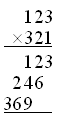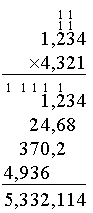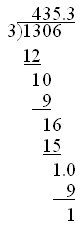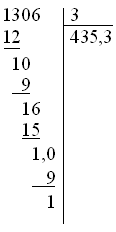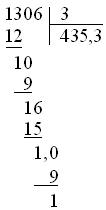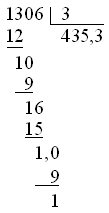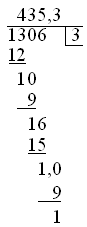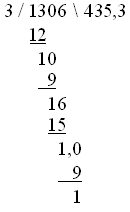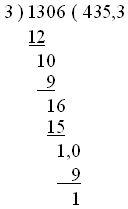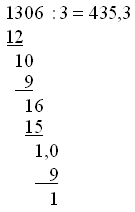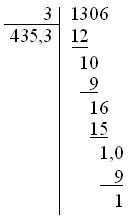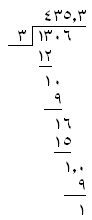MathML documents should be validated using the RelaxNG Schema for MathML, either in
the XML encoding (http://www.w3.org/Math/RelaxNG/mathml4/mathml4.rng)
or in compact notation (https://www.w3.org/Math/RelaxNG/mathml4/mathml4.rnc)
which is also shown below.
In contrast to DTDs there is no in-document method to associate a RelaxNG schema with
a document.
MathML Core is specified in MathML Core however the Schema is developed alongside the schema for MathML 4 and presented here, it can also be found at https://www.w3.org/Math/RelaxNG/mathml4/mathml4-core.rnc.
# MathML 4 (Core Level 1)
# #######################
# Copyright 1998-2022 W3C (MIT, ERCIM, Keio, Beihang)
#
# Use and distribution of this code are permitted under the terms
# W3C Software Notice and License
# http://www.w3.org/Consortium/Legal/2002/copyright-software-20021231
default namespace m = "http://www.w3.org/1998/Math/MathML"
namespace h = "http://www.w3.org/1999/xhtml"
start |= math
math = element math {math.attributes,ImpliedMrow}
MathMLoneventAttributes =
attribute onabort {text}?,
attribute onauxclick {text}?,
attribute onblur {text}?,
attribute oncancel {text}?,
attribute oncanplay {text}?,
attribute oncanplaythrough {text}?,
attribute onchange {text}?,
attribute onclick {text}?,
attribute onclose {text}?,
attribute oncontextlost {text}?,
attribute oncontextmenu {text}?,
attribute oncontextrestored {text}?,
attribute oncuechange {text}?,
attribute ondblclick {text}?,
attribute ondrag {text}?,
attribute ondragend {text}?,
attribute ondragenter {text}?,
attribute ondragleave {text}?,
attribute ondragover {text}?,
attribute ondragstart {text}?,
attribute ondrop {text}?,
attribute ondurationchange {text}?,
attribute onemptied {text}?,
attribute onended {text}?,
attribute onerror {text}?,
attribute onfocus {text}?,
attribute onformdata {text}?,
attribute oninput {text}?,
attribute oninvalid {text}?,
attribute onkeydown {text}?,
attribute onkeypress {text}?,
attribute onkeyup {text}?,
attribute onload {text}?,
attribute onloadeddata {text}?,
attribute onloadedmetadata {text}?,
attribute onloadstart {text}?,
attribute onmousedown {text}?,
attribute onmouseenter {text}?,
attribute onmouseleave {text}?,
attribute onmousemove {text}?,
attribute onmouseout {text}?,
attribute onmouseover {text}?,
attribute onmouseup {text}?,
attribute onpause {text}?,
attribute onplay {text}?,
attribute onplaying {text}?,
attribute onprogress {text}?,
attribute onratechange {text}?,
attribute onreset {text}?,
attribute onresize {text}?,
attribute onscroll {text}?,
attribute onsecuritypolicyviolation {text}?,
attribute onseeked {text}?,
attribute onseeking {text}?,
attribute onselect {text}?,
attribute onslotchange {text}?,
attribute onstalled {text}?,
attribute onsubmit {text}?,
attribute onsuspend {text}?,
attribute ontimeupdate {text}?,
attribute ontoggle {text}?,
attribute onvolumechange {text}?,
attribute onwaiting {text}?,
attribute onwebkitanimationend {text}?,
attribute onwebkitanimationiteration {text}?,
attribute onwebkitanimationstart {text}?,
attribute onwebkittransitionend {text}?,
attribute onwheel {text}?,
attribute onafterprint {text}?,
attribute onbeforeprint {text}?,
attribute onbeforeunload {text}?,
attribute onhashchange {text}?,
attribute onlanguagechange {text}?,
attribute onmessage {text}?,
attribute onmessageerror {text}?,
attribute onoffline {text}?,
attribute ononline {text}?,
attribute onpagehide {text}?,
attribute onpageshow {text}?,
attribute onpopstate {text}?,
attribute onrejectionhandled {text}?,
attribute onstorage {text}?,
attribute onunhandledrejection {text}?,
attribute onunload {text}?,
attribute oncopy {text}?,
attribute oncut {text}?,
attribute onpaste {text}?
# Sample set. May need preprocessing
# or schema extension to allow more see MathML Core (and HTML) spec
MathMLDataAttributes =
attribute data-other {text}?
# sample set, like data- may need preprocessing to allow more
MathMLARIAattributes =
attribute aria-label {text}?,
attribute aria-describedby {text}?,
attribute aria-details {text}?
MathMLintentAttributes =
attribute intent {text}?,
attribute arg {xsd:NCName}?
MathMLPGlobalAttributes = attribute id {xsd:ID}?,
attribute class {xsd:NCName}?,
attribute style {xsd:string}?,
attribute dir {"ltr" | "rtl"}?,
attribute mathbackground {color}?,
attribute mathcolor {color}?,
attribute mathsize {length-percentage}?,
attribute mathvariant {xsd:string{pattern="\s*([Nn][Oo][Rr][Mm][Aa][Ll]|[Bb][Oo][Ll][Dd]|[Ii][Tt][Aa][Ll][Ii][Cc]|[Bb][Oo][Ll][Dd]-[Ii][Tt][Aa][Ll][Ii][Cc]|[Dd][Oo][Uu][Bb][Ll][Ee]-[Ss][Tt][Rr][Uu][Cc][Kk]|[Bb][Oo][Ll][Dd]-[Ff][Rr][Aa][Kk][Tt][Uu][Rr]|[Ss][Cc][Rr][Ii][Pp][Tt]|[Bb][Oo][Ll][Dd]-[Ss][Cc][Rr][Ii][Pp][Tt]|[Ff][Rr][Aa][Kk][Tt][Uu][Rr]|[Ss][Aa][Nn][Ss]-[Ss][Ee][Rr][Ii][Ff]|[Bb][Oo][Ll][Dd]-[Ss][Aa][Nn][Ss]-[Ss][Ee][Rr][Ii][Ff]|[Ss][Aa][Nn][Ss]-[Ss][Ee][Rr][Ii][Ff]-[Ii][Tt][Aa][Ll][Ii][Cc]|[Ss][Aa][Nn][Ss]-[Ss][Ee][Rr][Ii][Ff]-[Bb][Oo][Ll][Dd]-[Ii][Tt][Aa][Ll][Ii][Cc]|[Mm][Oo][Nn][Oo][Ss][Pp][Aa][Cc][Ee]|[Ii][Nn][Ii][Tt][Ii][Aa][Ll]|[Tt][Aa][Ii][Ll][Ee][Dd]|[Ll][Oo][Oo][Pp][Ee][Dd]|[Ss][Tt][Rr][Ee][Tt][Cc][Hh][Ee][Dd])\s*"}}?,
attribute displaystyle {mathml-boolean}?,
attribute scriptlevel {xsd:integer}?,
attribute tabindex {xsd:integer}?,
attribute nonce {text}?,
MathMLoneventAttributes,
# Extension attributes, no defined behavior
MathMLDataAttributes,
# No specified behavior in Core, see MathML4
MathMLintentAttributes,
# No specified behavior in Core, see WAI-ARIA
MathMLARIAattributes
math.attributes = MathMLPGlobalAttributes,
attribute display {"block" | "inline"}?,
# No specified behavior in Core, see MathML4
attribute alttext {text}?
annotation = element annotation {MathMLPGlobalAttributes,encoding?,text}
anyElement = element (*) {(attribute * {text}|text| anyElement)*}
annotation-xml = element annotation-xml {annotation-xml.attributes,
(MathExpression*|anyElement*)}
annotation-xml.attributes = MathMLPGlobalAttributes, encoding?
encoding=attribute encoding {xsd:string}?
semantics = element semantics {semantics.attributes,
MathExpression,
(annotation|annotation-xml)*}
semantics.attributes = MathMLPGlobalAttributes
mathml-boolean = xsd:string {
pattern = '\s*([Tt][Rr][Uu][Ee]|[Ff][Aa][Ll][Ss][Ee])\s*'
}
length-percentage = xsd:string {
pattern = '\s*((-?[0-9]*([0-9]\.?|\.[0-9])[0-9]*(r?em|ex|in|cm|mm|p[xtc]|Q|v[hw]|vmin|vmax|%))|0)\s*'
}
MathExpression = TokenExpression|
mrow|mfrac|msqrt|mroot|mstyle|merror|mpadded|mphantom|
msub|msup|msubsup|munder|mover|munderover|
mmultiscripts|mtable|maction|
semantics
MathMalignExpression = MathExpression
ImpliedMrow = MathMalignExpression*
TableRowExpression = mtr
MultiScriptExpression = (MathExpression|none),(MathExpression|none)
color = xsd:string {
pattern = '\s*((#[0-9a-fA-F]{3}([0-9a-fA-F]{3})?)|[a-zA-Z]+|[a-zA-Z]+\s*\([0-9, %.]+\))\s*'}
TokenExpression = mi|mn|mo|mtext|mspace|ms
textorHTML = text | element (h:*) {attribute * {text}*,textorHTML*}
token.content = textorHTML
mi = element mi {mi.attributes, token.content}
mi.attributes =
MathMLPGlobalAttributes
mn = element mn {mn.attributes, token.content}
mn.attributes =
MathMLPGlobalAttributes
mo = element mo {mo.attributes, token.content}
mo.attributes =
MathMLPGlobalAttributes,
attribute form {"prefix" | "infix" | "postfix"}?,
attribute fence {mathml-boolean}?,
attribute separator {mathml-boolean}?,
attribute lspace {length-percentage}?,
attribute rspace {length-percentage}?,
attribute stretchy {mathml-boolean}?,
attribute symmetric {mathml-boolean}?,
attribute maxsize {length-percentage}?,
attribute minsize {length-percentage}?,
attribute largeop {mathml-boolean}?,
attribute movablelimits {mathml-boolean}?
mtext = element mtext {mtext.attributes, token.content}
mtext.attributes =
MathMLPGlobalAttributes
mspace = element mspace {mspace.attributes, empty}
mspace.attributes =
MathMLPGlobalAttributes,
attribute width {length-percentage}?,
attribute height {length-percentage}?,
attribute depth {length-percentage}?
ms = element ms {ms.attributes, token.content}
ms.attributes =
MathMLPGlobalAttributes
none = element none {none.attributes,empty}
none.attributes =
MathMLPGlobalAttributes
mprescripts = element mprescripts {mprescripts.attributes,empty}
mprescripts.attributes =
MathMLPGlobalAttributes
mrow = element mrow {mrow.attributes, ImpliedMrow}
mrow.attributes =
MathMLPGlobalAttributes
mfrac = element mfrac {mfrac.attributes, MathExpression, MathExpression}
mfrac.attributes =
MathMLPGlobalAttributes,
attribute linethickness {length-percentage}?
msqrt = element msqrt {msqrt.attributes, ImpliedMrow}
msqrt.attributes =
MathMLPGlobalAttributes
mroot = element mroot {mroot.attributes, MathExpression, MathExpression}
mroot.attributes =
MathMLPGlobalAttributes
mstyle = element mstyle {mstyle.attributes, ImpliedMrow}
mstyle.attributes =
MathMLPGlobalAttributes
merror = element merror {merror.attributes, ImpliedMrow}
merror.attributes =
MathMLPGlobalAttributes
mpadded = element mpadded {mpadded.attributes, ImpliedMrow}
mpadded.attributes =
MathMLPGlobalAttributes,
attribute height {mpadded-length-percentage}?,
attribute depth {mpadded-length-percentage}?,
attribute width {mpadded-length-percentage}?,
attribute lspace {mpadded-length-percentage}?,
attribute rspace {mpadded-length-percentage}?,
attribute voffset {mpadded-length-percentage}?
mpadded-length-percentage=length-percentage
mphantom = element mphantom {mphantom.attributes, ImpliedMrow}
mphantom.attributes =
MathMLPGlobalAttributes
msub = element msub {msub.attributes, MathExpression, MathExpression}
msub.attributes =
MathMLPGlobalAttributes
msup = element msup {msup.attributes, MathExpression, MathExpression}
msup.attributes =
MathMLPGlobalAttributes
msubsup = element msubsup {msubsup.attributes, MathExpression, MathExpression, MathExpression}
msubsup.attributes =
MathMLPGlobalAttributes
munder = element munder {munder.attributes, MathExpression, MathExpression}
munder.attributes =
MathMLPGlobalAttributes,
attribute accentunder {mathml-boolean}?
mover = element mover {mover.attributes, MathExpression, MathExpression}
mover.attributes =
MathMLPGlobalAttributes,
attribute accent {mathml-boolean}?
munderover = element munderover {munderover.attributes, MathExpression, MathExpression, MathExpression}
munderover.attributes =
MathMLPGlobalAttributes,
attribute accent {mathml-boolean}?,
attribute accentunder {mathml-boolean}?
mmultiscripts = element mmultiscripts {mmultiscripts.attributes,
MathExpression,
MultiScriptExpression*,
(mprescripts,MultiScriptExpression*)?}
mmultiscripts.attributes =
msubsup.attributes
mtable = element mtable {mtable.attributes, TableRowExpression*}
mtable.attributes =
MathMLPGlobalAttributes
mtr = element mtr {mtr.attributes, mtd*}
mtr.attributes =
MathMLPGlobalAttributes
mtd = element mtd {mtd.attributes, ImpliedMrow}
mtd.attributes =
MathMLPGlobalAttributes,
attribute rowspan {xsd:positiveInteger}?,
attribute columnspan {xsd:positiveInteger}?
maction = element maction {maction.attributes, ImpliedMrow}
maction.attributes =
MathMLPGlobalAttributes,
attribute actiontype {text}?,
attribute selection {xsd:positiveInteger}?
The grammar for Presentation MathML 4 builds on the grammar for the MathML
Core, and can be found at https://www.w3.org/Math/RelaxNG/mathml4/mathml4-presentation.rnc.
# MathML 4 (Presentation)
# #######################
# Copyright 1998-2022 W3C (MIT, ERCIM, Keio, Beihang)
#
# Use and distribution of this code are permitted under the terms
# W3C Software Notice and License
# http://www.w3.org/Consortium/Legal/2002/copyright-software-20021231
default namespace m = "http://www.w3.org/1998/Math/MathML"
namespace local = ""
# MathML Core
include "mathml4-core.rnc" {
# named lengths
length-percentage = xsd:string {
pattern = '\s*((-?[0-9]*([0-9]\.?|\.[0-9])[0-9]*(r?em|ex|in|cm|mm|p[xtc]|Q|v[hw]|vmin|vmax|%))|0|(negative)?((very){0,2}thi(n|ck)|medium)mathspace)\s*'
}
mpadded-length-percentage = xsd:string {
pattern = '\s*([\+\-]?[0-9]*([0-9]\.?|\.[0-9])[0-9]*\s*((%?\s*(height|depth|width)?)|r?em|ex|in|cm|mm|p[xtc]|Q|v[hw]|vmin|vmax|%|((negative)?((very){0,2}thi(n|ck)|medium)mathspace))?)\s*'
}
}
NonMathMLAtt = attribute (* - (local:* | m:*)) {xsd:string}
MathMLPGlobalAttributes &=
NonMathMLAtt*,
attribute xref {text}?,
attribute href {xsd:anyURI}?,
attribute other {text}?
MathMalignExpression |= MalignExpression
MathExpression |= PresentationExpression
TableRowExpression |= mlabeledtr
MstackExpression = MathMalignExpression|mscarries|msline|msrow|msgroup
MsrowExpression = MathMalignExpression|none
linestyle = "none" | "solid" | "dashed"
verticalalign =
"top" |
"bottom" |
"center" |
"baseline" |
"axis"
columnalignstyle = "left" | "center" | "right"
notationstyle =
"longdiv" |
"actuarial" |
"radical" |
"box" |
"roundedbox" |
"circle" |
"left" |
"right" |
"top" |
"bottom" |
"updiagonalstrike" |
"downdiagonalstrike" |
"verticalstrike" |
"horizontalstrike" |
"madruwb"
idref = text
unsigned-integer = xsd:unsignedLong
integer = xsd:integer
number = xsd:decimal
character = xsd:string {
pattern = '\s*\S\s*'}
positive-integer = xsd:positiveInteger
token.content |= mglyph|text
mo.attributes &=
attribute linebreak {"auto" | "newline" | "nobreak" | "goodbreak" | "badbreak"}?,
attribute lineleading {length-percentage}?,
attribute linebreakstyle {"before" | "after" | "duplicate" | "infixlinebreakstyle"}?,
attribute linebreakmultchar {text}?,
attribute indentalign {"left" | "center" | "right" | "auto" | "id"}?,
attribute indentshift {length-percentage}?,
attribute indenttarget {idref}?,
attribute indentalignfirst {"left" | "center" | "right" | "auto" | "id" | "indentalign"}?,
attribute indentshiftfirst {length-percentage | "indentshift"}?,
attribute indentalignlast {"left" | "center" | "right" | "auto" | "id" | "indentalign"}?,
attribute indentshiftlast {length-percentage | "indentshift"}?,
attribute accent {mathml-boolean}?,
attribute maxsize {"infinity"}?
mspace.attributes &=
attribute linebreak {"auto" | "newline" | "nobreak" | "goodbreak" | "badbreak" | "indentingnewline"}?,
attribute indentalign {"left" | "center" | "right" | "auto" | "id"}?,
attribute indentshift {length-percentage}?,
attribute indenttarget {idref}?,
attribute indentalignfirst {"left" | "center" | "right" | "auto" | "id" | "indentalign"}?,
attribute indentshiftfirst {length-percentage | "indentshift"}?,
attribute indentalignlast {"left" | "center" | "right" | "auto" | "id" | "indentalign"}?,
attribute indentshiftlast {length-percentage | "indentshift"}?
ms.attributes &=
attribute lquote {text}?,
attribute rquote {text}?
mglyph = element mglyph {mglyph.attributes,empty}
mglyph.attributes =
MathMLPGlobalAttributes,
attribute src {xsd:anyURI}?,
attribute width {length-percentage}?,
attribute height {length-percentage}?,
attribute valign {length-percentage}?,
attribute alt {text}?
msline = element msline {msline.attributes,empty}
msline.attributes =
MathMLPGlobalAttributes,
attribute position {integer}?,
attribute length {unsigned-integer}?,
attribute leftoverhang {length-percentage}?,
attribute rightoverhang {length-percentage}?,
attribute mslinethickness {length-percentage | "thin" | "medium" | "thick"}?
MalignExpression = maligngroup|malignmark
malignmark = element malignmark {malignmark.attributes, empty}
malignmark.attributes = MathMLPGlobalAttributes
maligngroup = element maligngroup {maligngroup.attributes, empty}
maligngroup.attributes = MathMLPGlobalAttributes
PresentationExpression = TokenExpression|
mrow|mfrac|msqrt|mroot|mstyle|merror|mpadded|mphantom|
mfenced|menclose|msub|msup|msubsup|munder|mover|munderover|
mmultiscripts|mtable|mstack|mlongdiv|maction
mfrac.attributes &=
attribute numalign {"left" | "center" | "right"}?,
attribute denomalign {"left" | "center" | "right"}?,
attribute bevelled {"true" | "false"}?
mstyle.attributes &=
mstyle.specificattributes,
mstyle.generalattributes
mstyle.specificattributes =
attribute Xscriptlevel {integer}?,
attribute Xdisplaystyle {"true" | "false"}?,
attribute scriptsizemultiplier {number}?,
attribute scriptminsize {length-percentage}?,
attribute infixlinebreakstyle {"before" | "after" | "duplicate"}?,
attribute decimalpoint {character}?
mstyle.generalattributes =
attribute accent {"true" | "false"}?,
attribute accentunder {"true" | "false"}?,
attribute align {"left" | "right" | "center"}?,
attribute alignmentscope {list {("true" | "false") +}}?,
attribute bevelled {"true" | "false"}?,
attribute charalign {"left" | "center" | "right"}?,
attribute charspacing {length-percentage | "loose" | "medium" | "tight"}?,
attribute close {text}?,
attribute columnalign {list {columnalignstyle+} }?,
attribute columnlines {list {linestyle +}}?,
attribute columnspacing {list {(length-percentage) +}}?,
attribute columnspan {positive-integer}?,
attribute columnwidth {list {("auto" | length-percentage | "fit") +}}?,
attribute crossout {list {("none" | "updiagonalstrike" | "downdiagonalstrike" | "verticalstrike" | "horizontalstrike")*}}?,
attribute denomalign {"left" | "center" | "right"}?,
attribute depth {length-percentage}?,
attribute dir {"ltr" | "rtl"}?,
attribute equalcolumns {"true" | "false"}?,
attribute equalrows {"true" | "false"}?,
attribute fence {"true" | "false"}?,
attribute form {"prefix" | "infix" | "postfix"}?,
attribute frame {linestyle}?,
attribute framespacing {list {length-percentage, length-percentage}}?,
attribute height {length-percentage}?,
attribute indentalign {"left" | "center" | "right" | "auto" | "id"}?,
attribute indentalignfirst {"left" | "center" | "right" | "auto" | "id" | "indentalign"}?,
attribute indentalignlast {"left" | "center" | "right" | "auto" | "id" | "indentalign"}?,
attribute indentshift {length-percentage}?,
attribute indentshiftfirst {length-percentage | "indentshift"}?,
attribute indentshiftlast {length-percentage | "indentshift"}?,
attribute indenttarget {idref}?,
attribute largeop {"true" | "false"}?,
attribute leftoverhang {length-percentage}?,
attribute length {unsigned-integer}?,
attribute linebreak {"auto" | "newline" | "nobreak" | "goodbreak" | "badbreak"}?,
attribute linebreakmultchar {text}?,
attribute linebreakstyle {"before" | "after" | "duplicate" | "infixlinebreakstyle"}?,
attribute lineleading {length-percentage}?,
attribute linethickness {length-percentage | "thin" | "medium" | "thick"}?,
attribute location {"w" | "nw" | "n" | "ne" | "e" | "se" | "s" | "sw"}?,
attribute longdivstyle {"lefttop" | "stackedrightright" | "mediumstackedrightright" | "shortstackedrightright" | "righttop" | "left/\right" | "left)(right" | ":right=right" | "stackedleftleft" | "stackedleftlinetop"}?,
attribute lquote {text}?,
attribute lspace {length-percentage}?,
attribute mathsize {"small" | "normal" | "big" | length-percentage}?,
attribute mathvariant {"normal" | "bold" | "italic" | "bold-italic" | "double-struck" | "bold-fraktur" | "script" | "bold-script" | "fraktur" | "sans-serif" | "bold-sans-serif" | "sans-serif-italic" | "sans-serif-bold-italic" | "monospace" | "initial" | "tailed" | "looped" | "stretched"}?,
attribute minlabelspacing {length-percentage}?,
attribute minsize {length-percentage}?,
attribute movablelimits {"true" | "false"}?,
attribute mslinethickness {length-percentage | "thin" | "medium" | "thick"}?,
attribute notation {text}?,
attribute numalign {"left" | "center" | "right"}?,
attribute open {text}?,
attribute position {integer}?,
attribute rightoverhang {length-percentage}?,
attribute rowalign {list {verticalalign+} }?,
attribute rowlines {list {linestyle +}}?,
attribute rowspacing {list {(length-percentage) +}}?,
attribute rowspan {positive-integer}?,
attribute rquote {text}?,
attribute rspace {length-percentage}?,
attribute selection {positive-integer}?,
attribute separator {"true" | "false"}?,
attribute separators {text}?,
attribute shift {integer}?,
attribute side {"left" | "right" | "leftoverlap" | "rightoverlap"}?,
attribute stackalign {"left" | "center" | "right" | "decimalpoint"}?,
attribute stretchy {"true" | "false"}?,
attribute subscriptshift {length-percentage}?,
attribute superscriptshift {length-percentage}?,
attribute symmetric {"true" | "false"}?,
attribute valign {length-percentage}?,
attribute width {length-percentage}?
math.attributes &= mstyle.specificattributes
math.attributes &= mstyle.generalattributes
math.attributes &= attribute overflow {"linebreak" | "scroll" | "elide" | "truncate" | "scale"}?
mfenced = element mfenced {mfenced.attributes, ImpliedMrow}
mfenced.attributes =
MathMLPGlobalAttributes,
attribute open {text}?,
attribute close {text}?,
attribute separators {text}?
menclose = element menclose {menclose.attributes, ImpliedMrow}
menclose.attributes =
MathMLPGlobalAttributes,
attribute notation {text}?
munder.attributes &=
attribute align {"left" | "right" | "center"}?
mover.attributes &=
attribute align {"left" | "right" | "center"}?
munderover.attributes &=
attribute align {"left" | "right" | "center"}?
msub.attributes &=
attribute subscriptshift {length-percentage}?
msup.attributes &=
attribute superscriptshift {length-percentage}?
msubsup.attributes &=
attribute subscriptshift {length-percentage}?,
attribute superscriptshift {length-percentage}?
mtable.attributes &=
attribute align {xsd:string {
pattern ='\s*(top|bottom|center|baseline|axis)(\s+-?[0-9]+)?\s*'}}?,
attribute rowalign {list {verticalalign+} }?,
attribute columnalign {list {columnalignstyle+} }?,
attribute alignmentscope {list {("true" | "false") +}}?,
attribute columnwidth {list {("auto" | length-percentage | "fit") +}}?,
attribute width {"auto" | length-percentage}?,
attribute rowspacing {list {(length-percentage) +}}?,
attribute columnspacing {list {(length-percentage) +}}?,
attribute rowlines {list {linestyle +}}?,
attribute columnlines {list {linestyle +}}?,
attribute frame {linestyle}?,
attribute framespacing {list {length-percentage, length-percentage}}?,
attribute equalrows {"true" | "false"}?,
attribute equalcolumns {"true" | "false"}?,
attribute displaystyle {"true" | "false"}?,
attribute side {"left" | "right" | "leftoverlap" | "rightoverlap"}?,
attribute minlabelspacing {length-percentage}?
mlabeledtr = element mlabeledtr {mlabeledtr.attributes, mtd+}
mlabeledtr.attributes =
mtr.attributes
mtr.attributes &=
attribute rowalign {"top" | "bottom" | "center" | "baseline" | "axis"}?,
attribute columnalign {list {columnalignstyle+} }?
mtd.attributes &=
attribute rowalign {"top" | "bottom" | "center" | "baseline" | "axis"}?,
attribute columnalign {columnalignstyle}?
mstack = element mstack {mstack.attributes, MstackExpression*}
mstack.attributes =
MathMLPGlobalAttributes,
attribute align {xsd:string {
pattern ='\s*(top|bottom|center|baseline|axis)(\s+-?[0-9]+)?\s*'}}?,
attribute stackalign {"left" | "center" | "right" | "decimalpoint"}?,
attribute charalign {"left" | "center" | "right"}?,
attribute charspacing {length-percentage | "loose" | "medium" | "tight"}?
mlongdiv = element mlongdiv {mlongdiv.attributes, MstackExpression,MstackExpression,MstackExpression+}
mlongdiv.attributes =
msgroup.attributes,
attribute longdivstyle {"lefttop" | "stackedrightright" | "mediumstackedrightright" | "shortstackedrightright" | "righttop" | "left/\right" | "left)(right" | ":right=right" | "stackedleftleft" | "stackedleftlinetop"}?
msgroup = element msgroup {msgroup.attributes, MstackExpression*}
msgroup.attributes =
MathMLPGlobalAttributes,
attribute position {integer}?,
attribute shift {integer}?
msrow = element msrow {msrow.attributes, MsrowExpression*}
msrow.attributes =
MathMLPGlobalAttributes,
attribute position {integer}?
mscarries = element mscarries {mscarries.attributes, (MsrowExpression|mscarry)*}
mscarries.attributes =
MathMLPGlobalAttributes,
attribute position {integer}?,
attribute location {"w" | "nw" | "n" | "ne" | "e" | "se" | "s" | "sw"}?,
attribute crossout {list {("none" | "updiagonalstrike" | "downdiagonalstrike" | "verticalstrike" | "horizontalstrike")*}}?,
attribute scriptsizemultiplier {number}?
mscarry = element mscarry {mscarry.attributes, MsrowExpression*}
mscarry.attributes =
MathMLPGlobalAttributes,
attribute location {"w" | "nw" | "n" | "ne" | "e" | "se" | "s" | "sw"}?,
attribute crossout {list {("none" | "updiagonalstrike" | "downdiagonalstrike" | "verticalstrike" | "horizontalstrike")*}}?
The grammar for Strict Content MathML 4 can be found at https://www.w3.org/Math/RelaxNG/mathml4/mathml4-strict-content.rnc.
# MathML 4 (Strict Content)
# #########################
# Copyright 1998-2022 W3C (MIT, ERCIM, Keio, Beihang)
#
# Use and distribution of this code are permitted under the terms
# W3C Software Notice and License
# http://www.w3.org/Consortium/Legal/2002/copyright-software-20021231
default namespace m = "http://www.w3.org/1998/Math/MathML"
start |= math.strict
CommonAtt =
attribute id {xsd:ID}?,
attribute xref {text}?
math.strict = element math {math.attributes,ContExp*}
math.attributes &= CommonAtt
ContExp = semantics-contexp | cn | ci | csymbol | apply | bind | share | cerror | cbytes | cs
cn = element cn {cn.attributes,cn.content}
cn.content = text
cn.attributes = CommonAtt, attribute type {"integer" | "real" | "double" | "hexdouble"}
semantics-ci = element semantics {CommonAtt,(ci|semantics-ci),
(annotation|annotation-xml)*}
semantics-contexp = element semantics {CommonAtt,MathExpression,
(annotation|annotation-xml)*}
annotation |= element annotation {CommonAtt,text}
anyElement |= element (* - m:*) {(attribute * {text}|text| anyElement)*}
annotation-xml |= element annotation-xml {annotation-xml.attributes,
(MathExpression*|anyElement*)}
annotation-xml.attributes &= CommonAtt, cd?, encoding?
encoding &= attribute encoding {xsd:string}
ci = element ci {ci.attributes, ci.content}
ci.attributes = CommonAtt, ci.type?
ci.type = attribute type {"integer" | "rational" | "real" | "complex" | "complex-polar" | "complex-cartesian" | "constant" | "function" | "vector" | "list" | "set" | "matrix"}
ci.content = text
csymbol = element csymbol {csymbol.attributes,csymbol.content}
SymbolName = xsd:NCName
csymbol.attributes = CommonAtt, cd
csymbol.content = SymbolName
cd = attribute cd {xsd:NCName}
name = attribute name {xsd:NCName}
src = attribute src {xsd:anyURI}?
BvarQ = bvar*
bvar = element bvar {CommonAtt, (ci | semantics-ci)}
apply = element apply {CommonAtt,apply.content}
apply.content = ContExp+
bind = element bind {CommonAtt,bind.content}
bind.content = ContExp,bvar*,ContExp
share = element share {CommonAtt, src, empty}
cerror = element cerror {cerror.attributes, csymbol, ContExp*}
cerror.attributes = CommonAtt
cbytes = element cbytes {cbytes.attributes, base64}
cbytes.attributes = CommonAtt
base64 = xsd:base64Binary
cs = element cs {cs.attributes, text}
cs.attributes = CommonAtt
MathExpression |= ContExp
The grammar for Content MathML 4 builds on the grammar for the Strict Content MathML
subset, and can be found at https://www.w3.org/Math/RelaxNG/mathml4/mathml4-content.rnc.
# MathML 4 (Content)
# ##################
# Copyright 1998-2022 W3C (MIT, ERCIM, Keio, Beihang)
#
# Use and distribution of this code are permitted under the terms
# W3C Software Notice and License
# http://www.w3.org/Consortium/Legal/2002/copyright-software-20021231
default namespace m = "http://www.w3.org/1998/Math/MathML"
namespace local = ""
include "mathml4-strict-content.rnc"{
cn.content = (text | sep | PresentationExpression)*
cn.attributes = CommonAtt, DefEncAtt, attribute type {text}?, base?
ci.attributes = CommonAtt, DefEncAtt, ci.type?
ci.type = attribute type {text}
ci.content = (text | PresentationExpression)*
csymbol.attributes = CommonAtt, DefEncAtt, attribute type {text}?,cd?
csymbol.content = (text | PresentationExpression)*
annotation-xml.attributes |= CommonAtt, cd?, name?, encoding?
bvar = element bvar {CommonAtt, ((ci | semantics-ci) & degree?)}
cbytes.attributes = CommonAtt, DefEncAtt
cs.attributes = CommonAtt, DefEncAtt
apply.content = ContExp+ | (ContExp, BvarQ, Qualifier*, ContExp*)
bind.content = apply.content
}
NonMathMLAtt |= attribute (* - (local:*|m:*)) {xsd:string}
math.attributes &=
attribute alttext {text}?
MathMLDataAttributes &=
attribute data-other {text}?
CommonAtt &=
NonMathMLAtt*,
MathMLDataAttributes,
attribute class {xsd:NCName}?,
attribute style {xsd:string}?,
attribute href {xsd:anyURI}?,
attribute other {text}?,
attribute intent {text}?,
attribute arg {xsd:NCName}?
base = attribute base {text}
sep = element sep {empty}
PresentationExpression |= notAllowed
DefEncAtt = attribute encoding {xsd:string}?,
attribute definitionURL {xsd:anyURI}?
DomainQ = (domainofapplication|condition|interval|(lowlimit,uplimit?))*
domainofapplication = element domainofapplication {ContExp}
condition = element condition {ContExp}
uplimit = element uplimit {ContExp}
lowlimit = element lowlimit {ContExp}
Qualifier = DomainQ|degree|momentabout|logbase
degree = element degree {ContExp}
momentabout = element momentabout {ContExp}
logbase = element logbase {ContExp}
type = attribute type {text}
order = attribute order {"numeric" | "lexicographic"}
closure = attribute closure {text}
ContExp |= piecewise
piecewise = element piecewise {CommonAtt, DefEncAtt,(piece* & otherwise?)}
piece = element piece {CommonAtt, DefEncAtt, ContExp, ContExp}
otherwise = element otherwise {CommonAtt, DefEncAtt, ContExp}
interval.class = interval
ContExp |= interval.class
interval = element interval { CommonAtt, DefEncAtt,closure?, ContExp,ContExp}
unary-functional.class = inverse | ident | domain | codomain | image | ln | log | moment
ContExp |= unary-functional.class
inverse = element inverse { CommonAtt, DefEncAtt, empty}
ident = element ident { CommonAtt, DefEncAtt, empty}
domain = element domain { CommonAtt, DefEncAtt, empty}
codomain = element codomain { CommonAtt, DefEncAtt, empty}
image = element image { CommonAtt, DefEncAtt, empty}
ln = element ln { CommonAtt, DefEncAtt, empty}
log = element log { CommonAtt, DefEncAtt, empty}
moment = element moment { CommonAtt, DefEncAtt, empty}
lambda.class = lambda
ContExp |= lambda.class
lambda = element lambda { CommonAtt, DefEncAtt, BvarQ, DomainQ, ContExp}
nary-functional.class = compose
ContExp |= nary-functional.class
compose = element compose { CommonAtt, DefEncAtt, empty}
binary-arith.class = quotient | divide | minus | power | rem | root
ContExp |= binary-arith.class
quotient = element quotient { CommonAtt, DefEncAtt, empty}
divide = element divide { CommonAtt, DefEncAtt, empty}
minus = element minus { CommonAtt, DefEncAtt, empty}
power = element power { CommonAtt, DefEncAtt, empty}
rem = element rem { CommonAtt, DefEncAtt, empty}
root = element root { CommonAtt, DefEncAtt, empty}
unary-arith.class = factorial | minus | root | abs | conjugate | arg | real | imaginary | floor | ceiling | exp
ContExp |= unary-arith.class
factorial = element factorial { CommonAtt, DefEncAtt, empty}
abs = element abs { CommonAtt, DefEncAtt, empty}
conjugate = element conjugate { CommonAtt, DefEncAtt, empty}
arg = element arg { CommonAtt, DefEncAtt, empty}
real = element real { CommonAtt, DefEncAtt, empty}
imaginary = element imaginary { CommonAtt, DefEncAtt, empty}
floor = element floor { CommonAtt, DefEncAtt, empty}
ceiling = element ceiling { CommonAtt, DefEncAtt, empty}
exp = element exp { CommonAtt, DefEncAtt, empty}
nary-minmax.class = max | min
ContExp |= nary-minmax.class
max = element max { CommonAtt, DefEncAtt, empty}
min = element min { CommonAtt, DefEncAtt, empty}
nary-arith.class = plus | times | gcd | lcm
ContExp |= nary-arith.class
plus = element plus { CommonAtt, DefEncAtt, empty}
times = element times { CommonAtt, DefEncAtt, empty}
gcd = element gcd { CommonAtt, DefEncAtt, empty}
lcm = element lcm { CommonAtt, DefEncAtt, empty}
nary-logical.class = and | or | xor
ContExp |= nary-logical.class
and = element and { CommonAtt, DefEncAtt, empty}
or = element or { CommonAtt, DefEncAtt, empty}
xor = element xor { CommonAtt, DefEncAtt, empty}
unary-logical.class = not
ContExp |= unary-logical.class
not = element not { CommonAtt, DefEncAtt, empty}
binary-logical.class = implies | equivalent
ContExp |= binary-logical.class
implies = element implies { CommonAtt, DefEncAtt, empty}
equivalent = element equivalent { CommonAtt, DefEncAtt, empty}
quantifier.class = forall | exists
ContExp |= quantifier.class
forall = element forall { CommonAtt, DefEncAtt, empty}
exists = element exists { CommonAtt, DefEncAtt, empty}
nary-reln.class = eq | gt | lt | geq | leq
ContExp |= nary-reln.class
eq = element eq { CommonAtt, DefEncAtt, empty}
gt = element gt { CommonAtt, DefEncAtt, empty}
lt = element lt { CommonAtt, DefEncAtt, empty}
geq = element geq { CommonAtt, DefEncAtt, empty}
leq = element leq { CommonAtt, DefEncAtt, empty}
binary-reln.class = neq | approx | factorof | tendsto
ContExp |= binary-reln.class
neq = element neq { CommonAtt, DefEncAtt, empty}
approx = element approx { CommonAtt, DefEncAtt, empty}
factorof = element factorof { CommonAtt, DefEncAtt, empty}
tendsto = element tendsto { CommonAtt, DefEncAtt, type?, empty}
int.class = int
ContExp |= int.class
int = element int { CommonAtt, DefEncAtt, empty}
Differential-Operator.class = diff
ContExp |= Differential-Operator.class
diff = element diff { CommonAtt, DefEncAtt, empty}
partialdiff.class = partialdiff
ContExp |= partialdiff.class
partialdiff = element partialdiff { CommonAtt, DefEncAtt, empty}
unary-veccalc.class = divergence | grad | curl | laplacian
ContExp |= unary-veccalc.class
divergence = element divergence { CommonAtt, DefEncAtt, empty}
grad = element grad { CommonAtt, DefEncAtt, empty}
curl = element curl { CommonAtt, DefEncAtt, empty}
laplacian = element laplacian { CommonAtt, DefEncAtt, empty}
nary-setlist-constructor.class = set | \list
ContExp |= nary-setlist-constructor.class
set = element set { CommonAtt, DefEncAtt, type?, BvarQ*, DomainQ*, ContExp*}
\list = element \list { CommonAtt, DefEncAtt, order?, BvarQ*, DomainQ*, ContExp*}
nary-set.class = union | intersect | cartesianproduct
ContExp |= nary-set.class
union = element union { CommonAtt, DefEncAtt, empty}
intersect = element intersect { CommonAtt, DefEncAtt, empty}
cartesianproduct = element cartesianproduct { CommonAtt, DefEncAtt, empty}
binary-set.class = in | notin | notsubset | notprsubset | setdiff
ContExp |= binary-set.class
in = element in { CommonAtt, DefEncAtt, empty}
notin = element notin { CommonAtt, DefEncAtt, empty}
notsubset = element notsubset { CommonAtt, DefEncAtt, empty}
notprsubset = element notprsubset { CommonAtt, DefEncAtt, empty}
setdiff = element setdiff { CommonAtt, DefEncAtt, empty}
nary-set-reln.class = subset | prsubset
ContExp |= nary-set-reln.class
subset = element subset { CommonAtt, DefEncAtt, empty}
prsubset = element prsubset { CommonAtt, DefEncAtt, empty}
unary-set.class = card
ContExp |= unary-set.class
card = element card { CommonAtt, DefEncAtt, empty}
sum.class = sum
ContExp |= sum.class
sum = element sum { CommonAtt, DefEncAtt, empty}
product.class = product
ContExp |= product.class
product = element product { CommonAtt, DefEncAtt, empty}
limit.class = limit
ContExp |= limit.class
limit = element limit { CommonAtt, DefEncAtt, empty}
unary-elementary.class = sin | cos | tan | sec | csc | cot | sinh | cosh | tanh | sech | csch | coth | arcsin | arccos | arctan | arccosh | arccot | arccoth | arccsc | arccsch | arcsec | arcsech | arcsinh | arctanh
ContExp |= unary-elementary.class
sin = element sin { CommonAtt, DefEncAtt, empty}
cos = element cos { CommonAtt, DefEncAtt, empty}
tan = element tan { CommonAtt, DefEncAtt, empty}
sec = element sec { CommonAtt, DefEncAtt, empty}
csc = element csc { CommonAtt, DefEncAtt, empty}
cot = element cot { CommonAtt, DefEncAtt, empty}
sinh = element sinh { CommonAtt, DefEncAtt, empty}
cosh = element cosh { CommonAtt, DefEncAtt, empty}
tanh = element tanh { CommonAtt, DefEncAtt, empty}
sech = element sech { CommonAtt, DefEncAtt, empty}
csch = element csch { CommonAtt, DefEncAtt, empty}
coth = element coth { CommonAtt, DefEncAtt, empty}
arcsin = element arcsin { CommonAtt, DefEncAtt, empty}
arccos = element arccos { CommonAtt, DefEncAtt, empty}
arctan = element arctan { CommonAtt, DefEncAtt, empty}
arccosh = element arccosh { CommonAtt, DefEncAtt, empty}
arccot = element arccot { CommonAtt, DefEncAtt, empty}
arccoth = element arccoth { CommonAtt, DefEncAtt, empty}
arccsc = element arccsc { CommonAtt, DefEncAtt, empty}
arccsch = element arccsch { CommonAtt, DefEncAtt, empty}
arcsec = element arcsec { CommonAtt, DefEncAtt, empty}
arcsech = element arcsech { CommonAtt, DefEncAtt, empty}
arcsinh = element arcsinh { CommonAtt, DefEncAtt, empty}
arctanh = element arctanh { CommonAtt, DefEncAtt, empty}
nary-stats.class = mean | median | mode | sdev | variance
ContExp |= nary-stats.class
mean = element mean { CommonAtt, DefEncAtt, empty}
median = element median { CommonAtt, DefEncAtt, empty}
mode = element mode { CommonAtt, DefEncAtt, empty}
sdev = element sdev { CommonAtt, DefEncAtt, empty}
variance = element variance { CommonAtt, DefEncAtt, empty}
nary-constructor.class = vector | matrix | matrixrow
ContExp |= nary-constructor.class
vector = element vector { CommonAtt, DefEncAtt, BvarQ, DomainQ, ContExp*}
matrix = element matrix { CommonAtt, DefEncAtt, BvarQ, DomainQ, ContExp*}
matrixrow = element matrixrow { CommonAtt, DefEncAtt, BvarQ, DomainQ, ContExp*}
unary-linalg.class = determinant | transpose
ContExp |= unary-linalg.class
determinant = element determinant { CommonAtt, DefEncAtt, empty}
transpose = element transpose { CommonAtt, DefEncAtt, empty}
nary-linalg.class = selector
ContExp |= nary-linalg.class
selector = element selector { CommonAtt, DefEncAtt, empty}
binary-linalg.class = vectorproduct | scalarproduct | outerproduct
ContExp |= binary-linalg.class
vectorproduct = element vectorproduct { CommonAtt, DefEncAtt, empty}
scalarproduct = element scalarproduct { CommonAtt, DefEncAtt, empty}
outerproduct = element outerproduct { CommonAtt, DefEncAtt, empty}
constant-set.class = integers | reals | rationals | naturalnumbers | complexes | primes | emptyset
ContExp |= constant-set.class
integers = element integers { CommonAtt, DefEncAtt, empty}
reals = element reals { CommonAtt, DefEncAtt, empty}
rationals = element rationals { CommonAtt, DefEncAtt, empty}
naturalnumbers = element naturalnumbers { CommonAtt, DefEncAtt, empty}
complexes = element complexes { CommonAtt, DefEncAtt, empty}
primes = element primes { CommonAtt, DefEncAtt, empty}
emptyset = element emptyset { CommonAtt, DefEncAtt, empty}
constant-arith.class = exponentiale | imaginaryi | notanumber | true | false | pi | eulergamma | infinity
ContExp |= constant-arith.class
exponentiale = element exponentiale { CommonAtt, DefEncAtt, empty}
imaginaryi = element imaginaryi { CommonAtt, DefEncAtt, empty}
notanumber = element notanumber { CommonAtt, DefEncAtt, empty}
true = element true { CommonAtt, DefEncAtt, empty}
false = element false { CommonAtt, DefEncAtt, empty}
pi = element pi { CommonAtt, DefEncAtt, empty}
eulergamma = element eulergamma { CommonAtt, DefEncAtt, empty}
infinity = element infinity { CommonAtt, DefEncAtt, empty}
The grammar for full MathML 4 is simply a merger of the above grammars,
and can be found at https://www.w3.org/Math/RelaxNG/mathml4/mathml4.rnc.
# MathML 4 (full)
# ##############
# Copyright 1998-2022 W3C (MIT, ERCIM, Keio)
#
# Use and distribution of this code are permitted under the terms
# W3C Software Notice and License
# http://www.w3.org/Consortium/Legal/2002/copyright-software-20021231
default namespace m = "http://www.w3.org/1998/Math/MathML"
# Presentation MathML
include "mathml4-presentation.rnc" {
anyElement = element (* - m:*) {(attribute * {text}|text| anyElement)*}
}
# Content MathML
include "mathml4-content.rnc"
Some elements and attributes that were deprecated in MathML 3
are removed from MathML 4. This schema extends the full MathML 4
schema, adding these constructs back, allowing validation of existing
MathML documents. It can be found at https://www.w3.org/Math/RelaxNG/mathml4/mathml4-legacy.rnc.
# MathML 4 (legacy)
# ################
# Copyright 1998-2022 W3C (MIT, ERCIM, Keio)
#
# Use and distribution of this code are permitted under the terms
# W3C Software Notice and License
# http://www.w3.org/Consortium/Legal/2002/copyright-software-20021231
default namespace m = "http://www.w3.org/1998/Math/MathML"
# MathML 4
include "mathml4.rnc" {
# unitless lengths
length-percentage = xsd:string {
pattern = '\s*((-?[0-9]*([0-9]\.?|\.[0-9])[0-9]*(e[mx]|in|cm|mm|p[xtc]|%)?)|(negative)?((very){0,2}thi(n|ck)|medium)mathspace)\s*'
}
}
# Removed MathML 1/2/3 elements
ContExp |= reln | fn | declare
reln = element reln {ContExp*}
fn = element fn {ContExp}
declare = element declare {attribute type {xsd:string}?,
attribute scope {xsd:string}?,
attribute nargs {xsd:nonNegativeInteger}?,
attribute occurrence {"prefix"|"infix"|"function-model"}?,
DefEncAtt,
ContExp+}
# legacy attributes
mglyph.deprecatedattributes =
attribute fontfamily {text}?,
attribute index {integer}?,
attribute mathvariant {"normal" | "bold" | "italic" | "bold-italic" | "double-struck" | "bold-fraktur" | "script" | "bold-script" | "fraktur" | "sans-serif" | "bold-sans-serif" | "sans-serif-italic" | "sans-serif-bold-italic" | "monospace" | "initial" | "tailed" | "looped" | "stretched"}?,
attribute mathsize {"small" | "normal" | "big" | length-percentage}?
mglyph.attributes &= mglyph.deprecatedattributes
mstyle.deprecatedattributes =
attribute veryverythinmathspace {length-percentage}?,
attribute verythinmathspace {length-percentage}?,
attribute thinmathspace {length-percentage}?,
attribute mediummathspace {length-percentage}?,
attribute thickmathspace {length-percentage}?,
attribute verythickmathspace {length-percentage}?,
attribute veryverythickmathspace {length-percentage}?
mstyle.attributes &= mstyle.deprecatedattributes
math.deprecatedattributes = attribute mode {xsd:string}?,
attribute macros {xsd:string}?
math.attributes &= math.deprecatedattributes
DeprecatedTokenAtt =
attribute fontfamily {text}?,
attribute fontweight {"normal" | "bold"}?,
attribute fontstyle {"normal" | "italic"}?,
attribute fontsize {length-percentage}?,
attribute color {color}?,
attribute background {color}?,
attribute mathsize {"small" | "normal" | "big" }?
mstyle.attributes &= DeprecatedTokenAtt
mglyph.attributes &= DeprecatedTokenAtt
mn.attributes &= DeprecatedTokenAtt
mi.attributes &= DeprecatedTokenAtt
mo.attributes &= DeprecatedTokenAtt
mtext.attributes &= DeprecatedTokenAtt
mspace.attributes &= DeprecatedTokenAtt
ms.attributes &= DeprecatedTokenAtt
semantics.attributes &= DefEncAtt
# malignmark in tokens
token.content |= malignmark
# malignmark in mfrac etc
MathExpression |= MalignExpression
maligngroup.attributes &=
attribute groupalign {"left" | "center" | "right" | "decimalpoint"}?
malignmark.attributes &=
attribute edge {"left" | "right"}?
mstyle.generalattributes &=
attribute edge {"left" | "right"}?
# groupalign
group-alignment = "left" | "center" | "right" | "decimalpoint"
group-alignment-list = list {group-alignment+}
group-alignment-list-list = xsd:string {
pattern = '(\s*\{\s*(left|center|right|decimalpoint)(\s+(left|center|right|decimalpoint))*\})*\s*' }
mstyle.generalattributes &=
attribute groupalign {group-alignment-list-list}?
mtable.attributes &=
attribute groupalign {group-alignment-list-list}?
mtr.attributes &=
attribute groupalign {group-alignment-list-list}?
mtd.attributes &=
attribute groupalign {group-alignment-list}?
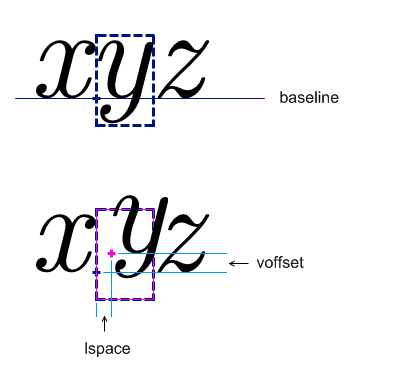
![[image of phasorangle notation for the angle negative pi over 2]](image/phasorangle.png)