A Special Considerations
A.3 Multiple Character Entities
In addition to the combining and variant character combinations
listed in the previous sections,
the following table lists the remaining entity replacement texts that
consist of more than one character.
| Entity | Set | Description | Unicode Character |
|---|
| fjlig | isopub | small fj ligature | U+0066 U+006A | 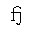 | fj ligature |
| ThickSpace | mmlextra | space of width 5/18 em | U+205F U+200A |  | space of width 5/18 em |
| race | isoamsb | reverse most positive, line below | U+223D U+0331 |  | REVERSED TILDE with underline |
| acE | isoamsb | most positive, two lines below | U+223E U+0333 |  | INVERTED LAZY S with double underline |
Unicode does not have an fj character, although the other common f ligatures
such as fi (U+FB01) are contained in the Alphabetic Presentation Forms block.
The fjlig entity is mapped to the pair of characters "fj";
modern typesetting engines should automatically use the fj ligature for this
combination if the font supplies such a ligature.
Unicode has a range of space characters (including all multiples of
1/18 em up to 6/18, except for 5/18 em) thus the ThickSpace entity is
mapped to a pair of space characters. An alternative would have been to use
U+2005 (1/4 em), but 1/4 em is not equal to 5/18 em, so the above definition was
chosen, despite the fact that the difference is unlikely to be visibly
noticeable at most typeset font sizes.
The entities race and acE denote underlined
characters for which Unicode does not have codepoints, thus combining
underline characters have been used, in a way analogous to the use of
combining strokes for negated operators.
A.4 Entities Defined to be a Combining Character
The following table lists the entity replacement texts that
consist of a combining character.
| Entity | Set | Description | Unicode Character |
|---|
| DownBreve | mmlextra | breve, inverted (non-spacing) | U+0311 | 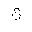 | COMBINING INVERTED BREVE |
| tdot | isotech | three dots above | U+20DB |  | COMBINING THREE DOTS ABOVE |
| TripleDot | mmlalias | alias ISOTECH tdot |
| DotDot | isotech | four dots above | U+20DC |  | COMBINING FOUR DOTS ABOVE |
For reasons explained further in [Charmod-norm], it is
not advisable to start the replacement text of an entity with a
combining character, as then potentially different results may be
produced depending on the order in which entity expansion and Unicode
normalisation are performed. As far as possible this specification
uses non-combining characters, however, in the cases DownBreve,
tdot, TripleDot and DotDot
Unicode only has combining forms of the accents.
Earlier versions of this specification defined these entities
with the replacement text starting with a space, to avoid the possibility that
the expansion of the entity combined with preceding text. However for various reasons
the entities as incorporated in HTML do not have a space here, and so the
definitions now consist just of the combining character so that HTML and XHTML
are consistent with any specifications using these definitions.
B Changes
B.1 Changes since 2014-04-10 (Second Edition Recommendation)
Source files updated to Unicode 15.0, affecting the character tables,
but with no changes to generated entity files or stylesheets.
New table for the U+FE01 Variation selector and greatly extended set of variations in the U+FE00 table (most of these standardised variants were added at Unicode 14). The script alphabet table has been extended to show both variants.
Reference added to the November 2021 W3C Process Document.
Some changes to the front matter including link to GitHub as
required by the latest W3C publication process.
Adjustments to CSS styling to match new W3C document style.
The source repository has been moved to github so the log is now public.
As detailed in A.4 Entities Defined to be a Combining Character DownBreve,
tdot, TripleDot and DotDot are no longer prefixed by a space.
B.2 Changes between 2010-04-01 and 2014-04-10 (First and Second Edition Recommendations)
Source files updated to Unicode 6.3, affecting the character tables,
but with no changes to generated entity files or stylesheets.
Source files updated Unicode 6.1 data on Arabic math alphabets (U+1EE??). Additional tables shown in Sections 3 and 4.
Section 2 Sets of names reorganized to highlight the htmlmathml set which is used in MathML and HTML. Also link to XSL and JSON formats for the HTML MathML set.
References updated: [MathML3], [HTML5] and [Unicode].
B.3 Changes between 2010-04-01 and 2010-02-11
Several example images improved, bringing them more in line with the Unicode reference images.
B.4 Changes between 2010-02-11 and 2009-11-17
Various editorial improvements, including using Unicode U+1234
notation more consistently rather than displaying the internal
IDs of the form U01234.
The combined entities file distributed with the 2009-11-17
draft introduced an error that if two entity names differed only
by case, only one was included. This has been corrected.
The combined entity set htmlmathml corresponding to the
entities usable in HTML and MathML is now explicitly provided. The
predefined set, corresponding to the entities predefined in XML
is now documented (it was previously used internally).
The entities xvee and xwedge had the correct
Unicode assignments (U+22C1 and U+22C0) but the entity descriptions
have been swapped, xvee is logical or and xwedge is logical and.
This error in [ISO9573-13-1991] was reported in 1999,
in a Proposed Technical Corrigendum,
but not previously fixed. The entity files are unaffected by this change.
The entity NotGreaterFullEqual which had been erroneously assigned to
a negated less than operator (U+2266 U+0338) has been corrected to be the negated greater than operator (U+2267 U+0338).
A sample catalog is now provided to redirect references to the entity files to copies on the local machine rather than the W3C server.
B.5 Changes between 2009-11-17 and 2008-07-21
The html5-uppercase set is now documented.
The entities ohm and angst have changed to U+03A9 and U+00C5 to match NFC. See
w3c bugzilla entry.
The entity race, which had been erroneously assigned U+29DA,
is now assigned the combination U+223D U+0331. (U+223D isn't
quite the shape shown in the original ISO document which is a
rotated S rather than a rotated tilde, but this appears to be
the closest character in Unicode 5.2.)
The entities bsolhsub and suphsol which were previously
mapped to two-character combinations U+005C U+2282 and U+2283 U+002F
are now mapped to the Unicode 5 characters that were added
specifically to support these entities, U+27C8 and U+27C9.
The source files have all been updated to match Unicode 5.2.
The entity ThickSpace now maps to the pair
U+205F U+200A rather than the triple U+2009 U+200A U+200A
(4/18 + 1/18)em rather than (3/18 + 1/18 + 1/18)em.
The entity UnderBar maps to the spacing character
_ rather than the combining character U+0332.
The entity OverBar maps to the spacing character
U+203E (like the XHTML entity oline) rather than the macron character U+00AF.
The entities epsiv and varepsilon are now mapped to the epsilon symbol
U+03F5 rather than being aliases for the entity epsilon, U+03B5.
The entities phiv and varphi are now mapped to the phi symbol U+03D5
rather than being aliases for the entity phi, U+03C6.
B.6 Changes between 2008-07-21 and 2007-12-14
The following entity definitions have changed at this draft:
phi, lang, rang,
OverParenthesis, UnderParenthesis,
OverBrace, UnderBrace,
lbbrk, rbbrk.