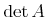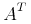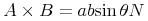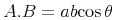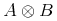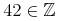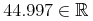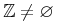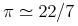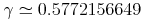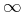A.2 Using the RelaxNG Schema for MathML3
MathML documents should be validated using the RelaxNG Schema for MathML, either in
the XML encoding (http://www.w3.org/Math/RelaxNG/mathml3/mathml3.rng)
or in compact notation (http://www.w3.org/Math/RelaxNG/mathml3/mathml3.rnc)
which is also shown below.
In contrast to DTDs there is no in-document method to associate a RelaxNG schema with
a document.
We provide five RelaxNG schema for MathML3 in five parts:
-
The grammar for full MathML
-
The grammar for elements common to Content and Presentation
-
The grammar for Presentation MathML
-
The grammar for Strict Content MathML
-
The grammar for Content MathML3
A.2.1 Full MathML
The RelaxNG schema for full MathML builds on the schema describing the various parts
of the language which are given in the following sections. It can be found at http://www.w3.org/Math/RelaxNG/mathml3/mathml3.rnc.
# This is the Mathematical Markup Language (MathML) 3.0, an XML
# application for describing mathematical notation and capturing
# both its structure and content.
#
# Copyright 1998-2010 W3C (MIT, ERCIM, Keio)
#
# Use and distribution of this code are permitted under the terms
# W3C Software Notice and License
# http://www.w3.org/Consortium/Legal/2002/copyright-software-20021231
default namespace m = "http://www.w3.org/1998/Math/MathML"
## Content MathML
include "mathml3-content.rnc"
## Presentation MathML
include "mathml3-presentation.rnc"
## math and semantics common to both Content and Presentation
include "mathml3-common.rnc"
A.2.2 Elements Common to Presentation and Content MathML
# This is the Mathematical Markup Language (MathML) 3.0, an XML
# application for describing mathematical notation and capturing
# both its structure and content.
#
# Copyright 1998-2014 W3C (MIT, ERCIM, Keio, Beihang)
#
# Use and distribution of this code are permitted under the terms
# W3C Software Notice and License
# http://www.w3.org/Consortium/Legal/2002/copyright-software-20021231
default namespace m = "http://www.w3.org/1998/Math/MathML"
namespace local = ""
start = math
math = element math {math.attributes,MathExpression*}
MathExpression = semantics
NonMathMLAtt = attribute (* - (local:*|m:*)) {xsd:string}
CommonDeprecatedAtt = attribute other {text}?
CommonAtt = attribute id {xsd:ID}?,
attribute xref {text}?,
attribute class {xsd:NMTOKENS}?,
attribute style {xsd:string}?,
attribute href {xsd:anyURI}?,
CommonDeprecatedAtt,
NonMathMLAtt*
math.attributes = CommonAtt,
attribute display {"block" | "inline"}?,
attribute maxwidth {length}?,
attribute overflow {"linebreak" | "scroll" | "elide" | "truncate" | "scale"}?,
attribute altimg {xsd:anyURI}?,
attribute altimg-width {length}?,
attribute altimg-height {length}?,
attribute altimg-valign {length | "top" | "middle" | "bottom"}?,
attribute alttext {text}?,
attribute cdgroup {xsd:anyURI}?,
math.deprecatedattributes
# the mathml3-presentation schema adds additional attributes
# to the math element, all those valid on mstyle
math.deprecatedattributes = attribute mode {xsd:string}?,
attribute macros {xsd:string}?
name = attribute name {xsd:NCName}
cd = attribute cd {xsd:NCName}
src = attribute src {xsd:anyURI}?
annotation = element annotation {annotation.attributes,text}
annotation-xml.model = (MathExpression|anyElement)*
anyElement = element (* - m:*) {(attribute * {text}|text| anyElement)*}
annotation-xml = element annotation-xml {annotation.attributes,
annotation-xml.model}
annotation.attributes = CommonAtt,
cd?,
name?,
DefEncAtt,
src?
DefEncAtt = attribute encoding {xsd:string}?,
attribute definitionURL {xsd:anyURI}?
semantics = element semantics {semantics.attributes,
MathExpression,
(annotation|annotation-xml)*}
semantics.attributes = CommonAtt,DefEncAtt,cd?,name?
length
# wrapped for display
= xsd:string {
pattern = '\s*((-?[0-9]*([0-9]\.?|\.[0-9])[0-9]*(e[mx]|in|cm|mm|p[xtc]|%)?)|(negative)?((very){0,2}thi(n|
ck)|medium)mathspace)\s*'
}
A.2.3 The Grammar for Presentation MathML
# This is the Mathematical Markup Language (MathML) 3.0, an XML
# application for describing mathematical notation and capturing
# both its structure and content.
#
# Copyright 1998-2014 W3C (MIT, ERCIM, Keio, Beihang)
#
# Use and distribution of this code are permitted under the terms
# W3C Software Notice and License
# http://www.w3.org/Consortium/Legal/2002/copyright-software-20021231
default namespace m = "http://www.w3.org/1998/Math/MathML"
MathExpression |= PresentationExpression
ImpliedMrow = MathExpression*
TableRowExpression = mtr|mlabeledtr
TableCellExpression = mtd
MstackExpression = MathExpression|mscarries|msline|msrow|msgroup
MsrowExpression = MathExpression|none
MultiScriptExpression = (MathExpression|none),(MathExpression|none)
mpadded-length
# wrapped for display
= xsd:string {
pattern = '\s*([\+\-]?[0-9]*([0-9]\.?|\.[0-9])[0-9]*\s*((%?\s*(height|depth|width)?)|
e[mx]|in|cm|mm|p[xtc]|((negative)?((very){0,2}thi(n|ck)|medium)mathspace))?)\s*' }
linestyle = "none" | "solid" | "dashed"
verticalalign =
"top" |
"bottom" |
"center" |
"baseline" |
"axis"
columnalignstyle = "left" | "center" | "right"
notationstyle =
"longdiv" |
"actuarial" |
"radical" |
"box" |
"roundedbox" |
"circle" |
"left" |
"right" |
"top" |
"bottom" |
"updiagonalstrike" |
"downdiagonalstrike" |
"verticalstrike" |
"horizontalstrike" |
"madruwb"
idref = text
unsigned-integer = xsd:unsignedLong
integer = xsd:integer
number = xsd:decimal
character = xsd:string {
pattern = '\s*\S\s*'}
color
# wrapped for display
= xsd:string {
pattern = '\s*((#[0-9a-fA-F]{3}([0-9a-fA-F]{3})?)|[aA][qQ][uU][aA]|[bB][lL][aA][cC][kK]|
[bB][lL][uU][eE]|[fF][uU][cC][hH][sS][iI][aA]|[gG][rR][aA][yY]|[gG][rR][eE][eE][nN]|
[lL][iI][mM][eE]|[mM][aA][rR][oO][oO][nN]|[nN][aA][vV][yY]|[oO][lL][iI][vV][eE]|[pP][uU][rR][pP][lL][eE]|
[rR][eE][dD]|[sS][iI][lL][vV][eE][rR]|[tT][eE][aA][lL]|[wW][hH][iI][tT][eE]|[yY][eE][lL][lL][oO][wW])\s*'}
group-alignment = "left" | "center" | "right" | "decimalpoint"
group-alignment-list = list {group-alignment+}
group-alignment-list-list = xsd:string {
pattern = '(\s*\{\s*(left|center|right|decimalpoint)(\s+(left|center|right|decimalpoint))*\})*\s*' }
positive-integer = xsd:positiveInteger
TokenExpression = mi|mn|mo|mtext|mspace|ms
token.content = mglyph|malignmark|text
mi = element mi {mi.attributes, token.content*}
mi.attributes =
CommonAtt,
CommonPresAtt,
TokenAtt
mn = element mn {mn.attributes, token.content*}
mn.attributes =
CommonAtt,
CommonPresAtt,
TokenAtt
mo = element mo {mo.attributes, token.content*}
mo.attributes =
CommonAtt,
CommonPresAtt,
TokenAtt,
attribute form {"prefix" | "infix" | "postfix"}?,
attribute fence {"true" | "false"}?,
attribute separator {"true" | "false"}?,
attribute lspace {length}?,
attribute rspace {length}?,
attribute stretchy {"true" | "false"}?,
attribute symmetric {"true" | "false"}?,
attribute maxsize {length | "infinity"}?,
attribute minsize {length}?,
attribute largeop {"true" | "false"}?,
attribute movablelimits {"true" | "false"}?,
attribute accent {"true" | "false"}?,
attribute linebreak {"auto" | "newline" | "nobreak" | "goodbreak" | "badbreak"}?,
attribute lineleading {length}?,
attribute linebreakstyle {"before" | "after" | "duplicate" | "infixlinebreakstyle"}?,
attribute linebreakmultchar {text}?,
attribute indentalign {"left" | "center" | "right" | "auto" | "id"}?,
attribute indentshift {length}?,
attribute indenttarget {idref}?,
attribute indentalignfirst {"left" | "center" | "right" | "auto" | "id" | "indentalign"}?,
attribute indentshiftfirst {length | "indentshift"}?,
attribute indentalignlast {"left" | "center" | "right" | "auto" | "id" | "indentalign"}?,
attribute indentshiftlast {length | "indentshift"}?
mtext = element mtext {mtext.attributes, token.content*}
mtext.attributes =
CommonAtt,
CommonPresAtt,
TokenAtt
mspace = element mspace {mspace.attributes, empty}
mspace.attributes =
CommonAtt,
CommonPresAtt,
TokenAtt,
attribute width {length}?,
attribute height {length}?,
attribute depth {length}?,
attribute linebreak {"auto" | "newline" | "nobreak" | "goodbreak" | "badbreak" | "indentingnewline"}?,
attribute indentalign {"left" | "center" | "right" | "auto" | "id"}?,
attribute indentshift {length}?,
attribute indenttarget {idref}?,
attribute indentalignfirst {"left" | "center" | "right" | "auto" | "id" | "indentalign"}?,
attribute indentshiftfirst {length | "indentshift"}?,
attribute indentalignlast {"left" | "center" | "right" | "auto" | "id" | "indentalign"}?,
attribute indentshiftlast {length | "indentshift"}?
ms = element ms {ms.attributes, token.content*}
ms.attributes =
CommonAtt,
CommonPresAtt,
TokenAtt,
attribute lquote {text}?,
attribute rquote {text}?
mglyph = element mglyph {mglyph.attributes,mglyph.deprecatedattributes,empty}
mglyph.attributes =
CommonAtt, CommonPresAtt,
attribute src {xsd:anyURI}?,
attribute width {length}?,
attribute height {length}?,
attribute valign {length}?,
attribute alt {text}?
mglyph.deprecatedattributes =
attribute index {integer}?,
attribute mathvariant {"normal" | "bold" | "italic" | "bold-italic" | "double-struck" | "bold-fraktur" |
"script" | "bold-script" | "fraktur" | "sans-serif" | "bold-sans-serif" | "sans-serif-italic" |
"sans-serif-bold-italic" | "monospace" | "initial" | "tailed" | "looped" | "stretched"}?,
attribute mathsize {"small" | "normal" | "big" | length}?,
DeprecatedTokenAtt
msline = element msline {msline.attributes,empty}
msline.attributes =
CommonAtt, CommonPresAtt,
attribute position {integer}?,
attribute length {unsigned-integer}?,
attribute leftoverhang {length}?,
attribute rightoverhang {length}?,
attribute mslinethickness {length | "thin" | "medium" | "thick"}?
none = element none {none.attributes,empty}
none.attributes =
CommonAtt,
CommonPresAtt
mprescripts = element mprescripts {mprescripts.attributes,empty}
mprescripts.attributes =
CommonAtt,
CommonPresAtt
CommonPresAtt =
attribute mathcolor {color}?,
attribute mathbackground {color | "transparent"}?
TokenAtt =
attribute mathvariant {"normal" | "bold" | "italic" | "bold-italic" | "double-struck" | "bold-fraktur" |
"script" | "bold-script" | "fraktur" | "sans-serif" | "bold-sans-serif" | "sans-serif-italic" |
"sans-serif-bold-italic" | "monospace" | "initial" | "tailed" | "looped" | "stretched"}?,
attribute mathsize {"small" | "normal" | "big" | length}?,
attribute dir {"ltr" | "rtl"}?,
DeprecatedTokenAtt
DeprecatedTokenAtt =
attribute fontfamily {text}?,
attribute fontweight {"normal" | "bold"}?,
attribute fontstyle {"normal" | "italic"}?,
attribute fontsize {length}?,
attribute color {color}?,
attribute background {color | "transparent"}?
MalignExpression = maligngroup|malignmark
malignmark = element malignmark {malignmark.attributes, empty}
malignmark.attributes =
CommonAtt, CommonPresAtt,
attribute edge {"left" | "right"}?
maligngroup = element maligngroup {maligngroup.attributes, empty}
maligngroup.attributes =
CommonAtt, CommonPresAtt,
attribute groupalign {"left" | "center" | "right" | "decimalpoint"}?
PresentationExpression = TokenExpression|MalignExpression|
mrow|mfrac|msqrt|mroot|mstyle|merror|mpadded|mphantom|
mfenced|menclose|msub|msup|msubsup|munder|mover|munderover|
mmultiscripts|mtable|mstack|mlongdiv|maction
mrow = element mrow {mrow.attributes, MathExpression*}
mrow.attributes =
CommonAtt, CommonPresAtt,
attribute dir {"ltr" | "rtl"}?
mfrac = element mfrac {mfrac.attributes, MathExpression, MathExpression}
mfrac.attributes =
CommonAtt, CommonPresAtt,
attribute linethickness {length | "thin" | "medium" | "thick"}?,
attribute numalign {"left" | "center" | "right"}?,
attribute denomalign {"left" | "center" | "right"}?,
attribute bevelled {"true" | "false"}?
msqrt = element msqrt {msqrt.attributes, ImpliedMrow}
msqrt.attributes =
CommonAtt, CommonPresAtt
mroot = element mroot {mroot.attributes, MathExpression, MathExpression}
mroot.attributes =
CommonAtt, CommonPresAtt
mstyle = element mstyle {mstyle.attributes, ImpliedMrow}
mstyle.attributes =
CommonAtt, CommonPresAtt,
mstyle.specificattributes,
mstyle.generalattributes,
mstyle.deprecatedattributes
mstyle.specificattributes =
attribute scriptlevel {integer}?,
attribute displaystyle {"true" | "false"}?,
attribute scriptsizemultiplier {number}?,
attribute scriptminsize {length}?,
attribute infixlinebreakstyle {"before" | "after" | "duplicate"}?,
attribute decimalpoint {character}?
mstyle.generalattributes =
attribute accent {"true" | "false"}?,
attribute accentunder {"true" | "false"}?,
attribute align {"left" | "right" | "center"}?,
attribute alignmentscope {list {("true" | "false") +}}?,
attribute bevelled {"true" | "false"}?,
attribute charalign {"left" | "center" | "right"}?,
attribute charspacing {length | "loose" | "medium" | "tight"}?,
attribute close {text}?,
attribute columnalign {list {columnalignstyle+} }?,
attribute columnlines {list {linestyle +}}?,
attribute columnspacing {list {(length) +}}?,
attribute columnspan {positive-integer}?,
attribute columnwidth {list {("auto" | length | "fit") +}}?,
attribute crossout {list {("none" | "updiagonalstrike" | "downdiagonalstrike" | "verticalstrike" | "horizontalstrike")*}}?,
attribute denomalign {"left" | "center" | "right"}?,
attribute depth {length}?,
attribute dir {"ltr" | "rtl"}?,
attribute edge {"left" | "right"}?,
attribute equalcolumns {"true" | "false"}?,
attribute equalrows {"true" | "false"}?,
attribute fence {"true" | "false"}?,
attribute form {"prefix" | "infix" | "postfix"}?,
attribute frame {linestyle}?,
attribute framespacing {list {length, length}}?,
attribute groupalign {group-alignment-list-list}?,
attribute height {length}?,
attribute indentalign {"left" | "center" | "right" | "auto" | "id"}?,
attribute indentalignfirst {"left" | "center" | "right" | "auto" | "id" | "indentalign"}?,
attribute indentalignlast {"left" | "center" | "right" | "auto" | "id" | "indentalign"}?,
attribute indentshift {length}?,
attribute indentshiftfirst {length | "indentshift"}?,
attribute indentshiftlast {length | "indentshift"}?,
attribute indenttarget {idref}?,
attribute largeop {"true" | "false"}?,
attribute leftoverhang {length}?,
attribute length {unsigned-integer}?,
attribute linebreak {"auto" | "newline" | "nobreak" | "goodbreak" | "badbreak"}?,
attribute linebreakmultchar {text}?,
attribute linebreakstyle {"before" | "after" | "duplicate" | "infixlinebreakstyle"}?,
attribute lineleading {length}?,
attribute linethickness {length | "thin" | "medium" | "thick"}?,
attribute location {"w" | "nw" | "n" | "ne" | "e" | "se" | "s" | "sw"}?,
attribute longdivstyle {"lefttop" | "stackedrightright" | "mediumstackedrightright" | "shortstackedrightright" |
"righttop" | "left/\right" | "left)(right" | ":right=right" | "stackedleftleft" |
"stackedleftlinetop"}?,
attribute lquote {text}?,
attribute lspace {length}?,
attribute mathsize {"small" | "normal" | "big" | length}?,
attribute mathvariant {"normal" | "bold" | "italic" | "bold-italic" | "double-struck" | "bold-fraktur" |
"script" | "bold-script" | "fraktur" | "sans-serif" | "bold-sans-serif" | "sans-serif-italic" |
"sans-serif-bold-italic" | "monospace" | "initial" | "tailed" | "looped" | "stretched"}?,
attribute maxsize {length | "infinity"}?,
attribute minlabelspacing {length}?,
attribute minsize {length}?,
attribute movablelimits {"true" | "false"}?,
attribute mslinethickness {length | "thin" | "medium" | "thick"}?,
attribute notation {text}?,
attribute numalign {"left" | "center" | "right"}?,
attribute open {text}?,
attribute position {integer}?,
attribute rightoverhang {length}?,
attribute rowalign {list {verticalalign+} }?,
attribute rowlines {list {linestyle +}}?,
attribute rowspacing {list {(length) +}}?,
attribute rowspan {positive-integer}?,
attribute rquote {text}?,
attribute rspace {length}?,
attribute selection {positive-integer}?,
attribute separator {"true" | "false"}?,
attribute separators {text}?,
attribute shift {integer}?,
attribute side {"left" | "right" | "leftoverlap" | "rightoverlap"}?,
attribute stackalign {"left" | "center" | "right" | "decimalpoint"}?,
attribute stretchy {"true" | "false"}?,
attribute subscriptshift {length}?,
attribute superscriptshift {length}?,
attribute symmetric {"true" | "false"}?,
attribute valign {length}?,
attribute width {length}?
mstyle.deprecatedattributes =
DeprecatedTokenAtt,
attribute veryverythinmathspace {length}?,
attribute verythinmathspace {length}?,
attribute thinmathspace {length}?,
attribute mediummathspace {length}?,
attribute thickmathspace {length}?,
attribute verythickmathspace {length}?,
attribute veryverythickmathspace {length}?
math.attributes &= CommonPresAtt
math.attributes &= mstyle.specificattributes
math.attributes &= mstyle.generalattributes
merror = element merror {merror.attributes, ImpliedMrow}
merror.attributes =
CommonAtt, CommonPresAtt
mpadded = element mpadded {mpadded.attributes, ImpliedMrow}
mpadded.attributes =
CommonAtt, CommonPresAtt,
attribute height {mpadded-length}?,
attribute depth {mpadded-length}?,
attribute width {mpadded-length}?,
attribute lspace {mpadded-length}?,
attribute voffset {mpadded-length}?
mphantom = element mphantom {mphantom.attributes, ImpliedMrow}
mphantom.attributes =
CommonAtt, CommonPresAtt
mfenced = element mfenced {mfenced.attributes, MathExpression*}
mfenced.attributes =
CommonAtt, CommonPresAtt,
attribute open {text}?,
attribute close {text}?,
attribute separators {text}?
menclose = element menclose {menclose.attributes, ImpliedMrow}
menclose.attributes =
CommonAtt, CommonPresAtt,
attribute notation {text}?
msub = element msub {msub.attributes, MathExpression, MathExpression}
msub.attributes =
CommonAtt, CommonPresAtt,
attribute subscriptshift {length}?
msup = element msup {msup.attributes, MathExpression, MathExpression}
msup.attributes =
CommonAtt, CommonPresAtt,
attribute superscriptshift {length}?
msubsup = element msubsup {msubsup.attributes, MathExpression, MathExpression, MathExpression}
msubsup.attributes =
CommonAtt, CommonPresAtt,
attribute subscriptshift {length}?,
attribute superscriptshift {length}?
munder = element munder {munder.attributes, MathExpression, MathExpression}
munder.attributes =
CommonAtt, CommonPresAtt,
attribute accentunder {"true" | "false"}?,
attribute align {"left" | "right" | "center"}?
mover = element mover {mover.attributes, MathExpression, MathExpression}
mover.attributes =
CommonAtt, CommonPresAtt,
attribute accent {"true" | "false"}?,
attribute align {"left" | "right" | "center"}?
munderover = element munderover {munderover.attributes, MathExpression, MathExpression, MathExpression}
munderover.attributes =
CommonAtt, CommonPresAtt,
attribute accent {"true" | "false"}?,
attribute accentunder {"true" | "false"}?,
attribute align {"left" | "right" | "center"}?
mmultiscripts = element mmultiscripts {mmultiscripts.attributes, MathExpression,MultiScriptExpression*,(mprescripts,MultiScriptExpression*)?}
mmultiscripts.attributes =
msubsup.attributes
mtable = element mtable {mtable.attributes, TableRowExpression*}
mtable.attributes =
CommonAtt, CommonPresAtt,
attribute align {xsd:string {
pattern ='\s*(top|bottom|center|baseline|axis)(\s+-?[0-9]+)?\s*'}}?,
attribute rowalign {list {verticalalign+} }?,
attribute columnalign {list {columnalignstyle+} }?,
attribute groupalign {group-alignment-list-list}?,
attribute alignmentscope {list {("true" | "false") +}}?,
attribute columnwidth {list {("auto" | length | "fit") +}}?,
attribute width {"auto" | length}?,
attribute rowspacing {list {(length) +}}?,
attribute columnspacing {list {(length) +}}?,
attribute rowlines {list {linestyle +}}?,
attribute columnlines {list {linestyle +}}?,
attribute frame {linestyle}?,
attribute framespacing {list {length, length}}?,
attribute equalrows {"true" | "false"}?,
attribute equalcolumns {"true" | "false"}?,
attribute displaystyle {"true" | "false"}?,
attribute side {"left" | "right" | "leftoverlap" | "rightoverlap"}?,
attribute minlabelspacing {length}?
mlabeledtr = element mlabeledtr {mlabeledtr.attributes, TableCellExpression+}
mlabeledtr.attributes =
mtr.attributes
mtr = element mtr {mtr.attributes, TableCellExpression*}
mtr.attributes =
CommonAtt, CommonPresAtt,
attribute rowalign {"top" | "bottom" | "center" | "baseline" | "axis"}?,
attribute columnalign {list {columnalignstyle+} }?,
attribute groupalign {group-alignment-list-list}?
mtd = element mtd {mtd.attributes, ImpliedMrow}
mtd.attributes =
CommonAtt, CommonPresAtt,
attribute rowspan {positive-integer}?,
attribute columnspan {positive-integer}?,
attribute rowalign {"top" | "bottom" | "center" | "baseline" | "axis"}?,
attribute columnalign {columnalignstyle}?,
attribute groupalign {group-alignment-list}?
mstack = element mstack {mstack.attributes, MstackExpression*}
mstack.attributes =
CommonAtt, CommonPresAtt,
attribute align {xsd:string {
pattern ='\s*(top|bottom|center|baseline|axis)(\s+-?[0-9]+)?\s*'}}?,
attribute stackalign {"left" | "center" | "right" | "decimalpoint"}?,
attribute charalign {"left" | "center" | "right"}?,
attribute charspacing {length | "loose" | "medium" | "tight"}?
mlongdiv = element mlongdiv {mlongdiv.attributes, MstackExpression,MstackExpression,MstackExpression+}
mlongdiv.attributes =
msgroup.attributes,
attribute longdivstyle {"lefttop" | "stackedrightright" | "mediumstackedrightright" | "shortstackedrightright" |
"righttop" | "left/\right" | "left)(right" | ":right=right" | "stackedleftleft" |
"stackedleftlinetop"}?
msgroup = element msgroup {msgroup.attributes, MstackExpression*}
msgroup.attributes =
CommonAtt, CommonPresAtt,
attribute position {integer}?,
attribute shift {integer}?
msrow = element msrow {msrow.attributes, MsrowExpression*}
msrow.attributes =
CommonAtt, CommonPresAtt,
attribute position {integer}?
mscarries = element mscarries {mscarries.attributes, (MsrowExpression|mscarry)*}
mscarries.attributes =
CommonAtt, CommonPresAtt,
attribute position {integer}?,
attribute location {"w" | "nw" | "n" | "ne" | "e" | "se" | "s" | "sw"}?,
attribute crossout {list {("none" | "updiagonalstrike" | "downdiagonalstrike" | "verticalstrike" | "horizontalstrike")*}}?,
attribute scriptsizemultiplier {number}?
mscarry = element mscarry {mscarry.attributes, MsrowExpression*}
mscarry.attributes =
CommonAtt, CommonPresAtt,
attribute location {"w" | "nw" | "n" | "ne" | "e" | "se" | "s" | "sw"}?,
attribute crossout {list {("none" | "updiagonalstrike" | "downdiagonalstrike" | "verticalstrike" | "horizontalstrike")*}}?
maction = element maction {maction.attributes, MathExpression+}
maction.attributes =
CommonAtt, CommonPresAtt,
attribute actiontype {text},
attribute selection {positive-integer}?
A.2.4 The Grammar for Strict Content MathML3
The grammar for Strict Content MathML3 can be found at http://www.w3.org/Math/RelaxNG/mathml3/mathml3-strict-content.rnc.
# This is the Mathematical Markup Language (MathML) 3.0, an XML
# application for describing mathematical notation and capturing
# both its structure and content.
#
# Copyright 1998-2014 W3C (MIT, ERCIM, Keio, Beihang)
#
# Use and distribution of this code are permitted under the terms
# W3C Software Notice and License
# http://www.w3.org/Consortium/Legal/2002/copyright-software-20021231
default namespace m = "http://www.w3.org/1998/Math/MathML"
ContExp = semantics-contexp | cn | ci | csymbol | apply | bind | share | cerror | cbytes | cs
cn = element cn {cn.attributes,cn.content}
cn.content = text
cn.attributes = CommonAtt, attribute type {"integer" | "real" | "double" | "hexdouble"}
semantics-ci = element semantics {semantics.attributes,(ci|semantics-ci),
(annotation|annotation-xml)*}
semantics-contexp = element semantics {semantics.attributes,ContExp,
(annotation|annotation-xml)*}
ci = element ci {ci.attributes, ci.content}
ci.attributes = CommonAtt, ci.type?
ci.type = attribute type {"integer" | "rational" | "real" | "complex" | "complex-polar" | "complex-cartesian" |
"constant" | "function" | "vector" | "list" | "set" | "matrix"}
ci.content = text
csymbol = element csymbol {csymbol.attributes,csymbol.content}
SymbolName = xsd:NCName
csymbol.attributes = CommonAtt, cd
csymbol.content = SymbolName
BvarQ = bvar*
bvar = element bvar {CommonAtt, (ci | semantics-ci)}
apply = element apply {CommonAtt,apply.content}
apply.content = ContExp+
bind = element bind {CommonAtt,bind.content}
bind.content = ContExp,bvar*,ContExp
share = element share {CommonAtt, src, empty}
cerror = element cerror {cerror.attributes, csymbol, ContExp*}
cerror.attributes = CommonAtt
cbytes = element cbytes {cbytes.attributes, base64}
cbytes.attributes = CommonAtt
base64 = xsd:base64Binary
cs = element cs {cs.attributes, text}
cs.attributes = CommonAtt
MathExpression |= ContExp
A.2.5 The Grammar for Content MathML
The grammar for Content MathML3 builds on the grammar for the Strict Content MathML subset, and can be found at http://www.w3.org/Math/RelaxNG/mathml3/mathml3-content.rnc.
# This is the Mathematical Markup Language (MathML) 3.0, an XML
# application for describing mathematical notation and capturing
# both its structure and content.
#
# Copyright 1998-2014 W3C (MIT, ERCIM, Keio, Beihang)
#
# Use and distribution of this code are permitted under the terms
# W3C Software Notice and License
# http://www.w3.org/Consortium/Legal/2002/copyright-software-20021231
include "mathml3-strict-content.rnc"{
cn.content = (text | mglyph | sep | PresentationExpression)*
cn.attributes = CommonAtt, DefEncAtt, attribute type {text}?, base?
ci.attributes = CommonAtt, DefEncAtt, ci.type?
ci.type = attribute type {text}
ci.content = (text | mglyph | PresentationExpression)*
csymbol.attributes = CommonAtt, DefEncAtt, attribute type {text}?,cd?
csymbol.content = (text | mglyph | PresentationExpression)*
bvar = element bvar {CommonAtt, ((ci | semantics-ci) & degree?)}
cbytes.attributes = CommonAtt, DefEncAtt
cs.attributes = CommonAtt, DefEncAtt
apply.content = ContExp+ | (ContExp, BvarQ, Qualifier*, ContExp*)
bind.content = apply.content
}
base = attribute base {text}
sep = element sep {empty}
PresentationExpression |= notAllowed
DomainQ = (domainofapplication|condition|interval|(lowlimit,uplimit?))*
domainofapplication = element domainofapplication {ContExp}
condition = element condition {ContExp}
uplimit = element uplimit {ContExp}
lowlimit = element lowlimit {ContExp}
Qualifier = DomainQ|degree|momentabout|logbase
degree = element degree {ContExp}
momentabout = element momentabout {ContExp}
logbase = element logbase {ContExp}
type = attribute type {text}
order = attribute order {"numeric" | "lexicographic"}
closure = attribute closure {text}
ContExp |= piecewise
piecewise = element piecewise {CommonAtt, DefEncAtt,(piece* & otherwise?)}
piece = element piece {CommonAtt, DefEncAtt, ContExp, ContExp}
otherwise = element otherwise {CommonAtt, DefEncAtt, ContExp}
DeprecatedContExp = reln | fn | declare
ContExp |= DeprecatedContExp
reln = element reln {ContExp*}
fn = element fn {ContExp}
declare = element declare {attribute type {xsd:string}?,
attribute scope {xsd:string}?,
attribute nargs {xsd:nonNegativeInteger}?,
attribute occurrence {"prefix"|"infix"|"function-model"}?,
DefEncAtt,
ContExp+}
interval.class = interval
ContExp |= interval.class
interval = element interval { CommonAtt, DefEncAtt,closure?, ContExp,ContExp}
unary-functional.class = inverse | ident | domain | codomain | image | ln | log | moment
ContExp |= unary-functional.class
inverse = element inverse { CommonAtt, DefEncAtt, empty}
ident = element ident { CommonAtt, DefEncAtt, empty}
domain = element domain { CommonAtt, DefEncAtt, empty}
codomain = element codomain { CommonAtt, DefEncAtt, empty}
image = element image { CommonAtt, DefEncAtt, empty}
ln = element ln { CommonAtt, DefEncAtt, empty}
log = element log { CommonAtt, DefEncAtt, empty}
moment = element moment { CommonAtt, DefEncAtt, empty}
lambda.class = lambda
ContExp |= lambda.class
lambda = element lambda { CommonAtt, DefEncAtt, BvarQ, DomainQ, ContExp}
nary-functional.class = compose
ContExp |= nary-functional.class
compose = element compose { CommonAtt, DefEncAtt, empty}
binary-arith.class = quotient | divide | minus | power | rem | root
ContExp |= binary-arith.class
quotient = element quotient { CommonAtt, DefEncAtt, empty}
divide = element divide { CommonAtt, DefEncAtt, empty}
minus = element minus { CommonAtt, DefEncAtt, empty}
power = element power { CommonAtt, DefEncAtt, empty}
rem = element rem { CommonAtt, DefEncAtt, empty}
root = element root { CommonAtt, DefEncAtt, empty}
unary-arith.class = factorial | minus | root | abs | conjugate | arg | real | imaginary | floor | ceiling | exp
ContExp |= unary-arith.class
factorial = element factorial { CommonAtt, DefEncAtt, empty}
abs = element abs { CommonAtt, DefEncAtt, empty}
conjugate = element conjugate { CommonAtt, DefEncAtt, empty}
arg = element arg { CommonAtt, DefEncAtt, empty}
real = element real { CommonAtt, DefEncAtt, empty}
imaginary = element imaginary { CommonAtt, DefEncAtt, empty}
floor = element floor { CommonAtt, DefEncAtt, empty}
ceiling = element ceiling { CommonAtt, DefEncAtt, empty}
exp = element exp { CommonAtt, DefEncAtt, empty}
nary-minmax.class = max | min
ContExp |= nary-minmax.class
max = element max { CommonAtt, DefEncAtt, empty}
min = element min { CommonAtt, DefEncAtt, empty}
nary-arith.class = plus | times | gcd | lcm
ContExp |= nary-arith.class
plus = element plus { CommonAtt, DefEncAtt, empty}
times = element times { CommonAtt, DefEncAtt, empty}
gcd = element gcd { CommonAtt, DefEncAtt, empty}
lcm = element lcm { CommonAtt, DefEncAtt, empty}
nary-logical.class = and | or | xor
ContExp |= nary-logical.class
and = element and { CommonAtt, DefEncAtt, empty}
or = element or { CommonAtt, DefEncAtt, empty}
xor = element xor { CommonAtt, DefEncAtt, empty}
unary-logical.class = not
ContExp |= unary-logical.class
not = element not { CommonAtt, DefEncAtt, empty}
binary-logical.class = implies | equivalent
ContExp |= binary-logical.class
implies = element implies { CommonAtt, DefEncAtt, empty}
equivalent = element equivalent { CommonAtt, DefEncAtt, empty}
quantifier.class = forall | exists
ContExp |= quantifier.class
forall = element forall { CommonAtt, DefEncAtt, empty}
exists = element exists { CommonAtt, DefEncAtt, empty}
nary-reln.class = eq | gt | lt | geq | leq
ContExp |= nary-reln.class
eq = element eq { CommonAtt, DefEncAtt, empty}
gt = element gt { CommonAtt, DefEncAtt, empty}
lt = element lt { CommonAtt, DefEncAtt, empty}
geq = element geq { CommonAtt, DefEncAtt, empty}
leq = element leq { CommonAtt, DefEncAtt, empty}
binary-reln.class = neq | approx | factorof | tendsto
ContExp |= binary-reln.class
neq = element neq { CommonAtt, DefEncAtt, empty}
approx = element approx { CommonAtt, DefEncAtt, empty}
factorof = element factorof { CommonAtt, DefEncAtt, empty}
tendsto = element tendsto { CommonAtt, DefEncAtt, type?, empty}
int.class = int
ContExp |= int.class
int = element int { CommonAtt, DefEncAtt, empty}
Differential-Operator.class = diff
ContExp |= Differential-Operator.class
diff = element diff { CommonAtt, DefEncAtt, empty}
partialdiff.class = partialdiff
ContExp |= partialdiff.class
partialdiff = element partialdiff { CommonAtt, DefEncAtt, empty}
unary-veccalc.class = divergence | grad | curl | laplacian
ContExp |= unary-veccalc.class
divergence = element divergence { CommonAtt, DefEncAtt, empty}
grad = element grad { CommonAtt, DefEncAtt, empty}
curl = element curl { CommonAtt, DefEncAtt, empty}
laplacian = element laplacian { CommonAtt, DefEncAtt, empty}
nary-setlist-constructor.class = set | \list
ContExp |= nary-setlist-constructor.class
set = element set { CommonAtt, DefEncAtt, type?, BvarQ*, DomainQ*, ContExp*}
\list = element \list { CommonAtt, DefEncAtt, order?, BvarQ*, DomainQ*, ContExp*}
nary-set.class = union | intersect | cartesianproduct
ContExp |= nary-set.class
union = element union { CommonAtt, DefEncAtt, empty}
intersect = element intersect { CommonAtt, DefEncAtt, empty}
cartesianproduct = element cartesianproduct { CommonAtt, DefEncAtt, empty}
binary-set.class = in | notin | notsubset | notprsubset | setdiff
ContExp |= binary-set.class
in = element in { CommonAtt, DefEncAtt, empty}
notin = element notin { CommonAtt, DefEncAtt, empty}
notsubset = element notsubset { CommonAtt, DefEncAtt, empty}
notprsubset = element notprsubset { CommonAtt, DefEncAtt, empty}
setdiff = element setdiff { CommonAtt, DefEncAtt, empty}
nary-set-reln.class = subset | prsubset
ContExp |= nary-set-reln.class
subset = element subset { CommonAtt, DefEncAtt, empty}
prsubset = element prsubset { CommonAtt, DefEncAtt, empty}
unary-set.class = card
ContExp |= unary-set.class
card = element card { CommonAtt, DefEncAtt, empty}
sum.class = sum
ContExp |= sum.class
sum = element sum { CommonAtt, DefEncAtt, empty}
product.class = product
ContExp |= product.class
product = element product { CommonAtt, DefEncAtt, empty}
limit.class = limit
ContExp |= limit.class
limit = element limit { CommonAtt, DefEncAtt, empty}
unary-elementary.class = sin | cos | tan | sec | csc | cot | sinh | cosh | tanh | sech | csch | coth | arcsin | arccos | arctan | arccosh | arccot | arccoth | arccsc | arccsch | arcsec | arcsech | arcsinh | arctanh
ContExp |= unary-elementary.class
sin = element sin { CommonAtt, DefEncAtt, empty}
cos = element cos { CommonAtt, DefEncAtt, empty}
tan = element tan { CommonAtt, DefEncAtt, empty}
sec = element sec { CommonAtt, DefEncAtt, empty}
csc = element csc { CommonAtt, DefEncAtt, empty}
cot = element cot { CommonAtt, DefEncAtt, empty}
sinh = element sinh { CommonAtt, DefEncAtt, empty}
cosh = element cosh { CommonAtt, DefEncAtt, empty}
tanh = element tanh { CommonAtt, DefEncAtt, empty}
sech = element sech { CommonAtt, DefEncAtt, empty}
csch = element csch { CommonAtt, DefEncAtt, empty}
coth = element coth { CommonAtt, DefEncAtt, empty}
arcsin = element arcsin { CommonAtt, DefEncAtt, empty}
arccos = element arccos { CommonAtt, DefEncAtt, empty}
arctan = element arctan { CommonAtt, DefEncAtt, empty}
arccosh = element arccosh { CommonAtt, DefEncAtt, empty}
arccot = element arccot { CommonAtt, DefEncAtt, empty}
arccoth = element arccoth { CommonAtt, DefEncAtt, empty}
arccsc = element arccsc { CommonAtt, DefEncAtt, empty}
arccsch = element arccsch { CommonAtt, DefEncAtt, empty}
arcsec = element arcsec { CommonAtt, DefEncAtt, empty}
arcsech = element arcsech { CommonAtt, DefEncAtt, empty}
arcsinh = element arcsinh { CommonAtt, DefEncAtt, empty}
arctanh = element arctanh { CommonAtt, DefEncAtt, empty}
nary-stats.class = mean | sdev | variance | median | mode
ContExp |= nary-stats.class
mean = element mean { CommonAtt, DefEncAtt, empty}
sdev = element sdev { CommonAtt, DefEncAtt, empty}
variance = element variance { CommonAtt, DefEncAtt, empty}
median = element median { CommonAtt, DefEncAtt, empty}
mode = element mode { CommonAtt, DefEncAtt, empty}
nary-constructor.class = vector | matrix | matrixrow
ContExp |= nary-constructor.class
vector = element vector { CommonAtt, DefEncAtt, BvarQ, DomainQ, ContExp*}
matrix = element matrix { CommonAtt, DefEncAtt, BvarQ, DomainQ, ContExp*}
matrixrow = element matrixrow { CommonAtt, DefEncAtt, BvarQ, DomainQ, ContExp*}
unary-linalg.class = determinant | transpose
ContExp |= unary-linalg.class
determinant = element determinant { CommonAtt, DefEncAtt, empty}
transpose = element transpose { CommonAtt, DefEncAtt, empty}
nary-linalg.class = selector
ContExp |= nary-linalg.class
selector = element selector { CommonAtt, DefEncAtt, empty}
binary-linalg.class = vectorproduct | scalarproduct | outerproduct
ContExp |= binary-linalg.class
vectorproduct = element vectorproduct { CommonAtt, DefEncAtt, empty}
scalarproduct = element scalarproduct { CommonAtt, DefEncAtt, empty}
outerproduct = element outerproduct { CommonAtt, DefEncAtt, empty}
constant-set.class = integers | reals | rationals | naturalnumbers | complexes | primes | emptyset
ContExp |= constant-set.class
integers = element integers { CommonAtt, DefEncAtt, empty}
reals = element reals { CommonAtt, DefEncAtt, empty}
rationals = element rationals { CommonAtt, DefEncAtt, empty}
naturalnumbers = element naturalnumbers { CommonAtt, DefEncAtt, empty}
complexes = element complexes { CommonAtt, DefEncAtt, empty}
primes = element primes { CommonAtt, DefEncAtt, empty}
emptyset = element emptyset { CommonAtt, DefEncAtt, empty}
constant-arith.class = exponentiale | imaginaryi | notanumber | true | false | pi | eulergamma | infinity
ContExp |= constant-arith.class
exponentiale = element exponentiale { CommonAtt, DefEncAtt, empty}
imaginaryi = element imaginaryi { CommonAtt, DefEncAtt, empty}
notanumber = element notanumber { CommonAtt, DefEncAtt, empty}
true = element true { CommonAtt, DefEncAtt, empty}
false = element false { CommonAtt, DefEncAtt, empty}
pi = element pi { CommonAtt, DefEncAtt, empty}
eulergamma = element eulergamma { CommonAtt, DefEncAtt, empty}
infinity = element infinity { CommonAtt, DefEncAtt, empty}
A.2.6 MathML as a module in a RelaxNG Schema
Normally, a MathML expression does not constitute an entire XML document. MathML is
designed to be used as the mathematics fragment of larger markup languages. In
particular it is designed to be used as a module in documents marked up
with the XHTML family of markup languages. As RelaxNG directly supports modular
development, this is usually very easy: an XHTML+MathML schema can be specified as simply as
# A RelaxNG Schema for XHTML+MathML
include "xhtml.rnc"
math = external "mathml3.rnc"
Inline.class |= math
Block.class |= math
assuming that we have access to a modular RelaxNG schema for XHTML that uses
Inline.class and Block.class to collect the the content models
for inline and block-level elements.
Customizing the MathML3 schema so that we can restrict the content of
annotation-xml elements is similarly simple, for example:
# A RelaxNG Schema for MathML with OpenMath3 annotations
omobj = external "openmath3.rnc"
include "mathml3.rnc" {anotation-xml.model = omobj}
The MathML3 schema is organized so that subsetting to one of the sublanguages specified here is easy.
To include strict content MathML3 in a schema just include
include "mathml3-common.rnc"
include "mathml3-strict-content.rnc"
instead of include mathml3.rnc.
For details about RelaxNG grammars and modularization see [RELAX-NG] or [RelaxNGBook].
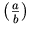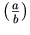 as opposed to the default rendering
as opposed to the default rendering
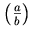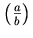 .
.
 .
.
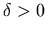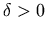 such that f(x) <1' is equivalent to
such that f(x) <1' is equivalent to
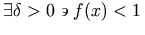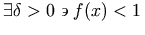 and could be represented as:
and could be represented as:
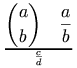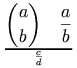
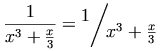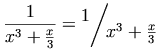
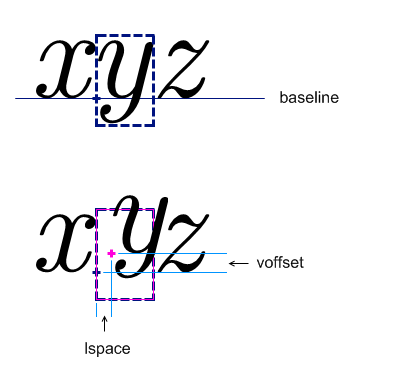
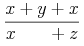
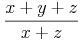
![[Image of a circle and box around x plus y]](image/circlebox.png)
![[image of actuarial notation for a angle n at i]](image/actuarial.png)
![[image of phasorangle notation for the angle negative pi over 2]](image/phasorangle.png)
![[Image of 12 factorial in Arabic style]](image/madruwb12.png)
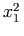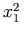 versus the staggered positioning of nested scripts as shown here
versus the staggered positioning of nested scripts as shown here
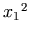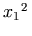 ;
the latter can be achieved by nesting an
;
the latter can be achieved by nesting an 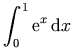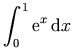
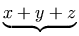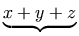 versus
versus
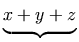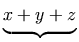 .
The MathML representation for this example is shown below.
.
The MathML representation for this example is shown below.
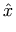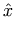 versus
versus
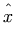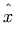 .
These differences also apply to "mathematical accents" such as
bars or braces over expressions:
.
These differences also apply to "mathematical accents" such as
bars or braces over expressions:
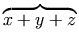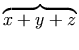 versus
versus
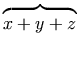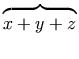 .
The MathML representation for each of these examples is shown below.
.
The MathML representation for each of these examples is shown below.
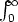 versus
versus
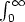 .
The MathML representation for this example is shown below.
.
The MathML representation for this example is shown below.
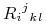 (where k and l are different indices)
(where k and l are different indices)
![[binomial(5,12) in english style]](image/binom5-12.png)
![[binomial(5,12) in Arabic style]](image/arbinom5-12.png)
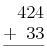
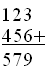
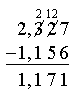
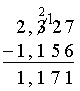
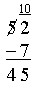
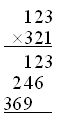
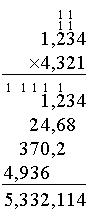
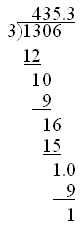
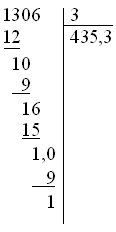
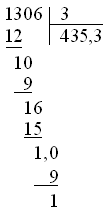
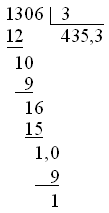
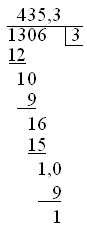
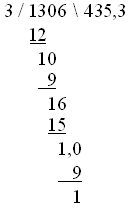
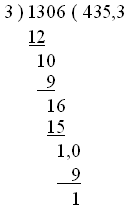
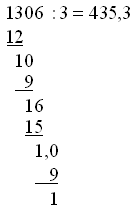
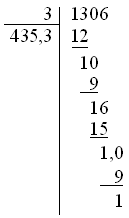
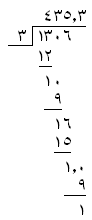
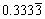
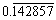
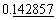
 He
He 
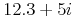
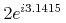
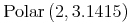
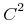
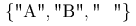
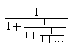 .
However, the procedure of building an expression tree by replacing
.
However, the procedure of building an expression tree by replacing
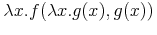 which has two sub-terms of the form
which has two sub-terms of the form
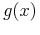 ,
one with
,
one with 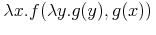 .
However, in this form, it is no longer possible to share the expression
.
However, in this form, it is no longer possible to share the expression
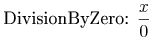
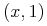
![{\left[{0},{1}\right]}](image/interval1-interval_cc-ex1.gif)
![{\left({0},{1}\right]}](image/interval1-interval_oc-ex1.gif)
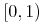
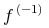
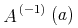
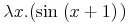
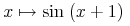
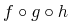
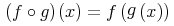
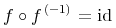
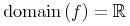
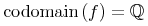
![{{\mathop{{\minormal{image}}}{\left({\minormal{sin}}\right)}}={\left[{\mn{-1}},{1}\right]}}](image/fns1-image-ex1.gif)
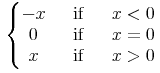
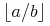
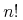
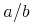
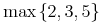
![{{\minormal{max}}{\left.\middle\{y^3\middle|{y\unicode{8712}{\left[{0},{1}\right]}}\middle\}\right.}}](image/minmax1-big_max-ex1.gif)
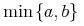

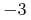
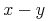
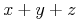
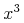
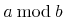
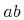
![\sqrt[{n}]{a}](image/arith1-root-ex1.gif)
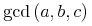
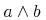
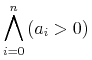
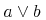
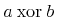
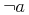
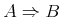
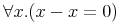
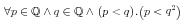
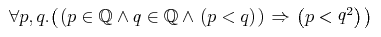
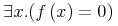
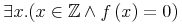
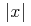
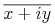
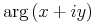
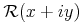
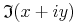
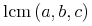
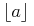
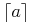
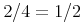
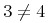
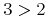
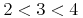
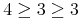
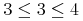
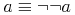
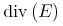
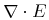
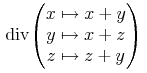
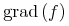
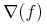
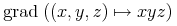
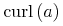
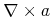
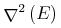
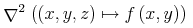
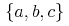
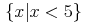
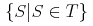
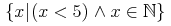
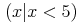
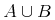
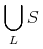
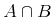
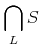
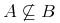
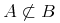
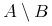
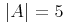
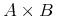
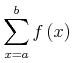
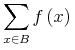
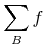
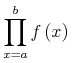
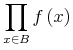
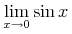
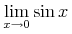
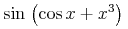
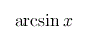
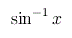
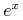
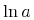
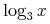
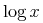
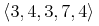


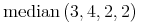
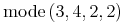
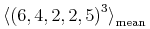
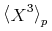
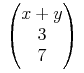
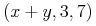
![{\left.[\msub{m}{{i,j}}\middle|{\msub{m}{{i,j}}=\msup{i}{j}};{{i\unicode{8712}{\left[1,5\right]}}\unicode{8743}{j\unicode{8712}{\left[5,9\right]}}}]\right.}](image/linalg6-matrix-ex1.gif)