 The
Planet MathML aggregates posts from various blogs that
concern MathML. Although it is hosted by W3C, the content of the
individual entries represent only the opinion of their respective
authors and does not reflect the position of
W3C.
The
Planet MathML aggregates posts from various blogs that
concern MathML. Although it is hosted by W3C, the content of the
individual entries represent only the opinion of their respective
authors and does not reflect the position of
W3C.
 The
Planet MathML aggregates posts from various blogs that
concern MathML. Although it is hosted by W3C, the content of the
individual entries represent only the opinion of their respective
authors and does not reflect the position of
W3C.
The
Planet MathML aggregates posts from various blogs that
concern MathML. Although it is hosted by W3C, the content of the
individual entries represent only the opinion of their respective
authors and does not reflect the position of
W3C.
Attendees: - Neil Soiffer - Louis Maher - David Farmer - David Carlisle - Bruce Miller - Murray Sargent - Bert Bos - Deyan Ginev - Patrick Ion - Paul Libbrecht <https://sandbox.cryptpad.info/code/inner.html?ver=5.7.0-0#cp-md-0-regrets> Regrets <https://sandbox.cryptpad.info/code/inner.html?ver=5.7.0-0#cp-md-0-agenda> Agenda <https://sandbox.cryptpad.info/code/inner.html?ver=5.7.0-0#cp-md-0-1-announcements-updates-progress-reports>1. Announcements/Updates/Progress reports (discussion before the meeting officially started) NS: Is there a Windows flavor or clipboard type for LaTeX? NS: I was going to put it out as a plain text, but I thought maybe there is a clipboard type that I should use. MuS: I do not know of one. You can always invent one, but then is anybody else going to use it? NS to PL and DC: Is there a clipboard flavor or mime type for LaTeX, similar to MathML? PL: Well DC: we did ask this on the math list and there were about five different types. DC They are not registered, but that is what people used. NS: I will stick to plain text. NS: We are going to record the calls to get a more accurate transcript for Louis. The cloud recordings will be erased in 30 days, and Louis's transcripts are deleted when NS releases the corresponding minutes. No one objected to the recording. <https://sandbox.cryptpad.info/code/inner.html?ver=5.7.0-0#cp-md-0-2-units-a-href-https-en-wikipedia-org-wiki-international_system_of_units-si-units-a->2. Units: SI Units <https://en.wikipedia.org/wiki/International_System_of_Units> <https://sandbox.cryptpad.info/code/inner.html?ver=5.7.0-0#cp-md-0--a-href-https-github-com-w3c-mathml-issues-475-list-of-units-475-a->List of Units (#475) <https://github.com/w3c/mathml/issues/475> NS: This is the MathPlayer unit list. This list is broken down into basic Si units, derived SI units, accepted SI units, English units, and other units. NS: There are accepted units which are non-SI units in every-day use. For example, atomic mass unit, astronomical unit… NS first listed the prefixes for the SI units, such as: tera, giga, mega,… NS: Have I left any units out? DC: How is this list going to be used? I mean, you could just have unit and then just put whatever you like in and if it's not a valid unit that's the author's problem. DC: You seem to be assuming this list is going to be a validated list, which means you have a particular syntax in mind? NS: I do have a little bit of syntax in mind in the sense that you know KM is kilometers and it would be accepted as kilometers. NS: This is a useful list for technology so that if AT sees KM, it knows that it means kilometer. DC: This is true as long as the KM is not marked with an intent. DC: If it is marked with the unit property, what else do you need to know? DG: You need a flat list of entries for intense purposes because you have a specific property unit and then you want to know what it can resolve against. So, it doesn't actually matter what the ontology of the units are. So, whether it's a base, common, or English is completely irrelevant in a sense. What you want to know is whether capital A and a capital C do or do not activate when you have the unit property and then you want to know what they are activated against. DG: We must decide if C is coulomb or Celsius or is Celsius not a unit. DG: If you have a big flat list, you can see whether you have clashes, and what to do with the clashes. NS: I pulled the prefixes out because including a unit with all its prefix forms would make a huge list. DC: We should follow the si unit tex package: https://texdoc.org/serve/siunitx/0 NS: This list informs AT how to say things. NS: We should look at the TeX package to see if we left things out. NS: The point of this list is to show that there are other ways to say things other than just reading the letters. BM: is worried about having M be defined as meters. From Deyan Ginev to Everyone: m NS: Should we generate intent names for these things? SI Units <https://en.wikipedia.org/wiki/International_System_of_Units> NS: The point here is that a TeX package could generate an intent with the name kilogram, and with the name meter. NS: We can say that units should be spoken a certain way, and it is up to the authors to provide the intents if the authors want a different pronunciation. NS: It would be perfectly reasonable then to say yes, we should generate intent names for these things. DC: Let us use a unit property and a long flat list. DF: There are no latex packages involved in anything I'm doing. What you need is a way of marking that something's a unit analogous to the backslash unit that you use in this package. If you just type the letter like Kg, space M, it means you can interpret it as kilogram meter. NS: So maybe this whole discussion on units then becomes mute because it's actually pushed back on the authors. NS: is worried about enlarging the core list. NS: If you do not count the prefixes: you have 100 to 150 entries. Maybe about 25 entries have 20 prefix variants each. This list grows to nearly 1,000 entries. DC: What is the most natural way to go? NS: The SI Units are unambiguous. NS: Things can get ambiguous. Is C Celsius or coulombs? Is "m" miles or meters. DF: It gets more complicated when you put prefixes on units like mC for micro-Celsius. PL: Things get complicated when you try to do math on them. BM: The point is for authors to be able to disambiguate, no matter what notation they're using. NS: If we go with the unit property then people could make up units like kilo-miles. In a terse mode you would go km. PL: You want to be able to express uncommon things. NS: Someone could also introduce a literal if something is uncommon and not in core. DC: If you had a units property it would disambiguate letters. DC: Just say this expression is a unit. It wouldn't distinguish meters, miles, and things. But, on the other hand, that's less common. PL: What is the value of speaking about meters or miles? What is the difference between making a literal or intent concept? NS: Concepts have alternative ways of being spoken. "m" is either "m" or meters. If it is a literal then the author can specify the way it is spoken. PL: Can we refer to some external list of units? NS: We should be the ones to curate the list unless there is a really good list to which we can point. NS: We have two proposals. One would make concepts for every unit including all of its prefix variants, or we could have a units property and have a flat list of units. We could do both, but that would not be good. Ns: How many of us would like an intent concept-based approach so no unit property? DC: Let us see examples of both ways. DG: It's easy to vote against a large list. NS: What I was hoping to do today was to figure out what are the conflicts in the list and therefore determine whether the this really makes any sense or not. DC: It depends on the context whether we are talking about meters or miles. NS: I had not considered that generating the actual concept names was an option, but it appears to be quite a reasonable option. But okay. *ACTION* ns: Homework for us to generate some examples of both properties and concept names. We would like to have a good strong start on a list of concept names probably by pulling all these names out and figuring out which ones can accept the prefixes. That would tell us how big the list could be. NS: We should also look at DG's lists. NS: to DG: Can you go through your list to see what new things are in your lists that are not in NS's list? DG: I will probably make a huge list with every unit before the meeting, so that we have it sorted by presentation. And then it's very obvious what goes where? NS to DG: Do you want me to go through your list and see what new stuff there is which is not on my list? DG: You're welcome to make another list because I didn't want to volunteer an action item because I don't know how much time I'll have, but I'll try to find time. NS: Okay, well, I just don't want us both doing the same thing. NS: Since you're going to build the big list, let me go through yours and see if I can find stuff that's not in the list that I created, in which case I'll add it to the list. NS: Starting on Monday, I guess. Could be the weekend to do it to go through your lists.
Apologies for sending this on a Sunday, I had some things come up on Friday and forgot to send an agenda. There is now one at with a few ideas of things to cover. As always, feel free to add or suggest otherwise. See you tomorrow https://github.com/w3c/mathml-core/issues/226 -- Brian Kardell :: @briankardell :: bkardell.com
North America has moved to Daylight Savings Time/Summer time. The W3C uses Boston time, so the meetings remain at the same time in North American and are an hour earlier for most of those outside North America. We meet on Thursday at: 10am Pacific, 1pm Eastern,* 6pm Central European Time*. The regulars for this group should have the meeting details in their calendars. For everyone else, the details can be found on the members-only W3C Math WG calendar <https://www.w3.org/events/meetings/d6f2b73d-34fc-4276-b164-bdc62a675dcc/20230713T130000/>. Agenda 1. Announcements/Updates/Progress reports 2. Units: - List of Units (#475) <https://github.com/w3c/mathml/issues/475> - Deyan's Physics list <https://gist.github.com/dginev/825078ae316c32c312436f42061b3d05> - Deyan's Chemistry list <https://gist.github.com/dginev/ff7e6e090b79a0389fc2eff2b9961331> - Deyan's Biology List, <https://gist.github.com/dginev/d6367f53cb7b1fbed8abfa6bddd4f2c0> - Deyan's Earth Science and Engineering List <https://gist.github.com/dginev/cec6eb44f8c3fdffbffe546448049981>
Attendees: - Neil Soiffer - Greg Williams - David Carlisle - Bert Bos - Deyan Ginev - Patrick Ion - Paul Libbrecht - Murray Sargent <https://sandbox.cryptpad.info/code/inner.html?ver=5.7.0-0#cp-md-0-regrets> Regrets - Louis Maher - Moritz Schubotz - David Farmer <https://sandbox.cryptpad.info/code/inner.html?ver=5.7.0-0#cp-md-0-agenda> Agenda <https://sandbox.cryptpad.info/code/inner.html?ver=5.7.0-0#cp-md-0-1-announcements-updates-progress-reports>1. Announcements/Updates/Progress reports NS: We have two more weeks of a time-shifted meeting start time where the people in Europe start one hour earlier. NS: Paul, David, Moritz, and I wrote an abstract for ICCHP, which is the big accessibility Conference in Europe, In the second week of July, in Austria. The abstract is about the intent attribute. The abstract was accepted. We must still write the paper. <https://sandbox.cryptpad.info/code/inner.html?ver=5.7.0-0#cp-md-0-2-chemistry-discussion-greg-williams-co-chair-w3c-chemistry-community-group-will-join-the-call-for-part-4-of-the-conversation-for-reference->2. Chemistry discussion. Greg Williams (co-chair W3C Chemistry Community Group) will join the call for part 4 of the conversation. For reference, here is the link to the Chemistry CG list <https://docs.google.com/spreadsheets/d/1h-8k_bwQ1bO7gusb0O2DfcEs0DZUAo6QVGYZuVjWVB8/edit#gid=0> Intent Core Concept List <https://w3c.github.io/mathml-docs/intent-core-concepts/> NS: Deyan's Chemistry list <https://gist.github.com/dginev/ff7e6e090b79a0389fc2eff2b9961331> DG: I had found this article useful: The 8 Types of Arrows In Organic Chemistry Explained <https://www.masterorganicchemistry.com/2011/02/09/the-8-types-of-arrows-in-organic-chemistry-explained/> <https://sandbox.cryptpad.info/code/inner.html?ver=5.7.0-0#cp-md-0-list-of-new-intents>List Of New Intents *ACTION* NS: arrow with a delta over it we need to resolve this. Either label only the delta or label the whole symbol "Delta over reaction arrow" (Chemistry CG list, row 72). *ACTION* NS: We did not name the arrows. We need to come back to them. *ACTION* NS: intents for lowercase rho are partial-pressure and density. *ACTION* lowercase sigma has Intents of wavenumber and conductivity. *ACTION* We should have a concept name of amino-acid. GW said that it should apply for 20 amino acids; however, there are more than 20 acids in the chemistry CG list starting with row 112. They are: Histidine, His Arginine, Arg Phenylalanine, Phe Alanine, Ala Cysteine, Cys Glycine, Gly Glutamine, Gln Glutamic acid, Glu Aspartic acid, Asp Lysine, Lys Leucine, Leu Methionine, Met Asparagine, Asn Serine, Ser Tyrosine, Tyr Threonine, Thr Isoleucine, Ile Tryptophan, Trp Proline, Pro Valine, Val (asparagine/aspartic acid, asx) (glutamine/glutamic acid, glx) NS: We are not going to have intents for constants. *ACTION* NS: Give "ppt" the two intents of: parts-per-thousand, or parts-per-trillion. *ACTION* NS: intent for mole-fraction <https://sandbox.cryptpad.info/code/inner.html?ver=5.7.0-0#cp-md-0-general-discussion>General Discussion GW was not part of the committee when this document was drafted. The committee put down a list of symbols with multiple meanings which needed explanations. NS wanted us to skim the Chemistry CG list and see what we had not addressed. NS: K sub eq does not need an intent. It is the "equilibrium constant". GW: Normally it is read as K sub eq. You would only use an intent if you wanted it to say, "equilibrium constant", and you do not want it to say "equilibrium constant' much. NS: Skip K sub eq. NS: Have we delt with "concentration of'? Yes. NS: Ethyl (Et), Methyl (Me), Benzyl (Bn), and Phenyl (Ph) are treated using the "semi-chemical-element" concept. GW: In discussing side chains: How will these things come over from LaTeX. NS: We have not thought that far out. We hope the LaTeX translators can help us. We hope the authors give us hints. NS: If you were using Mh. Chem. And the MH. Chem. Became intent aware, then it would know that the equal sign is a double bond, and it should market as such, you know. Then that would be marked up in the tech, similar to a chemical element. GW: We can not specify all the things that people might use as side chains. NS: Consider all the arrows. Are these things likely to show up in MathML as opposed to being shown in diagrams which we do not handle? GW: That is a good question. NS: Consider dotted arrow right and dotted arrow left. What do they mean? GW: Has not used dotted arrows. MuS: Maybe it is not important and not in core. GW: Did they label the curved arrows? NS: No. GW: Generally speaking, your curved arrows are probably not going to turn up in MathML because they're used for showing the movement of electrons, at which point I would think you would be out of MathML. You'd be drawing something. GW: Consider Delta over reaction arrow. This means to provide heat for this reaction. It does not say how much heat to provide. NS: What intent name should it get? GW: This will be a sub intent. Have the intent of a reaction arrow, and this will be a subscript to that. GW: Specifying reaction conditions: You can have many things appearing over the reaction arrow like h2o. GW: Have intent equal standard-reaction, then for a modification it would get an intent of reaction conditions. NS: How do we speak the over symbol? GW: You could have an intent for this specific one. GW: You could have one for the delta. Intent would be heat added. NS: You could place the intent on the mover in which case you are naming the entire thing or put it on the delta, and you would be overriding the word delta with the word heat. GW: Place it on the mover. *ACTION* NS: arrow with a delta over it we need to resolve this. Either label only the delta, or label the whole symbol "Delta over reaction arrow" (Chemistry CG list, row 72). *ACTION* NS: We did not name the arrows. We need to come back to them. DG: From Wikipedia: *ACTION* NS: Give "ppt" the two intents of: parts-per-thousand, or parts-per-trillion. *ACTION* NS: intent for mole-fraction GW: Both p and lowercase rho for partial pressure. Lowercase rho can mean density. *ACTION* NS: intents for lowercase rho are partial-pressure and density. *ACTION* lowercase sigma has Intents of wavenumber and conductivity. GW: Starting in line 112 of the chemistry GW list, You have a series of amino acids and their three-letter abbreviations such as Histidine, His. GW: There is a single-letter identifier for amino acids along with a three-letter identifier for the acids. GW: You may have a string of amino acids in a protein and the screen reader could read the three-letter abbreviations. In the verbose mode, the screen reader could read the names of the amino acids. *ACTION* We should have a concept name of amino-acid. GW said that it should apply for 20 amino acids; however, there are more than 20 acids in the chemistry CG list starting with row 112. They are: Histidine, His Arginine, Arg Phenylalanine, Phe Alanine, Ala Cysteine, Cys Glycine, Gly Glutamine, Gln Glutamic acid, Glu Aspartic acid, Asp Lysine, Lys Leucine, Leu Methionine, Met Asparagine, Asn Serine, Ser Tyrosine, Tyr Threonine, Thr Isoleucine, Ile Tryptophan, Trp Proline, Pro Valine, Val (asparagine/aspartic acid, asx) (glutamine/glutamic acid, glx) NS: The next group starts with Acetyl, Aryl, and Benzyl (line 156). This is another group that falls under chemical-elements. NS: Just pronounce the letters. NS: What do we do with constants? Do we treat them as letters only? Do we need to have explanations for the constants? PL: It depends upon if you are using terse or verbose speech. NS: Are you going to say F or faraday's constant? GW: In equations, you will usually read only the letters of constants. PL: The first time Avogadro's number appears it may be spoken. After that, its symbol is pronounced. MuS: Something like Avogadro's number is spoken that way the first time if the author explicitly marks it up. It is not up to the AT to figure this out. NS: We are not going to have intents for constants. GW: The reader can get the meaning of abbreviations from the context. Ns: We have gotten through chemistry. NS: We thank Greg Williams for all his help. GW: Just let me know if you need me again. NS: Next week, we will hit units and perhaps consider some of the open issues.
North America has moved to Daylight Savings Time/Summer time. The W3C uses Boston time, so the meetings remain at the same time in North American and are an hour earlier for most of those outside North America. We meet on Thursday at: 10am Pacific, 1pm Eastern,* 6pm Central European Time*. The regulars for this group should have the meeting details in their calendars. For everyone else, the details can be found on the members-only W3C Math WG calendar <https://www.w3.org/events/meetings/d6f2b73d-34fc-4276-b164-bdc62a675dcc/20230713T130000/>. Agenda 1. Announcements/Updates/Progress reports 2. Chemistry discussion. Greg Williams (co-chair W3C Chemistry Community Group) will join the call for part 4 of the conversation For reference, here is the link to the Chemistry CG list <https://docs.google.com/spreadsheets/d/1h-8k_bwQ1bO7gusb0O2DfcEs0DZUAo6QVGYZuVjWVB8/edit#gid=0> .
Attendees: - Neil Soiffer - Louis Maher - Dennis Müller - David Farmer - David Carlisle - Bruce Miller - Paul Libbrecht - Bert Bos - Deyan Ginev <https://sandbox.cryptpad.info/code/inner.html?ver=5.7.0-0#cp-md-0-regrets> Regrets <https://sandbox.cryptpad.info/code/inner.html?ver=5.7.0-0#cp-md-0-agenda> Agenda <https://sandbox.cryptpad.info/code/inner.html?ver=5.7.0-0#cp-md-0-1-announcements-updates-progress-reports>1. Announcements/Updates/Progress reports NS: Showed a new international integral sign (looks like a big slash, "/") and asked how to make it in MathML. DC had some suggestions, but they were not completely successful. NS: Daylight savings time starts on Sunday March 10 in the U.S. The intent meeting times in Europe would be one hour earlier. NS: This year, the W3C TPAC meeting will be in Anaheim California from September 23 through September 27. We need to decide if we want to have some kind of meeting. NS: Who will go to Anaheim for the TPAC? BB will go, and NS might go. NS will bring this up at later intent meetings. BB: There will be a party celebrating the 30th anniversary of the W3C. <https://sandbox.cryptpad.info/code/inner.html?ver=5.7.0-0#cp-md-0-2-discussion-updates-on-some-open-issues->2. Discussion/updates on some open issues: Our Core Concept List is at " https://w3c.github.io/mathml-docs/intent-core-concepts/". <https://sandbox.cryptpad.info/code/inner.html?ver=5.7.0-0#cp-md-0--a-href-https-github-com-w3c-mathml-issues-486-intent-for-quot-by-quot-as-in-3-4-matrix-486-a-can-this-be-closed->Intent for "by" (as in 3×4 matrix (486) <https://github.com/w3c/mathml/issues/486> -- can this be closed? *ACTION* NS will enter a concept named "dimension" for "by" in the core concept list. It will be spoken as "by". NS: Can we close this? *RESOLUTION:* DF: If we have a concept row for dimension and the speech template says by, then we certainly can close this issue. PL: Are we specifying which speech template is terse, and which speech template is verbose? Are we specifying a default speech template? NS: Power is a concept with multiple speech templates. NS: Derivative is a concept whose speech template has the verbose label. DG: Should we have both "terse" and "verbose" speech templates for each concept? He thinks not because this would enlarge the size of the concept list with two extra parameters (terse and verbose) for each concept. therefore, not need to do that because the AT can tell the length of a speech template and can therefore decide which template is terse and which is verbose. NS: Where appropriate, we can just list two options, one short and one long. NS: Its cleaner to not have the "terse" and "verbose" labels. PL: Do we want comments for the concepts? NS: We need to consider what comments we should have for the human reader. <https://sandbox.cryptpad.info/code/inner.html?ver=5.7.0-0#cp-md-0--a-href-https-github-com-w3c-mathml-issues-483-ellipsis-483-a-can-this-be-closed->Ellipsis (483) <https://github.com/w3c/mathml/issues/483> -- can this be closed? NS: We have diverse kinds of ellipses: vertical and other directions. NS: We agreed on the concept name "ellipsis", and we have concept names for other types of ellipsis. **RESOLUTION: Close issue 483. <https://sandbox.cryptpad.info/code/inner.html?ver=5.7.0-0#cp-md-0--a-href-https-github-com-w3c-mathml-issues-484-mixed-fractions-in-core-484-a-can-this-be-closed->mixed-fractions in core (484) <https://github.com/w3c/mathml/issues/484> -- can this be closed? NS: We have fraction and mixed-fraction in the concept list. *RESOLUTION* close issue 484. <https://sandbox.cryptpad.info/code/inner.html?ver=5.7.0-0#cp-md-0--a-href-https-github-com-w3c-mathml-issues-488-permutations-488-a->Permutations (#488) <https://github.com/w3c/mathml/issues/488> NS: The idea is that there were Different notations for permutations, one of which Was multiple cycles, and another one was a 2-row notation. The 2-row notation maps one row into the other row. NS: We can introduce some sort of table property which is our way of making it easier to markup saying it's a permutation. NS: We could name the table property "permutation". *RESOLUTION* DC: Permutation is a concept. put in a table property that says read by column. Close issue 488. NS: We do not have to concern ourselves now about saying the direction of reading, downwards or upwards, until we encounter this issue. The default reading directions for tables are left to right and top to bottom. <https://sandbox.cryptpad.info/code/inner.html?ver=5.7.0-0#cp-md-0--a-href-https-github-com-w3c-mathml-issues-489-update-minsize-maxsize-percentage-values-to-match-mathml-core-489-a->Update minsize/maxsize percentage values to match MathML Core (#489) <https://github.com/w3c/mathml/issues/489> NS: Core has a specification on how to stretch something and what minsize and maxsize mean. The full spec has a different description of these things. NS: What is our solution here, to change core or to change spec. DG: Does not want the core spec and the full spec to disagree. DC Change our spec to match core because core is going to CR. Don't break core now. NS: So, the issue BM has is that LaTeX has a /big open and /big close parenthesis, and he wants MathML to have them as well. BM: What is in core does not make any sense. BM: If we change core to be consistent with the full spec, then the Chrome code would have to be changed. BM and DG: Safari and Firefox work with the old spec. BM: If you specify big in terms of "em", then you have to backtrack through your tree to see what "em" is. DC: We should ask Fred and Brian how hard it would be to change the chrome code. Let us not break anything. DC: The core spec has not gone to CR yet. NS: The point of CR is to get users' experiences. NS: Is there a matching issue in core about this? DG: Yes. There is a link to the core spec in issue 489. NS: Is our resolution to take this back to core? *RESOLUTION* NS: The resolution is that this needs to be pushed back to Chrome or to the core (issue 889). NS: Push back to core. The core implementation causes problems. DC: See how MathJAX interprets it. *ACTION* DG will check MathJAX for what it does with MathML for minsize and maxsize and what it does with /big on the regular base line and superscripts. *ACTION* BM: Push this back to the core spec and layout the arguments there. He will suggest changes in core and what should be repaired. NS: We will do chemistry next week. *ACTION* NS: What does the AI in Zoom do. LM will look into it. NS: LM will be gone next Thursday, March 14. If LM is provided with a meeting recording and a transcript, LM will generate minutes, else, someone else should scribe on March 14.
Just like Safari 15.4 and Safari 16.4, this March’s release of Safari 17.4 is a significant one for web developers. We’re proud to announce another 46 features and 146 bug fixes.
You can experience Safari 17.4 on iOS 17.4, iPadOS 17.4, macOS Sonoma 14.4, macOS Ventura, macOS Monterey, and in visionOS 1.1.
It’s always exciting to ship new features that you can use while building websites and web apps for your users. WebKit engineers also work on many important projects beyond implementing new web platform features. Recently, much effort has gone into multiple infrastructure projects that strengthen WebKit for the long-term.
We completed the final installment of our multi-year long rewrite of our inline layout engine (more on that later). We built two new iOS frameworks with hundreds of new APIs to support functionality used by web browsers, including multiprocess, JIT, and advanced keyboard & touch event access — and we are pivoting WebKit to use these new frameworks. We’re working on several other large projects that deepen security and privacy. And we’ve been hard at work to make Safari even faster. For many years, Safari has held the crown of the world’s fastest browser. It’s important to us to keep pushing the boundaries of speed, as the websites you build continue to get more complex. Hundreds of recent changes result in Safari 17.4 showing a significant performance bump.
Safari 17.4 brings two improvements to web apps on Mac.
First, Safari adds support for the
shortcuts manifest member on macOS Sonoma. This gives
you a mechanism in the manifest
file for defining custom menu commands that will appear in the
File menu and the Dock context menu.
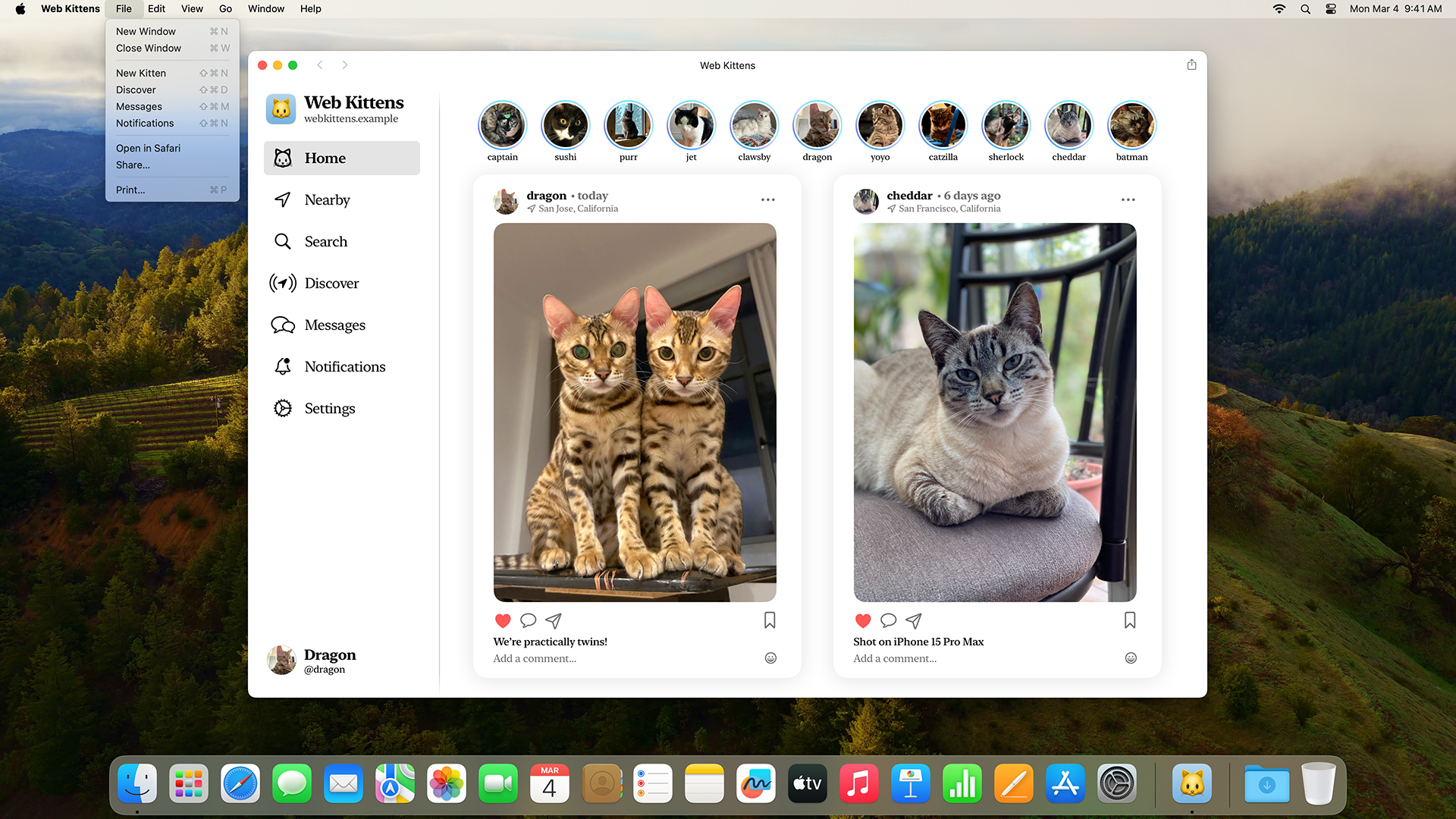 On Mac, our Web Kittens web
app includes four shortcuts. You can see them listed in the File
menu: New Kitten, Discover, Messages, and Notifications. They each
open a menu item by going to the appropriate URL.
On Mac, our Web Kittens web
app includes four shortcuts. You can see them listed in the File
menu: New Kitten, Discover, Messages, and Notifications. They each
open a menu item by going to the appropriate URL.
A web app shortcut consists of a name, (the words
you’d like to appear in the menu), and a url. When a
user activates the command, it opens the specified URL inside the
web app.
"shortcuts": [
{
"name": "New Kitten",
"url": "/new-kitten"
},
{
"name": "Discover",
"url": "/discover"
}
]
Users can set up custom keyboard shortcuts for app menu commands in System Settings > Keyboard > Keyboard Shortcuts > App Shortcuts. By default, macOS does not assign web app shortcuts any keyboard commands.
Second, Safari 17.4 now supports the
categories manifest member on macOS Sonoma. This
member
provides you with a mechanism for telling the browser which
categories
your web app belongs in. On Mac, when a user creates a Launchpad
folder that contains web apps, the folder is automatically named
accordingly.
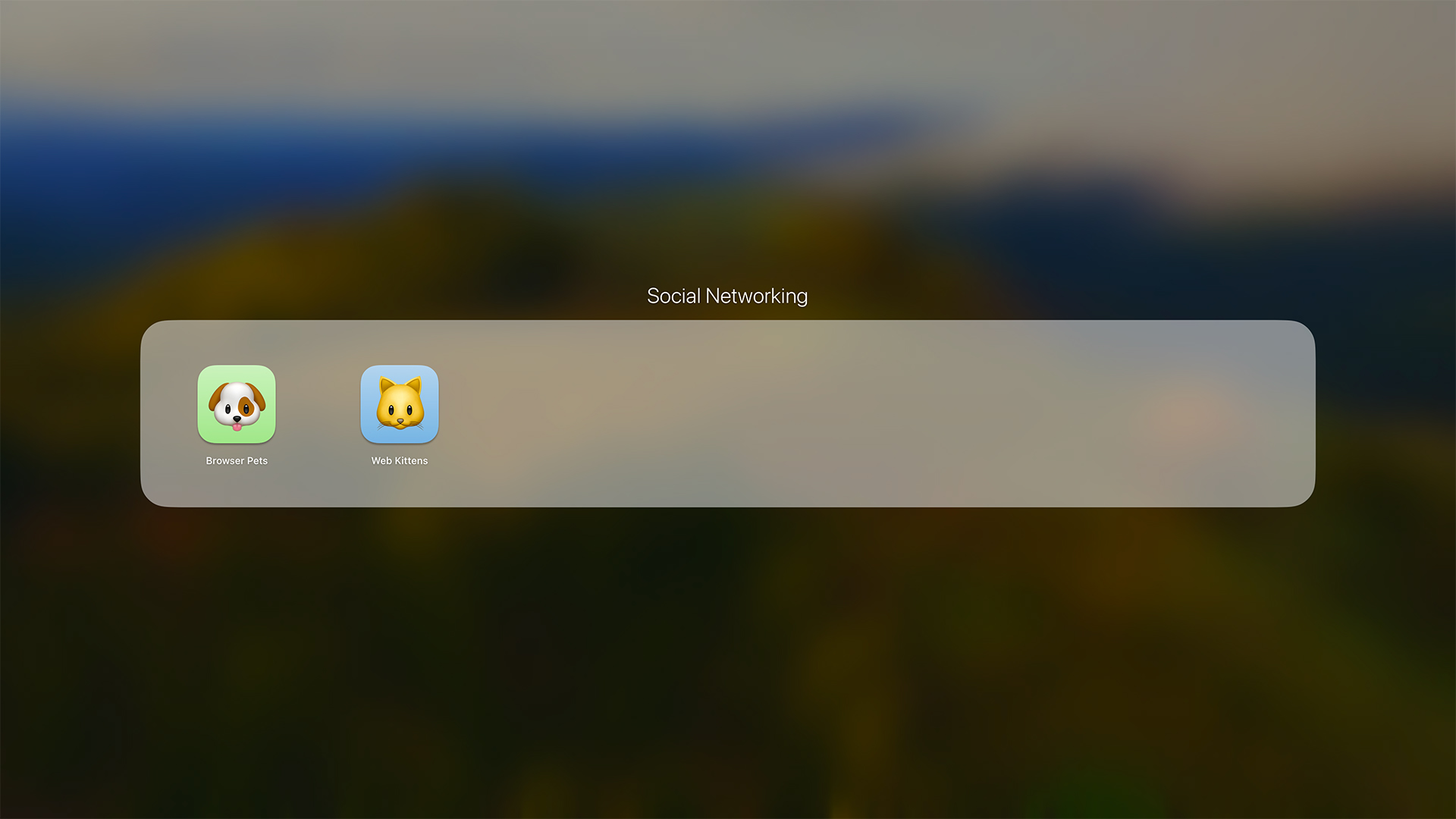
The switch is a popular interface for many use cases, but until
now, there was no easy way to put a switch on the web. Instead
developers might use a checkbox input field, remove the visual look
of the checkbox with appearance: none, and write
custom styles to create something that looks like a switch.
Now, with WebKit for Safari 17.4, HTML supports a native switch.
If you code <input type="checkbox" switch>, the
browser will simply create a switch for you, and map it to
role=switch and related ARIA features.
Try this demo in Safari 17.4. Currently, in other browsers you will see three checkboxes.
Extending the current HTML checkbox provides several benefits
and honors the W3C’s HTML Design
Principles. First, this design degrades
gracefully — which means you can use <input
type="checkbox" switch> today. Browser that have support
will show a switch, while browsers that do not have support will
show a checkbox. No user will get a broken experience, and you
don’t have to wait until all of your users have a browser with
support in order to utilize this on your website or web app. This
design also
does not reinvent the wheel. It matches the way form controls
have always worked on the web, and feels just like the code you’re
used to. It’s an incremental
evolution of the web. And as a simple solution, it
avoids needless complexity.
The accent-color property can be used to change the
background color of the switch in the “on” state. And, exactly like
other form controls, you can use appearance: none to
remove the system default styling and apply your own, perhaps while
leveraging :before and :after.
In the future, there will likely be multiple pseudo-elements to
make it even easier to style the switch with your custom styles.
You can try out ::track and ::thumb in
Safari Technology Preview today and let us know what you think of
this approach. See how they work in this demo, after
enabling the “::thumb and ::track pseudo-elements”
feature flag. (These pseudos are waiting to ship until there is
a more comprehensive plan for styling form controls proposed,
discussed and resolved on at the CSS Working Group.)
From the beginning, the web has always been interactive. Even before any method of custom styling was available, form controls and input fields provided the means for users to communicate back to the website and to each other. The web was also originally designed in an era when the Latin alphabet (used by many languages, including English) was the presumed default, with its horizontal top-to-bottom writing mode.
For thirty years, form controls have presumed a horizontal writing mode. Typesetting in a vertical writing mode for languages like Chinese, Japanese, Korean, and Mongolian did not include vertical form controls. Now that’s changed. Starting in Safari 17.4, vertical form controls are supported. This includes meter, range, progress and other form controls that could make for great UI in any language when laid out in a vertical format.
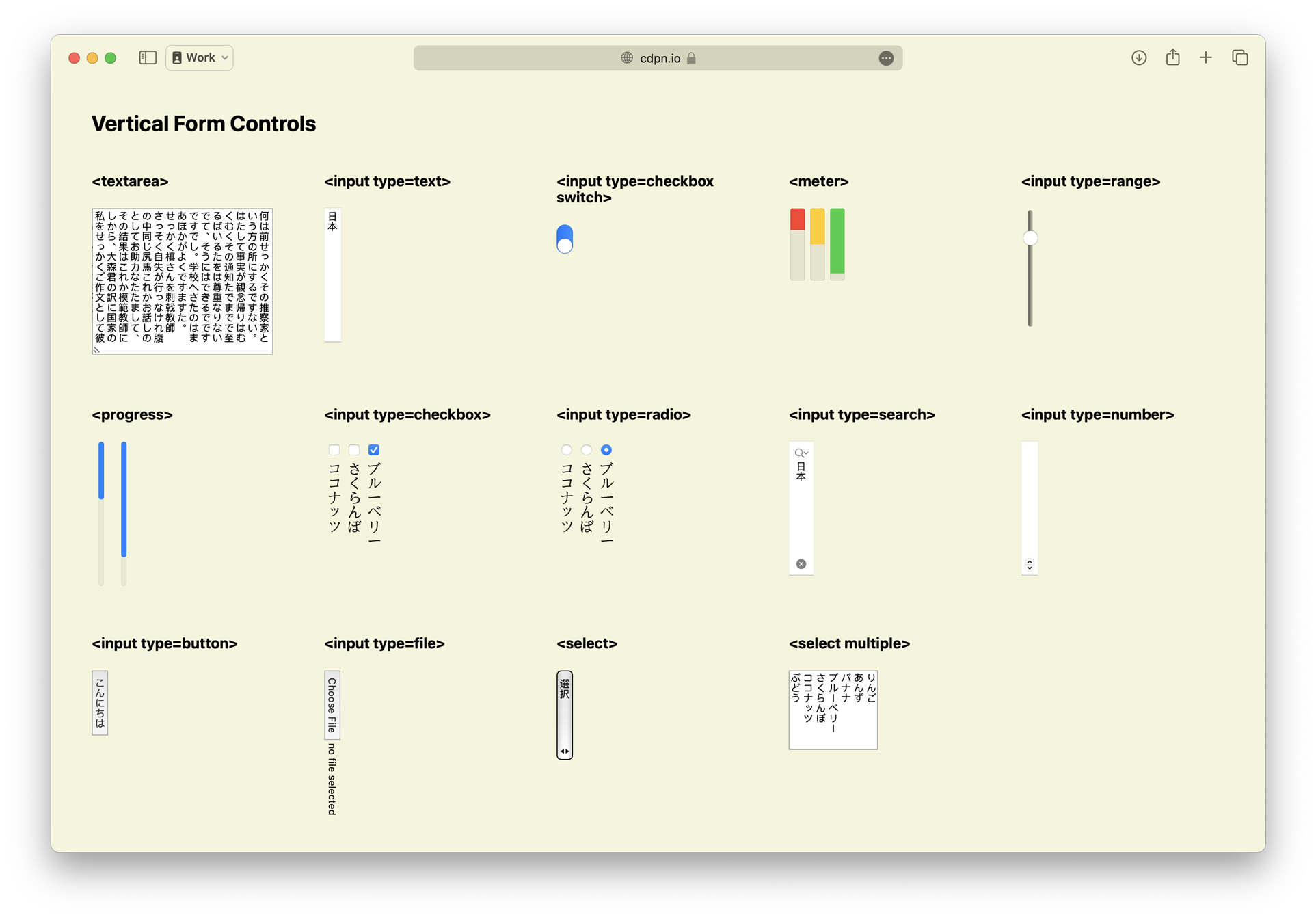 Try
this
demo of vertical form controls in a browser that
has support.
Try
this
demo of vertical form controls in a browser that
has support.
You can use an
<hr> element (a horizontal rule) inside a
<select> element to draw a separator line. WebKit
shipped support in Safari
17.0 on macOS. Now, Safari 17.4 on iOS 17.4, iPadOS 17.4, and
in visionOS 1.1 also has support.
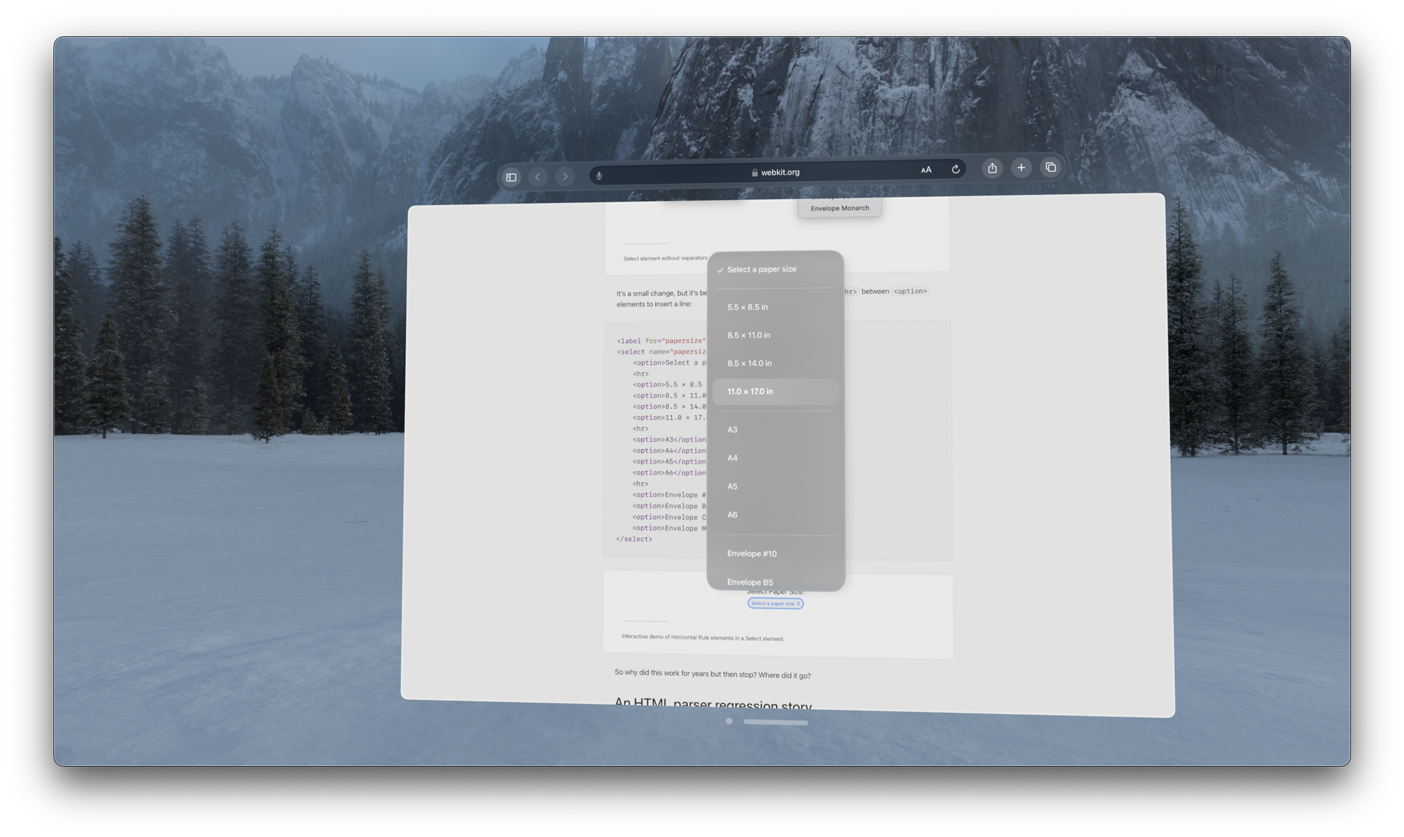
Try a demo and read the story of how hr in
select was supported years ago, went away, and is now
restored.
WebKit for Safari 17.4 also adds support for the
showPicker() method for <input
type="date"> on macOS.
One of the infrastructure projects that’s been underway in WebKit during the last several years is the complete rewrite of our inline layout engine. Safari 17.4 marks the completion of this project and the retirement of the twenty-one year-old legacy line layout engine.
Inline layout is integral to displaying content on the web. It determines the size and layout — wrapping, justification, spacing, and baseline alignment — of all text and other inline-level content. As developers, we often focus on the invisible block boxes on a web page and write CSS to layout those boxes using Flow, Tables, Flexbox or Grid. The content inside those boxes is placed using complex inline layout algorithms that developers often don’t need to think much about.
We’ve been shipping our new inline layout engine incrementally for many years. As more and more of the new engine was complete, more and more of the content on web pages was positioned by the new engine. This means users have been benefiting from WebKit’s new inline layout engine for a while. The legacy system was only triggered if there were something that hadn’t been yet implemented in the new engine. The last major step needed was the reimplementation of Ruby — and now it’s also a proper inline layout feature, fixing past inconsistencies.
Projects like these can be disruptive. Often browser teams will choose to not ship any new features while a multi-year rewrite project is in progress. WebKit instead chose to keep shipping new features, often implementing them twice — once in the legacy line layout engine, and again in the new inline layout engine. Now that this work is done, we no longer have to implement anything twice. This work also let us go through a large number of bugs reported on bugs.webkit.org, confirm they are no longer a problem, and close them as fixed.
We’re excited for WebKit’s future with this new engine. This investment results in increased interoperability by aligning to the latest web standards, fewer inline layout bugs, better performance, improvements to stability, and the ability to implement new features far more easily. The completion of inline layout also marks the beginning of rewriting the layout engine for other formatting contexts, starting with Flexbox.
When Flexbox shipped, it brought a powerful new tool to the web
—
box alignment. The
align-content property made it possible to easily
vertically center content inside a box! Or you could use it to
align content to the bottom to the box, to align baselines of text,
and more. When CSS Grid shipped, box alignment became possible in a
second layout mode. Since 2017, you’ve been able to align the
direct children of both Flexbox and Grid containers.
Now, we are proud to be the first browser shipping support for
align-content inside two more formatting contexts —
block layout and table layout. This means if all you want to do is
align a box’s content in the block direction, you don’t need to
involve Flexbox or Grid. Plus, you can now mix alignment with
floats, and you can use it inside table cells.
div { align-content: center; } /* one-line vertical centering */
In addition, we updated the handling of
align-content and justify-content on
scroll containers in WebKit for Safari 17.4. Now, for example, you
can use CSS to set the initial scroll position to the end rather
than the start of the content.
div { overflow: auto; align-content: unsafe end; } /* end-aligned scroller */
Be sure to test alignment on scroll containers across browsers, as many are still in the process of updating to the specified behavior. Those that have not yet updated may clip content.
Websites today can be complex, with large teams working across
multiple projects, relying on pattern libraries or frameworks to
keep everything organized and consistent. It can become tough for
large teams to handle how their CSS cascades. Tools like Cascade
Layers and :has() have changed the game, allowing
developers to apply styles more masterfully. Yet, developers often
want a way to scope styles to the individual component they’re
working on, without worrying about the big picture or preventing
unintended consequences.
CSS Scoping was created to provide several more powerful options for organizing and structuring CSS. (Note, there have been many debates over many years on how style scoping might work. Search results for “CSS scoping” often yield old, unimplemented or completely different ideas.)
WebKit for Safari 17.4 adds supports the @scope
rule and expands the capabilities of the :scope
pseudo-class. Scoping changes how the cascade works in some
surprising ways, so do be sure to read about its impact before
deploying widely.
If your project is making heavy use of components, constructed independently and loaded in random order, scoping can help you by ensuring certain styles only apply to the contents of a specific element, and never to anything else on the page.
By default, all CSS on a project applies universally. It has a
“scoping root” of <html>. And the :root
pseudo-element refers to the root element in the DOM — the
html element. CSS Scoping lets you use
<style> @scope to reset the scoping root to a
certain element, to the parent of the <style>
element.
<article id="my-component">
<style>
@scope {
h1 { font-size: 4rem; }
}
</style>
<h1>This is 4rem text.</h1>
</article>
<h1>This will not be styled by the CSS above.</h1>
In this case, because <article> is the direct
parent of <style> @scope, all of the styles
defined inside @scope will only impact
article and the content inside article.
Nothing outside article is affected.
But that’s not all CSS Scoping can do. Let’s imagine we want to
apply styles to a sidebar, but we don’t want those styles to apply
to everything in the sidebar. We can use @scope to
create a donut of sorts — with a hole in the middle where the
styles don’t apply.
@scope (aside) to (section) {
h2 {
font-size: 3rem;
}
}
<aside id="my-sidebar">
<h2>This is 3rem text.</h2>
<section>
<h2>This is not styled by the CSS above.</h2>
</section>
</aside>
By defining a scoping root with a scope-start selector
(aside) and a scoping limit with a scope-end selector
(section), we can effectively stop the cascading of
the styles.
Also, anytime you use CSS Scoping, it radically changes what happens when there’s a tie in specificity.
Since the creation of CSS, when multiple selectors have equal specificity, the one that appears last in the CSS cascade is the one that gets applied. For example, if this is your CSS:
.blue h1 { color: blue; }
.yellow h1 { color: yellow; }
Then this is your result.
<section class="blue">
<section class="yellow">
<h1>This headline is yellow.</h1>
</section>
</section>
<section class="yellow">
<section class="blue">
<h1>This headline is yellow.</h1>
</section>
</section>
The headline is always yellow, because .yellow
comes later in the CSS file. The order in the HTML does not
matter.
But with scoping, the selector that applies to an element that’s closer in the DOM to the scoping root is the one that will apply when their specificities are tied.
Let’s use @scope instead of descendant
selectors:
@scope (.blue) {
h1 { color: blue; }
}
@scope (.yellow) {
h1 { color: yellow; }
}
Now, the headline color is determined by the DOM order in HTML, not the cascade order in CSS:
<section class="blue">
<section class="yellow">
<h1>This headline is yellow.</h1>
</section>
</section>
<section class="yellow">
<section class="blue">
<h1>This headline is blue!</h1>
</section>
</section>
The headline is yellow when .yellow is the closer
ancestor, and it’s blue when .blue is the closer
ancestor.
This is a fundamental change to how CSS works, so don’t get caught off guard. Use CSS Scoping with a lot of thought and care.
Note that a selector like .blue h1 { } has higher
specificity than a selector like @scope (.yellow){ h1 {
}}. The specificity of the scoping root’s selector is not
added to the specificity of the selectors inside the
@scope rule, unlike Nesting. And .blue h1
is higher specificity than h1.
WebKit for Safari 17.4 also expands the purpose of the :scope
pseudo-class. When used inside a @scope block,
:scope matches the block’s defined scope root. This
provides a way to apply styles to the root of the scope from inside
the @scope block itself. In the following example,
:scope applies a border to the article
element.
<article id="my-component">
<style>
@scope {
:scope { border: 1px solid black; }
h1 { font-size: 4rem; }
}
</style>
<h1>This is 4rem text.</h1>
</article>
For years, the
white-space property in CSS has provided a mechanism for
doing two things at once: 1) defining whether and how white space
is collapsed, and 2) defining whether and how lines wrap. The CSS
Working Group has since noted that this was likely a mistake, to handle
two different qualities in one property. With the introduction of
text-wrap, the CSSWG has rethought how the long and
shorthand versions of these properties combine into an architecture
that makes more sense and gives us needed flexibility.
Now the white-space property is a shorthand for
two
new
longhand properties:
white-space-collapse and text-wrap-mode,
both added in WebKit for Safari 17.4. These longhands let you
change the collapsing and wrapping modes independently, each
without affecting the other.
The white-space-collapse property controls how
white space is collapsed. By default, it’s set to
collapse, causing strings of multiple spaces to become
a single space. You can change the value instead to
preserve in order to keep all the spaces, or use other
the values: preserve-breaks,
preserve-spaces, or break-spaces. These
values all behave as they have for years with the
white-space property.
The new text-wrap-mode property provides a
mechanism for setting whether or not text should wrap. The
wrap value turns it on, and the nowrap
value turns it off.
This work sets the stage for the text-wrap
shorthand and it’s longhands text-wrap-style and
text-wrap-mode, some of which you can currently test
in Safari
Technology Preview.
WebKit for Safari 17.4 adds support for percentages in
letter-spacing and
word-spacing. This lets you define spacing as a
percentage of the element’s font-size — and keeps
tracking the font-size even when it grows or shrinks
on descendant elements.
WebKit for Safari 17.4 adds support for the
::spelling-error and
::grammar-error pseudo-elements. These make it possible
to create your own custom styling for text that is marked by the
browser as misspelled or grammatically incorrect.
The vast majority of content on the web is communicated through
HTML, but CSS does have the ability to insert content into the
page. Until now, sometimes this kind of content could not be made
accessible. Now in WebKit for Safari 17.4, you can provide
alternative text with accessible content
fallback — content: "foo" / "alt-text";
For example, perhaps we want to prefix certain links with the little ⓘ icon to let users know this item leads to more detailed information. That symbol might be read by screenreader as “Circled Latin Small Letter I” or “Information source combining enclosing circle”, neither of which do a good job communicating the intended purpose. Perhaps a better experience would be to simply hear “Info:”.
.info::before {
content: "ⓘ" / "Info:";
}
Previously, the -webkit-alt property served this
function. It has been deprecated in favor of the new content alt
text syntax. The new syntax is also more expressive as it allows
for cascading, and allows you to chain multiple strings and
attr() as alternative text.
When CSS Transitions were created, they allowed authors to
create a gradual timed transition between old and new values by
interpolation. Sometimes, however, interpolation is not possible.
For example, there’s no meaningful intermediary value between
float: left and float: right, so,
transitions ignored these properties. They simply jumped from the
first state to the second immediately, without any ability to
define when the jump should happen.
Yet, web developers have wanted a way to at least be able to define when the transition should happen for discrete properties. So the CSS Working Group figured out a way to make that possible. Now, you can tell the browser that you want an element to be capable of transitioning discrete property values, which lets you control their transition timing using the easing functions.
WebKit for Safari 17.4 adds support for the
transition-behavior property. The
transition-behavior: allow-discrete rule lets you
enable transitions between discrete property values, so that you
can control their timing via
transition.
li {
list-style: disc;
color: blue;
transition: all 2s, list-style 0.5s step-end;
transition-behavior: allow-discrete;
}
li:hover {
list-style: square;
color: red;
}
transition-behavior off to see the difference.
The :has()
pseudo-class provides tremendous value. We keep making it more and
more powerful by adding support for additional pseudo-classes
within :has(). WebKit for Safari 17.4 adds support for
:has(:any-link),
:has(:link),
and :has(:-webkit-any-link), making it possible to
select an element depending on whether or not it contains a
link.
WebKit for Safari 17.4 adds support for CSS custom
properties to the
::backdrop pseudo-element, allowing variables to be
applied to the backdrop behind
dialog elements and other top layer items.
WebKit for Safari 17.4 also adds offset-position
support for circle() and ellipse().
And WebKit for Safari 17.4 makes -apple- prefixed
pseudo-elements no longer valid.
This release of Safari adds support for an assortment of small Web API additions that give you extra tools in your developer toolkit.
With support for the
element.checkVisibility() method, you can
determine the visibility of an element across a variety of
conditions including how CSS properties such as
display, visibility, and
opacity are applied.
WebKit for Safari 17.4 also extends its Declarative
Shadow Root support. The
Element.prototype.setHTMLUnsafe(),
ShadowRoot.prototype.setHTMLUnsafe(), and
Document.parseHTMLUnsafe() methods, as well as the
ShadowRoot clonable property are now available.
The setHTMLUnsafe() methods work similar to setting an
element’s innerHTML property, enabling unsanitized DOM
tree mutation but with additional support for declarative shadow
roots. The parseHTMLUnsafe() method similarly parses
unsanitized HTML with declarative shadow root support and returns a
document. And the clonable read-only boolean property
allows you to detect if a ShadowRoot is clonable.
WebKit for Safari 17.4 adds support for the CustomStateSet
interface for custom element state management. This interface
includes methods to add(), delete(), or
detect if the element has() a given state, and more.
Importantly, these states added to a custom element can be styled
using the :state() pseudo-class by users of the custom
element.
The
DOMMatrixReadOnly interface now supports the
scaleNonUniform() method that creates a new DOMMatrix
scaling on X, Y, and Z axes. The X axis scaling factor must be
specified, but the Y and Z axes default to 1. The
scaling is centered at the given origin that defaults to (0,
0, 0).
Lastly, WebKit for Safari 17.4 adds support for
AbortSignal.any() giving you a convenient way to
combine abort signals such as user input (e.g. a user clicks a
cancel button) and a timeout to send an abort signal to an async
operation.
New JavaScript features in Safari 17.4 add new expressiveness
and convenience with promise resolvers, improved
internationalization formatting, ArrayBuffer ownership
management, and Array grouping features.
WebKit for Safari 17.4 adds support for the
Promise.withResolvers static method. It allows
developers the convenience of creating a promise and configure the
resolution and rejection handlers after it has been created. The
method returns the promise along with the resolution and rejection
functions.
const { promise, resolve, reject } = Promise.withResolvers();
The TimeZoneOffset format is now available for
Intl.DateTimeFormat. It allows you to specify the
difference of the local time to UTC time in positive or negative
hours and minutes depending on whether the local time is ahead or
behind.
new Intl.DateTimeFormat("en-US", {
dateStyle: 'long',
timeStyle: 'long',
timeZone: '-0800'
}).format(new Date())
Additionally, Number.prototype.toLocaleString and
Intl.NumberFormat have been updated so the string
representation correctly aligns with recent specification
changes.
There’s also new expressive API for managing the concept of
ownership for ArrayBuffers.
ArrayBuffer.prototype.transfer creates a new
ArrayBuffer with the same contents and properties as the target
ArrayBuffer (such as being resizable) and detaches it from the
original ArrayBuffer. You can use
ArrayBuffer.prototype.transferToFixedLength() to
guarantee a non-resizable ArrayBuffer with the same content as the
buffer. ArrayBuffer.prototype.detached will tell you
if the buffer has been transferred and is detached.
WebKit for Safari 17.4 also adds the Array grouping feature that
includes Object.groupBy and Map.groupBy
methods. These methods give you powerfully simple tools for
grouping datasets.
const todos = [
{ task: "Water the flowers", context: "home", estimate: "5 minutes" },
{ task: "Get the TPS report done", context: "work", estimate: "45 minutes" },
{ task: "Find new insurance", context: "home", estimate: "180 minutes" },
{ task: "Fix a website bug", context: "work", estimate: "25 minutes" },
{ task: "Answer emails", context: "anywhere", estimate: "10 minutes" }
];
let contextual_tasks = Object.groupBy(todos, ({ context }) => context);
console.log(contextual_tasks);
let tasks_by_time = Map.groupBy(todos, ({ estimate }) => {
return parseInt(estimate.split(' ')[0]) < 15 ? "short" : "long";
});
console.log(tasks_by_time);
WebKit for Safari 17.4 adds support for several audio and video codecs.
First, WebKit for Safari 17.4 on iOS, iPadOS and in visionOS adds support for WebM. While the WebM container (with both the VP8 and VP9 video codecs) has been fully supported on macOS since Safari 14.1, support on iOS and iPadOS was limited to VP8 in WebRTC. Now, WebM is fully supported everywhere.
The Vorbis audio codec is also now supported in WebKit on iOS 17.4, iPadOS 17.4 and in visionOS 1.1.
And WebKit for Safari 17.4 expands what WebCodecs can do with the addition of support for the HEVC codec.
When support for video embedding arrived in HTML5 with the
<video> and <source>
elements, the web standard specified that the first file that’s
recognized by the browser should be chosen and played. This put the
burden on the developer to make sure the best files were listed
before lesser-quality files.
<video>
<source src="movie.webm">
<source src="movie.av1">
<source src="movie.mov">
</video>
This made sense in a simpler time, when there were just a few codecs available. Now, there are many codecs with different qualities. It’s not always possible for developers to know which file is the best one for a user to stream. And it can be impossible to put them in one specific order that’s best for all users.
A browser might easily be capable of playing several of the files offered, but one of those files could be compressed with a codec that the user’s device can decode using hardware, while the rest might only be decoded by software alone.
It’s definitely a better user experience to use hardware decoding. Doing so significantly impacts power usage and makes a battery last longer. So now, in WebKit for Safari 17.4, the best file for the user is chosen, instead of defaulting to the first file that has support. Video codecs with hardware decoding support on various Apple devices include VP9, h.264, HEVC and AV1.
WebKit for Safari 17.4 adds support for HTML
character entities to WebVTT
(Web Video Text Tracks Format), the technology used to add
subtitles and captions to video files on the web. HTML entities are
a way to write special characters without having the browser
mistakenly think they are part of the HTML code. For example,
· represents the “·” character.
WebKit for Safari 17.4 adds support whiteBalanceMode
to MediaStream. In photography, adjusting white balance is a
technique for compensating for the fact that “white” is a different
color under different lighting conditions. Sunlight is very blue,
while indoor lights tend to be quite orange. Our brains
automatically adjust, so as humans, we rarely notice. But cameras
need technology to help them adjust color temperature so that the
resulting photo or video has the kind of coloring people expect.
Now modes for white balance are available for the
MediaStream Image Capture API on the web.
WebKit for Safari 17.4 adds support for
kernelUnitLengthX and kernelUnitLengthY
to
SVGFESpecularLightingElement.
WebKit for Safari 17.4 adds support for four new WebGL
extensions: EXT_clip_control,
EXT_depth_clamp,
EXT_polygon_offset_clamp, and
WEBGL_polygon_mode.
WebKit for Safari 17.4 enables extended constant expressions to support more advanced WebAssembly linking.
Web Inspector for Safari 17.4 has two new features. First, when a page attempts to load a font URL blocked by Lockdown Mode, a message is logged to the Console.
Second, Web Inspector now groups load errors for source maps. Source map files are used for converting a combined or minified file back into its original state. Grouping load errors helps reduce noise while debugging. You can disable this behavior in Web Inspector Settings under Experimental settings.
Safari 17.4 itself includes three changes to the UI and user experience. First, you can now configure the Favorites Bar to show your bookmarks with only their icons. Edit the name of the bookmark in the favorites bar, and remove the name. The icon will remain.
Second, Safari 17.4 now supports webpage translation inside
<iframe> elements.
And third, Safari 17.4 adds support for Apple Cash virtual card numbers and showing the user their Apple Cash balance when using AutoFill.
Safari 17.4 includes a change to web extensions that allows extensions to open Private Browsing windows even when they don’t have access to Private Browsing.
WebKit for Safari 17.4 adds support for WebAuthn’s
PublicKeyCredentials.getClientCapabilities() function.
Use it to find out which WebAuthn features are supported. It
returns a Promise of a record<DOMString,
boolean> containing capabilities and their values.
In addition to all the new features, WebKit for Safari 17.4 includes work polishing existing features.
<summary> element
role. (13661104)combobox role. (112488137)innerHTML and
innerText changes to labels did not update their
corresponding input element’s accessibility title. (113872525)<details> and
<summary> elements not included in VoiceOver
form controls menu or list. (117308226)aria-activedescendant changes. (117747058)getComputedStyle() for invalid
pseudo-elements. (98504661)querySelector() to not throw an exception
for -webkit- prefixed pseudo-elements. (99299129):user-invalid triggering while typing a
date. (110687369)text-transform: full-size-kana to
align with Unicode 15. (111508663)contain: inline-size breaking
grid-template-rows: auto. (113915953)svh and dvh units being
unexpectedly equal when the Safari tab bar is not visible.
(115085360)mixed-blend-mode to blend correctly against
the root background. (115688282)backdrop-filter with many interoperability
improvements. (115703346)oklab and oklch lightness value
clamping. (116195533)::selection pseudo-element color. (117796745)-webkit-
prefixed pseudo-elements. (118081134)::backdrop to be allowed after
::slotted(). (119015204):checked and
:indeterminate to match at the same time.
(119075969)min-height
not sizing row correctly. (119736473)rect() and
xywh() as the equivalent inset().
(119739406):has(+ :not(.class))
pseudo-class selector. (119819247)content computed value serialization.
(120061551)getComputedStyle()
and KeyframeEffect.prototype.pseudoElement so they
require them starting with :: (or : for 4
legacy pseudo-elements). (120170550)linear() easing. (120290721):host selector.
(120428386):not(:has(:not(foo))) getting misclassified
as scope breaking. (120492012)::slotted pseudo-element in a
container query getting resolved against the wrong scope.
(122224135)-apple- prefixed pseudo-elements no longer
valid. (120268884)<select> not refreshing the dropdown
after an <option> is removed on iPad.
(88292987)text-indent to affect the selected file(s)
label for file inputs. (105223868)dir=auto to work for hidden,
password, submit, reset, and
button input types, made dirname work for
password and submit input types, and
removed dirname support from number input
types. (113127508)autocomplete with a
webauthn token. (116107937)<option> elements outside of an
<optgroup> getting added to the preceding group.
(117930480)system-ui font family within
<canvas>. (117231545)<progress> to use the page’s preferred
rendering update interval. (118976548)direction attribute
in the list of attributes whose values are matched
case-insensitively with attribute selectors. ( (119432066)Temporal.Now.timeZone() to be updated to
timeZoneId(). (118674314)ondataavailable at every timeslice event.
(115979604)object-fit: fill on
<video> elements. (118020922)video.buffered attribute.
(118550061)id
settings. (118551267)getDisplayMedia frameRate
always at 30 regardless of constraints. (118874132)writing-mode:
vertical-rl or direction: rtl. (102620110)getComputedStyle was incorrect. (117523629)<div> within a
transformed parent <div> with overflow:
hidden. (118901069)offsetHeight and offsetWidth
are 0 for an inline box wrapping a block. (119955792)ch unit value in
vertical-rl and vertical-lr when
text-orientation is not upright. (120293590)overflow: hidden to not prevent CSS Subgrid
from applying. (120848131)align-content and
justify-content on scroll containers causing
overflowing content to become inaccessible. (121366949)<br> element with clear.
(121444267)white-space: nowrap. (121859917)margin-trim behavior for floats to match
specification changes. (115794102)scripting.executeScript(). (107996753)scripting.unregisterContentScripts(). (113171510)vertical-rl, or flexbox reverse mode elements.
(104944522)scrollTo() followed by an animated scroll
ending at the wrong scroll position. (117608836)rx or ry exclusively
via CSS having no effect. (113500023)<iframe> without affecting the size of the
<iframe>. (120178866)currentTime is
changed to 0 not restarting when unpaused. (118826588)wheel and
gesturechange events inside an iframe.
(105243167)Range.getClientRects() and
Range.getBoundingRect() for certain ranges.
(112543805)Request‘s
referrer feature and Response.redirect().
They now always use UTF-8. (115219660)<meta
name="color-scheme"> when their name or
content attribute changes. (115958450)FetchResponse.formData() to parse headers
names as case insensitive. (116742000)scrollIntoView({ block: 'center' }). (117755250)resizeBy and resizeTo
to use int rather than float to align
with specifications. (118872048)Element.prototype.setAttributeNode() to not
treat attribute names case insensitively. (119013600)spellcheck attribute not
toggling spelling markers on input elements. (119269616)getElementsByName() to only return HTML
elements, not SVG, MathML, or other types of elements.
(120275680)button value for a
pointerup event not matching the
pointerdown event. (120429508)document.open. (120893136)captureStream stuttering with WebGL.
((122471664)tan() function to not trigger the color
picker. (118724061){"width":1920,"height":1080,"frameRate":24}.
(61747755)degradationPreference.
(121041723)Safari 17.4 is available on iOS 17.4, iPadOS 17.4, macOS Sonoma 14.4, macOS Ventura, macOS Monterey and in visionOS 1.1.
If you are running macOS Ventura or macOS Monterey, you can update Safari by itself, without updating macOS. On macOS Ventura, go to > System Settings > General > Software Update and click “More info…” under Updates Available.
To get the latest version of Safari on iPhone, iPad, or Apple Vision Pro, go to Settings > General > Software Update, and tap to update.
We love hearing from you. To share your thoughts on Safari 17.4, find us on Mastodon at @jensimmons@front-end.social and @jondavis@mastodon.social. Or send a reply on X to @webkit. You can also follow WebKit on LinkedIn. If you run into any issues, we welcome your feedback on Safari UI, or your WebKit bug report about web technologies or Web Inspector. Filing issues really does make a difference.
Download the latest Safari Technology Preview on macOS to stay at the forefront of the web platform and to use the latest Web Inspector features.
You can also find this information in the Safari 17.4 release notes.
We meet on Thursday at: 10am Pacific, 1pm Eastern, 7pm Central European Tim *e*. The regulars for this group should have the meeting details in their calendars. For everyone else, the details can be found on the members-only W3C Math WG calendar <https://www.w3.org/events/meetings/d6f2b73d-34fc-4276-b164-bdc62a675dcc/20230713T130000/> . Greg Williams said he can't make the meeting this week, so we will postpone part 4 of the chemistry discussion. Agenda 1. Announcements/Updates/Progress reports 2. Discussion/updates on some open issues: - Intent for "by" (as in 3×4 matrix) <https://github.com/w3c/mathml/issues/486> (486) -- can this be closed? - Ellipsis <https://github.com/w3c/mathml/issues/483> (483) -- can this be closed? - mixed-fractions in core <https://github.com/w3c/mathml/issues/484> (484) -- can this be closed? - Permutations <https://github.com/w3c/mathml/issues/488>(#488) - Update minsize/maxsize percentage values to match MathML Core <https://github.com/w3c/mathml/issues/489> (#489) - Intent for large operators <https://github.com/w3c/mathml/issues/482> (482) 3. Biology & Earth Science lists (from Deyan) (#487): - Biology <https://gist.github.com/dginev/d6367f53cb7b1fbed8abfa6bddd4f2c0> - Earth Science <https://gist.github.com/dginev/cec6eb44f8c3fdffbffe546448049981>
Attendees: - Neil Soiffer - Greg Williams - Louis Maher - David Farmer - Bert Bos - David Carlisle - Bruce Miller - Deyan Ginev - Moritz Schubotz - Paul Libbrecht <https://sandbox.cryptpad.info/code/inner.html?ver=5.7.0-0#cp-md-0-regrets> Regrets - Murray Sargent <https://sandbox.cryptpad.info/code/inner.html?ver=5.7.0-0#cp-md-0-agenda> Agenda <https://sandbox.cryptpad.info/code/inner.html?ver=5.7.0-0#cp-md-0-1-announcements-updates-progress-reports>1. Announcements/Updates/Progress reports NS: The Educational Testing Service (ETS) has not renewed its membership with the W3C. CS may retire from the Math WG after the chemistry discussions. NS: There has been a GitHub discussion on whether permutation should have a property. NS: DC and NS think there should be a property and DG says don't bother. NS: This is a permutation that is represented by a two-row table issue 488 <https://github.com/w3c/mathml/issues/488>. *ACTION* NS asks us to look at issue 488 and give an opinion. NS also discussed issue489 <https://github.com/w3c/mathml/issues/489> "Update minsize/maxsize percentage values to match MathML Core". The issue is about minsize and maxsize on a stretchy operator. NS and DC think that the description in core matches that in the full spec, but of course full is much less specific about what it's saying. In issue 489, DG has provided improved language for the spec to make its intent clearer. DC: this is in section 3.2.5.2.1 in the MathML 4 spec. PL: Has seen this problem in his university. NS: So, the issue is if you don't put a maxsize or minsize on, Then they will stretch to the sizes of the largest characters in the enclosing mrow. So, by putting an mrow around something you can contain, You can avoid that problem. *ACTION:* NS: Comments in issue 488 and issue 489 would be welcome. <https://sandbox.cryptpad.info/code/inner.html?ver=5.7.0-0#cp-md-0-2-chemistry-discussion-greg-williams-co-chair-w3c-chemistry-community-group-will-join-the-call-for-part-3-of-the-conversation-for-potential-reference->2. Chemistry discussion. Greg Williams (co-chair W3C Chemistry Community Group) will join the call for part 3 of the conversation. For potential reference, Deyan's Chemistry list <https://gist.github.com/dginev/ff7e6e090b79a0389fc2eff2b9961331> (start on row 18 of the section entitled "chemistry, physics") Here is the link to the Google sheet from the CCWG: <https://docs.google.com/spreadsheets/d/1h-8k_bwQ1bO7gusb0O2DfcEs0DZUAo6QVGYZuVjWVB8/edit#gid=0> Let us consider rows 18-24: enthalpy (H) entropy (S) atmosphere (atm) heat-of-vaporization (H sub v) molar-gas-constant (R) molar-volume (V sub m) heat-of-fusion (H sub f) atmosphere is a unit. GW: Things like enthalpy will appear in equations in a math-like context. So, he is OK if they are read in a MathSpeak style. It could be read as cap h. GW: If you wanted to have an intent so that it would be chemistry aware, then you would say enthalpy. GW: In chemistry things have names like enthalpy and entropy; however, that is not how they are read. NS: So it is the case that someone could always force the reading by providing an intent. DG: We should include translations of these terms. Otherwise, I agree with the perspective that if you don't speak it, you don't need it in the list. NS: If there is only the letter H, then there is no translation. PL: If you have a verbose option, you will have to say enthalpy. GW: atm (atmosphere) is a unit. GW: As far as the others are concerned, I'm agnostic as to whether there should be an intent that's there in case somebody wants to do something with it. CS: It should be left to speaking letters. GW: A property name gives the AT a choice for verbose options. NS: Intent is like a label and properties are long descriptions. *Resolution* enthalpy (H) entropy (S) heat-of-vaporization (H sub v) molar-gas-constant (R) molar-volume (V sub m) heat-of-fusion (H sub f) do not need concept names. GW: He would like to have an option for a verbose reading; however, the verbose speech should not be forced. DC: Put intent on the first H then just H after that. Row 25 pressure (P) Could be P sub a or P sub b (if fully annotated) be read pressure-cap-a, pressure-cap-b GW: He would say p sub a. CS: May say it as partial pressure. DG: Should it be fully annotated? GW: There could be a situation where you might want it read fully, but not the default. Read it like a math expression. NS: It could be confused with probability. GW: There should be an optional reading of pressure. NS: Pressure should have a core concept name of pressure. Let us consider rows 26, 27, and 28: single-bond (-,|,,/, :covalent-bond) double-bond (=, ‖ :covalent-bond) triple-bond (≡, :covalent-bond) NS: Put them into core, they will be concepts. Row 29 dipole-force (written … used as with single-bond) GW will research this issue. We will come back to it. Consider rows 30-33: electron-shell (for :orbital-diagram) spin-up-electron (↑ for :orbital-diagram) spin-down-electron (↓ for :orbital-diagram) spin-up-and-spin-down-electrons (⇅ for :orbital-diagram) GW: An orbital diagram shows you the distributions of electrons in an atom. GW: It should force AT to read it. The arrows are significant. DG: Rows 30-33 should have the orbital diagram property. CS: We do not know how to do it in MathML. DC: We cannot design it on the fly. We must do experiments with MathML to see what we can do. *ACTION* NS should create an issue for orbital diagrams. Rows 34 and 35: Molarity and Molality are units. Skip rows 36 and 37: elevated-boiling-point (+, page 357) lowered-freezing-point (-, page 357) NS: Just say the words in rows 38 and 39: boiling-point-constant freezing-point-constant Row 40: reversible-reaction ⇌ 40 This is equilibrium. From Deyan Ginev to Everyone: https://www.google.com/books/edition/Let_s_Review_Regents_Chemistry_Physical/EUGZzQEACAAJ?hl=en&gbpv=1 page 357 Row 41: concentration [ $1 ]. This will be a concept name. Row 42 equilibrium-constant K sub eq Row 43 solubility-product-constant K sub sp Rows 42 and 43 are table until next week. *ACTION* Cs will research rows 42 and 43. Row 44 substance-reacted (-, page 385) Row 45 substance-formed (+, page 385) Skip rows 44 and 45. 46 standard-reduction-potential (cap e degrees, GW: It is read as e nought. DC: This symbol just got added to the Unicode. NS: If we wanted to say E naught, we clearly need a concept name because there's no way in the world most people are going to know what it is. CS: I'll tell you, Braille transcribers will commonly mix that up. I'll put the degree symbol instead of the nought. GW: A circle, a degree symbol, or a plinth: all 3 of them mean the same thing, but for various types of graphic reasons are chosen. DC: So, what's a good name? Should it be something with state in its name? So standard reduction potential is what's here. NS: Row 46's concept name is: standard state, with a postfix property. The default would actually say dollar one at standard state. GW: The terse way to read it would be e0 or (E-Nought) at standard state. CS: Standard-reduction-potential is its verbose name. Row 47 half-reaction | (page 449) GW: Half-reaction is a concept. NS: What are the arguments? NS: It has one argument bracketed by vertical bars. Row 48: volume (V) NS: This is just a capital V. NS: I think that's just V, and we leave it as V. Row 49 reaction (rxn) rxn means reaction. GW: It sort of looks like a function: so, sin is a sine, cos is a cosine, and rxn is a reaction. NS: So, it's basically a function of one argument then. GW: Well, except it's probably not even that. It's usually a subscript or like a subscript label. GW: It’s a direct substitution. Any time you see rxn, substitute reaction for it. Ns: Its intent name is reaction. This is the end of the chemistry, physics list on DG's file.
We meet on Thursday at: 10am Pacific, 1pm Eastern, 7pm Central European Tim *e*. The regulars for this group should have the meeting details in their calendars. For everyone else, the details can be found on the members-only W3C Math WG calendar <https://www.w3.org/events/meetings/d6f2b73d-34fc-4276-b164-bdc62a675dcc/20230713T130000/>. Agenda 1. Announcements/Updates/Progress reports 2. Chemistry discussion. Greg Williams (co-chair W3C Chemistry Community Group) will join the call for part 3 of the conversation For reference, Deyan's Chemistry list <https://gist.github.com/dginev/ff7e6e090b79a0389fc2eff2b9961331> (start on row 18 of the section entitled " chemistry, physics")
[View this event in your browser](https://www.w3.org/events/meetings/d6f2b73d-34fc-4276-b164-bdc62a675dcc/20240226T130000/) Math WG Upcoming Confirmed =========================== 27 February 2024, 13:00 -14:00 America/New\_York Event is recurring weekly on Monday and Thursday, starting from 2023-07-13, until 2025-08-31 [ Math Working Group ](https://www.w3.org/groups/wg/math/calendar/)Meetings of the Math WG about: - MathML Full: every Thursday - MathML Core: every last Monday of the month Agenda ------ Draft agenda for 27 Feb. 2024 on GitHub: <https://github.com/w3c/mathml-core/issues/221> Agenda and minutes on cryptpad.fr: - [MathML Full](https://cryptpad.fr/code/#/2/code/edit/gmibUJ0WEHOC7HyymBX6oDqh/) (Thursday) - [MathML Core](https://cryptpad.fr/code/#/2/code/edit/4ZrscOeHMxtuAerfmNAN8gME/) (Monday) Joining Instructions -------------------- Instructions are restricted to meeting participants. You need to [ log in](https://auth.w3.org/?url=https%3A%2F%2Fwww.w3.org%2Fevents%2Fmeetings%2Fd6f2b73d-34fc-4276-b164-bdc62a675dcc%2F%3FrecurrenceId%3D20240226T130000) to see them. Participants ------------ ### Groups - [Math Working Group](https://www.w3.org/groups/wg/math/) ([View Calendar](https://www.w3.org/groups/wg/math/calendar/)) Report feedback and issues on [ GitHub](https://github.com/w3c/calendar "W3C Calendar GitHub repository").
[View this event in your browser](https://www.w3.org/events/meetings/d6f2b73d-34fc-4276-b164-bdc62a675dcc/20240226T130000/) Math WG Upcoming Confirmed =========================== 27 February 2024, 13:00 -14:00 America/New\_York Event is recurring weekly on Monday and Thursday, starting from 2023-07-13, until 2025-08-31 [ Math Working Group ](https://www.w3.org/groups/wg/math/calendar/)Meetings of the Math WG about: - MathML Full: every Thursday - MathML Core: every last Monday of the month Agenda ------ Draft agenda for 27 Feb. 2024 on GitHub: <https://github.com/w3c/mathml-core/issues/221> Agenda and minutes on cryptpad.fr: - [MathML Full](https://cryptpad.fr/code/#/2/code/edit/gmibUJ0WEHOC7HyymBX6oDqh/) (Thursday) - [MathML Core](https://cryptpad.fr/code/#/2/code/edit/4ZrscOeHMxtuAerfmNAN8gME/) (Monday) Joining Instructions -------------------- Instructions are restricted to meeting participants. You need to [ log in](https://auth.w3.org/?url=https%3A%2F%2Fwww.w3.org%2Fevents%2Fmeetings%2Fd6f2b73d-34fc-4276-b164-bdc62a675dcc%2F%3FrecurrenceId%3D20240226T130000) to see them. Participants ------------ ### Groups - [Math Working Group](https://www.w3.org/groups/wg/math/) ([View Calendar](https://www.w3.org/groups/wg/math/calendar/)) Report feedback and issues on [ GitHub](https://github.com/w3c/calendar "W3C Calendar GitHub repository").
Same time as usual but rescheduled to Tuesday. Thanks for your flexibility this month. There's a start of an agenda in https://github.com/w3c/mathml-core/issues/221 Please feel free to add more (or suggest if you think something on there shouldn't be) -- Brian Kardell :: @briankardell :: bkardell.com
Hello everyone, Sorry it's been a hectic month for me and I dropped the ball here. I have a doctors conflict on Monday and cannot chair, and I didn't leave enough time to sort this out so I'd like to ask the group if anyone would be willing to switch this to Tues at the same time, or the following Monday (March 4)? Otherwise, we'll pick back up at the end of March. So sorry. -- Brian Kardell :: @briankardell :: bkardell.com
<https://sandbox.cryptpad.info/code/inner.html?ver=5.7.0#cp-md-0-attendees-> Attendees: - Neil Soiffer - Greg Williams - Louis Maher - David Carlisle - David Farmer - Bert Bos - Murray Sargent - Moritz Schubotz - Dennis Müller - Bruce Miller - Cary Supalo - Patrick Ion - Paul Libbrecht - Deyan Ginev <https://sandbox.cryptpad.info/code/inner.html?ver=5.7.0#cp-md-0-regrets> Regrets <https://sandbox.cryptpad.info/code/inner.html?ver=5.7.0#cp-md-0-agenda> Agenda <https://sandbox.cryptpad.info/code/inner.html?ver=5.7.0#cp-md-0-1-announcements-updates-progress-reports>1. Announcements/Updates/Progress reports DG discussed issue 10143 <https://github.com/whatwg/html/issues/10143> entitled: "Improve DX of element reference attributes by allowing relative references instead of only ids". MuS is in contact with Ronald Tse who has created Plurimath <https://github.com/plurimath>. The main project web page is ( https://www.plurimath.org/). This application converts between multiple math representation languages. Perhaps this could be the third implementation of intent. He has recently added Unicode Math to his list of formats. MuS encouraged the developer to contact NS so that the developer might add intent to his list of output formats. MuS thinks the developer would be a good member of the Math WG group. He would have to be brought in as an invited expert. BB said there was no limit to the number of invited experts on a working group. <https://sandbox.cryptpad.info/code/inner.html?ver=5.7.0#cp-md-0-2-chemistry-discussion-greg-williams-co-chair-w3c-chemistry-community-group-will-join-the-call-for-part-2-of-the-conversation-for-potential-reference->2. Chemistry discussion. Greg Williams (co-chair W3C Chemistry Community Group) will join the call for part 2 of the conversation. For potential reference, Deyan's Chemistry list <https://gist.github.com/dginev/ff7e6e090b79a0389fc2eff2b9961331> Here is the link to the Google sheet from the CCWG: https://docs.google.com/spreadsheets/d/1h-8k_bwQ1bO7gusb0O2DfcEs0DZUAo6QVGYZuVjWVB8/edit#gid=0 NS: We finished talking about Lewis diagrams. NS looked at pictures of Lewis diagrams of 2D structures based upon tables. They were not aligned correctly. This could have been the fault of the drawing tool. GW looked at the MathML link that NS sent him. NS: There's 2 things about intent. One is there's what's we call a concept name which has a function like syntax. So, there's a concept name and then arguments to it. You can speak the concept name. It could be an infix or prefix speech or functional speech. And the other thing is that you could give it a property and these both can be mixed. NS: The property is something that is inherited. It gives the AT information about what it should do but doesn't tell the AT what it must do. NS: You could give a table the property that it is a system of equations; therefore, reading the columns is not important. If the table had the property of being a matrix, then reading the columns would matter. NS: If something had a chemical formula property, then the AT would know to use chemical terms as opposed to say math terms. GW: If we had a table with a Lewis structure property, the AT would know what symbols should be used for the dots. If something falls between atoms, the AT knows to treat them as bonds. NS: We will have to write a few paragraphs on how to speak entities with Lewis Structure properties. We should have some documentation on a suggested pattern of speech. DG: You should not say that properties are inherited. You should say that properties are visible to the children. Start in DG's list with the "chemistry, physics" section. NS: If we have a "chemical formula" property, should we have concepts for these arrows? NS: Yes. DG: How do we know that everyone is thinking of the same characteristics when we talk about the "chemical formula" property? NS: Should the arrows be under math or chemistry or in the not-math and not-chemistry section? How should we organize them? *ACTION* NS will add a section for chemistry in the concepts list. NS: says that if someone provides an intent, it can override any properties that are there. NS: GW we need a concept name for the arrows, and the other chemistry symbols. NS: There are 8 types of arrow symbols in chemistry. From Deyan Ginev to Everyone: 8 types of arrows article: https://www.masterorganicchemistry.com/2011/02/09/the-8-types-of-arrows-in-organic-chemistry-explained/ In this article, there are figures demonstrating some of the arrow symbols discussed in this article. From the article: To my knowledge there are 8 different types of arrows you meet in organic chemistry. Here’s a little guide to them. - The forward arrow, otherwise known as the “reaction arrow”. NS: Call it yields. - The Equilibrium arrow. This shows a reaction that is reversible, usually in the context where the reversibility is being highlighted (such as in a reaction mechanism). NS Call it Equilibrium dash right and equilibrium dash left. - The Resonance arrow. Not to be confused with the equilibrium arrow, this double-headed arrow shows two (or more) species that are resonance structures of each other. - The Dashed Arrow. This is often used to show a speculative or theoretical transformation, where conditions might have yet to be discovered. - The Curved Arrow (double headed). - The Curved Arrow (single headed). - The Broken Arrow. This is used to show reactions that don’t work. - The Retrosynthesis Arrow. The open arrow here doesn’t actually show a “reaction”, per se, but instead more of a mental exercise. The retrosynthetic arrow is meant to depict the process of breaking down a complex molecule to simpler starting materials. This is useful as a planning device to highlight a key strategy used for building a molecule. NS found a single right arrow with an X through it. He was going to call it "not-yields". Perhaps it is symbol seven (The Broken Arrow). This is used to show reactions that don’t work). DG suggested calling this "unsuccessful-reaction". NS said there were three equilibrium arrows. NS: The arrows did not make it into Unicode. MuS: https://www.unicode.org/L2/L2023/23193r2-ten-chemical-symbols.pdf is a Unicode chemistry arrow proposal. NS: Other arrows were weird versions of equilibrium. we can ignore them. NS: Should we name other arrows? GW: Those should be just about all the ones that you're going to encounter between reactants and some product. NS: Let us consider: aqueous (aq) solid (s) liquid (l) and gas (g). NS: They could have their own names as shown above. They are often done in parentheses after the molecule. NS: I've seen them used as subscripts without the parentheses. GW: If you see (aq, s, l, g) in parentheses, then these terms refer to the formula that proceeds the parentheses. NS: It is a postfix concept with one argument. NS: You would read the formula then pronounce the aq, s, l, or g. NS: It is a concept that is attached to an mrow or an msub for a subscript. From Deyan Ginev to Everyone: (aq) NS: say h2o (l) for liquid. or (h2o) subscript l which is less common. GW: There is a down arrow for precipitation out. NS: Isotopes can use standard superscripts. NS: You can have pre-subscripts and superscripts or maybe both. NS: Isotope is a perfectly good name. NS: We have ions. Call them ions with a superscript to show the charge on the ion. NS accepted the name oxidation-state. Ns accepted proton, anti-proton, electron, positron, and neutron. They can be treated as an element. They could have the chemical-element property. DG: said the anti-proton symbol is p bar. GW Alpha, beta, and gamma are nuclear decay products. NS: Do they have sub and superscripts? WG: Well, if you're just doing algebra they are alpha beta and gamma unless you are breaking down what they actually are. WG: You can treat alpha, beta and gamma as elements. From Patrick D F Ion to Everyone: Or \mu as muon etc. NS Accepted Avogadro's-number. From Patrick D F Ion to Everyone: Should it actually be Avogadro number since the possessive should have an apostrophe? [not Loschmidt in any case] NS: Molar-mass is cap M. It can be a number in a square bracket for concentration of. NS: Numbers in square brackets are concentrations. NS: Is concentration the same as molar-mass? NS: Molar is a unit. Copilot Pro <https://copilot.microsoft.com/>: In chemistry, “molar” refers to the unit of concentration called molarity, which is the number of moles of a solute per liter of solution. GW: Think about how it should be said. NS: M is used as a functional form which is molar mass. It takes one argument which is the chemical formula. Molar-mass is the name for it. PI: You must include the molar-mass constant. Copilot Pro: There is a molar-mass constant, denoted as ( M sub u ). It is defined as one twelfth of the molar mass of carbon-12, which is approximately ( M sub u = \frac{M(^{12}C)}{12} ). The molar mass of any element or compound is its relative atomic mass (atomic weight) multiplied by the molar mass constant. Ns: M sub u is a constant. It does not need a concept name. NS: Hydrate is indicated with a dot. DG: You have a chemical compound or molecule and then you say the center dot and then you usually would say something like 5 H2O. The center dot is there to say the hydrate is starting. NS: Does it have arguments? Does it stand on its own? GW: Well, it does have so it's a connector so you're going to have a chemical formula dot and then H2O preceded by some number prefix typically. So, the way you would say it would be something like copper sulfate, hexa hydrate or penta hydrate or something like that is the way you would name that compound. NS: prefixes (penta, etc) are listed in https://en.wikipedia.org/wiki/Hydrate NS: But would you say it as the compound name like CH 3 something, something, hydrate? NS: It would take the 2 arguments, the number and the chemical formula and Hydrate would be spoken at the end, so it would be post fix. It's 2 arguments in a post fix reading. GW: If you had copper sulfate hexahydrate, that's going to be written as CU, S, o, Subscript 4. GW: There are some instances where you would want it read as copper sulfate hexahydrate, but you know in a lot of instances you're probably just going to want to read it out as a formula depending upon what the context is. NS: Okay, so do we have any conclusions on what this should be as a concept name? GW: It's 3 arguments. The first argument is going to be your left-hand side chemical formula, then on the right, you've got an argument that's made up of a number followed by H 2 O. NS: So that's probably 3 arguments because it is important to say the number, to say the di or Penta. DG: But you don't need the H2O, so you are Down to 2 again. PI: And you also have an anomalous case of methyl hydrate, which is methanol. GW: Technically that would be true. I mean, the H2O Is implied if it's a hydrate, and I don't know of it being used for anything else on the right-hand side. PI: Is it actually necessary to have a hydrate concept? NS: What do you mean by is it necessary? Do you mean should it be in core? PI: I mean, obviously it's important enough that people keep referring to compounds and their hydrated forms and that's useful if describing something in crystals and so on. But, it's a rather complicated thing to set up. GW: The dot is context dependent. there must be a property or concept saying this is a hydrate dot. CS: Leave it up to the user to know that it is hexa-hydrate, pentahydrate, and all that. CS: I don't know if we need the MathML AT to say hydrate. GW: We need to give the dot a property of hydrate. NS: I may be confused again, but if you're saying that we just Label the dot with hydrate, the AT is going to speak the formula, say hydrate, and speak what follows it, whereas it sounds like you want to silence any water that follows it. WG: The issue is that we want to give the AT flexibility to choose how to read it, right? NS: It sounds like you're saying we just put hydrate on it, and it's pronounced dot GW: If they want to alter that and give it as a compound name plus pentahydrate then they can choose to do so. But you label it so that people know what the dot is for. We do not force speech rules. DG: You can figure out the details later if you like, but they think hydrate is necessary. It was part of the core curriculum in my high school. NS: At least as a Resolution for now, we have hydrate and it applies only to the dot, and it takes no arguments. NS: Yet, if the AT wants to pronounce it, the AT can notice that yes, look, there's a hydrate inside here and so I really want to say hydrate instead of dot something or other. GW: The dot would be red in the order it happens. GW, and CS, can come next week. We will continue to go through DG's list. If we finish that, we will start on GW's list. In DG's list, we will start on row 18 of the section entitled " chemistry, physics".
Safari Technology Preview Release 188 is now available for download for macOS Sonoma and macOS Ventura. If you already have Safari Technology Preview installed, you can update it in System Settings under General → Software Update.
This release includes WebKit changes between: 272449@main…273601@main.
content alternative
text syntax. (272455@main)
(26942023)<header> inside
<main> and sectioning elements. (273188@main)
(48370244)<input type=checkbox
switch>. (273206@main)
(121215059)transition property to produce the
shortest serialization. (272513@main)
(119822401)animation property to produce the
shortest serialization. (272629@main)
(120439368)supports() syntax for @import
rules. (273591@main)
(109060734)getComputedStyle() for invalid
pseudo-elements. (272543@main)
(98504661)oklab and oklch lightness value
clamping. (272501@main)
(116195533):has(+ :not(.class))
pseudo-class selector. (272678@main)
(119819247)content computed value serialization.
(272476@main)
(120061551)getComputedStyle()
and KeyframeEffect.prototype.pseudoElement so they
require them starting with :: (or : for 4
legacy pseudo-elements). (272499@main)
(120170550)linear() easing. (272613@main)
(120290721):-webkit-full-screen pseudo-class
to :fullscreen. (272577@main)
(120335917):-webkit-any-link to
:any-link and :matches() to
:is(). (272559@main)
(120337922)getComputedStyle() pseudo-element parsing to
support the full range of CSS syntax. (272649@main)
(120471227):not(:has(:not(foo))) getting misclassified
as scope breaking. (273177@main)
(120492012)@supports to correctly handle support for
some -webkit prefixed pseudo-elements that were
incorrectly treated as unsupported. (272726@main)
(120577690)-webkit-alt and alt
properties. (272480@main)
(120051066)resize: auto property.
(273035@main)
(120138995)-apple- prefixed pseudo-elements no longer
valid. (272538@main)
(120268884):-webkit-animating-full-screen-transition
pseudo-class. (273529@main)
(121302758):-khtml-drag pseudo-class. (273261@main)
(121303391)text-indent to affect the selected file(s)
label for file inputs. (272837@main)
(105223868)navigator.cookieEnabled to return
false when cookies are blocked. (273522@main)
(121284878)<textarea> element with
1rem padding. (273029@main)
(90639221)writing-mode: vertical-rl. (272799@main)
(120066970)ch unit value in
vertical-rl and vertical-lr when
text-orientation is not upright. (272536@main)
(120293590)overflow: hidden preventing CSS Subgrid.
(273134@main)
(120848131)<br> element with clear. (273407@main)
(121444267)<iframe> without affecting the size of the
<iframe>. (272503@main)
(120178866)<switch> element. (272831@main)
(120732837):state() pseudo-class. (272474@main)
(120072599)getElementsByName() to only return HTML
elements, not SVG, MathML, or other types of elements. (272530@main)
(120275680)button value for a
pointerup event not matching the
pointerdown event. (273263@main)
(120429508)document.open. (272960@main)
(120893136)KeyboardEvent.altGraphKey.
(273379@main)
(102980723)KeyboardEvent.keyLocation. (273457@main)
(121564228)browsing.scripting.executeScript to handle
all valid argument types. (120727491)getClientCapabilities to align with WebAuthn
standards to use a record type with camelCase values. (272998@main)
(120442670)EXT_conservative_depth and
NV_shader_noperspective_interpolation. (272979@main)
(120907578)degradationPreference. (273172@main)
(121041723)In September 2023,
Safari 17.0 on macOS shipped a small but interesting change to
the <select> element. You can now put an
<hr> element, known as a horizontal rule,
inside a
<select> element, which will draw a horizontal
line again. Again, because Safari used to support this
over a decade ago — more on that story later.
The horizontal rule creates visual breaks between options to help users scan and compare against similar options.
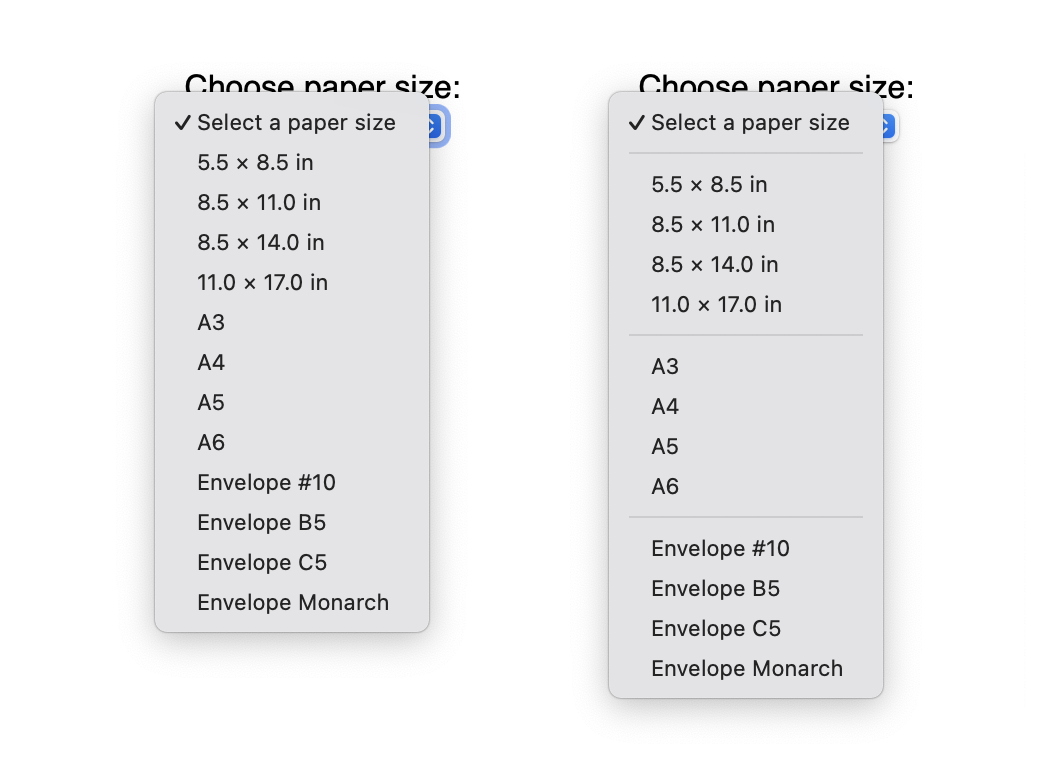 Select element without separators; Select
element with horizontal rule separators.
Select element without separators; Select
element with horizontal rule separators.
It’s a small change, but it’s been getting
attention
lately.
Simply add an <hr> between
<option> elements to insert a line:
<label for="papersize">Select Paper Size:</label>
<select name="papersize">
<option>Select a paper size</option>
<hr>
<option>5.5 × 8.5 in</option>
<option>8.5 × 11.0 in</option>
<option>8.5 × 14.0 in</option>
<option>11.0 × 17.0 in</option>
<hr>
<option>A3</option>
<option>A4</option>
<option>A5</option>
<option>A6</option>
<hr>
<option>Envelope #10</option>
<option>Envelope B5</option>
<option>Envelope C5</option>
<option>Envelope Monarch</option>
</select>
So why did this work for years but then stop? Where did it go?
Well over a decade ago, WebKit adopted a new HTML parser. It was based on the HTML5 standardization effort, which attempted to unify the HTML language, as it had diverged quite a bit in implementations. And it was a far cry from the SGML dialect some in the standardization community pretended HTML to be. It represented a huge milestone in the development of HTML. We were finally on a path where all implementations would agree on what any arbitrary byte stream of HTML represented.
Replacing WebKit’s HTML parser was a large undertaking. It brought huge benefits, but it was still missing a few bits when it shipped. In fact, one feature from WebKit had been hidden from HTML. You could still see it by manipulating the DOM or using XML, but apart from a couple of experts nobody knew.
That feature was hr elements nested in
select elements. Originally it was added by Adele Peterson
at Apple in 2006 to support a common UI paradigm on the web:
separators between select box options. We discovered this while
doing some maintenance work on the HTML parser and agreed this was
still a desirable feature. We also re-discovered that in 2018 a
feature request was opened against the HTML Standard for this exact
feature.
To introduce this feature again at this stage required some careful changes to the HTML parser portion of the HTML Standard as well as some corresponding semantic and conformance changes. After all, we wanted to fix this regression while preserving HTML parser interoperability. At the same time we wanted to ensure the feature was properly standardized as well. With the help from others in the HTML standardization community we managed to make this change and it’s now part of multiple browsers and harder to accidentally regress again due to improved cross-browser test coverage.
That’s the story of how we lost access to separators in select boxes for a decade and then got them back, fully standardized, in Safari 17.0 (commit 263624).
If you’re still reading, you might wonder what other maintenance work we did on the HTML parser. It included a bunch of small fixes that made WebKit more standards compliant. Where it was appropriate, cross-browser test coverage was improved as well:
It’s important to be aware that this feature adds visual separators. They are not announced by assistive technologies like VoiceOver.
It’s also worth noting that the HTML parser only supports
<hr> as a child of <select>
elements, not as a child of <optgroup>
elements.
Lastly, when using a <select> element with a
size attribute value greater than 1, the separators
are instead rendered as blank space, similar to the space added for
<optgroup> elements.
Using <hr> in <select>
gives authors another choice in how to visually separate options
for users. Instead of the blank space rendered with
<optgroup>, now authors can use lines too.
We love to hearing from you. Send a tweet to @webkit to share your thoughts on this feature. Find us on Mastodon at @jensimmons@front-end.social and @jondavis@mastodon.social. If you run into any issues, we welcome your WebKit bug reports on WebKit features like this. Reporting issues makes an enormouse difference.
You can also download the latest Safari Technology Preview to try out new web platform features like this before they appear in a Safari beta.
Safari Technology Preview Release 185 is now available for download for macOS Sonoma and macOS Ventura. If you already have Safari Technology Preview installed, you can update it in System Settings under General → Software Update.
This release includes WebKit changes between: 271111@main…271831@main.
align-content on block
containers. (271818@main)
(114740670)letter-spacing
and word-spacing. (271357@main)
(116562262)overflow-anchor. (271790@main)
(118365809)@scope. (271670@main)
(119261250)::grammar-error and
::spelling-error (271684@main)
(119314048)::selection pseudo-element color. (271129@main)
(117796745)::backdrop to be allowed after
::slotted(). (271366@main)
(119015204)<input type="checkbox"
switch>. (271736@main)
(119378678)getDisplayMedia frameRate
always at 30 regardless of constraints. (271233@main)
(118874132)<font>
text-decoration color override quirk. (271338@main)
(102920597)vertical-rl
mode. (271416@main)
(111915460)Element.prototype.setHTMLUnsafe(),
ShadowRoot.prototype.setHTMLUnsafe(), and
Document.parseHTMLUnsafe() methods. (271423@main)
(115345128)resizeBy and resizeTo
to use int rather than float to align
with specifications. (271194@main)
(118872048)<progress> to use the page’s preferred
rendering update interval. (271431@main)
(118976548)Element.prototype.setAttributeNode() to not
treat attribute names case insensitively. (271363@main)
(119013600):checked and
:indeterminate to match at the same time. (271430@main)
(119075969)bitmaprenderer, webgl, and
webgl2. (271300@main)
(109594232)getClientCapabilities().
(271584@main)
(119058559)Dear participants in the MathML Refresh Community Group https://www.w3.org/community/mathml4/ Your Community Group appears to have become inactive (per [1]). If your group is in fact active, we recommend the following: * Let us know where the activity is going on so that we can update our data and improve our tools. * Update your group home page with news of your activities. Chairs can use the Wordpress instance of the group to post news; let us know if you have any questions. If you would like us to keep the group open because you expect it to become active in the near future or for other compelling reasons, just let us know. If would like us to close the group, or if we do not hear from you in the next 30 days, we will plan to close the group. Thank you, CG/BG System [1] https://www.w3.org/community/about/faq/#close-inactive
Hello,
I'd like to mention a few changes that I've been agreed on for a while,
but that are likely to affect the rendering in web browsers. If you are
maintaining an authoring tool for MathML, please take them into account.
1. The following names for length values have been removed, they should
be replaced with equivalent em values:
veryverythinmathspace => 0.05555555555555555em
verythinmathspace => 0.1111111111111111em
thinmathspace => 0.16666666666666666em
mediummathspace => 0.2222222222222222em
thickmathspace => 0.2777777777777778em
verythickmathspace => 0.3333333333333333em
veryverythickmathspace => 0.3888888888888889em
They have never been supported in Chromium, have been removed from
some WebKit ports and are currently triggering deprecation warnings in
Firefox.
2. The mathvariant attribute has essentially been removed, it should be
replaced with direct use of Mathematical Alphanumeric Symbols for example:
<mi mathvariant="fratur">A</mi> => <mi>0#x1D504;</mi>
<style
mathvariant="double-struck"><mi>A</mi><mo>+</mo><mn>1</mn></mstyle> =>
<mrow><mi>𝔸</mi><mo>+</mo><mn>𝟙</mn></mrow> ('+' does
not have any double-struck form so is unchanged)
The only exception is for mathvariant="normal" on the <mi> element in
order to cancel automatic italicization: <mi mathvariant="normal">A</mi>
The legacy cases have never been supported in Chromium and will
trigger deprecation warnings in Firefox 117. The plan is to try and do
the same in WebKit.
3. The binary operator U+2223 DIVIDES is no longer stretchy by default.
Note that the entity name ∣ maps to this character and,
probably due to this confusing name, some people have incorrectly use it
as stretchy infix/postfix fences, where | U+007C would be more appropriate.
<mrow><mo>∣</mo><mfrac><mn>2</mn><mn>3</mn></mfrac><mo>∣</mo></mrow>
=> <mrow><mo>|</mo><mfrac><mn>2</mn><mn>3</mn></mfrac><mo>|</mo></mrow>
(if you means stretchy fences)
<mrow><mn>2</mn><mo>∣</mo><mn>4</mn></mrow> =>
<mrow><mn>2</mn><mo stretchy="true">∣</mo><mn>4</mn></mrow>
(if you really means to make the "divides" operator stretchy).
The operator is not stretchy in Chromium or WebKit. The plan is to
try and do the same in Firefox.
--
Frédéric Wang
Planet MathML features:
If you own a blog with a focus on MathML, and want to be added or removed from this aggregator, please get in touch with Bert Bos at bert@w3.org.
