To be effective, MathML must work well with a wide variety of renderers, processors, translators and editors. This chapter addresses some of the interface issues involved in generating and rendering MathML. Since MathML exists primarily to encode mathematics in Web documents, perhaps the most important interface issues are related to embedding MathML in [HTML4] and [XHTML].
There are three kinds of interface issues that arise in embedding MathML in other XML documents. First, MathML must be semantically integrated. MathML markup must be recognized as valid embedded XML content, and not as an error. This is primarily a question of managing namespaces in XML [Namespaces].
Second, in the case of HTML/XHTML, MathML rendering must be integrated into browser software. Some browsers already implement MathML rendering natively, and one can expect more browsers will do so in the future. At the same time, other browsers have developed infrastructure to facilitate the rendering of MathML and other embedded XML content by third-party software. Using these browser specific mechanisms generally requires some additional interface markup of some sort to activate them.
Third, other tools for generating and processing MathML must be able to intercommunicate. A number of MathML tools have been or are being developed, including editors, translators, computer algebra systems, and other scientific software. However, since MathML expressions tend to be lengthy, and prone to error when entered by hand, special emphasis must be given to insuring that MathML can be easily generated by user-friendly conversion and authoring tools, and that these tools work together in a dependable, platform and vendor independent way.
The W3C Math Working Group is committed to providing support to software vendors developing any kind of MathML tool. The Working Group monitors the public mailing list www-math@w3.org, and will attempt to answer questions about the MathML specification. The Working Group works with MathML developer and user groups. For current information about MathML tools, applications and user support activities, consult the home page of the W3C Math Working Group.
7.1 Embedding MathML in other Documents
While MathML can be used in isolation as a language for exchanging mathematical expressions between MathML-aware applications, the primary anticipated use of MathML is to encode mathematical expression within larger documents. MathML is ideal for embedding math expressions in other applications of XML.
In particular, the focus here is on the mechanics of embedding MathML in [XHTML]. XHTML is a W3C Recommendation formulating a family of current and future XML-based document types and modules that reproduce, subset, and extend HTML. While [HTML4] is the dominant language of the Web at the time of this writing, one may anticipate a shift from HTML to XHTML. Indeed, XHTML can already be made to render properly in most HTML user agents.
Since MathML and XHTML share a common XML framework, namespaces provide a standard mechanism for embedding MathML in XHTML. While some popular user agents also support inclusion of MathML directly in HTML as "XML data islands," this is a transitional strategy. Consult user agent documentation for specific information on its support for embedding XML in HTML.
7.1.1 MathML and Namespaces
Embedding MathML in XML-based documents in general, and XHTML in particular, is a matter of managing namespaces. See the W3C Recommendation "Namespaces in XML" [Namespaces] for full details.
An XML namespace is a collection of names identified by a URI. The URI for the MathML namespace is:
http://www.w3.org/1998/Math/MathML
Using namespaces, embedding a MathML expression in a larger XML document is merely a matter of identifying the MathML markup as residing in the MathML namespace. This can be accomplished by either explicitly identifying each MathML element name by attaching a namespace prefix, or by declaring a default namespace on an enclosing element.
To declare a namespace, one uses an xmlns
attribute, or an attribute
with an xmlns prefix. When the xmlns attribute is used alone, it sets
the default namespace for the element on which it
appears, and for any children elements.
Example:
<math xmlns="http://www.w3.org/1998/Math/MathML"> <mrow>...</mrow> </math>
When the xmlns attribute is used as a
prefix, it declares a
prefix which can then be used to explicitly associate other elements
and attributes with a particular namespace.
Example:
<body xmlns:m="http://www.w3.org/1998/Math/MathML"> ... <m:math><m:mrow>...</m:mrow></m:math> ... </body>
These two methods of namespace declaration can be used together.
For example, by using both an explicit document-wide namespace prefix,
and default namespace declarations on individual mathematical
elements, it is possible to localize namespace related markup to the
top-level math element. This is also
important for implementation with some user agents, since attaching
rendering behaviors to an element currently requires an explicit
namespace prefix in these browsers. At the same time, a number of
MathML authoring tools are not yet namespace-aware, and thus the
ability to use markup without prefixes is also desirable in the short
term.J
Example:
<body xmlns:m="http://www.w3.org/1998/Math/MathML"> ... <m:math xmlns="http://www.w3.org/1998/Math/MathML"> <mrow>...<mrow> </m:math> ... </body>
7.1.1.1 Document Validation Issues
The use of namespace prefixes creates an issue for DTD validation of documents embedding MathML. DTD validation requires knowing the literal (possibly prefixed) element names used in the document. However, the Namespaces in XML Recommendation [Namespaces] allows the prefix to be changed at arbitrary points in the document, since namespace prefixes may be declared on any element.
The 'historical' method of bridging this gap was to write a DTD with a fixed prefix, or in the case of XHTML and MathML, with no prefix, and mandate that the specified form must be used throughout the document. However, this is somewhat restricting for a modular DTD that is intended for use in conjunction with another DTD, which is exactly the situation with MathML in XHTML. In essence, the MathML DTD would have to allocate a prefix for itself and hope no other module uses the same prefix to avoid name clashes, thus losing one of the main benefits of XML namespaces.
One strategy for addressing this problem is to make every element name in the DTD be accessed by an entity reference. This means that by declaring a couple of entities to specify the prefix before the DTD is loaded, the prefix can be chosen by a document author, and compound DTDs that include several modules can, without changing the module DTDs, specify unique prefixes for each module to avoid clashes. The MathML DTD has been designed in this fashion. See Section A.2.5 The MathML DTD and [Modularization] for details.
An extra issue arises in the case where explicit prefixes are used
on the top-level math element, but a default
namespace is used for other MathML elements. In this case, one wants
the MathML module to be included into XHTML with the prefix set to
empty. However, the 'driver' DTD file that sets up the inclusion of
the MathML module would then need to define a new element called
m:math. This would allow the top-level math
element to use an explicit prefix, for attaching rendering behaviors
in current browsers, while the contents would not need an explicit
prefix, for ease of interoperability between authoring tools, etc.
7.1.1.2 Compatibility Suggestions
While the use of namespaces to embed MathML in other XML applications is completely described by the relevant W3C Recommendations, a certain degree of pragmatism is still called for at present. Support for XML, namespaces and rendering behaviors in popular user agents is not always fully in alignment with W3C Recommendations. In some cases, the software predates the relevant standards, and in other cases, the relevant standards are not yet complete.
During the transitional period, in which some software may not be fully namespace-aware, a few conventional practices will ease compatibility problems:
-
When using namespace prefixes with MathML markup, use m: as a conventional prefix for the MathML namespace. Using an explicit prefix is probably safer for compatibility in current user agents.
-
When using namespace prefixes, pick one and use it consistently within a document.
-
Explicitly declare the MathML namespace on all
mathelements.
Examples.
<body> ... <m:math xmlns:m="http://www.w3.org/1998/Math/MathML"> <m:mrow>...<m:mrow> </m:math> ... </body>
Or
<body> ... <math xmlns="http://www.w3.org/1998/Math/MathML"> <mrow>...<mrow> </math> ... </body>
Note that these suggestions alone may not be sufficient for creating functional Web pages containing MathML markup. It will generally be the case that some additional document-wide markup will be required. Additional work may also be required to make all MathML instances in a document compatible with document-wide declarations. This is particularly true when documents are created by cutting and pasting MathML expressions, since current tools will probably not be able to query global namespace information.
Consult the W3C Math Working Group home page for compatibility and implementation suggestions for current browsers and other MathML-aware tools.
7.1.2 The Top-Level
math Element
MathML specifies a single top-level or root math element, which encapsulates each instance of
MathML markup within a document. All other MathML content must be
contained in a math element; equivalently,
every valid, complete MathML expression must be contained in <math> tags. The math
element must always be the outermost element in a MathML expression;
it is an error for one math element to contain
another.
Applications that return sub-expressions of other MathML
expressions, for example, as the result of a cut-and-paste operation,
should always wrap them in <math>
tags. Ideally, the presence of enclosing <math>
tags should be a very good heuristic test for MathML
material. Similarly, applications which insert MathML expressions in
other MathML expressions must take care to remove the <math> tags from the inner expressions.
The math element can contain an arbitrary number
of children schemata. The children schemata render by default as if they
were contained in an mrow element.
The attributes of the math element are:
- class, id, style
-
Provided for use with stylesheets.
- xref
-
Provided along with
idfor use with XSL processing (See Section 5.4 Tools, Style Sheets and Macros for Combined Markup) - macros
-
This attribute provides a way of pointing to external macro definition files. Macros are not part of the MathML specification, and much of the functionality provided by macros in MathML can be accommodated by XSL transformations [XSLT]. However, the
macrosattribute is provided to make possible future development of more streamlined, MathML-specific macro mechanisms. The value of this attribute is a sequence of URLs or URIs, separated by whitespace - mode
-
The
modeattribute specifies whether the enclosed MathML expression should be rendered in a display style or an in-line style. Allowed values are "display" and "inline" (default). This attribute is deprecated in favor of the newdisplayattribute, or the CSS2 'display' property with the analogous block and inline values. - display
-
The
displayattribute replaces the deprecatedmodeattributeJ. It specifies whether the enclosed MathML expression should be rendered in a display style or an in-line style. Allowed values are "block" and "inline" (default).
The attributes of the math element affect
the entire enclosed expression. They are, in a sense, "inward
looking". However, to render MathML properly in a browser, and
to integrate it properly into an XHTML document, a second collection
of "outward looking" attributes are also useful.
While general mechanisms for attaching rendering behaviors to elements in XML documents are under development, wide variations in strategy and level of implementation remain between various existing user agents. Consequently, the remainder of this section describes attributes and functionality that are desirable for integrating third-party rendering modules with user agents:
- overflow
-
In cases where size negotiation is not possible or fails (for example in the case of an extremely long equation), this attribute is provided to suggest an alternative processing method to the renderer. Allowed values are
- scroll
-
The window provides a viewport into the larger complete display of the mathematical expression. Horizontal or vertical scrollbars are added to the window as necessary to allow the viewport to be moved to a different position.
- elide
-
The display is abbreviated by removing enough of it so that the remainder fits into the window. For example, a large polynomial might have the first and last terms displayed with "+ ... +" between them. Advanced renderers may provide a facility to zoom in on elided areas.
- truncate
-
The display is abbreviated by simply truncating it at the right and bottom borders. It is recommended that some indication of truncation is made to the viewer.
- scale
-
The fonts used to display the mathematical expression are chosen so that the full expression fits in the window. Note that this only happens if the expression is too large. In the case of a window larger than necessary, the expression is shown at its normal size within the larger window.
- altimg
-
This attribute provides a graceful fall-back for browsers that do not support embedded elements. The value of the attribute is an URL.
- alttext
-
This attribute provides a graceful fall-back for browsers that do not support embedded elements or images. The value of the attribute is a text string.
7.1.3 Invoking MathML Processors
In browsers where MathML is not natively supported, it is anticipated that MathML rendering will be carried out via embedded objects such as plug-ins, applets, or helper applications. The direction which has begun emerging for invoking third-party rendering and processing software is elucidated in the W3C Working Draft "Behavioral Extensions to CSS" [Behaviors].
Behavioral extensions use the linking mechanism of CSS to attach
executable components to elements. Typically, the executable
components involve script code which manipulate the DOM to instantiate
other MathML processing components. Using experimental
implementations of behavior extensions in current user agents, it is
possible to attach processing components to math elements which then carry out the rendering
of MathML markup in an XHTML page.
Work on on Behavior Extensions to CSS is ongoing at W3C, and existing implementations must be regarded as non-standard at this time. However, it offers a very promising direction for powerful and flexible invocation of third-party MathML processors.
MIME types [RFC2045], [RFC2046] offer
an alternative strategy that can also be used in current user agents
to invoke a MathML renderer. This is primarily useful when
referencing separate files containing MathML markup from an embed or object element.
[RFC3023] assigns MathML the MIME type
application/mathml+xml. The W3C Math Working Group
recommends the standard file extension .mml used for
browser registry.
In MathML 1.0, text/mathml was given as the suggested
MIME type. This has been superceded by RFC3023.
Although rendering MathML expressions typically occurs in place in a Web browser, other MathML processing functions take place more naturally in other applications. Particularly common tasks include opening a MathML expression in an equation editor or computer algebra system.
At present, there is no standard way of selecting between various applications which might be used to render or process embedded MathML. As work progresses on coordination between browsers and embedded elements and the Document Object Model [DOM], providing this kind of functionality should be a priority. Both authors and readers should be able to indicate a preference about what MathML application to use in a given context. For example, one might imagine that some mouse gesture over a MathML expression causes a browser to present the reader with a pop-up menu, showing the various kinds of MathML processing available on the system, and the MathML processors recommended by the author.
Since MathML is most often generated by authoring tools, it is
particularly important that opening a MathML expression in an editor should
be easy to do and to implement. In many cases, it will be desirable for an
authoring tool to record some information about its internal state along
with a MathML expression, so that an author can pick up editing where he or
she left off. The MathML specification does not explicitly contain
provisions for recording information about the authoring tool. In some
circumstances, it may be possible to include authoring tool information
that applies to an entire document in the form of meta-data; interested
readers are encouraged to consult the W3C Metadata Activity for current
information about metadata and resource definition. For encoding authoring
tool state information that applies to a particular MathML instance,
readers are referred to the possible use of the semantics element for this purpose Section 4.4.11.2 Semantics (semantics).
In the short term, regardless of the methodology, implementors of embedded MathML processing applications are encouraged to try to allow for the following kinds of functionality:
-
An author wishing to reach an audience as wide as possible might want MathML to be rendered by any available processor.
-
An author targeting a specific audience might want to indicate that a particular MathML processor be used.
-
A reader might wish to specify which of several available processors installed locally should be used.
7.1.4 Mixing and Linking MathML and HTML
In order to fully integrate MathML into XHTML, it should be possible not only to embed MathML in XHTML, but also to embed XHTML in MathML. However, the problem of supporting XHTML in MathML presents many difficulties. Therefore, at present, the MathML specification does not permit any XHTML elements within a MathML expression, although this may be subject to change in a future revision of MathML.
In most cases, XHTML elements (headings, paragraphs, lists, etc.) either do not apply in mathematical contexts, or MathML already provides equivalent or better functionality specifically tailored to mathematical content (tables, mathematics style changes, etc.). However, there are two notable exceptions, the XHTML anchor and image elements. For this functionality, MathML relies on the general XML linking and graphics mechanisms being developed by other W3C Activities.
7.1.4.1 Linking
MathML has no element that corresponds to the XHTML anchor element a. In XHTML, anchors are used both to make links, and to provide locations to which a link can be made. MathML, as an XML application, defines links by the use of the mechanism described in the W3C CandidateJ Recommendation "XML Linking Language" [XLink].The reader is cautioned that at the time of this writing, XLink is not yet a Recommendation, and is therefore subject to future revision. Since the MathML linking mechanism is defined in terms of the XML linking specification, the same proviso holds for it as well.J
A MathML element is designated as a link by the presence of the
attribute xlink:href. To use the attribute xlink:href, it is also necessary to declare the
appropriate namespace. Thus, a typical MathML link might look like:
<mrow xmlns:xlink="http://www.w3.org/1999/xlink"
xlink:href="sample.xml">
...
</mrow>
MathML designates that almost all elements can be used as XML linking
elements. The only elements that cannot serve as linking elements are those
such as the sep element, which exist primarily to
disambiguate other MathML constructs and in general do not correspond to
any part of a typical visual rendering. The full list of exceptional
elements that cannot be used as linking elements is given in the table
below.
| MathML elements that cannot be linking elements. | ||
|---|---|---|
mprescripts |
none |
sep |
malignmark |
maligngroup |
|
Note that the XML Linking [XLink] and XML Pointer Language [XPointer] specifications also define how to link into a MathML expressions. Be aware, however, that such links may or may not be properly interpreted in current software.
7.1.4.2 Images
The img element has no MathML
equivalent. The decision to omit a general mechanism for image
inclusion from MathML was based on several factors. However, the main
reason for not providing an image facility is that MathML takes great
pains to make the notational structure and mathematical content it
encodes easily available to processors, whereas information contained
in images is only available to a human reader looking at a visual
representation. Thus, for example, in the MathML paradigm, it would be
preferable to introduce new glyphs via the mglyph element which at a minimum identifies them
as glyphs, rather than simply including them as images.
7.1.5 MathML and Graphical Markup
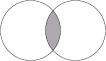
Apart from the introduction of new glyphs, many of the situations where one might be inclined to use an image amount to displaying labeled diagrams. For example, knot diagrams, Venn diagrams, Dynkin diagrams, Feynman diagrams and commutative diagrams all fall into this category. As such, their content would be better encoded via some combination of structured graphics and MathML markup. However, at the time of this writing, it is beyond the scope of the W3C Math Activity to define a markup language to encode such a general concept as "labeled diagrams." (See http://www.w3.org/Math for current W3C activity in mathematics and http://www.w3.org/Graphics for the W3C graphics activity.)
One mechanism for embedding additional graphical content is via the
semantics element, as in the following example:
<semantics>
<apply>
<intersect/>
<ci>A</ci>
<ci>B</ci>
</apply>
<annotation-xml encoding="SVG1.1">
<svg xmlns="http://www.w3.org/2000/svg" viewBox="0 0 290 180">
<clipPath id="a">
<circle cy="90" cx="100" r="60"/>
</clipPath>
<circle fill="#AAAAAA" cy="90" cx="190"
r="60" style="clip-path:url(#a)"/>
<circle stroke="black" fill="none" cy="90" cx="100" r="60"/>
<circle stroke="black" fill="none" cy="90" cx="190" r="60"/>
</svg>
</annotation-xml>
<annotation-xml encoding="application/xhtml+xml">
<img xmlns="http://www.w3.org/1999/xhtml" src="intersect.gif" alt="A intersect B"/>
</annotation-xml>
</semantics>
Here, the annotation-xml elements are used to indicate alternative
representations of the Content MathML depiction of the
intersection of two sets.
The first one is in the "Scalable Vector
Graphics" format [SVG1.1]
(see [XHTML-MathML-SVG] for the definition of an XHTML profile integrating MathML and SVG), the second one uses the
XHTML img element embedded as an XHTML fragment.
In this situation, a MathML processor can use any of these
representations for display, perhaps producing a graphical format
such as the image below.
Note that the semantics representation of this example is given
in the Content MathML markup, as the first child of the
semantics element. In this regard, it is the
representation most analogous to the alt attribute of the
img element in XHTML, and would likely be
the best choice for non-visual rendering.
7.1.6 Using CSS with MathML
When MathML is rendered in an environment that supports CSS, controlling mathematics style properties with a CSS stylesheet is obviously desirable. MathML 2.0 has significantly redesigned the way presentation element style properties are organized to facilitate better interaction between MathML renderers and CSS style mechanisms. It introduces four new mathematics style attributes with logical values. Roughly speaking, these attributes can be viewed as the proper selectors for CSS rules that affect MathML.
Controlling mathematics styling is not as simple as it might first appear
because mathematics styling and text styling are quite different in
character. In text, meaning is primarily carried by the relative
positioning of characters next to one another to form words. Thus,
although the font used to render text may impart nuances to the
meaning, transforming the typographic properties of the individual
characters leaves the meaning of text basically intact. By contrast,
in mathematical expressions, individual characters in specific
typefaces tend to function as atomic symbols. Thus, in the same
equation, a bold italic 'x' and a normal italic 'x' are almost always
intended to be two distinct symbols that mean different things. In
traditional usage, there are eight basic typographical categories
of symbols. These categories are described by mathematics style
attributes, primarily the mathvariant
attribute.
Text and mathematics layout also obviously differ in that mathematics uses 2-dimensional layout. As a result, many of the style parameters that affect mathematics layout have no textual analogs. Even in cases where there are analogous properties, the sensible values for these properties may not correspond. For example, traditional mathematical typography usually uses italic fonts for single character identifiers, and upright fonts for multicharacter identifier. In text, italicization does not usually depend on the number of letters in a word. Thus although a font-slant property makes sense for both mathematics and text, the natural default values are quite different.
Because of the difference between text and mathematics styling, only some aspects of MathML layout are good candidates for CSS control. MathML 2.0 captures the most important properties with the new mathematics style attributes, and users should try to use them whenever possible over more direct, but less robust, approaches. A sample CSS stylesheet illustrating the use of the mathematical style attributes is available in Appendix G Sample CSS Style Sheet for MathML
Generally speaking, the model for CSS interaction with the math style attributes runs as follows. A CSS style sheet might provide a style rule such as:
math *.[mathsize="small"] {
font-size: 80%
}
This rule sets the CSS font-size properties for all children of the
math element that have the mathsize attribute set to small. A MathML renderer
would then query the style engine for the CSS environment, and use the
values returned as input to its own layout algorithms. MathML does
not specify the mechanism by which style information is inherited from
the environment. However, some suggested rendering rules for the
interaction between properties of the ambient style environment and
MathML-specific rendering rules are discussed in Section 3.2.2 Mathematics style attributes common to token
elements, and more generally throughout Chapter 3 Presentation Markup.
It should be stressed, however, that some caution is required in writing CSS stylesheets for MathML. Because changing typographic properties of mathematics symbols can change the meaning of an equation, stylesheet should be written in a way such that changes to document-wide typographic styles do not affect embedded MathML expressions. By using the MathML 2.0 mathematics style attributes as selectors for CSS rules, this danger is minimized.
Another pitfall to be avoided is using CSS to provide typographic style information necessary to the proper understanding of an expression. Expressions dependent on CSS for meaning will not be portable to non-CSS environments such as computer algebra systems. By using the logical values of the new MathML 2.0 mathematics style attributes as selectors for CSS rules, it can be assured that style information necessary to the sense of an expression is encoded directly in the MathML.
MathML 2.0 does not specify how a user agent should process style information, because there are many non-CSS MathML environments, and because different users agents and renderers have widely varying degrees of access to CSS information. In general, however, developers are urged to provide as much CSS support for MathML as possible.
7.2 Conformance
Information is increasingly generated, processed and rendered by software tools. The exponential growth of the Web is fueling the development of advanced systems for automatically searching, categorizing, and interconnecting information. Thus, although MathML can be written by hand and read by humans, the future of MathML is largely tied to the ability to process it with software tools.
There are many different kinds of MathML processors: editors for authoring MathML expressions, translators for converting to and from other encodings, validators for checking MathML expressions, computation engines that evaluate, manipulate or compare MathML expressions, and rendering engines that produce visual, aural or tactile representations of mathematical notation.J What it means to support MathML varies widely between applications. For example, the issues that arise with a MathML-compliantJ validating parser are very different from those for a MathML-compliantJ equation editor.
In this section, guidelines are given for describing different types of MathML support, and for quantifying the extent of MathML support in a given application. Developers, users and reviewers are encouraged to use these guidelines in characterizing products. The intention behind these guidelines is to facilitate reuse and interoperability between MathML applications by accurately characterizing their capabilities in quantifiable terms.
The W3C Math Working Group maintains MathML 2.0 Conformance GuidelinesJ. Consult this document for future updates on conformance activities and resources.
7.2.1 MathML Conformance
JA valid MathML expression is an XML construct determined by the MathML DTD together with the additional requirements given in this specification.
Define a "MathML processor" to mean any application that can accept, produce, or "roundtrip" a valid MathML expression. An example of an application that might round-trip a MathML expression might be an editor that writes a new file even though no modifications are made.
Three forms of MathML conformanceJ are specified:
-
A MathML-input-conformantJ processor must accept all valid MathML expressions, and faithfully translate all MathML expressions into application-specific form allowing native application operations to be performed.
-
A MathML-output-conformantJ processor must generate valid MathML, faithfully representing all application-specific data.
-
A MathML-roundtrip-conformantJ processor must preserve MathML equivalence. Two MathML expressions are "equivalent" if and only if both expressions have the same interpretation (as stated by the MathML DTD and specification) under any circumstances, by any MathML processor. Equivalence on an element-by-element basis is discussed elsewhere in this document.
Beyond the above definitions, the MathML specification makes no demands of individual processors. In order to guide developers, the MathML specification includes advisory material; for example, there are many suggested rendering rules throughout Chapter 3 Presentation Markup. However, in general, developers are given wide latitude in interpreting what kind of MathML implementation is meaningful for their own particular application.
To clarify the difference between conformanceJ and interpretation of what is meaningful, consider some examples:
-
In order to be MathML-input-conformantJ, a validating parser needs only to accept expressions, and return "true" for expressions that are valid MathML. In particular, it need not render or interpret the MathML expressions at all.
-
A MathML computer-algebra interface based on content markup might choose to ignore all presentation markup. Provided the interface accepts all valid MathML expressions including those containing presentation markup, it would be technically correct to characterize the application as MathML-input-conformantJ.
-
An equation editor might have an internal data representation that makes it easy to export some equations as MathML but not others. If the editor exports the simple equations as valid MathML, and merely displays an error message to the effect that conversion failed for the others, it is still technically MathML-output-conformantJ.
7.2.1.1 MathML Test Suite and Validator
As the previous examples show, to be useful, the concept of MathML conformanceJ frequently involves a judgment about what parts of the language are meaningfully implemented, as opposed to parts that are merely processed in a technically correct way with respect to the definitions of conformanceJ. This requires some mechanism for giving a quantitative statement about which parts of MathML are meaningfully implemented by a given application. To this end, the W3C Math Working Group has provided a test suite.
The test suite consists of a large number of MathML expressions categorized by markup category and dominant MathML element being tested. The existence of this test suite makes it possible, for example, to characterize quantitatively the hypothetical computer algebra interface mentioned above by saying that it is a MathML-input-conformantJ processor which meaningfully implements MathML content markup, including all of the expressions in the content markup section of the test suite.
Developers who choose not to implement parts of the MathML specification in a meaningful way are encouraged to itemize the parts they leave out by referring to specific categories in the test suite.
For MathML-output-conformantJ processors, there is also a MathML validator accessible over the Web. Developers of MathML-output-conformantJ processors are encouraged to verify their output using this validator.
Customers of MathML applications who wish to verify claims as to which parts of the MathML specification are implemented by an application are encouraged to use the test suites as a part of their decision processes.
7.2.1.2 Deprecated MathML 1.x Features
MathML 2.0 contains a number of MathML 1.x features which are now deprecated. The following points define what it means for a feature to be deprecated, and clarify the relation between deprecated features and MathML 2.0 conformanceJ.
-
In order to be MathML-output-conformantJ, authoring tools may not generate MathML markup containing deprecated features.
-
In order to be MathML-input-conformantJ, rendering/reading tools must support deprecated features if they are to be in conformance with MathML 1.xJ. They do not have to support deprecated features to be considered in conformance with MathML 2.0J. However, all tools are encouraged to support the old forms as much as possible.
-
In order to be MathML-roundtrip-conformantJ, a processor need only preserve MathML equivalence on expressions containing no deprecated features.
7.2.1.3 MathML 2.0 Extension Mechanisms and Conformance
MathML 2.0 defines three extension mechanisms: The mglyph
element provides a way of displaying glyphs for non-Unicode
characters, and glyph variants for existing Unicode characters; the
maction element uses attributes from other namespaces to obtain
implementation-specific parameters; and content markup makes use of
the definitionURL attribute to point to external
definitions of mathematical semantics.
These extension mechanisms are important because they provide a way
of encoding concepts that are beyond the scope of MathML 2.0, which
allows MathML to be used for exploring new ideas not yet susceptible
to standardization. However, as new ideas take hold, they may become
part of future standards. For example, an emerging character that
must be represented by an mglyph element today may be
assigned a Unicode codepoint in the future. At that time,
representing the character directly by its Unicode codepoint would be
preferable.
Because the possibility of future obsolescence is inherent in the
use of extension mechanisms to facilitate the discussion of new ideas,
MathML 2.0 makes no conformance requirement concerning the use of
extension mechanisms, even when alternative standard markup is
available. For example, using an mglyph element to represent
an 'x' is permitted. However, authors and implementors are
strongly encouraged to use standard markup whenever possible.
Similarly, maintainers of documents employing MathML 2.0 extension
mechanisms are encouraged to monitor relevant standards activity
(e.g. Unicode, OpenMath, etc) and update documents as more
standardized markup becomes available.
7.2.2 Handling of Errors
If a MathML-input-conformantJ application receives input containing one or
more elements with an illegal number or type of attributes or child
schemata, it should nonetheless attempt to render all the input in an
intelligible way, i.e. to render normally those parts of the input that
were valid, and to render error messages (rendered as if enclosed in
an merror
element) in place of invalid expressions.
MathML-output-conformantJ applications such as editors and translators may
choose to generate merror expressions to signal
errors in their input. This is usually preferable to generating valid, but
possibly erroneous, MathML.
7.2.3 Attributes for unspecified data
The MathML attributes described in the MathML specification are necessary for presentation and content markup. Ideally, the MathML attributes should be an open-ended list so that users can add specific attributes for specific renderers. However, this cannot be done within the confines of a single XML DTD. Although it can be done using extensions of the standard DTD, some authors will wish to use non-standard attributes to take advantage of renderer-specific capabilities while remaining strictly in conformanceJ with the standard DTD.
To allow this, the MathML 1.0 specification [MathML1]J
allowed the attribute other on all elements, for use as a hook to pass
on renderer-specific information. In particular, it was intended as a hook for
passing information to audio renderers, computer algebra systems, and for pattern
matching in future macro/extension mechanisms. The motivation for this approach to
the problem was historical, looking to PostScript, for example, where comments are
widely used to pass information that is not part of PostScript.
In the meantime, however, the development of a general XML namespace
mechanism has made the use of the other
attribute obsolete. In MathML 2.0, the other
attribute is deprecated
in favor of the use of namespace
prefixes to identify non-MathML attributes.
For example, in MathML 1.0, it was recommended that if additional information
was used in a renderer-specific implementation for the maction element (Section 3.6.1 Bind Action to Sub-Expression (maction)),
that information should be passed in using the other attribute:
<maction actiontype="highlight" other="color='#ff0000'"> expression </maction>
In MathML 2.0, a color attribute from another
namespace would be used:
<body xmlns:my="http://www.example.com/MathML/extensions"> ... <maction actiontype="highlight" my:color="#ff0000"> expression </maction> ... </body>
Note that the intent of allowing non-standard attributes is not to encourage software developers to use this as a loophole for circumventing the core conventions for MathML markup. Authors and applications should use non-standard attributes judiciously.
7.3 Future Extensions
If MathML is to remain useful in the future, it is to be expected that MathML will need to be extended and revised in various ways. Some of these extensions can be easily foreseen; for example, as work on behavioral extensions to CSS proceeds, MathML will likely need to be extended as well.
Similarly, there are several kinds of functionality that are fairly obvious candidates for future MathML extensions. These include macros, style sheets, and perhaps a general facility for "labeled diagrams". However, there will no doubt be other desirable extensions to MathML that will only emerge as MathML is widely used. For these extensions, the W3C Math Working Group relies on the extensible architecture of XML, and the common sense of the larger Web community.
7.3.1 Macros and Style Sheets
The development of style-sheet mechanisms for XML is part of the ongoing XML activity of the World Wide Web Consortium. Both XSL and CSS are working to incorporate greater support for mathematics.
In particular, XSL Transformations [XSLT] are likely to have a large impact on the future development of MathML. Macros have traditionally contributed greatly the usability and effectiveness of mathematics encodings. Further work developing applications of XSLT tailored specifically to MathML is clearly called for.
Some of the possible uses of macro capabilities for MathML include:
- Abbreviation
-
One common use of macros is for abbreviation. Authors needing to repeat some complicated but constant notation can define a macro. This greatly facilitates hand authoring. Macros that allow for substitution of parameters facilitate such usage even further.
- Extension of Content Markup
-
By defining macros for semantic objects, for example a binomial coefficient, or a Bessel function, one can in effect extend the content markup for MathML. Such a macro could include an explicit semantic binding, or such a binding could be easily added by an external application. Narrowly defined disciplines should be able to easily introduce standardized content markup by using standard macro packages. For example, the OpenMath project could release macro packages for attaching OpenMath content markup.
- Rendering and Style Control
-
Another basic way in which macros are often used is to provide a way of controlling style and rendering behavior by replacing high-level macro definitions. This is especially important for controlling the rendering behavior of MathML content tags in a context sensitive way. Such a macro capability is also necessary to provide a way of attaching renderings to user-defined XML extensions to the MathML core.
- Accessibility
-
Reader-controlled style sheets are important in providing accessibility to MathML. For example, a reader listening to a voice renderer might, by default, hear a bit of MathML presentation markup read as "D sub x sup 2 of f". Knowing the context to be multi-variable calculus, the reader may wish to use a style sheet or macro package that instructs the renderer to render this
<msubsup>element as "second derivative with respect to x of f".
7.3.2 XML Extensions to MathML
The set of elements and attributes specified in the MathML specification are necessary for rendering common mathematical expressions. It is recognized that not all mathematical notation is covered by this set of elements, that new notations are continually invented, and that sub-communities within mathematics often have specialized notations; and furthermore that the explicit extension of a standard is a necessarily slow and conservative process. This implies that the MathML standard could never explicitly cover all the presentational forms used by every sub-community of authors and readers of mathematics, much less encode all mathematical content.
In order to facilitate the use of MathML by the widest possible audience, and to enable its smooth evolution to encompass more notational forms and more mathematical content (perhaps eventually covered by explicit extensions to the standard), the set of tags and attributes is open-ended, in the sense described in this section.
MathML is described by an XML DTD, which necessarily limits the elements and attributes to those occurring in the DTD. Renderers desiring to accept non-standard elements or attributes, and authors desiring to include these in documents, should accept or produce documents that conform to an appropriately extended XML DTD that has the standard MathML DTD as a subset.
MathML-compliantJ renderers are allowed, but not required, to accept
non-standard elements and attributes, and to render them in any way. If a
renderer does not accept some or all non-standard tags, it is encouraged
either to handle them as errors as described above for elements with the
wrong number of arguments, or to render their arguments as if they were
arguments to an mrow, in either case rendering all
standard parts of the input in the normal way.