1. Introduction
This section is not normative.
The CSS visual formatting model describes a coordinate system within each element is positioned. Positions and sizes in this coordinate space can be thought of as being expressed in pixels, starting in the origin of point with positive values proceeding to the right and down.
This coordinate space can be modified with the transform property. Using transform, elements can be translated, rotated and scaled.
1.1. Module Interactions
This module defines a set of CSS properties that affect the visual rendering of elements to which those properties are applied; these effects are applied after elements have been sized and positioned according to the visual formatting model from [CSS2]. Some values of these properties result in the creation of a containing block, and/or the creation of a stacking context.
Transforms affect the rendering of backgrounds on elements with a value of fixed for the background-attachment property, which is specified in [CSS3BG].
Transforms affect the client rectangles returned by the Element Interface Extensions getClientRects() and getBoundingClientRect(), which are specified in [CSSOM-VIEW].
Transforms affect the computation of the scrollable overflow region as described by [CSS-OVERFLOW-3].
1.2. CSS Values
This specification follows the CSS property definition conventions from [CSS2]. Value types not defined in this specification are defined in CSS Values & Units [CSS-VALUES-3]. Other CSS modules may expand the definitions of these value types.
In addition to the property-specific values listed in their definitions, all properties defined in this specification also accept the CSS-wide keywords keywords as their property value. For readability they have not been repeated explicitly.
2. Terminology
When used in this specification, terms have the meanings assigned in this section.
- transformable element
-
A transformable element is an element in one of these categories:
-
all elements whose layout is governed by the CSS box model except for non-replaced inline boxes, table-column boxes, and table-column-group boxes [CSS2],
-
all SVG paint server elements, the clipPath element and SVG renderable elements with the exception of any descendant element of text content elements [SVG2].
-
- transformed element
-
An element with a computed value other than none for the transform property.
- user coordinate system
- local coordinate system
-
In general, a coordinate system defines locations and distances on the current canvas. The current local coordinate system (also user coordinate system) is the coordinate system that is currently active and which is used to define how coordinates and lengths are located and computed, respectively, on the current canvas. The current user coordinate system has its origin at the top-left of a reference box specified by the transform-box property. Percentage values are relative to the dimension of this reference box. One unit equals one CSS pixel.
- transformation matrix
-
A matrix that defines the mathematical mapping from one coordinate system into another. It is computed from the values of the transform and transform-origin properties as described below.
- current transformation matrix (CTM)
-
A matrix that defines the mapping from the local coordinate system into the viewport coordinate system.
- 2D matrix
-
A 3x2 transformation matrix, or a 4x4 matrix where the items m31, m32, m13, m23, m43, m14, m24, m34 are equal to 0 and m33, m44 are equal to 1.
- identity transform function
-
A transform function that is equivalent to a identity 4x4 matrix (see Mathematical Description of Transform Functions). Examples for identity transform functions are translate(0), translateX(0), translateY(0), scale(1), scaleX(1), scaleY(1), rotate(0), skew(0, 0), skewX(0), skewY(0) and matrix(1, 0, 0, 1, 0, 0).
- post-multiply
- post-multiplied
-
Term A post-multiplied by term B is equal to A · B.
- pre-multiply
- pre-multiplied
-
Term A pre-multiplied by term B is equal to B · A.
- multiply
-
Multiply term A by term B is equal to A · B.
3. The Transform Rendering Model
This section is normative.
Specifying a value other than none for the transform property establishes a new local coordinate system at the element that it is applied to. The mapping from where the element would have rendered into that local coordinate system is given by the element’s transformation matrix.
The transformation matrix is computed from the transform and transform-origin properties as follows:
-
Start with the identity matrix.
-
Translate by the computed X and Y of transform-origin
-
Multiply by each of the transform functions in transform property from left to right
-
Translate by the negated computed X and Y values of transform-origin
An element has a transform property that is not none.
div {
transform-origin : 0 0 ;
transform : translate ( -10 px , -20 px ) scale ( 2 ) rotate ( 45 deg );
}
The transform-origin property is set to 0 0 and can be omitted. The transformation matrix TM gets computed by post-multying the <translate()>, <scale()> and <rotate()> <transform-function>s.

Transforms apply to transformable elements.
The coordinate space is a coordinate system with two axes: the X axis increases horizontally to the right; the Y axis increases vertically downwards.
Transformations are cumulative. That is, elements establish their local coordinate system within the coordinate system of their parent.
To map a point plocal with the coordinate pair xlocal and ylocal from the local coordinate system of an element into the parent’s coordinate system, post-multiply the transformation matrix TM of the element by plocal. The result is the mapped point pparent with the coordinate pair xparent and yparent in the parent’s local coordinate system.
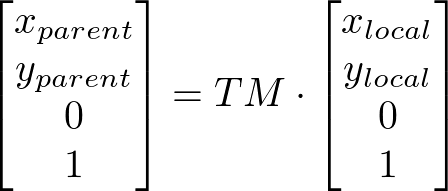
From the perspective of the user, an element effectively accumulates all the transform properties of its ancestors as well as any local transform applied to it. The accumulation of these transforms defines a current transformation matrix (CTM) for the element.
The current transformation matrix is computed by post-multiplying all transformation matrices starting from the viewport coordinate system and ending with the transformation matrix of an element.
< svg xmlns = "http://www.w3.org/2000/svg" >
< g transform = "translate(-10, 20)" >
< g transform = "scale(2)" >
< rect width = "200" height = "200" transform = "rotate(45)" />
</ g >
</ g >
</ svg >
-
translate(-10, 20) computes to the transformation matrix T1
-
scale(2) computes to the transformation matrix T2
-
rotate(45) computes to the transformation matrix T3
The CTM for the SVG rect element is the result of multiplying T1, T2 and T3 in order.
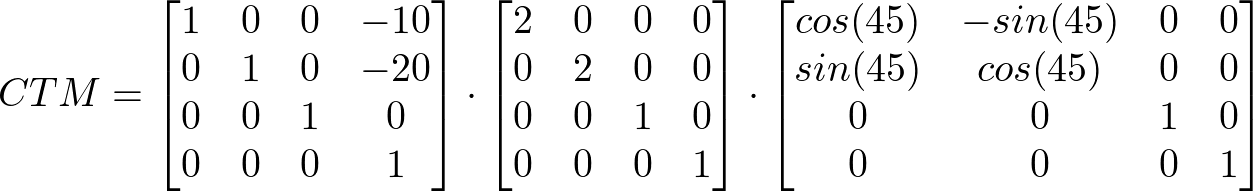
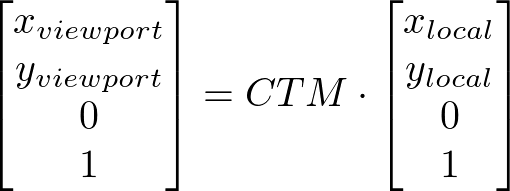
To map a point plocal with the coordinate pair xlocal and ylocal from the local coordinate system of the SVG rect element into the viewport coordinate system, post-multiply the current transformation matrix CTM of the element by plocal. The result is the mapped point pviewport with the coordinate pair xviewport and yviewport in the viewport coordinate system.
Note: Transformations do affect the visual rendering, but have no affect on the CSS layout other than affecting overflow. Transforms are also taken into account when computing client rectangles exposed via the Element Interface Extensions, namely getClientRects() and getBoundingClientRect(), which are specified in [CSSOM-VIEW].
div {
transform : translate ( 100 px , 100 px );
}
This transform moves the element by 100 pixels in both the X and Y directions.
div {
height : 100 px ; width : 100 px ;
transform-origin : 50 px 50 px ;
transform : rotate ( 45 deg );
}
The transform-origin property moves the point of origin by 50 pixels in both the X and Y directions. The transform rotates the element clockwise by 45° about the point of origin. After all transform functions were applied, the translation of the origin gets translated back by -50 pixels in both the X and Y directions.
div {
height : 100 px ; width : 100 px ;
transform : translate ( 80 px , 80 px ) scale ( 1.5 , 1.5 ) rotate ( 45 deg );
}
The visual appareance is as if the div element gets translated by 80px to the bottom left direction, then scaled up by 150% and finally rotated by 45°.
Each <transform-function> can get represented by a corresponding 4x4 matrix. To map a point from the coordinate space of the div box to the coordinate space of the parent element, these transforms get multiplied in the reverse order:
-
The rotation matrix gets post-multiplied by the scale matrix.
-
The result of the previous multiplication is then post-multiplied by the translation matrix to create the accumulated transformation matrix.
-
Finally, the point to map gets pre-multiplied with the accumulated transformation matrix.
For more details see The Transform Function Lists.
Note: The identical rendering can be obtained by nesting elements with the equivalent transforms:
< div style = "transform: translate(80px, 80px)" >
< div style = "transform: scale(1.5, 1.5)" >
< div style = "transform: rotate(45deg)" ></ div >
</ div >
</ div >
For elements whose layout is governed by the CSS box model, the transform property does not affect the flow of the content surrounding the transformed element. However, the extent of the overflow area takes into account transformed elements. This behavior is similar to what happens when elements are offset via relative positioning. Therefore, if the value of the overflow property is scroll or auto, scrollbars will appear as needed to see content that is transformed outside the visible area. Specifically, transforms can extend (but do not shrink) the size of the overflow area, which is computed as the union of the bounds of the elements before and after the application of transforms.
For elements whose layout is governed by the CSS box model, any value other than none for the transform property results in the creation of a stacking context. Implementations must paint the layer it creates, within its parent stacking context, at the same stacking order that would be used if it were a positioned element with z-index: 0. If an element with a transform is positioned, the z-index property applies as described in [CSS2], except that auto is treated as 0 since a new stacking context is always created.
For elements whose layout is governed by the CSS box model, any value other than none for the transform property also causes the element to establish a containing block for all descendants. Its padding box will be used to layout for all of its absolute-position descendants, fixed-position descendants, and descendant fixed background attachments.
< style >
# container {
width : 300 px ;
height : 200 px ;
border : 5 px dashed black ;
padding : 5 px ;
overflow : scroll ;
}
# bloat {
height : 1000 px ;
}
# child {
right : 0 ;
bottom : 0 ;
width : 10 % ;
height : 10 % ;
background : green ;
}
</ style >
< div id = "container" style = "transform:translateX(5px);" >
< div id = "bloat" ></ div >
< div id = "child" style = "position:fixed;" ></ div >
</ div >
versus
< div id = "container" style = "position:relative; z-index:0; left:5px;" >
< div id = "bloat" ></ div >
< div id = "child" style = "position:absolute;" ></ div >
</ div >
Fixed backgrounds on the root element are affected by any transform specified for that element. For all other elements that are effected by a transform (i.e. have a transform applied to them, or to any of their ancestor elements), a value of fixed for the background-attachment property is treated as if it had a value of scroll. The computed value of background-attachment is not affected.
Note: If the root element is transformed, the transformation applies to the entire canvas, including any background specified for the root element. Since the background painting area for the root element is the entire canvas, which is infinite, the transformation might cause parts of the background that were originally off-screen to appear. For example, if the root element’s background were repeating dots, and a transformation of scale(0.5) were specified on the root element, the dots would shrink to half their size, but there will be twice as many, so they still cover the whole viewport.
4. The transform Property
A transformation is applied to the coordinate system an element renders into through the transform property. This property contains a list of transform functions. The final transformation value for a coordinate system is obtained by converting each function in the list to its corresponding matrix like defined in Mathematical Description of Transform Functions, then multiplying the matrices.
| Name: | transform |
|---|---|
| Value: | none | <transform-list> |
| Initial: | none |
| Applies to: | transformable elements |
| Inherited: | no |
| Percentages: | refer to the size of reference box |
| Computed value: | as specified, but with lengths made absolute |
| Canonical order: | per grammar |
| Animation type: | transform list, see interpolation rules |
Any computed value other than none for the transform affects containing block and stacking context, as described in §3 The Transform Rendering Model.
<transform-list> = <transform-function>+
4.1. Serialization of <transform-function>s
To serialize the <transform-function>s, serialize as per their individual grammars, in the order the grammars are written in, avoiding <calc()> expressions where possible, avoiding <calc()> transformations, omitting components when possible without changing the meaning, joining space-separated tokens with a single space, and following each serialized comma with a single space.
4.2. Serialization of the computed value of <transform-list>
A <transform-list> for the computed value is serialized to one <matrix()> function by the following algorithm:
-
Let transform be a 4x4 matrix initialized to the identity matrix. The elements m11, m22, m33 and m44 of transform must be set to 1 all other elements of transform must be set to 0.
-
Post-multiply all <transform-function>s in <transform-list> to transform.
-
Serialize transform to a <matrix()> function.
5. The transform-origin Property
| Name: | transform-origin |
|---|---|
| Value: | [ left | center | right | top | bottom | <length-percentage> ] | [ left | center | right | <length-percentage> ] [ top | center | bottom | <length-percentage> ] <length>? | [[ center | left | right ] && [ center | top | bottom ]] <length>? |
| Initial: | 50% 50% |
| Applies to: | transformable elements |
| Inherited: | no |
| Percentages: | refer to the size of reference box |
| Computed value: | see background-position |
| Canonical order: | per grammar |
| Animation type: | by computed value |
The values of the transform and transform-origin properties are used to compute the transformation matrix, as described above.
If only one value is specified, the second value is assumed to be center. If one or two values are specified, the third value is assumed to be 0px.
If two or more values are defined and either no value is a keyword, or the only used keyword is center, then the first value represents the horizontal position (or offset) and the second represents the vertical position (or offset). A third value always represents the Z position (or offset) and must be of type <length>.
- <length-percentage>
-
A percentage for the horizontal offset is relative to the width of the reference box. A percentage for the vertical offset is relative to the height of the reference box. The value for the horizontal and vertical offset represent an offset from the top left corner of the reference box.
- <length>
-
A length value gives a fixed length as the offset. The value for the horizontal and vertical offset represent an offset from the top left corner of the reference box.
- top
-
Computes to 0% for the vertical position.
- right
-
Computes to 100% for the horizontal position.
- bottom
-
Computes to 100% for the vertical position.
- left
-
Computes to 0% for the horizontal position.
- center
-
Computes to 50% (left 50%) for the horizontal position if the horizontal position is not otherwise specified, or 50% (top 50%) for the vertical position if it is.
For SVG elements without associated CSS layout box the initial used value is 0 0 as if the user agent style sheet contained:
*:not(svg), *:not(foreignObject) > svg {
transform-origin : 0 0 ;
}
The transform-origin property is a resolved value special case property like height. [CSSOM]
6. Transform reference box: the transform-box property
| Name: | transform-box |
|---|---|
| Value: | content-box | border-box | fill-box | stroke-box | view-box |
| Initial: | view-box |
| Applies to: | transformable elements |
| Inherited: | no |
| Percentages: | N/A |
| Computed value: | specified keyword |
| Canonical order: | per grammar |
| Animation type: | discrete |
All transformations defined by the transform and transform-origin property are relative to the position and dimensions of the reference box of the element. The reference box is specified by one of the following:
- content-box
-
Uses the content box as reference box. The reference box of a table is the border box of its table wrapper box, not its table box.
- border-box
-
Uses the border box as reference box. The reference box of a table is the border box of its table wrapper box, not its table box.
- fill-box
-
Uses the object bounding box as reference box.
- stroke-box
-
Uses the stroke bounding box as reference box.
- view-box
-
Uses the nearest SVG viewport as reference box.
If a
viewBoxattribute is specified for the SVG viewport creating element:
For the SVG pattern element, the reference box gets defined by the patternUnits attribute [SVG2].
For the SVG linearGradient and radialGradient elements, the reference box gets defined by the gradientUnits attribute [SVG2].
For the SVG clipPath element, the reference box gets defined by the clipPathUnits attribute [CSS-MASKING].
A reference box adds an additional offset to the origin specified by the transform-origin property.
For SVG elements without associated CSS layout box, the used value for content-box is fill-box and for border-box is stroke-box.
For elements with associated CSS layout box, the used value for fill-box is content-box and for stroke-box and view-box is border-box.
7. The SVG transform Attribute
7.1. SVG presentation attributes
The transform-origin CSS property is also a presentation attribute and extends the list of existing presentation attributes [SVG2].
SVG 2 defines the transform, patternTransform, gradientTransform attributes as presentation attributes, represented by the CSS transform property [SVG2].
The participation in the CSS cascade is determined by the specificity of presentation attributes in the SVG specification. According to SVG, user agents conceptually insert a new author style sheet for presentation attributes, which is the first in the author style sheet collection [SVG2].
<svg xmlns= "http://www.w3.org/2000/svg" >
<style>
.container {
transform: translate(100px, 100px);
}
</style>
<g class= "container" transform= "translate(200 200)" >
<rect width= "100" height= "100" fill= "blue" />
</g>
</svg>
Because of the participation to the CSS cascade, the transform style property overrides the transform attribute. Therefore the container gets translated by 100px in both the horizontal and the vertical directions, instead of 200px.
7.2. Syntax of the SVG transform attribute
For backwards compatibility reasons, the syntax of the transform, patternTransform, gradientTransform attributes differ from the syntax of the transform CSS property. For the attributes, there is no support for additional <transform-function>s defined for the CSS transform property. Specifically, <translateX()>, <translateY()>, <scaleX()>, <scaleY()> and <skew()> are not supported by the transform, patternTransform, gradientTransform attributes.
The following list uses the Backus-Naur Form (BNF) to define values for the transform, patternTransform and gradientTransform attributes followed by an informative rail road diagram. The following notation is used:
-
*: 0 or more
-
+: 1 or more
-
?: 0 or 1
-
(): grouping
-
|: separates alternatives
-
double quotes surround literals. Literals consists of letters [CSS-SYNTAX-3], left parenthesis and right parenthesis.
-
<number-token> defined by the CSS Syntax module [CSS-SYNTAX-3].
Note: The syntax reflects implemented behavior in user agents and differs from the syntax defined by SVG 1.1.
- left parenthesis (
- U+0028 LEFT PARENTHESIS
- right parenthesis )
- U+0029 RIGHT PARENTHESIS
- comma
- U+002C COMMA.
- wsp
- Either a U+000A LINE FEED, U+000D CARRIAGE RETURN, U+0009 CHARACTER TABULATION, or U+0020 SPACE.
- comma-wsp
-
(wsp+ comma? wsp*) | (comma wsp*)
- translate
-
"translate" wsp* "(" wsp* number ( comma-wsp? number )? wsp* ")" - scale
-
"scale" wsp* "(" wsp* number ( comma-wsp? number )? wsp* ")" - rotate
-
"rotate" wsp* "(" wsp* number ( comma-wsp? number comma-wsp? number )? wsp* ")" - skewX
-
"skewY" wsp* "(" wsp* number wsp* ")" - skewY
-
"skewY" wsp* "(" wsp* number wsp* ")" - matrix
-
"matrix" wsp* "(" wsp* number comma-wsp? number comma-wsp? number comma-wsp? number comma-wsp? number comma-wsp? number wsp* ")" - transform
-
matrix | translate | scale | rotate | skewX | skewY
- transforms
-
transform | transform comma-wsp transforms
- transform-list
-
wsp* transforms? wsp*
7.3. SVG transform functions
SVG transform functions of the transform, patternTransform, gradientTransform attributes defined by the syntax above are mapped to CSS <transform-function>s as follows:
| SVG transform function | CSS <transform-function> | Additional notes |
|---|---|---|
| translate | <translate()> | Number values interpreted as CSS <length> types with px units. |
| scale | <scale()> | |
| rotate | <rotate()> | Only single value version. Number value interpreted as CSS <angle> type with deg unit. |
| skewX | <skewX()> | Number value interpreted as CSS <angle> type with deg unit. |
| skewY | <skewY()> | Number value interpreted as CSS <angle> type with deg unit. |
| matrix | <matrix()> |
The SVG transform function rotate with 3 values can not be mapped to a corresponding CSS <transform-function>. The 2 optional number values represent a horizontal translation value cx followed by a vertical translation value cy. Both number values get interpreted as CSS <length> types with px units and define the origin for rotation. The behavior is equivalent to an initial translation by cx, cy, a rotation defined by the first number value interpreted as <angle> type with deg unit followed by a translation by -cx, -cy.
A transform attribute can be the start or end value of a CSS Transition. If the value of a transform attribute is the start or end value of a CSS Transition and the SVG transform list contains at least one rotate transform function with 3 values, the individual SVG transform functions must get post-multiplied and the resulting matrix must get mapped to a <matrix()> CSS <transform-function> and used as start/end value of the CSS Transition.
7.4. User coordinate space
For the pattern element, the patternTransform attribtue and transform property define an additional transformation in the pattern coordinate system. See patternUnits attribute for details [SVG2].
For the linearGradient and radialGradient elements, the gradientTransform attribtue and transform property define an additional transformation in the gradient coordinate system. See gradientUnits attribute for details [SVG2].
For the clipPath element, the transform attribtue and transform property define an additional transformation in the clipping path coordinate space. See clipPathUnits attribute for details [CSS-MASKING].
For all other transformable elements the transform attribute and transform property define a transformation in the current user coordinate system of the parent. All percentage values of the transform attribute are relative to the element’s reference box.
The transform-origin property on the pattern in the following example specifies a 50% translation of the origin in the horizontal and vertical dimension. The transform property specifies a translation as well, but in absolute lengths.
<svg xmlns= "http://www.w3.org/2000/svg" >
<style>
pattern {
transform: rotate(45deg);
transform-origin: 50% 50%;
}
</style>
<defs>
<pattern id= "pattern-1" >
<rect id= "rect1" width= "100" height= "100" fill= "blue" />
</pattern>
</defs>
<rect width= "200" height= "200" fill= "url(#pattern-1)" />
</svg>
An SVG pattern element doesn’t have a bounding box. The reference box of the referencing rect element is used instead to solve the relative values of the transform-origin property. Therefore the point of origin will get translated by 100 pixels temporarily to rotate the user space of the pattern elements content.
7.5. SVG DOM interface for the transform attribute
The SVG specification defines the "SVGAnimatedTransformList" interface in the SVG DOM to provide access to the animated and the base value of the SVG transform, gradientTransform and patternTransform attributes. To ensure backwards compatibility, this API must still be supported by user agents.
baseVal gives the author the possibility to access and modify the values of the SVG transform, patternTransform, gradientTransform attributes. To provide the necessary backwards compatibility to the SVG DOM, baseVal must reflect the values of this author style sheet. All modifications to SVG DOM objects of baseVal must affect this author style sheet immediately.
animVal represents the computed style of the transform property. Therefore it includes all applied CSS3 Transitions, CSS3 Animations or SVG Animations if any of those are underway. The computed style and SVG DOM objects of animVal can not be modified.
8. SVG Animation
8.1. The animate and set element
With this specification, the animate element and the set element can animate the data type <transform-list>.
The animation effect is post-multiplied to the underlying value for additive animate animations (see below) instead of added to the underlying value, due to the specific behavior of <transform-list> animations.
From-to, from-by and by animations are defined in SMIL to be equivalent to a corresponding values animation. However, to animations are a mixture of additive and non-additive behavior [SMIL3].
To animations on animate provide specific functionality to get a smooth change from the underlying value to the to attribute value, which conflicts mathematically with the requirement for additive transform animations to be post-multiplied. As a consequence, the behavior of to animations for animate is undefined. Authors are suggested to use from-to, from-by, by or values animations to achieve any desired transform animation.
The value "paced" is undefined for the attribute calcMode on animate for animations of the data type <transform-list>. If specified, UAs may choose the value "linear" instead. Future versions of this specification may define how paced animations can be performed on <transform-list>.
Note: The following paragraphs extend Elements, attributes and properties that can be animated [SVG11].
The introduced presentation attributes transform, patternTransform, gradientTransform and transform-origin are animatable.
With this specification the SVG basic data type <transform-list> is equivalent to a list of <transform-function>s. <transform-list> is animatable and additive. The data type can be animated using the SVG animate element and the SVG set element. SVG animations must run the same animation steps as described in section Transitions and Animations between Transform Values.
| Data type | Additive? | animate
| set
| animateColor
| animateTransform
| Notes |
|---|---|---|---|---|---|---|
| <transform-list> | yes | yes | yes | no | yes | Additive for animateTransform means that a transformation is post-multiplied to the base set of transformations.
|
8.2. Neutral element for addition
Some animations require a neutral element for addition. For transform functions this is a scalar or a list of scalars of 0. Examples of neutral elements for transform functions are translate(0), scale(0), rotate(0), skewX(0), skewY(0).
Note: This paragraph focuses on the requirements of [SMIL] and the extension defined by [SVG11]. This specification does not provide definitions of neutral elements for the other transform functions than the functions listed above.
A by animation with a by value vb is equivalent to the same animation with a values list with 2 values, the neutral element for addition for the domain of the target attribute (denoted 0) and vb, and additive="sum". [SMIL3]
<rect width= "100" height= "100" >
<animateTransform attributeName= "transform" attributeType= "XML"
type= "scale" by= "1" dur= "5s" fill= "freeze" />
</rect>
The neutral element for addition when performing a by animation with type="scale" is the value 0. Thus, performing the animation of the example above causes the rectangle to be invisible at time 0s (since the animated transform list value is scale(0)), and be scaled back to its original size at time 5s (since the animated transform list value is scale(1)).
8.3. The SVG 1.1 'attributeName' attribute
SVG 1.1 Animation defines the "attributeName" attribute to specify the name of the target attribute. For the presentation attributes gradientTransform and patternTransform it will also be possible to use the value transform. The same transform property will get animated.
In this example the gradient transformation of the linear gradient gets animated.
<linearGradient gradientTransform= "scale(2)" >
<animate attributeName= "gradientTransform" from= "scale(2)" to= "scale(4)"
dur= "3s" additive= "sum" />
<animate attributeName= "transform" from= "translate(0, 0)" to= "translate(100px, 100px)"
dur= "3s" additive= "sum" />
</linearGradient>
The linearGradient element specifies the gradientTransform presentation attribute. The two animate elements address the target attribute gradientTransform and transform. Even so all animations apply to the same gradient transformation by taking the value of the gradientTransform presentation attribute, applying the scaling of the first animation and applying the translation of the second animation one after the other.
9. The Transform Functions
The value of the transform property is a list of <transform-function>. The set of allowed transform functions is given below. In the following functions, a <zero> behaves the same as 0deg ("unitless 0" angles are preserved for legacy compat). A percentage for horizontal translations is relative to the width of the reference box. A percentage for vertical translations is relative to the height of the reference box.
9.1. 2D Transform Functions
- matrix() = matrix( <number> [, <number> ]{5,5} )
-
specifies a 2D transformation in the form of a transformation matrix of the six values a, b, c, d, e, f.
- translate() = translate( <length-percentage> [, <length-percentage> ]? )
-
specifies a 2D translation by the vector [tx, ty], where tx is the first translation-value parameter and ty is the optional second translation-value parameter. If <ty> is not provided, ty has zero as a value.
- translateX() = translateX( <length-percentage> )
-
specifies a translation by the given amount in the X direction.
- translateY() = translateY( <length-percentage> )
-
specifies a translation by the given amount in the Y direction.
- scale() = scale( <number> [, <number> ]? )
-
specifies a 2D scale operation by the [sx,sy] scaling vector described by the 2 parameters. If the second parameter is not provided, it takes a value equal to the first. For example, scale(1, 1) would leave an element unchanged, while scale(2, 2) would cause it to appear twice as long in both the X and Y axes, or four times its typical geometric size.
- scaleX() = scaleX( <number> )
-
specifies a 2D scale operation using the [sx,1] scaling vector, where sx is given as the parameter.
- scaleY() = scaleY( <number> )
-
specifies a 2D scale operation using the [1,sy] scaling vector, where sy is given as the parameter.
- rotate() = rotate( [ <angle> | <zero> ] )
-
specifies a 2D rotation by the angle specified in the parameter about the origin of the element, as defined by the transform-origin property. For example, rotate(90deg) would cause elements to appear rotated one-quarter of a turn in the clockwise direction.
- skew() = skew( [ <angle> | <zero> ] [, [ <angle> | <zero> ] ]? )
-
specifies a 2D skew by [ax,ay] for X and Y. If the second parameter is not provided, it has a zero value.
skew() exists for compatibility reasons, and should not be used in new content. Use skewX() or skewY() instead, noting that the behavior of skew() is different from multiplying skewX() with skewY().
- skewX() = skewX( [ <angle> | <zero> ] )
-
specifies a 2D skew transformation along the X axis by the given angle.
- skewY() = skewY( [ <angle> | <zero> ] )
-
specifies a 2D skew transformation along the Y axis by the given angle.
9.2. Transform function primitives and derivatives
Some transform functions can be represented by more generic transform functions. These transform functions are called derived transform functions, and the generic transform functions are called primitive transform functions. Two-dimensional primitives and their derived transform functions are:
- translate()
- for <translateX()>, <translateY()> and <translate()>.
- scale()
- for <scaleX()>, <scaleY()> and <scale()>.
10. The Transform Function Lists
If a list of <transform-function>s is provided, then the net effect is as if each transform function had been specified separately in the order provided.
That is, in the absence of other styling that affects position and dimensions, a nested set of transforms is equivalent to a single list of transform functions, applied from the coordinate system of the ancestor to the local coordinate system of a given element. The resulting transform is the matrix multiplication of the list of transforms.
< div style = "transform: translate(-10px, -20px) scale(2) rotate(45deg)" />
is functionally equivalent to:
< div style = "transform: translate(-10px, -20px)" id = "root" >
< div style = "transform: scale(2)" >
< div style = "transform: rotate(45deg)" >
</ div >
</ div >
</ div >
If a transform function causes the current transformation matrix of an object to be non-invertible, the object and its content do not get displayed.
The object in the following example gets scaled by 0.
< style >
. box {
transform : scale( 0 );
}
</ style >
< div class = "box" >
Not visible
</ div >
The scaling causes a non-invertible CTM for the coordinate space of the div box. Therefore neither the div box, nor the text in it get displayed.
11. Interpolation of Transforms
Interpolation of transform function lists is performed as follows:
-
If both Va and Vb are none:
-
Vresult is none.
-
-
Treating none as a list of zero length,
if Va or Vb differ in length:
-
extend the shorter list to the length of the longer list, setting the function at each additional position to the identity transform function matching the function at the corresponding position in the longer list. Both transform function lists are then interpolated following the next rule.
-
-
Let Vresult be an empty list.
Beginning at the start of Va and Vb,
compare the corresponding functions at each position:
-
While the functions have either the same name, or are derivatives of the same primitive transform function, interpolate the corresponding pair of functions as described in §12 Interpolation of primitives and derived transform functions and append the result to Vresult.
-
If the pair do not have a common name or primitive transform function, post-multiply the remaining transform functions in each of Va and Vb respectively to produce two 4x4 matrices. Interpolate these two matrices as described in §13 Interpolation of Matrices, append the result to Vresult, and cease iterating over Va and Vb.
For example, if Va is rotate(0deg) scale(1) translate(20px) and Vb is rotate(270deg) translate(10px) scale(2), the rotate(0deg) and rotate(360deg) functions will be interpolated according to §12 Interpolation of primitives and derived transform functions while the remainder of each list—scale(1) translate(20px) and translate(10px) scale(2)— will first be converted to equivalent 4x4 matrices and then interpolated as described in §13 Interpolation of Matrices. A previous version of this specification did not attempt to interpolate matching pairs of transform functions unless all functions in the list matched. As a result, the two lists in this example would be interpolated using matrix interpolation only and the rotate(360deg) component of the second list would be lost.
-
In some cases, an animation might cause a transformation matrix to be singular or non-invertible. For example, an animation in which scale moves from 1 to -1. At the time when the matrix is in such a state, the transformed element is not rendered.
12. Interpolation of primitives and derived transform functions
Two transform functions with the same name and the same number of arguments are interpolated numerically without a former conversion. The calculated value will be of the same transform function type with the same number of arguments. Special rules apply to <matrix()>.
The two transform functions translate(0) and translate(100px) are of the same type, have the same number of arguments and therefore can get interpolated numerically. translateX(100px) is not of the same type and translate(100px, 0) does not have the same number of arguments, therefore these transform functions can not get interpolated without a former conversion step.
Two different types of transform functions that share the same primitive, or transform functions of the same type with different number of arguments can be interpolated. Both transform functions need a former conversion to the common primitive first and get interpolated numerically afterwards. The computed value will be the primitive with the resulting interpolated arguments.
The following example describes a transition from translateX(100px) to translateY(100px) in 3 seconds on hovering over the div box. Both transform functions derive from the same primitive translate() and therefore can be interpolated.
div {
transform : translateX ( 100 px );
}
div:hover {
transform : translateY ( 100 px );
transition : transform 3 s ;
}
For the time of the transition both transform functions get transformed to the common primitive. translateX(100px) gets converted to translate(100px, 0) and translateY(100px) gets converted to translate(0, 100px). Both transform functions can then get interpolated numerically.
If both transform functions share a primitive in the two-dimensional space, both transform functions get converted to the two-dimensional primitive. If one or both transform functions are three-dimensional transform functions, the common three-dimensional primitive is used.
In this example a two-dimensional transform function gets animated to a three-dimensional transform function. The common primitive is translate3d().
div {
transform : translateX ( 100 px );
}
div:hover {
transform : translateZ ( 100 px );
transition : transform 3 s ;
}
First translateX(100px) gets converted to translate3d(100px, 0, 0) and translateZ(100px) to translate3d(0, 0, 100px) respectively. Then both converted transform functions get interpolated numerically.
13. Interpolation of Matrices
When interpolating between two matrices, each matrix is decomposed into the corresponding translation, rotation, scale, skew. Each corresponding component of the decomposed matrices gets interpolated numerically and recomposed back to a matrix in a final step.
< style >
div {
transform : rotate( 45 deg );
}
div : hover {
transform : translate( 100 px , 100 px ) rotate( 1215 deg );
transition : transform 3 s ;
}
</ style >
< div ></ div >
The number of transform functions on the source transform rotate(45deg) differs from the number of transform functions on the destination transform translate(100px, 100px) rotate(1125deg). According to the last rule of Interpolation of Transforms, both transforms must be interpolated by matrix interpolation. With converting the transformation functions to matrices, the information about the three turns gets lost and the element gets rotated by just a quarter turn (90°).
To achieve the three and a quarter turns for the example above, source and destination transforms must fulfill the third rule of Interpolation of Transforms. Source transform could look like translate(0, 0) rotate(45deg) for a linear interpolation of the transform functions.
In the following we differ between the interpolation of two 2D matrices and the interpolation of two matrices where at least one matrix is not a 2D matrix.
If one of the matrices for interpolation is non-invertible, the used animation function must fall-back to a discrete animation according to the rules of the respective animation specification.
13.1. Supporting functions
The pseudo code in the next subsections make use of the following supporting functions:
Supporting functions (point is a 3 component vector, matrix is a 4x4 matrix, vector is a 4 component vector):
double determinant(matrix) returns the 4x4 determinant of the matrix
matrix inverse(matrix) returns the inverse of the passed matrix
matrix transpose(matrix) returns the transpose of the passed matrix
point multVecMatrix(point, matrix) multiplies the passed point by the passed matrix
and returns the transformed point
double length(point) returns the length of the passed vector
point normalize(point) normalizes the length of the passed point to 1
double dot(point, point) returns the dot product of the passed points
double sqrt(double) returns the root square of passed value
double max(double y, double x) returns the bigger value of the two passed values
double dot(vector, vector) returns the dot product of the passed vectors
vector multVector(vector, vector) multiplies the passed vectors
double sqrt(double) returns the root square of passed value
double max(double y, double x) returns the bigger value of the two passed values
double min(double y, double x) returns the smaller value of the two passed values
double cos(double) returns the cosines of passed value
double sin(double) returns the sine of passed value
double acos(double) returns the inverse cosine of passed value
double abs(double) returns the absolute value of the passed value
double rad2deg(double) transforms a value in radian to degree and returns it
double deg2rad(double) transforms a value in degree to radian and returns it
Decomposition also makes use of the following function:
point combine(point a, point b, double ascl, double bscl)
result[0] = (ascl * a[0]) + (bscl * b[0])
result[1] = (ascl * a[1]) + (bscl * b[1])
result[2] = (ascl * a[2]) + (bscl * b[2])
return result
13.2. Interpolation of 2D matrices
13.2.1. Decomposing a 2D matrix
The pseudo code below is based upon the "unmatrix" method in "Graphics Gems II, edited by Jim Arvo".
Matrices in the pseudo code use the column-major order. The first index on a matrix entry represents the column and the second index represents the row.
Input: matrix ; a 4x4 matrix
Output: translation ; a 2 component vector
scale ; a 2 component vector
angle ; rotation
m11 ; 1,1 coordinate of 2x2 matrix
m12 ; 1,2 coordinate of 2x2 matrix
m21 ; 2,1 coordinate of 2x2 matrix
m22 ; 2,2 coordinate of 2x2 matrix
Returns false if the matrix cannot be decomposed, true if it can
double row0x = matrix[0][0]
double row0y = matrix[0][1]
double row1x = matrix[1][0]
double row1y = matrix[1][1]
translate[0] = matrix[3][0]
translate[1] = matrix[3][1]
scale[0] = sqrt(row0x * row0x + row0y * row0y)
scale[1] = sqrt(row1x * row1x + row1y * row1y)
// If determinant is negative, one axis was flipped.
double determinant = row0x * row1y - row0y * row1x
if (determinant < 0)
// Flip axis with minimum unit vector dot product.
if (row0x < row1y)
scale[0] = -scale[0]
else
scale[1] = -scale[1]
// Renormalize matrix to remove scale.
if (scale[0])
row0x *= 1 / scale[0]
row0y *= 1 / scale[0]
if (scale[1])
row1x *= 1 / scale[1]
row1y *= 1 / scale[1]
// Compute rotation and renormalize matrix.
angle = atan2(row0y, row0x);
if (angle)
// Rotate(-angle) = [cos(angle), sin(angle), -sin(angle), cos(angle)]
// = [row0x, -row0y, row0y, row0x]
// Thanks to the normalization above.
double sn = -row0y
double cs = row0x
double m11 = row0x
double m12 = row0y
double m21 = row1x
double m22 = row1y
row0x = cs * m11 + sn * m21
row0y = cs * m12 + sn * m22
row1x = -sn * m11 + cs * m21
row1y = -sn * m12 + cs * m22
m11 = row0x
m12 = row0y
m21 = row1x
m22 = row1y
// Convert into degrees because our rotation functions expect it.
angle = rad2deg(angle)
return true
13.2.2. Interpolation of decomposed 2D matrix values
Before two decomposed 2D matrix values can be interpolated, the following
Input: translationA ; a 2 component vector
scaleA ; a 2 component vector
angleA ; rotation
m11A ; 1,1 coordinate of 2x2 matrix
m12A ; 1,2 coordinate of 2x2 matrix
m21A ; 2,1 coordinate of 2x2 matrix
m22A ; 2,2 coordinate of 2x2 matrix
translationB ; a 2 component vector
scaleB ; a 2 component vector
angleB ; rotation
m11B ; 1,1 coordinate of 2x2 matrix
m12B ; 1,2 coordinate of 2x2 matrix
m21B ; 2,1 coordinate of 2x2 matrix
m22B ; 2,2 coordinate of 2x2 matrix
// If x-axis of one is flipped, and y-axis of the other,
// convert to an unflipped rotation.
if ((scaleA[0] < 0 && scaleB[1] < 0) || (scaleA[1] < 0 && scaleB[0] < 0))
scaleA[0] = -scaleA[0]
scaleA[1] = -scaleA[1]
angleA += angleA < 0 ? 180 : -180
// Don’t rotate the long way around.
if (!angleA)
angleA = 360
if (!angleB)
angleB = 360
if (abs(angleA - angleB) > 180)
if (angleA > angleB)
angleA -= 360
else
angleB -= 360
Afterwards, each component of the decomposed values translation, scale, angle, m11 to m22 of the source matrix get linearly interpolated with each corresponding component of the destination matrix.
13.2.3. Recomposing to a 2D matrix
After interpolation, the resulting values are used to transform the elements user space. One way to use these values is to recompose them into a 4x4 matrix. This can be done following the pseudo code below.
Matrices in the pseudo code use the column-major order. The first index on a matrix entry represents the column and the second index represents the row.
Input: translation ; a 2 component vector
scale ; a 2 component vector
angle ; rotation
m11 ; 1,1 coordinate of 2x2 matrix
m12 ; 1,2 coordinate of 2x2 matrix
m21 ; 2,1 coordinate of 2x2 matrix
m22 ; 2,2 coordinate of 2x2 matrix
Output: matrix ; a 4x4 matrix initialized to identity matrix
matrix[0][0] = m11
matrix[0][1] = m12
matrix[1][0] = m21
matrix[1][1] = m22
// Translate matrix.
matrix[3][0] = translate[0] * m11 + translate[1] * m21
matrix[3][1] = translate[0] * m12 + translate[1] * m22
// Rotate matrix.
angle = deg2rad(angle);
double cosAngle = cos(angle);
double sinAngle = sin(angle);
// New temporary, identity initialized, 4x4 matrix rotateMatrix
rotateMatrix[0][0] = cosAngle
rotateMatrix[0][1] = sinAngle
rotateMatrix[1][0] = -sinAngle
rotateMatrix[1][1] = cosAngle
matrix = post-multiply(rotateMatrix, matrix)
// Scale matrix.
matrix[0][0] *= scale[0]
matrix[0][1] *= scale[0]
matrix[1][0] *= scale[1]
matrix[1][1] *= scale[1]
14. Mathematical Description of Transform Functions
Mathematically, all transform functions can be represented as 4x4 transformation matrices of the following form:
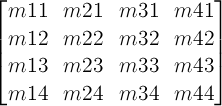
One translation unit on a matrix is equivalent to 1 pixel in the local coordinate system of the element.
-
A 2D 3x2 matrix with six parameters a, b, c, d, e and f is equivalent to the matrix:

-
A 2D translation with the parameters tx and ty is equivalent to a 3D translation where tz has zero as a value.
-
A 2D scaling with the parameters sx and sy is equivalent to a 3D scale where sz has one as a value.
-
A 2D rotation with the parameter alpha is equivalent to a 3D rotation with vector [0,0,1] and parameter alpha.
-
A 2D skew like transformation with the parameters alpha and beta is equivalent to the matrix:
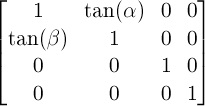
-
A 2D skew transformation along the X axis with the parameter alpha is equivalent to the matrix:
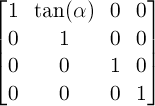
-
A 2D skew transformation along the Y axis with the parameter beta is equivalent to the matrix:
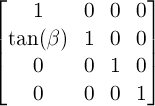
15. Privacy and Security Considerations
UAs must implement transform operations in a way attackers can not infer information and mount a timing attack.A timing attack is a method of obtaining information about content that is otherwise protected, based on studying the amount of time it takes for an operation to occur.
At this point there are no information about potential privacy or security concerns specific to this specification.
Changes
Since the 30 November 2018 Working Draft
-
No substantive changes
-
Boilerplate, styling updates for CR
Since the 30 November 2017 Working Draft
-
Remove specification text that makes patternTransform, gradientTransform presentation attributes representing the transform property. That is going to get specified by SVG 2 [SVG2].
-
Added privacy and security section.
-
Use [SVG2] definitions for transformable elements.
-
Added special syntax for transform,
gradientTransformandpatternTransformattributes. -
Clarify multiplication order by using terms post-multiply and pre-multiply.
-
Clarify index order of matrix entries in pseudo-code.
-
Clarify multiplication order in recomposition pseudo-code.
-
Clarify behavior of transform on overflow area.
-
Remove translateX(0), translateY(0), scaleX(0), scaleY(0) from the list of neutral elements.
-
Remove any reference of 3D transformations of transform function definitions.
-
Specify interpolation between <transform-list>s to match lengths and avoid matrix interpolation for the common prefix of the two lists.
-
No transform on non-replaced inline boxes, table-column boxes, and table-column-group boxes.
-
Define target coordinate space for transformations on
pattern,linearGradient,radialGradientandclipPathelements. -
Remove 3-value <rotate()> from transform function primitives.
-
Be more specific about computation of transformation matrix and current transformation matrix.
-
Define reference box for paint servers and
clipPathelement. -
Specify behavior of transform presentation attribute with 3-value-rotate as start or end value of a transition.
-
Add stroke-box and content-box to transform-box. Align box mapping behavior across all specifications.
-
Editorial changes.
Acknowledgments
The editors would like to thank Robert O’Callahan, Cameron McCormack, Tab Atkins, Gérard Talbot, L. David Baron, Rik Cabanier, Brian Birtles, Benoit Jacob, Ken Shoemake, Alan Gresley, Maciej Stochowiak, Sylvain Galineau, Rafal Pietrak, Shane Stephens, Matt Rakow, XiangHongAi, Fabio M. Costa, Nivesh Rajbhandari, Rebecca Hauck, Gregg Tavares, Graham Clift, Erik Dahlström, Alexander Zolotov, Amelia Bellamy-Royds and Boris Zbarsky for their careful reviews, comments, and corrections.