RIF Core Design

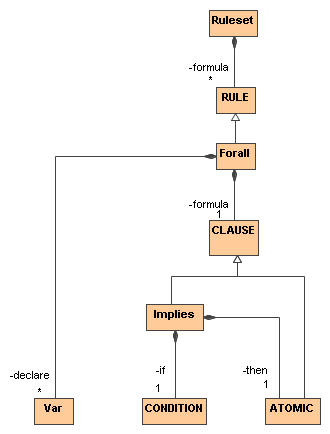
The language of positive RIF conditions determines what can appear as a body (the if-part) of a rule supported by RIF Core. As explained in Section Overview, RIF Core corresponds to definite Horn rules, and the bodies of such rules are conjunctions of atomic formulas without negation. However, it is well-known that disjunctions of such conditions can also be used in the bodies of rules without changing the essential properties of the rule language. This is based on the fundamental logical tautologies (h ← b ∨ c) ≡ ((h ← b) ∧ (h ← c)) and ∀ x (F ∧ G) ≡ (∀ x F ∧ ∀ x G). In other words, a rule with a disjunction in the body can be split into two or more rules that have no such disjunction.

In a later draft, positive RIF conditions will be extended to include builtins, i.e. calls to procedures defined outside the ruleset. The condition language will be shared among the bodies of the rules expressed in future RIF dialects, such as LP, FO, PR and RR. The condition language might also be used to uniformly express integrity contraints and queries.

This section presents a syntax and semantics for the RIF condition language, which supports primitive data types (such as xsd:long, xsd:string, xsd:decimal, xsd:time, xsd:dateTime), and the use of URIs to refer to individuals, predicates, and functions -- an essential ingredient in making RIF dialects suitable as Web languages.

To make RIF into a Web language and to provide for future higher-order dialects based on formalisms such as HiLog and Common Logic, the RIF Core language does not separate symbols used to denote individuals from symbols used as names for functions or predicates. Instead, all symbols are drawn from the same universal set. When desired, separation between the different kinds of symbols is achieved through the mechanism of sorts. In logic, the mechanism of sorts is used to classify symbols into separate groups. Currently RIF Core supports the sort rif:uri for URIs, and the sorts xsd:long (http://www.w3.org/2001/XMLSchema#long), xsd:decimal (http://www.w3.org/2001/XMLSchema#decimal), xsd:time (http://www.w3.org/2001/XMLSchema#time), xsd:string (http://www.w3.org/2001/XMLSchema#string), and xsd:dateTime (http://www.w3.org/2001/XMLSchema#dateTime). Other sorts (such as xsd:double, xsd:date, and a sort to represent temporal duration) might be added in future drafts.

To make RIF a Web language and to facilitate extensibility, the underlying logic of RIF is not only multi-sorted (i.e., allows multiple sorts), but it also allows symbols to be polymorphic (i.e., the same symbol is allowed to have several sorts). Some sorts can be disjoint and others not. RIF dialects will be able to decide which sorts will be allowed for predicate symbols, which for function symbols, and so on.

`For didactic reasons, we start with a single sort, which includes all constants, function symbols, and predicate names. The multisorted RIF logic is described in Section Multisorted RIF Logic.

2.1.1. Syntax

2.1.1.1. Abstract Syntax

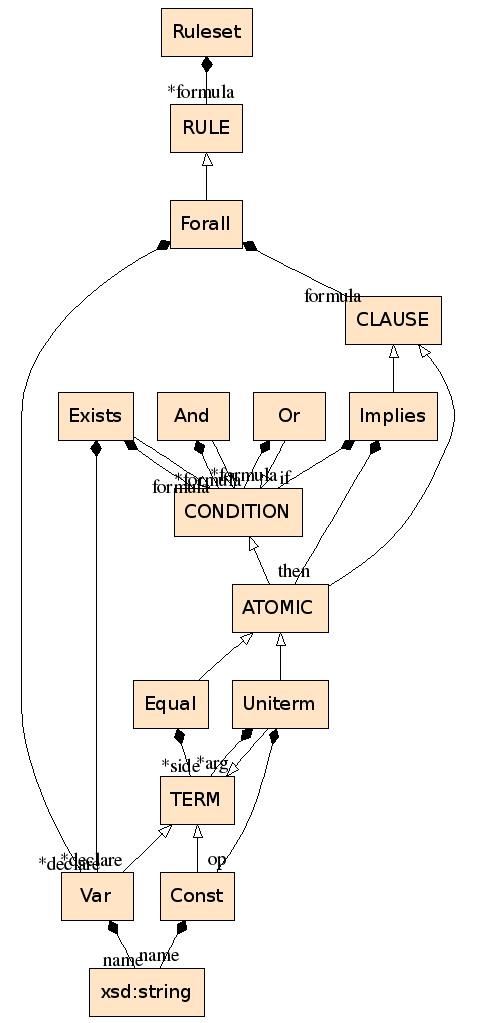
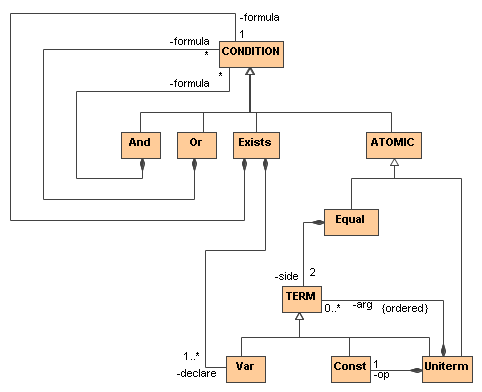
The abstract syntax of the condition language is given in asn06 as follows:

class CONDITION

    subclass And
        property formula : list of CONDITION

    subclass Or
        property formula : list of CONDITION

    subclass Exists
        property declare : list of Var
        property formula : CONDITION

    subclass ATOMIC

class ATOMIC

    subclass Equal
       property side: list of TERM

    subclass Uniterm

class TERM

    subclass Var
        property name: xsd:string

    subclass Const
        property name: xsd:string

    subclass Uniterm       
        property op: Const
        property arg: list of TERM

The multiplicity of the side property (role) of the Equal class is assumed to be exactly 2.

The abstract syntax is visualized by a UML diagram used as a schema-level device for specifying syntactic classes with generalizations as well as multiplicity- and role-labeled associations. Automatic asn06-to-UML transformation is available.

The central class of RIF, CONDITION, is specified recursively through its subclasses and their parts. The Equal class has two side roles. Two pairs of roles distinguish between the declare and formula parts of the Exists class, and between the operation (op) and arguments (arg) of the Uniterm class, where multiple arguments are subject to an ordered constraint (the natural "left-to-right" order):

The syntactic classes are partitioned into classes that will not be visible in serializations (written in all-uppercase letters) and classes that will be visible in instance markup (written with a leading uppercase letter only).

The three classes Var, CONDITION, and ATOMIC will be required in the abstract syntax of Horn Rules.

2.1.1.2. Concrete Syntax

The abstract syntax of Section Abstract Syntax can be instantiated to a concrete syntax. The EBNF syntax below, which instantiates the abstract syntax, is used throughout this document to explain and illustrate the main ideas. This syntax is similar in style to what in OWL is called the Abstract Syntax http://www.w3.org/TR/owl-semantics/syntax.html.

The concrete human-readable syntax, described in this (slightly modified) EBNF, is work in progress and under discussion.

  CONDITION   ::= CONJUNCTION | DISJUNCTION | EXISTENTIAL | ATOMIC
  CONJUNCTION ::= 'And' '(' CONDITION* ')'
  DISJUNCTION ::= 'Or' '(' CONDITION* ')'
  EXISTENTIAL ::= 'Exists' Var+ '(' CONDITION ')'
  ATOMIC      ::= Uniterm | Equal
  Uniterm     ::= Const '(' TERM* ')'
  Equal       ::= TERM '=' TERM
  TERM        ::= Const | Var | Uniterm
  Const       ::= CONSTNAME | '"'CONSTNAME'"''^^'SORTNAME
  Var         ::= '?'VARNAME | '?'VARNAME'^^'SORTNAME

The above is a standard syntax for a variant of first-order logic. The application of a symbol from Const to a sequence of terms is called Uniterm ("Universal term") since it can be used to play the role of a function term or an atomic formula depending on the syntactic context in which the application occurs. The non-terminal ATOMIC stands for (positive) atomic formula, which can later be complemented with "negated atomic formula". EXISTENTIAL stands for "existential formula", which in Horn-like conditions is the only quantified formula but in later conditions may be complemented with "universal formula" (Var+ denotes the list of free variables in CONDITION). The production CONJUNCTION defines conjunctions of conditions, and DISJUNCTION denotes disjunctions. Finally, CONDITION assembles everything into what we call RIF conditions. RIF dialects will extend these conditions in various ways.

Since initially we focus on an unsorted RIF language, individuals, function symbols, and predicate symbols all belong to the same set of symbols (Const). Variables are also unsorted, i.e., they range over the entire domain. Sorts are introduced in Section Multisorted RIF Logic. However, in preparation of the multisorted version, the above EBNF syntax already introduces SORTNAME-enriched choices for Const and Var that will be required in Section Multisorted RIF Logic.

The above EBNF, where TERM* is understood as TERM* ::= | TERM TERM*, uses spaces to indicate Lisp-like whitespace (SPACE, TAB, or NEWLINE) character sequences in the defined language; these must consist of at least one whitespace character when used as the separator between adjacent TERMs, and can consist of zero or more whitespace characters elsewhere. Where spaces are omitted from the EBNF, as between '?' and VARNAME in '?'VARNAME, there must be no whitespace character in the defined language.

At this point we do not commit to any particular vocabulary for the names of constants, variables, or sorts. For the moment, NamedElement in the UML model can be either CONSTNAME, or VARNAME, or SORTNAME. These are still assumed to be alphanumeric character sequences (except 'And' and 'Or'). For more details on this see Multisorted RIF Logic.

Note that variables in the RIF Condition Language can be free and quantified. All quantification is explicit. All variables introduced by quantification should also occur in the quantified formula. Initially, only existential quantification is used. Universal quantification will be introduced later. We adopt the usual scoping rules for quantifiers from first-order logic. Variables that are not explicitly quantified are free.

Free variables arise because CONDITION can occur in an if part of a rule. When this happens, the free variables in a condition formula are precisely those variables that also occur in the then part of the rule. We shall see in Section Horn Rules that such variables are quantified universally outside of the rule, and the scope of such quantification is the entire rule. For instance, the variable ?Y in the first RIF condition of Example 1 is quantified, existentially, but ?X is free. However, when this condition occurs in the if part of the second rule in Example 1, then this variable is quantified universally outside of the rule. (The precise syntax for RIF rules will be given in Section Horn Rules.)

Example 1 (A RIF condition in and outside of a rule)

 RIF condition:
                        Exists ?Y (condition(?X ?Y)) 

 RIF Horn rule:
        Forall ?X (then(?X) :-  Exists ?Y (condition(?X ?Y)))

When conditions are used as queries, their free variables are used to carry answer bindings back to the caller.

The following is a possible XML-serializing mapping of the abstract syntax in Section Abstract Syntax (and of the above EBNF syntax). This XML serialization is partially stripe-skipped in that it uses positional information instead of most role elements. The only place where role elements ('declare' and 'formula') are explicit is within the Exists element. Following the examples of Java and RDF, we use capitalized names for class elements and names that start with lowercase for role elements.

The all-uppercase non-terminals in EBNF, such as CONDITION, become XML entities. They act like macros and are not visible in instance markup. The other non-terminals and symbols (such as Exists or =) become XML elements, as shown below.

- And     (conjunction)
- Or      (disjunction)
- Exists  (quantified formula for 'Exists', containing declare and formula roles)
- declare (declare role, containing a Var)
- formula (formula role, containing a CONDITION formula)
- Uniterm (atomic or function-expression formula)
- Equal   (prefix version of term equation '=')
- Const   (individual, function symbol, or relation/predicate symbol)
- Var     (logic variable)

The following example illustrates XML serialization of RIF conditions.

Example 2 (A RIF condition and its XML serialization):

a. RIF condition:

  And ( Exists ?Buyer (purchase(?Buyer ?Seller book(?Author LeRif) $49)) ?Seller=?Author )

b. XML serialization:

  <And>
    <Exists>
      <declare><Var>Buyer</Var></declare>
      <formula>
        <Uniterm>
          <Const>purchase</Const>
          <Var>Buyer</Var>
          <Var>Seller</Var>
          <Uniterm>
            <Const>book</Const>
            <Var>Author</Var>
            <Const>LeRif</Const>
          </Uniterm>
          <Const>$49</Const>
        </Uniterm>
      </formula>
    </Exists>
    <Equal>
      <Var>Seller</Var>
      <Var>Author</Var>
    </Equal>
  </And>

2.1.2. Semantic Structures

The first step in defining a model-theoretic semantics for a logic-based language is to define the notion of a semantic structure, also known as an interpretation. (See end note on the rationale.)

A semantic structure, I, is a tuple of the form <D,I_C, I_V, I_F, I_R>, which determines the truth value of every formula, as explained below. Currently, by formula we mean anything produced by the CONDITION production in the EBNF. Later on this term will also include rules. Other dialects might extend this notion even further.

The set of truth values is denoted by TV. For RIF Core, TV includes only two values, t (true) and f (false). (See end note on truth values.)

The set TV has a total or partial order, called the truth order; it is denoted with <_t. In RIF Core, f <_t t, and it is a total order. (See end note on ordering truth values.)

To define how semantic structures determine the truth values of RIF formulas, we introduce the following sets:

• D - a non-empty set of elements called the domain of I,

• Const - the set of individuals, predicate names, and function symbols,

• Var - the set of variables.

As mentioned above, an interpretation, I, consists of a domain, D, and four mappings:

• I_C from Const to elements of D

• I_V from Var to elements of D

• I_F from Const to functions from D* into D (here D* is a set of all tuples of any length over the domain D)

• I_R from Const to truth-valued mappings D* → TV

We remark that f() and f can be interpreted differently by semantic structures, and the proposed XML serialization also treats them as distinct terms: the nullary function application <Uniterm><Const>f</Const></Uniterm> vs. the symbol <Const>f</Const>. Semantically, neither f() = f nor f() ≠ f are entailed a priori. However, if desirable, a particular application or a dialect may introduce axioms of the form f = f() to equate symbols and nullary terms.

Using these mappings, we can define a more general mapping, I, as follows:

• I(k) = I_C(k) if k is a symbol in Const

• I(?v) = I_V(?v) if ?v is a variable in Var

• I(f(t₁ ... t_n)) = I_F(f)(I(t₁),...,I(t_n))

Truth values for formulas in RIF Core are determined using the following function, denoted I_Truth:

• Atomic formulas: I_Truth(r(t₁ ... t_n)) = I_R(r)(I(t₁),...,I(t_n))

• Equality: I_Truth(t₁=t₂) = t iff I(t₁) = I(t₂); I_Truth(t₁=t₂) = f otherwise.

• Conjunction: I_Truth(And(c₁ ... c_n)) = min_t(I_Truth(c₁),...,I_Truth(c_n)), where min_t is minimum with respect to the truth order.

• Disjunction: I_Truth(Or(c₁ ... c_n)) = max_t(I_Truth(c₁),...,I_Truth(c_n)), where max_t is maximum with respect to the truth order.

• Quantification: I_Truth(Exists ?v₁ ... ?v_n (c)) = max_t(I*_Truth(c)), where max_t is taken over all interpretations I* of the form <D,I_C, I*_V, I_F, I_R>, where I*_V is the same as I_V except possibly on the variables ?v₁,...,?v_n (i.e., I* agrees with I everywhere except possibly in its interpretation of the variables ?v₁ ... ?v_n).

Notice that the mapping I_Truth is uniquely determined by the four mapping comprising I and, therefore, it does not need to be listed explicitly.

2.1.3. Multisorted RIF Logic

RIF uses multi-sorted logic to account for primitive data types, the use of URIs as identifiers for objects and concepts, and more. This framework is general enough to accommodate a number of popular extensions, such as Prolog, HiLog, F-logic, Common Logic, and RDF, which allow the same symbol to play multiple roles. For instance, the same symbol, foo, can be used to denote an individual, a predicate of several different arities, and as a function symbol of different arities.

In a multisorted RIF Core, each symbol from Const is associated with a sort and zero or more signatures. A signature can be an arrow signature, or a Boolean signature. Arrow signatures are also known as function signatures, and Boolean signatures are also known as predicate signatures. A variable may be associated with one sort, or it may be unsorted.

Sorts are drawn from a fixed collection of sorts PS₁, ..., PS_n. These sorts are intended to model primitive data types. For instance, RIF Core supports the sorts xsd:long, xsd:string, xsd:dateTime, and xsd:uri among others. The same symbol can be associated with more than one primitive sort. It is also possible that one sort would be a subsort of another. So, there is a partial order defined over the sorts. For example, the sort of short integers might be defined as a subsort of the sort of long integers, so every symbol of the sort xsd:short would also be associated with the sort xsd:long. In RIF, symbols of different sorts are distinguished syntactically. A concrete syntax for sorted symbols and variables is shown in Section Multisorted Syntax.

The language of the RIF sorted logic also provides a special sublanguage for defining the signatures of function symbols and predicates. An arrow signature is a statement of the form s₁ × ... × s_k → s, where s₁, ..., s_k, s are names of sorts (i.e., one of the PS₁, ..., PS_n). For instance, xsd:dateTime × xsd:long → xsd:dateTime could be an arrow signature for a function. A Boolean signature is a statement of the form s₁ × ... × s_k, where, again, s₁, ..., s_k are names of sorts. For instance, the predicate HappenedBefore may have a Boolean sort xsd:dateTime × xsd:dateTime. The arrow and Boolean sorts, along with the primitive sorts, are used in the definition of well-formed terms and formulas. This notion is defined in Section Formalization of the Multisorted RIF Logic. (See end note on using sorts to represent FOL, RDF, and other logics.)

2.1.3.1. Formalization of the Multisorted RIF Logic

In addition to the syntax for the sorted literals, RIF Core needs the following extensions. First, we introduce the following new functions:

• Sort: Const → Primitive_Sorts

• ASignature: Const → Arrow_Sorts

• BSignature: Const → Boolean_Sorts

Sort associates a sort with every symbol in Const. ASignature associates a (possibly empty) set of arrow signatures with every symbol. Similarly, BSignature associates a (possibly empty) set of Boolean signatures with every symbol in Const. The set of primitive sorts is assumed to be partially ordered. RIF Core defines a set of builtin sorts as well as the partial order on them. RIF dialects will add to this set and extend the order according to their needs.

The function Sort is also defined for variables:

• Sort: Var → Primitive_Sorts

It is a partial function in this case. The informal meaning is that if ?v ∈ Var and Sort(?v) = s then ?v can be bound only to terms that belong to the sort s (we define what it means for a term to belong to a particular sort below). If Sort(?v) is undefined then ?v is an unsorted variable, which can be bound to any term of any sort.

Well-formed function terms. Any symbol, c ∈ Const, is a well-formed function term of sort Sort(c). A variable, ?v, is a well-formed term of sort Sort(?v), if Sort(?v) is defined. If Sort(?v) is not defined then ?v is a well-formed term for every sort.

By induction, if f(t₁ ... t_k) is a function term then it is a well-formed function term of sort s if there is an arrow signature s₁, ..., s_k → s ∈ ASignature(f) such that t₁, ..., t_k are well-formed function terms of sorts s₁, ..., s_k, respectively. If t is a well-formed term of sort s and s' is a supersort of s then t is also a well-formed term of sort s'.

It is convenient to extend the mapping Sort from symbols in Const to terms created as function applications as follows:

• Sort(t) = { s | t is a well-formed term of sort s }

Well-formed atomic formula. We can now say that an atomic formula p(t₁, ..., t_k) is well-formed if and only if t₁, ..., t_k are well-formed function terms and there is a Boolean signature s₁ × ... × s_k ∈ BSignature(p) such that s₁ = Sort(t₁), ..., s_k = Sort(t_k).

From now on, we also require that all atomic formulas that occur in RIF conditions and rules must be well-formed.

Well-formed condition. A condition formula is well-formed if it is constructed out of well-formed atomic formulas.

2.1.3.2. Multisorted Syntax

Now we define how exactly the sorts are specified in RIF, i.e., how the functions Sort, ASignature, and BSignature are defined in practice.

Syntax for Primitive Sorts. In this document we will use the following syntax, following N-Triples, to specify the primitive sorts, which lie in the range of the function Sort:

   "value"^^sortname

For instance, "123"^^xsd:long is a symbol that belongs to the primitive sort xsd:long, "2007-11-23T03:55:44-02:30"^^xsd:dateTime is a symbol of sort xsd:dateTime, and "ftp://example.com/foobar"^^rif:uri is a symbol that belongs to the sort rif:uri. The part of such symbols that occurs inside the double quotes is called a literal of the sorted symbol. The surrounding double quotes are not part of the literal. If a double quote must be included as part of a literal, it must be escaped with the backslash. Some frequently used sorted literals, namely strings, long integers, and decimals, will have alternative short notation, as explained below.

Variables can also be sorted. A variable ?v of sort xsd:dateTime, for example, is represented as ?v^^xsd:dateTime. We will continue to use our old notation, ?v, for unsorted variables, i.e., variables that range over the entire domain, which includes all sorts. (See end note on polymorphic symbols.)

The XML syntax for sorts can utilize the 'sort' attribute associated with XML term elements such as Const. For instance, the earlier xsd:dateTime example can be represented as <Const sort="xsd:dateTime">2007-11-23T03:55:44-02:30</Const>. A correspondingly sorted variable xyz would be written as <Var sort="xsd:dateTime">xyz</Var>.

Many primitive sorts in RIF may be based on the XML Schema data types and thus it is expected that some names of RIF primitive types will be references to those XML Schema types. In this case, these sorts will be URI strings.

In this version of the RIF Core document, we define the following primitive sorts, where the prefix xsd refers to the XML Schema URI and rif is the prefix for the RIF language. The syntax such as xsd:long should be understood as a compact uri, i.e., a macro, which expands to a concatenation of the character sequence denoted by the prefix xsd and the string long. In the next version of this document we will introduce a syntax for defining prefixes for compact URIs and will also expand on the syntax for the symbols that can be used to denote RIF sorts.

• xsd:long. This sort corresponds to the XML data type xsd:long. Example: "123"^^xsd:long. Long integers also have a short notation, which does not require the "..."^^xsd:long wrapper. Example: 123.

• xsd:decimal. This sort corresponds to the XML data type xsd:decimal. Example: "123.45"^^xsd:decimal. Decimals also have an alternative short notation, which does not require the "..."^^xsd:decimal wrapper. Example: 123.45.

The sort xsd:decimal is a supersort of xsd:long.

• xsd:string. This corresponds to the XML data type xsd:string. Example: "a string"^^xsd:string. Double quotes that appear inside strings are escaped with a backslash and a backslash that is supposed to appear in the string must be escaped with another backslash. Strings have also an alternative short notation. Example: 'a string'. In this notation, single quotes and backslashes that occur inside such strings are escaped with backslashes.

• xsd:time. This corresponds to the XML data type xsd:time. Example: "18:33:44.2345"^^xsd:time.

• xsd:dateTime. This sort corresponds to the XML data type xsd:dateTime. Example: "2007-03-12T21:22:33.44-01:30"^^xsd:dateTime.

• rif:uri. Symbols of this sort have the form "XYZ"^^rif:uri, where XYZ is a URI as specified in RFC 3986.

Other XML data types that are likely to be incorporated as RIF sorts include xsd:double, xsd:date, and a sort for temporal duration. At present, the partial order on the above sorts is imposed by the XML Schema hierarchy, so the only subsort relationship is between xsd:long and xsd:decimal. This may be extended as more sorts are added.

The domain of the aforesaid primitive sorts, which correspond to XML primitive data types is defined to be the value space associated with the corresponding data type as specified in XML Schema Part 2: Datatypes. This means that, for example "1.2"^^xsd:decimal and "1.20"^^xsd:decimal represent the same symbol (i.e., I_C("1.2"^^xsd:decimal) = I_C("1.20"^^xsd:decimal) in every semantic structure). The same holds regarding the equalities defined for the value spaces of other data types.

The sort rif:uri is intended to be used in a way similar to RDFS resources. The domain of the sort rif:uri can be any set. Its concrete structure depends on the application. This domain is not the same as the value space of the XML primitive type anyURI. The exact semantics of the sort rif:uri will be elaborated upon in future drafts. The precise meaning of rif:uri is currently still an open issue for the group.

Specifying Arrow and Boolean Sorts. Arrow sorts are declared as follows. Note that multiple sorts can be declared for the same symbol.

• :- signature   NAME   s₁ * ... * s_n → s ,   r₁ * ... * r_k → r ,   ...

Boolean sorts are declared similarly:

• :- signature   NAME   s₁ * ... * s_n ,   r₁ * ... * r_k ,   ...

Note that NAME is a symbol from Const whose syntax was specified in Section Multisorted Syntax. In most cases functions and predicates are denoted by URIs, so such a symbol will have the syntax {{{"..."^^rif:uri}}}. In many cases sorts will be XML Schema data types referred to by strings that syntactically look like URI (in the sense of RFC 3986), but they should not be confused with RIF symbols of the sort rif:uri. For instance, in "1"^^'http://www.w3.org/2001/XMLSchema#long', the sort specification http://www.w3.org/2001/XMLSchema#long is a URI in the sense of RFC 3986, but it is not a rif:uri symbol, because it does not have the form "http://www.w3.org/2001/XMLSchema#long"^^rif:uri.

2.1.3.3. Semantics of the Multisorted RIF Conditions

The definition of RIF semantic structures needs only minor modifications. A multisorted semantic structure I, consists of a domain D = D_s1 ∪ ... ∪ D_sn, and the same four mappings as before. Each D_si is the domain of interpretation of the primitive sort s_i. Only the mappings I_C, I_V, and I_F require some changes. These changes are expressed as additional constraints as indicated below.

• I_C from Const to elements of D.

  • New constraint: If symbol c has sort s then I_C(c) ∈ D_s.

• I_V from Var to elements of D.

  • New constraint: If ?v is a variable of sort s then I_V(?v) ∈ D_s.

• I_F from Const to functions from D* into D (here D* is a set of all tuples of any length over the domain D).

  • New constraint: If f has an arrow signature s₁× ...× s_k → s ∈ ASignature(f) then I_F(f) must be a function of type D_s1 × ... × D_sk → D_s. The latter means that if d₁ ∈ D_s1, ..., d_k ∈ D_sk then I_F(f)(d₁,...,d_k) must be in D_s (but if the arguments are not in D_s1 × ... × D_sk then the result does not need to be in D_s). However, since the symbol f can have additional signatures, I_F(f) can have additional types, which restrict the behavior of this function.

• I_R from Const to truth-valued mappings D* → Truth.

Using these mappings, we can define a more general mapping, I, as follows:

• I(k) = I_C(k) if k is a symbol in Const

• I(?v) = I_V(?v) if ?v is a variable in Var

• I(f(t₁ ... t_n)) = I_F(f)(I(t₁),...,I(t_n)).

  • New constraint: Here f(t₁ ... t_n) must be a well-formed term as defined earlier.

The definition of I_Truth stays the same.

This section defines Horn rules for RIF Phase 1. The syntax and semantics incorporates RIF Positive Conditions defined in Section Positive Conditions.

3.1.1. Syntax

3.1.1.1. Abstract Syntax

The abstract syntax of the Horn rule language extending Positive Conditions is given in asn06 as follows:

class Ruleset
   property formula : list of RULE

class RULE

   subclass Forall
      property declare : list of Var
      property formula : CLAUSE

class CLAUSE

   subclass ATOMIC

   subclass Implies
      property if: CONDITION
      property then: ATOMIC

The abstract syntax is visualized by a UML diagram extending the UML diagram of Positive Conditions as shown below.

The central RIF Ruleset class contains zero or more RULEs, which are Forall-closed RIF CLAUSEs. The class Forall is specified through its parts, i.e. zero or more variable (Var) declarations and a CLAUSE formula, which can be an Implies or an ATOMIC formula. The Implies class distinguishes if-CONDITION from then-ATOMIC parts.

The classes Var, CONDITION, and ATOMIC were specified in the abstract syntax of Positive Conditions.

The combined RIF Core abstract syntax and its visualization are given in Appendix: Specification.

3.1.1.2. Concrete Syntax

The abstract syntax of Section Abstract Syntax can again be instantiated to a concrete syntax.

The concrete human-readable syntax, described in this EBNF extending the one for Positive Conditions by the following productions, is work in progress and under discussion:

  Ruleset  ::= RULE*
  RULE     ::= 'Forall' Var* CLAUSE
  CLAUSE   ::= Implies | ATOMIC
  Implies  ::= ATOMIC ':-' CONDITION

Var, ATOMIC, and CONDITION were defined as part of the syntax for positive conditions in Positive Conditions. The symbol :- denotes the implication connective used in rules. The statement ATOMIC :- CONDITION should be informally read as if CONDITION is true then ATOMIC is also true. RIF deliberately avoids using the connective ← here because in some RIF dialects, such as LP and PR, the implication :- will have different meaning from the meaning of the first-order implication ←.

Rules are generated by the Implies production. Facts are generated by the ATOMIC production, and can be viewed as the then part of an Implies with an empty conjunctive if (or with true as the if part). Finally, the CLAUSE production generates a universally closed rule or fact.

Note also that, since CONDITION permits disjunction and existential quantification, the rules defined by the Implies production are more general than pure Horn rules. This extension was explained in the introduction to Section Positive Conditions.

Well-formed rules. A rule is well-formed if its ATOMIC part is a well-formed atomic formula and the CONDITION part is a well-formed condition formula.

The following examples of EBNF and XML rule syntax use the unsorted version of the condition syntax and do not illustrate the use of URIs for predicates and concepts. This will be addressed in a future working draft.

The document RIF Use Cases and Requirements includes a use case "Negotiating eBusiness Contracts Across Rule Platforms", which discusses a business rule slightly modified here:

If an item is perishable and it is delivered to John more than 10 days after the
scheduled delivery date then the item will be rejected by him.

In the EBNF syntax used throughout this document, this rule can be written in one of these two equivalent ways:

Example 3 (A RIF rule in human-readable syntax)

a. Universal form:

  Forall ?item ?deliverydate ?scheduledate ?diffdate
      (
        reject(John ?item) :-
           And ( perishable(?item)
                 delivered(?item ?deliverydate John)
                 scheduled(?item ?scheduledate)
                 timediff(?diffdate ?deliverydate ?scheduledate)
                 greaterThan(?diffdate 10) )
      )

b. Universal-existential form:

  Forall ?item
      (
        reject(John ?item) :-
           Exists ?deliverydate ?scheduledate ?diffdate
               (
                 And ( perishable(?item)
                       delivered(?item ?deliverydate John)
                       scheduled(?item ?scheduledate)
                       timediff(?diffdate ?deliverydate ?scheduledate)
                       greaterThan(?diffdate 10) )
               )
      )

In form (a), all variables are quantified universally outside of the rule. In form (b), the variables that do not appear in the rule then part are instead quantified existentially in the if part. It is well-known that these two forms are logically equivalent.

The following extends the XML syntax of Positive Conditions, by serializing the above abstract syntax (and EBNF syntax) of RIF Horn rules in XML. The Forall element contains the role elements declare and formula, which were earlier used within the Exists element of Positive Conditions. The Implies element contains the role elements then and if to designate these two parts of a rule. With this, the order between the then and the if parts of a rule becomes immaterial.

- Ruleset (collection of rules)
- Forall  (quantified formula for 'Forall', containing declare and formula roles)
- Implies (implication, containing then and if roles in any order)
- then    (consequent role, containing ATOMIC)
- if      (antecedent role, containing CONDITION)

For instance, the rule in Example 3a can be serialized in XML as shown below as the first element of a rule set whose second element is a business rule for Fred.

Example 4 (A RIF rule set in XML syntax)

<Ruleset>
  <Forall>
    <declare><Var>item</Var></declare>
    <declare><Var>deliverydate</Var></declare>
    <declare><Var>scheduledate</Var></declare>
    <declare><Var>diffdate</Var></declare>
    <formula>
      <Implies>
        <then>
          <Uniterm>
            <Const>reject</Const>
            <Const>John</Const>
            <Var>item</Var>
          </Uniterm>
        </then>
        <if>
          <And>
            <Uniterm>
              <Const>perishable</Const>
              <Var>item</Var>
            </Uniterm>
            <Uniterm>
              <Const>delivered</Const>
              <Var>item</Var>
              <Var>deliverydate</Var>
              <Const>John</Const>
            </Uniterm>
            <Uniterm>
              <Const>scheduled</Const>
              <Var>item</Var>
              <Var>scheduledate</Var>
            </Uniterm>
            <Uniterm>
              <Const>timediff</Const>
              <Var>diffdate</Var>
              <Var>deliverydate</Var>
              <Var>scheduledate</Var>
            </Uniterm>
            <Uniterm>
              <Const>greaterThan</Const>
              <Var>diffdate</Var>
              <Const>10</Const>
            </Uniterm>
          </And>
        </if>
      </Implies>
    </formula>
  </Forall>
  <Forall>
    <declare><Var>item</Var></declare>
    <formula>
      <Implies>
        <then>
          <Uniterm>
            <Const>reject</Const>
            <Const>Fred</Const>
            <Var>item</Var>
          </Uniterm>
        </then>
        <if>
          <Uniterm>
            <Const>unsolicited</Const>
            <Var>item</Var>
          </Uniterm>
        </if>
      </Implies>
    </formula>
  </Forall>
</Ruleset>

3.1.2. Semantics

3.1.2.1. Interpretation and Models of Rules

Section Positive Conditions defined the notion of semantic structures and how such structures determine truth values of RIF conditions. The current section defines what it means for such a structure to satisfy a rule.

While semantic structures can be multivalued in RIF dialects that extend the core, rules are typically two-valued even in dialects that support inconsistency and uncertainty. Consider a rule of the form Q then :- if, where Q is a quantification prefix for all the variables in the rule. For the Horn subset, Q is a universal prefix, i.e., all variables in the rule are universally quantified outside of the rule. We first define the notion of rule satisfaction without the quantification prefix Q:

iff I_Truth(then) ≥_t I_Truth(if). (Recall that the sef of truth values, TV, has a partial order ≥_t.)

We define I |= Q then :- if iff I* |= then :- if for every I* that agrees with I everywhere except possibly on some variables mentioned in Q. In this case we also say that I is a model of the rule. I is a model of a rule set R if it is a model of every rule in the set, i.e., if it is a semantic structure such that I |= r for every rule r ∈ R.

The above defines the semantics of RIF Core using standard first-order semantics for Horn clauses. Various RIF dialects will extend this semantics in the required directions. Some of these extended semantics might not have a model theory (for example, production rules) and some will have non-first-order semantics. However, all these extensions are required to be compatible with the above definition when the rule set is completely covered by RIF Core. For further details on defining the semantics for RIF dialects see end note on intended models for rule sets.

This version of the specification of RIF Core does not detail compatibility with OWL; however, this is planned for future versions. There are several expressive features of OWL that are not expressible using a standard rule language such as RIF Core. These features include OWL's (classical) negation as well as its disjunction and existential quantification (outside of rule antecedents). The RIF Working Group will investigate different approaches to achieving interoperability between OWL and RIF Core. The approaches to be investigated include, but are not limited to, (a) translating a subset of OWL to RIF Core, (b) defining a query mechanism to allow the querying of OWL knowledge bases from RIF Core rules, and (c) using a hybrid formalism that combines OWL ontologies and RIF Core rule sets, but limits their interaction in order to attain certain desirable computational features.

This version of the specification of RIF Core does not detail compatibility with RDF; however, this is planned for future versions. There are several issues that arise when combining RDF with RIF Core, which will need to be addressed by the RIF Working Group. Among these issues are the blank nodes in RDF, which correspond to existentially quantified variables (beyond those allowed in RIF Core), the meta-modeling features of RDF (e.g., using classes as instances), and the possibility to use the RDFS ontology vocabulary in arbitrary locations, thereby changing its semantics. The RIF Working Group will investigate different approaches to interoperation, including, but not limited to, (a) integrating (a subset of) the RDF semantics with RIF Core, and (b) defining a query mechanism that allows the querying of RDF knowledge bases from RIF Core rules, possibly using a SPARQL query interface. Two specific considerations are: (i) whether to treat a triple s p o as a binary predicate p(s,o) or as the arguments of a special _triple predicate _triple(s,p,o), and (ii) whether to treat blank nodes as existentially quantified variables or as "skolem" constants.

These issues and considerations also need to be taken into account when considering interoperation with OWL Full.