Abstract
This document presents a framework for specifying the semantics
for the languages of the Semantic Web. Some of these languages
(notably RDF [RDF-PRIMER] [RDF-VOCABULARY] [RDF-SYNTAX] [RDF-CONCEPTS] [RDF-SEMANTICS], and OWL [OWL]) are currently in various stages of
development and we expect others to be developed in the future.
This framework is intended to provide a framework for specifying
the semantics of all of these languages in a uniform and coherent
way. The strategy is to translate the various languages into a
common 'base' language thereby providing them with a single
coherent model theory.
We describe a mechanism for providing a precise semantics for
the Semantic Web Languages (referred to as SWELs from now on. The
purpose of this is to define clearly the consequences and allowed
inferences from constructs in these languages.
Status of This Document
This section describes the status of this document at the
time of its publication. Other documents may supersede this
document. A list of current W3C Recommendations and other technical
reports is available at http://www.w3.org/TR/.
This document is a W3C NOTE for the use by W3C Members and other
interested parties. It may be updated, replaced or made obsolete by
other documents at any time.
This document results from discussions within the RDF Core Working
Group concerning the formalization of RDF and RDF-based
languages. The RDF Core Working Group is part of the W3C Semantic Web
Activity. The group's goals and requirements are discussed in
the RDF Core
Working Group charter. These include requirements that...
- The RDF Core group must take into account the various
formalizations of RDF that have been proposed since the
publication of the RDF Model and Syntax Recommendation. The group
is encouraged to make use both of formal techniques and
implementation-led test cases throughout their work.
- The RDF schema system must provide an extensibility
mechanism to allow future work (for example on Web Ontology and
logic-based Rule languages) to provide richer
facilities.
This document is motivated by these two requirements. It does
not present an RDF Core WG design for Semantic Web layering.
Rather, it documents a technique that the RDF Core WG are using in
our discussions and in the RDF
Semantics specification. The RDF Core WG solicit feedback from
other Working Groups and from the RDF implementor community on the
wider applicability of this technique.
Note that the use of the abbreviation "SWEL" in Lbase differs
from the prior use of "SWeLL" in the MIT/LCS DAML
project.
In conformance with W3C
policy requirements, known patent and IPR constraints
associated with this Note are detailed on the RDF Core Working Group Patent Disclosure
page.
Review comments on this document are invited and should be sent
to the public mailing list www-rdf-comments@w3.org.
An archive of comments is available at http://lists.w3.org/Archives/Public/www-rdf-comments/.
Discussion of this document is invited on the www-rdf-logic@w3.org list of
the RDF Interest
Group (public
archives).
A model-theoretic
semantics for a language assumes that the language refers to a
'world', and describes the minimal conditions that a world must
satisfy in order to assign an appropriate meaning for every
expression in the language. A particular world is called an
interpretation, so that model theory might be better called
'interpretation theory'. The idea is to provide a mathematical
account of the properties that any such interpretation must have,
making as few assumptions as possible about its actual nature or
intrinsic structure. Model theory tries to be metaphysically and
ontologically neutral. It is typically couched in the language of
set theory simply because that is the normal language of
mathematics - for example, this semantics assumes that names denote
things in a set IR called the 'universe' - but the use of
set-theoretic language here is not supposed to imply that the
things in the universe are set-theoretic in nature.
The chief utility of such a semantic theory is not to suggest
any particular processing model, or to provide any deep analysis of
the nature of the things being described by the language, but
rather to provide a technical tool to analyze the semantic
properties of proposed operations on the language; in particular,
to provide a way to determine when they preserve meaning. Any
proposed inference rule, for example, can be checked to see if it
is valid with respect to a model theory, i.e. if its conclusions
are always true in any interpretation which makes its antecedents
true.
We note that the word 'model' is often used in a rather
different sense, eg as in 'data model', to refer to a computational
system or data structures of some kind. To avoid misunderstanding,
we emphasise that the interpretations referred to in a model theory
are not, in general, intended to be thought of as things that can
be computed or manipulated by computers.
There will be many Semantic Web languages, most of which will be
built on top of more basic Semantic Web language(s). It is
important that this layering be clean and simple, not just
for human understandability, but also to enable the construction of
robust semantic web agents that use these languages. The emerging
current practice is for each of the SWELs to be defined in terms of
their own model theory, layering it on top of the model theories of
the languages they are layered upon. While having a model theory is
clearly desireable, and even essential, for a SWEL, this
direct-construction approach has several problems. It produces a
range of model theories, each with its own notion of consequence
and entailment. It requires expertise in logic to make sure that
model theories align properly, and model-theoretic alignment does
not always sit naturally with interoperability requirements.
Experience to date (particularly with the OWL standard under
development at the time of writing by the W3C Webont working
group) shows that quite difficult problems can arise when
layering model theories for extensions to the 'basic' RDF layer
[RDF] of the semantic web. Moreover, this strategy places a very
high burden on the 'basic' layer, since it is difficult to
anticipate the semantic demands which will be made by all future
higher layers, and the expectations of different development and
user communities may conflict. Further, we believe that a melange
of model theories will adversely impact developers building agents
that implement proof systems for these layers, since the proof
systems will likely be different for each layer, resulting in the
need to micro-manage small semantic variations for various dialects
and sub-languages (cf. the distinctions between various dialects of
OWL).
In this document, we use an alternative approach to for defining
the semantics for the different SWELs in a fashion which ensures
interoperability. We first define a basic language Lbase
which is expressive enough to state the content of all currently
proposed web languages, and has a fixed, clear model-theoretic
semantics. Then, the semantics of each SWEL Li is
defined by specifying how expressions in the Li map into
equivalent expressions in Lbase, and by providing axioms
written in Lbase which constrain the intended meanings
of the SWEL special vocabulary. The Lbase meaning of any
expression in any SWEL language can then be determined by
mapping it into Lbase and adding the appropriate
language axioms, if there are any.
The intended result is that the model theory of Lbase
is the model theory of all the Semantic Web Languages,
even though the languages themselves are different. This makes it
possible to use a single inference mechanism to work on these
different languages. Although it will possible to exploit
restrictions on the languages to provide better performance, the
existence of a reference proof system is likely to be of utility to
developers. This also allows the meanings of expressions in
different SWELs to be compared and combined, which is very
difficult when they all have distinct model theories.
The idea of providing a semantics for SWELs by
translating them into logic is not new [see for example
Marchiolri&Saarela, Fikes&McGuinness] but we plan to adopt
a somewhat different style than previous 'axiomatic semantics',
which have usually operated by mapping all RDF triples to instances
of a single three-place predicate. We propose rather to use the
logical form of the target language as an explication of the
intended meaning of the SWEL, rather than simply as an axiomatic
description of that meaning, so that RDF classes translate to unary
predicates, RDF properties to binary relations, the relation
rdf:type translates to application of a predicate to an argument,
and list-valued properties in OWL or DAML can be translated into
n-ary or variadic relations. The syntax and semantics of
Lbase have been designed with this kind of translation
in mind. It is our intent that the model theory of Lbase
be used in the spirit of its model theory and not as a programming
language, i.e., relations in Li should correspond to
relations in Lbase, variables should correspond to
variables and so on.
It is important to note that Lbase is not
being proposed as a SWEL. It is a tool for specifying the semantics
of different SWELs. The syntax of Lbase described here
is not intended to be accessible for machine processing; any such
proposal should be considered to be a proposal for a more
expressive SWEL.
By using a well understood logic (i.e., first order logic
[Enderton]) as the core of Lbase, and providing for
mutually consistent mappings of different SWELs into
Lbase, we ensure that the content expressed in several
SWELs can be combined consistently, avoiding paradoxes and other
problems. Mapping type/class language into predicate/application
language also ensures that set-theoretical paradoxes do not arise.
Although the use of this technique does not in itself guarantee
that mappings between the syntax of different SWELs will always be
consistent, it does provide a general framework for detecting and
identifying potential inconsistencies.
It is also important that the axioms defining the vocabulary
items introduced by a SWEL are internally consistent. Although
first-order logic (and hence Lbase) is only
semi-decideable, we are confident that it will be routine to
construct Lbase interpretations which establish the
relevant consistencies for all the SWELs currently contemplated. In
the general case, future efforts may have to rely on certifications
from particular automated theorem provers stating that they weren't
able to find an inconsistency with certain stated levels of effort.
The availablity of powerful inference engines for first-order logic
is of course relevant here.
In this document, we use a version of
first order logic with equality as Lbase. This imposes a
fairly strict monotonic discipline on the language, so that it
cannot express local default preferences and several other
commonly-used non-monotonic constructs. We expect
that as the Semantic Web grows to encompass more and our
understanding of the Semantic Web improves, we will need to replace
this Lbase with more expressive logics. However,
we expect that first order logic will be a proper subset of such
systems and hence we will be able to smoothly transition to more
expressive Lbase languages in the future. We note that
the computational advantages claimed for various sublanguages of
first-order logic, such as description logics, logical programming
languages and frame languages, are irrelevant for the purposes of
using Lbase as a semantic specification language.
We will use First Order Logic with suitable minor changes to
account for the use of referring expressions (such as URIs) on the
Web, and a few simple extensions to improve utility for the
intended purposes.
Any first-order logic is based on a set of atomic terms,
which are used as the basic referring expressions in the syntax.
These include names, which refer to entities in the domain,
special names, and variables. Lbase allows
character strings (not starting with the characters ')','(', '\',
'?','<' or ''' , and containing no whitespace characters) as
names, but distinguishes the special class of urirefs,
defined to be a URI reference in the sense of [URI]. Urirefs are
used to refer to both individuals and relations between the
individuals.
Lbase allows for various collections of special names
with fixed meanings defined by other specifications (external to
the Lbase specification). There is no assumption that
these could be defined by collections of Lbase axioms,
so that imposing the intended meanings on these special names may
go beyond strict first-order expressiveness. (In mathematical
terms, we allow that some sets of names refer to elements of
certain fixed algebras, even when the algebra has no characteristic
first-order description.) Each such set of names
has an associated predicate which is true of the things denoted by
the names in the set. At present, we assume three categories
of such fixed names: numerals, quoted strings, and XML structures,
with associated predicate names 'NatNumber', 'String', and
'XmlThing' respectively.
Numerals are defined to be strings of the characters
'0123456789', and are interpreted as decimal numerals in the usual
way. Since arithmetic is not first-order definable, this is the
first and most obvious place that Lbase goes beyond
first-order expressiveness.
Quoted strings are arbitrary character sequences enclosed in
(single) quotation marks, and are
interpreted as denoting the string inside the quotation marks. The
backslash character is used as a self-escaping prefix escape to
include a quote mark in a quoted string. Quoted strings denote the
strings they contain, i.e. any such string denotes the string
gotten by removing the two surrounding quote marks and unescaping
any inner quote marks which are then at the beginning or end. For
example,
'\'a\\\'b\''
is a quoted string which denotes the string:
'a\\\'b'
Double quote marks have no special
interpretation.
An XML structure is a character string which is a well-formed
piece of XML, possibly with an XML lang tag, and it is taken to
denote an abstract structure representing the parsed XML with the
lang tag attached to any enclosed literals.
The associated predicate names NatNumber,
String, XmlThing and Relation (see
below) are considered to be special names.
A variable is any non-white-space character string starting with
the character '?'.
The characters '(', ',' and ')' are considered to be punctuation
symbols.
The categories of punctuation, whitespace, names, special names
and variables are exclusive and each such string can be classified
by examining its first character. This is not strictly necessary
but is a useful convention.
Any Lbase language is defined with respect to a
vocabulary, which is a set of non-special names. We require
that every Lbase vocabulary contain all urirefs, but
other expressions are allowed. (We will require that every
Lbase interpretation provide a meaning for every special
name, but these interpretations are fixed, so special names are not
counted as part of the vocabulary.)
There are several aspects of meaning of expressions on the
semantic web which are not yet treated by this semantics; in
particular, it treats URIs as simple names, ignoring aspects of
meaning encoded in particular URI forms [RFC 2396] and does not
provide any analysis of time-varying data or of changes to URI
denotations. The model theory also has nothing to say about whether
an HTTP uri such as "http://www.w3.org/" denotes the World Wide Web
Consortium or the HTML page accessible at that URI or the web site
accessible via that URI. These complexities may be addressed in
future extensions of Lbase; in general, we expect that
Lbase will be extended both notationally and by adding
axioms in order to track future standardization efforts.
We do not take any position here on the way that urirefs may be
composed from other expressions, e.g. from relative URIs or Qnames;
the model theory simply assumes that such lexical issues have been
resolved in some way that is globally coherent, so that a single
uriref can be taken to have the same meaning wherever it
occurs.
Similarly, the model theory given here has no special provision
for tracking temporal changes. It assumes, implicitly, that urirefs
have the same meaning whenever they occur. To provide an
adequate semantics which would be sensitive to temporal changes is
a research problem which is beyond the scope of this document..
Even though the exact syntax chosen for Lbase is not
important, we do need a syntax for the specification. We follow the
same general conventions used in most standard presentations of
first-order logic, with one generalization which has proven useful.
We will assume that there are three sets of names (not special
names) which together constitute the vocabulary: individual names,
relation names, and function names, and that each function name has
an associated arity, which is a non-negative integer. In a
particular vocabulary these sets may or may not be disjoint.
Expressions in Lbase (speaking strictly,
Lbase expressions in this particular vocabulary) are
then constructed recursively as follows:
A term is either a name or a special name or a variable,
or else it has the form f(t1,...,tn) where f is an n-ary function
name and t1,...,tn are terms.
A formula is either atomic or boolean or quantified,
where:
an atomic formula has the form (t1=t2) where t1 and t2 are
terms, or else the form R(t1,...,tn) where R is a relation name or
a variable and t1,...,tn are terms;
a boolean formula has one of the forms
(W1 and W2 and ....and Wn)
(W1 or W2 or ... or Wn)
(W1 implies W2)
(W1 iff W2)
(not W1)
where W1, ...,Wn are formulae; and
a quantified formula has one of the forms
(forall (?v1 ...?vn) W)
(exists (?v1 ... ?vn) W)
where ?v1,...,?vn are variables and W is a formula. (The
subexpression just after the quantifier is the variable
list of the quantifier. Any occurrence of a variable in W is
said to be bound in the quantified formula by the
nearest quantifer to the occurrence which includes that variable in
its variable list, if there is one; otherwise it is said to be
free in the formula.)
Finally, an Lbase knowledge base is a set of
formulae.
Formulae are also called 'wellformed formulae' or 'wffs' or
simply 'expressions'. In general, surplus brackets may be omitted
from expressions when no syntactic ambiguity would arise.
Some comments may be in order. The only parts of this definition
which are in any way nonstandard are (1) allowing 'special names',
which was discussed earlier; (2) allowing variables to occur in
relation position, which might seem to be at odds with the claim
that Lbase is first-order - we discuss this further
below - and (3) not assigning a fixed arity to relation names. This
last is a useful generalization which makes no substantial changes
to the usual semantic properties of first-order logic, but which
eases the translation process for some SWEL syntactic constructs.
(The computational properties of such 'variadic relations' are
quite complex, but Lbase is not being proposed as a
language for computational use.)
The following definition of an interpretation is couched in
mathematical language, but what it amounts to intuitively is that
an interpretation provides just enough information about a possible
way the world might be - a 'possible world' - in order to fix the
truth-value (true or false) of any Lbase well formed
formula in that world. It does this by specifying for each uriref,
what it is supposed to be a name of; and also, if it is a function
symbol, what values the function has for each choice of arguments;
and further, if it is a relation symbol, which sequences of things
the relation holds between. This is just enough information to
determine the truth-values of all atomic formulas; and then this,
together with a set of recursive rules, is enough to assign a truth
value for any Lbase formula.
In specifying the following it is convenient to define use some
standard definitions. A relation over a set S is a set of finite
sequences (tuples) of members of S. If R is a relation and all the
elements of R have the same length n, then R is said to have
arity n, or to be a n-ary relation. Not every
relation need have an arity. If R is an (n+1)-ary relation over S
which has the property that for any sequence <s1,...,sn> of
members of S, there is exactly one element of R of the form <s0,
s1, ..., sn>, then R is an n-ary function; and s0 is the
value of the function for the arguments s1, ...sn. (Note
that an n-ary function is an (n+1)-ary relation, and that, by
convention, the function value is the first argument of the
relation, so that for any n-ary function f, f(y,x1,...,xn) means
the same as y = f(x1,...,xn).)
The conventional textbook treatment of first-order
interpretations assumes that relation symbols denote relations. We
will modify this slightly to require that relation symbols denote
entities with an associated relation, called the relational
extension, and will sometimes abuse terminology by referring to the
entities with relational extensions as relations. This device gives
Lbase some of the freedom to quantify over relations
which would be familiar in a higher-order logic, while remaining
strictly a first-order language in its semantic and metatheoretic
properties. We will use the special name
Relation to denote the property of having a relational
extension.
Let VV be the set of all variables, and NN be the set of all
special names.
We will assume that there is a globally fixed mapping
SN from elements of NN to a domain ISN (i.e, consisting of
character strings, integers and XML structures). The exact
specification of SN is given for numerals by the usual reading of a
decimal numeral to denote a natural number; for quoted strings by
the dequotation rules described earlier; and for XML structures by
the XML 1.0 specification [XML].
An interpretation I of a vocabulary V is then a
structure defined by:
- a set ID, called the domain or universe of I;
- a mapping IS from (V union VV) into ID;
- a mapping IEXT from IR, a subset of ID, into a relation over
ID+ISN (ie a set of tuples of elements of
ID+ISN).
which satisfies the following conditions:
- for any n-ary function symbol f in V, IEXT(I(f))
is an n-ary function over ID+ISN.
- IEXT(I(NatNum)) = {<n>, n a
natural number}
- IEXT(I(String)) = {<s>, s a
character string}
- IEXT(I(XmlThing)) = {<x>, x an XML
structure}
- IEXT(I(Relation)) = IR
An interpretation then specifies the value of any other
Lbase expression E according to the following rules:
| if E is: |
then I(E) is: |
| a name or a variable |
IS(E) |
| a special name |
SN(E) |
| a term f(t1,...,tn) |
the value of IEXT(I(f)) for the arguments
I(t1),...,I(tn) |
| an equation (A=B) |
true if I(A)=I(B), otherwise false |
| a formula of the form R(t1,...,t2) |
true if IEXT(I(R)) contains the sequence
<I(t1),...,I(tn)>, otherwise false |
| (W1 and ...and Wn) |
true if I(Wi)=true for i=1 through n,
otherwise false |
| (W1 or ...or Wn) |
false if I(Wi)=false for i=1 through n,
otherwise true |
| (W1 <=> W2) |
true if I(W1)=I(W2), otherwise false |
| (W1 => W2) |
false if I(W1)=true and I(W2)=false,
otherwise true |
| not W |
true if I(W)=false, otherwise false |
If B is a mapping from a set W of variables into ID, then define
[I+B] to be the interpretation which is like I except that
[I+B](?v)=B(?v) for any variable ?v in W.
| if E is: |
then I(E) is: |
| (forall (?v1,...,?vn) W) |
false if [I+B](W)=false for some
mapping B from {?v1,...,?vn} into ID, otherwise true |
| (exist (?v1,...,?vn) W) |
true if [I+B](W)=true for some
mapping B from {?v1,...,?vn} into ID, otherwise false |
Finally, a knowledge base is considered to be true if and only if
all its elements are true, .i.e. to be a conjunction of its
elements.
Intuitively, the meaning of an expression containing free
variables is not well specified (it is formally specified, but the
interpretation of the free variables is arbitrary.) To resolve any
confusion, we impose a familiar convention by which any free
variables in a sentence of a knowledge base are considered to be
universally quantified at the top level of the expression in which
they occur. (Equivalently, one could insist that all variables in
any knowledge-base expression be bound by a quantifier in that
expression; this would force the implicit quantification to be made
explicit.)
These definitions are quite conventional. The only unusual
features are the incorporation of special-name values into the
domain, the use of an explicit extension mapping, the fact that
relations are not required to have a fixed arity, and the
description of functions as a class of relations.
The explicit extension mapping is a technical device to allow
relations to be applied to other relations without going outside
first-order expressivity. We note that while this allows the same
name to be used in both an individual and a relation position, and
in a sense gives relations (and hence functions) a 'first-class'
status, it does not incorporate any comprehension principles or
make any logical assumptions about what relations are in the
domain. Notice that no special semantic conditions were invoked to
treat variables in relation position differently from other
variables. In particular, the language makes no comprehension
assumptions whatever. The resulting language is first-order in all
the usual senses: it is compact and satisfies the
downward Skolem-Lowenheim property, for example, and the
usual machine-oriented inference processes still apply, in
particular the unification algorithm. (One can obtain a translation
into a more conventional syntax by re-writing every atomic sentence
using a rule of the form R(t1,...,tn) => Holds(R, t1,...,tn),
where 'Holds' is a 'dummy' relation indicating that the relation R
is true of the remaining arguments. The presentation given here
eliminates the need for this artificial translation, but its
existence establishes the first-order properties of the language.
To translate a conventional first-order syntax
into the Lbase form, simply qualify all quantifiers to
range only over non-Relations. The issue is further
discussed in (Hayes & Menzel ref). )
Allowing relations with no fixed arity is a technical
convenience which allows Lbase to accept more natural
translations from some SWELs. It makes no significant difference to
the metatheory of the formalism compared to a fixed-arity sytnax
where each relation has a given arity. Treating functions as a
particular kind of relation allows us to use a function symbol in a
relation position (albeit with a fixed arity, which is one more
than its arity as a function); this enables some of the
translations to be specified more efficiently.
As noted earlier, incorporating special name interpretations (in
particular, integers) into the domain takes Lbase
outside strict first-order compliance, but these domains have
natural recursive definitions and are in common use throughout
computer science. Mechanical inference systems typically have
special-purpose reasoners which can effectively test for
satisfiability in these domains. Notice that the incorporation of
these special domains into an interpretation does not automatically
incorporate all truths of a full theory of such structures into
Lbase; for example, the presence of the integers in the
semantic domain does not in itself require all truths of arithmetic
to be valid or provable in Lbase.
2.4 Axiom schemes
An axiom scheme stands for an infinite set of Lbase
sentences all having a similar 'form'. We will allow schemes which
are like Lbase formulae except that expressions of the
form "<exp1>...<expn>", ie two
expressions of the same syntactic category separated by three dots,
can be used, and such a schema is intended to stand for the
infinite knowledge base containing all the Lbase
formulae gotten by substituting some actual sequence of appropriate
expressions (terms or variables or formulae) for the expression
shown, which we call the Lbase instances of the
scheme. (We have in fact been using this convention already, but
informally; now we are making it formal.) For example, the
following is an Lbase scheme:
(forall
(?v1...?vn)(R(?v1...?vn) implies
Q(a, ?v2...?vn)))
- where the expression after the first quantifier is an actual scheme expression, not a conventional
abbreviation - which has the following Lbase
instances, among others:
(forall (?x)(R(?x) implies Q(a, ?x)))
(forall (?y,?yy,?z)(R(?y, ?yy, ?z) implies Q(a,?y,?yy,?z)))
Axiom schemes do not take the language beyond first-order, since
all the instances are first-order sentences and the language is
compact, so if any Lbase sentence follows from (the
infinite set of instances of) an axiom scheme, then it must in fact
be entailed by some finite set of instances of that scheme.
We note that Lbase schemes should be understood only
as syntactic abbreviations for (infinite) sets of Lbase
sentences when stating translation rules and specifying axiom sets.
Since all Lbase expressions are required to be finite,
one should not think of Lbase schemes as themselves
being sentences; for example as making assertions, as being
instances or subexpressions of Lbase sentences, or as
being posed as theorems to be proved. Such usages would go beyond
the first-order Lbase framework. (They amount to a
convention for using infinitary logic: see [Hayes& Menzel] for
details.) This kind of restricted use of 'axiom schemes' is
familiar in many textbook presentations of logic.
Following conventional
terminology, we say that I satisfies E if I(E)=true, and
that a set S of expressions
entails E if every interpretation which satisfies every
member of S also satisfies E. If the set S contains schemes,
they are understood to stand for the infinite sets of all their
instances. Entailment is the key idea which connects
model-theoretic semantics to real-world applications. As noted
earlier, making an assertion amounts to claiming that the world is
an interpretation which assigns the value true to the assertion. If
A entails B, then any interpretation that makes A true also makes B
true, so that an assertion of A already contains the same "meaning"
as an assertion of B; we could say that the meaning of B is somehow
contained in, or subsumed by, that of A. If A and B entail each
other, then they both "mean" the same thing, in the sense that
asserting either of them makes the same claim about the world. The
interest of this observation arises most vividly when A and B are
different expressions, since then the relation of entailment is
exactly the appropriate semantic licence to justify an application
inferring or generating one of them from the other. Through the
notions of satisfaction, entailment and validity, formal semantics
gives a rigorous definition to a notion of "meaning" that can be
related directly to computable methods of determining whether or
not meaning is preserved by some transformation on a representation
of knowledge.
Any process or technique which
constructs a well formed formula Foutput from some other
Finput is said to be valid if Finput
entails Foutput, otherwise invalid. Note
that being an invalid process does not mean that the conclusion is
false, and being valid does not guarantee truth. However, validity
represents the best guarantee that any assertional language can
offer: if given true inputs, it will never draw a false conclusion
from them.
Imagine we have a Semantic Web Language Li. To provide a
semantics for Li using Lbase, we must
provide:
-
a procedure for translating expressions in Li to
expressions in Lbase. This process will also
consequently define the subset of Lbase that is used
by Li.
-
a set of vocabulary items introduced by Li
-
a set of axioms and/or axiom schemas (expressed in
Lbase or Lbase schema) that define the
semantics of the terms in (2).
Given a set of expressions G in Li, we apply the
procedure above to obtain a set of equivalent well formed formulae
in Lbase. We then conjoin these with the axioms
associated with the vocabulary introduced by Li (and any
other language upon which Li is layered). If there are
associated axiom schemata, we appropriately instantiate these and
conjoin them to these axioms. The resulting set, referred to as
A(G), is the axiomatic equivalent of G.
As an illustrative example, we give in the following table a
sketch of the axiomatic equivalent for RDF graphs
using the RDF(S) and OWL vocabularies, in the form of a translation
from N-triples. The translations given for the OWL vocabulary
reflect the 'OWL-Full' version of the language; to accurately
reflect the more restricted OWL-DL version would require the
Lbase axioms to make finer distinctions such as between
the meanings of rdfs:Class and owl:Class.
The next table gives some of the axioms which wouild also be
required to support the meanings of the various namespaces. Therse
are largely simple trascriptions of conditions described in the RDF
Semantics documentation. Note, this should not be referred
to as an accurate or normative semantic description. It is
given here only to illustrate the axiomatic technique which
Lbase is designed to support.
| RDF expression E |
Lbase expression
TR[E] |
add axiom |
"s"^^rdf:XMLLiteral where s is well-formed
XML |
the XML canonical form of s |
Lbase:XMLThing(TR[E]) |
"s"@tag^^rdf:XMLLiteral |
the XML canonical form of
<rdf-wrapper lang='tag'> s
</rdf-wrapper>
|
Lbase:XMLThing(TR[E]) |
| a plain literal "s" |
's' with all occurrences of the
symbols ',\,(,),<,> prefixed by \ |
| a plain literal "s"@tag |
| a typed literal a^^d |
the term
L2V(TR[a],TR[d]) |
| a blank node |
a variable (one distinct variable per blank
node) |
any uriref a not in the rdf:,
rdfs: or owl: namespaces |
a |
any uriref of the form rdf:_nnn |
rdf-member(nnn) |
rdfs:Resource |
T |
owl:Thing |
T |
owl:Nothing |
F |
owl:sameIndividualAs |
= |
a owl:differentIndividualFrom b |
not TR[a] =
TR[b] |
a owl:sameClassAs b . |
(forall (?u)(
TR[a](?u) iff TR[b](?u)
)) |
a owl:samePropertyAs b . |
(forall (?u ?v)(
TR[a](?u ?v) iff TR[b](?u
?v) )) |
a rdfs:SubClassOf b . |
(forall (?u)(
TR[a](?u) implies
TR[b](?u) ) |
a rdfs:subPropertyOf b . |
(forall (?u ?v)(
TR[a](?u ?v) implies
TR[b](?u ?v) ) |
|
a rdf:type owl:SymmetricProperty
|
(forall (?u ?v)(
TR[a](?u ?v) iff TR[a](?v
?u)) |
|
a rdf:type owl:FunctionalProperty
|
(forall (?u ?v ?w)((TR[a](?u
?v) and TR[a](?u ?w)) implies
?v=?w)
|
|
a rdf:type owl:InverseFunctionalProperty
|
(forall (?u ?v
?w)((TR[a](?v ?u) and
TR[a](?w ?u)) implies ?v=?w) |
|
a rdf:type owl:TransitiveProperty
|
(forall (?u ?v ?w)
((TR[a](?u ?v) and
TR[a](?v ?w)) implies
TR[a](?u ?w)) |
|
a owl:inverseOf b .
|
(forall (?u
?v)(TR[a](?u ?v) iff
TR[b](?v ?u)) |
a owl:disjointWith b . |
not (exists (?u)( TR[a](?u)
and TR[b](?u) )) |
a owl:complementOf b . |
(forall (?u)(TR[a](?u) iff
not TR[b](?u) )) |
a owl:oneOf [[ b1 ... bn ]] |
(forall (?u)(TR[a](?u) iff
(a=TR[b1] or ... or
a=TR[bn]))) |
a owl:unionOf [[ b1 ... bn ]] |
(forall (?u)(TR[a](?u) iff
( TR[b1](?u) or ... or
TR[bn](?u) ))) |
a owl:intersectionOf [[ b1 ... bn ]] |
(forall (?u)(TR[a](?u) iff
( TR[b1](?u) and ... and
TR[bn](?u) ))) |
a owl:onProperty b .
a owl:someValuesFrom c . |
(forall (?u)( TR[a](?u) iff
(exists (?v)(TR[b](?u ?v) and
TR[c](?v) )))) |
a owl:onProperty b .
a owl:allValuesFrom c . |
(forall (?u)( TR[a](?u) iff
(forall (?v)(TR[b](?u ?v) implies
TR[c](?v) )))) |
a owl:onProperty b .
a owl:hasValue c . |
(forall (?u) TR[a](?u)
iff TR[b](?u TR[c]) ) |
a owl:onProperty b .
a owl:minCardinality n . |
(forall (?u)( TR[a](?u)
iff
(exists (?x1 ... ?xn) (?x1 =/= ?x2 and ...and ?xn-1 =/= ?xn
and TR[b](?u ?x1) and ...and TR[b](?u
?xn) )) |
a owl:onProperty b .
a owl:maxCardinality n . |
(forall (?u)( TR[a](?u)
iff
(not (exists (?x1 ... ?xn+1) (?x1 =/= ?x2 and ...and ?xn =/=
?xn+1 and TR[b](?u ?x1) and ...and
TR[b](?u ?xn+1) ))) |
a owl:onProperty b .
a owl:Cardinality n . |
(forall (?u)( TR[a](?u) iff
(exists (?x1 ... ?xn) (?x1 =/= ?x2 and ...and ?xn-1 =/= ?xn
and TR[b](?u ?x1) and ...and
TR[b](?u ?xn)
and
(not (exists (?x1 ... ?xn+1) (?x1 =/= ?x2 and
...and ?xn =/= ?xn+1 and TR[b](?u ?x1) and
...and TR[b](?u ?xn+1) )
))
|
| any other uriref a |
a |
|
any other triple of the form a rdf:type b
.
|
TR[b](TR[a]) |
rdfs:Class(TR[b]) |
|
any other triple a b c .
|
TR[b](TR[a],TR[c]) |
rdfs:Property(TR[b]) |
Some Lbase axioms for RDF, RDFS and OWL
|
rdf:type(?x,?y) implies ?y(?x)
rdf:Property(rdf:type)
rdf:List(rdf:nil)
pair(?x,?y)=pair(?u,?v) iff (?x=?u and ?y=?v) .
Lbase:XMLThing(?x) implies
L2V(?x,rdf:XMLLiteral)=XMLCanonical(?x)
(Lbase:XMLThing(?x) and LanguageTag(?y)) implies
L2V(pair(?x,?y),rdf:XMLLiteral)=XMLCanonical(withLang(?x,?y))
T(?x)
not F(?x)
rdfs:Class(?y) implies (?y(?x) iff rdf:type(?x,?y))
(rdfs:range(?x,?y) and ?x(?u,?v)) implies ?y(?v)
(rdfs:domain(?x,?y) and ?x(?u,?v)) implies ?y(?u)
(rdfs:subClassOf(?x ?y) iff
(rdfs:Class(?x) and rdfs:Class(?y) and (forall
(?u)(?x(?u) implies ?y(?u)))
)
(rdfs:subPropertyOf(?x,?y) iff
(rdf:Property(?x) and rdf:Property(?y) and
(forall (?u ?v)(?x(?u,?v) implies ?y(?u,?v)))
)
rdfs:ContainerMembershipProperty(?x) implies
rdfs:subPropertyOf(?x,rdfs:member)
rdf:XMLLiteral(?x) implies rdfs:Literal(?x)
Lbase:String(?y) implies
rdfs:Literal(?y)
LanguageTag(?x) implies
Lbase:String(?x)
(Lbase:String(?x) and LanguageTag(?y))
implies rdfs:Literal(pair(?x,?y))
rdfs:Datatype(rdf:XMLLiteral)
Lbase:NatNumber(?x) implies
rdfs:ContainerMembershipProperty(rdf-member(?x))
rdfs:Class(T)
rdfs:Class(rdf:Property)
rdfs:Class(rdfs:Class)
rdfs:Class(rdfs:Datatype)
rdfs:Class(rdf:Seq)
rdfs:Class(rdf:Bag)
rdfs:Class(rdf:Alt)
rdfs:Class(rdfs:Container)
rdfs:Class(rdf:List)
rdfs:Class(rdfs:ContainerMembershipProperty)
rdfs:Class(rdf:Statement)
rdf:Property(rdfs:domain)
rdf:Property(rdfs:range)
rdf:Property(rdfs:subClassOf)
rdf:Property(rdfs:subPropertyOf)
rdf:Property(rdfs:comment)
rdf:Property(rdf:predicate)
rdf:Property(rdf:subject)
rdf:Property(rdf:object)
rdf:Property(rdf:first)
rdf:Property(rdf:rest)
rdf:Property(rdfs:seeAlso)
rdf:Property(rdfs:isDefinedBy)
rdf:Property(rdfs:label)
rdf:Property(rdf:value)
rdfs:domain(rdfs:subPropertyOf,rdf:Property)
rdfs:domain(rdfs:subClassOf,rdfs:Class)
rdfs:domain(rdfs:domain,rdf:Property)
rdfs:domain(rdfs:range,rdf:Property)
rdfs:domain(rdf:subject,rdf:Statement)
rdfs:domain(rdf:predicate,rdf:Statement)
rdfs:domain(rdf:object,rdf:Statement)
rdfs:domain(rdf:first,rdf:List)
rdfs:domain(rdf:rest,rdf:List)
rdfs:range(rdfs:subPropertyOf,rdf:Property)
rdfs:range(rdfs:subClassOf,rdfs:Class)
rdfs:range(rdfs:domain,rdfs:Class)
rdfs:range(rdfs:range,rdfs:Class)
rdfs:range(rdf:type,rdfs:Class)
rdfs:range(rdfs:comment,rdfs:Literal)
rdfs:range(rdfs:label,rdfs:Literal)
rdfs:range(rdf:rest,rdf:List)
rdfs:subClassOf(rdfs:Datatype,rdfs:Literal)
rdfs:subClassOf(rdf:Alt,rdfs:Container)
rdfs:subClassOf(rdf:Bag,rdfs:Container)
rdfs:subClassOf(rdf:Seq, rdfs:Container)
rdfs:subClassOf(rdfs:ContainerMembershipProperty,rdf:Property)
rdfs:subPropertyOf(rdfs:isDefinedBy,rdfs:seeAlso)
rdfs:Datatype(?x) implies ( LegalLexicalForm(?y,?x)) iff
?x(L2V(?y,?x)) )
( rdfs:Datatype(?x) and LegalLexicalForm(?y,?x) and ?x(?y))
implies rdfs:Literal(?y)
Lbase:XMLThing(?x) iff
LegalLexicalForm(?x,rdf:XMLLiteral)
|
3.1 Relation between the two kinds
of semantics
Given a SWEL Li, we can provide a semantics for it
either by providing it with a model or by mapping it into
Lbase and utilizing the model theory associated with
Lbase. Given a set of expressions G in Li and its
axiomatic equivalent in Lbase A(G), any Lbase
interpretation of A(G) defines an Li interpetation for G. The
natural Li interpretation from its own model theory will in general
be simpler than the Lbase interpretation: for example,
interpretations of RDF will not make use of the universal
quantification, negation or disjunction rules, and the underlying
structures need have no functional relations. In general,
therefore, the most 'natural' semantics for Li will be obtained by
simply ignoring some aspects of the Lbase interpretation
of A(G). (In category-theoretic terms, it will be the result of
applying an appropriate forgetful functor to the Lbase
structure.) Nevertheless, this extra structure is harmless, since
it does not affect entailment in Li considered in isolation; and it
may be useful, since it provides a natural way to define
consistency across several SWELs at the same time, and to define
entailment from KBs which express content in different, or even in
mixed, SWELs simultaneously. For these reasons we propose to adopt
it as a convention that the appropriate notion of satisfaction for
any SWEL expression G is in fact defined relative to an
Lbase interpretation of A(G).
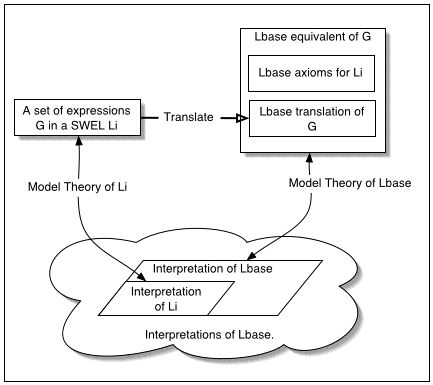
The following diagram illustrates the relation between Li,
Lbase, G and interpretations of G according to the
different model theories.
The important point to note about the above diagram is that if
the Li to Lbase mapping and model theory for Li are done
consistently, then the two 'routes' from G to a satisfying
interpretation will be equivalent. This is because the
Li axioms included in the Lbase equivalent of
G should be sufficient to guarantee that any satisfying
interpretation in the Lbase model theory of the
Lbase equivalent of G will contain a substructure which
is a satisfying interpretation of G according to the Li model
theory, and vice versa.
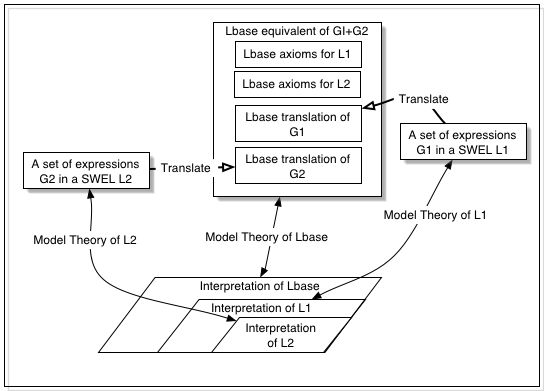
The utility of this framework for combining assertions in
several different SWELs is illustrated by the following diagram,
which is an 'overlay' of two copies of the previous diagram.
Note that the G1+G2 equivalent in this case contains axioms for
both languages, ensuring (if all is done properly) that any
Lbase interpretation will contain appropriate
substructures for both sentences.
If the translations into Lbase are appropriately
defined at a sufficient level of detail, then even tighter semantic
integration could be achieved, where expressions which 'mix'
vocabulary from several SWELs could be given a coherent
interpretation which satisfies the semantic conditions of both
languages. This will be possible only when the SWELS have a
particularly close relationship, however. In the particular case
where one SWEL (the one used by G2) is layered on top of another
(the one used by G1), the interpretations of G2 will be a subset of
those of G1
The Lbase described above has several deficiencies as a
base system for the Semantic Web. In particular,
- It does not capture the social meaning of URIs. It merely
treats them as opaque symbols. A future web logic should go
further towards capturing this intention.
- At the moment, Lbase does not provide any
facilities related to the representation of time and change.
However, many existing techniques for temporal representation use
languages similar to Lbase in expressive power, and we
are optimistic that Lbase can provide a useful
framework in which to experiment with temporal ontologies for Web
use.
- It might turn out that some aspects of what we want to
represent on the the semantic web requires more than can be
expressed using the Lbase described in this document.
In particular, Lbase does not provide a mechanism for
expressing propositional attitudes or true second order
constructs.
A future version of Lbase, which includes the above
Lbase as a proper subset, might have to include such
facilities.
We would like to thank members of the RDF Core working group, Tim
Berners-Lee, Richard Fikes, Sandro Hawke and Jim Hendler for
comments on various versions of this document.
- [Enderton]
- A Mathematical Introduction to Logic, H.B.Enderton,
2nd edition, 2001, Harcourt/Academic Press.
- [Fikes & McGuinness]
- R. Fikes, D. L. McGuinness,
An Axiomatic Semantics for RDF, RDF Schema, and DAML+OIL, KSL
Technical Report KSL-01-01, 2001
- [Hayes & Menzel]
- P. Hayes, C. Menzel,
A Semantics for the Knowledge Interchange Format , 6 August
2001 (Proceedings of 2001 Workshop on the
IEEE Standard Upper Ontology)
- [OWL]
- Web
Ontology Language (OWL) Reference Version 1.0, Mike Dean, Dan
Connolly, Frank van Harmelen, James Hendler, Ian Horrocks,
Deborah L. McGuinness, Peter F. Patel-Schneider, and Lynn Andrea
Stein. W3C Working Draft 12 November 2002. This
version is http://www.w3.org/TR/2002/WD-owl-ref-20021112/ .
Latest version is available at http://www.w3.org/TR/owl-ref/.
- [Marchiori & Saarela]
- M. Marchioi, J. Saarela, Query +
Metadata + Logic = Metalog, 1998
- [RDF-CONCEPTS]
- Resource
Description Framework (RDF): Concepts and Abstract
Syntax, Klyne G., Carroll J. (Editors), World Wide Web
Consortium Working Draft, 17 January 2003 (work in progress). This
version is
http://www.w3.org/TR/2003/WD-rdf-concepts-20030123/. The latest version is
http://www.w3.org/TR/rdf-concepts/
- [RDF-SYNTAX]
- RDF/XML
Syntax Specification (Revised), Beckett D. (Editor),
World Wide Web Consortium Working Draft, 17 January 2003 (work in
progress). This
version is
http://www.w3.org/TR/2003/WD-rdf-syntax-grammar-20030123/. The latest
version is http://www.w3.org/TR/rdf-syntax-grammar/
- [RDF-SEMANTICS]
- RDF
Semantics, Hayes P. (Editor), World Wide Web
Consortium Working Draft, 17 January 2003 (work in progress). This
version is http://www.w3.org/TR/2003/WD-rdf-mt-20030123/. The
latest version is
http://www.w3.org/TR/rdf-mt/
- [RDF-TESTS]
- RDF
Test Cases, Grant J., Beckett D. (Editors) World Wide
Web Consortium Working Draft, 17 January 2003 (work in progress).
This
version is
http://www.w3.org/TR/2003/WD-rdf-testcases-20030123/. The latest version is
http://www.w3.org/TR/rdf-testcases/.
- [RDFMS]
- Resource
Description Framework (RDF) Model and Syntax, W3C
Recommendation, 22 February 1999
http://www.w3.org/TR/1999/REC-rdf-syntax-19990222/
- [RDF-PRIMER]
- RDF
Primer, Manola F., Miller E. (Editors), World Wide Web
Consortium Working Draft, 17 January 2003 (work in progress). This
version is http://www.w3.org/TR/2003/WD-rdf-primer-20030123/.
The latest version
is http://www.w3.org/TR/rdf-primer/
- [RDF-VOCABULARY]
- RDF
Vocabulary Description Language 1.0: RDF Schema,
Brickley D., Guha R.V. (Editors), World Wide Web Consortium,
November 2002. Consortium Working Draft, 17 January 2003 (work in
progress). This
version is http://www.w3.org/TR/2003/WD-rdf-schema-20030123/.
The latest version
is http://www.w3.org/TR/rdf-schema/
- [URI]
- T. Berners-Lee, Fielding and Masinter, RFC 2396 - Uniform
Resource Identifiers (URI): Generic Syntax, August 1998.
- [WebOnt]
- The Web Ontology
Working Group
- [XML]
- T. Bray, J. Paoli, C.M. Sperberg.McQueen, E. Maler. Extensible Markup Language
(XML) 1.0 (Second Edition), W3C Recommendation 6 October
2000