RecordDescription
RDF has explicit support for unary and binary relations, but some propositions, for example Chicago is between New York and Los Angeles don't fit naturally in either of those forms. However, NaryRelations can be reduced to binary using various patterns.
We can write this as a RecordDescription. For example, in NotationThree:
[ :betweenMiddle :Chicago; :betweenThisEnd :NewYork; :betweenThatEnd :LosAngeles ].
This harks somewhat to use of columns in SQL or selector
arguments in smalltalk, or scheme records. If you're an ML programmer, you might prefer the CurriedFunction
approach. C/lisp programmers would probably prefer an ArgumentList.
- Hmm... how much is it like UML composition arrows?*
discussion: Boley in www-rdf-logic, Hayes in scl
I read this twice now and I don't see the point. -- DanConnolly
Taking an example that is likely to have information added imagine modeling "Joe teaches math."  We can observe the awkward adaptation from a simple relation:
We can observe the awkward adaptation from a simple relation:
:joe :teaches0 :math.
to a record description stating "Joe teaches math to grade 3." 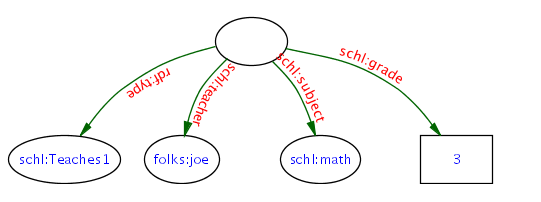 :
:
[ a teaches1; :teacher :joe; :subject :math; :grade :3 ].
In n-ary predicates (for prolog or relational databases), we could write the teaches relationship between joe, math and 3 as:
teaches(joe, math, 3)
yes, but why would we?
This leaves the relationships between joe/math, joe/3 and math/3 unexpressed. Expressing this relation as a RecordDescription forces all those relationships to be explicit because the relationship to the record is named (teacher, subject, grade). Now we have more opportunities to re-use existing properties (because the set of assertions about a teacher and a grade is a subset of assertions about all three). We can also ask questions about a subset of the relation:
[ :teacher ?teacher . :grade 3 ]
If we extend the teaches relation to include a school:
teaches(joe, math, 3, Sunnydale Elementary)
we define a new relation that is backwords compatible with the old relation. Assertions in the new relation could answer questions asked of the old relation. In prolog, there is no automatic relationship between the 3-ary teaches and the 4-ary teaches. quite; so? Does the next sentence not say why this matters? Thus, the query
teaches(WHO, _, grade3)
would not match the 4-ary relation that included a school. A sublanguage could be defined where this "backward compatibility" was assumed and the 4-ary teaches would imply the 3-ary teaches when compiled. In relational databases, this is often the case. An administrator will often add a field to a table without having to re-visit all of the SQL queries that use the previous fields. @@ do relational calculus specifications encourage this? @@ The extension of the teaches1 record to include extra properties 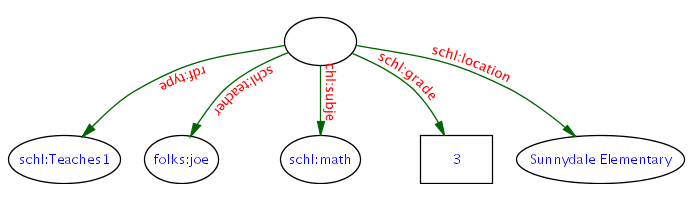 is trivial and the 3-ary 4-ary records have the maximum practical interoperability (4-ary records can answer queries tuned to the 3-ary records). Contrast this with the less desirable data extensibility charateristics of the ArgumentList and CurriedFunction approaches.
is trivial and the 3-ary 4-ary records have the maximum practical interoperability (4-ary records can answer queries tuned to the 3-ary records). Contrast this with the less desirable data extensibility charateristics of the ArgumentList and CurriedFunction approaches.
Expressing this as an ArgumentList, we'd
:joe :teaches ( :math :grade3 :sunnydale ).
Once again, the relationships between math/grade3, math/sunnydale and grade3/sunnydale are not explicit. However, 3-ary queries will work on 4-ary data so long as they are left sufficiently open:
?who :teaches ?list. ?list first ?subject. ?list rest ?a. ?a first grade3.
will match the 4-ary data as it doesn't expect ?a to have a rest of nil. However, the terse expression of this query:
?who :teaches ( ?subject ?grade ).
will fail to match the 4-ary data as it does expect the cddr to be nil.
Expressing this data as a CurriedFunction explodes with unintuitive verbosity:
:joe :teaches :joeteach2. :math :joeteach2 :joeteach3. :grade3 :joeteach3 :sunnydale.
which requires someknowlege of the answer joe as the predicate joeteach2 is already tailored to its subject, or a very loose query
:who :teaches ?p1. ?subject ?p1 ?grade.
which gives an unfortunate (inaccurate) answer that ?grade is joeteach3 when applied to the 4-ary data.
(This is true of a naive implementation, but see my discussion about generalizing relations for an example that avoids this problem. -- Dave Menendez)
It as safer to express data that may evolve in a RecordDescription. How can we say what data won't evolve?