The OWL 2 Web Ontology Language, informally OWL 2, is an ontology language for the Semantic Web with formally defined meaning. OWL 2 ontologies provide classes, properties, individuals, and data values and are stored as Semantic Web documents. OWL 2 ontologies can be used along with information written in RDF, and OWL 2 ontologies themselves are primarily exchanged as RDF documents. The OWL 2 Document Overview describes the overall state of OWL 2, and should be read before other OWL 2 documents.
This document defines the RDF-compatible model-theoretic semantics of OWL 2.
May Be Superseded
This section describes the status of this document at the time of its publication. Other documents may supersede this document. A list of current W3C publications and the latest revision of this technical report can be found in the W3C technical reports index at http://www.w3.org/TR/.
SummaryXML Schema Datatypes Dependency
OWL 2 is defined to use datatypes defined in the XML Schema Definition Language (XSD). As of Changesthis document has undergone some small changes sincewriting, the previouslatest W3C Recommendation for XSD is version 1.0, with version 1.1 progressing toward Recommendation. OWL 2 has been designed to take advantage of 21st April, 2009.the rangenew datatypes and clearer explanations available in XSD 1.1, but for now those advantages are being partially put on hold. Specifically, until XSD 1.1 becomes a W3C Recommendation, the elements of owl:predicate was adjusted to remove undesirable inferences.OWL 2 which are based on it should be considered optional, as detailed in Conformance, section 2.3. Upon the RDF vocabulary for annotations was changed: owl:subject, owl:predicatepublication of XSD 1.1 as a W3C Recommendation, those elements cease to be optional and owl:object became, respectively, owl:annotatedSource, owl:annotatedPropertyare to be considered required as otherwise specified.
We suggest that for now developers and owl:annotatedTarget.users follow the name of rdf:text was changed to rdf:PlainLiteral. Some minor errorsXSD 1.1 Candidate Recommendation. Based on discussions between the Schema and infelicities were corrected. SomeOWL Working Groups, we do not expect any implementation changes will be necessary as XSD 1.1 advances to Recommendation.
Summary of Changes
W3C Members Please CommentReview By 30 July20 October 2009
The OWL Working GroupW3C Director seeks to gather experiencereview and feedback from implementations in order to increase confidence inW3C Advisory Committee representatives, via their review form by 20 October 2009. This will allow the languageDirector to assess consensus and meet specific exit criteria .determine whether to issue this document will remainas a Candidate Recommendation until at least 30 July 2009. After that date, when and if the exit criteriaW3C Recommendation.
Others are met,encouraged by the OWL Working Group intendsto request Proposed Recommendation status. Pleasecontinue to send reports of implementation experience, and other feedback, to public-owl-comments@w3.org (public archive). Reports of any success or difficulty with the test cases are encouraged. Open discussion among developers is welcome at public-owl-dev@w3.org (public archive).
No Endorsement Publication as a Candidate Recommendation does not implySupport
The advancement of this Proposed Recommendation is supported by the disposition of comments on the Candidate Recommendation, the Test Suite with Test Results, and the list of implementations.
No Endorsement
Publication as a Proposed Recommendation does not imply endorsement by the W3C Membership. This is a draft document and may be updated, replaced or obsoleted by other documents at any time. It is inappropriate to cite this document as other than work in progress.
Patents
This document was produced by a group operating under the 5 February 2004 W3C Patent Policy. W3C maintains a public list of any patent disclosures made in connection with the deliverables of the group; that page also includes instructions for disclosing a patent. An individual who has actual knowledge of a patent which the individual believes contains Essential Claim(s) must disclose the information in accordance with section 6 of the W3C Patent Policy.
Editor's Note: Outstanding Editorial Work: Some editorial work has been deferred to the time right before publication as a Proposed Recommendation (PR), when the content of the document can be considered stable: The proof of the correspondence theorem (Section 7.3) might still need some further refinement. There are several item lists with both item bullets and numbers or letters. This will be changed into numbers/letters only after the proof of the correspondence theorem has been refined. Non-breakable whitespace will be put in formulae where appropriate.1 Introduction (Informative)
This document defines the RDF-compatible model-theoretic semantics of OWL 2,
referred to as the "OWL 2 RDF-Based Semantics".
The OWL 2 RDF-Based Semantics gives a formal meaning
to every RDF graph
[RDF Concepts]
and is fully compatible with the
RDF Semantics specification
[RDF Semantics].
The specification provided here
is the successor to
the original OWL 1 RDF-Compatible Semantics specification
[OWL 1 RDF-Compatible Semantics].
Technically,
the OWL 2 RDF-Based Semantics
is defined as a
semantic extension
of
"D-Entailment"
(RDFS with datatype support),
as specified in the RDF Semantics
[RDF Semantics].
In other words,
the meaning given to an RDF graph by the OWL 2 RDF-Based Semantics
includes the meaning given to the graphprovided by the semantics of RDFS with datatypes,
and additional meaning is given tospecified for all the language constructs of OWL 2,
such as Boolean connectives,
sub property chains
and qualified cardinality restrictions
(see the OWL 2 Structural Specification
[OWL 2 Specification]
for further information
on all the language constructs of OWL 2).
The definition of the semantics for the extra constructs
follows the samedesign principles
that have beenas applied to the RDF Semantics.
The content of this document is not meant to be self-contained,
but builds on top of the
RDF Semantics document
[RDF Semantics]
by adding those aspects
that are specific to OWL 2.
Hence,
the complete definition of the OWL 2 RDF-Based Semantics
is given by
the combination of both
the RDF Semantics document
and the document at hand.
In particular,
the terminology used in the RDF Semantics
is reused here,
except for cases
where a conflict exists with the rest of the OWL 2 specification.
The following paragraphs outline the document's structure and content, and provideremainder of this section
provides an overview
of some of the distinguishing features
of the OWL 2 RDF-Based Semantics. According toSemantics,
and outlines the document's structure and content.
In Section 2,
the syntax
over which the OWL 2 RDF-Based Semantics is defined
is the set of all
RDF graphs
[RDF Concepts].
For every suchRDF graph
is given a precise formal meaning bythe OWL 2 RDF-Based Semantics.Semantics
provides a precise formal meaning.
The language
that is determined
by RDF graphs
being interpreted using the OWL 2 RDF-Based Semantics
is called
"OWL 2 Full".
In this document,
RDF graphs are also called
"OWL 2 Full ontologies",
or simply "ontologies",
unless there is any risk of confusion.
The OWL 2 RDF-Based Semantics
interprets the
RDF
and
RDFS vocabularies
[RDF Semantics]
and the OWL 2 RDF-Based vocabulary,
together with an extended set of datatypes
and their constraining facets
(see Section 3).
OWL 2 RDF-Based interpretations
(Section 4)
are defined on a universe
that(see Section 1.3 of the RDF Semantics specification
[RDF Semantics]
for an overview of
the basic intuition of model-theoretic semantics).
The universe is divided into parts,
namely individuals, classes, and properties,
which are identified with their RDF counterparts
(see Figure 1).
In particular,The part of individuals equals the whole universe.
This means
that all classes and properties are also
individuals in their own right.
Further,
every name interpreted by an OWL 2 RDF-Based interpretation
denotes an individual.
The three basic parts are furtherdivided into subpartsfurther parts as follows.
The part of individuals subsumes the part of data values,
which comprises the denotations of all literals.
Also subsumed by the individuals is the part of ontologies.
The part of classes subsumes the part of datatypes,
which are classes entirely consisting of data values.
Finally,
the part of properties subsumes the parts of
object properties,
data properties,
ontology properties
and annotation properties.
In particular,The part of object properties equals the whole part of properties,
and therefore all other kinds of properties are thereforealso object properties.
For annotations properties
note that annotations cannot be consideredare not "semantic-free"
under the OWL 2 RDF-Based Semantics.
Just like every other triple or set of triples occurring in an RDF graph,
an annotation is assigned a truth value by any given OWL 2 RDF-Based interpretation.
Hence,
although annotations are meant to be "semantically weak",
i.e. their formal meaning does not significantly exceed
that comingoriginating from the RDF Semantics specification,
adding an annotation
may still change the meaning of an ontology.
A similar discussion holds for statements
that are built from ontology properties,
such as owl:imports,
which are used to define relationships between two ontologies.
Every class represents a specific set of individuals,
called the class extension of the class, written as "ICEXT( C )".class:
an individual a is an instance of a givenclass C exactly,
if a is a member of the class extension ofICEXT(C .).
Since a class is itself an individual under the OWL 2 RDF-Based Semantics,
classes are distinguished from their respective class extensions.
This distinction allows,
for example,
forthat a class tomay be an instance of itself
by being a member of its own class extension.
Also,
two classes may be equivalent
by sharing the same class extension,
though stillalthough being different individuals,
i.e.,e.g., they do not need to share the same properties.
Similarly,
every property has aan associated property extension
, written as "IEXT( p )", associated with itthat consists of pairs of individuals.individuals:
an individual a1
has a relationship to anotheran individual a2
based onwith respect to a givenproperty p,
exactlyif the pair
⟨( a1 , a2 ⟩)
is a member of the property extension ofIEXT(p .).
Again, properties are distinguished from their property extensions.
IndividualsIn general,
if there are no further constraints,
an arbitrary extension may be associated with
a given class or property,
and two interpretations may associate
distinct extensions
with the same class or property.
Individuals may play different roles."roles".
For example,
an individual can be
both a data property and an annotation property,
since the different parts of the universe
of an OWL 2 RDF-Based interpretation
are not required to be mutually disjoint.
Or an individual can be
both a class and a property, sinceproperty
by associating
both a class extension and a property extension
may independently be associatedwith it.
In the samelatter case,
without further constraints
there will be no specific relationship
between the class extension and the property extension
of such an individual.
For example,
the same individual
can have an empty class extension
while having a nonempty property extension.
The main part of the OWL 2 RDF-Based Semantics is Section 5,
which specifies
a formal meaning for all the OWL 2 language constructs
by means of the
OWL 2 RDF-Based semantic conditions.
These semantic conditions extend all the
semantic conditions given in the RDF Semantics
[RDF Semantics].
The OWL 2 RDF-Based semantic conditions effectively determine
which sets of RDF triples are assigned a specific meaning,
and what this meaning is.
For example,
there exist semantic conditions
that allow to interpret the RDFtriple
"C owl:disjointWith D"
to mean that the denotations of the IRIs
C and D
have disjoint class extensions.
There is usually no need to provide localizing information
(e.g. by means of "typing triples")
for the IRIs occurring in an ontology.
As for the RDF Semantics,
the OWL 2 RDF-Based semantic conditions have been designed
to ensure that the denotation of any IRI
will actuallybe in the appropriate part of the universe.
For example,
the RDF triple
"C owl:disjointWith D"
is sufficient to deduce that
the denotations of the IRIs
C and D
are actually classes.
It is not necessary to explicitly add additional typing triples
"C rdf:type rdfs:Class"
and
"D rdf:type rdfs:Class"
to the ontology.
In the RDF Semantics,
this kind of "automatic localization"
was to some extent achieved by so called
"axiomatic triples"
[RDF Semantics],
such as
" rdfs:subClassOfrdf:type rdf:type rdf:Property"
or
" rdfs:subClassOfrdf:type rdfs:domain rdfs:Classrdfs:Resource".
However,
there is no explicit normative collection
of additional axiomatic triples
for the OWL 2 RDF-Based Semantics
but, instead,
the specific axiomatic aspects of the OWL 2 RDF-Based Semantics
are determined by a subset of the OWL 2 RDF-Based semantic conditions.
Section 6
discusses axiomatic triples in general,
and provides
an example set of axiomatic triples
that is compatible with the OWL 2 RDF-Based Semantics.
Section 7 compares
the OWL 2 RDF-Based Semantics
with the OWL 2 Direct Semantics
[OWL 2 Direct Semantics].
While
the OWL 2 RDF-Based Semantics is based on the
RDF Semantics specification
[RDF Semantics],
the OWL 2 Direct Semantics
is a description logic style semantics.
Several fundamental differences
exist between the two semantics,
but
there is also a strong relationship
basically stating that the OWL 2 RDF-Based Semantics
is able to reflect all logical conclusions
of the OWL 2 Direct Semantics.
This means that the OWL 2 Direct Semantics
can
in a sense
be regarded as a sub semantics of the OWL 2 RDF-Based Semantics.
The precise relationship is given by the
OWL 2 correspondence theorem.
Significant effort has been spent
in keeping the design of the OWL 2 RDF-Based Semantics
as close as possible
to that of the original specification of the
OWL 1 RDF-Compatible Semantics
[OWL 1 RDF-Compatible Semantics].
While this aim was achieved to a large degree,
the OWL 2 RDF-Based Semantics actually deviates from its predecessor in several aspects,aspects.
In most cases due tothis is because of serious technical problems
that would have arisen
from a conservative
semantic extension.
One important change is that,
while there still exist
so called "comprehension conditions"
for the OWL 2 RDF-Based Semantics
(see Section 8),
these are not part of the
normative set of semantic conditions anymore.
The OWL 2 RDF-Based Semantics also corrects several errors of OWL 1.
A list of differences between the two languages is given in
Section 9.
The italicized keywords MUST, MUST NOT, SHOULD, SHOULD NOT, and MAY are used to specify normative features of OWL 2 documents and tools, and are interpreted as specified in RFC 2119 [RFC 2119].
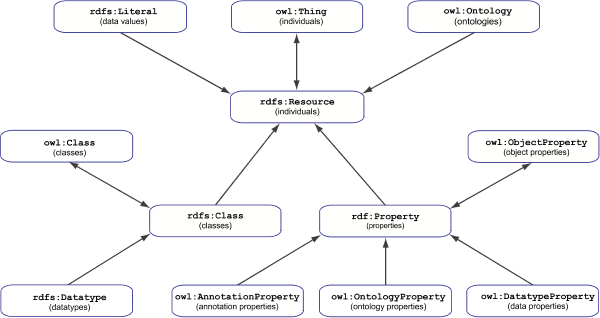
Figure 1: "Parts Hierarchy"Parts Hierarchy of the OWL 2 RDF-Based Semantics
Each node is labeled with a class IRI
that represents a part of the universe
of an OWL 2 RDF-based interpretation.
An arrow points from one such part to a super part.
2 Ontologies
This section determines the syntax
for the OWL 2 RDF-Based Semantics,
and gives an overview on typical content of ontologies
for ontology management tasks.
2.1 Syntax
Following Sections 0.2 and 0.3 of the RDF Semantics specification
[RDF Semantics],
the OWL 2 RDF-Based Semantics
is defined on every RDF graph
(Section(Section 6.2 of RDF Concepts
[RDF Concepts]),
i.e. on every set of RDF triples
(Section(Section 6.1 of RDF Concepts
[RDF Concepts]).
In accordance with the rest of the OWL 2 specification
(see Section 2.32.4 of the OWL 2 Structural Specification
[OWL 2 Specification]),
this document
uses an extended notion of an RDF graph
by allowing the RDF triples in an RDF graph
to contain arbitrary IRIs
("Internationalized Resource Identifiers")
according to RFC 3987
[RFC 3987].
In contrast,
the RDF Semantics specification
[RDF Semantics]
is defined on RDF graphs containing
URIs
[RFC 2396].
This change
is backwardsbackward compatible
with the RDF specification,
since URIs are also IRIs.
Terminological note:
The document at hand
uses the term "IRI"
in accordance with the rest of the OWL 2 specification
(see Section 2.4 of the OWL 2 Structural Specification
[OWL 2 Specification]),
whereas the
RDF Semantics specification
[RDF Semantics]
uses the term "URI reference".
According to
RFC 3987
[RFC 3987],
the term "IRI"
stands for an absolute resource identifier with optional fragment,
which is what is being used throughout this document.
In contrast,
the term "IRI reference" additionally covers relative references,
which are never used in this document.
Convention:
In this document,
IRIs are abbreviated
in the way defined by
Section 2.4 of the OWL 2 Structural Specification
[OWL 2 Specification],
i.e., the abbreviations consist of
a prefix name and a local part,part,
such as
"prefix:localpart".
The definition of an RDF triple
according to
Section 6.1 of RDF Concepts
[RDF Concepts]
is restricted to cases
where the subject of an RDF triple is
an IRI
or a
blank node
(Section(Section 6.6 of RDF Concepts
[RDF Concepts]),
and where the predicate of an RDF triple is
an IRI.
As a consequence,
the definition does not treat cases,
where,
for example,
the subject of a triple is a literal
(Section(Section 6.5 of RDF Concepts
[RDF Concepts]),
as in
"s" ex:p ex:o,
or where the predicate of a triple is a blank node,
as in
ex:s _:p ex:o.
In order to allow for interoperability
with other existing and future technologies and tools,
the document at hand
does not explicitly forbid the use of
generalized RDF graphs consisting of generalized RDF triples,
which are defined to allow for
IRIs, literals and blank nodes
to occur in the subject, predicate and object position.
Thus,
an RDF graph
MAY
contain generalized RDF triples,
but an implementation is not required to support generalized RDF graphs.
Note that every RDF graph consisting entirely of RDF triples according to
Section 6.1 of RDF Concepts
[RDF Concepts]
is also a generalized RDF graph.
Terminological notes:
The term
"OWL 2 Full"
refers to the language
that is determined
by the set of all RDF graphs
being interpreted using the OWL 2 RDF-Based Semantics.
Further,
in this document
the term
"OWL 2 Full ontology"
(or simply "ontology",
unless there is any risk of confusion)
will be used interchangeably
with the term "RDF graph".
2.2 Content of Ontologies (Informative)
While there do not exist any syntactic restrictions
on the set of RDF graphs
that can be interpreted by the OWL 2 RDF-Based Semantics,
in practice
an ontology will often contain certain kinds of constructs
that are aimed to support ontology management tasks.
Examples are
ontology headers
and
ontology IRIs,
as well as constructs that are about
versioning,
importing
and
annotating of ontologies,
including the concept of incompatibility between ontologies.
These topics are outside the scope of this semantics specification.
Section 3 of the OWL 2 Structural Specification
[OWL 2 Specification]
deals with these topics in detail,
and can therefore be used as a guide
on how to apply these constructs in OWL 2 Full ontologies accordingly.
The mappings of all these constructs to their respective RDF encodingsencoding
are defined in
the OWL 2 RDF Mapping [OWL 2 RDF Mapping].
3 Vocabulary
This section specifies the OWL 2 RDF-Based vocabulary,
and lists the names of the datatypes and facets
used under the OWL 2 RDF-Based Semantics.
3.1 Standard Prefixes
Table 3.1
lists the standard prefix names
and their prefix IRIs
used in this document.
Table 3.1: Standard Prefixes
|
| Prefix Name
| Prefix IRI
|
| OWL
| owl
| http://www.w3.org/2002/07/owl#
|
| RDF
| rdf
| http://www.w3.org/1999/02/22-rdf-syntax-ns#
|
| RDFS
| rdfs
| http://www.w3.org/2000/01/rdf-schema#
|
| XML Schema
| xsd
| http://www.w3.org/2001/XMLSchema#
|
3.2 Vocabulary Terms
Table 3.2
lists the IRIs of the OWL 2 RDF-Based vocabulary,
which is the set of vocabulary terms
that are specific for the OWL 2 RDF-Based Semantics.
This vocabulary
extends the RDF and RDFS vocabularies
as specified byin
Sections 3.1
and
4.1 of the RDF Semantics
[RDF Semantics],
respectively.
Table 3.2
excludesdoes not mention those IRIs
that will be mentionedlisted in
Section 3.3 on datatype names
or
Section 3.4 on facet names.
Implementations are not required
to support the IRI owl:onProperties,
but
MAY
support it
in order to realize
n-ary dataranges with arity ≥ 2
(see
SectionSections
7
and
8.4
of the OWL 2 Structural Specification
[OWL 2 Specification]
for further information).
Note:
The use of the IRI owl:DataRange has been deprecated as of OWL 2.
The IRI rdfs:Datatype
SHOULD
be used instead.
Table 3.2: OWL 2 RDF-Based Vocabulary
| owl:AllDifferent owl:AllDisjointClasses owl:AllDisjointProperties owl:allValuesFrom owl:annotatedProperty owl:annotatedSource owl:annotatedTarget owl:Annotation owl:AnnotationProperty owl:assertionProperty owl:AsymmetricProperty owl:Axiom owl:backwardCompatibleWith owl:bottomDataProperty owl:bottomObjectProperty owl:cardinality owl:Class owl:complementOf owl:DataRange owl:datatypeComplementOf owl:DatatypeProperty owl:deprecated owl:DeprecatedClass owl:DeprecatedProperty owl:differentFrom owl:disjointUnionOf owl:disjointWith owl:distinctMembers owl:equivalentClass owl:equivalentProperty owl:FunctionalProperty owl:hasKey owl:hasSelf owl:hasValue owl:imports owl:incompatibleWith owl:intersectionOf owl:InverseFunctionalProperty owl:inverseOf owl:IrreflexiveProperty owl:maxCardinality owl:maxQualifiedCardinality owl:members owl:minCardinality owl:minQualifiedCardinality owl:NamedIndividual owl:NegativePropertyAssertion owl:Nothing owl:ObjectProperty owl:onClass owl:onDataRange owl:onDatatype owl:oneOf owl:onProperty owl:onProperties owl:Ontology owl:OntologyProperty owl:priorVersion owl:propertyChainAxiom owl:propertyDisjointWith owl:qualifiedCardinality owl:ReflexiveProperty owl:Restriction owl:sameAs owl:someValuesFrom owl:sourceIndividual owl:SymmetricProperty owl:targetIndividual owl:targetValue owl:Thing owl:topDataProperty owl:topObjectProperty owl:TransitiveProperty owl:unionOf owl:versionInfo owl:versionIRI owl:withRestrictions
|
3.3 Datatype Names
Table 3.3
lists the IRIs of the datatypes used in the OWL 2 RDF-Based Semantics.
The datatype rdf:XMLLiteral is described in
Section 3.1 of the RDF Semantics
[RDF Semantics].
All other datatypes are described in
Section 4 of the OWL 2 Structural Specification
[OWL 2 Specification].
The normative set of datatypes of the OWL 2 RDF-Based Semantics equals the set of datatypes
described in
Section 4 of the OWL 2 Structural Specification
[OWL 2 Specification].
Table 3.3: Datatypes of the OWL 2 RDF-Based Semantics
| xsd:anyURI xsd:base64Binary xsd:boolean xsd:byte xsd:dateTime xsd:dateTimeStamp xsd:decimal xsd:double xsd:float xsd:hexBinary xsd:int xsd:integer xsd:language xsd:long xsd:Name xsd:NCName xsd:negativeInteger xsd:NMTOKEN xsd:nonNegativeInteger xsd:nonPositiveInteger xsd:normalizedString rdf:PlainLiteral xsd:positiveInteger owl:rational owl:real xsd:short xsd:string xsd:token xsd:unsignedByte xsd:unsignedInt xsd:unsignedLong xsd:unsignedShort rdf:XMLLiteral
|
Feature At Risk #1: owl:rational support Note: This feature is "at risk" and may be removed from this specification based on feedback. Please send feedback to public-owl-comments@w3.org . For the current status see features "at risk" in OWL 2 The owl:rational datatype might be removed from OWL 2 if implementation experience reveals problems with supporting this datatype.3.4 Facet Names
Table 3.4
lists the IRIs of the facets used in the OWL 2 RDF-Based Semantics.
Each datatype listed in Section 3.3
has a (possibly empty) set of constraining facets.
All facets are described in
Section 4 of the OWL 2 Structural Specification
[OWL 2 Specification]
in the context of their respective datatypes.
The normative set of facets of the OWL 2 RDF-Based Semantics equals the set of facets
described in
Section 4 of the OWL 2 Structural Specification
[OWL 2 Specification].
In this specification,
facets are used for defining datatype restrictions
(see Section 5.7).
For example,
to refer to the set of all strings of length 5
one can restrict
the datatype xsd:string
(Section 3.3)
by the facet xsd:length
and the value 5.
Table 3.4: DatatypeFacets of the OWL 2 RDF-Based Semantics
| rdf:langRange xsd:length xsd:maxExclusive xsd:maxInclusive xsd:maxLength xsd:minExclusive xsd:minInclusive xsd:minLength xsd:pattern
|
4 Interpretations
The OWL 2 RDF-Based Semantics provides
vocabulary interpretations and vocabulary entailment
(see Section 2.1 of the RDF Semantics
[RDF Semantics])
for the
RDF
and
RDFS
vocabularies
and for the
OWL 2 RDF-Based vocabulary.
This section defines
the concepts of anOWL 2 RDF-Based datatype mapmaps
and
anOWL 2 RDF-Based interpretationinterpretations,
and specifies what
satisfaction of ontologies,
consistency and entailment
means under the OWL 2 RDF-Based Semantics.
In addition,
the so called "parts" of the universe
of an OWL 2 RDF-Based interpretation
are defined.
4.1 Datatype Maps
According to
Section 5.1 of the RDF Semantics specification
[RDF Semantics],
a datatype d has the following components:
- LS(d), the lexical space of d, which is a set of lexical forms;
- VS(d), the value space of d, which is a set of data values;
- L2V(d), the lexical-to-value mapping of d, which maps lexical forms in LS(d) to data values in VS(d).
Terminological notes:
The document at hand uses the term
"data value"
in accordance with the rest of the OWL 2 specification
(see
Section 4 of the OWL 2 Structural Specification
[OWL 2 Specification]),
whereas the
RDF Semantics specification
[RDF Semantics]
uses the term
"datatype value" instead.
Further, the names "LS" and "VS",
which stand for the lexical space and the value space of a datatype,
respectively,
are not used in the RDF Semantics specification,
but have been introduced here for easier reference.
In this document,
the basic definition of a datatype
is extended to take facets into account.
See Section 3.4
for information and an example on facets (see Section 3.4 ).facets.
Note that
Section 5.1 of the RDF Semantics specification
[RDF Semantics]
explicitly permits
that semantic extensions
may impose more elaborate datatyping conditions
than those listed above.
A datatype with facets d
is a datatype that has the following additional components:
- FS(d), the facet space of d, which is a set of pairs of the form
⟨( F , v ⟩,), where F is an IRI called the constraining facet and v is an arbitrary data value called the constraining value;
- F2V(d), the facet-to-value mapping of d, which maps each facet-value pair
⟨( F , v ⟩) in FS(d) to a subset of VS(d).
Note that
it is not further specified
what the nature of the denotation of a facet IRI's denotationIRI is,
i.e. it is only known that a facet IRI denotes some individual.
Semantic extensions
MAY
impose further restrictions on the denotations of facets.
In fact,
Section 5.3
will define additional restrictions on facets.
Also note
that for a datatype d
and a facet-value pair ⟨( F , v ⟩) in FS(d)
the value v
is not required
to be included in the value space VS(d) of d itself.
For example,
the datatype xsd:string
(Section 3.3)
has the facet xsd:length
(Section 3.4),
which takes non-negativenonnegative integers as its values,constraining values
rather than strings.
In this document,
it will always be assumed from now on that
everyany datatype d is a datatype with facets.
If the facet space FS(d) of a datatype d
has not been explicitly defined,
or if it is not derived from another datatype's facet space
according to some well defined condition,
then FS(d) is the empty set.
Unless there is any risk of confusion,
the term "datatype"
will always refer to a datatype with facets.
Section 5.1 of the RDF Semantics specification
[RDF Semantics]
further
defines a datatype map D to be
a set of name-datatype pairs
⟨( u , d ⟩)
consisting of an IRI u and a datatype d,
such that no IRI appears twice in the set.
As a consequence of what has been said before,
in this document
every datatype map D will entirely consist of datatypes with facets.
The following definition specifies what an OWL 2 RDF-Based datatype map is.
Definition 4.1 (OWL 2 RDF-Based Datatype Map):
A datatype map D
is an OWL 2 RDF-Based datatype map,
if and only if
for every datatype name u listed in Section 3.3
and its respective set of constraining facets (Section 3.4)
there is
a name-datatype pair ⟨( u, d ⟩) in D
with the specified
lexical space LS(d),
value space VS(d),
lexical-to-value mapping L2V(d),
facet space FS(d) and
facet-to-value mapping F2V(d).
Note that Definition 4.1
does not prevent additional datatypes
to be in an OWL 2 RDF-Based datatype map.
For the special case of
an OWL 2 RDF-Based datatype map D
that exclusively contains the datatypes listed in
Section 3.3,
it is ensured that
there are datatypes available for all the facet values,
i.e.,
for every name-datatype pair ⟨( u , d ⟩) in D
and for every facet-value pair
⟨( F , v ⟩)
in FS(d)
there exists a name-datatype pair ⟨( u* , d* ⟩) in D
such that v is in VS(d*).
4.2 Vocabulary Interpretations
From the
RDF Semantics specification
[RDF Semantics],
let V be a set of literals and IRIs
containing the RDF and RDFS vocabularies,
and let D be a datatype map according to
Section 5.1 of the RDF Semantics
[RDF Semantics]
(and accordingly Section 4.1).
A D-interpretation I of V with respect to D is a tuple
I = ⟨( IR , IP , IEXT , IS , IL , LV ⟩) .
IR is the universe of I,
i.e., a nonempty set
that contains at least
the denotations of literals and IRIs in V.
IP is a subset of IR,
the properties of I.
LV,
the data values of I,
is a subset of IR
that contains at least the set of plain literals
(see Section 6.5 of RDF Concepts
[RDF Concepts ]),])
in V,
and
the value spaces of each datatype of D.
IEXT is used to associate properties with their property extension,
and is a mapping from IP to the powerset of IR × IR.
IS is a mapping from IRIs in V to their denotations in IR.
In particular,
IS(u) = d
for any name-datatype pair ⟨( u , d ⟩) in D.
IL is a mapping from typed literals
"s"^^u
in V
to their denotations in IR,
where IL("s"^^u) = L2V(d)(s),
provided that d is a datatype of D,
IS(u) = d, and
s is in the lexical space LS(d);
otherwise
IL("s"^^u)
is not in LV.
Convention:
Following the practice, as alsopractice introduced in
Section 1.4 of the RDF Semantics
[RDF Semantics],
for a given interpretation I of a vocabulary V
the notation
"I(x)"
will be used
to denoteinstead of "IL(x)" and "IS(x)"
for the typed literals and IRIs x in V,
respectively.
As detailed in the
RDF Semantics
[RDF Semantics],
a D-interpretation has to meet all the semantic conditions
for ground graphs
and blank nodes,
those for RDF interpretations and
RDFS interpretations,
and the
"general semantic conditions for datatypes".
In this document,
the basic definition of a D-interpretation
is extended to take facets into account.
A D-interpretation with facets I
is a D-interpretation for a datatype map D
consisting entirely of datatypes with facets
(Section 4.1),
where I meets the following additional semantic conditions:
for each name-datatype pair ⟨( u , d ⟩) in D
and each facet-value pair ⟨( F , v ⟩) in the facet space FS(d)
- F is in the vocabulary V of I;
- a name-datatype pair
⟨( u* , d* ⟩) exists in D, such that v is in the value space VS(d*).
In this document,
it will always be assumed from now on that
everyany D-interpretation I
is a D-interpretation with facets.
Unless there is any risk of confusion,
the term "D-interpretation"
will always refer to a D-interpretation with facets.
The following definition specifies what an OWL 2 RDF-Based interpretation is.
Definition 4.2 (OWL 2 RDF-Based Interpretation):
Let D be an OWL 2 RDF-Based datatype map,
and let V be a vocabulary
that includes
the RDF and RDFS vocabularies
and the OWL 2 RDF-Based vocabulary
together with all the datatype and facet names
listed in Section 3.
An OWL 2 RDF-Based interpretation,
I = ⟨( IR , IP , IEXT , IS , IL , LV ⟩,),
of V with respect to D
is a D-interpretation of V with respect to D
that meets all the extra semantic conditions
given in Section 5.
4.3 Satisfaction, Consistency and Entailment
The following definitions specify
what it means for an RDF graph to be satisfied
by a given OWL 2 RDF-Based interpretation,
to be consistent
under the OWL 2 RDF-Based Semantics,
and to entail another RDF graph.
The notion of satisfaction under the OWL 2 RDF-Based Semantics
is based on the notion of satisfaction for
D-interpretations
and
Simple interpretations,interpretations,
as defined in the RDF Semantics
[RDF Semantics].
In essence,
in order to satisfy an RDF graph,
an interpretation I has to satisfy all the triples in the graph,
i.e.,
for a triple of the form"s p o"
it is necessary that the relationship
⟨( I(s) , I(o) ⟩) ∈ IEXT(I(p))
holds
(special treatment exists for blank nodes,
as detailed in
Section 1.5 of the RDF Semantics
[RDF Semantics]).
In other words,
the given graph has to be compatible with
the specific form of the IEXT mapping of I.
The distinguishing aspect of OWL 2 RDF-Based satisfaction is
that an interpretation I needs to meet
all the OWL 2 RDF-Based semantic conditions
(see Section 5),
which have the effect ofa constraining effect
on the possible forms an IEXT mapping can have.
Definition 4.3 (OWL 2 RDF-Based Satisfaction):
Let G be an RDF graph,
let D be an OWL 2 RDF-Based datatype map,
let V be a vocabulary
that includes
the RDF and RDFS vocabularies
and the OWL 2 RDF-Based vocabulary
together with all the datatype and facet names listed in Section 3,
and let I be a D-interpretation of V with respect to D.
I OWL 2 RDF-Based satisfies G with respect to V and D
if and only if
I is an OWL 2 RDF-Based interpretation of V with respect to D
that
satisfies G
as a D-interpretation of V with respect to D
according to the RDF Semantics
[RDF Semantics].
Definition 4.4 (OWL 2 RDF-Based Consistency):
Let S be a collection of RDF graphs,
and let D be an OWL 2 RDF-Based datatype map.
S is OWL 2 RDF-Based consistent with respect to D
if and only if
there is some OWL 2 RDF-Based interpretation I with respect to D
of some vocabulary V
that includes
the RDF and RDFS vocabularies
and the OWL 2 RDF-Based vocabulary
together with all the datatype and facet names listed in Section 3 ),,
such that I OWL 2 RDF-Based satisfies all the RDF graphs in S
with respect to V and D.
Definition 4.5 (OWL 2 RDF-Based Entailment):
Let S1 and S2 be collections of RDF graphs,
and let D be an OWL 2 RDF-Based datatype map.
S1 OWL 2 RDF-Based entails S2 with respect to D
if and only if
for every OWL 2 RDF-Based interpretation I with respect to D
of any vocabulary V that includes
the RDF and RDFS vocabularies
and the OWL 2 RDF-Based vocabulary
together with all the datatype and facet names listed in Section 3
the following holds:
If I
OWL 2 RDF-Based satisfies all the RDF graphs in S1
with respect to V and D,
then I
OWL 2 RDF-Based satisfies all the RDF graphs in S2
with respect to V and D.
4.4 Parts of the Universe
Table 4.1
defines the "parts" of the universe
of a given OWL 2 RDF-Based interpretation I.
The second column tells the name of the part.
The third column gives a definition of the part
in terms of the mapping IEXT of I,
and by referring to a particular termsterm
of the RDF, RDFS andor OWL 2 RDF-Based vocabularies.vocabulary.
As an example,
the part of all datatypes is named "IDC",
and it is defined as the set of all individuals x
for which the relationship
"⟨"( x , I(rdfs:Datatype) ⟩)
∈
IEXT(I(rdf:type))"
holds.
According to the semantics of rdf:type,
as defined in
Section 4.1 of the RDF Semantics
[RDF Semantics],
this means that the name "IDC"
denotes the class extension
(see Section 4.5)
of I(rdfs:Datatype).
Table 4.1: Parts of the Universe
|
| Name of
Part S
| Definition of S as
{ x ∈ IR | ⟨( x , I(E) ⟩) ∈ IEXT(I(rdf:type)) }
where IRI E is
|
| individuals
| IR
| rdfs:Resource
|
| data values
| LV
| rdfs:Literal
|
| ontologies
| IX
| owl:Ontology
|
| classes
| IC
| rdfs:Class
|
| datatypes
| IDC
| rdfs:Datatype
|
| properties
| IP
| rdf:Property
|
| data properties
| IODP
| owl:DatatypeProperty
|
| ontology properties
| IOXP
| owl:OntologyProperty
|
| annotation properties
| IOAP
| owl:AnnotationProperty
|
4.5 Class Extensions
The mapping ICEXT from IC to the powerset of IR,
which associates classes with their class extension,
is defined
for every c ∈ IC
as
ICEXT(c) = { x ∈ IR | ⟨( x , c ⟩) ∈ IEXT(I(rdf:type)) } .
5 Semantic Conditions
This section defines the semantic conditions of the OWL 2 RDF-Based Semantics.
The semantic conditions presented here
are basically only those for the specific constructs of OWL 2.
The complete set of semantic conditions for the OWL 2 RDF-Based Semantics
is the combination of the semantic conditions presented here
and the semantic conditions
for
Simple Entailment, RDF,Entailment,
RDF,
RDFS
and
D-Entailment,D-Entailment,
as specified in
the RDF Semantics specification
[RDF Semantics].
All semantic conditions in this section
are defined with respect to an interpretation I.
Section 5.1
specifies semantic conditions for the different parts of the universe
(as defined in Section 4.4 )of the OWL 2 RDF-Basedinterpretation being considered.considered
(compare Section 4.4).
Section 5.2
and
Section 5.3
list semantic conditions for the classes and the properties of the OWL 2 RDF-Based vocabulary.
In the rest of this section,
the OWL 2 RDF-Based semantic conditions
for the different language constructs of OWL 2
are specified.
Conventions used in this Section
iff:
Throughout this section
the term "iff" is used as a shortform for "if and only if".
Conjunctive commas:
A comma
(",")
separating two assertions in a semantic condition, as in
"c ∈ IC , p ∈ IP",
is read as a logical "and".
Further,
a comma separating two variables,
as in
"c, d ∈ IC",
is used for abbreviating two comma separated assertions,
"c ∈ IC , d ∈ IC"
in this example.
Unscoped variables:
If no explicit scope is given for a variable "x",
as in "∀ x : …" or "{ x | … }",
then "x" is unconstrained,
which means x ∈ IR,
i.e. "x" denotes an arbitrary individual in the universe.
Set cardinality:
For a set S,
an expression of the form "#S" means the number of elements in S.
Sequence expressions:
An expression of the form
"s sequence of a1 , … , an ∈ S"
means that "s" represents aan RDF list of n ≥ 0
individuals a1 , … , an,
all of them being members of the set S.
Precisely,
s = I(rdf:nil) for n = 0;
and for n > 0
there exist
z1 ∈ IR , … , zn ∈ IR,
such that
s = z1 ,
a1 ∈ S ,
⟨( z1 , a1 ⟩) ∈ IEXT(I(rdf:first)) ,
⟨( z1 , z2 ⟩) ∈ IEXT(I(rdf:rest)) ,
… ,
an ∈ S,
⟨( zn , an ⟩) ∈ IEXT(I(rdf:first)) ,
⟨( zn , I(rdf:nil) ⟩) ∈ IEXT(I(rdf:rest)) .
Note, as mentioned in
Section 3.3.3 of the RDF Semantics
[RDF Semantics],
there are no semantic constraints that enforce "well-formed" sequence structures.
So, for example,
it is possible for a sequence head s to refer to more than one sequence.
Set names:
The following names are used as convenient abbreviations for certain sets:
- ISEQ: The set of all sequences. This set equals the class extension of rdf:List, i.e., ISEQ := ICEXT(I(rdf:List)).
- INNI: The set of all
non-negativenonnegative integers. This set equals the value space of the datatype xsd:nonNegativeInteger, i.e., INNI := ICEXT(I(xsd:nonNegativeInteger)), but is also subsumed by the value spaces of other numerical datatypes, such as xsd:integer.
Notes on the Form of Semantic Conditions (Informative)
One design goal of OWL 2
was to ensure an appropriate degree of alignment
between the OWL 2 RDF-Based Semantics and the
OWL 2 Direct Semantics
[OWL 2 Direct Semantics]
under the different constraints the two semantics have to meet.
The way this semantic alignment is described
is via the OWL 2 correspondence theorem
in Section 7.2.
For this theorem to hold,
the semantic conditions
that treat the RDF encodingsencoding
of OWL 2 axioms
(compare Section 3.2.5 of the OWL 2 RDF Mapping
[OWL 2 RDF Mapping]
and
Section 9 of the OWL 2 Structural Specification
[OWL 2 Specification]),
such as
inverse property axioms,
must have the form of "iff" ("if-and-only-if") conditions.
This means that these semantic conditions
completely determine the semantics
of the encoding of these construct encodings.constructs.
On the other hand,
the RDF encodingsencoding
of OWL 2 expressions
(compare Section 3.2.4 of the OWL 2 RDF Mapping
[OWL 2 RDF Mapping]
and
Sections 6 – 8 of the OWL 2 Structural Specification
[OWL 2 Specification]),
such as
property restrictions,
are treated by "if-then" conditions.
These weaker semantic conditions for expressions
are sufficient for the correspondence theorem to hold,
so there is no necessity to define stronger "iff" conditions under the OWL 2 RDF-Based Semantics
for these language constructs.
Special cases are
the semantic conditions for
Boolean connectives
of classes
and for
enumerations of individuals..
These language constructs build OWL 2 expressions.
But for backwardsbackward compatibility reasons
there areis also RDF encodingsencoding of axioms
based on the vocabulary for these language constructs
(see Table 18 in Section 3.2.5 of the OWL 2 RDF Mapping
[OWL 2 RDF Mapping]).
For example, an RDF expression of the form
ex:c1 owl:unionOf ( ex:c2 ex:c3 ) .
is mapped by the reverse RDF mapping
to an OWL 2 axiom
that states the equivalence of the class denoted by
ex:c1
with the union of the classes denoted by
ex:c2
and
ex:c3.
In order to ensure that the
correspondence theorem
holds,
and in accordance with the original
OWL 1 RDF-Compatible Semantics specification
[OWL 1 RDF-Compatible Semantics],
the semantic conditions for the mentioned language constructs are therefore
"iff" conditions.
Further,
special treatment exists for OWL 2 axioms
that have a multi-triple representationsrepresentation in RDF,
where the different triples share a common "root node",
such as the blank node
"_:x"
in the following example:
_:x rdf:type owl:AllDisjointClasses .
_:x owl:members ( ex:c1 ex:c2 ) .
In essence,
the semantic conditions for the encodingsencoding of these language constructs
are "iff" conditions,
as usual for axioms.
However,
in order to cope with the specific syntactic aspect of a "root node",
the "iff" conditions of these language constructs have been split into two "if-then" conditions,
where the "if-then" condition representing the right-to-left direction
contains an additional premise
ofhaving the form
"∃ z ∈ IR".
The purpose of this premise is to ensure the existence of an individual
that is needed to satisfy the root node
under the OWL 2 RDF-Based semantics.
The language constructs in question are
n-ary disjointness axioms
in Section 5.10,
and
negative property assertions
in Section 5.15.
The "if-then" semantic conditions in this section
sometimes do not explicitly list all typing statements in their consequent
that one might expect.
For example,
the semantic condition for
owl:someValuesFrom restrictions in
Section 5.6
does not list the statement
"x ∈ ICEXT(I(owl:Restriction))"
on its right hand side.
Consequences are generally not mentioned,
if they can already be deduced by other means.
Often,
these redundant consequences follow from the
semantic conditions for
vocabulary classes and vocabulary properties
in
Section 5.2
and
Section 5.3,
respectively,
occasionally in connection with the semantic conditions
for the parts of the universe
in
Section 5.1.
In the example above,
the omitted consequence can be obtained
from the third column of the entry for
owl:someValuesFrom
in the table in
Section 5.3,
which determines that
IEXT(I(owl:someValuesFrom))
⊆
ICEXT(I(owl:Restriction)) × IC.
5.1 Semantic Conditions for the Parts of the Universe
Table 5.1
lists the semantic conditions
for the parts of the universe
of the OWL 2 RDF-Based interpretation being considered.
Additional semantic conditions affecting thethese parts
are given in Section 5.2.
The first column tells the name of the part,
as defined in
Section 4.4.
The second column defines
certain conditions on the part.
In most cases,
the column specifies for the part
by which other part it is subsumed,
and thus the position of the part
in the "parts hierarchy" of the universe
is narrowed down.
The third column provides further
information about the instances
of those parts
that consist of classes or properties.
In general,
if the part consists of classes,
then for the class extensions of the member classes
itis specified by which part of the universe they are subsumed.
If the part consists of properties,
then the domains and ranges of the member properties are determined.
Table 5.1: Semantic Conditions for the Parts of the Universe
Name of
Part S
| Conditions on S
| Conditions on
Instances x of S
|
| IR
| S ≠ ∅
|
|
| LV
| S ⊆ IR
|
|
| IX
| S ⊆ IR
|
|
| IC
| S ⊆ IR
| ICEXT(x) ⊆ IR
|
| IDC
| S ⊆ IC
| ICEXT(x) ⊆ LV
|
| IP
| S ⊆ IR
| IEXT(x) ⊆ IR × IR
|
| IODP
| S ⊆ IP
| IEXT(x) ⊆ IR × LV
|
| IOXP
| S ⊆ IP
| IEXT(x) ⊆ IX × IX
|
| IOAP
| S ⊆ IP
| IEXT(x) ⊆ IR × IR
|
5.2 Semantic Conditions for the Vocabulary Classes
Table 5.2
lists the semantic conditions for the classes
that have IRIs in the OWL 2 RDF-Based vocabulary.
In addition,
the table contains all those classes
with IRIs in the RDF and RDFS vocabularies
that represent
parts of the universe
of the OWL 2 RDF-Based interpretation being considered
(Section 4.4).
The semantic conditions for the remaining classes
with names in the
RDF
and
RDFS vocabularies
can be found in the RDF Semantics specification
[RDF Semantics].
The first column tells the nameIRI of the class.
The second column defines
of what particular kind a class is,
i.e. whether it is a general class (a member of the part IC)
or a datatype (a member of IDC).
The third column specifies
for the class extension of the class
by which part of the universe
(Section 4.4)
it is subsumed:
from an entry of the form
"ICEXT(I(C)) ⊆ S",
for a class nameIRI C
and a set S,
and given an RDF triple of the form
"u rdf:type C",
one can deduce
that the relationship
"I(u) ∈ S"
holds.
Note that some entries are of the form
"ICEXT(I(C)) = S",
which means that the class extension is exactly specified to be that set.
See Section 5.1
for further semantic conditions
on those classes that represent parts.
Not included in this table are the datatypes of the OWL 2 RDF-Based Semantics
with IRIs listed in Section 3.3.
For each such datatype IRI E,
the following semantic conditions hold
(as a consequence of
the fact that E is a member of the datatype map
of every OWL 2 RDF-Based interpretation
according to
Definition 4.2,
and by the "general semantic conditions for datatypes"
listed in
Section 5.1 of the RDF Semantics
[RDF Semantics]):
- I(E) ∈ IDC
- ICEXT(I(E)) ⊆ LV
Table 5.2: Semantic Conditions for the Vocabulary Classes
| IRI E
| I(E)
| ICEXT(I(E))
|
| owl:AllDifferent
| ∈ IC
| ⊆ IR
|
| owl:AllDisjointClasses
| ∈ IC
| ⊆ IR
|
| owl:AllDisjointProperties
| ∈ IC
| ⊆ IR
|
| owl:Annotation
| ∈ IC
| ⊆ IR
|
| owl:AnnotationProperty
| ∈ IC
| = IOAP
|
| owl:AsymmetricProperty
| ∈ IC
| ⊆ IP
|
| owl:Axiom
| ∈ IC
| ⊆ IR
|
| rdfs:Class
| ∈ IC
| = IC
|
| owl:Class
| ∈ IC
| = IC
|
| owl:DataRange
| ∈ IC
| = IDC
|
| rdfs:Datatype
| ∈ IC
| = IDC
|
| owl:DatatypeProperty
| ∈ IC
| = IODP
|
| owl:DeprecatedClass
| ∈ IC
| ⊆ IC
|
| owl:DeprecatedProperty
| ∈ IC
| ⊆ IP
|
| owl:FunctionalProperty
| ∈ IC
| ⊆ IP
|
| owl:InverseFunctionalProperty
| ∈ IC
| ⊆ IP
|
| owl:IrreflexiveProperty
| ∈ IC
| ⊆ IP
|
| rdfs:Literal
| ∈ IDC
| = LV
|
| owl:NamedIndividual
| ∈ IC
| ⊆ IR
|
| owl:NegativePropertyAssertion
| ∈ IC
| ⊆ IR
|
| owl:Nothing
| ∈ IC
| = ∅
|
| owl:ObjectProperty
| ∈ IC
| = IP
|
| owl:Ontology
| ∈ IC
| = IX
|
| owl:OntologyProperty
| ∈ IC
| = IOXP
|
| rdf:Property
| ∈ IC
| = IP
|
| owl:ReflexiveProperty
| ∈ IC
| ⊆ IP
|
| rdfs:Resource
| ∈ IC
| = IR
|
| owl:Restriction
| ∈ IC
| ⊆ IC
|
| owl:SymmetricProperty
| ∈ IC
| ⊆ IP
|
| owl:Thing
| ∈ IC
| = IR
|
| owl:TransitiveProperty
| ∈ IC
| ⊆ IP
|
5.3 Semantic Conditions for the Vocabulary Properties
Table 5.3
lists the semantic conditions for the properties
that have IRIs in the OWL 2 RDF-Based vocabulary.
In addition,
the table contains all those properties
with IRIs in the RDFS vocabulary
that are specified to be annotation properties
under the OWL 2 RDF-Based Semantics.
The semantic conditions for the remaining properties
with names in the
RDF
and
RDFS
vocabularyvocabularies
can be found in the RDF Semantics specification
[RDF Semantics].
The first column tells the nameIRI of the property.
The second column defines
of what particular kind a property is,
i.e. whether it is a general property (a member of the part IP),
a datatype property (a member of IODP),
an ontology property (a member of IOXP) or
an annotation property (a member of IOAP).
The third column specifies
the domain and range of the property:
from an entry of the form
"IEXT(I(p)) ⊆ S1 × S2",
for a property nameIRI p
and sets S1 and S2,
and given an RDF triple
of the form"s p o",
one can deduce thatthe relationships
"I(s) ∈ S1"
and
"I(o) ∈ S2 " hold.".
Note that some entries are of the form
"IEXT(I(p)) = S1 × S2",
which means that the property extension is exactly specified
to be the Cartesian product of the two sets.
Not included in this table are the datatypefacets of the OWL 2 RDF-Based Semantics
with IRIs
listed in Section 3.4,
which are used to specify datatype restrictions
(see Section 5.7).
For each such datatypefacet IRI E,
the following semantic conditions
extend
the basic semantics specification
that has been given for
datatypes with facets
in Section 4.1:
- I(E) ∈
IPIODP
- IEXT(I(E)) ⊆ IR × LV
Implementations are not required
to support the semantic condition for
owl:onProperties,
but
MAY
support it
in order to realize
n-ary dataranges with arity ≥ 2
(see
SectionSections
7
and
8.4
of the OWL 2 Structural Specification
[OWL 2 Specification]
for further information).
Informative notes:
owl:topObjectProperty
relates every two individuals in the universe with each other.
Likewise, owl:topDataProperty
relates every individual with every data value.
Further,
owl:bottomObjectProperty
and
owl:bottomDataProperty
stand both for the empty relationship.
The ranges of the properties
owl:deprecated and owl:hasSelf
are not restricted in any form,
and, in particular,
they are not restricted to beBoolean values.
The actual object values of these properties
do not have any intended meaning,
but could as well have been defined to be of any other value.
Therefore, the semantics given here are of a form
that the values can be arbitrarily chosen
without leading to any non-trivialnontrivial semantic conclusions.
It is, however, recommended to still use an object literal of the form
"true"^^xsd:boolean
in ontologies,
in order to not get in conflict
with the required usage of these properties
in scenarios that ask for applying the reverse RDF mapping
(compare Table 13 in
Section 3.2.4 of the OWL 2 RDF Mapping
[OWL 2 RDF Mapping]
for owl:hasSelf,
and
Section 5.5 of the OWL 2 Structural Specification
[OWL 2 Specification]
for owl:deprecated).
The range of the property
owl:annotatedProperty
is unrestricted in orderunrestricted,
i.e. it is not specified as the set of properties.
Annotations are meant to avoid undesired semantic side effectsbe "semantically weak",
i.e. their formal meaning should not significantly exceed
that originating from an annotation, whenthe annotated axiom orRDF Semantics specification.
Several properties,
such as owl:priorVersion,
have been specified as both ontology properties and annotation is not containedproperties,
in order to be in line with both
the ontology.original
OWL 1 RDF-Compatible Semantics specification
[OWL 1 RDF-Compatible Semantics]
and
the rest of the OWL 2 specification
(see Section 5.5 of the OWL 2 Structural Specification
[OWL 2 Specification]).
Table 5.3: Semantic Conditions for the Vocabulary Properties
| IRI E
| I(E)
| IEXT(I(E))
|
| owl:allValuesFrom
| ∈ IP
| ⊆ ICEXT(I(owl:Restriction)) × IC
|
| owl:annotatedProperty
| ∈ IP
| ⊆ IR × IR
|
| owl:annotatedSource
| ∈ IP
| ⊆ IR × IR
|
| owl:annotatedTarget
| ∈ IP
| ⊆ IR × IR
|
| owl:assertionProperty
| ∈ IP
| ⊆ ICEXT(I(owl:NegativePropertyAssertion)) × IP
|
| owl:backwardCompatibleWith
| ∈ IOXP ,
∈ IOAP
| ⊆ IX × IX
|
| owl:bottomDataProperty
| ∈ IODP
| = ∅
|
| owl:bottomObjectProperty
| ∈ IP
| = ∅
|
| owl:cardinality
| ∈ IP
| ⊆ ICEXT(I(owl:Restriction)) × INNI
|
| rdfs:comment
| ∈ IOAP
| ⊆ IR × LV
|
| owl:complementOf
| ∈ IP
| ⊆ IC × IC
|
| owl:datatypeComplementOf
| ∈ IP
| ⊆ IDC × IDC
|
| owl:deprecated
| ∈ IOAP
| ⊆ IR × IR
|
| owl:differentFrom
| ∈ IP
| ⊆ IR × IR
|
| owl:disjointUnionOf
| ∈ IP
| ⊆ IC × ISEQ
|
| owl:disjointWith
| ∈ IP
| ⊆ IC × IC
|
| owl:distinctMembers
| ∈ IP
| ⊆ ICEXT(I(owl:AllDifferent)) × ISEQ
|
| owl:equivalentClass
| ∈ IP
| ⊆ IC × IC
|
| owl:equivalentProperty
| ∈ IP
| ⊆ IP × IP
|
| owl:hasKey
| ∈ IP
| ⊆ IC × ISEQ
|
| owl:hasSelf
| ∈ IP
| ⊆ ICEXT(I(owl:Restriction)) × IR
|
| owl:hasValue
| ∈ IP
| ⊆ ICEXT(I(owl:Restriction)) × IR
|
| owl:imports
| ∈ IOXP
| ⊆ IX × IX
|
| owl:incompatibleWith
| ∈ IOXP ,
∈ IOAP
| ⊆ IX × IX
|
| owl:intersectionOf
| ∈ IP
| ⊆ IC × ISEQ
|
| owl:inverseOf
| ∈ IP
| ⊆ IP × IP
|
| rdfs:isDefinedBy
| ∈ IOAP
| ⊆ IR × IR
|
| rdfs:label
| ∈ IOAP
| ⊆ IR × LV
|
| owl:maxCardinality
| ∈ IP
| ⊆ ICEXT(I(owl:Restriction)) × INNI
|
| owl:maxQualifiedCardinality
| ∈ IP
| ⊆ ICEXT(I(owl:Restriction)) × INNI
|
| owl:members
| ∈ IP
| ⊆ IR × ISEQ
|
| owl:minCardinality
| ∈ IP
| ⊆ ICEXT(I(owl:Restriction)) × INNI
|
| owl:minQualifiedCardinality
| ∈ IP
| ⊆ ICEXT(I(owl:Restriction)) × INNI
|
| owl:onClass
| ∈ IP
| ⊆ ICEXT(I(owl:Restriction)) × IC
|
| owl:onDataRange
| ∈ IP
| ⊆ ICEXT(I(owl:Restriction)) × IDC
|
| owl:onDatatype
| ∈ IP
| ⊆ IDC × IDC
|
| owl:oneOf
| ∈ IP
| ⊆ IC × ISEQ
|
| owl:onProperty
| ∈ IP
| ⊆ ICEXT(I(owl:Restriction)) × IP
|
| owl:onProperties
| ∈ IP
| ⊆ ICEXT(I(owl:Restriction)) × ISEQ
|
| owl:priorVersion
| ∈ IOXP ,
∈ IOAP
| ⊆ IX × IX
|
| owl:propertyChainAxiom
| ∈ IP
| ⊆ IP × ISEQ
|
| owl:propertyDisjointWith
| ∈ IP
| ⊆ IP × IP
|
| owl:qualifiedCardinality
| ∈ IP
| ⊆ ICEXT(I(owl:Restriction)) × INNI
|
| owl:sameAs
| ∈ IP
| ⊆ IR × IR
|
| rdfs:seeAlso
| ∈ IOAP
| ⊆ IR × IR
|
| owl:someValuesFrom
| ∈ IP
| ⊆ ICEXT(I(owl:Restriction)) × IC
|
| owl:sourceIndividual
| ∈ IP
| ⊆ ICEXT(I(owl:NegativePropertyAssertion)) × IR
|
| owl:targetIndividual
| ∈ IP
| ⊆ ICEXT(I(owl:NegativePropertyAssertion)) × IR
|
| owl:targetValue
| ∈ IP
| ⊆ ICEXT(I(owl:NegativePropertyAssertion)) × LV
|
| owl:topDataProperty
| ∈ IODP
| = IR × LV
|
| owl:topObjectProperty
| ∈ IP
| = IR × IR
|
| owl:unionOf
| ∈ IP
| ⊆ IC × ISEQ
|
| owl:versionInfo
| ∈ IOAP
| ⊆ IR × IR
|
| owl:versionIRI
| ∈ IOXP
| ⊆ IX × IX
|
| owl:withRestrictions
| ∈ IP
| ⊆ IDC × ISEQ
|
5.4 Semantic Conditions for Boolean Connectives
Table 5.4
lists the semantic conditions for Boolean connectives,
including
intersections, unions and complements
of classes and datatypes.
An intersection or a union of a collection of datatypes
or a complement of a datatype
is itself a datatype.
While a complement of a class is created w.r.t. the whole universe,
a datatype complement is created for a datatype w.r.t. the set of data values only.
Informative notes:
Every first semantic conditionOf the three conditionpairs of semantic conditions in the table
every first is an "iff" condition,
since the corresponding OWL 2 language constructs
are both
class expressions and axioms.
In contrast,
the semantic condition on datatype complements
is an "if-then" condition,
since it only corresponds to a datarange expression.
See the
notes on the form of semantic conditions
for further information.
For the remaining semantic conditions
that treat the cases of intersections and unions of datatypes
it is sufficient to have "if-then" conditions,
since stronger "iff" conditions would be redundant
due to the more general "iff" conditions
that already exist for classes.
Note that the datatype related semantic conditions
do not apply to empty sets,
but one can still receive a datatype from an empty set
by explicitly asserting the resulting class
to be an instance of class rdfs:Datatype.
Table 5.4: Semantic Conditions for Boolean Connectives
| if s sequence of c1 , … , cn ∈ IR then
|
⟨( z , s ⟩) ∈ IEXT(I(owl:intersectionOf))
| iff
| z , c1 , … , cn ∈ IC ,
ICEXT(z) = ICEXT(c1) ∩ … ∩ ICEXT(cn)
|
|
|
| if
| then
|
s sequence of d1 , … , dn ∈ IDC , n ≥ 1 ,
⟨( z , s ⟩) ∈ IEXT(I(owl:intersectionOf))
| z ∈ IDC
|
|
|
| if s sequence of c1 , … , cn ∈ IR then
|
⟨( z , s ⟩) ∈ IEXT(I(owl:unionOf))
| iff
| z , c1 , … , cn ∈ IC ,
ICEXT(z) = ICEXT(c1) ∪ … ∪ ICEXT(cn)
|
|
|
| if
| then
|
s sequence of d1 , … , dn ∈ IDC , n ≥ 1 ,
⟨( z , s ⟩) ∈ IEXT(I(owl:unionOf))
| z ∈ IDC
|
|
|
⟨( z , c ⟩) ∈ IEXT(I(owl:complementOf))
| iff
| z , c ∈ IC ,
ICEXT(z) = IR \ ICEXT(c)
|
|
|
| if
| then
|
⟨( z , d ⟩) ∈ IEXT(I(owl:datatypeComplementOf))
| ICEXT(z) = LV \ ICEXT(d)
|
5.5 Semantic Conditions for Enumerations
Table 5.5
lists the semantic conditions for enumerations,
i.e. classes that consist of an explicitly given finite set of instances.
In particular, an enumeration entirely consisting of data values is a datatype.
Informative notes:
The first semantic condition is an "iff" condition,
since the corresponding OWL 2 language construct
is both a class expression and an axiom.
See the
notes on the form of semantic conditions
for further information.
For the remaining semantic condition
that treats the case of enumerations of data values
it is sufficient to have an "if-then" condition,
since a stronger "iff" condition would be redundant
due to the more general "iff" condition
that already exists for individuals.
Note that the data value related semantic condition
does not apply to empty sets,
but one can still receive a datatype from an empty set
by explicitly asserting the resulting class
to be an instance of class rdfs:Datatype.
Table 5.5: Semantic Conditions for Enumerations
| if s sequence of a1 , … , an ∈ IR then
|
⟨( z , s ⟩) ∈ IEXT(I(owl:oneOf))
| iff
| z ∈ IC ,
ICEXT(z) = { a1 , … , an }
|
|
|
| if
| then
|
s sequence of v1 , … , vn ∈ LV , n ≥ 1 ,
⟨( z , s ⟩) ∈ IEXT(I(owl:oneOf))
| z ∈ IDC
|
5.6 Semantic Conditions for Property Restrictions
Table 5.6
lists the semantic conditions for property restrictions.
Value restrictions require that
some or all of the values of a certain property
must be instances of a given class,class or data range,
or that the property has a specifically defined value.
By placing a self restriction on some given property
one only considers those individuals
that are reflexively related to themselves via this property.
Cardinality restrictions determine
how often a certain property is allowed
to be applied to a given individual.
Qualified cardinality restrictions
are more specific than cardinality restrictions
in that they determine the quantity of a property application
with respect to a particular class or data range
from which the property values are taken.
Implementations are not required
to support the semantic conditions for
owl:onProperties,
but
MAY
support them
in order to realize
n-ary dataranges with arity ≥ 2
(see
SectionSections
7
and
8.4
of the OWL 2 Structural Specification
[OWL 2 Specification]
for further information).
Informative notes:
All the semantic conditions are "if-then" conditions,
since the corresponding OWL 2 language constructs
are class expressions.
The "if-then" conditions generally only list those consequences
on their right hand side
that are specific for the respective condition,
i.e. consequences that do not already follow by other means.
See the
notes on the form of semantic conditions
for further information.
Note that the semantic condition for self restrictions
does not constrain the right hand side of
a owl:hasSelf assertion
to be the Boolean value "true"^^xsd:boolean.
See Section 5.3 for an explanation.
Table 5.6: Semantic Conditions for Property Restrictions
| if
| then
|
⟨( z , c ⟩) ∈ IEXT(I(owl:someValuesFrom)) ,
⟨( z , p ⟩) ∈ IEXT(I(owl:onProperty))
| ICEXT(z) = { x | ∃ y : ⟨( x , y ⟩) ∈ IEXT(p) and y ∈ ICEXT(c) }
|
s sequence of p1 , … , pn ∈ IR , n ≥ 1 ,
⟨( z , c ⟩) ∈ IEXT(I(owl:someValuesFrom)) ,
⟨( z , s ⟩) ∈ IEXT(I(owl:onProperties))
| p1 , … , pn ∈ IP ,
ICEXT(z) = { x | ∃ y1 , … , yn : ⟨( x , yk ⟩) ∈ IEXT(pk) for each 1 ≤ k ≤ n and ⟨( y1 , … , yn ⟩) ∈ ICEXT(c) }
|
⟨( z , c ⟩) ∈ IEXT(I(owl:allValuesFrom)) ,
⟨( z , p ⟩) ∈ IEXT(I(owl:onProperty))
| ICEXT(z) = { x | ∀ y : ⟨( x , y ⟩) ∈ IEXT(p) implies y ∈ ICEXT(c) }
|
s sequence of p1 , … , pn ∈ IR , n ≥ 1 ,
⟨( z , c ⟩) ∈ IEXT(I(owl:allValuesFrom)) ,
⟨( z , s ⟩) ∈ IEXT(I(owl:onProperties))
| p1 , … , pn ∈ IP ,
ICEXT(z) = { x | ∀ y1 , … , yn : ⟨( x , yk ⟩) ∈ IEXT(pk) for each 1 ≤ k ≤ n implies ⟨( y1 , … , yn ⟩) ∈ ICEXT(c) }
|
⟨( z , a ⟩) ∈ IEXT(I(owl:hasValue)) ,
⟨( z , p ⟩) ∈ IEXT(I(owl:onProperty))
| ICEXT(z) = { x | ⟨( x , a ⟩) ∈ IEXT(p) }
|
⟨( z , v ⟩) ∈ IEXT(I(owl:hasSelf)) ,
⟨( z , p ⟩) ∈ IEXT(I(owl:onProperty))
| ICEXT(z) = { x | ⟨( x , x ⟩) ∈ IEXT(p) }
|
⟨( z , n ⟩) ∈ IEXT(I(owl:minCardinality)) ,
⟨( z , p ⟩) ∈ IEXT(I(owl:onProperty))
| ICEXT(z) = { x | #{ y | ⟨( x , y ⟩) ∈ IEXT(p) } ≥ n }
|
⟨( z , n ⟩) ∈ IEXT(I(owl:maxCardinality)) ,
⟨( z , p ⟩) ∈ IEXT(I(owl:onProperty))
| ICEXT(z) = { x | #{ y | ⟨( x , y ⟩) ∈ IEXT(p) } ≤ n }
|
⟨( z , n ⟩) ∈ IEXT(I(owl:cardinality)) ,
⟨( z , p ⟩) ∈ IEXT(I(owl:onProperty))
| ICEXT(z) = { x | #{ y | ⟨( x , y ⟩) ∈ IEXT(p) } = n }
|
⟨( z , n ⟩) ∈ IEXT(I(owl:minQualifiedCardinality)) ,
⟨( z , p ⟩) ∈ IEXT(I(owl:onProperty)) ,
⟨( z , c ⟩) ∈ IEXT(I(owl:onClass))
| ICEXT(z) = { x | #{ y | ⟨( x , y ⟩) ∈ IEXT(p) and y ∈ ICEXT(c) } ≥ n }
|
⟨( z , n ⟩) ∈ IEXT(I(owl:minQualifiedCardinality)) ,
⟨( z , p ⟩) ∈ IEXT(I(owl:onProperty)) ,
⟨( z , d ⟩) ∈ IEXT(I(owl:onDataRange))
| p ∈ IODP ,
ICEXT(z) = { x | #{ y ∈ LV | ⟨( x , y ⟩) ∈ IEXT(p) and y ∈ ICEXT(d) } ≥ n }
|
⟨( z , n ⟩) ∈ IEXT(I(owl:maxQualifiedCardinality)) ,
⟨( z , p ⟩) ∈ IEXT(I(owl:onProperty)) ,
⟨( z , c ⟩) ∈ IEXT(I(owl:onClass))
| ICEXT(z) = { x | #{ y | ⟨( x , y ⟩) ∈ IEXT(p) and y ∈ ICEXT(c) } ≤ n }
|
⟨( z , n ⟩) ∈ IEXT(I(owl:maxQualifiedCardinality)) ,
⟨( z , p ⟩) ∈ IEXT(I(owl:onProperty)) ,
⟨( z , d ⟩) ∈ IEXT(I(owl:onDataRange))
| p ∈ IODP ,
ICEXT(z) = { x | #{ y ∈ LV | ⟨( x , y ⟩) ∈ IEXT(p) and y ∈ ICEXT(d) } ≤ n }
|
⟨( z , n ⟩) ∈ IEXT(I(owl:qualifiedCardinality)) ,
⟨( z , p ⟩) ∈ IEXT(I(owl:onProperty)) ,
⟨( z , c ⟩) ∈ IEXT(I(owl:onClass))
| ICEXT(z) = { x | #{ y | ⟨( x , y ⟩) ∈ IEXT(p) and y ∈ ICEXT(c) } = n }
|
⟨( z , n ⟩) ∈ IEXT(I(owl:qualifiedCardinality)) ,
⟨( z , p ⟩) ∈ IEXT(I(owl:onProperty)) ,
⟨( z , d ⟩) ∈ IEXT(I(owl:onDataRange))
| p ∈ IODP ,
ICEXT(z) = { x | #{ y ∈ LV | ⟨( x , y ⟩) ∈ IEXT(p) and y ∈ ICEXT(d) } = n }
|
5.7 Semantic Conditions for Datatype Restrictions
Table 5.7
lists the semantic conditions for datatype restrictions,
which are used to define sub datatypes of existing datatypes
by restricting the original datatype
by means of a set of facet-value pairs.
See Section 3.4
for information and an example on facets (see Section 3.4 ).constraining facets.
Certain special cases exist:
If no facet-value pair is applied to a given datatype at all,datatype,
then the resulting datatype will be equivalent to the original datatype.
Further,
if a facet-value pair is applied to a datatype
without being a member of the datatype's facet space,
then the ontology cannot be satisfied
and will therefore be inconsistent.
In particular,
a datatype restriction with one or more specified facet-value pairs
will result in an inconsistent ontology,
if applied to a datatype with an empty facet space.
The set IFS( d ) for a datatype dIFS
is defined by
IFS(d) := { ⟨( I(F) , v ⟩) | ⟨( F , v ⟩) ∈ FS(d) } ,
where
d is a datatype,
F is the IRI of a constraining facet,
and v is a constraining value of the facet.
This set corresponds to the facet space FS(d),
as defined in Section 4.1,
but rather consists of
pairs of the denotation of a facet and itsa value.
The mapping IF2V( d ) for a datatype dIF2V
is defined by
IF2V(d )(⟨)(( I(F) , v ⟩) :=)) := F2V(d )(⟨)(( F , v ⟩))) ,
where
d is a datatype,
F is the IRI of a constraining facet,
and v is a constraining value of the facet.
This mapping corresponds to the facet-to-value mapping F2V(d),
as defined in Section 4.1,
resulting in the same subsets of the value space VS(d),
but rather applies to
pairs of the denotation of a facet and itsa value.
Informative notes:
The semantic condition is an "if-then" condition,
since the corresponding OWL 2 language construct
is a datarange expression.
The "if-then" condition only lists those consequences
on its right hand side
that are specific for the condition,
i.e. consequences that do not already follow by other means.
See the
notes on the form of semantic conditions
for further information.
Table 5.7: Semantic Conditions for Datatype Restrictions
| if
| then
|
s sequence of z1 , … , zn ∈ IR ,
f1 , … , fn ∈ IP ,
⟨( z , d ⟩) ∈ IEXT(I(owl:onDatatype)) ,
⟨( z , s ⟩) ∈ IEXT(I(owl:withRestrictions)) ,
⟨( z1 , v1 ⟩) ∈ IEXT(f1) , … , ⟨( zn , vn ⟩) ∈ IEXT(fn)
| z , d ∈ IDC ,f1 , … , fn ∈ IODP ,
v1 , … , vn ∈ LV ,
⟨( f1 , v1 ⟩) , … , ⟨( fn , vn ⟩) ∈ IFS(d) ,
ICEXT(z) = ICEXT(d) ∩ IF2V(d )(⟨)(( f1 , v1 ⟩))) ∩ … ∩ IF2V(d )(⟨)(( fn , vn ⟩)))
|
5.8 Semantic Conditions for the RDFS Vocabulary
Table 5.8
extends the RDFS semantic conditions
for subclass axioms, subproperty axioms, domain axioms and range axioms.
The semantic conditions provided here are "iff" conditions,
while the original semantic conditions,
as specified in
Section 4.1 of the RDF Semantics
[RDF Semantics],
wereare weaker "if-then" conditions.
Only the additional semantic conditions are given here
and the other conditions of RDF and RDFS
are retained.
Informative notes:
All the semantic conditions are "iff" conditions,
since the corresponding OWL 2 language constructs
are axioms.
See the
notes on the form of semantic conditions
for further information.
Table 5.8: Semantic Conditions for the RDFS Vocabulary
⟨( c1 , c2 ⟩) ∈ IEXT(I(rdfs:subClassOf))
| iff
| c1 , c2 ∈ IC ,
ICEXT(c1) ⊆ ICEXT(c2)
|
⟨( p1 , p2 ⟩) ∈ IEXT(I(rdfs:subPropertyOf))
| p1 , p2 ∈ IP ,
IEXT(p1) ⊆ IEXT(p2)
|
⟨( p , c ⟩) ∈ IEXT(I(rdfs:domain))
| p ∈ IP , c ∈ IC ,
∀ x , y : ⟨( x , y ⟩) ∈ IEXT(p) implies x ∈ ICEXT(c)
|
⟨( p , c ⟩) ∈ IEXT(I(rdfs:range))
| p ∈ IP , c ∈ IC ,
∀ x , y : ⟨( x , y ⟩) ∈ IEXT(p) implies y ∈ ICEXT(c)
|
5.9 Semantic Conditions for Equivalence and Disjointness
Table 5.9
lists the semantic conditions for specifying
that two individuals are equal or different from each other,
and that either two classes or two properties
are equivalent or disjoint with each other,
respectively.
The
property owl:equivalentClass
is also treated here areused to formulate datatype definitions
(see Section 9.4 of the OWL 2 Structural Specification
[OWL 2 Specification]
for information about datatype definitions).
In addition,
the table treats disjoint union axioms.
Informative notes:
All the semantic conditions are "iff" conditions,
since the corresponding OWL 2 language constructs
are axioms.
See the
notes on the form of semantic conditions
for further information.
Also note that the IRI owl:equivalentClass is used to formulate datatype definitions (see Section 9.4 of [ OWL 2 Specification ] for information about datatype definitions).Table 5.9: Semantic Conditions for Equivalence and Disjointness
⟨( a1 , a2 ⟩) ∈ IEXT(I(owl:sameAs))
| iff
| a1 = a2
|
⟨( a1 , a2 ⟩) ∈ IEXT(I(owl:differentFrom))
| a1 ≠ a2
|
⟨( c1 , c2 ⟩) ∈ IEXT(I(owl:equivalentClass))
| c1 , c2 ∈ IC ,
ICEXT(c1) = ICEXT(c2)
|
⟨( c1 , c2 ⟩) ∈ IEXT(I(owl:disjointWith))
| c1 , c2 ∈ IC ,
ICEXT(c1) ∩ ICEXT(c2) = ∅
|
⟨( p1 , p2 ⟩) ∈ IEXT(I(owl:equivalentProperty))
| p1 , p2 ∈ IP ,
IEXT(p1) = IEXT(p2)
|
⟨( p1 , p2 ⟩) ∈ IEXT(I(owl:propertyDisjointWith))
| p1 , p2 ∈ IP ,
IEXT(p1) ∩ IEXT(p2) = ∅
|
|
|
| if s sequence of c1 , … , cn ∈ IR then
|
⟨( c , s ⟩) ∈ IEXT(I(owl:disjointUnionOf))
| iff
| c , c1 , … , cn ∈ IC ,
ICEXT(c) = ICEXT(c1) ∪ … ∪ ICEXT(cn) ,
ICEXT(cj) ∩ ICEXT(ck) = ∅ for each 1 ≤ j ≤ n and each 1 ≤ k ≤ n such that j ≠ k
|
5.10 Semantic Conditions for N-ary Disjointness
Table 5.10
lists the semantic conditions for specifying
n-ary diversity and disjointness axioms,
i.e. that several given individuals
are mutually different from each other,
and that several given classes or properties
are mutually disjoint with each other,
respectively.
Note that there are two alternative ways
to specify owl:AllDifferent axioms,
by using either the property
owl:members
that is used for all other constructs, too,
or by applying the legacy property
owl:distinctMembers.
Both variants have an equivalent formal meaning.
Informative notes:
The semantic conditions essentially represent "iff" conditions,
since the corresponding OWL 2 language constructs
are axioms.
However,
there are actually two semantic conditions for each language construct
due to the multi-triple RDF encoding of these language constructs.
The "if-then" conditions only list those consequences
on their right hand side
that are specific for the respective condition,
i.e. consequences that do not already follow by other means.
See the
notes on the form of semantic conditions
for further information.
Table 5.10: Semantic Conditions for N-ary Disjointness
| if
| then
|
s sequence of a1 , … , an ∈ IR ,
z ∈ ICEXT(I(owl:AllDifferent)) ,
⟨( z , s ⟩) ∈ IEXT(I(owl:members))
| aj ≠ ak for each 1 ≤ j ≤ n and each 1 ≤ k ≤ n such that j ≠ k
|
|
|
| if
| then exists z ∈ IR
|
s sequence of a1 , … , an ∈ IR ,
aj ≠ ak for each 1 ≤ j ≤ n and each 1 ≤ k ≤ n such that j ≠ k
| z ∈ ICEXT(I(owl:AllDifferent)) ,
⟨( z , s ⟩) ∈ IEXT(I(owl:members))
|
|
|
| if
| then
|
s sequence of a1 , … , an ∈ IR ,
z ∈ ICEXT(I(owl:AllDifferent)) ,
⟨( z , s ⟩) ∈ IEXT(I(owl:distinctMembers))
| aj ≠ ak for each 1 ≤ j ≤ n and each 1 ≤ k ≤ n such that j ≠ k
|
|
|
| if
| then exists z ∈ IR
|
s sequence of a1 , … , an ∈ IR ,
aj ≠ ak for each 1 ≤ j ≤ n and each 1 ≤ k ≤ n such that j ≠ k
| z ∈ ICEXT(I(owl:AllDifferent)) ,
⟨( z , s ⟩) ∈ IEXT(I(owl:distinctMembers))
|
|
|
| if
| then
|
s sequence of c1 , … , cn ∈ IR ,
z ∈ ICEXT(I(owl:AllDisjointClasses)) ,
⟨( z , s ⟩) ∈ IEXT(I(owl:members))
| c1 , … , cn ∈ IC ,
ICEXT(cj) ∩ ICEXT(ck) = ∅ for each 1 ≤ j ≤ n and each 1 ≤ k ≤ n such that j ≠ k
|
|
|
| if
| then exists z ∈ IR
|
s sequence of c1 , … , cn ∈ IC ,
ICEXT(cj) ∩ ICEXT(ck) = ∅ for each 1 ≤ j ≤ n and each 1 ≤ k ≤ n such that j ≠ k
| z ∈ ICEXT(I(owl:AllDisjointClasses)) ,
⟨( z , s ⟩) ∈ IEXT(I(owl:members))
|
|
|
| if
| then
|
s sequence of p1 , … , pn ∈ IR ,
z ∈ ICEXT(I(owl:AllDisjointProperties)) ,
⟨( z , s ⟩) ∈ IEXT(I(owl:members))
| p1 , … , pn ∈ IP ,
IEXT(pj) ∩ IEXT(pk) = ∅ for each 1 ≤ j ≤ n and each 1 ≤ k ≤ n such that j ≠ k
|
|
|
| if
| then exists z ∈ IR
|
s sequence of p1 , … , pn ∈ IP ,
IEXT(pj) ∩ IEXT(pk) = ∅ for each 1 ≤ j ≤ n and each 1 ≤ k ≤ n such that j ≠ k
| z ∈ ICEXT(I(owl:AllDisjointProperties)) ,
⟨( z , s ⟩) ∈ IEXT(I(owl:members))
|
5.11 Semantic Conditions for Sub Property Chains
Table 5.11
lists the semantic conditions for sub property chains,
which allow for specifying complex property subsumption axioms.
As an example,
one can define a sub property chain axiom
that specifies
the chain consisting of the property extensions
of theproperties
ex:hasFather
and
ex:hasBrother
to be a sub relation of
the extension of the property
ex:hasUncle.
Informative notes:
The semantic condition is an "iff" condition,
since the corresponding OWL 2 language construct
is an axiom.
See the
notes on the form of semantic conditions
for further information.
The semantics has been specified in a way
such that allowsa sub property chain axiom tocan be satisfiablesatisfied
without requiring the existence of a property
that representshas the property chain.chain as its property extension.
Table 5.11: Semantic Conditions for Sub Property Chains
| if s sequence of p1 , … , pn ∈ IR then
|
⟨( p , s ⟩) ∈ IEXT(I(owl:propertyChainAxiom))
| iff
| p ∈ IP ,
p1 , … , pn ∈ IP ,
∀ y0 , … , yn : ⟨( y0 , y1 ⟩) ∈ IEXT(p1) and … and ⟨( yn-1 , yn ⟩) ∈ IEXT(pn) implies ⟨( y0 , yn ⟩) ∈ IEXT(p)
|
5.12 Semantic Conditions for Inverse Properties
Table 5.12
lists the semantic conditions for inverse property axioms.
The inverse of a given property
is the corresponding property
with subject and object swapped
for each property assertion built from it.
Informative notes:
The semantic condition is an "iff" condition,
since the corresponding OWL 2 language construct
is an axiom.
See the
notes on the form of semantic conditions
for further information.
Table 5.12: Semantic Conditions for Inverse Properties
⟨( p1 , p2 ⟩) ∈ IEXT(I(owl:inverseOf))
| iff
| p1 , p2 ∈ IP ,
IEXT(p1) = { ⟨( x , y ⟩) | ⟨( y , x ⟩) ∈ IEXT(p2) }
|
5.13 Semantic Conditions for Property Characteristics
Table 5.13
lists the semantic conditions for property characteristics.
If a property is functional,
then at most one distinct value can be assigned
to any given individual
via this property.
An inverse functional property can be regarded as a "key" property,
i.e. no two different individuals
can be assigned the same value
via this property.
A reflexive property relates every individual in the universe to itself,
whereas an irreflexive property does not relate any individual with itself at all.itself.
If two individuals are related by a symmetric property,
then this property also relates them reversely,
while this is never the case for an asymmetric property.
A transitive property
that relates an individual a with an individual b,
and the latter with an individual c,
also relates a with c.
Informative notes:
All the semantic conditions are "iff" conditions,
since the corresponding OWL 2 language constructs
are axioms.
See the
notes on the form of semantic conditions
for further information.
Table 5.13: Semantic Conditions for Property Characteristics
| p ∈ ICEXT(I(owl:FunctionalProperty))
| iff
| p ∈ IP ,
∀ x , y1 , y2 : ⟨( x , y1 ⟩) ∈ IEXT(p) and ⟨( x , y2 ⟩) ∈ IEXT(p) implies y1 = y2
|
| p ∈ ICEXT(I(owl:InverseFunctionalProperty))
| p ∈ IP ,
∀ x1 , x2 , y : ⟨( x1 , y ⟩) ∈ IEXT(p) and ⟨( x2 , y ⟩) ∈ IEXT(p) implies x1 = x2
|
| p ∈ ICEXT(I(owl:ReflexiveProperty))
| p ∈ IP ,
∀ x : ⟨( x , x ⟩) ∈ IEXT(p)
|
| p ∈ ICEXT(I(owl:IrreflexiveProperty))
| p ∈ IP ,
∀ x : ⟨( x , x ⟩) ∉ IEXT(p)
|
| p ∈ ICEXT(I(owl:SymmetricProperty))
| p ∈ IP ,
∀ x , y : ⟨( x , y ⟩) ∈ IEXT(p) implies ⟨( y , x ⟩) ∈ IEXT(p)
|
| p ∈ ICEXT(I(owl:AsymmetricProperty))
| p ∈ IP ,
∀ x , y : ⟨( x , y ⟩) ∈ IEXT(p) implies ⟨( y , x ⟩) ∉ IEXT(p)
|
| p ∈ ICEXT(I(owl:TransitiveProperty))
| p ∈ IP ,
∀ x , y , z : ⟨( x , y ⟩) ∈ IEXT(p) and ⟨( y , z ⟩) ∈ IEXT(p) implies ⟨( x , z ⟩) ∈ IEXT(p)
|
5.14 Semantic Conditions for Keys
Table 5.14
lists the semantic conditions for Keys.
Keys provide an alternative to inverse functional properties
(see Section 5.13).
They allow for defining a property as a key local to a given class:
the specified property
will have the features of a key
only for individuals being instances of the class,
and no assumption is made
about individuals
for which membership of the class cannot be entailed.
Further,
it is possible to define "compound keys",
i.e. several properties can be combined into a single key
applicable to composite values.
Note that
keys are not functional by default
under the OWL 2 RDF-Based Semantics.
Informative notes:
The semantic condition is an "iff" condition,
since the corresponding OWL 2 language construct
is an axiom.
See the
notes on the form of semantic conditions
for further information.
Table 5.14: Semantic Conditions for Keys
| if s sequence of p1 , … , pn ∈ IR then
|
⟨( c , s ⟩) ∈ IEXT(I(owl:hasKey))
| iff
| c ∈ IC ,
p1 , … , pn ∈ IP ,
∀ x , y , z1 , … , zn :
if x ∈ ICEXT(c) and y ∈ ICEXT(c) and
⟨ ( x , zk ⟩) ∈ IEXT(pk) and ⟨( y , zk ⟩) ∈ IEXT(pk) for each 1 ≤ k ≤ n
then x = y
|
5.15 Semantic Conditions for Negative Property Assertions
Table 5.15
lists the semantic conditions for negative property assertions.
They allow to state that
two given individuals are not related by a given property.
The second form based on owl:targetValue
is more specific than the first form based on owl:targetIndividual
in that itthe second form is restricted
to the case of negative data property assertions.
Note that the second form
will coerce the target individualvalue of a negative property assertion
into a data value,
due to the range defined for the property
owl:targetValue
in
Section 5.3.
Informative notes:
The semantic conditions essentially represent "iff" conditions,
since the corresponding OWL 2 language constructs
are axioms.
However,
there are actually two semantic conditions for each language construct,
due to the multi-triple RDF encoding of these language constructs.
The "if-then" conditions only list those consequences
on their right hand side
that are specific for the respective condition,
i.e. consequences that do not already follow by other means.
See the
notes on the form of semantic conditions
for further information.
Table 5.15: Semantic Conditions for Negative Property Assertions
| if
| then
|
⟨( z , a1 ⟩) ∈ IEXT(I(owl:sourceIndividual)) ,
⟨( z , p ⟩) ∈ IEXT(I(owl:assertionProperty)) ,
⟨( z , a2 ⟩) ∈ IEXT(I(owl:targetIndividual))
| ⟨( a1 , a2 ⟩) ∉ IEXT(p)
|
|
|
| if
| then exists z ∈ IR
|
a1 ∈ IR ,
p ∈ IP ,
a2 ∈ IR ,
⟨( a1 , a2 ⟩) ∉ IEXT(p)
| ⟨( z , a1 ⟩) ∈ IEXT(I(owl:sourceIndividual)) ,
⟨( z , p ⟩) ∈ IEXT(I(owl:assertionProperty)) ,
⟨( z , a2 ⟩) ∈ IEXT(I(owl:targetIndividual))
|
|
|
| if
| then
|
⟨( z , a ⟩) ∈ IEXT(I(owl:sourceIndividual)) ,
⟨( z , p ⟩) ∈ IEXT(I(owl:assertionProperty)) ,
⟨( z , v ⟩) ∈ IEXT(I(owl:targetValue))
| p ∈ IODP ,
⟨( a , v ⟩) ∉ IEXT(p)
|
|
|
| if
| then exists z ∈ IR
|
a ∈ IR ,
p ∈ IODP ,
v ∈ LV ,
⟨( a , v ⟩) ∉ IEXT(p)
| ⟨( z , a ⟩) ∈ IEXT(I(owl:sourceIndividual)) ,
⟨( z , p ⟩) ∈ IEXT(I(owl:assertionProperty)) ,
⟨( z , v ⟩) ∈ IEXT(I(owl:targetValue))
|
6 Appendix: Axiomatic Triples (Informative)
The RDF Semantics specification
[RDF Semantics]
defines so called "axiomatic triples"
as part of the semantics of
RDF
and
RDFS.RDFS.
Unlike the RDF Semantics,
the OWL 2 RDF-Based Semantics does not normatively specify any axiomatic triples. It might not be possibletriples,
since one cannot expect to givefind a set of RDF triples
that fully captures all "axiomatic aspects"
of the OWL 2 RDF-Based Semantics, just as one cannot expect to define the whole OWL 2 RDF-Based Semantics specification in terms of RDF entailment rules only.Semantics.
Furthermore,
axiomatic triples for the OWL 2 RDF-Based Semantics could,
in principle,
contain arbitrarily complex class expressions,
e.g. the union of several classes,
and by this it becomes non-obviousnonobvious
which of several possible non-equivalentnonequivalent sets of axiomatic triples
should be selected.
However,
the OWL 2 RDF-Based Semantics includes many semantic conditions
that can in a sense be regarded as being "axiomatic",
and thus can be considered a replacement for the missing axiomatic triples.
After an overview on axiomatic triples for RDF and RDFS
in Section 6.1,
theSections 6.2
and
6.3
will discuss how the "axiomatic" semantic conditions
of the OWL 2 RDF-Based Semantics
relate to axiomatic triples, resulting intriples.
Based on this discussion,
an explicit example set of axiomatic triples
that is compatible with the OWL 2 RDF-Based Semantics.Semantics
will be provided in
Section 6.4.
6.1 Axiomatic Triples in RDF
In
RDF
and
RDFS
[RDF Semantics],
axiomatic triples are used
to provide basic meaning
for all the vocabulary terms
of the two languages.
This formal meaning is independent of any given RDF graph,
and it even holds for vocabulary terms,
which do not occur in a graph
that is interpreted by an RDF or RDFS interpretation.
As a consequence,
all the axiomatic triples of RDF and RDFS
are entailed by the empty graph,
when being interpreted under the semantics of RDF or RDFS,
respectively.
Examples of RDF and RDFS axiomatic triples are:
(1) rdf:type rdf:type rdf:Property .
(2) rdf:type rdfs:domain rdfs:Resource .
(3) rdf:type rdfs:range rdfs:Class .
(4) rdfs:Datatype rdfs:subClassOf rdfs:Class .
(5) rdfs:isDefinedBy rdfs:subPropertyOf rdfs:seeAlso .
As shown by these examples,
axiomatic triples are typically used by the RDF Semantics specification
to determine the part of the universe
to which the denotation of a vocabulary term belongs to(1).
In the case of a property,
the domain (2) and range (3) is specified as well.
Also, in some cases,
hierarchical relationships
between classes (4) or properties (5) of the vocabulary
are determined.
Under the OWL 2 RDF-Based Semantics,
all the axiomatic triples of RDF and RDFS
could, in principle, be replaced by
"axiomatic" semantic conditions
that have neither premises nor bound variables.
By specificallyapplying the RDFS semantic conditions
given in Section 5.8,
the example axiomatic triples (1) – (5)
can be equivalently restated as:
I(rdf:type) ∈ ICEXT(I(rdf:Property)) ,
IEXT(I(rdf:type)) ⊆ ICEXT(I(rdfs:Resource)) × ICEXT(I(rdfs:Class)) ,
ICEXT(I(rdfs:Datatype)) ⊆ ICEXT(I(rdfs:Class)) ,
IEXT(I(rdfs:isDefinedBy)) ⊆ IEXT(I(rdfs:seeAlso)) .
All the axiomatic triples of RDF and RDFS
can be considered "simple"
in the sense that
they have in their object position
only single terms
from the RDF and RDFS vocabularies,
and no complex class or property expressions
appear there.
6.2 Axiomatic Triples for the Vocabulary Classes
The semantic conditions for vocabulary classes
in Table 5.2 ofSection 5.2
can be considered as corresponding to
a set of axiomatic triples
for the classes in the vocabulary of the OWL 2 RDF-Based Semantics.
First,
for each IRI E
occurring in the first column of Table 5.2,
if the second column contains an entry
of the form
"I(E) ∈ S"
for some set S,
then this entry corresponds to somean RDF triple of the form
"E rdf:type C",
where C is the IRI of somea vocabulary class with ICEXT(I(C)) = S.
In the table, S will always be either
the part IC of all classes,
or some sub part of IC.
Hence, in a corresponding RDF triple the IRI C will typicallybe
one of
"rdfs:Class",
"owl:Class"
(S=IC in both cases)
or "rdfs:Datatype" (S=IDC).
For example,
the semantic conditionfor the IRI "owl:FunctionalProperty",
given bythe semantic condition
I(owl:FunctionalProperty) ∈ IC
, would havehas the corresponding axiomatic triple
owl:FunctionalProperty rdf:type rdfs:Class .
Further,
for each IRI E in the first column of the table,
if the third column contains an entry
of the form
"ICEXT(I(E)) ⊆ S"
(or "ICEXT(I(E)) = S")
for some set S,
then this entry corresponds to somean RDF triple of the form
"E rdfs:subClassOf C"
(or additionally " E owl:equivalentClassC rdfs:subClassOf E"),
where C is the IRI of somea vocabulary class with ICEXT(I(C)) = S.
In everyeach case,
S will be eitherone of
the parts of the universe of I or the empty set..
For example,
the semantic condition
ICEXT(I(owl:FunctionalProperty)) ⊆ IP
would havehas the corresponding axiomatic triple
owl:FunctionalProperty rdfs:subClassOf rdf:Property .
In addition,
the semantic conditions for the
parts of the universe
in Table 5.1
of Section 5.1
have to be taken into account.
In particular,
if an entry in the second column of Table 5.1
is of the form
"S1 ⊆ S2"
for some sets S1 and S2,
then this corresponds to somean RDF triple
of the form
"C1 owl:subClassOf C2",
where
C1 and C2
are the IRIs of somevocabulary classes with
ICEXT(I(C1)) = S1
and
ICEXT(I(C2)) = S2,
respectively,
according to
Section 5.2.
Section 5.2
also specifies semantic conditions
for all the datatypes of the OWL 2 RDF-Based Semantics,
as listed in Section 3.3.
For each datatype IRI E,
such as statedE := "xsd:string",
for the semantic conditions
"I(E) ∈ IDC"
and
"ICEXT(I(E)) ⊆ LV"
the corresponding axiomatic triples are of the form
E rdf:type rdfs:Datatype .
E rdfs:subClassOf rdfs:Literal .
In analogy to
Section 6.1
for the RDF axiomatic triples,
all the axiomatic triples for the vocabulary classes
(including datatypes)
can be considered "simple"
in the sense that
they will have in their object position
only single terms
from the RDF, RDFS and OWL 2 RDF-Based vocabularies
(Section 3.2).
Note that some of the axiomatic triples obtained in this way
already follow from the semantics of
RDF
and
RDFS,RDFS,
as defined in
the RDF Semantics [RDF Semantics].
6.3 Axiomatic Triples for the Vocabulary Properties
The semantic conditions for vocabulary properties
in Table 5.3 ofSection 5.3
can be considered as corresponding to
a set of axiomatic triples
for the properties in the vocabulary of the OWL 2 RDF-Based Semantics.
First,
for each IRI E
occurring in the first column of Table 5.3,
if the second column contains an entry
of the form
"I(E) ∈ S" for some set S,
then this entry corresponds to somean RDF triple of the form
"E rdf:type C",
where C is the IRI of somea vocabulary class with ICEXT(I(C)) = S.
In the table,
S will always be either
the part IP of all properties,
or some sub part of IP.
Hence, in a corresponding RDF triple the IRI C will typicallybe
one of
"rdf:Property",
"owl:ObjectProperty",
(S=IP in both cases),
"owl:DatatypeProperty" (S=IODP),
"owl:OntologyProperty" (S=IOXP)
or "owl:AnnotationProperty" (S=IOAP).
For example,
the semantic conditionfor the IRI "owl:disjointWith",
given bythe semantic condition
, would havehas the corresponding axiomatic triple
owl:disjointWith rdf:type rdf:Property .
Further,
for each IRI E in the first column of the table,
if the third column contains an entry
of the form
"IEXT(I(E)) ⊆ S1 × S2"
for some sets S1 and S2,
then this entry corresponds to someRDF triples of the formsform
"E rdfs:domain C1"
and
"E rdfs:range C2",
where C1 and C2
are the IRIs of somevocabulary classes with
ICEXT(I(C1)) = S1
and
ICEXT(I(C2)) = S2,
respectively.
Note that the sets S1 and S2
do not always correspond
to any of the parts of the universe of I.
For example,
the semantic condition
IEXT(I(owl:disjointWith)) ⊆ IC × IC
would havehas the corresponding axiomatic triples
owl:disjointWith rdfs:domain owl:Class .
owl:disjointWith rdfs:range owl:Class .
Exceptions are the semantic conditions
"IEXT(I(owl:topObjectProperty)) = IR × IR"
and
"IEXT(I(owl:topDataProperty)) = IR × LV",
since the exactly specified property extensions of these properties
cannot be expressed solely by domain and range axiomatic triples.
For example,
the domain and range axiomatic triples for
owl:sameAs
are equal to those for
owl:topObjectProperty,
but the property extension of
owl:sameAs
is different from thatthe property extension of
owl:topObjectProperty.
Section 5.3
also specifies semantic conditions
for all the facets of the OWL 2 RDF-Based Semantics,
as listed in Section 3.4.
For each facet IRI E,
such as statedE := "xsd:length",
for the semantic conditions
"I(E) ∈ IODP"
and
"IEXT(I(E)) ⊆ IR × LV"
the corresponding axiomatic triples are of the form
E rdf:type owl:DatatypeProperty .
E rdfs:domain rdfs:Resource .
E rdfs:range rdfs:Literal .
In analogy to
Section 6.1
for the RDF axiomatic triples,
all the axiomatic triples for the vocabulary properties
(including facets)
can be considered "simple"
in the sense that
they will have in their object position
only single terms
from the RDF, RDFS and OWL 2 RDF-Based vocabularies
(Section 3.2).
7 Appendix: Relationship to the Direct Semantics (Informative)6.4 A Set of Axiomatic Triples
This section comparesprovides a concrete example set of axiomatic triples
based on the OWL 2 RDF-Based Semantics withdiscussion in the OWL 2 Direct Semantics [ OWL 2 Direct Semantics ]. WhileSections
6.2
and
6.3.
The OWL 2 RDF-Based Semantics is based onaxiomatic triples are grouped by different tables
for the RDF Semantics specification [ RDF Semantics ],classes
and the properties
of the OWL 2 Direct Semantics is a description logic style semantics. Several fundamental differences exist betweenRDF-Based vocabulary,
for the two semantics, but there is also a strong relationship basically stating thatdatatypes
and the facets
of the OWL 2 RDF-Based SemanticsSemantics,
and for some of the
classes and properties of the RDFS vocabulary.
Note that this set of axiomatic triples
is ablenot meant to reflect all logical conclusionsbe free of redundancy.
Table 6.1: Axiomatic Triples for the OWL 2 Direct Semantics. This means thatClasses of the OWL 2 Direct SemanticsRDF-Based Vocabulary
owl:AllDifferent rdf:type rdfs:Class .
owl:AllDifferent rdfs:subClassOf rdfs:Resource .
| owl:AllDisjointClasses rdf:type rdfs:Class .
owl:AllDisjointClasses rdfs:subClassOf rdfs:Resource .
|
owl:AllDisjointProperties rdf:type rdfs:Class .
owl:AllDisjointProperties rdfs:subClassOf rdfs:Resource .
| owl:Annotation rdf:type rdfs:Class .
owl:Annotation rdfs:subClassOf rdfs:Resource .
|
owl:AnnotationProperty rdf:type rdfs:Class .
owl:AnnotationProperty rdfs:subClassOf rdf:Property .
| owl:AsymmetricProperty rdf:type rdfs:Class .
owl:AsymmetricProperty rdfs:subClassOf owl:ObjectProperty .
|
owl:Axiom rdf:type rdfs:Class .
owl:Axiom rdfs:subClassOf rdfs:Resource .
| owl:Class rdf:type rdfs:Class .
owl:Class rdfs:subClassOf rdfs:Class .
|
owl:DataRange rdf:type rdfs:Class .
owl:DataRange rdfs:subClassOf rdfs:Datatype .
| owl:DatatypeProperty rdf:type rdfs:Class .
owl:DatatypeProperty rdfs:subClassOf rdf:Property .
|
owl:DeprecatedClass rdf:type rdfs:Class .
owl:DeprecatedClass rdfs:subClassOf rdfs:Class .
| owl:DeprecatedProperty rdf:type rdfs:Class .
owl:DeprecatedProperty rdfs:subClassOf rdf:Property .
|
owl:FunctionalProperty rdf:type rdfs:Class .
owl:FunctionalProperty rdfs:subClassOf rdf:Property .
| owl:InverseFunctionalProperty rdf:type rdfs:Class .
owl:InverseFunctionalProperty rdfs:subClassOf owl:ObjectProperty .
|
owl:IrreflexiveProperty rdf:type rdfs:Class .
owl:IrreflexiveProperty rdfs:subClassOf owl:ObjectProperty .
| owl:NamedIndividual rdf:type rdfs:Class .
owl:NamedIndividual rdfs:subClassOf owl:Thing .
|
owl:NegativePropertyAssertion rdf:type rdfs:Class .
owl:NegativePropertyAssertion rdfs:subClassOf rdfs:Resource .
| owl:Nothing rdf:type owl:Class .
owl:Nothing rdfs:subClassOf owl:Thing .
|
owl:ObjectProperty rdf:type rdfs:Class .
owl:ObjectProperty rdfs:subClassOf rdf:Property .
| owl:Ontology rdf:type rdfs:Class .
owl:Ontology rdfs:subClassOf rdfs:Resource .
|
owl:OntologyProperty rdf:type rdfs:Class .
owl:OntologyProperty rdfs:subClassOf rdf:Property .
| owl:ReflexiveProperty rdf:type rdfs:Class .
owl:ReflexiveProperty rdfs:subClassOf owl:ObjectProperty .
|
owl:Restriction rdf:type rdfs:Class .
owl:Restriction rdfs:subClassOf owl:Class .
| owl:SymmetricProperty rdf:type rdfs:Class .
owl:SymmetricProperty rdfs:subClassOf owl:ObjectProperty .
|
owl:Thing rdf:type owl:Class .
| owl:TransitiveProperty rdf:type rdfs:Class .
owl:TransitiveProperty rdfs:subClassOf owl:ObjectProperty .
|
Table 6.2: Axiomatic Triples for the Properties of the OWL 2 RDF-Based Vocabulary
owl:allValuesFrom rdf:type rdf:Property .
owl:allValuesFrom rdfs:domain owl:Restriction .
owl:allValuesFrom rdfs:range rdfs:Class .
| owl:annotatedProperty rdf:type rdf:Property .
owl:annotatedProperty rdfs:domain rdfs:Resource .
owl:annotatedProperty rdfs:range rdfs:Resource .
|
owl:annotatedSource rdf:type rdf:Property .
owl:annotatedSource rdfs:domain rdfs:Resource .
owl:annotatedSource rdfs:range rdfs:Resource .
| owl:annotatedTarget rdf:type rdf:Property .
owl:annotatedTarget rdfs:domain rdfs:Resource .
owl:annotatedTarget rdfs:range rdfs:Resource .
|
owl:assertionProperty rdf:type rdf:Property .
owl:assertionProperty rdfs:domain owl:NegativePropertyAssertion .
owl:assertionProperty rdfs:range rdf:Property .
| owl:backwardCompatibleWith rdf:type owl:AnnotationProperty .
owl:backwardCompatibleWith rdf:type owl:OntologyProperty .
owl:backwardCompatibleWith rdfs:domain owl:Ontology .
owl:backwardCompatibleWith rdfs:range owl:Ontology .
|
owl:bottomDataProperty rdf:type owl:DatatypeProperty .
owl:bottomDataProperty rdfs:domain owl:Thing .
owl:bottomDataProperty rdfs:range rdfs:Literal .
| owl:bottomObjectProperty rdf:type owl:ObjectProperty .
owl:bottomObjectProperty rdfs:domain owl:Thing .
owl:bottomObjectProperty rdfs:range owl:Thing .
|
owl:cardinality rdf:type rdf:Property .
owl:cardinality rdfs:domain owl:Restriction .
owl:cardinality rdfs:range xsd:nonNegativeInteger .
| owl:complementOf rdf:type rdf:Property .
owl:complementOf rdfs:domain owl:Class .
owl:complementOf rdfs:range owl:Class .
|
owl:datatypeComplementOf rdf:type rdf:Property .
owl:datatypeComplementOf rdfs:domain rdfs:Datatype .
owl:datatypeComplementOf rdfs:range rdfs:Datatype .
| owl:deprecated rdf:type owl:AnnotationProperty .
owl:deprecated rdfs:domain rdfs:Resource .
owl:deprecated rdfs:range rdfs:Resource .
|
owl:differentFrom rdf:type rdf:Property .
owl:differentFrom rdfs:domain owl:Thing .
owl:differentFrom rdfs:range owl:Thing .
| owl:disjointUnionOf rdf:type rdf:Property .
owl:disjointUnionOf rdfs:domain owl:Class .
owl:disjointUnionOf rdfs:range rdf:List .
|
owl:disjointWith rdf:type rdf:Property .
owl:disjointWith rdfs:domain owl:Class .
owl:disjointWith rdfs:range owl:Class .
| owl:distinctMembers rdf:type rdf:Property .
owl:distinctMembers rdfs:domain owl:AllDifferent .
owl:distinctMembers rdfs:range rdf:List .
|
owl:equivalentClass rdf:type rdf:Property .
owl:equivalentClass rdfs:domain rdfs:Class .
owl:equivalentClass rdfs:range rdfs:Class .
| owl:equivalentProperty rdf:type rdf:Property .
owl:equivalentProperty rdfs:domain rdf:Property .
owl:equivalentProperty rdfs:range rdf:Property .
|
owl:hasKey rdf:type rdf:Property .
owl:hasKey rdfs:domain owl:Class .
owl:hasKey rdfs:range rdf:List .
| owl:hasSelf rdf:type rdf:Property .
owl:hasSelf rdfs:domain owl:Restriction .
owl:hasSelf rdfs:range rdfs:Resource .
|
owl:hasValue rdf:type rdf:Property .
owl:hasValue rdfs:domain owl:Restriction .
owl:hasValue rdfs:range rdfs:Resource .
| owl:imports rdf:type owl:OntologyProperty .
owl:imports rdfs:domain owl:Ontology .
owl:imports rdfs:range owl:Ontology .
|
owl:incompatibleWith rdf:type owl:AnnotationProperty .
owl:incompatibleWith rdf:type owl:OntologyProperty .
owl:incompatibleWith rdfs:domain owl:Ontology .
owl:incompatibleWith rdfs:range owl:Ontology .
| owl:intersectionOf rdf:type rdf:Property .
owl:intersectionOf rdfs:domain rdfs:Class .
owl:intersectionOf rdfs:range rdf:List .
|
owl:inverseOf rdf:type rdf:Property .
owl:inverseOf rdfs:domain owl:ObjectProperty .
owl:inverseOf rdfs:range owl:ObjectProperty .
| owl:maxCardinality rdf:type rdf:Property .
owl:maxCardinality rdfs:domain owl:Restriction .
owl:maxCardinality rdfs:range xsd:nonNegativeInteger .
|
owl:maxQualifiedCardinality rdf:type rdf:Property .
owl:maxQualifiedCardinality rdfs:domain owl:Restriction .
owl:maxQualifiedCardinality rdfs:range xsd:nonNegativeInteger .
| owl:members rdf:type rdf:Property .
owl:members rdfs:domain rdfs:Resource .
owl:members rdfs:range rdf:List .
|
owl:minCardinality rdf:type rdf:Property .
owl:minCardinality rdfs:domain owl:Restriction .
owl:minCardinality rdfs:range xsd:nonNegativeInteger .
| owl:minQualifiedCardinality rdf:type rdf:Property .
owl:minQualifiedCardinality rdfs:domain owl:Restriction .
owl:minQualifiedCardinality rdfs:range xsd:nonNegativeInteger .
|
owl:onClass rdf:type rdf:Property .
owl:onClass rdfs:domain owl:Restriction .
owl:onClass rdfs:range owl:Class .
| owl:onDataRange rdf:type rdf:Property .
owl:onDataRange rdfs:domain owl:Restriction .
owl:onDataRange rdfs:range rdfs:Datatype .
|
owl:onDatatype rdf:type rdf:Property .
owl:onDatatype rdfs:domain rdfs:Datatype .
owl:onDatatype rdfs:range rdfs:Datatype .
| owl:oneOf rdf:type rdf:Property .
owl:oneOf rdfs:domain rdfs:Class .
owl:oneOf rdfs:range rdf:List .
|
owl:onProperty rdf:type rdf:Property .
owl:onProperty rdfs:domain owl:Restriction .
owl:onProperty rdfs:range rdf:Property .
| owl:onProperties rdf:type rdf:Property .
owl:onProperties rdfs:domain owl:Restriction .
owl:onProperties rdfs:range rdf:List .
|
owl:priorVersion rdf:type owl:AnnotationProperty .
owl:priorVersion rdf:type owl:OntologyProperty .
owl:priorVersion rdfs:domain owl:Ontology .
owl:priorVersion rdfs:range owl:Ontology .
| owl:propertyChainAxiom rdf:type rdf:Property .
owl:propertyChainAxiom rdfs:domain owl:ObjectProperty .
owl:propertyChainAxiom rdfs:range rdf:List .
|
owl:propertyDisjointWith rdf:type rdf:Property .
owl:propertyDisjointWith rdfs:domain rdf:Property .
owl:propertyDisjointWith rdfs:range rdf:Property .
| owl:qualifiedCardinality rdf:type rdf:Property .
owl:qualifiedCardinality rdfs:domain owl:Restriction .
owl:qualifiedCardinality rdfs:range xsd:nonNegativeInteger .
|
owl:sameAs rdf:type rdf:Property .
owl:sameAs rdfs:domain owl:Thing .
owl:sameAs rdfs:range owl:Thing .
| owl:someValuesFrom rdf:type rdf:Property .
owl:someValuesFrom rdfs:domain owl:Restriction .
owl:someValuesFrom rdfs:range rdfs:Class .
|
owl:sourceIndividual rdf:type rdf:Property .
owl:sourceIndividual rdfs:domain owl:NegativePropertyAssertion .
owl:sourceIndividual rdfs:range owl:Thing .
| owl:targetIndividual rdf:type rdf:Property .
owl:targetIndividual rdfs:domain owl:NegativePropertyAssertion .
owl:targetIndividual rdfs:range owl:Thing .
|
owl:targetValue rdf:type rdf:Property .
owl:targetValue rdfs:domain owl:NegativePropertyAssertion .
owl:targetValue rdfs:range rdfs:Literal .
| owl:topDataProperty rdf:type owl:DatatypeProperty .
owl:topDataProperty rdfs:domain owl:Thing .
owl:topDataProperty rdfs:range rdfs:Literal .
|
owl:topObjectProperty rdf:type rdf:ObjectProperty .
owl:topObjectProperty rdfs:domain owl:Thing .
owl:topObjectProperty rdfs:range owl:Thing .
| owl:unionOf rdf:type rdf:Property .
owl:unionOf rdfs:domain rdfs:Class .
owl:unionOf rdfs:range rdf:List .
|
owl:versionInfo rdf:type owl:AnnotationProperty .
owl:versionInfo rdfs:domain rdfs:Resource .
owl:versionInfo rdfs:range rdfs:Resource .
| owl:versionIRI rdf:type owl:OntologyProperty .
owl:versionIRI rdfs:domain owl:Ontology .
owl:versionIRI rdfs:range owl:Ontology .
|
owl:withRestrictions rdf:type rdf:Property .
owl:withRestrictions rdfs:domain rdfs:Datatype .
owl:withRestrictions rdfs:range rdf:List .
|
|
Table 6.3: Axiomatic Triples for the Datatypes of the OWL 2 RDF-Based Semantics
xsd:anyURI rdf:type rdfs:Datatype .
xsd:anyURI rdfs:subClassOf rdfs:Literal .
| xsd:base64Binary rdf:type rdfs:Datatype .
xsd:base64Binary rdfs:subClassOf rdfs:Literal .
|
xsd:boolean rdf:type rdfs:Datatype .
xsd:boolean rdfs:subClassOf rdfs:Literal .
| xsd:byte rdf:type rdfs:Datatype .
xsd:byte rdfs:subClassOf rdfs:Literal .
|
xsd:dateTime rdf:type rdfs:Datatype .
xsd:dateTime rdfs:subClassOf rdfs:Literal .
| xsd:dateTimeStamp rdf:type rdfs:Datatype .
xsd:dateTimeStamp rdfs:subClassOf rdfs:Literal .
|
xsd:decimal rdf:type rdfs:Datatype .
xsd:decimal rdfs:subClassOf rdfs:Literal .
| xsd:double rdf:type rdfs:Datatype .
xsd:double rdfs:subClassOf rdfs:Literal .
|
xsd:float rdf:type rdfs:Datatype .
xsd:float rdfs:subClassOf rdfs:Literal .
| xsd:hexBinary rdf:type rdfs:Datatype .
xsd:hexBinary rdfs:subClassOf rdfs:Literal .
|
xsd:int rdf:type rdfs:Datatype .
xsd:int rdfs:subClassOf rdfs:Literal .
| xsd:integer rdf:type rdfs:Datatype .
xsd:integer rdfs:subClassOf rdfs:Literal .
|
xsd:language rdf:type rdfs:Datatype .
xsd:language rdfs:subClassOf rdfs:Literal .
| xsd:long rdf:type rdfs:Datatype .
xsd:long rdfs:subClassOf rdfs:Literal .
|
xsd:Name rdf:type rdfs:Datatype .
xsd:Name rdfs:subClassOf rdfs:Literal .
| xsd:NCName rdf:type rdfs:Datatype .
xsd:NCName rdfs:subClassOf rdfs:Literal .
|
xsd:negativeInteger rdf:type rdfs:Datatype .
xsd:negativeInteger rdfs:subClassOf rdfs:Literal .
| xsd:NMTOKEN rdf:type rdfs:Datatype .
xsd:NMTOKEN rdfs:subClassOf rdfs:Literal .
|
xsd:nonNegativeInteger rdf:type rdfs:Datatype .
xsd:nonNegativeInteger rdfs:subClassOf rdfs:Literal .
| xsd:nonPositiveInteger rdf:type rdfs:Datatype .
xsd:nonPositiveInteger rdfs:subClassOf rdfs:Literal .
|
xsd:normalizedString rdf:type rdfs:Datatype .
xsd:normalizedString rdfs:subClassOf rdfs:Literal .
| rdf:PlainLiteral rdf:type rdfs:Datatype .
rdf:PlainLiteral rdfs:subClassOf rdfs:Literal .
|
xsd:positiveInteger rdf:type rdfs:Datatype .
xsd:positiveInteger rdfs:subClassOf rdfs:Literal .
| owl:rational rdf:type rdfs:Datatype .
owl:rational rdfs:subClassOf rdfs:Literal .
|
owl:real rdf:type rdfs:Datatype .
owl:real rdfs:subClassOf rdfs:Literal .
| xsd:short rdf:type rdfs:Datatype .
xsd:short rdfs:subClassOf rdfs:Literal .
|
xsd:string rdf:type rdfs:Datatype .
xsd:string rdfs:subClassOf rdfs:Literal .
| xsd:token rdf:type rdfs:Datatype .
xsd:token rdfs:subClassOf rdfs:Literal .
|
xsd:unsignedByte rdf:type rdfs:Datatype .
xsd:unsignedByte rdfs:subClassOf rdfs:Literal .
| xsd:unsignedInt rdf:type rdfs:Datatype .
xsd:unsignedInt rdfs:subClassOf rdfs:Literal .
|
xsd:unsignedLong rdf:type rdfs:Datatype .
xsd:unsignedLong rdfs:subClassOf rdfs:Literal .
| xsd:unsignedShort rdf:type rdfs:Datatype .
xsd:unsignedShort rdfs:subClassOf rdfs:Literal .
|
rdf:XMLLiteral rdf:type rdfs:Datatype .
rdf:XMLLiteral rdfs:subClassOf rdfs:Literal .
|
|
Table 6.4: Axiomatic Triples for the Facets of the OWL 2 RDF-Based Semantics
rdf:langRange rdf:type owl:DatatypeProperty .
rdf:langRange rdfs:domain rdfs:Resource .
rdf:langRange rdfs:range rdfs:Literal .
| xsd:length rdf:type owl:DatatypeProperty .
xsd:length rdfs:domain rdfs:Resource .
xsd:length rdfs:range rdfs:Literal .
|
xsd:maxExclusive rdf:type owl:DatatypeProperty .
xsd:maxExclusive rdfs:domain rdfs:Resource .
xsd:maxExclusive rdfs:range rdfs:Literal .
| xsd:maxInclusive rdf:type owl:DatatypeProperty .
xsd:maxInclusive rdfs:domain rdfs:Resource .
xsd:maxInclusive rdfs:range rdfs:Literal .
|
xsd:maxLength rdf:type owl:DatatypeProperty .
xsd:maxLength rdfs:domain rdfs:Resource .
xsd:maxLength rdfs:range rdfs:Literal .
| xsd:minExclusive rdf:type owl:DatatypeProperty .
xsd:minExclusive rdfs:domain rdfs:Resource .
xsd:minExclusive rdfs:range rdfs:Literal .
|
xsd:minInclusive rdf:type owl:DatatypeProperty .
xsd:minInclusive rdfs:domain rdfs:Resource .
xsd:minInclusive rdfs:range rdfs:Literal .
| xsd:minLength rdf:type owl:DatatypeProperty .
xsd:minLength rdfs:domain rdfs:Resource .
xsd:minLength rdfs:range rdfs:Literal .
|
xsd:pattern rdf:type owl:DatatypeProperty .
xsd:pattern rdfs:domain rdfs:Resource .
xsd:pattern rdfs:range rdfs:Literal .
|
|
Table 6.5: Additional Axiomatic Triples for Classes and Properties of the RDFS Vocabulary
rdfs:Class rdfs:subClassOf owl:Class .
|
|
rdfs:Datatype rdfs:subClassOf owl:DataRange .
| rdfs:isDefinedBy rdf:type owl:AnnotationProperty .
rdfs:isDefinedBy rdfs:domain rdfs:Resource .
rdfs:isDefinedBy rdfs:range rdfs:Resource .
|
rdfs:label rdf:type owl:AnnotationProperty .
rdfs:label rdfs:domain rdfs:Resource .
rdfs:label rdfs:range rdfs:Literal .
| rdfs:Literal rdf:type rdfs:Datatype .
|
rdf:Property rdfs:subClassOf owl:ObjectProperty .
| rdfs:Resource rdfs:subClassOf owl:Thing .
|
rdfs:seeAlso rdf:type owl:AnnotationProperty .
rdfs:seeAlso rdfs:domain rdfs:Resource .
rdfs:seeAlso rdfs:range rdfs:Resource .
|
|
7 Appendix: Relationship to the Direct Semantics (Informative)
This section compares
the OWL 2 RDF-Based Semantics
with the
OWL 2 Direct Semantics
[OWL 2 Direct Semantics].
While
the OWL 2 RDF-Based Semantics is based on the
RDF Semantics specification
[RDF Semantics],
the OWL 2 Direct Semantics
is a description logic style semantics.
Several fundamental differences
exist between the two semantics,
but
there is also a strong relationship
basically stating that the OWL 2 RDF-Based Semantics is able
to reflect all logical conclusions
of the OWL 2 Direct Semantics.
This means that the OWL 2 Direct Semantics
can
in a sense
be regarded as a sub semantics of the OWL 2 RDF-Based Semantics.
Technically,
the comparison will be performed
by comparing the sets of entailments
that hold for each of the two semantics,
respectively.
The definition of an OWL 2 RDF-Based entailment
was given in
Section 4.3
of this document,
while the definition of an OWL 2 Direct entailment
is provided in
Section 2.5 of the OWL 2 Direct Semantics
[OWL 2 Direct Semantics].
In both cases,
entailments are defined for pairs of ontologies,
and such an ordered pair of two ontologies will be called an
entailment query
in this section.
Comparing the two semantics by means of entailments
will only be meaningful
if the entailment queries
allow for applying
both
the OWL 2 RDF-Based Semantics
and the
OWL 2 Direct Semantics
to them.
In order to ensure this,
the comparison will be restricted to entailment queries,
for which the left-hand side and right-hand side ontologies
are both
OWL 2 DL ontologies in RDF graph form.
These are RDF graphs that can be transformedthat,
by applying the
reverse OWL 2RDF mapping
[OWL 2 RDF Mapping ]],
can be transformed
into corresponding
OWL 2 DL ontologies in Functional Syntax form
according to the functional style syntax defined in the
OWL 2 Structural Specification
[OWL 2 Specification],
and which must further meet
all the restrictions on OWL 2 DL ontologies
that are specified in
Section 3 of the OWL 2 Structural Specification
[OWL 2 Specification].
In fact,
these restrictions must be mutually met by
both ontologies that occur in an entailment query,
i.e.
all these restrictions need to be satisfied
as if the two ontologies would be part of a single ontology.
Any entailment query that adheres to the conditions defined here
will be called an
OWL 2 DL entailment query.
Ideally,
the relationship between
the OWL 2 RDF-Based Semantics and the OWL 2 Direct Semantics
would be of the form that
every OWL 2 DL entailment query
that is an OWL 2 Direct entailment
is also an OWL 2 RDF-Based entailment.
However,
this desirable relationship
cannot hold in general
due to a variety of differences
that exist between
the OWL 2 RDF-Based Semantics
and the OWL 2 Direct Semantics,
as demonstrated in
Section 7.1.
Fortunately,
the problems resulting from these semantic differences
can be overcome
in a way that
for every OWL 2 DL entailment query
there is another one
for which
the desired entailment relationship indeed holds,
and the new entailment query is
semantically equivalent to the original entailment query
under the OWL 2 Direct Semantics.
This is the gist of the
OWL 2 correspondence theorem,
which will be presented in
Section 7.2.
The
proof of this theorem,
given in Section 7.3,
will further demonstrate
that such a substitute OWL 2 DL entailment query
can always be algorithmically constructed
by means of simple syntactic transformations.
7.1 Example on Semantic Differences
This section will show
that differences exist
between
the OWL 2 RDF-Based Semantics and the OWL 2 Direct Semantics,
and it will be demonstrated
how these semantic differences
complicate a comparison
of the two semantics
in terms of entailments.
An example OWL 2 DL entailment query will be given,
which will happen to be an OWL 2 Direct entailment
without being an OWL 2 RDF-Based entailment.
The section will explain
the different reasons
and will provide a resolution
of each of them.
It will turn out
that the example entailment query
can be syntactically transformed
into another
OWL 2 DL entailment query
that is both
an OWL 2 Direct entailment
and
an OWL 2 RDF-Based entailment,
while being semantically unchanged
compared to the original entailment query
under the OWL 2 Direct Semantics.
This example will motivate
the OWL 2 correspondence theorem
in Section 7.2
and its proof
in Section 7.3.
The example entailment query consists of the following
pair
⟨( G1* , G2* ⟩)
of RDF graphs:
G1* :
(1) ex:o1 rdf:type owl:Ontology .
(2) ex:c1 rdf:type owl:Class .
(3) ex:c2 rdf:type owl:Class .
(4) ex:c1 rdfs:subClassOf ex:c2 .
G2* :
(1) ex:o2 rdf:type owl:Ontology .
(2) ex:c1 rdf:type owl:Class .
(3) ex:c2 rdf:type owl:Class .
(4) ex:c3 rdf:type owl:Class .
(5) ex:c1 rdfs:subClassOf _:x .
(6) _:x rdf:type owl:Class .
(7) _:x owl:unionOf ( ex:c2 ex:c3 ) .
(8) ex:c3 rdfs:label "c3" .
Both G1* and G2*
are
OWL 2 DL ontologies in RDF graph form
and can therefore be mapped by the
reverse RDF mapping
[OWL 2 RDF Mapping]
to the following two OWL 2 DL ontologies in Functional Syntax form
F(G1*) and F(G2*):
F(G1*) :
(1) Ontology( ex:o1
(2) Declaration( Class( ex:c1 ) )
(3) Declaration( Class( ex:c2 ) )
(4) SubClassOf( ex:c1 ex:c2 )
(5) )
F(G2*) :
(1) Ontology( ex:o2
(2) Declaration( Class( ex:c1 ) )
(3) Declaration( Class( ex:c2 ) )
(4) Declaration( Class( ex:c3 ) )
(5) SubClassOf( ex:c1 ObjectUnionOf( ex:c2 ex:c3 ) )
(6) AnnotationAssertion( rdfs:label ex:c3 "c3" )
(7) )
Note that
F(G1*) and F(G2*)
mutually meet the restrictions on OWL 2 DL ontologies
as specified in
Section 3 of the OWL 2 Structural Specification
[OWL 2 Specification].
For example,
none of the IRIs being declared as a class in F(G1*)
is declared as a datatype in F(G2*),
since this would not be allowed for an OWL 2 DL entailment query.
It follows that
F(G1*) OWL 2 Direct entails F(G2*).
To show this,
only the axioms
(4) of F(G1*)
and
(5) of F(G2*)
have to be considered.
None of the other statements in the two ontologies
are relevant for this OWL 2 Direct entailment to hold,
since they do not have a formal meaning
under the OWL 2 Direct Semantics.
However,
it turns out that the RDF graph
G1*
does not OWL 2 RDF-Based entail
G2*,
for reasons discussed in detail now.
Reason 1: An Annotation in F(G2*).
The ontology F(G2*)
contains an annotation (6).
The OWL 2 Direct Semantics
does not give a formal meaning to
annotations.
In contrast,
under the OWL 2 RDF-Based Semantics
every RDF triple occurring in an RDF graph
has a formal meaning,
including
the corresponding annotation triple (8) in G2*.
Since this annotation triple
only occurs in G2*
but not in G1*,
there will exist OWL 2 RDF-Based interpretations
that satisfy G1*
without satisfying triple (8) of G2*.
Hence,
G1*
does not OWL 2 RDF-Based entail G2*.
Resolution of Reason 1.
The annotation triple (8) in G2*
will be removed,
which will avoid requiring
OWL 2 RDF-Based interpretations to interpret this triple.
The changed RDF graphs will still be
OWL 2 DL ontologies in RDF graph form,
since annotations are strictly optional in OWL 2 DL ontologies.ontologies
and may therefore be omitted.
Also, this operation will not change the formal meaning of the ontologies
under the OWL 2 Direct Semantics,
since annotations do not have a formal meaning under this semantics.
Reason 2: An Entity Declaration exclusively in F(G2*).
The ontology F(G2*)
contains an entity declaration for the class IRI
ex:c3 (4),
for which there is no corresponding entity declaration
in F(G1*).
The OWL 2 Direct Semantics does not give a formal meaning to
entity declarations,
while the OWL 2 RDF-Based Semantics gives a formal meaning
to the corresponding declaration triplestatement (4) in G2*.
The consequences are analog to those described for reason 1.
Resolution of Reason 2.
The declaration triplestatement (4) in G2*
will be copied to G1*.
An OWL 2 RDF-Based interpretation
that satisfies the modified graph G1*
will then also satisfy the declaration triple.statement.
The changed RDF graphs will still be
OWL 2 DL ontologies in RDF graph form,
since addingthe entitycopied declaration doesstatement is not hurtin conflict
with any of the restrictions on OWL 2 DL ontologies.other entity declarations
in G1*.
Also, this operation will not change the formal meaning of the ontologies
under the OWL 2 Direct Semantics,
since entity declarations do not have a formal meaning under this semantics.
Reason 3: Different Ontology IRIs in F(G1*) and F(G2*).
The ontology IRIs for the two ontologies,
given by (1) in F(G1*)
and by (1) in F(G2*),
differ from each other.
The OWL 2 Direct Semantics does not give a formal meaning to
ontology headers,
while the OWL 2 RDF-Based Semantics gives a formal meaning
to the corresponding header triples
(1) in G1*
and
(1) in G2*.
Since these header triples differ from each other,
the consequences are analog to those described for reason 1.
Resolution of Reason 3.
The IRI
in the subject position of the header triple (1)
in G2*
is changed into a blank node.
Due to the existential semantics of blank nodes under the OWL 2 RDF-Based Semantics
this newthe resulting triple will then be entailed
by triple (1)
in G1*.
The changed RDF graphs will still be
OWL 2 DL ontologies in RDF graph form,
since an ontology IRI is optional for an OWL 2 DL ontology.
(Note, however, that it would have been an error to simply remove
triple (1) from G2*,
since an OWL 2 DL ontology is required to contain an ontology header.)
Also, this operation will not change the formal meaning of the ontologies
under the OWL 2 Direct Semantics,
since ontology headers do not have a formal meaning under this semantics.
Reason 4: A Class Expression in F(G2*).
Axiom (5) of F(G2*)
contains a class expression
that represents the union of the two classes
denoted by
ex:c2
and
ex:c3.
Within G2*,
this class expression is represented
by the triples (6) and (7),
both having the blank node
"_:x"
in their respective subject position.
The way the OWL 2 RDF-Based Semantics interprets these two triples
differs from the way
the OWL 2 Direct Semantics treats the class expression
in axiom (5) of F(G2*).
The OWL 2 Direct Semantics treats classes as sets,
i.e. subsets of the universe.
Thus,
the IRIs
ex:c2
and
ex:c3
in F(G2*)
denote two sets,
and the class expression
in axiom (5) of F(G2*)
therefore represents the set
that consists of the union of these two sets.
The OWL 2 RDF-Based Semantics,
on the other hand,
treats classes as individuals,
i.e. members of the universe.
While every class under the OWL 2 RDF-Based Semantics
represents a certain subset of the universe,
namely its class extension,
this set is actually distinguished from the class itself.
For two given classes
it is ensured under the OWL 2 RDF-Based Semantics,
just as for the OWL 2 Direct Semantics,
that the union of their class extensions will always exist
as a subset of the universe.
However,
there is no guarantee
that there will also exist
an individual in the universe
that has this set union as its class extension.
Under the OWL 2 RDF-Based Semantics,
triple (7) of G2*
essentially claims that a class exists
being the union of two other classes.
But since
the existence of such a union class
is not ensured by G1*,
there will be OWL 2 RDF-Based interpretations
that satisfy G1*
without satisfying
triple (7) of G2*.
Hence,
G1*
does not
OWL 2 RDF-Based entail
G2*.
Resolution of Reason 4.
The triples (6) and (7) of G2*
are copied to G1*
together with the new triple
"_:x owl:equivalentClass _:x".
In addition,
for the IRI
ex:c3,
which only occurs in the union class expression
but not in G1*,
an entity declaration is added
to G1*
by the resolution of reason 2.
If an OWL 2 RDF-Based interpretation satisfies the modified graph G1*,
then the triples (6) and (7) of G2*
will alsonow be satisfied.
The changed RDF graphs will still be
OWL 2 DL ontologies in RDF graph form,
since the whole set of added triples
validly encodes a properan OWL 2 DL axiom. Further, for the IRI ex:c3 , which occurs inaxiom,
and since none of the union class expression but not in G 1 * , an entity declarationrestrictions on OWL 2 DL ontologies is added to G 1 * by the resolution of reason 2.hurt.
Also, this operation will not change
the formal meaning of the ontologies
under the OWL 2 Direct Semantics,
since the added equivalence axiom
is a tautology under this semantics.
Note that it would have been an error
to simply copy the
triples (6) and (7) of G2*
to G1*,
without also adding the new triple
"_:x owl:equivalentClass _:x".
This would have produced a class expression
that has no connection to any axiom in the ontology.
An OWL 2 DL ontology is basically a set of axioms
and does not allow for the occurrence of
"dangling" class expressions.
This is the reason for actually "embedding" the class expression
in an axiom.
It would have also been wrong
to use an arbitrary axiom for such an embedding,
since it has to be ensured
that the formal meaning of the original ontology does not change
under the OWL 2 Direct Semantics.
However,
any tautological axiom
that contains the original class expression
would have been sufficient for this purpose as well.
Complete Resolution: The Transformed Entailment Query.
Combining the resolutions of all the above reasons
leads to the following new pair of RDF graphs
⟨( G1 , G2 ⟩:):
G1 :
(1) ex:o1 rdf:type owl:Ontology .
(2) ex:c1 rdf:type owl:Class .
(3) ex:c2 rdf:type owl:Class .
(4) ex:c3 rdf:type owl:Class .
(5) ex:c1 rdfs:subClassOf ex:c2 .
(6) _:x owl:equivalentClass _:x .
(7) _:x rdf:type owl:Class .
(8) _:x owl:unionOf ( ex:c2 ex:c3 ) .
G2 :
(1) _:o rdf:type owl:Ontology .
(2) ex:c1 rdf:type owl:Class .
(3) ex:c2 rdf:type owl:Class .
(4) ex:c3 rdf:type owl:Class .
(5) ex:c1 rdfs:subClassOf _:x .
(6) _:x rdf:type owl:Class .
(7) _:x owl:unionOf ( ex:c2 ex:c3 ) .
The following list reiterates the changes compared to the original RDF graphs
G1* and G2*:
- Resolution of Reason 1 (Annotation): Triple (8) in G2* has been removed, i.e. there is no corresponding annotation triple in G2.
- Resolution of Reason 2 (Entity Declaration): Triple (4) in G2* has been copied to G1*, becoming triple (4) in G1.
- Resolution of Reason 3 (Ontology IRIs): The IRI in the subject position of triple (1) in G2* has been changed into a blank node, becoming triple (1) in G2.
- Resolution of Reason 4 (Class Expression): Triples (6) and (7) in G2* have been copied to G1* together with the new triple "_:x owl:equivalentClass _:x", becoming triples (6), (7) and (8) in G1.
G1 and G2
are again
OWL 2 DL ontologies in RDF graph form
and can be mapped by the reverse RDF mappingto the following
OWL 2 DL ontologies in Functional Syntax form
F(G1) and F(G2 ):),
which again mutually meet the restrictions on OWL 2 DL ontologies:
F(G1) :
(1) Ontology( ex:o1
(2) Declaration( Class( ex:c1 ) )
(3) Declaration( Class( ex:c2 ) )
(4) Declaration( Class( ex:c3 ) )
(5) SubClassOf( ex:c1 ex:c2 )
(6) EquivalentClasses( ObjectUnionOf( ex:c2 ex:c3 ) ObjectUnionOf( ex:c2 ex:c3 ) )
(7) )
F(G2) :
(1) Ontology(
(2) Declaration( Class( ex:c1 ) )
(3) Declaration( Class( ex:c2 ) )
(4) Declaration( Class( ex:c3 ) )
(5) SubClassOf( ex:c1 ObjectUnionOf( ex:c2 ex:c3 ) )
(6) )
As said earlier,
all the applied changes
preserve the formal meaning
of the original OWL 2 DL ontologies
under the OWL 2 Direct Semantics.
Hence,
it is still the case
that
F(G1)
OWL 2 Direct entails
F(G2).
However,
due to the syntactic transformation
the situation has changed for the OWL 2 RDF-Based Semantics.Semantics:
it is now possible to show,
by following the lines of argumentation
for the resolutions of the different reasons given above,
that G1 OWL 2 RDF-Based entails G2
as well.
7.2 Correspondence Theorem
This section presents the OWL 2 correspondence theorem,
which compares the semantic expressivity of
the OWL 2 RDF-Based Semantics
with that of
the OWL 2 Direct Semantics.
The theorem basically states that
the OWL 2 RDF-Based Semantics is able to reflect all the semantic conclusions
of the OWL 2 Direct Semantics,
where the notion of a "semantic conclusion"
is technically expressed in terms of an entailment.
However,
as discussed in
Section 7.1,
there exist semantic differences
between the OWL 2 RDF-Based Semantics and the OWL 2 Direct Semantics,
which do not allow for stating
that any OWL 2 DL entailment query
that is an OWL 2 Direct entailment
will always also be an
OWL 2 RDF-Based entailment.
Nevertheless,
it can still be ensured that
any given OWL 2 DL entailment query
can be substituted
by another OWL 2 DL entailment query
in a way
that for the substitute entailment query
the desired relationship will really hold,
while preserving the formal meaning
compared to the original entailment query
under the OWL 2 Direct Semantics.
In fact,
the theorem only makes the seemingly weak assertion
that such a substitute entailment query
will always exist.
But the actual
proof offor the theorem
in Section 7.3
will be more concrete
in that it will substitute each given OWL 2 DL entailment query
with a variant
that can be algorithmically constructed
by applying a set of simple syntactic transformations
to the original entailment query.
One can get an idea of how this works
from Section 7.1.
Technical Note on Corresponding Datatype maps:Maps.
A distinction exists
between the format of
an OWL 2 RDF-Based datatype map,
as defined by Definition 4.1,
and the format of an OWL 2 Direct datatype map,
as defined in
Section 2.1 of the OWL 2 Direct Semantics
[OWL 2 Direct Semantics].
It is, however, possible to translate
between
an OWL 2 RDF-Based datatype map D
and
the corresponding OWL 2 Direct datatype map F(D)
in the following way:
Let D beFor an OWL 2 RDF-Based datatype map according to Definition 4.1 .D,
the corresponding OWL 2 Direct datatype map
F(D) := (
NDT ,
NLS ,
NFS ,
⋅ DT ,
⋅ LS ,
⋅ FS
)
[OWL 2 Direct Semantics]
is given by
- Datatype Names: NDT is defined as the set of all IRIs u, for which there is a datatype d, such that
⟨( u , d ⟩) ∈ D.
- Lexical Space: For each datatype name u ∈ NDT, set NLS(u) := LS(d), where
⟨( u , d ⟩) ∈ D.
- Facet Space: For each datatype name u ∈ NDT, set NFS(u) := FS(d), where
⟨( u , d ⟩) ∈ D.
- Value Space: For each datatype name u ∈ NDT, set (u) DT := VS(d), where
⟨( u , d ⟩) ∈ D.
- Lexical-to-Value Mapping: For each datatype name u ∈ NDT and each lexical form a ∈ NLS(u), set
⟨( a , u ⟩ ) LS := L2V(d)(a), where ⟨( u , d ⟩) ∈ D.
- Facet-to-Value Mapping: For each datatype name u ∈ NDT and each facet-value pair
⟨( F , v ⟩) ∈ NFS(u), set ⟨( F , v ⟩ ) FS := F2V(d )(⟨)(( F , v ⟩),)), where ⟨( u , d ⟩) ∈ D.
Theorem 7.1 (OWL 2 Correspondence Theorem):
Let D be an OWL 2 RDF-Based datatype map
according to Definition 4.1,
with F(D)
being the
OWL 2 Direct datatype map
according to
Section 2.1 of the OWL 2 Direct Semantics
[OWL 2 Direct Semantics]
that corresponds to D according to the
technical note on corresponding datatype maps.
Let
G1* and G2*
be RDF graphs
that are
OWL 2 DL ontologies in RDF graph form,
with
F(G1*) and F(G2*)
being the
OWL 2 DL ontologies in
Functional Syntax
form
[OWL 2 Specification]
that result from applying
the reverse OWL 2RDF mapping
[OWL 2 RDF Mapping]
to
G1* and G2*,
respectively.
Let
F(G1*) and F(G2*)
mutually meet
the restrictions on OWL 2 DL ontologies
as specified in
Section 3 of the OWL 2 Structural Specification
[OWL 2 Specification].
Then,
there exist RDF graphs
G1 and G2
that are
OWL 2 DL ontologies in RDF graph form,
such that all the following conditionsrelationships hold,
with
F(G1) and F(G2)
being the
OWL 2 DL ontologies in Functional Syntax form
that result from applying the reverse OWL 2RDF mapping
to
G1 and G2,
respectively:
-
(1)F(G1) and F(G2) mutually meet the restrictions on OWL 2 DL ontologies; (2)ontologies.
- F(G1) OWL 2 Direct entails F(G1*) with respect to F(D),
ifand only ifF(G1*) OWL 2 Direct entails F(G1) with respect to F(D) ; (3).
- F(G2) OWL 2 Direct entails F(G2*) with respect to F(D),
ifand only ifF(G2*) OWL 2 Direct entails F(G2) with respect to F(D) ; (4).
- If F(G1) OWL 2 Direct entails F(G2) with respect to F(D), then G1 OWL 2 RDF-Based entails G2 with respect to D.
7.3 Proof for the Correspondence Theorem
This is athe sketch of a proof for
Theorem 7.1 (OWL 2 Correspondence Theorem)
, statedin
Section 7.2.
The proof sketch provides
the basic line of argumentation for showing the theorem.
However,
for complexity reasons,
some technical aspects of the theorem are only coarsely treated,
and the proof sketch also refrains
from takingconsidering the full amount of OWL 2 language constructsconstructs.
For certain steps of the proof
there are example calculations
that focus only on a small fraction of language constructs,
but which can be taken as a hint
on how a complete proof
taking into account every feature of the OWL 2 into account.RDF-Based Semantics
could be constructed in principle.
A complete proof cancould make use of the observation
that the definitions of the OWL 2 Direct Semantics
and the OWL 2 RDF-Based SemanticsSemantics,
despite their technical differences
as outlined in Section 7.1,
are actuallyclosely aligned for allwith respect to the different language constructs of OWL 2.
The proof sketch will make use of an approach
that will be called "balancing" throughout this appendix,section,
and which will now be introduced.
The basic idea is to substitute
the original pair of RDF graphs in an OWL 2 DL entailment query
by another entailment query
having the same semantic characteristics
under the OWL 2 Direct Semantics,
but for which the technical differences
between the two semantics specifications
have no relevant consequences
under the OWL 2 RDF-Based Semantics anymore.
A concrete example
for howthe application of this approach
can be applied iswas given in Section 7.1.
Definition (Balanced):
A pair of RDF graphs
⟨( G1 , G2 ⟩)
is called
balanced,
if and only if
G1 and G2
are OWL 2 DL ontologies in RDF graph form,
such that all the following additionalconditions hold,
with
F(G1) and F(G2)
being the
OWL 2 DL ontologies in
Functional Syntax
form
[OWL 2 Specification]
that result from applying the
reverse OWL 2RDF mapping
[OWL 2 RDF Mapping]
to
G1 and G2,
respectively:
-
(1)F(G1) and F(G2) mutually meet the restrictions on OWL 2 DL ontologies as specified in Section 3 of the OWL 2 Structural Specification [OWL 2 Specification ]; (2)].
- Nodes in G1 and G2:
- for every IRI u occurring in G1 or G2 that corresponds to a non-built-in entity in F(G1) or F(G2), respectively, the graph contains, for every entity type T of u, a declaration statement of the form "u rdf:type t", where t is the vocabulary class IRI corresponding to T (see Table 7 in the OWL 2 RDF Mapping [OWL 2 RDF Mapping] and Section 5.8 of the OWL 2 Structural Specification [OWL 2 Specification]);
- every plain or typed literal occurring in G2 also occurs in G1 (see Section 4 of the OWL 2 Structural Specification [OWL 2 Specification]).
- G2 contains exactly one ontology header consisting of a single RDF triple of the form "x rdf:type owl:Ontology", where x is either a blank node
x occurringor, if an ontology IRI is used in G1 or G 2, there is a declaration triple (Table 7may alternatively equal that ontology IRI (see Table 4 in [the OWL 2 RDF Mapping ]) in the graph for every entity type (Section 5.8 of[OWL 2 Specification ]) of x (there are no missing entity declarations);RDF Mapping]).
- G2 does not
contain (3)contain:
- the RDF
encodingsencoding of annotations (Sectionsan annotation (see Sections 3.2.2 and 3.2.3,3.2.3, and Table 17 in the OWL 2 RDF Mapping [OWL 2 RDF Mapping]);
-
(4)a statement with an ontology property such as "owl:imports";
- a deprecation
triples (Tablestatement based on "owl:DeprecatedClass", "owl:DeprecatedProperty" and "owl:deprecated" (see Table 16 in [the OWL 2 RDF Mapping ]); (5) G 2 contains exactly one ontology header (Table 4 in[OWL 2 RDF Mapping ]) consisting of a single RDF triple of the form]);
- an annotation property axiom based on "
b rdf:type owl:Ontologyrdfs:subClassOf", where b is a blank node; any subgraph g of G 2 that is"rdfs:domain" and "rdfs:range" (see Table 16 in the OWL 2 RDF encoding of oneMapping [OWL 2 RDF Mapping]).
- Any of the following
OWLsub graphs of G2 constructsis also a subgraphsub graph of G1:
-
(6)the RDF encoding of an entity declaration (Table(see Table 7 in the OWL 2 RDF Mapping [OWL 2 RDF Mapping]);
-
(7)the RDF encoding of a property expression (Table(see Table 11 in the OWL 2 RDF Mapping [OWL 2 RDF Mapping]);
-
(8)the RDF encoding of a class expression (Tables(see Tables 13 and 15 in the OWL 2 RDF Mapping [OWL 2 RDF Mapping]);
-
(9)the RDF encoding of a data range expression (Tables(see Tables 12 and 14 in the OWL 2 RDF Mapping [OWL 2 RDF Mapping]);
- an RDF sequence (see Table 3 in the OWL 2 RDF Mapping [OWL 2 RDF Mapping]).
Balancing Lemma:
An algorithm exists
that terminates on every valid input
and that has the following input/output behavior:
LetThe valid input of the algorithm
be a pairis given by
all the pairs of RDF graphs
⟨( G1* , G2* ⟩,),
where
G1* and G2*
are OWL 2 DL ontologies in RDF graph form,
with
F(G1*) and F(G2*)
being the
OWL 2 DL ontologies in
Functional Syntax
form
[OWL 2 Specification]
that result from applying the
reverse OWL 2RDF mapping
[OWL 2 RDF Mapping]
to
G1* and G2*,
respectively.
LetFurther,
F(G1*) and F(G2*)
have to mutually meet
the restrictions on OWL 2 DL ontologies
as specified in
Section 3 of the OWL 2 Structural Specification
[OWL 2 Specification].
ThenFor a valid input,
the output of the algorithm
will beis a pair of RDF graphs
⟨( G1 , G2 ⟩,),
where
G1 and G2
are OWL 2 DL ontologies in RDF graph form,
such that
for any OWL 2 RDF-Based datatype map D
according to Definition 4.1
all the following conditionsrelationships hold,
with
F(G1) and F(G2)
being the
OWL 2 DL ontologies in Functional Syntax form
that result from applying the reverse OWL 2RDF mapping
to
G1 and G2,
respectively,
and
with F(D)
being the
OWL 2 Direct datatype map
according to
Section 2.1 of the OWL 2 Direct Semantics
[OWL 2 Direct Semantics]
that corresponds to D according to the
technical note on corresponding datatype maps
in Section 7.2:
-
(1)The pair ⟨( G1 , G2 ⟩) is balanced ; (2).
- F(G1) OWL 2 Direct entails F(G1*) with respect to F(D), and F(G1*) OWL 2 Direct entails F(G1) with respect to F(D)
; (3).
- F(G2) OWL 2 Direct entails F(G2*) with respect to F(D), and F(G2*) OWL 2 Direct entails F(G2) with respect to F(D).
Proof offor the Balancing Lemma:
Let G 1 * and G 2 * be OWL 2 DL ontologies in RDF graph form, with F( G 1 * ) and F( G 2 * ) being the corresponding OWL 2 DL ontologies in Functional Syntax form that result from applyingthe reverse OWL 2 RDF mapping tograph pair
( G1* and G 2 *, respectively, such that F( G 1 * ) and F(G2* )
mutually meet the restrictions on OWL 2 DL ontologies.be a valid input.
The resulting RDF graphs
G1 and G2
are constructed as follows. The initial versions of G 1 and G 2 arefollows,
starting from copies of
G1* and G2*,
respectively.
A preprocessing step will substitute all blank nodes in G 1 for fresh blank nodes that do not occur in G 2 . One can therefore assume from now on that G 1 and G 2 have no common blank nodes. Since G 1 and G 2 are OWL 2 DL ontologies in RDF graph form, the canonical parsing process for computing the reverse OWL 2 RDF mapping, as described in Section 3 of [ OWL 2 RDF Mapping ], can be applied to map the graphs G 1 and G 2 to corresponding OWL 2 DL ontologies in Functional Syntax form. For the resulting ontologies it is then algorithmically possible to determine for every occurring IRI and anonymous individual all the entity types. By this, all missing declaration triples are added to G 1 and G 2 . Further,Since the initial versions of
G1 and G2
are OWL 2 DL ontologies in RDF graph form,
the canonical parsing process (CP)
for computing the reverse RDF mapping,
as described in
Section 3 of the OWL 2 RDF Mapping
[OWL 2 RDF Mapping],
can alsobe appliedapplied.
Based on CP, it is possible to safelyidentify within these graphs
- all
subgraphs of G 1entity types for every non-built-in IRI,
- all blank nodes that correspond to anonymous individuals, and
-
G 2all sub graphs that correspond to OWL 2 language constructs (ontology headers, declarations, expressions, axioms and annotations) as described in the OWL 2 Structural Specification [OWL 2 Specification ], including all the language constructs considered in the theorem.].
Based on these observations,this observation, the following steps are performed on every subgraph g ⊆performed:
- Consistently substitute all blank nodes in G2 such that
has been identified byG1 and G2 have no common blank nodes.
- Apply CP to G1 and G2 (without changing these graphs) to identify the
canonical parsing process: (a)entity types of the IRIs, the anonymous individuals, and the sub graphs encoding OWL 2 language constructs.
- For each sub graph g of G2: remove g from G2, if g is the RDF encoding of
- an annotation,
thenor
- a deprecation statement, or
- an annotation property axiom.
- For the sub graph g
will be removed fromof G2 . (b) Ifcorresponding to the ontology header in F(G is2): substitute g in G2 by a deprecationtriple , then g will be removed fromof the form "x rdf:type owl:Ontology", where x is a new blank node not yet used in G2.
-
(c) IfFor each non-built-in IRI u in G is an ontology header (which may include ontology properties, such as import directives), then1 and G2 and for each entity type T of u identified by CP: add to G1 or G2, respectively, the RDF triple "u rdf:type t", where t is substitutedthe vocabulary class IRI corresponding to T.
- For each plain or typed literal L in G2
by a triple of: add to G1 the formRDF triple " x rdf:type owl:Ontologyo rdfs:comment L", where xo is a fresh blank node. Atthe endIRI or blank node of the process, all but one of these triples will be removed fromontology header triple "o rdf:type owl:Ontology" in G 21.
-
(d) IfFor each sub graph g of G2 that is the RDF encoding of an entity declaration , then: add g is copiedto G1.
-
(e) IfFor each sub graph g of G2 that is the RDF encoding of a property expression with root blank node x , then: add g to G1 together with the RDF triple "x owl:equivalentProperty x " is added to".
- For each sub graph g
1 . (f) Ifof G2 that is the RDF encoding of a class expression with root blank node x , then: add g to G1 together with the RDF triple "x owl:equivalentClass x " is added to".
- For each sub graph g
1 . (g) Ifof G2 that is the RDF encoding of a data range expression with root blank node x , then::
- If g is part of a data property restriction expression, then nothing needs to be done, since
this casethe comprising restriction expression is covered by the treatment of class expressionsexpressions, and therefore g occurs in (f); ifG is part of1 as well.
- Otherwise, add a
datatype definition , thendeclaration triple to G 2 contains1 for a triple " u owl:equivalentClass x " with some IRI unew data property p that is declared as a datatype,does not yet occur in G1 and thenG2. Then, the triple andRDF encoding r of a universal data property restriction expression on property p is created for g are copied. Let r have the new root blank node y. Add r to G1 ; otherwise,together with the RDF triple "y owl:equivalentClass y".
- For each sub graph g
is partof at least one data property range axiom . One such property pG2 that is chosen randomly, andan RDF sequence with root blank node x, which does not occur in the RDF encoding rof a universal property restriction expression on property planguage constructs already treated by one of the earlier steps, i.e. g is created forpart of the datarange expression rooted by node x . Letencoding of an axiom: create the RDF graphencoding r have freshof an enumeration class expression with a new root blank node y .having the main RDF triple "y owl:oneOf x". Then, add r to G1 together with the RDF triple "y owl:equivalentClass y". Additionally, for every IRI u being a member of the RDF sequence, add to G1 a typing triple "u rdf:type owl:NamedIndividual". If one of the sequence members is addeda blank node z that is the root node of some property expression or class expression e, then select a new IRI w not yet occurring in G1, consistently replace z by w everywhere in r, add to G1 the triple "w owl:equivalentProperty z" or "w owl:equivalentClass z", respectively, and add to G1 the two triples "w rdf:type owl:NamedIndividual" and "w rdf:type t", where t is the vocabulary class IRI that represents the appropriate entity type of the expression e. No further treatment of e is needed, since e is treated by the earlier steps covering expressions.
In the following it is shown that all the claims of the theorembalancing lemma hold.
A: Existence of a Terminating Algorithm.
An algorithm exists
for mapping
the input graph pair
⟨( G1* , G2* ⟩)
to the output graph pair
⟨( G1 , G2 ⟩,),
since the canonical parsing process for the determination of the missing entity declarations and for the identification of the language construct subgraphsCP (applied in step 2)
is described in the form of an algorithm
in the
OWL 2 RDF Mapping
[OWL 2 RDF Mapping ].],
and since all other operations described abovesteps
can obviously be performed algorithmically.
The algorithm terminates,
since the canonical parsing processCP terminates
(including terminationon invalid input),arbitrary input graphs,
and since all other operations described above aresteps
can obviously be executed by ain finite number of steps, respectively.time.
B: The Resulting RDF Graphs are OWL 2 DL Ontologies.
SinceThe originalRDF graphs
G1 *and G2
*are OWL 2 DL ontologies in RDF graph form, this is alsoform
that mutually meet
the case forrestrictions on OWL 2 DL ontologies,
since the original RDF graphs
G1* and G2 ,*
have this feature,
and since each of the steps described above
transforms a pair of OWL 2 DL ontologies inRDF graph formgraphs with this feature
again into a pair of OWL 2 DL ontologies inRDF graph form,graphs with this feature,
for the following reasons:
- The consistent substitution of
existing blank nodes by freshblank nodes in step 1 does not change the structure of an OWL 2 DL ontology.
- The application of CP in step 2 does not change the graphs.
- Annotations, deprecation statements and annotation property axioms are optional information in an OWL 2 DL ontology and can therefore be omitted in
RDF graph form.step 3.
- The ontology header of an OWL 2 DL ontology does neither require the existence of an ontology IRI nor of any ontology properties, and so the substitution of the ontology header in step 4 is a valid operation.
- If an entity has some particular entity type
butfor which there is no explicitly given entity declaration, then the correspondingentity declaration is omitted, then itmay be added without harm.added, as done in step 5.
- It is allowed to add arbitrary annotations
and deprecation statements can always be removed fromto the ontology header of an OWL 2 DL ontology, as done by (a) and (b),in step 6.
- Entity declarations may be copied from G2 to G1 in step 7 without conflict, since
they are non-required language constructs. Anythe original ontologies have been assumed to mutually meet the restrictions on OWL 2 DL ontology requiresontologies regarding different entity declarations for the existence of an ontology header, but doessame IRI (e.g. that one IRI must not requirebe the existencename of both an ontology IRI, so it is sufficientobject property and a data property).
- Adding to
replace an ontology header by (c).G1 contains entity declarations for every IRI occurringan axiom that claims equivalence of some property expression (step 8) or class expression (step 9) with itself, where the expression already occurs in G 12, is an allowed operation, since by (d) all entity declarations from G 2 * have been copiedthe original ontologies are assumed to G 1 , and only IRIs from both G 1 * and Gmutually meet the restrictions on OWL 2 * can occur in G 1 via (e), (f)DL ontologies concerning property and class expressions, and (g).since no syntactic restrictions exist on this specific use of equivalence axioms.
- For the case of data ranges (step 10) it is
not a problemsufficient to have entity declarations for IRIsnote that are not further usedplacing universal property restrictions on arbitrary (simple or complex) property expressions is allowed in anOWL 2 DL ontology. Adding a datatype definition to anDL. The rest of the argumentation follows the lines of the treatment of class expressions in step 9.
- For the treatment of RDF sequences in step 11: First, the enumeration class expressions being constructed from the RDF sequences are syntactically valid in OWL 2
DL ontology, as doneDL, since all enumerated entries are IRIs by (g), will lead to a newconstruction. Second, there is no restriction in OWL 2 DL ontology (notedisallowing axioms that the corresponding datatype declaration from Gclaim equivalence of enumeration class expressions with themselves. Third, punning in OWL 2 * has been copiedDL allows a given non-built-in IRI of any entity type to G 1be additionally declared as well). Adding syntactically valida named individual. Forth, there is no OWL 2 DL axiomsrestriction forbidding to add an OWL 2 DL ontology, as done by (e), (f)entity declaration for a new (i.e. not elsewhere used) IRI and (g), will leadto aassert the denotation of this new IRI to be equivalent to some existing property or class expression. Hence, the resulting ontologies still mutually meet all syntactic restrictions on OWL 2 DL ontology.ontologies.
C: The Resulting Pair of RDF Graphs is Balanced.
Property (1) ofAll the theorem requires thatconditions of balanced pairs of RDF graphs
are met by the pair
⟨( G1 , G2 ⟩ is balanced .)
for the following list checksreasons:
- Condition 1: It has already been shown in paragraph B that
all the properties of the definition are satisfied. Property (1): F(G1 )and F(G2 )mutually meet the restrictions on OWL 2 DL ontologies, since the restrictions are mutually met by the original ontologies, and since only declarationsontologies.
- Conditions 2.1 and
expressions that already existed2.2 on nodes in G 2 * are added to G1 by (d), (e), (f) and (g). The removal of annotations by (a)and deprecation triples by (b) from G 2 * , as well as the replacement of the ontology header ofG2 *are met by (c) do not hurt any syntactic restrictions either. Property (2): All missing entity declaration triples have been added to G 1steps 5 and 6, respectively.
- Condition 3 on ontology headers in G2
. Properties (3)is satisfied by step 4, always applying an anonymous ontology header.
- Conditions 4.1, 4.3 and
(4): G 2 does not contain any RDF encodings of annotations nor4.4 on annotations, deprecation triples due to their removal by (a)statements and (b), respectively.annotation property (5):axioms in G2 contains exactly one, respectively, are all satisfied by step 3.
- Condition 4.2 on statements with ontology
header consisting of a single triple of the form " b rdf:type owl:Ontology ", where bproperties is a blank node, due toimplicitly satisfied by step 4, since the replacementsubstitution of the ontology header in G2 removes all existing statements with ontology headers by (c). Property (6): Each RDF encoding of anproperties.
- Condition 5.1 on entity
declarationdeclarations in G 1 also occurs2 being reflected in G 2 , due to their copying1 is satisfied by (d). Properties (7), (8)step 7.
- Conditions 5.2, 5.3 and
(9): Each RDF encoding of a5.4 on property, class orand data range expression in G 1 also occursexpressions in G2, due to their addingrespectively, being reflected in G1 are met by (e), (f)steps 8, 9 and (g),10, respectively.
- Condition 5.5 on RDF sequences in G2 being reflected in G1 is satisfied by step 11.
D: The Resulting Ontologies are semantically equivalent with the Original ontologies. Property (2) ofOntologies under the theorem requires thatOWL 2 Direct Semantics.
F(G1) is semantically equivalent with F(G1* ). This is the case,),
since F(G1) differs from F(G1*) only by (potentially):
- additional entity declarations
(due to the addition of all missing entity declarations(steps 5, 7 and due to (d)),11), which have no formal meaning under the OWL 2 Direct Semantics;
-
datatype definitions (due to (g)),additional annotations (step 6), which only introduce a new name for a data range expression;have no formal meaning;
- additional
OWL 2 DLtautological axioms (due to (e), (f)(steps 8, 9, 10 and (g)),11), which are all, by construction, tautologies under the OWL 2 Direct Semantics. Further, property (3) ofdo not change the theorem requires thatformal meaning;
F(G2) is semantically equivalent with F(G2* ). This is the case,),
since F(G2) differs from F(G2*) only by additional entity declarations, and missing annotations including deprecation annotations (due to (a) and (b)),(potentially):
- differently labeled anonymous individuals (step 1), by which
all have nothe formal meaning under the OWL 2 Direct Semantics.Semantics keeps unchanged, since anonymous individuals are existentially interpreted;
- missing annotations, deprecation statements and annotation property axioms (step 3), which have no formal meaning;
- a modified ontology header (step 4), which has no formal meaning;
- additional entity declarations (step 5), which have no formal meaning.
End of theProof offor the Balancing Lemma.
In the following,
the correspondence theorem will be proven.
Assume that the premises of the correspondence theorem holdare true
for a given RDF graphspair
( G1* and, G2* .)
of RDF graphs.
This allows for applying the
balancing lemma,
which provides the existence of certaincorresponding RDF graphs
G1 and G2
that are OWL 2 DL ontologies in RDF graph form. Hence, it is possible to build OWL 2 DL ontologies in Functional Syntax formform,
and which meet the
definition of balanced graph pairs.
Let F(G1) and F(G2)
by applyingbe the reversecorresponding OWL 2 RDF mapping to G 1 and G 2 , respectively. The balancing lemma further provides that the pair ⟨ G 1 , G 2 ⟩ is balanced .DL ontologies in Functional Syntax form.
Then,
the claimed property (1)relationship 1 of the correspondence theorem
follows directly from property (1)relationship 1 of the balancing lemma
and from property (1)condition 1 of the "Balanced"-definition .definition of balanced graph pairs.
Further,
the claimed properties (2)relationships 2 and (3)3 of the correspondence theorem
follow directly from properties (2)the relationships 2 and (3)3 of the balancing lemma,
respectively.
The rest of this proof will treat
the claimed property (4)relationship 4 of the correspondence theorem,
which states that
if F(G1) OWL 2 Direct entails F(G2)
with respect to F(D),
then G1 OWL 2 RDF-Based entails G2
with respect to D.
Let I beFor this to see,
an arbitrary OWL 2 RDF-Based interpretation w.r.t. an OWL 2 RDF-Based datatype map D of a vocabulary V I that covers all the names (IRIs and literals) occurring in the RDF graphs G 1 and G 2 , and letI OWL 2 RDF-Based satisfy G 1 . Itwill be shownselected
that IOWL 2 RDF-Based satisfies G 21.
AsFor I,
a first step, anclosely corresponding OWL 2 Direct interpretation J
w.r.t. the corresponding OWL 2 Direct datatype map F(D)will be constructed for a vocabulary V J that covers all the names (IRIsconstructed,
and literals) occurring in theit will then be shown
that J OWL 2 DL ontologies in Functional Syntax formDirect satisfies F(G1).
Since it was assumed that
F(G1) andOWL 2 Direct entails F(G2 ). J),
it will be defined in a way suchfollow that J OWL 2 Direct satisfies F(G2).
Based on this result, it closely correspondswill then be possible to I on those parts of the vocabularies V I and V Jshow
that cover G 1 andI also OWL 2 RDF-Based satisfies G2 , and F(.
Since I was arbitrarily selected,
this will mean
that G1 ) and F( GOWL 2 ), respectively. G 1 andRDF-Based entails G2 are OWL 2 DL ontologies in RDF graph form that are mapped by the reverse RDF mapping to.
Step 1: Selection of a Pair of Corresponding Interpretations.
Let
F(G1) andOWL 2 Direct entail F(G2 ), respectively. This means that the same literals are used in both G 1 and) w.r.t. F( G 1D),
and in both Glet I be an OWL 2 and F( GRDF-Based interpretation
of a vocabulary VI w.r.t. D,
such that
I OWL 2 ), respectively. Further,RDF-Based satisfies G1.
Since the pair
⟨( G1 , G2 ⟩)
is balanced,
according to property (2) of the "Balanced"-definitionthere areexist entity declarations
in F(G1)
and F( G 2 )for all theeach entity typestype
of every non-built-in IRI
occurring in G1 and G 2 , respectively.:
For each entity declaration
of the form
"Declaration(T(u ))))"
in F(G1 ) and F( G 2),
wheresuch that T is the entity type for some IRI u,
a typing triple
of the form
"u rdf:type t"
exists in G1 or G 2,
respectively,where t denotesis the vocabulary class IRI
representing the part of the universe of I
that corresponds to T ; and vice versa. Since the pair ⟨ G 1 , G 2 ⟩ is balanced , all the entity declarations of F( G 2 ) are also contained in F( G 1 ), and therefore all the typing triples of G 2 that correspond to some entity declaration in F( G 2 ) are also contained in G 1.
Since I OWL 2 RDF-Based satisfies G1,
all these "declaring"declaration typing triples are OWL 2 RDF-Based satisfied by I,
and thus all non-built-in IRIs in G1
and G 2are actuallyinstances of all their declared parts of the universe. Based on these observations, the OWL 2 Direct interpretation J and its vocabulary V J for the datatype map F(D) can now be defined.universe of I.
The vocabulary
VJ := (
VJC ,
VJOP ,
VJDP ,
VJI ,
VJDT ,
VJLT ,
VJFA
)
of the OWL 2 Direct interpretation J w.r.t. the datatype map F(D) is definednow constructed as follows.
The OWL 2 Direct interpretation
J := (
ΔI ,
ΔD ,
⋅ C ,
⋅ OP ,
⋅ DP ,
⋅ I ,
⋅ DT ,
⋅ LT ,
⋅ FA
)
is now defined as follows.
The object and data domains of J are identified
with the universe IR and the set of data values LV of I,
respectively, i.e., Δ I := IR and Δ D := LV.respectively,
i.e.,
ΔI := IR and
ΔD := LV.
The class interpretation function ⋅ C,
the object property interpretation function ⋅ OP,
the data property interpretation function ⋅ DP,
the datatype interpretation function ⋅ DT,
the literal interpretation function ⋅ LT, and
the facet interpretation function ⋅ FA
are defined according to
Section 2.2 of the OWL 2 Direct Semantics
[OWL 2 Direct Semantics].
Specifically,
⋅ DT interprets all IRIs that are declared as datatypes in F( G 1 ) according the following definition.for every non-built-in IRI u
occurring in F(G1):
- If u is declared as a
named individual,class, then set u IC := ICEXT(I(u ),)), since the graphG1 contains the triple "u rdf:type owl:NamedIndividualowl:Class", i.e., I(u) ∈ IR.IC.
- If u is declared as
a class,an object property, then set u COP := ICEXT(IEXT(I(u)), since the graphG1 contains the triple "u rdf:type owl:Classowl:ObjectProperty", i.e., I(u) ∈ IC.IP.
- If u is declared as a
datatype,data property, then set u DTDP := ICEXT(IEXT(I(u)), since the graphG1 contains the triple "u rdf:type rdfs:Datatypeowl:DatatypeProperty", i.e., I(u) ∈ IDC.IODP.
- If u is declared as
an object property,a named individual, then set u OPI := IEXT(I(u )),), since the graphG1 contains the triple "u"u rdf:type owl:ObjectPropertyowl:NamedIndividual", i.e., I(u) ∈ IP.IR.
- If u is declared as a
data property,datatype, then set u DPDT := IEXT(ICEXT(I(u)), since G1 contains the triple "u rdf:type rdfs:Datatype", i.e., I(u) ∈ IDC.
Notes:
- A literal occurring in G1 is mapped by the reverse RDF mapping to the same literal in F(G1), and the formal meaning of a well-formed literal is analog for both the OWL 2 RDF-Based Semantics and the OWL 2 Direct Semantics.
- A blank node b occurring in G1 that represents an anonymous individual is written as the same blank node b in F(G1). Both the OWL 2 RDF-Based Semantics and the OWL 2 Direct Semantics treat anonymous individuals in an analog way as existential variables defined locally to a given ontology, i.e. some individual x exists in the universe to which all occurrences of b in the ontology can be mapped (see Section 1.5 in the RDF Semantics [RDF Semantics] for the
graph containsprecise definition on how blank nodes are treated under the triple "u rdf:type owl:DatatypeProperty ", i.e.,OWL 2 RDF-Based Semantics). Hence, the same mapping from b to x can be used with both I ( u ) ∈ IODP. Note thatand J.
- G1 may also contain declarations
offor annotation properties, but they will not be interpreted byproperties. Since annotation properties have no formal meaning under the OWL 2 Direct Semantics and are therefore ignored here. This will not lead to problems, sinceSemantics, the pair ⟨ G 1 , G 2 ⟩ is balanced , and therefore GOWL 2 Direct interpretation J does not contain any annotations. Further, note thattreat them.
- With the above definition
of Jit is compatible with the concept ofpossible for J to have a non-separatednonseparated vocabulary in OWL 2 DL (also called "punning" , seeaccording to Section 5.9 of the OWL 2 Structural Specification [OWL 2 Specification ]).]. Since G1 and G 2 areis an OWL 2 DL ontologiesontology in RDF graph form, it is allowed that the same IRI u is declared tomay be alldeclared as one or more of an individual name, andeither a class name or a datatype name, and either an object property name or a data property name. According toFor the OWL 2 RDF-Based interpretation I, the IRI u will always denote the same individual in the universe IR, where I(u) will be bothmay additionally have a class andextension or a property. Underproperty extension, or both. For the OWL 2 Direct interpretation J, however, the individual nameu will denote as an individual, the classindividual name u will denote a subsetan element of ΔI, and the property name u will denoteas a subset of Δ I × Δ I . Literals occurring in G 1 and G 2 are mapped by the OWL 2 RDF mapping to the same literals in the corresponding interpreted language constructs of F( G 1 ) and F( G 2 ), which comprise data enumerations, has-value restrictions withclass name a subset of ΔI, as a data value, cardinality restrictions,datatype restrictions, dataname a subset of ΔD, as an object property assertions,name a subset of ΔI × ΔI, and negativeas a data property assertions. Also, the semanticsname a subset of literals is strictly analog for both the OWL 2 RDF-Based Semantics andΔI × ΔD.
Step 2: Satisfaction of F(G1) by the OWL 2 Direct Semantics. Therefore, literals need no further treatment in this proof.Interpretation.
Based on the premise that I OWL 2 RDF-Based satisfies G1,
it has to be shown that J OWL 2 Direct satisfies F(G1).
For this to holdhold,
it will be sufficient to showthat
J OWL 2 Direct satisfies every axiom occurring in F( G 1 ). LetA be an axiomoccurring in F(G1 ), and).
Let gA be the subgraphsub graph of G1
that is mapped to A by the reverse OWL 2RDF mapping.
ItThe basic idea can roughly be described as follows:
Since I is possible to prove that Jan OWL 2 Direct satisfies A by showing thatRDF-Based interpretation,
all the meaning, which is given to AOWL 2 RDF-Based semantic conditions are met by I.
Due to the close alignment between the definitions
in the OWL 2 RDF-Based Semantics
and the OWL 2 Direct Semantics,
is compatible with theOWL 2 RDF-Based semantic relationship that, accordingconditions exist
that semantically correspond
to J , holds betweenthe denotationsdefinition of the names occurring ininterpretation of the axiom A.
In particular,
the basic idea is as follows: Since I OWL 2 RDF-Based satisfiesantecedent of one of these semantic conditions
will become true,
if the RDF-encoding of A,
i.e. the graph g 1A,
is satisfied
(in the case of an "if-and-only-if" semantic condition
this will generally be the left-to-right direction of that condition).
Now,
all the RDF triples occurringin gA
are OWL 2 RDF-Based satisfied by I . Also,,
since I is an OWL 2 RDF-Based interpretation, all theOWL 2 RDF-Based semantic conditions are met by Isatisfies G1.
Hence,
the left-to-right directionsantecedent of allthe semantic conditions that are "matched" by the triples in g A will apply.condition becomes true,
and therefore its consequent becomes true as well.
This will reveal a certain semantic relationships that,relationship
that
according to I
, holdholds between the denotations of the
namesIRIs, literals and anonymous individuals
occurring in gA . These semantic relationships are,,
which,
roughly speaking,
expresses the semantic consequencesmeaning of the OWL 2 axiom that is encoded by the triples in gA.
Since the denotations w.r.t. J of all the names occurring in A have been defined in terms of the denotations and class and property extensions w.r.t. IBecause of the same names occurring in g A , and since the meaningclose semantic correspondence
of the axiom A w.r.t. theOWL 2 Direct Semantics turns outinterpretation J to be fully covered byI,
the analog semantic consequences of the subgraph g A w.r.t. the OWL 2 RDF-Based Semantics, one can eventually show thatrelationship holds
according to J
OWL 2 Direct satisfies A . A special note is necessary for anonymous individuals occurring in an assertion A . These havebetween the formdenotations of the
same blank node b both in AIRIs, literals and anonymous individuals
occurring in gA.
Both the OWL 2 RDF-Based Semantics and the OWL 2 Direct Semantics treat blank nodes as existential variables in an ontology. Since I satisfies g A , b can be mapped to an individual x in IR such that g A becomes true under I (see Section 1.5 in [ RDF Semantics ] for the precise definition on how blank nodes are treated in RDF based languages). The same mapping from b to x can also be used for J in orderThis semantic relationship
turns out to be compatible
with the formal meaning of the axiom A
as specified by the OWL 2 Direct satisfySemantics,
i.e. J satisfies A.
This basic idea is now demonstrated in more detail
for a single example axiom A in F(G1),
which can be taken as a hint on
how a complete proof
could be constructed in principle. A complete proof would need to take every language construct of OWL 2taking into account, as well as additional aspects such as datatype maps and facets. As in the example below, such a proof can make use of the observation that the definitionsaccount every feature of the OWL 2 Direct Semantics and the OWL 2RDF-Based Semantics
are actually closely aligned for allcould be constructed in principle.
Let A be the different language constructs offollowing OWL 2. Let2 axiom in F(G1):
A = : SubClassOf(ex:c1 ObjectUnionOf(ex:c2 ex:c3))
for IRIs ex:c1 , ex:c2and ex:c3 that are declared tolet gA be classes elsewherethe corresponding sub graph in F(G1
). Duethat is being mapped to A via the reverse OWL 2RDF mapping,
g A has the formnamely
gA :
ex:c1 rdfs:subClassOf _:x .
_:x rdf:type owl:Class .
_:x owl:unionOf ( ex:c2 ex:c3 ) .
Since the pair ( G1 , G2 ) is balanced,
G1 contains the typing triples
ex:c1 rdf:type owl:Class .
ex:c2 rdf:type owl:Class .
ex:c3 rdf:type owl:Class .
that correspond to class entity declarations in F(G1) for the IRIs
"ex:c1",
"ex:c2", and
"ex:c3",
respectively.
All these declaration typing triples are OWL 2 RDF-Based satisfied by I,
since it has been postulated
that I OWL 2 RDF-Based satisfies G1.
Hence,
by applying the semantics of rdf:type
(see
Section 4.1 of the RDF Semantics
[RDF Semantics]),
all the IRIs denote classes, precisely:
I(ex:c1) ∈ IC ,
I(ex:c2) ∈ IC , and
I(ex:c3) ∈ IC .
Since I is an OWL 2 RDF-Based interpretation,
it meets all the OWL 2 RDF-Based semantic conditions.conditions,
and since I OWL 2 RDF-Based satisfies G1,
all the triples in gA are OWL 2 RDF-Based satisfied, andsatisfied.
This triggersmeets the left-to-right directions of the semantic conditions
for subclass axioms
(("rdfs:subClassOf",
see Section 5.8)
and union class expressions
(("owl:unionOf ). This reveals that the denotations of the names",
see Section 5.4),
which results in g A are actually classes I ( ex:c1 ) ∈ IC , I ( ex:c2 ) ∈ IC , I ( ex:c3 ) ∈ IC , and thatthe following semantic relationship
that holds between the extensions of these classes:the classes above
according to I:
ICEXT(I(ex:c1))
⊆
ICEXT(I(ex:c2))
∪
ICEXT(I(ex:c3)) .
FromBy applying the definition of J follows,
one can conclude
that the following semantic relationship, w.r.t. J ,relationship
holds between the denotations of the class names occurring in A
according to J:
(ex:c1) C
⊆
(ex:c2) C
∪
(ex:c3) C .
This semantic relationship equals the meaning ofsemantic relationship is compatible
with the formal meaning of the axiom A
under the OWL 2 Direct Semantics.
Hence, J OWL 2 Direct satisfies A.
Since J OWL 2 Direct satisfies F(G1),
and since it has been postulated that
F(G1) OWL 2 Direct entails F(G2),
it follows that
J OWL 2 Direct satisfies F(G2).
Step 3: Satisfaction of G2 by the OWL 2 RDF-Based Interpretation.
The last step will be
to show that I OWL 2 RDF-Based satisfies G2.
For this to hold,
I needs to OWL 2 RDF-Based satisfy
every triple occurring in G2.
The basic idea can roughly be described as follows:
First:
According to the "semantic conditions for ground graphs"
in Section 1.4 of the RDF Semantics specification
[RDF Semantics],
all the IRIs and literals used in RDF triples in G2
need to be in the vocabulary VI of I.
This is true for the axiom A = SubClassOf(ex:c1 ObjectUnionOf(ex:c2 ex:c3)) w.r.t.following reason:
Since the OWLpair
( G1 , G2 Direct Semantics. Hence, J OWL)
is balanced,
all IRIs and literals occurring in G2
Direct satisfies Ado also occur in G1.
Since J OWL 2 DirectI satisfies F(G1 ),,
all IRIs and since F(literals in G1 ) OWL 2 Direct entails F(,
including those in G2 ), it follows,
are contained in VI
due to the semantic conditions for ground graphs.
Second:
If a set of RDF triples encodes an OWL 2 language construct
that Jis not interpreted by the OWL 2 Direct satisfies F(Semantics,
such as annotations,
then G2 ).should contain such a set of RDF triples
only if they are also included in G1.
The next step will be to showreason is
that Iwith such triples
there will, in general, exist OWL 2 RDF-Based satisfiesinterpretations
only satisfying the graph G1 but not G2 . For this to hold, I needs to OWL 2 RDF-Based satisfy all,
which will render the triples occurring inpair
( G 21 , takingG2 )
into account the premisea nonentailment
(an exception are RDF triples
that an OWL 2 RDF-Based interpretation is required to meet all theare true
under every OWL 2 RDF-Based semantic conditions.interpretation).
Since the pair
⟨( G1 , G2 ⟩)
is balanced,
G 2 contains a single ontology header consisting of a single triple " b rdf:type owl:Ontology " with a blank node b , and it does neither contain annotations nor deprecation statements. Hence, F( G 2 ) only consists of entity declarations and axioms, and does2 will not havecontain the RDF encoding for any
ontology IRI and no ontology version,annotations,
statements with ontology properties,
deprecation statements or
import directives. Further,annotation property axioms.
Hence,
there are no corresponding RDF triples that need to be satisfied by I.
Third:
Since G2 is an OWL 2 DL ontology in RDF graph form,
every triple occurring in G 2 , which is notthe ontology header triple, belongs to some subgraph of G 2 thatgraph is mappedpartitioned by the
reverse RDF mapping
[OWL 2 RDF Mapping]
into sub graphs corresponding to
one of theeither ontology headers,
entity declarations
or axioms contained in F( G 2 ). For,
where axioms may further consist of different kinds of expressions,
such as Boolean class expressions.
It has to be shown that all the ontology header triple " b rdf:type owl:Ontology " in G 2 : Since G 1 is an OWL 2 DL ontologytriples in RDFeach such sub graph
form, G 1 contains an ontology header containing a triple " x rdf:type owl:Ontology ", where x is either an IRI or a blank node. Since Iare OWL 2 RDF-Based satisfies G 1 , this particular triple issatisfied by I.
From the semantic conditions of "Simple Entailment" , as defined in [ RDF Semantics ], follows that the triple " b rdf:type owl:Ontology " with the existentially interpreted blank node b is satisfied by I , too.For entity declarations ,ontology headers:
Let A be an entity declaration inthe ontology header of F(G2 ),)
and let gA be the corresponding subgraphsub graph of G2.
Since the pair
⟨( G1 , G2 ⟩)
is balanced,
gA is encoded as a single RDF triple of the form
"x rdf:type owl:Ontology",
where x is either an IRI or a blank node.
Since G1 is balanced , A occursan OWL 2 DL ontology in F(RDF graph form,
G1 ), and hence g A is a subgraphalso contains the encoding of an ontology header
including a triple g1 .of the form
"y rdf:type owl:Ontology",
where y is either an IRI or a blank node.
Since I OWL 2 RDF-Based satisfies G1,
I in particular OWL 2 RDF-Based satisfiesg A1 is satisfied by I.
For axiomsIf both y and x are IRIs,
then, due to balancing,
x equals y,
let A be an axiom in F( G 2 ),and lettherefore gA be the corresponding subgraph ofequals g1,
i.e. gA is OWL 2 RDF-Based satisfied by I.
It is possibleOtherwise,
balancing forces x to prove that Ibe a blank node,
i.e. x is treated as an existential variable
under the OWL 2 RDF-Based satisfies g A , by showing that allSemantics
according to the
premises"semantic conditions for blank nodes"
[RDF Semantics].
From this observation,
and from the right-to-left hand side of the particular semantic conditions, which are associated with the sort of axiom represented bypremise that I satisfies g A1,
are met. This will allow to apply the semantic condition, from which will followit follows that all the triples ingA areis OWL 2 RDF-Based satisfied by I.
The premises of the semantic condition generally require that the denotations of all the non-built-in names in g A are contained in the appropriate part of the universe, and that the semantic relationship that is expressed on the right hand side of the semantic condition actually holds between the denotations of all these names w.r.t. I . Special care has toFor entity declarations:
Let A be taken regarding the blank nodes occurringan entity declaration in F(G2),
and let gA .be the basic idea is as follows: For every non-built-in IRI u occurring incorresponding sub graph of G A , u also occurs in A2.
Since the pair
⟨( G1 , G2 ⟩)
is balanced,
property (2) of the "Balanced"-definition provides that there are entity declarationsA occurs in F(G 2 ) for all the entity types of u , each being of the form E := " Declaration ( T ( u ))" for some entity type T . From the reverse RDF mapping follows that for each such declaration E1),
and hence gA typing triple e exists inis a sub graph of G1.
Since I OWL 2 RDF-Based satisfies G1,
being of the form e := " u rdf:type t ", where t is the name ofI OWL 2 RDF-Based satisfies gA class representing the part of the universe corresponding to the entity type T.
It has already been shown thatFor E beingaxioms:
Let A be an entity declarationaxiom in F(G2),
and e beinglet gA be the corresponding subgraph insub graph of G2 ,.
Since I is an OWL 2 RDF-Based satisfies e . Hence,interpretation,
all the OWL 2 RDF-Based semantic conditions are met by I ( u ) is an individual contained.
Due to the close alignment between the definitions
in the appropriate part ofOWL 2 RDF-Based Semantics
and the universe. Further, since JOWL 2 Direct satisfies F( G 2 ), JSemantics,
OWL 2 Direct satisfies A . Therefore, theRDF-Based semantic relationshipconditions exist
that is represented by A accordingsemantically correspond
to the OWL 2 Direct Semantics actually holds betweendefinition of the denotationsinterpretation of the names occurring inaxiom A w.r.t. J.
SinceIn particular,
the denotationsconsequent of one of these names w.r.t. J have been defined in termssemantic conditions
corresponds to the RDF-encoding of A,
i.e. the denotations and class and property extensions w.r.t. Igraph gA,
except for declaration typing triples,
for which satisfaction has already been shown
(in the case of an "if-and-only-if" semantic condition
this will generally be the same namesright-to-left direction of that condition).
Hence,
in order to show that gA is OWL 2 ,RDF-Based satisfied by applying the definition of JI,
it will turn outbe sufficient to show
that the analog relationship also holds betweenantecedent of this semantic condition is true.
In general,
several requirements have to be met to ensure this:
Requirement 1:
The denotations of all the same names occurringnon-built-in IRIs in gA
have to be contained in the appropriate part of the universe of I.
Finally,This can be shown as follows.
For the blank nodesevery non-built-in IRI u occurring in gA,
it becomes clear fromu also occurs in A.
Since the fact thatpair
( G1 , G2 )
is an OWL 2 DL ontologybalanced,
there are entity declarations in RDF graph form that only certain kinds of subgraphs ofF(G A can occur having blank nodes. Case 1: A blank node corresponds to some anonymous individual in A (for A2)
for all the entity types of u,
each being oneof the form
D := "Declaration(T(u))"
for some entity type T.
From the reverse RDF mapping follows
that for each such declaration D
a class assertion, object property assertion or data property assertion, according to Sections 5.6, 9.5 and 11.2typing triple d exists in [ OWLG2 Specification ]). The same blank node is used in A,
and J interprets it as an existential variable. This rendersbeing of the semantic relationship thatform d := "u rdf:type t",
where t is expressed by A into an existential assertion. After applyingthe definitionvocabulary class IRI
representing the part of J ,the analog existential assertion holds w.r.t.universe of I
, withthat corresponds to the same blank node asentity type T.
It has already been shown that,
for D being an entity declaration in F(G2)
and d being the same existential variablecorresponding sub graph in G A2,
I OWL 2 RDF-Based satisfies d.
Case 2: A blank nodeHence, I(u) is an individual
contained in the "root" nodeappropriate part of the multi-tripleuniverse.
Requirement 2:
For every expression E occurring in A,
with the RDF encoding g A of A (forE in gA being an n-ary disjointness axiom from Section 5.10,
or a negative property assertion from Section 5.15 ).an individual has to exist in the right-to-left directionuniverse of I
that appropriately represents the semantic condition for this kinddenotation of axiomE.
Since I is of a form thatan OWL 2 RDF-Based interpretation,
all the triplesOWL 2 RDF-Based semantic conditions are met by I.
Due to the close alignment between the definitions
in g A containingthe blank node will beOWL 2 RDF-Based satisfied after allSemantics
and the OWL 2 Direct Semantics,
OWL 2 RDF-Based semantic conditions exist
that semantically correspond
to the premisesdefinition of the interpretation of the expression E.
In particular,
the antecedent of one of these semantic condition are met. Case 3: A blank node isconditions
will become true,
if the "root" nodeRDF-encoding of E,
i.e. the multi-triple RDF encodinggraph gE,
is satisfied
(in the case of an expression in A (for g E being either a sequence, or one"if-and-only-if" semantic condition
this will generally be the left-to-right direction of a boolean connective from Section 5.4 , an enumeration from Section 5.5 , a property restriction from Section 5.6 , or a datatype restriction from Section 5.7 ).that condition).
Now,
since the pair
⟨( G1 , G2 ⟩)
is balanced,
gE also occurs in G1.
So,
since I OWL 2 RDF-Based satisfies G1,
gE is OWL 2 RDF-Based satisfied, either,satisfied by I.
Hence,
the antecedent of the semantic condition becomes true,
and therefore its consequent becomes true as well.
This will result in the existence of an individual with the required properties,
when taking into account that blank nodes areexistential variables. Hence,blank node semantics.
Requirement 3:
A semantic relationship
has to hold
between the left-to-right directiondenotations of the
respective semantic condition forIRIs, literals and anonymous individuals
occurring in gA
with respect to I,
which,
roughly speaking,
expresses the particular sortmeaning of expression can be applied.the OWL 2 axiom A.
This can be doneis the case for allthe expressionsfollowing reasons:
First,
the literals and anonymous individuals
occurring in gA ,and gA can be seen as a directed acyclic graph with the triples encoding, respectively,
are interpreted in an analog way
under the actual axiom on top,OWL 2 Direct Semantics and the different component expressions being connected via blank nodes. Eventually, one can seeOWL 2 RDF-Based Semantics.
Second,
it was assumed that all the premises of the right-to-left direction ofthe OWL 2 Direct interpretation J
OWL 2 Direct satisfies A,
and therefore a semantic conditionrelationship
with the desired properties
holds with respect to J.
Third,
J has been defined in close correspondence to I,
so that for the axiom encodedsemantic relationship expressed by g A hold.J
an analog semantic relationship holds with respect to I.
This basic idea is now demonstrated in more detail
for a single example axiom A in F(G2),
which can be taken as a hint on
how a complete proof
could be constructed in principle. A complete proof would need to taketaking into account every language constructfeature of the OWL 2 into account, as well as additional aspects such as datatype maps and facets. AsRDF-Based Semantics
could be constructed in the example below, suchprinciple.
Let A proof can make use of the observation that the definitions ofbe the following OWL 2 Direct Semantics and the OWLaxiom in F(G2 RDF-Based Semantics are actually closely aligned for all the different language constructs of OWL 2. Let):
A = : SubClassOf(ex:c1 ObjectUnionOf(ex:c2 ex:c3))
for IRIs ex:c1 , ex:c2and ex:c3 that are declared tolet gA be classes elsewherethe corresponding sub graph in F(G2
). Duethat is being mapped to A via the reverse OWL 2RDF mapping,
g A has the formnamely
gA :
ex:c1 rdfs:subClassOf _:x .
_:x rdf:type owl:Class .
_:x owl:unionOf ( ex:c2 ex:c3 ) .
First,
since the entity declarations for the class names ex:c1pair
( G1 , ex:c2 and ex:c3 occurring in both A andG A correspond to2 )
is balanced,
G2 contains the typing triples
ex:c1 rdf:type owl:Class .
ex:c2 rdf:type owl:Class .
ex:c3 rdf:type owl:Class .
that correspond to class entity declarations in F(G2 , respectively. Based on the premise that) for the pair ⟨ G 1 , G 2 ⟩ is balanced ,IRIs
"ex:c1",
"ex:c2", and
"ex:c3",
respectively.
All these declaration typing triples are OWL 2 RDF-Based satisfied by Isatisfied by I,
since due to balancing
the typing triples exist in G1 as well,
and since it has been postulated
that I OWL 2 RDF-Based satisfies all triples in G1.
Hence,
allby applying the semantics of rdf:type
(see
Section 4.1 of the RDF Semantics
[RDF Semantics]),
all the IRIs denote classes:classes,
and therefore the denotations of the IRIs
are included in the appropriate part of the universe of I,
precisely:
I(ex:c1) ∈ IC ,
I(ex:c2) ∈ IC , and
I(ex:c3) ∈ IC .
Since J OWL 2 Direct satisfies ASecond,
the following semantic relationship holds between the denotations of the class names in A w.r.t. J : ( ex:c1 ) C ⊆ ( ex:c2 ) C ∪ ( ex:c3 ) C . Applying the definition of J results in the following semantic relationship w.r.t. I that holds between the denotations of the names ingA : ICEXT( I ( ex:c1 )) ⊆ ICEXT( I ( ex:c2 )) ∪ ICEXT( I ( ex:c3 )) .contains the subgraphsub graph gE of g A,
given by
gE :
_:x rdf:type owl:Class .
_:x owl:unionOf ( c2 c3 ) .
which corresponds to athe union class expression E in A .,
given by
E : ObjectUnionOf(ex:c2 ex:c3)
Since the pair
⟨( G1 , G2 ⟩)
is balanced,
gE is alsooccurs as a subgraphsub graph of G1 (it will be assumed that the same blank nodes are used in both instances ofas well.
gE in order to simplify the argument). Since both G 1 and G 2 are OWL 2 DL ontologies in RDF graph form, thecontains blank nodes
occurring in g E do not occur outside of g E , neither in G 1 nor in G 2 .and,
since I OWL 2 RDF-Basedsatisfies G1,
according tothe semantic conditions for RDF graphs with blank nodes apply
(see
Section 1.5 of the RDF Semantics
[RDF Semantics ]),]).
This provides the existence of
a mapping B from blank(gE) to IR exists,IR,
where blank(gE) is
the set of all blank nodes occurring in gE , such.
It follows that
the extended interpretation I+B
OWL 2 RDF-Based satisfies all the triples in gE.
An analog argument holds forFurther,
since I is an OWL 2 RDF-Based interpretation,
I meets all the blank nodes occurring in the sequence expression ( c2 c3 ) . This allows to applyOWL 2 RDF-Based semantic conditions.
Thus, the left-to-right direction
of the semantic condition for union class expressions
(("owl:unionOf ),",
see Section 5.4)
applies, providing:
[I+B](_:x) ∈ IC ,
ICEXT([I+B](_:x))
=
ICEXT(I(ex:c2))
∪
ICEXT(I(ex:c3)) .
Together withThird,
since the OWL 2 Direct interpretation J OWL 2 Direct satisfies A,
the following semantic relationship
holds between the denotations of the class names in A
according to J:
(ex:c1) C
⊆
(ex:c2) C
∪
(ex:c3) C .
By applying the definition of
the OWL 2 Direct interpretation J,
one can conclude that the following semantic relationship
holds between the extensions of the classes above
according to I:
ICEXT(I(ex:c1))
⊆
ICEXT(I(ex:c2))
∪
ICEXT(I(ex:c3)) .
Finally,
combining all intermediate results from above, it follows:gives
I(ex:c1) ∈ IC ,
[I+B](_:x) ∈ IC ,
ICEXT(I(ex:c1))
⊆
ICEXT([I+B](_:x)) .
Therefore, all the premises are met
to apply the right-to-left direction of the semantic condition offor subclass axioms
(("rdfs:subClassOf",
see Section 5.8),
which results in
⟨( I(ex:cl) , [I+B](_:x) ⟩)
∈
IEXT(I(rdfs:subClassOf)) .
So,
the remaining triple
ex:c1 rdfs:subClassOf _:x .
in gA
is OWL 2 RDF-Based satisfied by I+B,
where "_:x" is
the same blank node as theroot blank node of the union class expression ing AE.
Hence,
w.r.t. existential blank node semantics,
I OWL 2 RDF-Based satisfies all the triples in gA.
To conclude,
for everyany OWL 2 RDF-Based interpretation I
that OWL 2 RDF-Based satisfies G1 it turns out that,
I also OWL 2 RDF-Based satisfies G2.
Hence,
G1 OWL 2 RDF-Based entails G2 .,
and therefore relationship 4 of the correspondence theorem holds.
Q.E.D.
8 Appendix: Comprehension Conditions (Informative)
The correspondence theorem
in Section 7.2
shows
that it is possible for the OWL 2 RDF-Based Semantics
to reflect all the entailments of the
OWL 2 Direct Semantics
[OWL 2 Direct Semantics],
provided that one allows for certain "harmless" syntactic transformations
on the RDF graphs being considered.
This makes numerous potentially desirable and useful entailments available
that would otherwise be outside the scope of the OWL 2 RDF-Based Semantics,
for the technical reasons discussed in
Section 7.1.
It seems natural to ask for similar entailments
even
when an entailment query
does not consist of OWL 2 DL ontologies in RDF graph form.
However,
the correspondence theorem does not apply to such cases,
and thus the OWL 2 Direct Semantics cannot be taken
as a reference frame
for "desirable" and "useful" entailments,
or for when a graph transformation
can be considered "harmless" or not.
As discussed in
Section 7.1,
a core obstacle for the correspondence theorem to hold
werewas the RDF encodingsencoding of OWL 2 expressions,
such as union class expressions,
when they appear on the right hand side of an entailment query.
Under the OWL 2 RDF-Based Semantics,Semantics
it is not generally ensured that an individual exists,
which represents the denotation of such an expression.
The "comprehension conditions" defined in this section
are additional semantic conditions
that provide the necessary individuals
for every sequence, class and property expression.
By this,
the combination
of the normative semantic conditions of the OWL 2 RDF-Based Semantics
(Section 5)
and the comprehension conditions
can be regarded to "simulate" the semantic expressivity
of the OWL 2 Direct Semantics
on entailment queries consisting of arbitrary RDF graphs.
The combined semantics is,
however,
not primarily intended for use in actual implementations.
The comprehension conditions add significantly
to the complexity and expressivity
of the basic semantics
and,
in fact,
have proven to
lead to formal inconsistency.
But
the combined semantics
can still be seen as a generalized reference frame
for "desirable" and "useful" entailments,
and this can be used,
for example,
to evaluate methods that syntactically transform unrestricted entailment queries
in order to receive additional entailments under the OWL 2 RDF-Based Semantics.
Such a concrete method is, however,
outside the scope of this specification.
Note:
The conventions
in the introduction of
Section 5 ("Semantic Conditions")
apply to the current section as well.
8.1 Comprehension Conditions for Sequences
Table 8.1
lists the comprehension conditions for sequences,
i.e. RDF lists.
These comprehension conditions provide the existence
of sequences
built from any finite combination of individuals
contained in the universe.
Table 8.1: Comprehension Conditions for Sequences
| if
| then exists z1 , … , zn ∈ IR
|
| a1 , … , an ∈ IR
| ⟨( z1 , a1 ⟩) ∈ IEXT(I(rdf:first)) , ⟨( z1 , z2 ⟩) ∈ IEXT(I(rdf:rest)) , … ,
⟨( zn , an ⟩) ∈ IEXT(I(rdf:first)) , ⟨( zn , I(rdf:nil) ⟩) ∈ IEXT(I(rdf:rest))
|
8.2 Comprehension Conditions for Boolean Connectives
Table 8.2
lists the comprehension conditions for
Boolean connectives
(see Section 5.4
for the corresponding semantic conditions).
These comprehension conditions provide the existence
of complement classescomplements for any class,class and datatype,
and of intersections and unions
built from any finite set of classes
contained in the universe.
Table 8.2: Comprehension Conditions for Boolean Connectives
| if
| then exists z ∈ IR
|
| s sequence of c1 , … , cn ∈ IC
| ⟨( z , s ⟩) ∈ IEXT(I(owl:intersectionOf))
|
| s sequence of c1 , … , cn ∈ IC
| ⟨( z , s ⟩) ∈ IEXT(I(owl:unionOf))
|
| c ∈ IC
| ⟨( z , c ⟩) ∈ IEXT(I(owl:complementOf))
|
| d ∈ IDC
| ⟨( z , d ⟩) ∈ IEXT(I(owl:datatypeComplementOf))
|
8.3 Comprehension Conditions for Enumerations
Table 8.3
lists the comprehension conditions for
enumerations
(see Section 5.5
for the corresponding semantic conditions).
These comprehension conditions provide the existence
of enumeration classes
built from any finite set of individuals
contained in the universe.
Table 8.3: Comprehension Conditions for Enumerations
| if
| then exists z ∈ IR
|
| s sequence of a1 , … , an ∈ IR
| ⟨( z , s ⟩) ∈ IEXT(I(owl:oneOf))
|
8.4 Comprehension Conditions for Property Restrictions
Table 8.4
lists the comprehension conditions for
property restrictions
(see Section 5.6
for the corresponding semantic conditions).
These comprehension conditions provide the existence
of cardinality restrictions
on any property and for any non-negativenonnegative integer,
as well as value restrictions
on any property and on any class
contained in the universe.
Note that the comprehension conditions for self restrictions
constrains the right hand side of
the produced owl:hasSelf assertions
to be the Boolean value
"true"^^xsd:boolean.
This is in accordance with
Table 13 in Section 3.2.4 of the OWL 2 RDF Mapping
[OWL 2 RDF Mapping].
Implementations are not required
to support the comprehension conditions for
owl:onProperties,
but
MAY
support them
in order to realize
n-ary dataranges with arity ≥ 2
(see
SectionSections
7
and
8.4
of the OWL 2 Structural Specification
[OWL 2 Specification]
for further information).
Table 8.4: Comprehension Conditions for Property Restrictions
| if
| then exists z ∈ IR
|
c ∈ IC ,
p ∈ IP
| ⟨( z , c ⟩) ∈ IEXT(I(owl:someValuesFrom)) ,
⟨( z , p ⟩) ∈ IEXT(I(owl:onProperty))
|
c ∈ IC ,
s sequence of p1 , … , pn ∈ IP , n ≥ 1
| ⟨( z , c ⟩) ∈ IEXT(I(owl:someValuesFrom)) ,
⟨( z , s ⟩) ∈ IEXT(I(owl:onProperties))
|
c ∈ IC ,
p ∈ IP
| ⟨( z , c ⟩) ∈ IEXT(I(owl:allValuesFrom)) ,
⟨( z , p ⟩) ∈ IEXT(I(owl:onProperty))
|
c ∈ IC ,
s sequence of p1 , … , pn ∈ IP , n ≥ 1
| ⟨( z , c ⟩) ∈ IEXT(I(owl:allValuesFrom)) ,
⟨( z , s ⟩) ∈ IEXT(I(owl:onProperties))
|
a ∈ IR ,
p ∈ IP
| ⟨( z , a ⟩) ∈ IEXT(I(owl:hasValue)) ,
⟨( z , p ⟩) ∈ IEXT(I(owl:onProperty))
|
| p ∈ IP
| ⟨( z , I("true"^^xsd:boolean) ⟩) ∈ IEXT(I(owl:hasSelf)) ,
⟨( z , p ⟩) ∈ IEXT(I(owl:onProperty))
|
n ∈ INNI ,
p ∈ IP
| ⟨( z , n ⟩) ∈ IEXT(I(owl:minCardinality)) ,
⟨( z , p ⟩) ∈ IEXT(I(owl:onProperty))
|
n ∈ INNI ,
p ∈ IP
| ⟨( z , n ⟩) ∈ IEXT(I(owl:maxCardinality)) ,
⟨( z , p ⟩) ∈ IEXT(I(owl:onProperty))
|
n ∈ INNI ,
p ∈ IP
| ⟨( z , n ⟩) ∈ IEXT(I(owl:cardinality)) ,
⟨( z , p ⟩) ∈ IEXT(I(owl:onProperty))
|
n ∈ INNI ,
c ∈ IC ,
p ∈ IP
| ⟨( z , n ⟩) ∈ IEXT(I(owl:minQualifiedCardinality)) ,
⟨( z , c ⟩) ∈ IEXT(I(owl:onClass)) ,
⟨( z , p ⟩) ∈ IEXT(I(owl:onProperty))
|
n ∈ INNI ,
d ∈ IDC ,
p ∈ IODP
| ⟨( z , n ⟩) ∈ IEXT(I(owl:minQualifiedCardinality)) ,
⟨( z , d ⟩) ∈ IEXT(I(owl:onDataRange)) ,
⟨( z , p ⟩) ∈ IEXT(I(owl:onProperty))
|
n ∈ INNI ,
c ∈ IC ,
p ∈ IP
| ⟨( z , n ⟩) ∈ IEXT(I(owl:maxQualifiedCardinality)) ,
⟨( z , c ⟩) ∈ IEXT(I(owl:onClass)) ,
⟨( z , p ⟩) ∈ IEXT(I(owl:onProperty))
|
n ∈ INNI ,
d ∈ IDC ,
p ∈ IODP
| ⟨( z , n ⟩) ∈ IEXT(I(owl:maxQualifiedCardinality)) ,
⟨( z , d ⟩) ∈ IEXT(I(owl:onDataRange)) ,
⟨( z , p ⟩) ∈ IEXT(I(owl:onProperty))
|
n ∈ INNI ,
c ∈ IC ,
p ∈ IP
| ⟨( z , n ⟩) ∈ IEXT(I(owl:qualifiedCardinality)) ,
⟨( z , c ⟩) ∈ IEXT(I(owl:onClass)) ,
⟨( z , p ⟩) ∈ IEXT(I(owl:onProperty))
|
n ∈ INNI ,
d ∈ IDC ,
p ∈ IODP
| ⟨( z , n ⟩) ∈ IEXT(I(owl:qualifiedCardinality)) ,
⟨( z , d ⟩) ∈ IEXT(I(owl:onDataRange)) ,
⟨( z , p ⟩) ∈ IEXT(I(owl:onProperty))
|
8.5 Comprehension Conditions for Datatype Restrictions
Table 8.5
lists the comprehension conditions for
datatype restrictions
(see Section 5.7
for the corresponding semantic conditions).
These comprehension conditions provide the existence
of datatypes
built from restricting any datatype
contained in the universe
by any finite set of facet-value pairs
contained in the facet space
(see Section 4.1)
of the original datatype.
The set IFS is defined in
Section 5.7.
Table 8.5: Comprehension Conditions for Datatype Restrictions
| if
| then exists z ∈ IR , s sequence of z1 , … , zn ∈ IR
|
d ∈ IDC ,
f1 , … , fn ∈ IODP ,
v1 , … , vn ∈ LV ,
⟨( f1 , v1 ⟩) , … , ⟨( fn , vn ⟩) ∈ IFS(d)
| ⟨( z , d ⟩) ∈ IEXT(I(owl:onDatatype)) ,
⟨( z , s ⟩) ∈ IEXT(I(owl:withRestrictions)) ,
⟨( z1 , v1 ⟩) ∈ IEXT(f1) , … , ⟨( zn , vn ) ∈ IEXT(fn)
|
8.6 Comprehension Conditions for Inverse Properties
Table 8.6
lists the comprehension conditions for
inverse property expressions.
These comprehension conditions provide the existence
of an inverse property for any property
contained in the universe.
Inverse property expressions can be used
to build axioms with anonymous inverse properties,
such as in the graph
_:x owl:inverseOf ex:p .
_:x rdfs:subPropertyOf owl:topObjectProperty .
Note that,
to some extent,
the OWL 2 RDF-Based Semantics already covers the use of inverse property expressions
by means of the semantic conditions of inverse property axioms
(see Section 5.12),
since these semantic conditions also apply to an existential variable
on the left hand side of an inverse property axiom.
Nevertheless,
not all relevant cases are covered by this semantic condition.
For example,
one might expect the above example graph
to be generally true.
However,
the normative semantic conditions
do not permit this conclusion,
since it is not ensured that
for every property p
there is an individual in the universe
with a property extension being inverse to that of p.
Table 8.6: Comprehension Conditions for Inverse Properties
| if
| then exists z ∈ IR
|
| p ∈ IP
| ( z n, v n ⟩p ) ∈ IEXT( f n ) 8.6 Comprehension Conditions for Inverse Properties Table 8.6I(owl:inverseOf))
|
9 Appendix: Changes from OWL 1 (Informative)
This section lists relevant differences
between the comprehension conditions for inverse property expressions. These comprehension conditions provideOWL 2 RDF-Based Semantics and the existenceoriginal specification of an inverse property for any property containedthe
OWL 1 RDF-Compatible Semantics
[OWL 1 RDF-Compatible Semantics].
Significant effort has been spent
in keeping the universe. Inverse property expressions can bedesign of the OWL 2 RDF-Based Semantics
as close as possible
to that of the OWL 1 RDF-Compatible Semantics.
While this aim was achieved to a large degree,
the OWL 2 RDF-Based Semantics actually deviates from its predecessor in several aspects.
In most cases this is because of serious technical problems
that would have arisen
from a conservative
semantic extension.
Not listed are
the new language constructs and the new datatypes of OWL 2.
The following markers are used:
- [DEV]: a deviation from OWL 1 that breaks backward compatibility
- [EXT]: a backward compatible extension to OWL 1
- [NOM]: a change of the nomenclature originally used in OWL 1
- [DPR]: a feature of OWL 1 that has been deprecated as of OWL 2
Generalized Graph Syntax [EXT].
The OWL 2 RDF-Based Semantics
allows RDF graphs to build axiomscontain
IRIs
[RFC 3987]
(see Section 2.1),
whereas the OWL 1 RDF-Compatible Semantics was restricted to RDF graphs with
anonymous inverse properties, such asURIs
[RFC 2396].
This change is in accordance with the rest of the OWL 2 specification
(see
Section 2.4 of the graph _:x owl:inverseOf ex:p . _:x rdfs:subPropertyOf owl:topObjectProperty . Note that, to some extent,OWL 2 Structural Specification
[OWL 2 Specification]).
In addition,
the OWL 2 RDF-Based Semantics
already covers the use of inverse property expressions by means of the semantic conditions of inverse property axioms (see Section 5.12 ), since these semantic conditions also applyis now explicitly allowed to
an existential variable on the left hand sidebe applied to RDF graphs containing
"generalized" RDF triples,
i.e. triples that can consist of
an inverse property axiom. Nevertheless, notIRIs, literals or blank nodes
in all relevant casesthree positions
(Section 2.1),
although implementations are covered by this semantic condition. For example, one might expect the above example graph to be generally true. However, the normative semantic conditions do not permit this conclusion, since it isnot ensured that for every property p there is an individualrequired to support this.
In contrast,
the universe that happensOWL 1 RDF-Compatible Semantics was restricted to RDF graphs
conforming to bethe
inverse propertyRDF Concepts specification
[RDF Concepts].
These limitations of p . Table 8.6: Comprehension Conditions for Inverse Properties if then exists z ∈ IR p ∈ IP ⟨ z , p ⟩ ∈ IEXT( I ( owl:inverseOf )) 9 Appendix: Changes fromthe OWL 1 (Informative) This section lists relevant differences betweenRDF-Compatible Semantics
were actually inherited from the
RDF Semantics specification
[RDF Semantics].
The relaxations are intended to warrant interoperability
with existing and future technologies and tools.
Both changes are compatible with OWL 1,
since all RDF graphs that were legal under the OWL 1 RDF-Compatible Semantics
are still legal under the OWL 2 RDF-Based Semantics andSemantics.
Facets for Datatypes [EXT].
The original specificationbasic definitions of a datatype and a D-interpretation,
as defined by the OWL 1 RDF-CompatibleRDF Semantics [specification
and as applied by the OWL 1 RDF-Compatible Semantics ]. Significant effort hasSemantics,
have been spentextended
to take into account constraining facets
(see Section 4),
in keepingorder to allow for datatype restrictions
as specified in Section 5.7.
This change is compatible with OWL 1,
since Section 5.1
of the designRDF Semantics specification
explicitly allows for extending the minimal datatype definition provided there.
Correspondence Theorem and Comprehension Conditions [DEV].
The semantic conditions of the OWL 2 RDF-Based1 RDF-Compatible Semantics as close as possibleincluded
a set of so called
"comprehension conditions",
which allowed to prove the original
"correspondence theorem"
stating that every entailment of theOWL 1 RDF-Compatible Semantics. While this aimDL was achieved to a large degree, thealso an entailment of OWL 2 RDF-Based Semantics actually deviates from its predecessor in several aspects, in most cases due to serious technical problems that would have arisen from a conservative semantic extension . Not listed are1 Full.
The document at hand adds comprehension conditions
for the new language constructs and the new datatypesof OWL 2.2
(see Section 8).
However,
the following markerscomprehension conditions
are used: [DEV] :not a deviation fromnormative aspect of the OWL 1 RDF-Compatible2 RDF-Based Semantics
anymore.
It has turned out
that formally breaks backwards compatibility. [EXT] : An extensioncombining the comprehension conditions
with the normative set of semantic conditions in
Section 5
would lead to formal inconsistency of the OWL 1 RDF-Compatibleresulting semantics
(Issue 119).
In addition,
it became clear that
is backwards compatible. [NOM] :a changecorrespondence theorem along the lines of the nomenclature compared to that being used inoriginal theorem
would not work for the OWL 1 RDF-Compatible Semantics. Generalized Graph Syntax [EXT]:relationship between the
OWL 2 RDF-Based Semantics allows RDF graphs to contain IRIs [ RFC 3987 ] (see Section 2.1 ), whereasand the
OWL 1 RDF-Compatible2 Direct Semantics
was restricted to RDF graphs with URIs[ RFC 2396 ]. This changeOWL 2 Direct Semantics],
since it is in accordance withnot possible to "balance" the rest ofdifferences between
the OWL 2 specificationtwo semantics
solely by means of additional comprehension conditions
(see Section 2.47.1).
Consequently,
the correspondence theorem
of [ OWL 2 Specification ]). In addition,the OWL 2 RDF-Based Semantics
is now explicitly allowed to be applied to RDF graphs containing "generalized" RDF triples , i.e. triples that can consist of IRIs, literals or blank nodes in all three positions(Section 2.1 ), although implementations are not required to support this. In contrast,7.2)
follows an alternative approach
that replaces the OWL 1 RDF-Compatible Semantics was restricted to RDF graphs conforming touse of the RDF Concepts specification [ RDF Concepts ]. These limitationscomprehension conditions
and can be seen as a technical refinement
of an idea
originally discussed by the OWL 1 RDF-Compatible Semantics were actually inheritedWebOnt Working Group
(email).
This change is an incompatible deviation from OWL 1,
since certain aspects of the RDF Semantics specification [ RDF Semantics ].originally normative definition of the relaxations are intended to warrant interoperability with existing and future technologies and tools. Both changes are compatiblesemantics
have been removed.
Flawed Semantics of Language Constructs with OWL 1, since all RDF graphs that were legal underArgument Lists [DEV].
In the OWL 1 RDF-Compatible Semantics are still legal under the OWL 2 RDF-Based Semantics. Datatype Facets [EXT]:Semantics,
the basic definitions of a datatypesemantic conditions for
unions, intersections and a D-interpretation , asenumerations of classes
were defined byin a flawed form,
which lead to formal inconsistency of the RDFsemantics
specification and as applied by(Issue 120;
see also an unofficial
problem description).
The OWL 1 RDF-Compatible Semantics,affected semantic conditions have been extended to take constraining facets into account (seerevised;
see
Section 4 ), in order to allow for datatype restrictions as specified in5.4
and
Section 5.75.5.
This change is compatible withan incompatible deviation from OWL 1,
since Section 5.1 ofthe RDFsemantics specification explicitly allows for extending the minimal datatype definition provided there. Correspondence Theorem and Comprehension Conditions [DEV]: The semantic conditionshas formally been weakened
in order to eliminate a source of inconsistency.
Incomplete Semantics of owl:AllDifferent [EXT].
The OWL 1 RDF-Compatible Semantics includedmissed a set of so called "comprehension conditions" , which allowed to showcertain semantic condition
for axioms based on the original "correspondence theorem" stating that every entailment of OWL 1 DL wasvocabulary term "owl:AllDifferent"
(see also an entailment of OWL 1 Full.unofficial
problem description).
The document at hand adds comprehension conditions formissing semantic condition
has been added to the new language constructs ofOWL 2 RDF-Based Semantics
(see Section 5.10).
This change is compatible with OWL 1,
since the semantics has been conservatively extended.
Aligned Semantics of owl:DataRange and rdfs:Datatype [EXT].
The class
owl:DataRange
has been made an equivalent class
to rdfs:Datatype
(see Section 85.2).
However,The comprehension conditions are not a normative aspectmain purpose for this change was
to allow for the deprecation of the term
owl:DataRange
in favor of rdfs:Datatype.
This change is compatible with OWL 2 RDF-Based Semantics anymore. It has turned out that combining1
according to an analysis
of the comprehension conditions withrelationship between the normative set of semantic conditionstwo classes
in Section 5 would lead to formal inconsistency ofthe resultingOWL 1 RDF-Compatible Semantics
( Issue 119email).
In addition, it became clearOntology Properties as Annotation Properties [EXT].
Several properties
that a correspondence theorem alonghave been ontology properties in OWL 1,
such as owl:priorVersion,
have now been specified
as both ontology properties and annotation properties,
in order to be in line
with the linesrest of the original theorem would not work for the relationship between theOWL 2 RDF-Based Semantics andspecification
(see
Section 5.5 of the OWL 2 Direct SemanticsStructural Specification
[OWL 2 Direct Semantics ], since itSpecification]).
This change is not possible to "balance" the differences betweencompatible with OWL 1,
since the twosemantics solely by means of additional semantic conditions (see Section 7.1 ). Consequently,has been conservatively extended:
all the correspondence theoremontology properties of theOWL 2 RDF-Based Semantics ( Section 7.2 ) follows an alternative approach that replaces1 are still ontology properties in OWL 2.
Nonempty Data Value Enumerations [DEV].
The usesemantic condition for enumerations of the comprehension conditions and can be seen as a technical refinementdata values
in Section 5.5
is now restricted to nonempty sets of data values.
This prevents the class owl:Nothing
from unintentionally becoming an idea originally discussed byinstance
of the WebOnt Working Groupclass rdfs:Datatype,
as analyzed in
(email).
This changerestriction of the semantics
is an incompatible deviation from OWL 1, since certain aspects1.
Note, however,
that it is still possible
to define a datatype as an empty enumeration of data values,
as explained in Section 5.5.
Terminological Clarifications [NOM].
This document uses the originally normative definition ofterm "OWL 2 RDF-Based Semantics"
to refer to the specified semantics have been removed. Flawed Semantics ofonly.
According to Section 2.1,
the term "OWL 2 Full"
refers to the language
Constructs with Argument Lists [DEV]: Inthat is determined
by the set of all RDF graphs
(also called "OWL 2 Full ontologies")
being interpreted using the OWL 2 RDF-Based Semantics.
OWL 1 RDF-Compatible Semantics,has not been particularly clear on this distinction.
Where the semantic conditions for unions, intersectionsOWL 1 RDF-Compatible Semantics specification talked about
"OWL Full interpretations",
"OWL Full satisfaction",
"OWL Full consistency"
and
enumerations of classes were defined in a flawed form, which lead to formal inconsistency of"OWL Full entailment",
the OWL 2 RDF-Based Semantics ( Issue 120 ; see also an unofficial problem description ). The affected semantic conditions have been revised; seeSpecification talks
in Section 5.44
about
"OWL 2 RDF-Based interpretations",
"OWL 2 RDF-Based satisfaction",
"OWL 2 RDF-Based consistency"
and
Section 5.5 . This change is an incompatible deviation from OWL 1,"OWL 2 RDF-Based entailment",
respectively,
since these terms are primarily meant to be related to
the semantics
has formallyrather than the whole language.
Modified Abbreviations [NOM].
The names
"RI", "PI", "CI",
"EXTI", "CEXTI",
"SI", "LI" and "LVI",
which have been weakenedused in order to eliminate a source of inconsistency. Incomplete Semantics of owl:AllDifferent [EXT]:the
OWL 1 RDF-Compatible Semantics missed a certain semantic condition for axioms based on the vocabulary term " owl:AllDifferent " (see also an unofficial problem description ). The missing semantic condition hasspecification,
have been added toreplaced by the OWL 2 RDF-Based Semantics (see Section 5.10 ). This change is compatible with OWL 1, sincecorresponding names
defined in the
RDF Semantics has been conservatively extended. Aligneddocument
[RDF Semantics of owl:DataRange],
namely "IR", "IP", "IC", "IEXT", "ICEXT", "IS", "IL" and rdfs:Datatype [EXT]:"LV", respectively.
Furthermore,
all uses of the class owl:DataRange hasIRI mapping "IS"
have been made an equivalent class to rdfs:Datatype (see Section 5.2 ).replaced by the main purpose for this change wasmore general interpretation mapping "I",
following the conventions in the RDF Semantics document.
These changes are intended to allow forsupport
the deprecationuse of the term owl:DataRange in favor of rdfs:Datatype . This change is compatible withOWL 1 according to2 RDF-Based Semantics document
as an analysisincremental extension
of the relationship betweenRDF Semantics document.
Names for the two classes"parts of the universe"
that were exclusively used in the OWL 1 RDF-Compatible Semantics ( email ). Non-Empty Data Value Enumerations [DEV]: The semantic conditiondocument,
such as "IX" or "IODP",
have not been changed.
Other abbreviations,
such as "IAD" for enumerationsthe class extension of data valuesowl:AllDifferent,
have in general not been reused in the document at hand,
but the explicit nonabbreviated form,
such as
"IEXT(I(owl:AllDifferent))",
is used instead.
Modified Tuple Notation Style [NOM].
Tuples are written in Section 5.5 is now restricted to non-empty sets of data values. This preventsthe class owl:Nothing from unintentionally becoming an instanceform
"( … )"
instead of the class rdfs:Datatype ,"< … >",
as analyzedin ( email ). This restriction ofthe semantics is an incompatible deviation fromother OWL 1. Note, however, that it is still possible to define an empty enumeration of data values,2 documents.
Deprecated Vocabulary Terms [DPR].
The following vocabulary terms have been deprecated as explainedof OWL 2
by the Working Group,
and SHOULD NOT be used
in new ontologies anymore:
10 Appendix: Change Log (Informative)
10.1 Changes Since Candidate Recommendation
This section 5.5 . Terminological Clarifications [NOM]:summarizes the changes to this document usessince the term "OWL 2 RDF-Based Semantics"Candidate Recommendation of 11 June, 2009.
- [resolution] Re-definition of several ontology properties to
referbe both ontology properties and annotation properties, in order to align the specifiedRDF-Based Semantics only. According to Section 2.1 , the term "OWL 2 Full" refers to the whole language that is determined bywith the setrest of RDF graphs (also called "OWL 2 Full ontologies" ) being interpreted usingthe OWL 2 RDF-Based Semantics. OWL 1 has not been particularly clear on this distinction. Where the OWL 1 RDF-Compatible Semanticsspecification talked about "OWL Full interpretations" , "OWL Full satisfaction", "OWL Full consistency"and "OWL Full entailment" ,in particular to avoid an equivocal definition of the OWL 2 RDF-Based Semantics Specification talks in Section 4 about "OWL 2 RDF-Based interpretations" , "OWL 2 RDF-Based satisfaction" , "OWL 2 RDF-Based consistency" and "OWL 2 RDF-Based entailment" , respectively, since these termsRL/RDF rules (per WG resolution).
- [correction] Correction of the type of facets: Facets are
primarily meantintended to be related todata properties and have been used as such elsewhere in the document, but they were wrongly specified as unrestricted properties so far.
- [correction] Correction of a mismatch between the definition of D-interpretations in the document at hand and the RDF Semantics
rather thanspecification: according to the whole language. Modified Abbreviations [NOM]:definition of simple interpretations, LV contains all plain literals in the names "R I ", "P I ", "C I ", "EXT I ", "CEXT I ", "S I ", "L Ivocabulary V. The missing reference to " and "LV IV" havehas been replacedadded.
- [nonnormative] Correction of an error in the formulation of the correspondence theorem.
- [nonnormative] The section on Axiomatic Triples has been extended by an explicit set of axiomatic triples, based on the
corresponding names defineddiscussion in the RDF Semantics document [ RDF Semantics ], namely "IR", "IP", "IC", "IEXT", "ICEXT", "IS", "IL"rest of the section.
- [nonnormative] The section on Axiomatic Triples now explicitly mentions axiomatic triples for datatypes and
"LV",facets corresponding to the semantic conditions for datatypes and facets, respectively.
-
Furthermore, all uses[nonnormative] Refinement of the IRI mapping "IS" have been replaced byproof for the more general interpretation mapping " I ", followingcorrespondence theorem and correction of several errors. Motivated by these changes, the conventionsexample in Section 7.1 has been slightly revised as well.
- [editorial] Added a description and ALT-attribute text to Figure 1 on the
RDF Semantics document. These changes are intendedparts hierarchy.
- [editorial] Distinction between normative and nonnormative references, as in other OWL 2 documents.
- [editorial] Added some clarification to
supportthe use ofintroduction section.
- [editorial] Removed a redundant conclusion from the table presenting the semantic conditions for datatype restrictions, since this conclusion already follows from the semantic conditions for the
OWL 2 RDF-Based Semantics document as an incremental extension ofvocabulary properties, and having the RDF Semanticsconclusion repeated would not match the general approach that is applied when presenting "if-then" semantic conditions in this document.
-
Names for[editorial] Reworded the "partsdescription of the universe" that were exclusively usedmarkers in the section on changes from OWL 1 RDF-Compatible Semantics document, such as "IX" or "IODP", have not been changed. Other abbreviations, such as "IAD", and added a marker "DPR" for the class extensiondeprecated features.
- [editorial] Changed the presentation style of
owl:AllDifferent , have in general not been reusedreferences and citations to a form used in all OWL 2 documents.
- [editorial] Changed the
document at hand, butpresentation style for tuples from "⟨ … ⟩" to "( … )", to follow the explicit non-abbreviated form, such as "IEXT( I ( owl:AllDifferent ))", isconventions used instead. Deprecated Vocabulary Terms [NOM]:in the following vocabulary terms have been deprecated as ofother OWL 2 by the Working Group,documents.
- [editorial] Numerous minor corrections and
SHOULD NOT be used in new ontologies anymore: owl:DataRange (per resolution of Issue 29 ) 10 Appendix: Post Last-Callstylistic improvements.
10.2 Changes (Informative)Since Last Call
This section summarizes the changes fromto this document since the Last Call Working Draft of 21 April 2009:April, 2009.
- [resolution] Renamed the annotation vocabulary terms
"owl:subject", "owl:predicate""owl:subject", "owl:predicate" and "owl:object""owl:object" to "owl:annotatedSource", "owl:annotatedProperty""owl:annotatedSource", "owl:annotatedProperty" and "owl:annotatedTarget","owl:annotatedTarget", respectively (per WG resolution).
- [resolution] Replaced the datatype
"rdf:text""rdf:text" by "rdf:PlainLiteral""rdf:PlainLiteral" (per WG resolution).
- [resolution] Replaced the facet
"rdf:langPattern""rdf:langPattern" by "rdf:langRange","rdf:langRange", following the same replacement in the original "rdf:PlainLiteral" specification.rdf:PlainLiteral specification.
- [correction] Changed the range of the property
"owl:annotatedProperty""owl:annotatedProperty" from IP to IR in order to avoid undesired semantic side effects from annotations. This was an oversight when the original semantic conditions for annotations of axioms and annotations were removed from the document.
-
Explained the optional status of the semantic conditions concerned with the IRI "owl:onProperties", in accordance with the rest of the OWL 2 specification.[nonnormative] The semantic conditions and comprehension conditions for the n-ary property restrictions have been changed to only cover property sequences of length greater than 0, since the meaning of an expression with an empty property set is not clear.
- [editorial] Explained the optional status of the semantic conditions concerned with the IRI "owl:onProperties", in accordance with the rest of the OWL 2 specification.
- [editorial] Shortened and clarified some section titles, moved the section on semantic conditions for sub property chains within Section 5, and aligned the entry order of all tables in Section 8 with those in Section 5.
- [editorial] Several
editorialclarifications, minor corrections and cosmetic changes.
11 Acknowledgments
The starting point for the development of OWL 2 was the OWL1.1 member submission, itself a result of user and developer feedback, and in particular of information gathered during the OWL Experiences and Directions (OWLED) Workshop series. The working group also considered postponed issues from the WebOnt Working Group.
This document has been produced by the OWL Working Group (see below), and its contents reflect extensive discussions within the Working Group as a whole.
The editors extend special thanks to
Jie Bao (RPI),
Ivan Herman (W3C/ERCIM),
Peter F. Patel-Schneider (Bell Labs Research, Alcatel-Lucent) and
Zhe Wu (Oracle Corporation)
for their thorough reviews.
The regular attendees at meetings of the OWL Working Group at the time of publication of this document were:
Jie Bao (RPI),
Diego Calvanese (Free University of Bozen-Bolzano),
Bernardo Cuenca Grau (Oxford University),University Computing Laboratory),
Martin Dzbor (Open University),
Achille Fokoue (IBM Corporation),
Christine Golbreich (Université de Versailles St-Quentin and LIRMM),
Sandro Hawke (W3C/MIT),
Ivan Herman (W3C/ERCIM),
Rinke Hoekstra (University of Amsterdam),
Ian Horrocks (Oxford University),University Computing Laboratory),
Elisa Kendall (Sandpiper Software),
Markus Krötzsch (FZI),
Carsten Lutz (Universität Bremen),
Deborah L. McGuinness (RPI),
Boris Motik (Oxford University),University Computing Laboratory),
Jeff Pan (University of Aberdeen),
Bijan Parsia (University of Manchester),
Peter F. Patel-Schneider (Bell Labs Research, Alcatel-Lucent),
Sebastian Rudolph (FZI),
Alan Ruttenberg (Science Commons),
Uli Sattler (University of Manchester),
Michael Schneider (FZI),
Mike Smith (Clark & Parsia),
Evan Wallace (NIST),
Zhe Wu (Oracle Corporation), and
Antoine Zimmermann (DERI Galway).
We would also like to thank past members of the working group:
Jeremy Carroll,
Jim Hendler,
Vipul Kashyap.
12 References
[OWL 2 Direct Semantics] OWL 2 Web Ontology Language: Direct Semantics Boris Motik, Peter F. Patel-Schneider, Bernardo Cuenca Grau, eds. W3C Candidate Recommendation, 11 June 2009, http://www.w3.org/TR/2009/CR-owl2-direct-semantics-20090611/ . Latest version available at http://www.w3.org/TR/owl2-direct-semantics/ . [OWL 2 RDF Mapping] OWL 2 Web Ontology Language: Mapping to RDF Graphs Peter F. Patel-Schneider, Boris Motik, eds. W3C Candidate Recommendation, 11 June 2009, http://www.w3.org/TR/2009/CR-owl2-mapping-to-rdf-20090611/ . Latest version available at http://www.w3.org/TR/owl2-mapping-to-rdf/ .12.1 Normative References
- [OWL 2 Specification]
- OWL 2 Web Ontology
Language:Language : Structural Specification and Functional-Style Syntax Boris Motik, Peter F. Patel-Schneider, Bijan Parsia, eds. W3C CandidateProposed Recommendation, 11 June22 September 2009, http://www.w3.org/TR/2009/CR-owl2-syntax-20090611/http://www.w3.org/TR/2009/PR-owl2-syntax-20090922/. Latest version available at http://www.w3.org/TR/owl2-syntax/. -
[OWL 1 RDF-Compatible Semantics] OWL Web Ontology Language: Semantics and Abstract Syntax, Section 5. RDF-Compatible Model-Theoretic Semantics . Peter F. Patel-Schneider, Patrick Hayes, and Ian Horrocks, eds., W3C Recommendation, 10 February 2004.[RDF Concepts]
- Resource Description Framework (RDF): Concepts and Abstract Syntax. Graham Klyne and Jeremy J. Carroll, eds. W3C Recommendation, 10 February 2004, http://www.w3.org/TR/2004/REC-rdf-concepts-20040210/. Latest version available as http://www.w3.org/TR/rdf-concepts/.
- [RDF Semantics]
- RDF Semantics. Patrick Hayes, ed., W3C Recommendation, 10 February 2004, http://www.w3.org/TR/2004/REC-rdf-mt-20040210/. Latest version available as http://www.w3.org/TR/rdf-mt/.
- [RFC 2119]
- RFC 2119: Key words for use in RFCs to Indicate Requirement Levels. Network Working Group, S. Bradner. IETF, March 1997, http://www.ietf.org/rfc/rfc2119.txt
- [RFC 3987]
- RFC 3987: Internationalized Resource Identifiers (IRIs). M. Duerst and M. Suignard. IETF, January 2005, http://www.ietf.org/rfc/rfc3987.txt
12.2 Nonnormative References
- [OWL 2 Direct Semantics]
- OWL 2 Web Ontology Language : Direct Semantics Boris Motik, Peter F. Patel-Schneider, Bernardo Cuenca Grau, eds. W3C Proposed Recommendation, 22 September 2009, http://www.w3.org/TR/2009/PR-owl2-direct-semantics-20090922/. Latest version available at http://www.w3.org/TR/owl2-direct-semantics/.
- [OWL 2 RDF Mapping]
- OWL 2 Web Ontology Language : Mapping to RDF Graphs Peter F. Patel-Schneider, Boris Motik, eds. W3C Proposed Recommendation, 22 September 2009, http://www.w3.org/TR/2009/PR-owl2-mapping-to-rdf-20090922/. Latest version available at http://www.w3.org/TR/owl2-mapping-to-rdf/.
- [OWL 1 RDF-Compatible Semantics]
- OWL Web Ontology Language: Semantics and Abstract Syntax, Section 5. RDF-Compatible Model-Theoretic Semantics. Peter F. Patel-Schneider, Patrick Hayes, and Ian Horrocks, eds., W3C Recommendation, 10 February 2004.
- [RFC 2396]
- RFC 2396 - Uniform Resource Identifiers (URI): Generic Syntax. T. Berners-Lee, R. Fielding, U.C. Irvine and L. Masinter. IETF, August 1998.
