8.1 Introduction
The primary role of MathML content elements is to provide a mechanism for recording that a particular notational structure has a particular mathematical meaning. To this end, every content element must have a mathematical definition associated with it in some form. These definitions are provided in the form of content dictionaries, XML files of a certain structure (see Section 8.2 MathML3 Content Dictionaries Infrastructure and Metadata).
The concept of a content dictionary has initially been introduced by the OpenMath1 format [OpenMath2000], and has been stabilized and generalized to abstract content dictionaries in the OpenMath2 standard [OpenMath2004], keeping a variant of OpenMath1 CDs as a reference encoding.
MathML 3 introduces a content dictionary format that is designed to support the MathML language, while meeting the requirements of OpenMath abstract CDs. We will introduce the format in the rest of the section and give an overview over the MathML3 content dictionaries for the K-14 fragment of Mathematics which is part of the MathML3 recommendation.
| Editorial note: MiKo | |
| reference the final resting place or joint OM/W3C document here. | |
We will now detail the MathML3 Content Dictionary format, on an abstract level and discuss the special case of the MathML Recommendation CDs. Note that the latter are not the only possible ones, any individual or group can set up and publish CDs for the purposes of communication.
8.2 MathML3 Content Dictionaries Infrastructure and Metadata
MathML uses the namespace URI http://www.w3.org/ns/mathml-cd for the
XML encoding of MathML content dictionaries. In the examples below, we will use the
namespace prefix mcd for visual disambiguation and assume that it is
bound to the URI above by the context of the example.
A MathML Content Dictionary consists of a set of symbol
declarations (see Section 8.3 Symbol Declarations) together with
administrative information about them. A MathML content dictionary is represented by
the mcd:mcd element. The first child of the mcd:mcd element is a
mcd:description element that contains a description of the collection of
symbols defined by the CD. The content of the mcd:description is ????.
| Issue mcd_text_format | wiki (member only) |
|---|---|
| Text Format for MathML CDs? | |
|
We need to fix a content model for text fields in MCDs. This should probably be some fragment of XHTML+MathML, most probably the inline content model |
|
| Resolution | None recorded |
Further administrative information about the CD as a whole is given by the
following required attributes of the mcd:mcd element.
-
The CD name is given in the
xml:idattribute. -
The revision date, i.e. the date of the last change to the Content Dictionary is specified in the
revision-date. Dates in MathML CDs are stored in the ISO-compliant format YYYY-MM-DD, e.g. 1966-02-03. For the MathML specification CDs the revision date is the date of the publication of the respective MathML recommendation. -
The review date, i.e. a date until which the content dictionary is guaranteed to remain unchanged is specified in the
review-dateattribute. -
The CD version number consists of a major and minor part, it is specified in the
versionattribute. For the MathML specification CDs, this is the version number of the respective MathML recommendation. -
The status of the CD is given in the
statusattribute. Its value is one of-
"official": i.e. approved by W3C as part of the MathML specification
-
experimental: under development and thus liable to change; -
private: used by a private group of users; -
obsolete: an obsolete Content Dictionary kept only for archival purposes.
-
-
The CD base is a URI which, when combined with the CD name, forms a unique identifier for the Content Dictionary. It may or may not refer to an actual location from which it can be retrieved. The CD base is specified by the
cdbaseattribute.
8.3 Symbol Declarations
| Editorial note: MiKo | |
| the material here still contains material that is just copied form OM-style abstract content, it will be reworked into a description of the MathML3 CD format soon. dictionaries. | |
MathML Content Dictionaries use the mcd:MMLdefinition element for symbol
declarations. This element carries a mandatory name attribute that
specifies the name of the declared symbol. Its value is an XML1.1 name
[xml11]. The role of the symbol is specified in the
optional role attribute (see Section 8.5 Symbol Roles for details and
values. The syntactic and semantic properties symbol are given by the following
specialized elements in the body of the mcd:MMLdefinition element:
-
A short description of the symbol. It can be accompanied by a
discussion, which can be as formal or informal as the author likes. These are given asdescriptionanddiscussionelements whose content are ???. -
A mandatory default rendering specification given in the form of a
mcd:notationelement (see Section 8.6 Rendering of Content Elements for details). -
Zero or more attribute specifications for the case, where the MathML token takes attributes.
Editorial note: MiKo specify this -
Zero or more signature declarations for type information (see Section 8.4 Type Declarations for details).
-
Zero or more commented mathematical properties which are mathematical properties of the symbol expressed in a human-readable way.
-
Zero or more properties which are mathematical properties of the symbol. A property can be expressed in natural language and as a MathML expression tree in the same property. The former is directly aimed at human readers, and the latter could be used for validation or evaluation in mathematical software systems.
property may be given an optional kind attribute. An author of a Content Dictionary may use this to indicate whether, for example, the property provides an algorithm for evaluation of the concept it is associated with. At present no fixed scheme is mandated for how this information should be encoded or used by an application.
-
Zero or more mathematical examples which are intended to demonstrate the use of the symbol within a content MathML expression tree.
8.4 Type Declarations
| Editorial note: MiKo | |
copy parts of the types note here, develop
signature declarations for all symbols in the CDs, and make mathmltypes
and STS CDs.
|
|
8.5 Symbol Roles
We say that a symbol is used to construct an MathML expression tree
if it is the first child of an apply, bind or error
element. The role of a symbol is a restriction on how it may be used to
construct a compound expression tree and, in the case of the key in an attribution
object, a clarification of how that attribution should be interpreted. The possible
roles are:
-
binder The symbol may appear as the first child of a
bindelement. -
application The symbol may appear as the first child of an
applyelement. -
constant The symbol cannot be used to construct a compound expression tree.
-
error The symbol may appear as the first child of a
errorelement.
| Issue mathml_roles | wiki (member only) |
|---|---|
| More Roles for MathML? | |
|
Those are the roles in OpenMath. Do we need more in MathML? We could have one
for constructor (so that we know that it is a container element in legacy
markup)... That could later be mapped to application. But maybe this would be
better done by the |
|
| Resolution | None recorded |
A symbol cannot have more than one role and cannot be used to construct a compound expression tree object in a way which requires a different role (using the definition of construct given earlier in this section). This means that one cannot use a symbol which binds some variables to construct, say, an application object. However it does not prevent the use of that symbol as an argument in an application object (where by argument we mean a child with index greater than 1).
If no role is indicated then the symbol can be used anywhere. Note that this is not the same as saying that the symbol's role is constant.
8.6 Rendering of Content Elements
While the primary role of the MathML content element set is to directly encode the mathematical structure of expressions independent of the notation used to present the objects, rendering issues cannot be ignored. Therefore it is important that content MathML have a native infrastructure for specifying notations for content symbols. These specifications can be used either directly as a parameter to a generic rendering process that can thus adapt to extensible mathematical vocabularies or to inform the implementation of specialized rendering processes for restricted vocabularies.
As notations are tied to content symbols, content dictionaries seem like a natural
place: a generic rendering process can look up notation definitions in the CD specified
in the csymbol element; a specialized rendering procedure can delimit it's area
of applicability by the CDs it covers (e.e. the MathML3 CDs). As mathematical notation
is highly variable even for fundamental concepts, CDs can only contain (sets of) of
default notation specifications that can be overridden e.g. by user
preferences. The MathML3 specification does not specify any mechanism for building
generic or specialized rendering processors, or for selecting the relevant notations in
a given context. Instead we specify a function from content MathML expressions to
presentation MathML expressions that takes a list of notation specifications as an
input. We will call this function the MathML3 rendering function, even
though strictly speaking its values are presentation MathML expressions that have to be
rendered by a MathML-aware processor to be rendered for visual or aural consumption.
Note that the mechanism of notation specifications can directly be transferred for generating renderings or representations in other target formats. In fact it can even be reversed to be a source of information for interpretation procedures.
In the rest of the section we will specify the format of notation specifications and then define the MathML3 rendering function based on this.
8.6.1 Notation Specifications
MathML specifies notations using a template-based mechanism. In essence, a notation specification is a pair consisting of schematic content MathML expression (called the prototype) together with a schematic presentation MathML expression (called the rendering). Schematic MathML expressions are expressions that can contain metavariables, and thus stand for a set of MathML expressions. A prototype/rendering pair directly specifies a correspondence between a set of content MathML expressions (those that match the prototype) and presentation MathML expressions (the result of instantiating the metavariables in the rendering with the pMathML expressions corresponding to the values of the matcher). Consider, for instance the following prototype/rendering pair:
<apply> <mrow> <csymbol cd="algebra_logic" name="minus"/> <mcd:render name="left"/> <mcd:expr name="left"/> <mo>-</mo> <mcd:expr name="right"/> <mcd:render name="right"/> </apply> </mrow>
This specifies that any application expression whose first child is a
"minus" symbol will correspond to an mrow with an infix
"-" operator. The meta-variables in the prototype are represented by
expr elements and by mcd:render elements in the rendering, they correspond if
they share the value of the name attribute. Thus the content MathML expression
<apply><csymbol cd="algebra_logic" name="minus"/><cn>2</cn><cn>1</cn></apply>
corresponds to the presentation MathML expression
<mrow><mn>2</cn><mo>-</moL<mn>1</mn></mrow>
assuming a suitable correspondence for numbers.
MathML3 uses four elements for representing metavariables, i.e. named variables that
stand for arbitrary MathML expression trees or tree lists: expr,
exprlist, mcd:render, and iterate. The first two are called
content metavariables and the latter two rendering
metavariables. The expr and mcd:render elements are called
element metavariables and stand for single MathML expressions, while the
exprlist iterate elements are called sequence metavariables
and stand for possibly empty sequences of MathML expressions. Content metavariables stand
for (lists of) cMathML expressions whereas rendering metavariables stand for (lists of)
pMathML expressions. Finally, we call a MathML expression schematic, if it
contains one or more metavariables.
All metavariables carry the required name attribute, whose value is an XML
name. The expr el is empty, and the exprlist can contain an arbitrary
schematic cMathML expression. The mcd:rendering element contains an arbitrary
sequence of schematic pMathML expressions. The iterate element carries the
optional reverse attribute, whose values can be "yes" and
"no". The body of the iterate element consists of a
separator element arbitrary sequence of schematic pMathML expressions. Finally,
the content of the separator element is a arbitrary sequence of schematic pMathML
expressions.
Prototypes and renderings are represented by the mcd:prototype and
mcd:rendering elements in notation specification. The former contains schematic
content MathML expression with input metavariables, and the latter contains a schematic
presentation MathML expression with rendering metavariables. A prototype may not contain
two sibling exprlist elements and no two content metavariables may have the same
name attribute. The mcd:prototype element carries the optional
priority attribute whose value is a natural number; if the attribute is
missing, the priority of the prototype defaults to 0. The mcd:rendering
element carries the optional xml:lang, context, and
variant attributes. The values of the xml:lang attribute are ISO 639
language specifiers. The values of the context and variant attribute
are currently not specified and left to applications.
Intuitively, a cMathML expression E matches a prototype
P, iff there is a mapping σ from metavariables in P
to (lists of) cMathML expressions, such that if σ is applied to
P, then the result is E. The formal definition of matching schematic
content MathML expressions below is somewhat more complicated, since we need to take
sequence metavariables into account, and the semantics elements have a built-in
notion of flattening. For given E and P, we know that if
E matches P, then σ is unique; it is called the
matcher for E and P.
Let σ be a mapping from metavariable names to lists of MathML expressions. We say that a sequence E of cMathML expressions matches a sequence of prototypes P via σ, iff one of the following holds
-
P is a single
exprmetavariable with name n and σ(n)=E -
P and E are flattened
semanticselements, P' and E', their first children and the Q=Q(1) ... Q(n) and C=C(1)...C(n+k) are the sequences of thoseannotation-xmlchildren of P and E whose keys have the role "semantic-annotation", sorted lexicographically via theircdbasecd, andnameattributes. Then E matches P via σ, iff Q(i) match C(i+k) for 1⋜i⋜n, and<semantics>E' C(1) ... C(k-1)</semantics>matches P' σ. -
P and E are single elements that have the same name, and the attributes of P is a subset of those of E and their values coincide, and the sequence of children of E matches that of P via σ.
-
P and E are sequences of the form P(1) ... P(n) and E(1) ... E(m) and
-
none of the Pi is a sequence metavariable and n=m and
-
all the E(i) match P(i) via σ.
-
-
P and E are sequences of the form P(1) ... P(n) and E(1) ... E(m) and
-
P(j) is a
exprlistelement with name ν for some 1⋜j⋜n (thus none of the P(i) are by the no-sibling-constraint above). -
E(i) match P(i) via σ for i<j.
-
E(n-i) match P(m-i) via σ for 1⋜i<n-j.
-
σ(ν)=E(j) ... E(m-j)
-
P(j) has children C=C(1) ... C(l) and m-n=kl
-
σ(ν) matches the sequence given by the k-fold concatenation of C with itself via σ.
-
For given prototype P and expression E, we know that there is at most one mapping σ such that E matches P via σ.
A notation element usually occurs as part of a MMLdefinition element
for its top symbol (i.e. the highest token or csymbol in the pattern expression
trees). If it appears in some other context (e.g. as part of a user's notation preferences
file), then it should reference the top symbol via the cd, name, and
possibly cdbase attributes to ensure that it can be found by the rendering
process.
For representation conciseness and manageability, MathML3 groups prototypes and
renderings in notation elements. We call a list of mcd:rendering elements in
a notation element a rendering block, iff it is delimited by
mcd:prototype elements or the end tag of the notation element itself. No two
mcd:rendering elements in a rendering block may have the same values for all three of
the xml:lang, context, and variant attributes. We say
that a cMathML expression selects the rendering block following the prototype
with the highest priority among those that it matches.
Multiple mcd:prototype elements can be used e.g. to make a notation specification
applicable to both strict and pragmatic cMathML expressions e.g. by adding a prototype
involving the element <plus/> element. Multiple mcd:rendering
elements in a rendering block can be used to model different notations or language
conventions; they are differentiated by their xml:lang, context, and
variant attributes. The xml:lang and context attributes
allows to select a rendering variant via a global context. The former by language context
to enable multilingual rendering. The selection mechanism of the context
attribute is currently unspecified and left to applications. The variant
attribute allows to select a notation variant locally on a cMathML element via its
variant attribute. If a content element carries a class attribute
and matches one of the prototypes of a notation element, then the mcd:rendering
element whose variant attribute value has the same value will be chosen for
rendering. (see Section 8.6.4 General Rules)
The intended meaning of a notation element is that a cMathML expression
corresponds to that rendering in the selected rendering block that is suitable in the
current context.
| Issue style-selector | wiki (member only) |
|---|---|
| Style Selector Specified? | |
|
We could have a possibility to re-use the selector language of CSS 2.1, which is big but well accepted, or we could have a possibility to restrict to style class-names (as described above). Both would offer some predictability for authors. |
|
| Resolution | None recorded |
A simple example is provided below, it describes the notations for the open real interval in English and other languages:
<notation cd="basic_content_elements" name="interval-oo">
<mcd:prototype>
<apply><interval type="open"/>
<mcd:expr name="a"/>
<mcd:expr name="b"/>
</apply>
</mcd:prototype>
<mcd:prototype>
<apply>
<csymbol cd="basic_content_elements" name="interval-oo"/>
<mcd:expr name="a"/>
<mcd:expr name="b"/>
</apply>
</mcd:prototype>
<mcd:rendering xml:lang="en">
<math>
<mrow>
<mo>(</mo><mcd:render name="a"/><mo>,</mo><mcd:render name="b"/><mo>)</mo>
</mrow>
</math>
</mcd:rendering>
<mcd:rendering>
<math>
<mrow>
<mo>]</mo><mcd:render name="a"/><mo>,</mo><mcd:render name="b"/><mo>[</mo>
</mrow>
</math>
</mcd:rendering>
</notation>The cMathML expression
<apply> <interval type="open"/> <apply><minus/><ci>n</ci><ci>ε</ci></apply> <apply><plus/><ci>n</ci><ci>ε</ci></apply> </math>
matches the first prototype in the notation specification above. The matcher
σ maps <arg name="a"/> to
<apply><minus/><ci>n</ci><ci>ε</ci></apply> and <arg
name="b"/> to
<apply><minus/><ci>n</ci><ci>ε</ci></apply>. In a French language
environment, the second mcd:rendering is selected, since the English notation in
the first target does not apply. Therefore the cMathML expression renders to
<mrow><mo>]</mo><mrow>a-ε</mrow><mo>,</mo><mrow>a+ε</mrow><mo>[</mo></mrow>
assuming suitable notation specifications for plus and minus elements.
Multiple notation specifications per symbol are explicitly allowed, they can be used e.g. when writing a notation specification for the derivative which would be presented differently if applied on a simple function or a function defined using the lambda binding which indicates explicitly the variable of derivation. Thus the following notation specification with two rendering blocks is used:
<notation cd="calculus_veccalc" name="diff">
<mcd:prototype>
<apply>
<csymbol cd="calculus_veccalc" name="diff"/>
<bind>
<csymbol name="basic_content_elements" name="lambda"/>
<bvar><mcd:expr name="x"/></<bvar>
<mcd:expr name="f"/>
</bind>
</apply>
</mcd:prototype>
<mcd:rendering>
<mfrac>
<mrow><mo>d</mo><mcd:render name="f"/></mrow>
<mrow><mod>d</mod><mcd:render name="x"/></mrow>
</mfrac>
</mcd:rendering>
<mcd:prototype>
<apply>
<csymbol cd="calculus_veccalc" name="diff"/>
<mcd:expr name="f"/>
</apply>
</mcd:prototype>
<mcd:rendering><mrow><mcd:render name="f"/><mo>'</mo></mrow></mcd:rendering>
</notation>Many operations take an arbitrary number of arguments. These are modeled using
schematic MathML expressions containing the exprlist metavariable, which matches a
list of cMathML expressions in a prototype. In a mcd:rendering element, an
exprlist element can contain arbitrary pMathML content. Consider for instance the
notation specification for addition:
<notation cd="algebra_logic" name="plus">
<mcd:prototype>
<apply>
<plus/>
<mcd:exprlist name="summands">
<mcd:expr name="sumand"/>
</mcd:exprlist>
</apply>
</mcd:prototype>
<mcd:rendering>
<mcd:iterate name="summands">
<separator><mo>+</mo></separator>
<render name="summand"/>
</iterate>
</mcd:rendering>
</notation>If we apply this notation specification to the cMathML expression
<apply><plus/><ci>a</ci><ci>b</ci><ci>c</ci></apply>
then the metavariable summands matches the list
<ci>a</ci><ci>b</ci><ci>c</ci>. In this situation, rendering of
the corresponding exprlist is the list of rendered elements interleaved by the
content of the exprlist. In our case we obtain
<mi>a</mi><mo>+</mo><mi>b</mi><mo>+</mo><mi>c</mi>
| Editorial note: MiKo | |
| The following examples might be material for the primer though | |
To further fortify our intuition, let us consider a complex example. We want to render a content representation of a multiple integral expression e.g.:
<bind>
<apply><int/><ci>P</ci><ci>Q</ci><ci>R</ci></apply>
<bvar><ci>x</ci><ci>y</ci><ci>z</ci></bvar>
<condition>
<apply><and/>
<apply><gt/><ci>x</ci><cn>1</cn></apply>
<apply><gt/><ci>y</ci><cn>0</cn></apply>
<apply><gt/><ci>z</ci><cn>-1</cn></apply>
</apply>
</condition>
<apply><plus/>
<ci>x</ci>
<apply><times/>
<cn>2</cn>
<apply><power/><ci>y</ci><cn>2</cn></apply>
</apply>
<apply><times/>
<cn>3</cn>
<apply><power/><ci>z</ci><cn>3</cn></apply>
</apply>
</apply>
</bind>The intended rendering
<mrow>
<mtable rowalign="center">
<mtr><mo>∫<!--INTEGRAL-->∫<!--INTEGRAL-->∫<!--INTEGRAL--></mo></mtr>
<mtr><mi>P</mi><mi>Q</mi><mi>R</mi></mtr>
<mrow>
<mrow><mi>x</mi><mo>><!--GREATER-THAN SIGN--></mo><mn>1</mn></mrow>
<mo>∧<!--LOGICAL AND--></mo>
<mrow><mi>y</mi><mo>><!--GREATER-THAN SIGN--></mo><mn>0</mn></mrow>
<mo>∧<!--LOGICAL AND--></mo>
<mrow><mi>z</mi><mo>><!--GREATER-THAN SIGN--></mo><mn>-1</mn></mrow>
</mrow>
</mtable>
<mrow>
<mi>x</mi>
<mo>+</mo>
<mrow><mn>2</mn><mo>⁢<!--INVISIBLE TIMES--></mo><msup><mi>y</mi><mn>2</mn></msup></mrow>
<mo>+</mo>
<mrow><mn>3</mn><mo>⁢<!--INVISIBLE TIMES--></mo><msup><mi>z</mi><mn>3</mn></msup></mrow>
</mrow>
<mrow><mo>d</mo><mi>x</mi><mo>d</mo><mi>y</mi><mo>d</mo><mi>z</mi></mrow>
</mrow>can be obtained with the following notation specification:
<notation for="int">
<mcd:prototype>
<bind>
<apply><int/>
<mcd:exprlist name="sets"><mcd:expr name="set"/></mcd:exprlist>
</apply>
<bvar>
<mcd:exprlist name="bvars"><mcd:expr name="bvar"/></mcd:exprlist>
</bvar>
<condition><mcd:expr="cond"/></condition>
<mcd:expr name="scope"/>
</bind>
</mcd:prototype>
<mcd:rendering>
<mrow>
<mtable rowalign="center">
<mtr><mo><iterate name="sets"><separator>∫<!--INTEGRAL--></separator></iterate></mo></mtr>
<mtr>
<iterate name="sets">
<separator><mo>×<!--MULTIPLICATION SIGN--></mo></separator>
<mcd:render name="set"/>
</iterate>
</mtr>
<mcd:render name="cond"/>
</mtable>
<mcd:render name="scope"/>
<iterate name="bvars"><mo>d</mo><mcd:render name="bvar"/></iterate>
</mrow>
</mcd:rendering>
</notation>
Note that the prototype picks up the structural backbone of the integral expression in the
mcd:prototype element, and introduces metavariables for the variable parts of
integral expressions. While matching the example, the meta variable sets is
bound to the list P, Q, R of sets that are integrated
over. This list is used twice in the rendering: once for generating the three integral
glyphs in the integration operator (here we do not have a mcd:render element so the
sets themselves are not rendered) and once in the cartesian product under the integration
operator. The list of bound variables is picked up in the end of the rendering to generate
the dx dy dz postfix.
The final example shows the use of non-empty exprlist metavariables
<mcd:notation>
<mcd:prototype>
<bind>
<apply mcd:cr="multint"><int/>
<mcd:exprlist name="domains">
<apply>
<interval mcd:cr="int"/>
<mcd:expr name="lower_bound"/>
<mcd:expr name="upper_bound"/>
</apply>
</mcd:exprlist>
</apply>
<bvars>
<mcd:exprlist name="variables"><mcd:expr name="var"/></mcd:exprlist>
</bvars>
<condition><mcd:expr name="condition"/></condition>
<mcd:expr name="body"/>
</bind>
</mcd:prototype>
<mcd:rendering>
<mrow>
<msub mcd:cr="multint">
<mrow>
<mcd:iterate name="domains">
<msubsup>
<mo mcd:cr="int">∫<!--INTEGRAL--></mo>
<mcd:render name="lower_bound"/>
<mcd:render name="upper_bound"/>
</msubsup>
</mcd:iterate>
</mrow>
<mcd:render name="condition"/>
</msub>
<mcd:render name="body"/>
<mcd:iterate name="variables" reverse="yes">
<mo>d</mo>
<mcd:render name="var"/>
</mcd:iterate>
</mrow>
</mcd:rendering>
<mcd:notation>This notation renders the cMathML expression
<bind>
<apply><int/>
<apply><interval/><ci>a</ci><ci>b</ci></apply>
<apply><interval/><ci>c</ci><ci>d</ci></apply>
</apply>
<bvars><ci>x</ci><ci>y</ci></bvars>
<condition><apply><gt/><ci>x</ci><ci>y</ci></apply></condition>
<apply><ci>f</ci><ci>x</ci><ci>y</ci></apply>
</bind>as
<mrow>
<msub>
<mrow>
<msubsup><mo>∫<!--INTEGRAL--></mo><mi>a</mi><mi>b</mi></msubsup>
<msubsup><mo>∫<!--INTEGRAL--></mo><mi>c</mi><mi>d</mi></msubsup>
</mrow>
<mrow><mi>x</mi><mo>><!--GREATER-THAN SIGN--></mo><mi>y</mi></mrow>
</msub>
<mrow><mi>f</mi><mo>(</mo><mi>x</mi><mi>y</mi><mo>)</mo></mrow>
<mo>d</mo><mi>y</mi>
<mo>d</mo><mi>x</mi>
</mrow>
Note that the matcher here consists of two mappings, one binds the top-level metavariables
domain, variables, condition, and
body, and the second one is indexed by the sequence variable
domain and binds the metavariables lower_bound and
upper_bound in its scope. The latter two can only be used in the rendering
inside the iterate element that renders domains.
8.6.2 Precedence-based Elisions
In content MathML expressions, the function/argument relation is fully specified by the prefix notation in expression trees. In traditional mathematical notation, operator placement is much less restricted and brackets are used sparingly to disambiguate the functional structure. However, the use of brackets is usually restricted to cases, where the functional structure cannot be derived from the two-dimensional structure of the notations and conventions about binding strength of operators. This distribution of brackets has to be re-created to obtain high-quality renderings for cMathML expressions, and therefore the binding strengths have to be modeled in notation specifications.
To account for this MathML3 add an precedence attributes to the
mcd:rendering element (to specify the the operator precedence) and the
mcd:render and iterate elements (to specify the the argument
precedence). The value of this attribute is an integer or +∞ or
-∞. If the precedence attribute is not present on a
mcd:rendering element, its operator precedence the default value 0. If the
precedence attribute is not present on a mcd:render or iterate
element the respective argument precedence is the same as the operator precedence.
The operator precedence allows rendering agents to decide on fencing the constructed rendering. Intuitively operators with larger precedence bind more strongly, so need not be fenced. Correspondingly, the rendering of an expression is enclosed in fences, iff the operator precedence is greater than the current precedence. For the next level of rendering this is set to the respective argument precedence of the rendering metavariable that triggers the recursive rendering. For top-level formulae renderings the current precedence has the default value 0. This ensures that outer brackets are usually elided, since most operators have positive operator precedence.
In MathML, fences are considered as a special case of semantic components that are
subject to elision, i.e. components that can be left out of the presentation
in certain situations. Even though brackets are the prime examples other components of
mathematical formulae, e.g. bases of logarithms, are also commonly elided, if they can be
derived from the context with little effort. In MathML, a component of a rendering is
marked to be elidable by adding the mcd:egroup attribute. This attribute
specifies the elision group. MathML reserves the
values "fence" and "separator" for fences and separators in
correpsondence to the attributes fence and separator (see
Section 3.2.5 Operator, Fence, Separator or Accent
(mo)). In a situation, where the current precedence is c
and the operator precedence of the fence (i.e. the value of the precedence
attribute on the
notation element that contains it) is o, then the fence is given a
visibility level of o-c (we take ∞-∞ to
be ∞ to make fences visible for safety in this degenerate
case). Rendering applications can specify other elision groups and give elidable
components an explicit visibility level as integers using the mcd:elevel
attribute. If none is given it defaults to the value 0.
Elision can take various forms in print and digital media. In static media like traditional print on paper or the PostScript format, we have to fix the elision level, and can decide at presentation time which elidable tokens will be printed and which will not. In this case, the presentation algorithm will take visibility thresholds T(g) for every elision group g as a user parameter and then elide (i.e. not render) all tokens in visibility group g with level l>T(g).
In an output format that is capable of interactively changing its appearance, e.g. dynamic XHTML+MathML (i.e. XHTML with embedded Presentation MathML formulae, which can be manipulated via JavaScript in browsers), an application can export the the information about elision groups and levels to the target format, and can then dynamically change the visibility thresholds by user interaction.
For example, the following notation element could be used for the factorial
operator:
<notation cd="algebra-logic" name="factorial">
<mcd:prototype>
<apply><factorial/><mcd:expr name="arg"/></apply>
</mcd:prototype>
<mcd:rendering precedence="500">
<mrow>
<mo mcd:egroup="fence">(</mo>
<mcd:render name="arg"/>
<mo mcd:egroup="fence">)</mo>
<mo>!</mo>
</mrow>
</mcd:rendering>
</notation>In a situation with a current precedence (c) of 800 and a threshold T(fence)=0 the following cMathML expression
<apply> <csymbol cd="algebra-logic" name="#factorial"/> <apply><csymbol cd="algebra-logic" name="plus"/><ci>x</ci><ci>y</ci></apply> </apply>
would be rendered by a static renderer as
<mrow>
<mo>(</mo>
<mrow><mi>x</mi><mo>+</mo><mi>y</mi></mrow>
<mo>)</mo>
<mo>!</mo>
</mrow>assuming an operator precedence of 100 for the addition operator (the argument precedences do not matter here, since identifiers are never fenced): 500-800=-300<0, so the outer fences are elided, and 500-100=400>0, so the factorial fences are rendered. In a situation with a smaller current precedence e.g. 400, the outer fences would be rendered as well.
A dynamic renderer would pass the computed visibility levels to the rendering. In our situation with a current precedence of 800 we would obtain
<mo mcd:egroup="fence" mcd:elevel="-300">(</mo>
<mrow>
<mo mcd:egroup="fence" mcd:elevel="400">(</mo>
<mrow><mi>x</mi><mo>+</mo><mi>y</mi></mrow>
<mo mcd:egroup="fence" mcd:elevel="400">)</mo>
<mo>!</mo>
</mrow>
<mo mcd:egroup="fence" mcd:elevel="-300">)</mo>Thus for a fencing threshold of 0 we would get the same result. With a user-given threshold larger than 400 (only components of a high visibility level are not elided) all fences would be elided, and with a threshold smaller than -300, all brackets would be made visible.
The requirement to have operator and argument precedences is probably most clearly seen in the case of binary associative operators we would use the following notation specification:
<notation cd="binary" name="plus">
<mcd:prototype>
<apply><csymbol cd="binary" name="plus"/>
<mcd:expr name="left"/>
<mcd:expr name="right"/>
</apply>
</mcd:prototype>
<mcd:rendering precedence="500">
<mrow mcd:egroup="fence">
<mo mcd:egroup="fence">(</mo>
<mcd:render name="left" precedence="501"/>
<mo>+</mo>
<mcd:render name="right" precedence="501"/>
<mo mcd:egroup="fence">)</mo>
</mrow mcd:egroup="fence">
</mcd:rendering>
</notation>In fact the content MathML expression
<apply><csymbol cd="binary" name="plus"/>
<apply><csymbol cd="binary" name="plus"/>
<ci>x</ci>
<ci>y</ci>
</apply>
<apply><csymbol cd="binary" name="plus"/>
<ci>z</ci>
<ci>w</ci>
</apply>
</apply>would be rendered as
<mrow> <mi>x</mi> <mo>+</mo> <mi>y</mi> <mo>+</mo> <mi>z</mi> <mo>+</mo> <mi>w</mi> </mrow>
Left- or right-associative binary operators (i.e. operators like the function space constructor that only elide parentheses in one of their arguments) are simply constructed by decreasing only one of their argument precedences.
8.6.3 Rendering Cross-References for Parallel Markup
The metavariable correspondence in notation elements is a good source for
crossreferences in parallel markup with crossreferences (see Section 5.5.2 Parallel Markup via Cross-References: xml:id and xref): If the rendering application constructs parallel markup, then it can
crossreference the top-level elements in corresponding prototype and
rendering elements, as well as the metavariables that have the name value of
the name element. If this is not enough, then additional crossreferencing
opportunities can be specified by adding mcd:cr attributes with equal values
to corresponding elements in the prototypes and renderings in a notation
declaration. For instance, in above example
we add cross-references for the multiple integral operator
and for the integrals operators it is made up of. Note that mcd:cr attributes
can be added to all MathML elements, but their values have to be unique in any
prototype and rendering elements.
8.6.4 General Rules
In this section we will specify the default rendering of cMathML expressions that do not match any of the notation definitions given to the rendering function. The default renderings of pragmatic content MathML are given by the default rendering of the corresponding strict ones. We will go over the cases for strict MathML expressions in turn:
8.6.4.1 Numbers
The default rendering of a simple cn-tagged object is the same as for
the presentation element mn with some provision for overriding the
presentation of the PCDATA by providing explicit mn tags. This is
described in detail in Section 4.2.3 Numbers.
8.6.4.2 Symbols and Identifiers
If the content of a ci or csymbol element is tagged using
presentation tags, that presentation is used. If no such tagging is supplied then
the PCDATA content is rendered as if it were the content
of an mi element. In particular if an application supports bidirectional
text rendering, then the rendering follows the Unicode bidirectional rendering.
8.6.4.3 Applications
If F is the rendering of f and Ai those of ai, then the default rendering of an application element of the form
<apply>f a1 ... an</apply>
is
<mrow>
F
<mo mcd:egroup="fence" fence="true">(</mo>
A1
<mo mcd:egroup="separator" separator="true">,</mo>
...
<mo mcd:egroup="separator" separator="true">,</mo>
An
<mo mcd:egroup="fence" fence="true">)</mo>
</mrow>This general rule could also be expressed by the following notation definition:
<mcd:notation>
<mcd:prototype>
<apply>
<mcd:expr name="fun"/>
<mcd:exprlist name="args"><mcd:expr name="arg"/></mcd:exprlist>
</apply>
<mcd:prototype>
<mcd:rendering>
<mrow>
<mcd:render name="fun"/>
<mo fence="true">(</mo>
<mcd:iterate name="args"/>
<mcd:separator><mo separator="true">,</mo></mcd:separator>
<mcd:render name="arg"/>
</mcd:iterate>
<mo fence="true">)</mo>
</mrow>
<mcd:rendering>
</mcd:notation>8.6.4.4 Binders
If b, c, xi, c, and s render to B, C, Xi, C, and S, then the default rendering of a binding element of the form
<bind>b<bvar>x1 ... xn</bvar>C S</bind>
is
<mrow> B x1 <mo mcd:egroup="separator" separator="true">,</mo> ... <mo mcd:egroup="separator" separator="true">,</mo> xn <mo mcd:egroup="separator" separator="true">:</mo> C <mo mcd:egroup="separator" separator="true">.</mo> S </mrow>
If the condition is not present, then the fragment
<mo mcd:egroup="separator" separator="true">:</mo>C
is omitted from the rendering.
This general rule could also be expressed by the following notation definition:
<mcd:notation>
<mcd:prototype>
<bind>
<mcd:expr name="bex"/>
<bvar><exprlist name="bvars"><expr name="bvar"/></mcd:exprlist>
<condition><mcd:expr name="condition"/></condition>
<mcd:expr name="body"/>
</bind>
<mcd:prototype>
<mcd:rendering>
<mrow>
<mcd:render name="bex"/>
<mcd:iterate name="bvars"/>
<mcd:separator><mo mcd:egroup="separator" separator="true">,</mo></mcd:separator>
<mcd:render name="bvar"/>
</mcd:iterate>
<mo mcd:egroup="separator" separator="true">:</mo>
<mcd:render name="condition"/>
<mo mcd:egroup="separator" separator="true">.</mo>
<mcd:render name="body"/>
</mrow>
<mcd:rendering>
<mcd:prototype>
<mcd:expr name="bex"/>
<bvar><exprlist name="bvars"><expr name="bvar"/></mcd:exprlist>
<mcd:expr name="body"/>
</bind>
<mcd:prototype>
<mcd:rendering>
<mrow>
<mcd:render name="bex"/>
<mcd:iterate name="bvars"/>
<mcd:separator><mo mcd:egroup="separator" separator="true">,</mo></mcd:separator>
<mcd:render name="bvar"/>
</mcd:iterate>
<mo mcd:egroup="separator" separator="true">.</mo>
<mcd:render name="body"/>
</mrow>
<mcd:rendering>
</mcd:notation>8.6.4.5 Attributions
The default rendering of a semantics element is the default rendering of
its first child: the annotation and annotation-xml are not
rendered. When a MathML-presentation annotation is provided, a MathML renderer may
optionally use this information to render the MathML construct. This would typically
be the case when the first child is a MathML content construct and the annotation is
provided to give a preferred rendering differing from the default for the content
elements.
8.6.5 Limitations and Extensions of Notation Documents
The elements proposed in this section provide a basis for exchangeable notation-documents which can be processed by rendering agents for the conversion of content-elements, to presentation MathML.
There is a great wealth of conversion tools from content to presentation. Compared to
hand-written XSLT stylesheets, such as ctop.xsl (TODO: quote), the expression matching is
quite poor and the programming facilities are almost nonexistent (thus it seems not
possible, yet, to specify that the 7 in 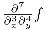 is computed
automatically), the approach of notation-documents is more declarative and opens the door
to exchangeability, moreover, it has the potential to respect user and language-dependent
notations.
is computed
automatically), the approach of notation-documents is more declarative and opens the door
to exchangeability, moreover, it has the potential to respect user and language-dependent
notations.
For the many more dynamic rendering agents, which includes all content-oriented input-editors, notation-documents may be a good way to render dynamically symbols just found on the web.