
RDF Semantics
W3C Recommendation 10 February 2004
PRE-PUBLICATION DRAFT. This document is being prepared for
possible publication by the W3C, but it may change, be
delayed, or never be published. The "Version" URIs and
"Status of this Document" section may reflect its
planned location and status, not present reality.
- This Version:
- http://www.w3.org/2001/sw/RDFCore/TR/WD-rdf-mt-20030117/
- Latest Version:
- http://www.w3.org/TR/rdf-mt/
- Previous Version:
- http://www.w3.org/TR/2003/PR-rdf-mt-20031215/
- Editor:
- Patrick Hayes (IHMC)<
phayes@ihmc.us>
- Series Editor
- Brian McBride (Hewlett
Packard Labs)<bwm@hplb.hpl.hp.com>
Please refer to the errata
for this document, which may include some normative corrections.
See also translations.
Copyright
© 2004 W3C®
(MIT,
ERCIM, Keio),
All Rights Reserved. W3C
liability,
trademark, document
use and software
licensing rules apply.
Abstract
This is a specification of a precise semantics, and
corresponding complete systems of inference rules, for the Resource Description
Framework (RDF) and RDF Schema (RDFS).
Table of Contents
0. Introduction
0.1 Specifying a formal semantics: scope and limitations
0.2 Graph Syntax
0.3 Graph Definitions
1. Interpretations
1.1 Technical Note (Informative)
1.2 URI references, Resources and Literals
1.3 Interpretations
1.4 Denotations of Ground Graphs
1.5 Blank nodes as Existential variables
2. Simple Entailment between RDF graphs
2.1 Vocabulary interpretations and vocabulary entailment
3. Interpreting the RDF vocabulary
3.1 RDF Interpretations
3.2 RDF Entailment
3.3 Reification, Containers, Collections and rdf:value
3.3.1 Reification
3.3.2 RDF Containers
3.3.3 RDF Collections
3.3.4 rdf:value
4. Interpreting the RDFS Vocabulary
4.1 RDFS Interpretations
4.2 Extensional Semantic Conditions (Informative)
4.3 A Note on rdfs:Literal
4.4 RDFS Entailment
5. Interpreting Datatypes
5.1 Datatyped Interpretations
5.2 D-Entailment
6. Monotonicity of Semantic Extensions
7. Entailment Rules (Informative)
7.1 Simple Entailment Rules
7.2 RDF Entailment Rules
7.3 RDFS Entailment Rules
7.3.1 Extensional Entailment Rules
7.4 Datatype Entailment Rules
Appendix A. Proofs of lemmas (Informative)
Appendix B. Glossary (Informative)
Appendix C. Acknowledgements
References
Appendix D. Change Log (Informative)
RDF is an assertional language intended to be used to express propositions using precise formal
vocabularies, particularly those specified using RDFS [RDF-VOCABULARY],
for access and use over the World Wide Web, and is intended to provide a basic
foundation for more advanced assertional languages with a similar purpose. The
overall design goals emphasise generality and precision in expressing propositions
about any topic, rather than conformity to any particular processing model:
see the RDF Concepts document [RDF-CONCEPTS] for more discussion.
Exactly what is considered to be the 'meaning' of an assertion in RDF or RDFS in some
broad sense may depend on many factors, including social conventions, comments
in natural language or links to other content-bearing documents. Much of this
meaning will be inaccessible to machine processing and is mentioned here only
to emphasize that the formal semantics described in this document is not intended to
provide a full analysis of 'meaning' in this broad sense; that would be a large
research topic. The semantics given here restricts itself to a formal notion of meaning which could be characterized
as the part that is common to all other accounts of meaning, and can be captured
in mechanical inference rules.
This document uses a basic technique called model theory for specifying the semantics of a formal
language. Readers unfamiliar with model theory may find the glossary
in appendix B helpful; throughout the text, uses of terms in a technical sense
are linked to their glossary definitions. Model theory assumes that the language
refers to a 'world', and describes the minimal conditions that a world
must satisfy in order to assign an appropriate meaning for every expression
in the language. A particular world is called an interpretation, so that
model theory might be better
called 'interpretation theory'. The idea is to provide an abstract, mathematical
account of the properties that any such interpretation must have, making as
few assumptions as possible about its actual nature or intrinsic structure,
thereby retaining as much generality as possible. The chief utility of a formal
semantic theory is not to provide any deep analysis of the nature of the things
being described by the language or to suggest any particular processing model,
but rather to provide a technical way to determine when inference processes
are valid, i.e. when they preserve truth. This provides the
maximal freedom for implementations while preserving a globally coherent notion
of meaning.
Model theory tries to be metaphysically and ontologically neutral. It is typically couched in the
language of set theory simply because that is the normal language of mathematics
- for example, this semantics assumes that names denote things in a set
IR called the 'universe' - but the use of set-theoretic
language here is not supposed to imply that the things in the universe are set-theoretic
in nature. Model theory is usually most relevant to implementation via the notion
of entailment, described later, which
makes it possible to define valid inference rules.
An alternative way to specify a semantics is to give a translation from RDF
into a formal logic with a model
theory already attached, as it were. This 'axiomatic semantics' approach
has been suggested and used previously with various alternative versions of
the target logical language [Conen&Klapsing] [Marchiori&Saarela] [McGuinness&al]. Such a translation
for RDF and RDFS is also given in the Lbase specification [LBASE].
The axiomatic semantics style has some advantages for machine processing and
may be more readable, but in the event that any axiomatic semantics fails to
conform to the model-theoretic semantics described in this document, the model
theory should be taken as normative.
There are several aspects of meaning in RDF which are ignored by this semantics;
in particular, it treats URI references as simple names, ignoring aspects of
meaning encoded in particular URI forms [RFC 2396]
and does not provide any analysis of time-varying data or of changes to URI
references. It does not provide any analysis of indexical uses of URI references, for example to mean
'this document'. Some parts of the RDF and RDFS vocabularies are not assigned
any formal meaning, and in some cases, notably the reification and container
vocabularies, it assigns less meaning than one might expect. These cases are
noted in the text and the limitations discussed in more detail. RDF is an assertional
logic, in which each triple expresses a simple proposition.
This imposes a fairly strict monotonic discipline on the language, so that it cannot
express closed-world assumptions, local default preferences, and several other
commonly used non-monotonic constructs.
Particular uses
of RDF, including as a basis for more expressive languages such as DAML+OIL
[DAML] and OWL [OWL], may impose further semantic conditions in
addition to those described here, and such extra semantic conditions can also
be imposed on the meanings of terms in particular RDF vocabularies.
Extensions or dialects of RDF which are obtained by imposing such extra semantic
conditions may be referred to as semantic extensions of RDF. Semantic
extensions of RDF are constrained in this recommendation using the keywords
MUST , MUST
NOT, SHOULD
and MAY of
[RFC 2119]. Semantic extensions of RDF
MUST conform
to the semantic conditions for simple interpretations described in sections
1.3 and 1.4 and 1.5 and those
for RDF interpretations described in section 3.1 of
this document. Any name for entailment in a semantic extension SHOULD
be indicated by the use of a vocabulary
entailment term. The semantic conditions imposed on an RDF semantic extension
MUST define
a notion of vocabulary entailment
which is valid according to the model-theoretic semantics described
in the normative parts of this document; except that if the semantic extension
is defined on some syntactically restricted subset of RDF
graphs, then the semantic conditions need only apply to this subset. Specifications
of such syntactically restricted semantic extensions MUST
include a specification of their syntactic conditions which are sufficient to
enable software to distinguish unambiguously those RDF
graphs to which the extended semantic conditions apply. Applications based
on such syntactically restricted semantic extensions MAY
treat RDF graphs which do not conform
to the required syntactic restrictions as syntax errors.
An example of a semantic extension of RDF is RDF Schema [RDF-VOCABULARY],
abbreviated as RDFS, the semantics of which are defined in later parts of this
document. RDF Schema imposes no extra syntactic restrictions.
Any semantic theory must be attached to a syntax. This semantics is defined
as a mapping on the abstract
syntax of RDF described in the RDF concepts and abstract syntax document
[RDF-CONCEPTS]. This document uses
the following terminology defined there: URI
reference,
literal, plain
literal, typed
literal, XML
literal,
XML value, node,
blank
node, triple
and RDF
graph. Throughout this document we use the term 'character string'
or 'string' to refer to a sequence of Unicode characters, and 'language tag'
in the sense of RFC 3066, c.f. section
6.5 in [RDF-CONCEPTS]. Note
that strings in an RDF graph SHOULD
be in Normal Form C.
This document uses the N-Triples syntax described
in the RDF test cases document [RDF-TESTS]
to describe RDF graphs. This notation
uses a node identifier (nodeID)
convention to indicate blank nodes in the triples of a graph. While node identifiers such as '_:xxx'
serve to identify blank nodes in the surface syntax, these expressions are not
considered to be the label of the graph node they identify; they are not names,
and do not occur in the actual graph. In particular, the RDF
graphs described by two N-Triples documents
which differ only by re-naming their node identifiers will be understood to
be equivalent
. This re-naming convention should be
understood as applying only to whole documents, since re-naming the node identifiers
in part of a document may result in a document describing a different RDF
graph.
The N-Triples syntax requires that URI references be given in full,
enclosed in angle brackets. In the interests of brevity, the
imaginary URI scheme 'ex:' is used to provide illustrative examples. To
obtain a more realistic view of the normal appearance of the
N-Triples syntax, the reader should imagine this replaced with
something like 'http://www.example.org/rdf/mt/artificial-example/'.
The QName prefixes
rdf:, rdfs: and xsd: are defined
as follows:
Prefix rdf: namespace URI:
http://www.w3.org/1999/02/22-rdf-syntax-ns#
Prefix rdfs: namespace URI:
http://www.w3.org/2000/01/rdf-schema#
Prefix xsd: namespace URI:
http://www.w3.org/2001/XMLSchema#
Since QName syntax is not legal N-Triples syntax, and in the
interests of brevity and readability, examples use the convention
whereby a QName is used without surrounding angle brackets to
indicate the corresponding URI reference enclosed in angle brackets, e.g.
the triple
<ex:a> rdf:type rdfs:Class .
should be read as an abbreviation for the N-Triples syntax
<ex:a>
<http://www.w3.org/1999/02/22-rdf-syntax-ns#type>
<http://www.w3.org/2000/01/rdf-schema#Class> .
In stating general semantic conditions, single characters
or character sequences without a colon indicate an arbitrary name, blank node,
character string and so on. The exact meaning will be specified in context.
An RDF
graph, or simply a graph, is a set of RDF triples.
A subgraph of an RDF graph is a subset
of the triples in the graph. A triple is identified with the singleton set
containing it, so that each triple in a graph is considered to be a subgraph.
A proper subgraph is a proper subset of the triples in the graph.
A ground RDF graph is one with no blank
nodes.
A name is a URI reference or a literal.
These are the expressions that need to be assigned a meaning by an interpretation. Note that a typed literal comprises
two names: itself and its internal type
URI reference.
A set of names
is referred to as a vocabulary. The vocabulary of a graph is
the set of names which occur as the subject, predicate or object of any triple
in the graph. Note that URI references which occur only inside typed literals
are not required to be in the vocabulary of the graph.
Suppose that M is a mapping from a set of blank
nodes to some set of literals, blank nodes and URI references; then any graph obtained
from a graph G by replacing some or all of the blank nodes N in G by M(N) is
an instance of G. Note that any graph is an instance of itself,
an instance of an instance of G is an instance of G,
and if H is an instance of G then every triple in H is an instance of some triple
in G.
An instance with respect to a vocabulary
V is an instance in which all the
names in the instance that were substituted
for blank nodes in the original are names
from V.
A proper instance of a graph
is an instance in which a blank node has been replaced by a name, or two blank
nodes in the graph have been mapped into the same node in the instance.
Any instance of a graph in which a blank node is mapped to a new blank node
not in the original graph is an instance of the original and also has it as
an instance, and this process can be iterated so that any 1:1 mapping between
blank nodes defines an instance of a graph which has the original graph as an
instance. Two such graphs, each an instance of the other but neither a proper
instance, which differ only in the identity of their blank nodes, are considered
to be equivalent.
We will treat such equivalent graphs as identical; this allows us to ignore
some issues which arise from 're-naming' nodeIDs, and is in conformance with
the convention that blank nodes have
no label. Equivalent graphs are mutual instances with an invertible instance
mapping.
An RDF graph is lean if it has no instance which is
a proper subgraph of the graph. Non-lean graphs have internal redundancy
and express the same content as their lean subgraphs. For example, the graph
<ex:a> <ex:p> _:x .
_:y <ex:p> _:x .
is not lean, but
<ex:a> <ex:p> _:x .
_:x <ex:p> _:x .
is lean.
A
merge of a set of RDF graphs is defined as follows. If the graphs in
the set have no blank nodes in common, then the union of the graphs is a merge;
if they do share blank nodes, then it is the union of a set of graphs that is
obtained by replacing the graphs in the set by equivalent graphs that share
no blank nodes. This is often described by saying that the blank nodes have
been 'standardized apart'. It
is easy to see that any two merges are equivalent, so we will refer to the
merge, following the convention on equivalent graphs.
Using the convention on equivalent graphs and identity, any graph in the original
set is considered to be a subgraph of the merge.
One does not, in general, obtain the merge of a set of graphs by concatenating
their corresponding N-Triples documents
and constructing the graph described by the merged document. If some of the
documents use the same node identifiers, the merged document will describe a
graph in which some of the blank nodes have been 'accidentally' identified.
To merge N-Triples documents
it is necessary to check if the same nodeID is used in two or more documents,
and to replace it with a distinct nodeID in each of them, before merging the
documents. Similar cautions apply to merging graphs described by RDF/XML documents
which contain nodeIDs, see RDF/XML
Syntax Specification (Revised) [RDF-SYNTAX].
RDF does not impose any logical restrictions on the domains and ranges of properties;
in particular, a property may be applied to itself. When classes
are introduced in RDFS, they may contain themselves. Such 'membership loops'
might seem to violate the axiom of foundation, one of the axioms of standard
(Zermelo-Fraenkel) set theory, which forbids infinitely descending chains of
membership. However, the semantic model given here distinguishes properties
and classes considered as objects from their extensions - the sets of object-value pairs which satisfy
the property, or things that are 'in' the class - thereby allowing the extension
of a property or class to contain the property or class itself without violating
the axiom of foundation. In particular, this use of a class extension mapping
allows classes to contain themselves. For example, it is quite OK for (the extension
of) a 'universal' class to contain the class itself as a member, a convention
that is often adopted at the top of a classification hierarchy. (If an extension
contained itself then the axiom would be violated, but that case never arises.)
The technique is described more fully in [Hayes&Menzel].
In this respect, RDFS differs from many conventional ontology frameworks such
as UML which assume a more structured hierarchy of individuals, sets of individuals,
etc., or which draw a sharp distinction between data and meta-data. However,
while RDFS does not assume the existence of such structure, it does not prohibit
it. RDF allows membership loops, but it does not mandate their use for all parts
of a user vocabulary. If this aspect of RDFS is found worrying, then it is possible
to restrict oneself to a subset of RDF graphs which do not contain any such
'loops' of class membership or property application while retaining much of
the expressive power of RDFS for many practical purposes, and semantic
extensions may impose syntactic conditions which forbid such looped constructions.
The use of the explicit extension mapping also makes it possible for two properties
to have exactly the same values, or two classes to contain the same instances,
and still be distinct entities. This means that RDFS classes can be considered
to be rather more than simple sets; they can be thought of as 'classifications'
or 'concepts' which have a robust notion of identity which goes beyond a simple
extensional correspondence. This property of the model
theory has significant consequences in more expressive languages built on
top of RDF, such as OWL [OWL], which are capable of expressing identity
between properties and classes directly. This 'intensional'
nature of classes and properties is sometimes claimed to be a useful property
of a descriptive language, but a full discussion of this issue is beyond the
scope of this document.
Notice that the question of whether or not a class contains itself as a member is quite different
from the question of whether or not it is a subclass of itself. All classes are subclasses of themselves.
Readers who are familiar with conventional logical semantics may find it useful
to think of RDF as a version of existential binary relational logic in which
relations are first-class entities in the universe of quantification. Such a
logic can be obtained by encoding the relational atom R(a,b) into a conventional
logical syntax, using a notional three-place relation Triple(a,R,b); the basic
semantics described here can be reconstructed from this intuition by defining
the extension of y as the set {<x,z> : Triple(x,y,z)} and noting that
this would be precisely the denotation of R in the conventional Tarskian model
theory of the original form R(a,b) of the relational atom. This construction
can also be traced in the semantics of the Lbase axiomatic description
[LBASE].
This document does not take any position on the way that URI references
may be composed from other expressions, e.g. from relative URIs or QNames;
the semantics simply assumes that such lexical issues have been
resolved in some way that is globally coherent, so that a single
URI reference can be taken to have the same meaning wherever it occurs.
Similarly, the semantics has no special provision for tracking
temporal changes. It assumes, implicitly, that URI references have the
same meaning whenever they occur. To provide an adequate
semantics which would be sensitive to temporal changes is a
research problem which is beyond the scope of this document.
The semantics does not assume any particular relationship
between the denotation of a URI reference and a document or Web
resource which can be retrieved by using that URI reference in an HTTP
transfer protocol, or any entity which is considered to be the
source of such documents. Such a requirement could be added as a
semantic extension, but the formal semantics described here makes
no assumptions about any connection between the denotations of
URI references and the uses of those URI references in other protocols.
The semantics treats all RDF names
as expressions which denote. The things denoted are called 'resources', following
[RFC 2396], but no assumptions are made here about
the nature of resources; 'resource' is treated here as synonymous with
'entity', i.e. as a generic term for anything in the
universe of discourse.
The different syntactic forms of names
are treated in particular ways. URI references are treated simply as logical
constants. Plain literals are considered to denote themselves, so have a fixed
meaning. The denotation of a typed literal is the value mapped from its enclosed
character string by the datatype associated with its enclosed type. RDF assigns
a particular meaning to literals typed with rdf:XMLLiteral, described
in section 3.
The basic intuition of model-theoretic semantics is that asserting a sentence
makes a claim about the world: it is another way of saying that the world is,
in fact, so arranged as to be an interpretation which makes
the sentence true. In other words, an assertion amounts to stating a constraint
on the possible ways the world might be. Notice that there is no presumption
here that any assertion contains enough information to specify a single unique
interpretation. It is usually impossible to assert enough in any language to
completely constrain the interpretations to a single possible world, so there
is no such thing as 'the' unique interpretation of an RDF graph.
In general, the larger an RDF graph is - the more it says about the world -
then the smaller the set of interpretations that an assertion of the graph allows to be true - the fewer the
ways the world could be, while making the asserted graph true of it.
The following definition of an interpretation is couched in
mathematical language, but what it amounts to intuitively is that
an interpretation provides just enough information about a possible
way the world might be - a 'possible world' - in order to fix the
truth-value (true or false) of any ground RDF triple. It does this
by specifying for each URI reference, what it is supposed to be a name of;
and also, if it is used to indicate a property, what values that
property has for each thing in the universe; and if it is used to indicate a
datatype, that the datatype defines a mapping between
lexical forms and datatype values. This is just enough information
to fix the truth-value of any ground triple, and hence any ground RDF
graph. (Non-ground
graphs are considered in the following section.) Note that if any of
this information were omitted, it would be possible for some well-formed triple to
be left without a determinate value; and also that any other
information - such as the exact nature of the things in the universe - would,
regardless of its intrinsic interest, be irrelevant to the actual
truth-values of any triple.
All interpretations will be relative to a set of names,
called the vocabulary of the interpretation; so that one should speak, strictly,
of an interpretation of an RDF vocabulary, rather than of RDF itself. Some interpretations
may assign special meanings to the symbols in a particular vocabulary. Interpretations
which share the special meaning of a particular vocabulary will be named for
that vocabulary, e.g. 'rdf-interpretations',
'rdfs-interpretations', etc. An
interpretation with no particular extra conditions on a vocabulary (including
the RDF vocabulary itself) will be called a simple interpretation, or
simply an interpretation.
RDF uses several forms of literal. The chief semantic characteristic of literals
is that their meaning is largely determined by the form of the string they contain.
Plain literals, without an embedded type URI reference, are always interpreted
as referring to themselves: either a character string or a pair consisting of
a character string and a language
tag; in either case, the character string is referred to as the "literal
character string". In the case of typed literals, however, the full specification
of the meaning depends on being able to access datatype
information which is external to RDF itself. A full discussion of the meaning
of typed literals is described in section 5 , where
a special notion of datatype interpretation is introduced. Each interpretation
defines a mapping IL from typed literals to their interpretations. Stronger
conditions on IL will be defined as the notion of 'interpretation' is extended
in later sections.
Throughout this document, precise semantic conditions will be set out in tables
which state semantic conditions, tables containing true assertions and valid inference rules, and tables listing syntax, which
are distinguished by background color. These tables, taken together, amount
to a formal summary of the entire semantics. Note that the semantics of RDF
does not depend on that of RDFS. The full semantics of RDF is defined in sections
1 and 3 ; the full semantics
of RDFS in sections 1, 3 and
4.
Definition of a simple interpretation.
A simple interpretation I of a vocabulary V is
defined by:
1. A non-empty set IR of resources, called the domain or universe
of I.
2. A set IP, called the set of properties of I.
3. A mapping IEXT from IP into the powerset of IR x IR i.e. the
set of sets of pairs <x,y> with x and y in IR .
4. A mapping IS from URI references in V into (IR union IP)
5. A mapping IL from typed literals in V into IR.
6. A distinguished subset LV of IR, called the set of literal values,
which contains all the plain literals in V |
IEXT(x), called
the extension of x, is a
set of pairs which identify the arguments for which the property is true,
that is, a binary
relational extension.
This trick of distinguishing a relation as an object from its
relational extension allows a property to occur in its own
extension, as noted earlier.
The assumption that LV is a subset of IR amounts to saying that literal values
are thought of as real entities that 'exist'. This amounts to saying that literal
values are resources. However, this does not imply that literals should be identified
with URI references. Note that LV may contain other items in addition to plain
literals. There is a technical reason why the range of IL is IR rather than
restricted to LV. When interpretations take account of datatype
information, it is syntactically possible for a typed literal to be internally
inconsistent, and such ill-typed literals are required to denote a non-literal
value, as explained in section
5.
The next sections define how an interpretation of a vocabulary determines the
truth-values of any RDF graph, by a recursive definition of the denotation -
the semantic "value" - of any RDF expression in terms of those of its immediate
subexpressions. These apply to all subsequent semantic extensions. RDF has two
kinds of denotation: names denote things
in the universe, and sets of triples denote truth-values.
The denotation of a ground RDF graph in I is given recursively by the following
rules, which extend the interpretation mapping I from names
to ground graphs. These rules (and extensions of them given later) work by defining
the denotation of any piece of RDF syntax E in terms of the denotations of the
immediate syntactic constituents of E, hence allowing the denotation of any
piece of RDF to be determined by a kind of syntactic recursion.
In this table, and throughout this document, the equality sign = indicates
identity and angle brackets <x,y> are used to indicate an ordered pair
of x and y. RDF graph syntax is indicated using the notational conventions of
the N-Triples syntax described
in the RDF test cases document [RDF-TESTS]:
literal strings are encloded within double quote marks, language tags indicated
by the use of the @ sign, and triples terminate with a 'code dot'
. .
Semantic conditions for ground graphs.
| if E is a plain literal "aaa" in V
then I(E) = aaa |
if E is a plain literal "aaa"@ttt
in V then I(E) = <aaa, ttt> |
| if E is a typed literal in V then I(E) = IL(E) |
| if E is a URI reference in V then I(E) = IS(E) |
if E is a ground triple s p o.
then I(E) = true if
s, p and o are in V, I(p) is in IP and <I(s),I(o)>
is in IEXT(I(p))
otherwise I(E)= false. |
| if E is a ground RDF graph then I(E) = false if I(E') =
false for some triple E' in E, otherwise I(E) =true. |
If the vocabulary of an RDF graph contains names that are not in the vocabulary
of an interpretation I - that is, if I simply does not give a semantic value
to some name that is used in the graph
- then these truth-conditions will always yield the value false for some triple
in the graph, and hence for the graph itself. Turned around, this means that
any assertion of a graph implicitly asserts that all the names
in the graph actually refer to something in the world. The final condition implies
that an empty graph (an empty set of triples) is trivially true.
Note that the denotation of plain literals is always in LV; and that
those of the subject and object of any true triple must be in IR; so any URI
reference which occurs in a graph both as a predicate and as a subject or object
must denote something in the intersection of IR and IP in any interpretation
which satisfies the graph.
As an illustrative example, the following is a small interpretation for the
artificial vocabulary {ex:a, ex:b, ex:c,
"whatever", "whatever"^^ex:b}.
Integers are used to indicate the non-literal 'things' in the universe. This
is not meant to imply that interpretations should be interpreted as being about
arithmetic, but more to emphasize that the exact nature of the things in the
universe is irrelevant. LV can be any set satisfying the semantic conditions.
(In this and subsequent examples the greater-than and less-than symbols are
used in several ways: following mathematical usage to indicate abstract pairs
and n-tuples; following N-Triples syntax to enclose URI references, and also
as arrowheads when indicating mappings.)
IR = LV union{1, 2}
IP={1}
IEXT: 1=>{<1,2>,<2,1>}
IS: ex:a=>1, ex:b=>1, ex:c=>2
IL: "whatever"^^ex:b =>2
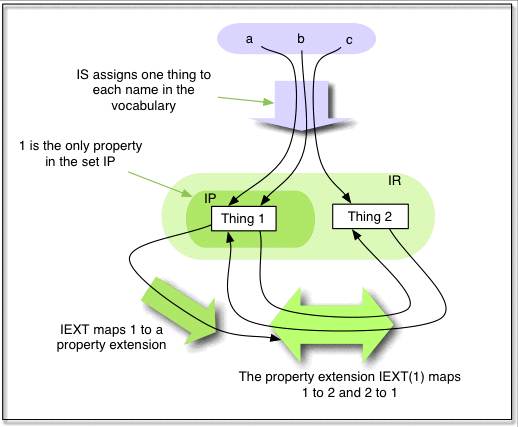
Figure 1: An example of an interpretation. Note, this is
not a picture of an RDF graph.
The figure does not show the infinite number of members of
LV.
This interpretation makes these triples true:
<ex:a> <ex:b> <ex:c>
.
<ex:c> <ex:a> <ex:a>
.
<ex:c> <ex:b> <ex:a>
.
<ex:a> <ex:b>
"whatever"^^<ex:b> .
For example, I(<ex:a> <ex:b> <ex:c>
.) = true if
<I(ex:a),I(ex:c)> is in
IEXT(I(<ex:b>)), i.e. if <1,2> is in
IEXT(1), which is {<1,2>,<2,1>} and so does contain
<1,2> and so I(<ex:a <ex:b> ex:c>)
is true.
The truth of the fourth triple is a consequence of the rather
idiosyncratic interpretation chosen here for typed literals.
In this interpretation IP is a subset of IR; this will be typical of RDF semantic
interpretations, but is not required.
It makes these triples false:
<ex:a> <ex:c> <ex:b>
.
<ex:a> <ex:b> <ex:b>
.
<ex:c> <ex:a> <ex:c>
.
<ex:a> <ex:b> "whatever"
.
For example, I(<ex:a> <ex:c> <ex:b> .) = true
if <I(ex:a), I(<ex:b>)>, i.e.<1,1>,
is in IEXT(I(ex:c)); but I(ex:c)=2 which is not in
IP, so IEXT is not defined on 2, so the condition fails and I(<ex:a>
<ex:c> <ex:b> .) = false.
It also makes all triples containing a plain literal false, since the property
extension does not have any pairs containing a plain literal.
To emphasize; this is only one possible interpretation of this vocabulary;
there are (infinitely) many others. For example, if this interpretation were
modified by attaching the property extension to 2 instead of 1, none of the
above triples would be true.
This example illustrates that any interpretation which maps any URI reference
which occurs in the predicate position of a triple in a graph to something not
in IP will make the graph false.
Blank nodes are treated as simply indicating the existence of a thing, without
using, or saying anything about, the name of that thing. (This is not the same
as assuming that the blank node indicates an 'unknown' URI reference; for example,
it does not assume that there is any URI reference which refers to the thing.
The discussion of Skolemization in appendix
A is relevant to this point.)
An interpretation can specify the truth-value of a graph containing blank nodes.
This will require some definitions, as the theory so far provides no meaning
for blank nodes. Suppose I is an interpretation and A is a mapping from some
set of blank nodes to the universe IR of I, and define I+A to be an extended
interpretation which is like I except that it uses A to give the interpretation
of blank nodes. Define blank(E) to be the set of blank nodes in E. Then the
above rules can be extended to include the two new cases that are introduced
when blank nodes occur in the graph:
Semantic conditions for blank nodes.
| If E is a blank node and A(E) is defined then
[I+A](E) = A(E) |
| If E is an RDF graph then I(E) = true if [I+A'](E) =
true for some mapping A' from blank(E) to IR, otherwise
I(E)= false. |
Notice that this does not change the definition of an interpretation;
it still consists of the same values IR, IP, IEXT, IS, LV and IL. It simply
extends the rules for defining denotations under an interpretation, so that
the same interpretation that provides a truth-value for ground graphs also assigns
truth-values to graphs with blank nodes, even though it provides no denotation
for the blank nodes themselves. Notice also that the blank nodes themselves
are perfectly well-defined entities; they differ from other nodes only in not
being assigned a denotation by an interpretation, reflecting the intuition that
they have no 'global' meaning (i.e. outside the graph in which they occur).
For example, the graph defined
by the following triples is false in the interpretation shown in figure 1:
_:xxx <ex:a> <ex:b> .
<ex:c> <ex:b> _:xxx .
since if A' maps the blank node to 1 then the first triple is
false in I+A', and if it maps it to 2 then the second triple is
false.
Note that each of these triples, if thought of as a single
graph, would be true in I, but the whole graph is not; and that if
a different nodeID were used in the two triples, indicating that
the RDF graph had two blank nodes instead of one, then A' could map
one node to 2 and the other to 1, and the resulting graph would be
true under the interpretation I.
This effectively treats all blank nodes as having the same meaning as existentially
quantified variables in the RDF graph in which they occur, and which have the
scope of the entire graph. In terms of the N-Triples syntax, this amounts to
the convention that would place the quantifiers just outside, or at the outer
edge of, the N-Triples document corresponding to the graph. This in turn means
that there is a subtle but important distinction in meaning between the operation
of forming the union of two graphs and that of forming the merge.
The simple union of two graphs corresponds to the conjunction ( 'and' ) of all
the triples in the graphs, maintaining the identity of any blank nodes which
occur in both graphs. This is appropriate when the information in the graphs
comes from a single source, or where one is derived from the other by means
of some valid inference process, as for example when applying
an inference rule to add a triple to a graph. Merging two graphs treats the
blank nodes in each graph as being existentially quantified in that graph,
so that no blank node from one graph is allowed to stray into the scope of the
other graph's surrounding quantifier. This is appropriate when the graphs come
from different sources and there is no justification for assuming that a blank
node in one refers to the same entity as any blank node in the other.
Following conventional terminology, I satisfies E if I(E)=true, and a set
S of RDF graphs (simply) entails a graph E if every interpretation
which satisfies every member of S also satisfies E. In later sections these
notions will be adapted to other classes of interpretations, but throughout
this section 'entailment' should be interpreted as meaning simple entailment.
Entailment is the key idea which connects model-theoretic
semantics to real-world applications. As noted earlier, making an
assertion amounts to claiming that the world is an interpretation
which assigns the value true to the assertion. If A entails B, then
any interpretation that makes A true also makes B true, so that an
assertion of A already contains the same "meaning" as an assertion
of B; one could say that the meaning of B is somehow contained in,
or subsumed by, that of A. If A and B entail each other, then they
both "mean" the same thing, in the sense that asserting either of
them makes the same claim about the world. The interest of this
observation arises most vividly when A and B are different
expressions, since then the relation of entailment is exactly the
appropriate semantic license to justify an application inferring or
generating one of them from the other. Through the notions of
satisfaction, entailment and validity, formal semantics gives a
rigorous definition to a notion of "meaning" that can be related
directly to computable methods of determining whether or not
meaning is preserved by some transformation on a representation of
knowledge.
Any process which constructs a
graph E from some other graph(s) S is said to be (simply)
valid if S entails E in every case,
otherwise invalid. Note
that being an invalid process does not mean that the conclusion is
false, and being valid does not guarantee truth. However, validity
represents the best guarantee that any assertional language can
offer: if given true inputs, it will never draw a false conclusion
from them.
This section gives a few basic results about simple entailment and valid inference. Simple entailment can be recognized by relatively
simple syntactic comparisons. The two basic forms of simply valid inference
in RDF are, in logical terms, the inference from (P and Q) to P, and the inference
from foo(baz) to (exists (?x) foo(?x)).
These results apply only to simple entailment, not to the extended notions
of entailment introduced in later sections. Proofs, all of which are straightforward,
are given in appendix A, which also describes some other
properties of entailment which may be of interest.
Empty Graph Lemma. The empty set of triples is entailed by
any graph, and does not entail any graph except itself. [Proof]
Subgraph Lemma. A graph
entails all its subgraphs. [Proof]
Instance Lemma. A graph
is entailed by any of its instances.[Proof]
The relationship between merging and entailment is simple,
and obvious from the definitions:
Merging lemma. The merge
of a set S of RDF graphs is entailed by S, and entails every member of S. [Proof]
This means that a set of graphs can be treated as equivalent to its
merge, i.e. a single graph, as far as the model theory is
concerned. This can
be used to simplify the terminology somewhat: for example, the definition
of
S entails E, above, can be paraphrased by saying that S entails E when every
interpretation which satisfies S also
satisfies E.
The example given in section 1.5 shows that it is not the case, in general,
that the simple union of a set of graphs is entailed by the set.
The main result for simple RDF inference is:
Interpolation Lemma.
S entails a graph E if and only if a subgraph of S is an instance of E.[Proof]
The interpolation lemma completely characterizes simple RDF entailment in syntactic
terms. To tell whether a set of RDF graphs entails another, check that
there is some instance of the entailed graph which is a subset of the merge
of the original set of graphs. Of course, there is no need to actually
construct the merge. If working backwards from the consequent E, an efficient technique
would be to treat blank nodes as variables in a process of subgraph-matching,
allowing them to bind to 'matching' names
in the antecedent graph(s) in S, i.e. those which may entail
the consequent graph. The interpolation lemma shows that this
process is valid, and is also complete if the subgraph-matching algorithm is. The existence
of complete subgraph-checking algorithms also shows that
RDF entailment is decidable, i.e. there is a terminating algorithm which will
determine for any finite set S and any graph E, whether or not S entails E.
Such a variable-binding process would only be appropriate when applied to the
conclusion of a proposed entailment. This corresponds to using the
document as a goal or a query, in contrast to asserting it, i.e. claiming it
to be true. If an RDF document is asserted, then it would be invalid to bind
new values to any of its blank nodes, since the resulting graph might not be
entailed by the assertion.
The interpolation lemma has an immediate consequence a criterion for non-entailment:
Anonymity lemma. Suppose
E is a lean graph and E' is a proper instance of E. Then E does
not entail E'.[Proof]
Note again that this applies only to simple entailment, not to the vocabulary
entailment relationships defined in rest of the document.
Several basic properties of entailment follow directly from the above definitions
and results but are stated here for completeness sake:
Monotonicity
Lemma. Suppose S is a subgraph of S' and S entails E. Then S' entails
E.[Proof]
The property of finite expressions always being derivable from a finite set
of antecedents is called compactness. Semantic theories which support
non-compact notions of entailment do not have corresponding computable inference
systems.
Compactness Lemma.
If S entails E and E is a finite graph, then some finite subset S' of S entails
E.
2.1
Vocabulary interpretations and vocabulary entailment
Simple interpretations and simple entailment capture the semantics of RDF
graphs when no attention is paid to the particular meaning of any of the names
in the graph. To obtain the full meaning of an RDF graph written using a particular
vocabulary, it is usually necessary to add further semantic conditions which
attach stronger meanings to particular URI references and typed literals in
the graph. Interpretations which are required to satisfy extra semantic conditions
on a particular vocabulary will be generically referred to as vocabulary
interpretations. Vocabulary entailment means entailment with respect to
such vocabulary interpretations. These stronger notions of interpretation and
entailment are indicated by the use of a namespace prefix, so that we will refer
to rdf-entailment, rdfs-entailment and so on in what follows.
In each case, the vocabulary whose meaning is being restricted, and the exact
conditions associated with that vocabulary, are spelled out in detail.
The RDF vocabulary, rdfV, is a
set of URI references in the rdf: namespace:
| RDF vocabulary |
rdf:type rdf:Property
rdf:XMLLiteral rdf:nil rdf:List rdf:Statement rdf:subject rdf:predicate
rdf:object rdf:first rdf:rest rdf:Seq rdf:Bag rdf:Alt rdf:_1 rdf:_2
... rdf:value |
rdf-interpretations
impose extra semantic conditions on rdfV
and on typed literals with the type rdf:XMLLiteral, which is
referred to as the RDF built-in datatype. This datatype is fully
described in the RDF
Concepts and Abstract Syntax document [RDF-CONCEPTS].
Any character string sss which satisfies the conditions for being
in the
lexical space of rdf:XMLLiteral will be called a well-typed
XML literal string. The corresponding value will be called the XML
value of the literal. Note that the XML values of well-typed XML
literals are in precise 1:1 correspondence with the XML literal strings of
such literals, but are not themselves character strings. An XML literal
whose literal string is well-typed will be called a well-typed XML literal;
other XML literals will be called ill-typed.
An rdf-interpretation
of a vocabulary V is a simple interpretation I of (V union rdfV)
which satisfies the extra conditions described in the following table
and all the triples in the subsequent table. These triples are called the rdf
axiomatic triples.
RDF semantic conditions.
x is
in IP if and only if <x, I(rdf:Property)> is in IEXT(I(rdf:type)) |
If
"xxx"^^rdf:XMLLiteral
is in V and xxx is a well-typed XML literal string, then
IL("xxx"^^rdf:XMLLiteral)
is the XML value of xxx;
IL("xxx"^^rdf:XMLLiteral)
is in LV;
IEXT(I(rdf:type)) contains <IL("xxx"^^rdf:XMLLiteral),
I(rdf:XMLLiteral)>
|
If
"xxx"^^rdf:XMLLiteral
is in V and xxx is an ill-typed XML literal string, then
IL("xxx"^^rdf:XMLLiteral)
is not in LV;
IEXT(I(rdf:type)) does not contain <IL("xxx"^^rdf:XMLLiteral),
I(rdf:XMLLiteral)>. |
The first condition could be regarded as defining IP to be the set of
resources in the universe of the interpretation which have the value I(rdf:Property)
of the property I(rdf:type). Such subsets of the universe will
be central in interpretations of RDFS. Note that this condition requires
IP to be a subset of IR. The third condition requires that ill-typed XML literals
denote something other than a literal value: this will be the standard way of
handling ill-formed typed literals.
RDF axiomatic triples.
rdf:type rdf:type rdf:Property .
rdf:subject rdf:type rdf:Property .
rdf:predicate rdf:type rdf:Property .
rdf:object rdf:type rdf:Property .
rdf:first rdf:type rdf:Property .
rdf:rest rdf:type rdf:Property .
rdf:value rdf:type rdf:Property .
rdf:_1 rdf:type rdf:Property .
rdf:_2 rdf:type rdf:Property .
...
rdf:nil rdf:type rdf:List . |
The rdfs-interpretations described
in section 4 below assign further semantic
conditions (range and domain conditions) to the properties used in the RDF
vocabulary, and other semantic extensions MAY
impose further conditions so as to further restrict their meanings, provided
that such conditions
MUST be compatible with the conditions described in this section.
For example, the following rdf-interpretation extends the simple interpretation
in figure 1 to the case where V contains rdfV.
For simplicity, we ignore XML literals in this example.
IR = LV union {1, 2, T , P}
IP = {1, T}
IEXT: 1=>{<1,2>,<2,1>},
T=>{<1,P>,<T,P>}
IS: ex:a=>1, ex:b=>1,
ex:c=> 2, rdf:type=>T,
rdf:Property=>P, rdf:nil=>1,
rdf:List=>P, rdf:Statement=>P,
rdf:subject=>1, rdf:predicate=>1, rdf:object=>1,
rdf:first=>1, rdf:rest=>1, rdf:Seq=>P,
rdf:Bag=>P, rdf:Alt=>P, rdf:_1, rdf:_2, ...
=>1
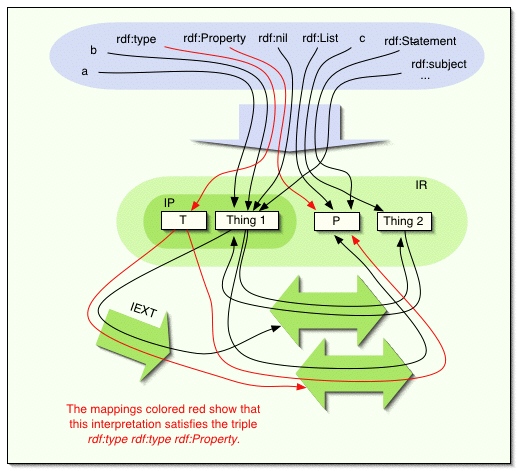
Figure 2: An rdf-interpretation.
This is not the smallest rdf-interpretation which extends the
earlier example, since one could have made
IEXT(T) be
{<1,2>,<T,2>}, and managed without having P in the
universe. In general, a given entity in an interpretation may play
several 'roles' at the same time, as long as this can be done
without violating any of the required semantic conditions. The
above interpretation identifies properties with lists, for example;
of course, other interpretations might not make such an
identification.
Every rdf-interpretation is also a simple interpretation. The 'extra' structure
does not prevent it acting in the simpler role.
3.2. RDF entailment
S rdf-entails E when every rdf-interpretation which satisfies every
member of S also satisfies E. This follows the wording of the definition of
simple entailment in
Section 2, but refers only to rdf-interpretations
instead of all simple interpretations. Rdf-entailment is an example of
vocabulary entailment.
It is easy to see that the lemmas in Section 2 do not all apply to rdf-entailment:
for example, the triple
rdf:type rdf:type rdf:Property .
is true in every rdf-interpretation, so is rdf-entailed by the empty graph,
contradicting the interpolation lemma for rdf-entailment. Section 7.2 describes
exact conditions for detecting RDF entailment.
The RDF semantic conditions impose significant formal constraints on the meaning
only of the central RDF vocabulary, so the notions of rdf-entailment and rdf-interpretation
apply to the remainder of the vocabulary without further change. This includes
vocabulary which is intended for use in describing containers and bounded collections,
and a reification vocabulary to enable an RDF graph to describe, as well as
exhibit, triples. In this section we review the intended meanings of this vocabulary,
and note some intuitive consequences which are not supported by the formal model theory. Semantic extensions
MAY limit the
formal interpretations of these vocabularies to conform to these intended meanings.
The omission of these conditions from the formal semantics is a design decision
to accomodate variations in existing RDF usage and to make it easier to implement
processes to check formal RDF entailment. For example, implementations may decide
to use special procedural techniques to implement the RDF collection vocabulary.
| RDF reification vocabulary |
rdf:Statement rdf:subject rdf:predicate
rdf:object |
Semantic extensions MAY limit the interpretation of these so
that a triple of the form
aaa rdf:type rdf:Statement .
is true in I just when I(aaa) is a token of an RDF triple in some RDF document,
and the three properties, when applied to such a denoted triple,
have the same values as the respective components of that
triple.
This may be illustrated by considering the following two RDF
graphs, the first of which consists of a single triple.
<ex:a> <ex:b> <ex:c> .
and
_:xxx rdf:type rdf:Statement .
_:xxx rdf:subject <ex:a> .
_:xxx rdf:predicate <ex:b> .
_:xxx rdf:object <ex:c> .
The second graph is called a reification of the triple in the first
graph, and the node which is intended to refer to the first triple
- the blank node in the second graph - is called, rather
confusingly, a reified triple. (This can be a blank node
or a URI reference.) In the intended interpretation of the reification
vocabulary, the second graph would be made true in an
interpretation I by interpreting the reified triple to refer to a
token of the triple in the first graph in some concrete RDF
document, considering that token to be valid RDF syntax, and then
using I to interpret the syntactic triple which the token
instantiates, so that the subject, predicate and object of that
triple are interpreted in the same way in the reification as in the
triple described by the reification. This could be stated formally
as follows: <x,y> is in IEXT(I(rdf:subject))
just when x is a token of an RDF triple of the form
aaa bbb ccc .
and y is I(aaa); similarly for predicate and object. Notice that
the value of the rdf:subject property is not the
subject URI reference itself but its interpretation, and so this condition
involves a two-stage interpretation process: one has to interpret
the reified node - the subject of the triples in the reification -
to refer to another triple, then treat that triple as RDF syntax
and apply the interpretation mapping again to get to the referent
of its subject. This requires triple tokens to exist as first-class
entities in the universe IR of an interpretation. In sum: the
meaning of the reification is that a document exists containing a
triple token which means whatever the first graph means.Note
that this way of understanding the reification vocabulary does not interpret
reification as a form of quotation. Rather, the reification describes the
relationship between a token of a triple and the resources that triple refers
to. The reification can be read intuitively as saying "'this piece of
RDF talks about these things" rather than "this piece of RDF has
this form".
The semantic extension described here requires
the reified triple that the reification describes -
I(_:xxx) in the above example - to be a particular token
or instance of a triple in a (real
or notional) RDF document, rather than an 'abstract' triple
considered as a grammatical form. There could be several such
entities which have the same subject, predicate and object
properties. Although a graph is defined as a set of triples,
several such tokens with the same triple structure might occur in
different documents. Thus, it would be meaningful to claim that the
blank node in the second graph above does not refer to the triple
in the first graph, but to some other triple with the same
structure. This particular interpretation of reification was chosen
on the basis of use cases where properties such as dates of
composition or provenance information have been applied to the
reified triple, which are meaningful only when thought of as
referring to a particular instance or token of a triple.
Although RDF applications may use reification to refer to triple tokens in
RDF documents, the connection between the document and its reification must
be maintained by some means external to the RDF graph
syntax. (In the RDF/XML syntax described in RDF/XML
Syntax Specification (Revised) [RDF-SYNTAX],
the rdf:ID attribute can be used in the description of a triple to create a
reification of that triple in which the reified triple is a URI constructed
from the baseURI of the XML document and the value of rdf:ID as a fragment.)
Since an assertion of a reification of a triple does not implicitly assert the
triple itself, this means that there are no entailment relationships
which hold between a triple and a reification of it. Thus the reification vocabulary
has no effective semantic constraints on it, other than those that apply to
an rdf-interpretation.
A reification of a triple does not entail the triple, and is not
entailed by it. (The
reification only says that the triple token exists and what it is about,
not that it is true. The second non-entailment is a consequence of the
fact
that asserting a triple does not automatically assert that any
triple tokens exist in the universe being described by the triple.
For example, the triple might be part of an ontology describing
animals, which could be satisfied by an interpretation in which the
universe contained only animals, and in which a reification of it was therefore
false.)
Since the relation between triples and reifications of triples
in any RDF graph or graphs need not be one-to-one, asserting a
property about some entity described by a reification need not
entail that the same property holds of another such entity, even if
it has the same components. For example,
_:xxx rdf:type rdf:Statement .
_:xxx rdf:subject <ex:subject> .
_:xxx rdf:predicate <ex:predicate> .
_:xxx rdf:object <ex:object> .
_:yyy rdf:type rdf:Statement .
_:yyy rdf:subject <ex:subject> .
_:yyy rdf:predicate <ex:predicate> .
_:yyy rdf:object <ex:object> .
_:xxx <ex:property> <ex:foo> .
does not entail
_:yyy <ex:property> <ex:foo> .
| RDF Container Vocabulary |
rdf:Seq rdf:Bag rdf:Alt rdf:_1 rdf:_2
... |
RDF provides vocabularies for describing three classes of
containers. Containers have a type, and their members can
be enumerated by using a fixed set of container membership
properties. These properties are indexed by integers to
provide a way to distinguish the members from each other, but these
indices should not necessarily be thought of as defining an
ordering of the container itself; some containers are considered to be unordered.
The RDFS vocabulary, described below, adds a generic membership
property which holds regardless of position, and classes containing
all the containers and all the membership properties.
One should understand this RDF vocabulary as describing
containers, rather than as a vocabulary for constructing them, as
would typically be supplied by a programming language. On this
view, the actual containers are entities in the semantic universe,
and RDF graphs which use the vocabulary simply provide very basic
information about these entities, enabling an RDF graph to
characterize the container type and give partial information about
the members of a container. Since the RDF container vocabulary is
so limited, many 'natural' assumptions concerning RDF containers
are not formally sanctioned by the RDF model theory. This should not be taken as
meaning that these assumptions are false, but only that RDF does
not formally entail that they must be true.
There are no special semantic conditions on the container
vocabulary: the only 'structure' which RDF presumes its containers
to have is what can be inferred from the use of this vocabulary and
the general RDF semantic conditions. In
general, this amounts to knowing the type of a container, and having a partial
enumeration
of the items in the container. The intended mode of use is that things
of type rdf:Bag
are considered to be unordered but to allow duplicates; things of
type rdf:Seq are considered to be ordered, and things
of type rdf:Alt are considered to represent a
collection of alternatives, possibly with a preference ordering.
The ordering of items in an ordered container is intended to be
indicated by the numerical ordering of the container membership
properties, which are assumed to be single-valued.
However, these informal interpretations are not reflected in any formal RDF
entailments.
RDF does not support any entailments which could arise from enumerating
the elements of an rdf:Bag in a different order. For example,
_:xxx rdf:type rdf:Bag .
_:xxx rdf:_1 <ex:a> .
_:xxx rdf:_2 <ex:b> .
does not entail
_:xxx rdf:_1 <ex:b> .
_:xxx rdf:_2 <ex:a> .
Notice that if this conclusion were valid, then the result of
conjoining it to the original graph would also be a valid
entailment, which would assert that both elements were in both
positions. This is a consequence of the fact that RDF is a purely
assertional language.
There is no assumption that a property of a container applies to
any of the elements of the container, or vice versa.
There is no formal requirement that
the three container classes are disjoint, so that for example
something can be asserted to be both an rdf:Bag and an rdf:Seq.
There is no assumption that containers are gap-free, so that for example
_:xxx rdf:type rdf:Seq.
_:xxx rdf:_1 <ex:a> .
_:xxx rdf:_3 <ex:c> .
does not entail
_:xxx rdf:_2 _:yyy .
There is no way in RDF to 'close' a container, i.e. to assert
that it contains only a fixed number of members. This is a
reflection of the fact that it is always consistent to add a triple
to a graph asserting a membership property of any container. And
finally, there is no built-in assumption that an RDF container has
only finitely many members.
3.3.3 RDF collections
| RDF Collection Vocabulary |
rdf:List rdf:first rdf:rest rdf:nil |
RDF provides a vocabulary for describing collections, i.e.'list
structures', in terms of head-tail links. Collections differ from
containers in allowing branching structure and in having an
explicit terminator, allowing applications to determine the exact
set of items in the collection.
As with containers, no special semantic conditions are imposed on this vocabulary
other than the type of rdf:nil being rdf:List. It
is intended for use typically in a context where a container is described using
blank nodes to connect a 'well-formed' sequence of items, each described by
two triples of the form
_:c1 rdf:first aaa .
_:c1 rdf:rest _:c2
where the final item is indicated by the use of rdf:nil as the
value of the property rdf:rest. In a familiar convention, rdf:nil
can be thought of as the empty collection. Any such graph amounts to an assertion
that the collection exists, and since the members of the collection can be determined
by inspection, this is often sufficient to enable applications to determine
what is meant. Note however that the semantics does not require any collections
to exist other than those mentioned explicitly in a graph (and the empty collection).
For example, the existence of a collection containing two items does not automatically
guarantee that the similar collection with the items permuted also exists:
_:c1 rdf:first <ex:aaa> .
_:c1 rdf:rest _:c2 .
_:c2 rdf:first <ex:bbb> .
_:c2 rdf:rest rdf:nil .
does not entail
_:c3 rdf:first <ex:bbb> .
_:c3 rdf:rest _:c4 .
_:c4 rdf:first <ex:aaa> .
_:c4 rdf:rest rdf:nil .
Also, RDF imposes no 'well-formedness' conditions on the use of this
vocabulary, so that it is possible to write RDF graphs which assert
the existence of highly peculiar objects such as lists with forked
or non-list tails, or multiple heads:
_:666 rdf:first <ex:aaa> .
_:666 rdf:first <ex:bbb> .
_:666 rdf:rest <ex:ccc> .
_:666 rdf:rest rdf:nil .
It is also possible to write a set of triples which underspecify a collection
by failing to specify its rdf:rest property value.
Semantic extensions MAY
place extra syntactic well-formedness restrictions on the use of this vocabulary
in order to rule out such graphs. They MAY
exclude interpretations of the collection vocabulary which violate the convention
that the subject of a 'linked' collection of two-triple items of the form described
above, ending with an item ending with rdf:nil, denotes a totally
ordered sequence whose members are the denotations of the rdf:first
values of the items, in the order got by tracing the rdf:rest properties
from the subject to rdf:nil. This permits sequences which contain
other sequences.
Note that the RDFS semantic conditions, described below, require that any
subject of the rdf:first property, and any subject or object of
the rdf:rest property, be of rdf:type rdf:List.
3.3.4 rdf:value
The intended use for rdf:value is explained
intuitively in the RDF Primer
document [RDF-PRIMER]. It is typically
used to identify a 'primary' or 'main' value of a property which has several
values, or has as its value a complex entity with several facets or properties
of its own.
Since the range of possible uses for rdf:value is so wide, it
is difficult to give a precise statement which covers all the intended meanings
or use cases. Users are cautioned, therefore, that the
meaning of rdf:value may vary from application to application.
In practice, the intended meaning is often clear from the context, but may be
lost when graphs are merged or when conclusions are inferred.
RDF Schema [RDF-VOCABULARY]
extends RDF to include a larger vocabulary
rdfsV with more complex semantic constraints:
| RDFS vocabulary |
rdfs:domain rdfs:range rdfs:Resource rdfs:Literal
rdfs:Datatype rdfs:Class rdfs:subClassOf rdfs:subPropertyOf
rdfs:member rdfs:Container rdfs:ContainerMembershipProperty
rdfs:comment rdfs:seeAlso rdfs:isDefinedBy
rdfs:label |
(rdfs:comment, rdfs:seeAlso, rdfs:isDefinedBy
and rdfs:label are included here because some constraints which
apply to their use can be stated using rdfs:domain, rdfs:range
and rdfs:subPropertyOf. Other than this, the formal semantics does
not assign them any particular meanings.)
Although not strictly necessary, it is convenient to state the RDFS semantics
in terms of a new semantic construct, a 'class', i.e. a resource which represents
a set of things in the universe which all have that class as the value of their
rdf:type property. Classes are defined to be things of type rdfs:Class,
and the set of all classes in an interpretation will be called IC.
The semantic conditions are stated in terms of a mapping ICEXT (for the Class
Extension in I) from IC to the set of subsets of IR. The meanings of
ICEXT and IC in a rdf-interpretation
of the RDFS vocabulary are completely defined by the first two conditions in
the table of RDFS semantic conditions, below. Notice that a class may have an
empty class extension; that (as noted
earlier) two different class entities could have the same class extension; and
that the class extension of rdfs:Class contains the class rdfs:Class.
An rdfs-interpretation
of V is an rdf-interpretation I
of (V union rdfV union
rdfsV) which satisfies the following
semantic conditions and all the triples in the subsequent table, called the
RDFS axiomatic triples.
RDFS semantic conditions.
| x
is in ICEXT(y) if and only if <x,y> is in IEXT(I(rdf:type))
IC = ICEXT(I(rdfs:Class))
IR = ICEXT(I(rdfs:Resource))
LV = ICEXT(I(rdfs:Literal)) |
| If
<x,y> is in IEXT(I(rdfs:domain)) and <u,v> is
in IEXT(x) then u is in ICEXT(y) |
| If
<x,y> is in IEXT(I(rdfs:range)) and <u,v> is
in IEXT(x) then v is in ICEXT(y) |
IEXT(I(rdfs:subPropertyOf))
is transitive and reflexive on IP |
| If
<x,y> is in IEXT(I(rdfs:subPropertyOf)) then x and
y are in IP and IEXT(x) is a subset of IEXT(y) |
If
x is in IC then <x, I(rdfs:Resource)> is in IEXT(I(rdfs:subClassOf)) |
| If
<x,y> is in IEXT(I(rdfs:subClassOf)) then x and y are
in IC and ICEXT(x) is a subset of ICEXT(y) |
IEXT(I(rdfs:subClassOf))
is transitive and reflexive on IC |
If
x is in ICEXT(I(rdfs:ContainerMembershipProperty)) then:
< x, I(rdfs:member)> is in IEXT(I(rdfs:subPropertyOf))
|
If
x is in ICEXT(I(rdfs:Datatype)) then <x,
I(rdfs:Literal)> is in IEXT(I(rdfs:subClassOf)) |
RDFS axiomatic triples.
rdf:type rdfs:domain rdfs:Resource .
rdfs:domain rdfs:domain rdf:Property .
rdfs:range rdfs:domain rdf:Property .
rdfs:subPropertyOf rdfs:domain rdf:Property .
rdfs:subClassOf rdfs:domain
rdfs:Class .
rdf:subject rdfs:domain rdf:Statement .
rdf:predicate rdfs:domain rdf:Statement .
rdf:object rdfs:domain rdf:Statement .
rdfs:member rdfs:domain rdfs:Resource .
rdf:first rdfs:domain rdf:List .
rdf:rest rdfs:domain rdf:List .
rdfs:seeAlso rdfs:domain rdfs:Resource .
rdfs:isDefinedBy rdfs:domain rdfs:Resource .
rdfs:comment rdfs:domain rdfs:Resource .
rdfs:label rdfs:domain rdfs:Resource .
rdf:value rdfs:domain rdfs:Resource .
rdf:type rdfs:range rdfs:Class .
rdfs:domain rdfs:range rdfs:Class .
rdfs:range rdfs:range rdfs:Class .
rdfs:subPropertyOf rdfs:range rdf:Property .
rdfs:subClassOf rdfs:range
rdfs:Class .
rdf:subject rdfs:range rdfs:Resource .
rdf:predicate rdfs:range rdfs:Resource .
rdf:object rdfs:range rdfs:Resource .
rdfs:member rdfs:range rdfs:Resource .
rdf:first rdfs:range rdfs:Resource .
rdf:rest rdfs:range rdf:List .
rdfs:seeAlso rdfs:range rdfs:Resource .
rdfs:isDefinedBy rdfs:range rdfs:Resource .
rdfs:comment rdfs:range rdfs:Literal .
rdfs:label rdfs:range rdfs:Literal .
rdf:value rdfs:range rdfs:Resource .
rdf:Alt rdfs:subClassOf rdfs:Container .
rdf:Bag rdfs:subClassOf rdfs:Container .
rdf:Seq rdfs:subClassOf rdfs:Container .
rdfs:ContainerMembershipProperty rdfs:subClassOf rdf:Property .
rdfs:isDefinedBy rdfs:subPropertyOf rdfs:seeAlso .
rdf:XMLLiteral rdf:type rdfs:Datatype .
rdf:XMLLiteral rdfs:subClassOf rdfs:Literal .
rdfs:Datatype rdfs:subClassOf rdfs:Class .
rdf:_1 rdf:type rdfs:ContainerMembershipProperty .
rdf:_1 rdfs:domain rdfs:Resource .
rdf:_1 rdfs:range rdfs:Resource .
rdf:_2 rdf:type rdfs:ContainerMembershipProperty .
rdf:_2 rdfs:domain rdfs:Resource .
rdf:_2 rdfs:range rdfs:Resource .
... |
Since I is an rdf-interpretation, the first condition implies that IP
= ICEXT(I(rdf:Property)).
These axioms and conditions have some redundancy: for example, all but one
of the RDF axiomatic triples can be derived from the RDFS axiomatic triples
and the semantic conditions on ICEXT, rdfs:domain and rdfs:range.
Other triples which must be true in all rdfs-interpretations
include the following:
Some triples which are rdfs-valid.
rdfs:Resource rdf:type rdfs:Class .
rdfs:Class rdf:type rdfs:Class .
rdfs:Literal rdf:type rdfs:Class .
rdf:XMLLiteral rdf:type rdfs:Class .
rdfs:Datatype rdf:type rdfs:Class .
rdf:Seq rdf:type rdfs:Class .
rdf:Bag rdf:type rdfs:Class .
rdf:Alt rdf:type rdfs:Class .
rdfs:Container rdf:type rdfs:Class .
rdf:List rdf:type rdfs:Class .
rdfs:ContainerMembershipProperty rdf:type rdfs:Class .
rdf:Property rdf:type rdfs:Class .
rdf:Statement rdf:type rdfs:Class .
rdfs:domain rdf:type rdf:Property .
rdfs:range rdf:type rdf:Property .
rdfs:subPropertyOf rdf:type rdf:Property .
rdfs:subClassOf rdf:type rdf:Property .
rdfs:member rdf:type rdf:Property .
rdfs:seeAlso rdf:type rdf:Property .
rdfs:isDefinedBy rdf:type rdf:Property .
rdfs:comment rdf:type rdf:Property .
rdfs:label rdf:type rdf:Property .
|
Note that datatypes are allowed to
have class extensions, i.e. are considered to be classes, in RDFS. As illustrated
by the semantic condition on the class extension of rdf:XMLLiteral,
the members of a datatype class are the values of the datatype.
This is explained in more detail in section 5 below.
The class rdfs:Literal contains all literal values; however,
typed literals whose strings do not conform to the lexical requirements of their
datatype are required to have meanings
not in this class. The semantic conditions on rdf-interpretations
imply that ICEXT(I(rdf:XMLLiteral)) contains all XML values of
well-typed XML literals.
The conditions on rdf:XMLLiteral and rdfs:range
taken together make it possible to write a contradictory statement in RDFS,
by asserting that a property value must be in the class rdf:XMLLiteral
but applying this property with a value which is an ill-formed XML literal,
and therefore required to not be in that class: for example
<ex:a> <ex:p> "<notLegalXML"^^rdf:XMLLiteral
.
<ex:p> rdfs:range rdf:XMLLiteral .
cannot be true in any rdfs-interpretation; it is rdfs-inconsistent.
4.2 Extensional Semantic
Conditions (Informative)
The semantics given above is deliberately chosen to be the weakest 'reasonable'
interpretation of the RDFS vocabulary. Semantic extensions MAY
strengthen the range, domain, subclass and subproperty semantic conditions to
the following 'extensional'
versions:
Extensional alternatives for some RDFS semantic conditions.
| <x,y> is in IEXT(I(rdfs:subClassOf))
if and only if x and y are in IC and ICEXT(x) is a subset of ICEXT(y) |
| <x,y> is in IEXT(I(rdfs:subPropertyOf))
if and only if x and y are in IP and IEXT(x) is a subset of IEXT(y) |
| <x,y> is in IEXT(I(rdfs:range))
if and only if (if <u,v> is in IEXT(x) then v is in ICEXT(y)) |
| <x,y> is in IEXT(I(rdfs:domain))
if and only if (if <u,v> is in IEXT(x) then u is in ICEXT(y)) |
which would guarantee that the subproperty and subclass properties were transitive
and reflexive, but would also have further consequences.
These stronger conditions would be trivially satisfied when properties are
identified with property extensions, classes with class extensions, and rdfs:SubClassOf
understood to mean subset, and hence would be satisfied by an extensional semantics
for RDFS. In some ways the extensional versions provide a simpler semantics,
but they require more complex inference rules. The 'intensional' semantics described
in the main text provides for most common uses of subclass and subproperty assertions,
and allows for simpler implementations of a
complete set of RDFS entailment rules, described in section 7.3.
Although the semantic conditions on rdfs-interpretations include the intuitively
sensible condition that ICEXT(I(rdfs:Literal)) must be the set
LV, there is no way to impose this condition by any RDF assertion or inference
rule. This limitation is due to the fact that RDF does not allow literals to
occur in the subject position of a triple, so there are severe restrictions
on what can be said about literals in RDF. Similarly, while properties
may be asserted of the class rdfs:Literal, none of these can be
validly transferred to literals themselves.
For example, a triple of the form
<ex:a> rdf:type rdfs:Literal .
is consistent even though 'ex:a' is a URI reference rather
than a literal. What it says is that I(ex:a) is a
literal value, ie that the URI reference 'ex:a'
denotes a literal value. It does not specify exactly which
literal value it denotes.
The semantic conditions guarantee that any triple containing a plain literal
object entails a similar triple with a blank node as object:
<ex:a> <ex:b> "10" .
entails
<ex:a> <ex:b> _:xxx .
This means that the literal denotes an entity, which could therefore also be
named, at least in principle, by a URI reference.
4.4 RDFS Entailment
S rdfs-entails E when every rdfs-interpretation
which satisfies every member of S also satisfies E. This follows the wording
of the definition of simple entailment
in Section 2, but refers only to rdfs-interpretations
instead of all simple interpretations. Rdfs-entailment is an example
of vocabulary entailment.
Since every rdfs-interpretation is an rdf-interpretation, if S rdfs-entails
E then it rdf-entails E; but rdfs-entailment is stronger than rdf-entailment.
Even the empty graph has a large number of rdfs-entailments which are not rdf-entailments,
for example all triples of the form
xxx rdf:type rdfs:Resource .
are true in all rdfs-interpretations
of any vocabulary containing the URI reference xxx.
An rdfs-inconsistent graph rdfs-entails any graph, by the
definition of entailment; such 'trivial entailments' by an inconsistent set
are not usually considered useful inferences to draw in practice, however.
RDF provides for the use of externally defined datatypes
identified by a particular URI reference. In the interests of generality, RDF imposes
minimal conditions on a datatype. It also includes a single built-in datatype
rdf:XMLLiteral.
This semantics for datatypes is minimal. It makes no provision for associating
a datatype with a property so that it applies to all values of the property,
and does not provide any way of explicitly asserting that
a blank node denotes a particular datatype value. Semantic
extensions and future versions of RDF may impose more elaborate datatyping
conditions. Semantic extensions may also refer to other kinds of information
about a datatype, such as orderings of the value space.
A datatype
is an entity characterized by a set of character strings called lexical
forms and a mapping from that set to a set of values. Exactly
how these sets and mappings are defined is a matter external to
RDF.
Formally, a datatype d is defined by three items:
1. a non-empty set of character strings called the lexical space
of d;
2. a non-empty set called the value space of d;
3. a mapping from the lexical space of d to the value space of d, called the
lexical-to-value mapping of d.
The lexical-to-value mapping of a datatype d is written as
L2V(d).
In stating the semantics we assume that interpretations are relativized
to a particular set of datatypes each of which is identified by a
URI reference.
Formally, let D be a set of
pairs consisting of a URI reference and a datatype
such that no URI reference appears twice in the set, so that D can be regarded
as a function from a set of URI references to a set of datatypes: call this
a datatype map. (The particular URI references must be mentioned explicitly
in order to ensure that interpretations conform to any naming conventions imposed
by the external authority responsible for defining the datatypes.) Every datatype
map is understood to contain <rdf:XMLLiteral, x> where
x is the built-in XML Literal datatype whose lexical and value spaces and lexical-to-value
mapping are defined
in the RDF Concepts and Abstract
Syntax document [RDF-CONCEPTS].
The datatype map which also contains
the set of all pairs of the form <http://www.w3.org/2001/XMLSchema#sss,
sss>, where sss is a built-in datatype named sss
in XML Schema Part 2: Datatypes
[XML-SCHEMA2] and listed in the following
table, is referred to here as XSD.
| XSD datatypes |
xsd:string,
xsd:boolean,
xsd:decimal,
xsd:float,
xsd:double,
xsd:dateTime,
xsd:time,
xsd:date,
xsd:gYearMonth,
xsd:gYear,
xsd:gMonthDay,
xsd:gDay,
xsd:gMonth,
xsd:hexBinary,
xsd:base64Binary,
xsd:anyURI,
xsd:normalizedString,
xsd:token,
xsd:language,
xsd:NMTOKEN,
xsd:Name,
xsd:NCName,
xsd:integer,
xsd:nonPositiveInteger,
xsd:negativeInteger,
xsd:long,
xsd:int,
xsd:short,
xsd:byte,
xsd:nonNegativeInteger,
xsd:unsignedLong,
xsd:unsignedInt,
xsd:unsignedShort,
xsd:unsignedByte,
xsd:positiveInteger
|
The other built-in XML Schema datatypes are unsuitable for various reasons,
and SHOULD NOT
be used: xsd:duration
does not have a well-defined value space (this may be corrected in later revisions
of XML Schema datatypes, in which case the revised datatype would be suitable
for use in RDF datatyping); xsd:QName
and xsd:ENTITY
require an enclosing XML document context; xsd:ID
and xsd:IDREF
are for cross references within an XML document; xsd:NOTATION
is not intended for direct use; xsd:IDREFS,
xsd:ENTITIES
and xsd:NMTOKENS
are sequence-valued datatypes which do not fit the RDF datatype
model.
If D is a datatype
map, a D-interpretation of a vocabulary V is any rdfs-interpretation
I of V union {aaa: < aaa, x > in D for some x } which satisfies the following extra conditions for every pair < aaa,
x > in D:
General semantic conditions for datatypes.
| if <aaa,x> is in D then I(aaa) = x |
| if <aaa,x> is in D then ICEXT(x) is the value space of x and is
a subset of LV |
if <aaa,x> is in D then for any typed literal "sss"^^ddd
in V with I(ddd) = x ,
if sss is in the lexical space of x then IL("sss"^^ddd)
= L2V(x)(sss), otherwise IL("sss"^^ddd) is not in LV |
if <aaa,x> is in D then I(aaa) is in ICEXT(I(rdfs:Datatype)) |
The first condition ensures that I interprets the URI reference according to
the datatype map provided. Note that this does not prevent other URI references
from also denoting the datatype.
The second condition ensures that the datatype URI reference, when used as
a class name, refers to the value space of the datatype,
and that all elements of a value space must be literal values.
The third condition ensures that typed literals in the vocabulary respect
the datatype lexical-to-value mapping. For example, if I is an XSD-interpretation
then I("15"^^xsd:decimal)
must be the number fifteen. The
condition also requires that an ill-typed literal, where the literal
string is not in the lexical space of the datatype,
not denote any literal value. Intuitively, such a name does not denote
any value, but in order to avoid the semantic complexities which arise
from empty names, the semantics requires such a typed literal to denote
an 'arbitrary' non-literal value. Thus for example, if I is an XSD-interpretation,
then all that can be concluded about I("arthur"^^xsd:decimal)
is that it is not in LV, i.e. not in ICEXT(I(rdfs:Literal)). An
ill-typed literal does not in itself constitute an inconsistency, but
a graph which entails that an ill-typed literal has rdf:type rdfs:Literal, or
that an ill-typed XML literal has rdf:type rdf:XMLLiteral, would
be inconsistent.
Note that this third condition applies only to datatypes
in the range of D. Typed literals whose type is not in the datatype
map of the interpretation are treated as before, i.e. as denoting some unknown
thing. The condition does not require that the URI reference in the typed literal
be the same as the associated URI reference of the datatype;
this allows semantic extensions which can express identity conditions on URI
references to draw appropriate conclusions.
The fourth condition ensures that the class rdfs:Datatype contains
the datatypes used in any satisfying
D-interpretation. Notice that this
is a necessary, but not a sufficient, condition; it allows the class I(rdfs:Datatype)
to contain other datatypes.
The semantic conditions for rdf-interpretations
impose the correct interpretation on literals typed by 'rdf:XMLLiteral'.
However, a D-interpretation recognizes the datatype to exist as an entity,
rather than simply being a semantic condition imposed on the RDF typed
literal syntax. Semantic extensions which can express identity conditions
on resources could therefore draw stronger conclusions from D-interpretations
than from rdfs-interpretations.
If the datatypes
in the datatype map D impose disjointness conditions on their value spaces,
it is possible for an RDF graph to have no D-interpretation
which satisfies it. For example, XML Schema defines the value spaces of xsd:string
and xsd:decimal to be disjoint, so it is impossible to construct
a XSD-interpretation satisfying
the graph
<ex:a> <ex:b> "25"^^xsd:decimal .
<ex:b> rdfs:range xsd:string .
This situation could be characterized by saying that the graph is XSD-inconsistent,
or more generally as a datatype clash. Note that it is possible to
construct a satisfying rdfs-interpretation
for this graph, but it would violate the XSD conditions, since the class extensions
of I(xsd:decimal) and I(xsd:string) would have a nonempty
intersection.
Datatype clashes can arise in several other ways. For example, any assertion
that something is in both of two disjoint dataype classes:
_:x rdf:type xsd:string .
_:x rdf:type xsd:decimal .
or that a property with an 'impossible' range has a value:
<ex:p> rdfs:range xsd:string .
<ex:p> rdfs:range xsd:decimal .
_:x <ex:p> _:y .
would constitute a datatype clash. A datatype clash may also arise from the
use of a particular lexical form, for example:
<ex:a> <ex:p> "2.5"^^xsd:decimal .
<ex:p> rdfs:range xsd:integer .
or by the use of an ill-typed lexical form:
<ex:a> <ex:p> "abc"^^xsd:integer .
<ex:p> rdfs:range xsd:integer .
Datatype clashes are the only inconsistencies recognized by
this model theory; note however that
datatype clashes involving XML literals can arise in RDFS.
If D is a subset of D', then restricting interpretations
of a graph to D'-interpretations amounts to a semantic extension compared
to the same restriction with respect to D. In effect, the extension of
the datatype map makes implicit assertions about typed literals, by requiring
them
to denote entities in the value space of a datatype. The extra semantic
constraints associated with the larger datatype map will force interpretations
to make more triples true, but they may also reveal datatype clashes
and violations, so that a D-consistent graph could be D'-inconsistent.
Say that an RDF graph recognizes a datatype
URI reference aaa when the graph rdfs-entails a datatyping triple of the form
aaa rdf:type rdfs:Datatype .
The semantic conditions for rdfs-interpretations
require the built-in datatype URI reference 'rdf:XMLLiteral' to
be recognized.
If every recognized URI reference in a graph is the name of a known datatype,
then there is a natural datatype map
DG which pairs each recognized URI reference to that known datatype (and 'rdf:XMLLiteral'
to rdf:XMLLiteral). Any rdfs-interpretation
I of that graph then has a corresponding 'natural' DG-interpretation which is
like I except that I(aaa) is the appropriate datatype
and the class extension of rdfs:Datatype is modified appropriately.
Applications MAY
require that RDF graphs be interpreted by D-interpretations
where D contains a natural datatype map of the graph. This amounts to treating
datatyping triples as 'declarations' of datatypes
by the graph, and making the fourth semantic condition into an 'iff' condition.
Note however that a datatyping triple does not in itself provide the information
necessary to check that a graph satisfies the other datatype semantic conditions,
and it does not formally rule out other interpretations, so that adopting this
requirement as a formal entailment principle would violate the general
monotonicity lemma described in section
6, below.
5.2 D-entailment
S D-entails E when every D-interpretation
which satisfies every member of S also satisfies E. This follows the wording
of the definition of simple entailment
in Section 2, but refers only to D-interpretations
instead of all simple interpretations. D-entailment is an example of
vocabulary entailment.
As noted above, it is
possible that a graph which is consistent in one vocabulary becomes inconsistent
in a semantic extension defined on a larger vocabulary, and D-interpretations
allow for inconsistencies in an RDF graph. The definition of vocabulary entailment
means that an inconsistent graph will entail any graph in the stronger
vocabulary entailment. For example, a D-inconsistent graph D-entails any RDF
graph. However, it will usually not be appropriate to consider such 'trivial'
entailments as useful consequences, since they may not be valid entailments in a smaller vocabulary.
6. Monotonicity of semantic extensions
Given a set of RDF graphs, there are various ways in which one can 'add' information
to it. Any of the graphs may have some triples added to it; the set of graphs
may be extended by extra graphs; or the vocabulary of the graph may be interpreted
relative to a stronger notion of vocabulary entailment, i.e. with a larger set
of semantic conditions understood to be imposed on the interpretations. All
of these can be thought of as an addition of information, and may make more
entailments hold than held before the change. All of these additions are monotonic,
in the sense that entailments which hold before the addition of information,
also hold after it. We can sum up this in a single lemma:
General monotonicity lemma. Suppose
that S, S' are sets of RDF graphs with every member of S a subset
of some member of S'. Suppose that Y indicates a semantic extension
of X, S X-entails E, and S and
E satisfy any syntactic restrictions of Y. Then S' Y-entails E.
In particular, if D' is a datatype map, D a subset of D' and if S D-entails
E then S also D'-entails E.
7. Entailment
rules (Informative)
The following tables list some inference patterns which capture some of the
various forms of vocabulary entailment, and could be used as a guide for the
design of software to check RDF graphs for RDF and RDFS entailment. Implementations
may be based on applying the rules forwards, or treating the conclusion as a
pattern to be recognized in the consequent of a proposed entailment and searching
backwards for an appropriate match with other rule conclusions or the proposed
antecedent. Other strategies are also possible.
The rules are all stated with the form add a triple to a graph when it
contains triples conforming to a pattern, and they are all valid
in the following sense: a graph entails (in the appropriate sense listed) any
larger graph that is obtained by applying the rules to the original graph. Notice
that applying such a rule to a graph amounts to forming a simple union with
the conclusion, rather than a merge,
and hence preserves any blank nodes already in the graph.
These rules all use the following conventions: aaa, bbb, etc., stand for any
URI reference, i.e. any possible predicate of a triple; uuu, vvv, etc. for any
URI reference or blank node identifier, i.e any possible subject of a triple;
xxx, yyy etc. for any URI reference, blank node identifier or literal, i.e.
any possible subject or object of a triple; lll for any literal; and _:nnn,
etc., for blank node identifiers.
7.1 Simple Entailment Rules
The interpolation lemma in Section
2 can be characterized by the following entailment rules which generate
generalizations, i.e. graphs which have the original graph as an instance.
Being a subgraph requires no explicit formulation as an inference rule
on triples.
simple entailment rules.
| Rule name |
If E contains |
then add |
| se1 |
uuu aaa xxx . |
uuu aaa _:nnn .
where _:nnn identifies a blank node allocated to xxx by rule
se1 or se2. |
| se2 |
uuu aaa xxx . |
_:nnn aaa xxx .
where _:nnn identifies a blank node allocated to uuu by rule
se1 or se2. |
The terminology 'allocated
to' means that the blank node must have been created by an earlier application
of the specified rules on the same URI reference, blank node or literal, or
if there is no such blank node then it must be a 'new' node which does not occur
in the graph. This rather complicated condition ensures that the resulting graph,
obtained by adding the new blank-node triples, has the original graph as a proper
instance and that any such graph will have a subgraph which is the same as one
which can be generated by these rules. For example, the graph
<ex:a> <ex:p> <ex:b> .
<ex:c> <ex:q> <ex:a> .
could be expanded as follows
_:x <ex:p> <ex:b> . by se1 using a new _:x
which is allocated to ex:a
<ex:c> <ex:q> _:x . by se2 using the same _:x allocated
to ex:a
_:x <ex:p> _:y . by se2 using a new _:y which is allocated to ex:b
but it would not be correct to infer
** _:x <ex:q> <ex:a> . ** by se2 (** since
_:x is not allocated to ex:c )
These rules allow blank nodes to proliferate, producing highly non-lean
graphs; they sanction entailments such as
<ex:a> <ex:p> <ex:b> .
<ex:a> <ex:p> _:x . by xse1 with _:x allocated to ex:b
<ex:a> <ex:p> _:y . by xse1 with _:y allocated to _:x
_:z <ex:p> _:y . by xse2 with _:z allocated to ex:a
_:u <ex:p> _:y . by xse2 with _:u allocated to _:z
_:u <ex:p> _:v . by xse1 with _:v allocated to _:y
It is easy to see that S is an instance of E if and only if one can derive
E from S by applying these rules in a suitable sequence; the rule applications
required can be discovered by examination of the instance mapping. So, by the
interpolation lemma, S simply entails E iff one can derive (a graph containing)
E from S by the application of these rules. However, it is also clear that applying
these rules naively would not result in an efficient search process, since the
rules will not terminate and can produce arbitrarily many redundant derivations
of equivalent triples.
The general problem of determining simple entailment between arbitrary RDF
graphs is decideable but NP-complete. This can be shown by encoding the problem
of detecting a subgraph of an arbitrary directed graph as an RDF entailment,
using only blank nodes to represent the graph (observation due to Jeremy Carroll.)
Subsequent rule sets for detecting RDF and RDFS entailment use a special case
of rule se1 which applies only to literals:
literal generalization rule.
| Rule Name |
If E contains |
then add |
| lg |
uuu aaa lll .
|
uuu aaa _:nnn .
where _:nnn identifies a blank node allocated to the literal
lll by this rule. |
Note that this rule is just sufficient to reproduce any subgraph of E consisting
of triples all containing a given literal as an isomorphic subgraph in which
the literal is replaced by a unique blank node. The significance of this lies
in the fact the blank nodes can stand in a subject position in an RDF triple,
allowing conclusions to be drawn by the other rules which express properties
of the literal value denoted by that literal.
For RDFS entailment one additional rule is required, which inverts rule
lg:
literal instantiation rule.
| Rule Name |
If E contains |
then add |
| gl |
uuu aaa _:nnn .
where _:nnn identifies a blank node allocated to
the literal lll by rule lg. |
uuu aaa lll . |
Clearly rule gl will simply produce a redundancy, except in cases where the
allocated blank node has been introduced into the object position of a new
triple by some other inference rule. The effect of these rules
is to ensure that any triple containing a literal, and the similar triple containing
the allocated blank node, are always derivable from one another, so that a
literal can be identified with its allocated blank node for purposes of applying
these rules.
7.2 RDF Entailment Rules
RDF entailment rules
| Rule Name |
if E contains |
then add |
| rdf1 |
uuu aaa yyy . |
aaa rdf:type rdf:Property . |
| rdf2 |
uuu aaa lll .
where lll is a well-typed XML literal . |
_:nnn rdf:type rdf:XMLLiteral .
where _:nnn identifies a blank node allocated
to lll by rule lg. |
These rules are complete
in the following sense.
RDF entailment lemma. S rdf-entails
E if and only if there is a graph which can be derived from S plus the RDF
axiomatic triples by the application of rule
lg and the RDF entailment rules
and which simply entails E.
(Proof in Appendix
A)
Note that this does not require the use of rule
gl.
7.3 RDFS Entailment Rules
RDFS entailment rules.
| Rule Name |
If E contains: |
then add: |
| rdfs1 |
uuu aaa lll.
where lll is a plain literal (with or without a language tag). |
_:nnn rdf:type rdfs:Literal .
where _:nnn identifies a blank node allocated
to lll by rule rule lg. |
| rdfs2 |
aaa rdfs:domain xxx .
uuu aaa yyy . |
uuu rdf:type xxx . |
| rdfs3 |
aaa rdfs:range xxx .
uuu aaa vvv . |
vvv rdf:type xxx . |
| rdfs4a |
uuu aaa xxx . |
uuu rdf:type rdfs:Resource . |
| rdfs4b |
uuu aaa vvv. |
vvv rdf:type rdfs:Resource . |
| rdfs5 |
uuu rdfs:subPropertyOf vvv .
vvv rdfs:subPropertyOf xxx . |
uuu rdfs:subPropertyOf xxx . |
| rdfs6 |
uuu rdf:type rdf:Property . |
uuu rdfs:subPropertyOf uuu . |
| rdfs7 |
aaa rdfs:subPropertyOf bbb .
uuu aaa yyy . |
uuu bbb yyy . |
| rdfs8 |
uuu rdf:type rdfs:Class . |
uuu rdfs:subClassOf rdfs:Resource . |
| rdfs9 |
uuu rdfs:subClassOf xxx .
vvv rdf:type uuu . |
vvv rdf:type xxx . |
| rdfs10 |
uuu rdf:type rdfs:Class . |
uuu rdfs:subClassOf uuu . |
| rdfs11 |
uuu rdfs:subClassOf vvv .
vvv rdfs:subClassOf xxx . |
uuu rdfs:subClassOf xxx . |
| rdfs12 |
uuu rdf:type rdfs:ContainerMembershipProperty . |
uuu rdfs:subPropertyOf rdfs:member . |
| rdfs13 |
uuu rdf:type rdfs:Datatype . |
uuu rdfs:subClassOf rdfs:Literal . |
Stating completeness for these
rules requires more care, since it is possible for a graph to be rdfs-inconsistent
by virtue of containing unsatisfiable assertions about ill-typed XML literals,
for example:
<ex:a> rdfs:subClassOf rdfs:Literal .
<ex:b> rdfs:range <ex:a> .
<ex:c> rdfs:subPropertyOf <ex:b>.
<ex:d> <ex:c> "<"^^rdf:XMLLiteral .
where the denotation of the ill-typed XML literal is required not to be a literal
value but can be inferred to be on the basis of the other assertions. Since
such an rdfs-inconsistent graph rdfs-entails
all RDF graphs, even when they are syntactically unrelated to the antecedent,
we have to exclude this case.
There is a characteristic signal of inconsistency which can be recognized by
the entailment rules, by the derivation of a triple of the form
xxx rdf:type rdfs:Literal .
where xxx is allocated to an ill-typed
XML literal by rule lg. Call such a triple
an XML clash. The derivation of such a clash from the above example
is straightforward:
<ex:d> <ex:c> _:1 . (by rule
lg, with _:1 allocated
to "<"^^rdf:XMLLiteral)
<ex:d> <ex:b> _:1 . (by rule rdfs7)
_:1 rdf:type <ex:a>. (by rule rdfs3)
_:1 rdf:type rdfs:Literal . (by rule rdfs9)
These rules are then complete
in the following sense:
RDFS entailment lemma. S rdfs-entails
E if and only if there is a graph which can be derived from S plus the RDF
and RDFS axiomatic triples
by the application of rule lg, rule gl and
the
RDF and RDFS
entailment rules and which either simply
entails E or contains an XML clash. (Proof
in Appendix A)
The RDFS rules are somewhat redundant. All but one of the RDF
axiomatic triples can be derived from the rules rdfs2
and rdfs3 and the RDFS
axiomatic triples, for example.
The outputs of these rules will often trigger others. These rules will propagate
all rdf:type assertions in the graph up the subproperty and subclass
hierarchies, re-asserting them for all super-properties and superclasses. rdf1
will generate type assertions for all the property names used in the graph,
and rdfs3 together with the last RDFS
axiomatic triple will add all type assertions for all the class names used.
Any subproperty or subclass assertion will generate appropriate type assertions
for its subject and object via rdfs2
and rdfs3 and the domain and range
assertions in the RDFS axiomatic triple set. The rules will generate all assertions
of the form
uuu rdf:type rdfs:Resource .
for every uuu in V, and of the form
uuu rdfs:subClassOf rdfs:Resource .
for every class name uuu; and several more 'universal' facts, such as
rdf:Property rdf:type rdfs:Class .
7.3.1 Extensional Entailment
Rules
The stronger extensional semantic conditions described in
Section 4.1 sanction further entailments which are not covered by the RDFS
rules. The following table lists some entailment patterns which are valid in
this stronger semantics. This is not a
complete set of rules for the extensional semantic conditions. Note that
none of these rules are rdfs-valid; they apply only to semantic extensions which
apply the strengthened extensional semantic conditions described in
Section 4.1. These rules have other consequences, eg that rdfs:Resource
is a domain and range of every property.
Rules ext5-ext9 follow a common pattern; they reflect the fact that the strengthened
extensional conditions require domains (and ranges for transitive properties)
of the properties in the rdfV and rdfsV vocabularies to be as large as possible,
so any attempt to restrict them will be subverted by the semantic conditions.
Similar rules apply to superproperties of rdfs:range and rdfs:domain.
None of these cases are likely to arise in practice.
Some additional inferences which would be valid under the extensional
versions of the RDFS semantic conditions.
| ext1 |
uuu rdfs:domain vvv .
vvv rdfs:subClassOf zzz . |
uuu rdfs:domain zzz . |
| ext2 |
uuu rdfs:range vvv .
vvv rdfs:subClassOf zzz . |
uuu rdfs:range zzz . |
| ext3 |
uuu rdfs:domain vvv .
www rdfs:subPropertyOf uuu . |
www rdfs:domain vvv . |
| ext4 |
uuu rdfs:range vvv .
www rdfs:subPropertyOf uuu . |
www rdfs:range vvv . |
| ext5 |
rdf:type rdfs:subPropertyOf www
.
www rdfs:domain vvv .
|
rdfs:Resource rdfs:subClassOf vvv . |
| ext6 |
rdfs:subClassOf rdfs:subPropertyOf
www .
www rdfs:domain vvv .
|
rdfs:Class rdfs:subClassOf vvv . |
| ext7 |
rdfs:subPropertyOf rdfs:subPropertyOf
www .
www rdfs:domain vvv .
|
rdf:Property rdfs:subClassOf vvv . |
| ext8 |
rdfs:subClassOf rdfs:subPropertyOf
www .
www rdfs:range vvv .
|
rdfs:Class rdfs:subClassOf vvv . |
| ext9 |
rdfs:subPropertyOf rdfs:subPropertyOf
www .
www rdfs:range vvv .
|
rdf:Property rdfs:subClassOf vvv . |
7.4 Datatype
Entailment Rules
In order to capture datatype entailment
in terms of assertions and entailment rules, the rules need to refer to information
supplied by the datatypes themselves;
and to state the rules it is necessary to assume syntactic conditions which
can only be checked by consulting the datatype
sources.
For each kind of information which is available about a datatype,
inference rules for information of that kind can be stated, which can be thought
of as extending the table of RDFS entailment rules. These should be understood
as applying to datatypes other than
the built-in datatype, the rules for which are part of the RDFS entailment rules.
The rules stated below assume that information is available about the datatype
denoted by a recognized URI reference, and they use that URI reference to refer
to the datatype.
The basic information specifies, for each literal string, whether or not it
is a legal lexical form for the datatype, i.e. one which maps to some value
under the lexical-to-value mapping of the datatype.
This corresponds to the following rule, for each string sss that is a legal
lexical form for the datatype denoted
by ddd:
| rdfD1 |
ddd rdf:type rdfs:Datatype .
uuu aaa "sss"^^ddd . |
_:nnn rdf:type ddd .
where _:nnn identifies a blank node allocated
to "sss"^^ddd by rule rule
lg. |
Suppose it is known that two lexical forms sss and ttt map to the same value
under the datatype denoted by ddd; then the following rule applies:
| rdfD2 |
ddd rdf:type rdfs:Datatype .
uuu aaa "sss"^^ddd .
|
uuu aaa "ttt"^^ddd . |
Suppose it is known that the lexical form sss of the datatype denoted by ddd
and the lexical form ttt of the datatype denoted by eee map to the same value.
Then the following rule applies:
| rdfD3 |
ddd rdf:type rdfs:Datatype .
eee rdf:type rdfs:Datatype .
uuu aaa "sss"^^ddd .
|
uuu aaa "ttt"^^eee . |
In addition, if it is known that the value space of the datatype
denoted by ddd is a subset of that of the datatype
denoted by eee, then it would be appropriate to assert that
ddd rdfs:subClassOf eee .
but this needs to be asserted explicitly; it does not follow from the subset
relationship alone.
Assuming that the information encoded in these rules is correct, applying these
and the earlier rules will produce a graph which is
D-entailed by the original.
The rules rdfD2 and 3 are essentially substitutions by virtue of equations
between lexical forms. Such equations may be capable of generating infinitely
many conclusions, e.g. it is possible to add any number of leading zeros to
any lexical form for xsd:integer without it ceasing to be a correct
lexical form for xsd:integer. To avoid such correct
but unhelpful inferences, it is sufficient to restrict rdfD2 to cases which
replace a lexical form with the canonical form for the datatype in question,
when such a canonical form is defined. In order not to omit some valid entailments,
however, such canonicalization rules should be applied to the conclusions as
well as the antecedents of any proposed entailments, and the corresponding rules
of type rdfD3 would need to reflect knowledge of identities between canonical
forms of the distinct datatype.
In particular cases other information might be available, which could be expressed
using a particular RDFS vocabulary. Semantic extensions may also define further
such datatype-specific meanings.
These rules allow one to conclude that any well-formed typed literal of a recognized
datatype will denote something in the class rdfs:Literal.
<ex:a> <ex:p> "sss"^^<ex:dtype> .
<ex:dtype> rdf:type rdfs:Datatype .
<ex:a> <ex:p> _:nnn . (by rule lg)
_:nnn rdf:type <ex:dtype> .
<ex:dtype> rdfs:subClassOf rdfs:Literal .
_:nnn rdf:type rdfs:Literal .
The rule rdfD1 is sufficient to expose some cases of a datatype
clash, by a chain of reasoning of the following form:
<ex:p> rdfs:range <ex:dtype> .
<ex:a> <ex:p> "sss"^^<ex:otherdtype> .
<ex:a> <ex:p> _:nnn .
_:nnn rdf:type <ex:otherdtype> . (by rule rdfD1)
_:nnn rdf:type <ex:dtype> . (by rule rdfs3)
These rules may not provide a complete set of inference principles for D-entailment,
since there may be valid D-entailments for particular datatypes which depend
on idiosyncratic properties of the particular datatypes, such as the size of
the value space (e.g. xsd:boolean has only two elements, so anything
established for those two values must be true for all literals with this datatype.)
In particular, the value space and lexical-to-value mapping of the XSD datatype
xsd:string
sanctions the identification of typed literals with plain literals without language
tags for all character strings which are in the lexical space of the datatype,
since both of them denote the Unicode character string which is displayed in
the literal; so the following inference rule is valid in all XSD-interpretations.
Here, 'sss' indicates any RDF string in the lexical space of
xsd:string.
| xsd 1a |
uuu aaa "sss". |
uuu aaa "sss"^^xsd:string
. |
| xsd 1b |
uuu aaa "sss"^^xsd:string . |
uuu aaa "sss". |
Again, as with the rules rdfD2 and rdfD3, applications may
use a systematic replacement of one of these equivalent forms for the other
rather than apply these rules directly.
"One of the merits of a proof is that it instills a certain
doubt as to the result proved." -Bertrand Russell
Empty Graph
Lemma. The empty set of triples is entailed by any graph, and does
not entail any graph except itself.
Proof. Let N be the empty set of triples. The semantic conditions
on graphs require that N is true in I, for any I; so the first part follows
from the definition of entailment. Suppose G is any nonempty graph and s p
o . is a triple in G, then an interpretation I with IEXT(I(p))
= { } does not satisfy G but does satisfy N; so N does not entail G. QED.
This means that most of the subsequent results are trivial for empty graphs,
which is what one would expect.
Subgraph Lemma. A graph
entails all its subgraphs.
Proof. Obvious, from definitions of subgraph and entailment. If the graph is true in
I then for some A, all its triples are true in I+A, so every subset of triples
is true in I. QED
Merging lemma.
The merge of a set S of RDF graphs is
entailed by S, and entails every member of S.
Proof. Obvious, from definitions of entailment and merge. All members
of S are true if and only if all triples in the merge of S are true. QED.
This means that, as noted in the text, a set of graphs can be treated as a
single graph when discussing satisfaction and entailment. This convention will
be adopted in the rest of the appendix, where a reference to an interpretation
of a set of graphs, a set of graphs entailing a graph, and so on, should be
understood in each case to refer to the merge of the set of graphs, and references
to 'graph' in the following can be taken to refer to graphs or to sets of graphs.
Instance Lemma. A graph
is entailed by all its instances.
Proof. Suppose I satisfies E' and E' is an instance of E. Then for some mapping
A on the blank nodes of E', I+A satisfies every triple in E'. For each blank
node b in E, define B(b)=I+A(c), where c is the blank node or name
that is substituted for b in E', or c=b if nothing was substituted for it.
Then I+B(E)=I+A(E')=true, so I satisfies E. But I was arbitrary; so E' entails
E. QED.
Skolemization is a syntactic transformation
routinely used in automatic inference systems in which existential variables
are replaced by 'new' functions - function names not used elsewhere - applied
to any enclosing universal variables. In RDF, Skolemization amounts to replacing
every blank node in a graph by a 'new' name, i.e. a URI reference which is guaranteed
to not occur anywhere else. In effect, it gives 'arbitrary' names to the anonymous
entities whose existence was asserted by the use of blank nodes: the arbitrariness
of the names ensures that nothing can be inferred that would not follow from
the bare assertion of existence represented by the blank node. (Using a literal
would not do. Literals are never 'new' in the required sense.)
To be precise, a Skolemization of E (with respect to V) is a ground
instance of E with respect to V with a 1:1 instance mapping that maps each
blank node in G to a URI reference that does not appear in G (so the Skolem
vocabulary V must be disjoint from the vocabulary of E)
While not itself strictly a valid operation, Skolemization adds no new content to
an expression, in the sense that a Skolemized expression has the same entailments
as the original expression provided they do not contain names from the Skolem
vocabulary:
Skolemization Lemma.
Suppose sk(E) is a skolemization of E with respect to V. Then sk(E) entails
E; and if sk(E) entails F and the vocabulary of F is disjoint from V, then E
entails F .
Proof. sk(E) entails E by the instance lemma.
Now, suppose that sk(E) entails F where F shares no vocabulary with V; and
suppose I is some interpretation satisfying E. Then for some mapping A from
the blank nodes of E, I+A satisfies E. Define an interpretation I' of the
vocabulary of sk(E) by: IR'=IR, IEXT'=IEXT, I'(x)=I(x) for x in the vocabulary
of E, and I'(x)=[I+A](y) for x in V, where y is the blank node in E that is
replaced by x in sk(E). Clearly I' satisfies sk(E), so I' satisfies F. But
I'(F)=[I+A](F) since the vocabulary of F is disjoint from that of V; so I
satisfies F. But I was arbitrary; so E entails F.
QED.
Intuitively, this lemma shows that asserting a Skolemization expresses a similar
content to asserting the original graph, in many respects. However, a graph
should not be thought of as being equivalent to its Skolemization, since these
'arbitrary' names would have the same status as any other URI references once
published. Also, Skolemization would not be an appropriate operation when applied
to anything other than the antecendent of an entailment. A Skolemization of
a query would represent a completely different query. Nevertheless, for many
purposes when proving results about entailment, we need only consider ground
graphs: for provided E does not contain any Skolem vocabulary, S entails E iff
S' entails E.
The proof of the subsequent lemmas uses a way of constructing an interpretation
of a graph by using the lexical items in the graph itself. (This was
Herbrand's idea; we here modify it slightly to handle literals appropriately.)
Given a nonempty graph G, the
(simple) Herbrand interpretation of G, written Herb(G),
is the interpretation defined as follows.
LVHerb(G) = the set of all plain literals in G;
IRHerb(G) = the set of all names
and blank nodes which occur in a subject or object position in a triple
in G;
IPHerb(G) = the set of URI references which occur in the property
position of a triple in G;
IEXTHerb(G) = {<s,o>: G contains a triple s p o .
}
ISHerb(G) and ILHerb(G) are both identity mappings
on the appropriate parts of the vocabulary of G. |
Clearly Herb(G)+B, where B is the identity map on blank nodes in G, satisfies
every triple in G, by construction, so Herb(G) satisfies G.
Herbrand interpretations treat
URI references and typed literals (and blank nodes) in the same way as plain literals, i.e. as denoting their own syntactic forms. Of course this may not
be what was intended by the writer of the RDF, but the construction shows that
any graph can be interpreted in this way. This therefore establishes
that any RDF graph has a satisfying simple interpretation, i.e. there cannot be
a simple inconsistency in RDF.
Notice that the universe of the Herbrand interpretation of G contains the blank
nodes of G; they are 'standing for' the entities that they assert the existence
of, in effect. Since blank nodes must be interpreted to denote themselves in
order to satisfy the graph, the Herbrand interpretation of a Skolemization of
a graph is isomorphic with the Herbrand interpretation of the graph together
with the blank node mapping: Herb(sk(G)) = Herb(G)+B (using a familiar abuse
of notation where a blank node in a Herbrand interpretation is treated as a
Skolem name.)
Interpolation Lemma. S entails E if and
only if a subgraph of S is an instance of E.
Proof. 'if' follows from the subgraph and instance lemmas.
'only if' uses the Herbrand construction. Suppose S simply entails E. Herb(S)
satisfies S, so Herb(S) satisfies E,
i.e. for some mapping A from the blank nodes of E to IRHerb(S),
[Herb(S)+A] satisfies every triple
s p o .
in E, so S must contain the triple
[Herb(E)+A](s) p [Herb(E)+A](o)
.
which is the instance of the previous triple under the instance mapping A.
So the set of all such triples is a subgraph of S which is an instance of
E.
QED
The following are direct consequences of the interpolation lemma:
Anonymity lemma.
Suppose E is a lean graph and E' is a
proper instance of E. Then E does not entail E'.
Proof. Suppose E entails E', then a subgraph of E is an
instance of E' and therefore a proper instance of E; so E is not lean , contrary to hypothesis. So E
does not entail E'.
QED
Compactness Lemma.
If S entails E and E is a finite graph, then some finite subset S' of S entails
E.
Proof. By the interpolation lemma, a subgraph S' of S is
an instance of E; so S' is finite, and S' entails E.
QED
Although compactness is trivial for simple entailment, it becomes progressively
less trivial in more elaborate semantic extensions.
Monotonicity
Lemma. Suppose S is a subgraph of S' and S entails E. Then S' entails
E. (Special case of general
monotonicity lemma) QED
General
monotonicity lemma. Suppose that S, S' are sets of RDF graphs with
every member of S a subset of some member of S'. Suppose that Y indicates a
semantic extension of X, S X-entails E, and S and E satisfy any syntactic
restrictions of Y. Then S' Y-entails E.
Proof. This follows simply by tracing the definitions. Suppose
that I is a Y-interpretation of S'; then since Y is a semantic extension of
X, I is an X-interpretation; and by the subgraph and merge lemmas, I satisfies
S; so I satisfies E.
QED
Both of the following proofs follow a common pattern which generalizes that
used in the proof of the interpolation lemma, by using a modification of the
Herbrand construction applied to a 'closure' obtained by applying rules to exhaustion.
The proofs operate by showing that the resulting interpretation is both appropriate
to the vocabulary and also acts similarly to the Herbrand
interpretation. Much of the complexity of the proofs arises from the need
to adapt the Herbrand construction in order to take proper account of literal
values. Herbrand interpretations ignore literal typing and treat all typed literals
as non-literal values; this is irrelevant when considering simple entailment,
which treats typed literals simply as denoting names; but more care will be
needed when considering rdf- and rdfs-interpretations.
Both proofs use a single basic idea which requires rather an awkward notation
but is basically straightforward to understand. The simple Herbrand interpretation
treats all vocabulary items as denoting themselves, and builds the interpretation
out of these syntactic items. The semantic conditions on rdf- and rdfs-interpretations
do not permit this in all cases: XML literals in particular are required to
denote other kinds of entity. We therefore distinguish between the 'real' semantic
values and their syntactic 'surrogates' in these cases, by defining a mapping
sur from the universe of the intepretation to the vocabulary of the
graph (plus blank nodes) which is as close as possible to being an identity
mapping, but which when applied to these special literal values, identifies
the particular blank node which acts as a witness for that value in the graph.
In the case of RDFS, the surrogate mapping is extended to all literal values,
since the blank node allocated to the literal can occur in a subject position,
and hence record information about the literal value which must be applied back
to that value in the interpretation.
RDF
entailment lemma. S rdf-entails
E if and only if there is a graph which can be derived from S plus the RDF
axiomatic triples by the application of rule
lg and the RDF entailment rules
and which simply entails E.
Proof. To show 'if' one has only to check that the rules
are rdf-valid, which is left as an exercise for the reader; and if S or E
is empty then the result follows trivially; so suppose they are both non-empty.
To establish 'only if', the proof proceeds by constructing an rdf Herbrand
interpretation RH of S which serves the same role for rdf-interpretations
that the simple Herbrand interpretation does for simple interpretations. The
construction follows the Herbrand construction as far as possible, but interprets
well-formed XML literals so as to satisfy the RDF semantic conditions, guided
by the triples in the RDF closure, C, defined to be the graph resulting
from the following process:
add to S all the RDF
axiomatic triples;
apply rule
lg to any triple containing a well-typed XML literal until the graph is
unchanged by the rule;
apply rule rdf2 until the graph is
unchanged;
apply rule rdf1 until the graph is
unchanged.
Note that C contains precisely one new blank node _:nnn allocated
to each literal in S by the rule rule lg,
and that the subgraph of triples in S containing any well-typed XML literal
is reproduced exactly in C with this blank node replacing the literal and
with the extra triple
_:nnn rdf:type rdf:XMLLiteral .
introduced by rule rdf2. Note also
that the proof only requires that rule
lg is used on well-typed XML literals, so that it actually establishes
a slightly tighter result.
Blank nodes introduced by rule lg
stand as surrogates for well-formed XML literals in the subject position
of a triple. (In the proof of the next lemma, this will be extend to all literals.)
In order to construct an RDF interpretation, XML literals and their surrogates
must be replaced by the appropriate literal values in the domain of the interpretation,
but the proof requires that each XML literal value be uniquely associated
with a lexical item that denotes it. This requires some delicacy in the following
construction.
If lll is a well-formed XML literal, let xml(lll) be the XML value
of lll; and for each XML value x of any well-formed XML literal in C, let
sur(x) be the blank node allocated to that XML literal by rule
lg; and extend sur to be the identity mapping on URI references,
blank nodes and all other literals in C.
RH is then defined by:
LVRH = all plain literals in C plus {xml(x):
x a well-typed XML literal in S}
IRRH = LVRH plus the set of URI references, blank
nodes and other typed literals occurring in C
IPRH = {x: C contains the triple: x rdf:type rdf:Property
.}
If x is in IPRH then IEXTRH(x) = {<s,o>:
C contains the triple sur(s) x sur(o) .
}
ISRH is the identity map on URIrefs in S
If x is a well-formed XML literal in S then ILRH(x) =
xml(x), otherwise ILRH(x) = x
|
Define a mapping B on blank nodes in C as follows: B(x)=xml(lll)
if x is allocated to a well-formed XML literal lll, otherwise B(x)=x, then
clearly [RH+B] satisfies C and therefore S, so RH satisfies S.
Since C contains all the required RDF axiomatic triples, RH satisfies them.
It is easy to see that J satisfies the first two RDF semantic conditions,
by construction; for the triples introduced by rule rdf2
require that IEXTRH(rdf:type) contains <xml(lll),rdf:XMLLiteral>
for every well-typed XML literal lll.
The third RDF semantic condition
is the only negative semantic condition which cannot be satisfied simply by
construction, but it is satisfied trivially. Ill-typed XML literals denote
themselves in RH, and so are excluded from LVRH by construction.
The pair <lll, rdf:XMLLiteral> cannot occur in IEXTRH(rdf:type)
because a literal cannot occur in subject position; so the condition is satisfied,
so RH is an rdf-interpretation.
Since S rdf-entails E, RH satisfies E: so for some mapping A from the blank
nodes of E to IRRH, [RH+A] satisfies every triple
s p o .
in E, i.e. IEXTRH(p) contains <[RH+A](s),[RH+A](o)>, i.e.C
contains a triple
sur([RH+A](s)) p sur([RH+A](o)).
but this is an instance of the first triple under the instantiation
mapping x -> sur(A(x)); so a subgraph of C is an instance of E;
so C simply entails E.
QED
This lemma also shows that any graph has a satisfying rdf-interpretation, and
the proof illustrates how to construct it from a Herbrand interpretation of
the closure, by interpreting well-formed XML literals appropriately and allowing
the possible existence of properties which have no extensions. Note that if
E is finite then the derived subgraph of C is also finite.
The proof of the RDFS entailment lemma is similar in structure and uses closely
similar definitions, but is of course longer and requires a more elaborate construction
to ensure that the class extensions of rdfs:Literal and rdfs:Resource
contain all literal values.
RDFS
entailment lemma. S rdfs-entails
E if and only if there is a graph which can be derived from S plus the RDF
and RDFS axiomatic triples
by the application of rule lg, rule
gl and the
RDF and RDFS
entailment rules and which either simply entails E or is an XML clash.
Proof. Again, to show 'if' it is sufficient to show that
the RDFS entailment
rules are rdfs-valid, which is again left as an exercise; and again,
the empty cases are trivial.
The proof of 'only if' is similar to that used in the previous lemma, and
similar constructions and terminology will be used, except that the RDFS closure,
D, is defined to be the graph resulting from the following process:
add to S all the RDF
and RDFS axiomatic triples;
apply rule
lg to any triple containing a literal until the graph is unchanged by
the rule;
apply rules rdf2 and rdfs1
until the graph is unchanged;
apply rule rdf1, rule gl and the
remaining
RDFS entailment rules until the
graph is unchanged.
Unlike the previous
lemma, this proof requires that rule
lg is applied to all literals, even ill-typed XML literals, and it
requires the inverse rule gl. Rule
gl needs to be used only after an application of rules
rdfs6 or rdfs10,
since those are the only rules which can move a blank node from subject
to object position. Note
that D contains precisely one new blank node _:nnn allocated
to each literal in S by the rule rule
lg,
and that the subgraph of triples in S containing any literal is reproduced
exactly in D with this blank node replacing the literal and with the extra
triple
_:nnn rdf:type rdfs:Literal .
introduced by rule rdfs1,
and possibly also
_:nnn rdf:type rdf:XMLLiteral .
introduced by rule rdf2 when appropriate.
This means that after this point in the construction, literals can effectively
be ignored, since any of the subsequent rules which applies to triples containing
a literal will also apply equally well to the similar triples where the
literal is replaced by its allocated blank node. The rest of the proof uses
this by requiring literal values in the interpretation to satisfy just the
semantic conditions imposed on the blank nodes allocated to the corresponding
literal, and ignoring triples in the graph which contain literals. The use
of rule gl ensures that D contains
any triple containing a literal if and only if it contains the similar triple
with the literal replaced by its allocated blank node.
As in the previous proof, if lll is a well-formed XML literal, let xml(lll)
be the XML value of lll; the surrogate mapping sur is then extended
as follows. First, the domain of sur is the set containing just the
URI references, literals and blank nodes occurring in D and all XML values
of well-formed XML literals in D. (This is the universe of the rdfs-Herbrand
interpretation, defined below.) Now, if lll is a well-formed XML literal in
D, let sur(xml(lll)) be the blank node allocated to lll
by rule lg; for any other literal lll
in D, let sur(lll) be the blank node allocated to lll by rule
lg, and for all URI references and blank nodes in D, let sur(x)
= x . Note that the range of sur contains only URI references
and blank nodes which occur in D.
The rdfs-Herbrand interpretation SH of S is then constructed similarly
to the previous lemma.
LVSH = {x: D contains the triple: sur(x) rdf:type
rdfs:Literal .}
IRSH = LVSH plus the set of URI references, blank
nodes and literals other than well-formed XML literals occurring in D
IPSH = {x: D contains the triple: sur(x)
rdf:type rdf:Property .}
If x is in IPRH then IEXTRH(x) = {<s,o>:
D contains the triple sur(s) x sur(o) .
}
ISSH is the identity map on URI references in S
If x is a well-formed XML literal in S then ILSH(x) = xml(x),
otherwise ILSH(x) = x
|
Define B(x) as follows: if x is a blank node allocated to a well-formed XML
literal lll in D then B(x) = xml(lll); if it is allocated to any
other literal lll in D then B(x)=lll; and otherwise B(x)=x; then clearly [SH+B]
satisfies D and therefore S, so SH satisfies S.
As in the previous lemma, SH satisfies all the required RDF and RDFS axiomatic
triples and the first two RDF semantic conditions by construction.
SH satisfies the third RDF semantic condition just in case D does not contain
an XML clash. Note that the presence of surrogates for ill-typed XML literals
invalidates the argument used in the previous lemma to the effect that this
condition is trivally satisfied. So assume that D does not contain an XML
clash.
As noted in the text, we can regard the first RDFS semantic condition as
defining ICEXT and IC: we will do so without further comment and describe
all the conditions in terms of IEXT. To show that SH satisfies
the remaining RDFS semantic conditions we argue case by case, using the minimality
of the Herbrand interpretation and the completeness of the closure.
All of these conditions can be mirrored by a corresponding sequence of rule
applications. The general form of the argument can be illustrated with the
case of the second RDFS semantic condition.
Suppose <x,y> is in IEXTSH(rdfs:domain) and
<u,v> is in IEXTSH(x); then D must contain the triples
sur(x) rdfs:domain sur(y) .
sur(u) x sur(v).
so x must be a URIref, so sur(x)=x; and then by rule rdfs2,
it must also contain the triple
sur(u) rdf:type sur(y).
so IEXTSH(rdf:type) contains <u,v> ; so the
condition is satisfied.
The other cases proceed similarly, by translating the semantic condition
into a derivation using the rules and axiomatic triples. The argument forms
are summarized in the following table. Some of the semantic conditions split
into several subconditions, and some also have special subcases.
| RDFS semantic condition |
Derivation |
if x in IR then
<x,rdfs:Resource> in IEXT(rdf:type) |
URIref or bnode in subject:
x a b
x rdf:type rdfs:Resource |
rdfs4a |
Literal:
_:x rdf:type rdfs:Literal
rdfs:type rdfs:range rdfs:Class
rdfs:Literal rdf:type rdfs:Class
rdfs:Literal rdfs:subClassOf rdfs:Resource
_:x rdf:type rdfs:Resource |
see below
axiomatic
rdfs3
rdfs8
rdfs9 |
URIref or bnode in object:
a b x
x rdf:type rdfs:Resource |
rdfs4b |
URIref in predicate:
a x b
x rdf:type rdf:Property
rdf:type rdfs:domain rdfs:Resource
x rdf:type rdfs:Resource |
rdf1
axiomatic
rdfs2 |
x in LV iff
<x,rdfs:Literal> in IEXT(rdf:type) |
well-typed XML literal lll:
a b lll
_:x rdf:type rdf:XMLLiteral
rdf:XMLLiteral rdfs:subClassOf rdfs:Literal
_:x rdf:type rdfs:Literal |
lg, rdf2,
sur(xml(lll))=_:x
axiomatic
rdfs9 |
other literal lll :
a b lll
_:x rdf:type rdfs:Literal |
lg, rdfs1,
sur(lll)=_:x |
if
<x,y> in IEXT(rdfs:domain) and <u,v> in IEXT(x)
then
<u,y> in IEXT(rdf:type) |
x rdfs:domain y .
u x v .
u rdf:type y . |
rdfs2 |
if
<x,y> in IEXT(rdfs:range) and <u,v> in IEXT(x)
then
<v,y> in IEXT(rdf:type) |
x rdfs:range y .
u x v .
v rdf:type y . |
rdfs3 |
if
<x,rdf:Property> in IEXT(rdf:type)
then
<x,x> in IEXT(rdfs:subPropertyOf) |
x rdf:type rdf:Property
x rdfs:subPropertyOf x |
rdfs6 |
if
<x,rdf:Property> in IEXT(rdf:type)
<y,rdf:Property>
in IEXT(rdf:type)
<z,rdf:Property> in IEXT(rdf:type)
<x,y> in IEXT(rdfs:subPropertyOf)
<y,z> in IEXT(rdfs:subPropertyOf)
then
<x,z> in IEXT(rdfs:subPropertyOf) |
x rdfs:subPropertyOf y
y rdfs:subPropertyOf z
x subPropertyOf z |
rdfs5 |
if
<x,y> in IEXT(rdfs:subPropertyOf)
<u,v> in IEXT(x)
then
<x,rdf:Property> in IEXT(rdf:type)
<y,rdf:Property> in IEXT(rdf:type)
<u,v> in IEXT(y) |
x rdfs:subPropertyOf y
u x v
rdfs:subPropertyOf rdfs:domain rdf:Property
x type rdf:Property
rdfs:subPropertyOf rdfs:domain rdf:Property
y rdf:type rdf:Property
u y v |
axiomatic triple
rdfs2
axiomatic triple
rdfs3
rdfs7 |
if
<x,rdfs:Class> in IEXT(rdf:type)
then
<x,rdfs:Resource> in IEXT(rdfs:subClassOf) |
x rdf:type rdfs:Class
x rdfs:subClassOf rdfs:Resource |
rdfs8 |
if
<x,y> in IEXT(rdfs:subClassOf)
<u,x> in IEXT(rdf:type)
then
<x,rdfs:Class> in IEXT(rdf:type)
<y,rdfs:Class> in IEXT(rdf:type)
<u,y> in IEXT(rdf:type) |
x rdfs:subClassOf y
u rdf:type x
rdfs:subClassOf rdfs:domain rdfs:Class
x rdf:type rdfs:Class
rdfs:subClassOf rdfs:range rdfs:Class
y rdf:type rdfs:Class
u rdf:type y |
axiomatic triple
rdfs2
axiomatic triple
rdfs3
rdfs9 |
if
<x,rdfs:Class> in IEXT(rdf:type)
then
<x,x> in IEXT(rdfs:subClassOf) |
x rdf:type rdfs:Class
x rdfs:subClassOf x |
rdfs10 |
if
<x,rdfs:Class> in IEXT(rdf:type)
<y,rdfs:Class>
in IEXT(rdf:type)
<z,rdfs:Class> in IEXT(rdf:type)
<x,y>
in IEXT(rdfs:subClassOf)
<y,z> in IEXT(rdfs:subClassOf)
then
<x,z> in IEXT(rdfs:subClassOf) |
x rdfs:subClassOf y
y rdfs:subClassOf z
x rdfs:subClassOf z |
rdfs11 |
if
<x,rdfs:ContainerMembershipProperty> in IEXT(rdf:type)
then
<x,rdfs:member> in IEXT(rdfs:subPropertyOf) |
x rdf:type rdfs:ContainerMembershipProperty
x rdfs:subPropertyOf rdfs:member |
rdfs12 |
if
<x,rdfs:Datatype> in IEXT(rdf:type)
then
<x,rdfs:Literal> in IEXT(rdfs:subClassOf) |
x rdf:type rdfs:Datatype
x rdfs:subClassOf rdfs:Literal |
rdfs13 |
so SH is an rdfs-interpretation.
Since S rdfs-entails E, SH satisfies E: so for some mapping A from the blank
nodes of E to IRSH, [SH+A] satisfies every triple
s p o .
in E, i.e. IEXTSH(p) contains <[SH+A](s),[SH+A](o)>, i.e.D
contains a triple
sur([SH+A](s)) p sur([SH+A](o)).
which is an instance of the first triple under the instantiation mapping
x -> sur(A(x)), unless o is a literal. If o is a
literal, then sur([SH+A](o) is the blank node
allocated to o, and so D also contains the triple
sur([SH+A](s)) p o .
which is an instance of the first triple under the instantiation mapping
x -> sur(A(x)). So a subgraph of D is an instance of E under
the instantiation mapping
x -> sur(A(x)); so D simply entails E.
So either D contains an XML clash or D simply entails E, so D satisfies the
conditions of the lemma.
QED
Note that if E is finite, or if D contains an XML clash, then a finite subgraph
of D also satisfies the conditions of the lemma.
Appendix B: Glossary of Terms (Informative)
Antecedent (n.) In an inference, the
expression(s) from which the conclusion is derived. In an entailment relation, the
entailer. Also assumption.
Assertion (n.) (i) Any expression
which is claimed to be true. (ii) The act of claiming something to
be true.
Class
(n.) A general concept, category or classification. Something used primarily to
classify or categorize other things. Formally, in RDF, a resource of type
rdfs:Class with an associated set of resources all of which
have the class as a value of the rdf:type property.
Classes are often called 'predicates' in the formal logical
literature.
(RDF distinguishes class from set, although the two are often
identified. Distinguishing classes from sets allows RDF more
freedom in constructing class hierarchies, as explained earlier.)
Complete (adj., of an inference system). (1)
Able to detect all entailments between any two expressions.
(2) Able to draw all valid inferences. See Inference. Also used with a qualifier: able to
detect entailments or draw all valid inferences in a certain limited form or kind (e.g.
between expressions in a certain normal form, or meeting certain syntactic conditions.)
(These definitions are not exactly equivalent, since the first requires that
the system has access to the consequent of the entailment, and may be unable
to draw 'trivial' inferences such as (p and p) from p. Typically, efficient
mechanical inference systems may be complete in the first sense but not necessarily
in the second.)
Consequent (n.) In an inference,
the expression constructed from the antecedent. In an entailment relation, the
entailee. Also conclusion.
Consistent (adj., of an expression) Having
a satisfying interpretation; not internally contradictory. (Also used
of an inference system as synonym for Correct.)
Correct (adj., of an inference system). Unable
to draw any invalid inferences, or unable to make false claims of entailment. See Inference.
Decideable
(adj., of an inference system). Able to determine for any pair of expressions,
in a finite time with finite resources, whether or not the first entails the
second. (Also: adj., of a logic:) Having a decideable inference system which
is complete and correct for the semantics of the logic.
(Not all logics can have inference systems which are both complete and decideable,
and decideable inference systems may have arbitrarily high computational complexity.
The relationships between logical syntax, semantics and complexity of an inference
system continue to be the subject of considerable research.)
Entail (v.),
entailment (n.). A semantic relationship between
expressions which holds whenever the truth of the first guarantees
the truth of the second. Equivalently, whenever it is logically
impossible for the first expression to be true and the second one
false. Equivalently, when any interpretation which satisfies the first also satisfies the second.
(Also used between a set of expressions and an expression.)
Equivalent (prep., with
to) True under exactly the same conditions; making
identical claims about the world, when asserted. Entails and is entailed
by.
Extensional (adj., of a logic) A
set-based theory or logic of classes, in which classes are
considered to be sets, properties considered to be sets of
<object, value> pairs, and so on. A theory which admits no
distinction between entities with the same extension. See Intensional.
Formal (adj.) Couched in language
sufficiently precise as to enable results to be established using
conventional mathematical techniques.
Iff
(conj.) Conventional abbreviation for 'if and only if'. Used to
express necessary and sufficient conditions.
Inconsistent (adj.) False under
all interpretations; impossible to satisfy. Inconsistency
(n.), any inconsistent expression or graph.
(Entailment and inconsistency are closely
related, since A entails B just when (A and not-B) is inconsistent, c.f. the
second definition for entailment. This is the basis of many
mechanical inference systems.
Although the definitions of consistency
and inconsistency are exact duals, they are computationally dissimilar. It is
often harder to detect consistency in all cases than to detect inconsistency
in all cases.)
Indexical (adj., of an expression) having
a meaning which implicitly refers to the context of use. Examples from English
include words like 'here', 'now', 'this'.
Inference (n.) An act or
process of constructing new expressions from existing expressions, or the result
of such an act or process. Inferences corresponding to entailments are described as correct or valid.
Inference rule, formal description of a type of inference;
inference system, organized system of inference rules; also,
software which generates inferences or checks inferences for validity.
Intensional (adj., of a logic)
Not extensional. A
logic which allows distinct entities with the same extension.
(The merits and demerits of intensionality have been extensively debated in
the philosophical logic literature. Extensional semantic theories are simpler,
and conventional semantics for formal logics usually assume an extensional view,
but conceptual analysis of ordinary language often suggests that intensional
thinking is more natural. Examples often cited are that an extensional logic
is obliged to treat all 'empty' extensions as identical, so must identify 'round
square' with 'santa clause', and is unable to distinguish concepts that 'accidentally'
have the same instances, such as human beings and bipedal hominids without body
hair. The semantics described in this document is basically intensional.)
Interpretation
(of) (n.) A minimal formal description of those
aspects of a world which
is just sufficient to establish the truth or falsity of any
expression of a logic.
(Some logic texts distinguish between a interpretation
structure, which is a 'possible world' considered as something
independent of any particular vocabulary, and an interpretation
mapping from a vocabulary into the structure. The RDF
semantics takes the simpler route of merging these into a single
concept.)
Logic
(n.) A formal language which expresses propositions.
Metaphysical (adj.).
Concerned with the true nature of things in some absolute or
fundamental sense.
Model Theory (n.) A
formal semantic theory which relates expressions to
interpretations.
(The name 'model theory' arises from the usage, traditional in
logical semantics, in which a satisfying interpretation is called a
"model". This usage is often found confusing, however, as it is
almost exactly the inverse of the meaning implied by terms like
"computational modelling", so has been avoided in this
document.)
Monotonic (adj., of a logic or
inference system) Satisfying the condition that if S entails E then
(S + T) entails E, i.e. adding information to some antecedents
cannot invalidate a valid entailment.
(All logics based on a conventional model theory and a standard notion of
entailment are monotonic. Monotonic logics have the property that
entailments remain valid outside of the context in which they were
generated. This is why RDF is designed to be monotonic.)
Nonmonotonic (adj.,of a logic
or inference system) Not monotonic. Non-monotonic formalisms have been
proposed and used in AI and various applications. Examples of
nonmonotonic inferences include default reasoning, where
one assumes a 'normal' general truth unless it is contradicted by
more particular information (birds normally fly, but penguins
don't fly); negation-by-failure, commonly assumed in logic
programming systems, where one concludes, from a failure to prove a
proposition, that the proposition is false; and implicit
closed-world assumptions, often assumed in database
applications, where one concludes from a lack of information about
an entity in some corpus that the information is false (e.g. that
if someone is not listed in an employee database, that he or she is not
an employee.)
(The relationship between monotonic and nonmonotonic inferences
is often subtle. For example, if a closed-world assumption is made
explicit, e.g. by asserting explicitly that the corpus is complete
and providing explicit provenance information in the conclusion,
then closed-world reasoning is monotonic; it is the implicitness
that makes the reasoning nonmonotonic. Nonmonotonic conclusions can
be said to be valid only in some kind of 'context', and are liable
to be incorrect or misleading when used outside that context.
Making the context explicit in the reasoning and visible in the
conclusion is a way to map them into a monotonic framework.)
Ontological (adj.) (Philosophy)
Concerned with what kinds of things really exist. (Applied)
Concerned with the details of a formal description of some topic or
domain.
Proposition (n.) Something that
has a truth-value; a statement or expression that is true or
false.
(Philosophical analyses of language traditionally distinguish
propositions from the expressions which are used to state them, but
model theory does not require this distinction.)
Reify
(v.), reification (n.) To categorize as an object;
to describe as an entity. Often used to describe a convention
whereby a syntactic expression is treated as a semantic object and
itself described using another syntax. In RDF, a reified triple is
a description of a triple-token using other RDF triples.
Resource (n.)(as used in RDF)(i) An
entity; anything in the universe. (ii) As a class name: the class
of everything; the most inclusive category possible.
Satisfy (v.t.),
satisfaction,(n.) satisfying
(adj., of an interpretation). To make true. The basic semantic
relationship between an interpretation and an expression. X
satisfies Y means that if the
world conforms to the conditions described by X, then Y must be
true.
Semantic (adj.) ,
semantics (n.). Concerned with the specification
of meanings. Often contrasted with syntactic to emphasize
the distinction between expressions and what they denote.
Skolemization (n.) A
syntactic transformation in which blank nodes are replaced by 'new'
names.
(Although not strictly valid, Skolemization retains the
essential meaning of an expression and is often used in mechanical
inference systems. The full logical form is more complex. It is
named after the logician
A. T. Skolem)
Token
(n.) A particular physical inscription of a symbol or expression in
a document. Usually contrasted with type, the abstract
grammatical form of an expression.
Universe (n., also Universe of
discourse) The universal classification, or the set of all
things that an interpretation considers to exist. In RDF/S, this is
identical to the set of resources.
Use (v.)
contrasted with mention; to use a piece of syntax to
denote or refer to something else. The normal way that language is
used.
("Whenever, in a sentence, we wish to say something about a
certain thing, we have to use, in this sentence, not the thing
itself but its name or designation." - Alfred
Tarski)
Valid
(adj., of an inference or inference process) Corresponding to an entailment, i.e. the
conclusion of the inference is entailed by the antecedent of the
inference. Also correct.
Well-formed (adj., of an
expression). Syntactically legal.
World
(n.) (with the:) (i) The actual world. (with
a:) (ii) A way that the actual world might be arranged.
(iii) An interpretation (iv) A possible world.
(The metaphysical status of 'possible
worlds' is highly controversial. Fortunately, one does not need to commit
oneself to a belief in parallel universes in order to use the concept in its
second and third senses, which are sufficient for semantic purposes.)
Appendix C: Acknowledgements
This document reflects the joint effort of the members of the RDF Core Working Group. Particular
contributions were made by Jeremy Carroll, Dan Connolly, Jan Grant, R. V. Guha,
Graham Klyne, Ora Lassilla, Brian McBride, Sergey Melnick, Jos deRoo and Patrick
Stickler.
The basic idea of using an explicit extension mapping to allow
self-application without violating the axiom of foundation was
suggested by Christopher Menzel.
Peter Patel-Schneider and Herman ter Horst found several major problems in
earlier drafts, and suggested several important technical improvements.
Patrick Hayes' work on this document was supported in part by DARPA under contract
#2507-225-22.
- [RDF-CONCEPTS]
- Resource Description Framework (RDF): Concepts and Abstract Syntax, Graham Klyne and Jeremy J. Carroll, Editors, W3C Recommendation, 10 February 2004, http://www.w3.org/2001/sw/RDFCore/TR/staging/rdf-concepts/ . Latest version available at http://www.w3.org/TR/rdf-concepts/ .
- [RDF-SYNTAX]
- RDF/XML Syntax Specification (Revised), Dave Beckett, Editor, W3C Recommendation, 10 February 2004, http://www.w3.org/2001/sw/RDFCore/TR/staging/rdf-syntax-grammar/ . Latest version available at http://www.w3.org/TR/rdf-syntax-grammar/ .
- [RDF-TESTS]
- RDF Test Cases, Jan Grant and Dave Beckett, Editors, W3C Recommendation, 10 February 2004, http://www.w3.org/2001/sw/RDFCore/TR/staging/rdf-testcases/ . Latest version available at http://www.w3.org/TR/rdf-testcases/ .
- [RDFMS]
- Resource
Description Framework (RDF) Model and Syntax Specification , O.
Lassila and R. Swick, Editors. World Wide Web Consortium. 22 February 1999.
This version is http://www.w3.org/TR/1999/REC-rdf-syntax-19990222/. The latest
version of RDF M&S is available at http://www.w3.org/TR/REC-rdf-syntax/.
- [RFC 2119]
- RFC 2119 - Key words
for use in RFCs to Indicate Requirement Levels , S. Bradner, IETF.
March 1997. This document is http://www.ietf.org/rfc/rfc2119.txt.
- [RFC 2396]
- RFC 2396 - Uniform
Resource Identifiers (URI): Generic Syntax Berners-Lee,T., Fielding
and Masinter, L., August 1998
- [XSD]
- XML Schema Part 2: Datatypes,
Biron, P. V., Malhotra, A. (Editors) World Wide Web Consortium Recommendation,
2 May 2001
- [OWL]
- OWL Web Ontology Language Reference, Mike Dean and Guus Schreiber, Editors, W3C Recommendation, 10 February 2004, http://www.w3.org/2001/sw/WebOnt/TR/STAGE-owl-ref/ . Latest version available at http://www.w3.org/TR/owl-ref/ .
- [Conen&Klapsing]
-
A Logical Interpretation of RDF, Conen, W., Klapsing, R..Circulated
to
RDF Interest Group, August 2000.
- [DAML]
- Frank van Harmelen, Peter F. Patel-Schneider, Ian Horrocks (editors), Reference Description
of the DAML+OIL (March 2001) ontology markup language
- [Hayes&Menzel]
-
A Semantics for the Knowledge Interchange Format, Hayes, P., Menzel,
C., Proceedings of 2001 Workshop on the IEEE Standard
Upper Ontology, August 2001.
- [KIF]
- Michael R. Genesereth et. al., Knowledge Interchange
Format, 1998 (draft American National Standard).
- [Marchiori&Saarela]
- Query + Metadata
+ Logic = Metalog, Marchiori, M., Saarela, J. 1998.
- [LBASE]
- Lbase: Semantics
for Languages of the Semantic Web, Guha, R. V., Hayes, P., W3C
Note, 10 October 2003.
- [McGuinness&al]
-
DAML+OIL:An Ontology Language for the Semantic Web, McGuinness,
D. L., Fikes, R., Hendler J. and Stein, L.A., IEEE Intelligent Systems, Vol.
17, No. 5, September/October 2002.
- [RDF-PRIMER]
- RDF Primer, Frank Manola and Eric Miller, Editors, W3C Recommendation, 10 February 2004, http://www.w3.org/2001/sw/RDFCore/TR/staging/rdf-primer/ . Latest version available at http://www.w3.org/TR/rdf-primer/ .
- [RDF-VOCABULARY]
- RDF Vocabulary Description Language 1.0: RDF Schema, Dan Brickley and R. V. Guha, Editors, W3C Recommendation, 10 February 2004, http://www.w3.org/2001/sw/RDFCore/TR/staging/rdf-schema/ . Latest version available at http://www.w3.org/TR/rdf-schema/ .
Appendix D: Change Log. (Informative)
Changes since the 15 December 2003 Proposed Recommendation.
An error in the wording of the RDFS entailment lemma in appendix A was corrected.
Some typos in the glossary and main text were corrected.
After considering comments
by ter Horst, the definition of D-interpretation has been modified so as
to apply to an extended vocabulary including the datatype names.
Older entries in the change log were removed. They can be found in the previous version.


