Abstract

This document defines the Semantic Web Services Language (SWSL), which is used to specify the Semantic Web Services Ontology (SWSO) as well as individual Web services. The language consists of two parts: SWSL-FOL, a full first-order logic language, and SWSL-Rules, as rule-based language. SWSL-FOL is primarily used for formal specification of the ontology and is intended to provide interoperability with other first-order based process models and service ontologies. In contrast, SWSL-Rules is designed to be an actual language for service specification.

Status of this document

Table of contents

1 Introduction
2 The Language
  2.1 Overview of SWSL-Rules and SWSL-FOL
  2.2 Basic Definitions
  2.3 Horn Rules
  2.4 The Monotonic Lloyd-Topor Layer
  2.5 The NAF Layer
  2.6 The Nonmonotonic Lloyd-Topor Layer
  2.7 The Courteous Rules Layer
  2.8 The HiLog Layer
  2.9 The Equality Layer
  2.10 The Frames Layer
  2.11 Reification
  2.12 Skolemization in SWSL-Rules
  2.13 SWSL-Rules and XML Schema Data Types
  2.16 Semantics of SWSL-Rules
  2.15 SWSL-FOL: The First-order Subset of SWSL
  2.16 Semantics of SWSL-FOL
  2.17 Future Extensions
3 Combining SWSL-Rules and SWSL-FOL
4 Serialization of SWSL in RuleML
   4.1 Serialization of the HiLog Layer
   4.2 Serialization of Explicit Equality
   4.3 Serialization of the Frames Layer
   4.4 Serialization of Reification
   4.5 Serialization of SWSL-FOL
5 Glossary
6 References

1 Introduction

This document is part of the technical report of the Semantic Web Services Language (SWSL) Committee of the Semantic Web Services Initiative (SWSI). The overall structure of the report is described in the document titled Semantic Web Services Framework Overview.

SWSL is a logic-based language for specifying formal characterizations of Web service concepts and descriptions of individual services. It includes two sublanguages: SWSL-FOL -- a full first-order logic language, which is used to specify the service ontology (SWSO), and SWSL-Rules -- a rule-based sublanguage, which can be used both as a specification and an implementation language. As a language, SWSL is domain-independent and does not include any constructs specific to services. Those constructs are defined by the Semantic Web Service Ontology, which appears in a separate document.

SWSL-Rules includes a novel combination of features that hitherto have not been present in a single system. However, almost all of the features of SWSL-Rules have been implemented in either FLORA-2 [Yang04], SweetRules [Grosof2004b], or the commercial Ontobroker [Ontobroker] system. Extensive feedback collected from the users of these systems has been incorporated in the design of the corresponding features in SWSL-Rules.

In contrast to SWSL-Rules, we do not envision the need for a full first-order reasoner based on SWSL-FOL. Instead, SWSL-FOL is intended largely as a specification language for SWSO, and specialized reasoners will be used to reason with the service ontology. In addition, SWSL-FOL will serve as a common platform to support semantic interoperability among the different first-order based service ontologies, such as OWL-S [OWL-S 1.1].

Relationship between SWSL-FOL and SWSL-Rules. SWSL includes two separate sublanguages, because we believe that different tasks associated with Semantic Web services are better served by different knowledge representation formalisms.

SWSL-Rules is a rule-based language with non-monotonic semantics. Such languages are better suited for tasks that have programming flavor and that naturally rely on default information and inheritance. These tasks include service discovery, contracting, policy specification, and others. In addition, rule-based languages are quite common both in the industry and research, and many people are more comfortable using them even for tasks that may not require defaults, such as service profile specification. Applications of SWSL and of the ontology built using SWSL are discussed in the Application Scenarios document.

In contrast, first-order logic is found more suitable for specifying process ontologies. One of the most prominent examples that uses this approach is PSL [Gruninger03a]. SWSL-FOL was developed to satisfy this need. Unfortunately, first-order and nonmonotonic semantics cannot be used together in the same language, so SWSL provides a "bridge" between the two sublanguages by describing how one can work in either sublanguage and use specifications written in the other sublanguage. This bridge is described in section titled Combining SWSL-Rules and SWSL-FOL.

The basic idea is as follows. First, as shown in Figure 2.2, both sublanguages share a common and useful core where they coincide both syntactically and semantically. Second, section Combining SWSL-Rules and SWSL-FOL describes a methodology for translating SWSL-FOL specifications into SWSL-Rules with "minimal loss." This means that inferences made using the translated specification are sound with respect to the original SWSL-FOL specification, and the "lost" inferences (i.e., formulas that are derivable from the original but not from the translated specification) are, in some sense, minimized. This approach was used in translating the axioms of PSL Core and PSL Outer Core into SWSL-Rules in section PSL in SWSL-FOL and SWSL-Rules.

The layered structure of SWSL. Both SWSL-Rules and SWSL-FOL are presented as layered languages. Unlike OWL, the layers are not organized based on the expressive power and computational complexity. Instead, each layer includes a number of new concepts that enhance the modeling power of the language. This is done in order to make it easier to learn the language and to help understand the relationship between the different features. Furthermore, most layers that extend the core of the language (either SWSL-Rules or SWSL-FOL) are independent from each other -- they can be implemented all at once or in any partial combination. This can provide certain guidance to vendors who might be interested only in a particular subset of the features.

Complexity. The layers of SWSL are not organized around the complexity. In fact, except for the equality layer, which boosts the complexity, all layers have the same complexity and decidability properties. For SWSL-Rules, the most important reasoning task is query answering. The general problem of query answering is known to be only semi-decidable. However, there are large classes of problems that are decidable in polynomial time. The best-known, and perhaps the most useful, subclass consists of rules that do not use function symbols. However, many decidable classes of rules with function symbols are also known [Lindenstrauss97].

2 The Language

2.1 Overview of SWSL-Rules and SWSL-FOL

As mentioned in the introduction, SWSL consists of two separate sublanguages, which have layered structure. This section gives an overview of these layers.

The SWSL-Rules language is designed to provide support for a variety of tasks that range from service profile specification to service discovery, contracting, policy specification, and so on. The language is layered to make it easier to learn and to simplify the use of its various parts for specialized tasks that do not require the full expressive power of SWSL-Rules. The layers of SWSL-Rules are shown in Figure 2.1.

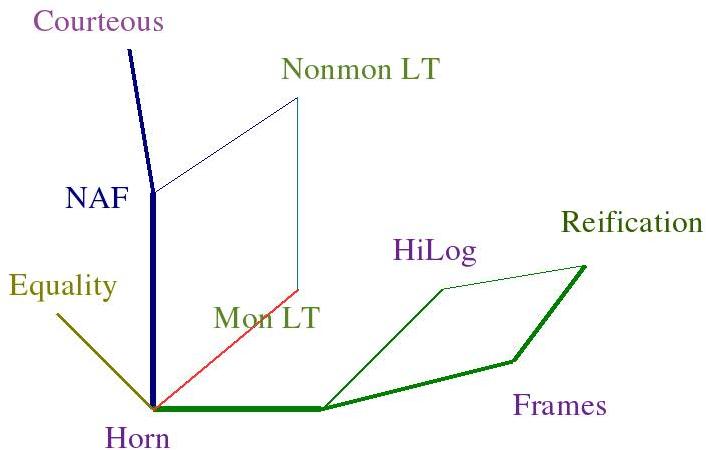
Figure 2.1: The Layered Structure of SWSL-Rules

The core of the language consists of the pure Horn subset of SWSL-Rules. The monotonic Lloyd-Topor (Mon LT) extension [Lloyd87] of the core permits disjunctions in the rule body and conjunction and implication in the rule head. NAF is an extension that allows negation in the rule body, which is interpreted as negation-as-failure. More specifically, negation is interpreted using the so called well-founded semantics [VanGelder91]. The nonmonotonic Lloyd-Topor extension (Nonmon LT) further permits quantifiers and implication in the rule body. The Courteous rules [Grosof99a] extension introduces two new features: restricted classical negation and prioritized rules. HiLog and Frames extend the language with a different kind of ideas. HiLog [Chen93] enables high degree of meta-programming by allowing variables to range over predicate symbols, function symbols, and even formulas. Despite these second-order features, the semantics of HiLog remains first-order and tractable. It has been argued [Chen93] that this semantics is more appropriate for many common tasks in knowledge representation than the classical second-order semantics. The Frames layer of SWSL-Rules introduces the most common object-oriented features, such as the frame syntax, types, and inheritance. The syntax and semantics of this extension is inspired by F-logic [Kifer95] and the followup works [Frohn94, Yang02, Yang03]. Finally, the Reification layer provides a mechanism for making objects out of a large class of SWSL-Rules formulas, which puts such formulas into the domain of discourse and allows reasoning about them.

All of the above layers have been implemented in one system or another and have been found highly valuable in knowledge representation. For instance, FLORA-2 [Yang04] includes all layers except Courteous rules and Nonmonotonic Lloyd-Topor. SweetRules [Grosof2004b] supports Courteous extensions, and Ontobroker [Ontobroker] supports Nonmonotonic Lloyd-Topor and frames.

Four points should be noted about the layering structure of SWSL-Rules.

1. The lines in Figure 2.1 represent inclusion dependencies among layers. For instance, Nonmonotonic LT layer includes both NAF and Monotonic LT. Reification includes HiLog and Frames, Courteous includes NAF, etc.
2. The different branches of Figure 2.1 are orthogonal and they all can be combined. For instance, the Frames and HiLog layers can be combined with the Courteous and Nonmon LT layers. Likewise, the equality layer can be combined with any other layer. Thus, SWSL-Rules is a unified language that combines all the layers into a coherent and powerful knowledge representation language.
3. Second, the Lloyd-Topor extensions and the Courteous rules extensions endow SWSL-Rules with all the normal first-order connectives. Therefore, syntactically SWSL-Rules contains all the connectives of the full first-order logic, which provides a bridge to SWSL-FOL. However, semantically the two sublanguages of SWSL are incompatible. Their semantics agree only over a relatively small, but useful subset of Horn rules. Section 5 discusses how the two sublanguages can be used together.
4. SWSL-Rules distinguishes between connectives with the classical first-order semantics and connectives that have nonmonotonic semantics. For instance, it uses two different forms of negation—naf, for negation-as-failure, and neg, for classical negation. Likewise, it distinguishes between the classical implication, <== and ==>, and the if-then connective :- used for rules.

SWSL-FOL is used to specify the dynamic properties of services, namely, the processes that they are intended to carry out. SWSL-FOL also has layered structure, which is depicted in Figure 2.2.

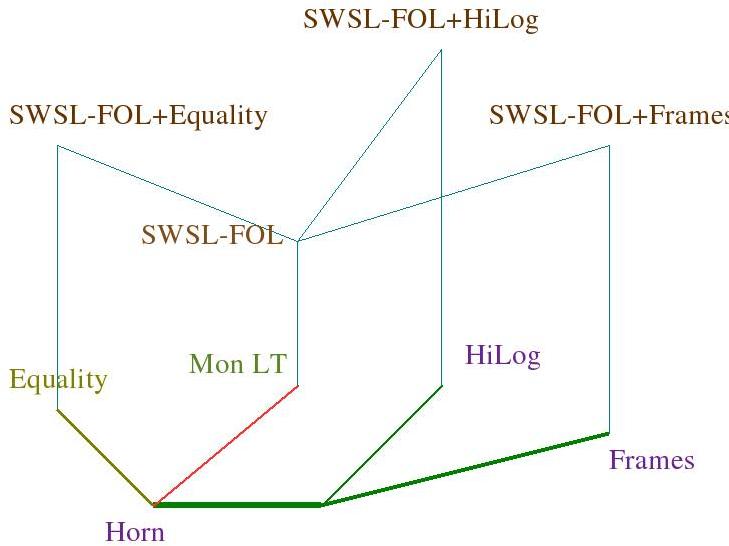
Figure 2.2: The Layers of SWSL-FOL and Their Relationship to SWSL-Rules

The bottom of Figure 2.2 shows those layers of SWSL-Rules that have monotonic semantics and therefore can be extended to full first-order logic. Above each layer of SWSL-Rules, the figure shows corresponding SWSL-FOL extension. The most basic extension is SWSL-FOL. The other three layers, SWSL-FOL+Equality, SWSL-FOL+HiLog, and SWSL-FOL+Frames extend SWSL-FOL both syntactically and semantically. Some of these extensions can be further combined into more powerful FOL languages. We discuss these issues in Section SWSL-FOL: The First-order Subset of SWSL.

2.2 Basic Definitions

In this section we define the basic syntactic components that are common to all layers of SWSL-Rules. Additional syntax will be added as more layers are introduced.

A constant is either a numeric value, a symbol, a string, or a URI.

• A numeric value is either an integer, a decimal, or a floating point number. For instance, 123, 34.9, 45e-11. See the section on SWSL data types for more details on the relationship between SWSL data types and the primitive data types in XML Schema.
• A symbol is a string of characters enclosed between a pair of single quotes. For instance, 'abc#$%'. Single quotes that are part of a symbol are escaped with the backslash. For instance, the symbol a'bc''d is represented as 'a\'bc\'\'d'. The backslash is escaped with another backslash. Symbols that consist exclusively of alphanumeric characters and the underscore (_) and begin with a letter or an underscore do not need to be quoted.
• Strings are sequences of characters that are enclosed between a pair of double quote symbols, e.g., "ab'%#cd". A double quote symbol that occurs in a string must be escaped with the backslash. For instance, the string ab"cd"""gf is represented as "ab\"cd\"\"\"gf".
• A SWSL-URI can come either in the form of a full URI or in the abbreviated form of an sQName.

  A full URI is a sequence of characters that has the form of a URI, as specified by IETF, and is enclosed between _" and ". For instance, _"http://w3.org/".

  An sQName has the form prefix#local-name. Here prefix is an alphanumeric symbol that is defined to be a shortcut for a URI as specified below; local-name is a string that must be acceptable as a path component in a URI. If local-name contains non-alphanumeric symbols, it must be enclosed in double quotes: e.g., "ab%20". An sQName is treated as a macro that expands into a full URI by concatenating the expansion of prefix (the URI represented by the prefix) with local-name. For the rationale behind the use of sQName see the entry for sQName in the Glossary.

A prefix declaration is a statement of the form

The prefix can then be used instead of the URI in sQNames. For instance, if we define

then the SWSL-URI _"http://www.w3.org/TR/xquery/" is considered to be equivalent to w3#"TR/xquery/"

A variable is an alphanumeric symbol (plus the underscore), which is prefixed with the ?-sign. Examples: ?_, ?abc23.

A first-order term is either a constant, a variable, or an expression of the form t(t1,...,tn), where t is a constant and t1,...,tn are first-order terms. Here the constant t is said to be used as a function symbol and t1,...,tn are used as arguments. Variable-free terms are also called ground.

Following Prolog, we also introduce special notation for lists: [t1,...,tn] and [t1,...,tn|rest], where t1,...,tn and rest are first-order terms. The first form shows all the elements of the list explicitly and the latter shows explicitly only a prefix of the list and uses the first-order term rest to represent the tail. We should note that, like in Prolog, this is just a convenient shorthand notation. Lists are nothing but first-order terms that are representable with function symbols. For instance, if cons denotes a function symbol that prepends a term to the head of a list then [a,b,c] is represented as first-order term cons(a,cons(b,c)).

A first-order atomic formula has the same form as first-order terms except that a variable cannot be a first-order atomic formula. We do not distinguish predicates as a separate class of constants, as this is usually not necessary, since first-order atomic formulas can be distinguished from first-order terms by the context in which they appear.

As many other rule-based languages, SWSL-Rules has a special unification operator, denoted =. The semantics of the unification operator is fixed and therefore it cannot appear in a rule head. An atomic formula of the form

where both terms are ground, is true if and only if the two terms are identical. If term₁ and term₂ have variables, then an occurrence of the above formula in a rule body is interpreted as a test of whether a substitution exists that can make the two terms identical. The = predicate is related to the equality predicate :=: introduced by the Equality Layer, which is discussed later.

To test that two terms do not unify SWSL-Rules uses the disunification operator !=. For ground terms, term₁ != term₂ iff the two terms are not identical. For non-ground terms, this is true if the two terms do not unify.

A conjunctive formula is either an atomic formula or a formula of the form

where and is a conjunction connective. Here and henceforth in similar definitions, italicized words will be meta-symbols that denote classes of syntactic entities. For instance, atomic formula above means ``any atomic formula.'' An and/or formula is either a conjunctive formula or a formula of either of the forms

In other words, an and/or formula can be an arbitrary Boolean combination of atomic formulas that involves the connectives and and or.

Comments. SWSL-Rules has two kinds of comments: single line comments and multiline comments. The syntax is the same as in Java. A single-line comment is any text that starts with a // and continues to the end of the current line. If // starts within a string ("...") or a symbol ('...') then these characters are considered to be part of the string or the symbol, and in this case they do not start a comment. A multiline comment begins with /* and end with a matching */. The combination /* does not start a comment if it appears inside a string or a symbol. The /* - */ pairs can be nested and a nested occurrence of */ does not close the comment. For instance, in

only the second */ closes the comment.

2.3 Horn Rules

A Horn rule has the form

where head is an atomic formula and body is a conjunctive formula.

A Horn query is of the form

where query is a conjunctive formula.

Rules can be recursive, i.e., the predicate in the head of a rule can occur (with the same arity) in the body of the rule; or they can be mutually recursive, i.e., a head predicate can depend on itself through a sequence of rules.

All variables in a rule are considered implicitly quantified with ∀ outside of the rule, i.e., ∀?X,?Y,...(head :- body). A variable that occurs in the body of a rule but not its head can be equivalently considered as being implicitly existentially quantified in the body. For instance,

is equivalent to

Sets of Horn rules have the nice property that their semantics can be characterized in three different and independent ways: through the regular first-order entailment, as a minimal model (which in this case happens to be the intersection of all Herbrand models of the rule set) and as a least fixpoint of the immediate consequence operator corresponding to the rule set [Lloyd87].

2.4 The Monotonic Lloyd-Topor Layer

This layer extends the Horn layer with three kinds of syntactic sugar:

1. Disjunction in the rule body
2. Conjunction in the rule head
3. It introduces the new symbols of classical implication and allows their use in the rule head.

A classical implication is a statement of either of the following forms:

The Lloyd-Topor implication (abbr., LT implication) is a special case of the classical implication where the formula in the head is a conjunction of atomic formulas and the formula in the body can contain both conjunctions and disjunctions of atomic formulas.

A classical bi-implication is a statement of the form

The Lloyd-Topor bi-implication (abbr., LT bi-implication) is a special case of the classical bi-implication where both formulas are conjunctions of atomic formulas.

The monotonic LT layer extends Horn rules in the following way. A rule still has the form

but head can now be a conjunction of atomic formulas and/or LT implications (including bi-implications) and body can consist of atomic formulas combined in arbitrary ways using the and and the or connectives.

This extension is considered a syntactic sugar, since semantically any set of extended rules reduces to another set of pure Horn rules as follows:

• head :- body1 or body2.

  reduces to

        head :- body1.
      head :- body2.
• head1 and head2 :- body.

  reduces to

        head1 :- body.
      head2 :- body.
• (head1 <== head2) :- body.

  reduces to

        head1 :- head2 and body.
• (head1 ==> head2) :- body.

  reduces to

        head2 :- head1 and body.

Complex formulas in the head are broken down using the last three reductions. Rule bodies that contain both disjunctions and conjunctions are first converted into disjunctive normal form and then are broken down using the first reduction rule.

2.5 The NAF Layer

The NAF layer add the negation-as-failure symbol, naf. For instance,

In SWSL-Rules we adopt the well-founded semantics [VanGelder91] as a way to interpret negation as failure. This semantics has good computational properties when no first-order terms of arity greater than 0 are involved, and the well-founded model is always defined and is unique. This model is three-valued, so some facts may have the ``unknown'' truth value.

We should note one important convention regarding the treatment of variables that occur under the scope of naf and that do not occur anywhere outside of naf in the same rule. The well-founded semantics was defined only for ground atoms and the interpretation of unbound variables was left open. Therefore, if Z does not occur elsewhere in the rule then the meaning of

can be defined as

or as

In practice, the second interpretation is preferred, and this is also a convention used in SWSL-Rules.

2.6 The Nonmonotonic Lloyd-Topor Layer

This layer introduces explicit bounded quantifiers (both exist and forall), classical implication symbols, <== and ==>, and the bi-implication symbol <==> in the rule body. This essentially permits arbitrary first-order-looking formulas in the body of SWSL-rules. We say "first-order-looking" because it should be kept in mind that the semantics of SWSL-Rules is not first-order and, for example, classical implication A <== B is interpreted in a non-classical way: as (A or naf B) rather than (A or neg B) (where neg denotes classical negation).

Recall that without explicit quantification, all variables in a rule are considered implicitly quantified with forall outside of the rule, i.e., forall ?X,?Y,...(head :- body). A variable that occurs in the body of a rule but not its head can be equivalently considered as being implicitly existentially quantified in the body. For instance,

is equivalent to

In the scope of the naf operator, unbound variables have a different interpretation under negation as failure. For instance, if ?X is bound and ?Y is unbound then

is actually supposed to mean

If we allow explicit universal quantification in the rule bodies then implicit existential quantification is not enough and explicit existential quantifier is needed. This is because forall and exist do not commute and so, for example, forall ?X exist ?Y and exist ?Y forall ?X mean different things. If only implicit existential quantification were available, it would not be possible to differentiate between the above two forms.

Formally, the Nonmonotonic Lloyd-Topor layer permits the following kinds of rules. The rule heads are the same as in the monotonic LT extension. The rule bodies are defined as follows.

• Any atomic formula is a legal rule body
• If f and g are legal rule bodies then so are
  •   f and g
  •   f or g
  •   naf f
  •   f ==> g
  •   f <== g
  •   f <==> g
• If f is a legal rule body then so is
  •   exist ?X1,...,?Xn(f)
  where ?X1, ..., ?Xn are variables that occur positively (defined below) in f.
• If g₁, g₂ are legal rule bodies then
  •   forall ?X1,...,?Xn(g₁ ==> g₂)
  •   forall ?X1,...,?Xn(g₂ <== g₁)
  are legal rule bodies provided that ?X1, ..., ?Xn occur positively in g₁

Positive occurrence of a free variable in a formula is defined as follows:

• Any variable occurs positively in an atomic formula
• A free variable occurs positively in f and g iff it occurs positively in either f or g.
• A free variable occurs positively in f or g iff it occurs positively in both f and g.
• A free variable occurs positively in f ==> g iff it occurs positively in g. Similarly for f <== g, except that now the variable must occur positively in f. Since f <==> g is a conjunction of two clauses, the definition of positive occurrence follows from the previous cases: the variable must occur positively in f or g.
• A free variable occurs positively in exist ?X1,...,?Xn(f) or forall ?X1,...,?Xn(f) iff it occurs positively in f.

The semantics of Lloyd-Topor extensions is defined via a transformation into the NAF layer as shown below. The theory behind this transformation is described in [Lloyd87].

Lloyd-Topor transformation: The transformation is designed to eliminate the extended forms that may occur in the bodies of the rules compared to the NAF layer. These extended forms involve the various types of implication and the explicit quantifiers. Note that the rules, below, must be applied top-down, that is, to the conjuncts that appear directly in the rule body. For instance, if the rule body looks like

then one should first apply the rule for <==, then the rules for forall should be applied to the result, and finally the rules for exist.

• Let the rule be of the form

        head :- body₁ and (f ==> g) and body₂.

  Then the LT transformation replaces it with the following pair of rules:

        head :- body₁ and naf f and body₂.
        head :- body₁ and g and body₂.

  The transformations for <== and <==> are similar.

• Let the rule be

        head :- body₁ and forall ?X1,...,?Xn(g₁ ==> g₂) and body₂.
  where ?X1,...,?Xn are free variables that occur positively in g₁.

  The LT transformation replaces this rule with the following pair of rules, where q(?X'1,...,?X'n) is a new predicate of arity n and ?X'1,...,?X'n are new variables:

        head :- body₁ and naf q(?X'1,...,?X'n) and body₂
        q(?X1,...,?Xn) :- g₁ and naf g₂.

  The transformation for <== is similar.

• Let the rule be

        head :- body₁ and exist ?X1,...,?Xn(f) and body₂.

  where ?X1,...,?Xn are free variables that occur positively in f.

  The LT transformation replaces this rule with the following:

        head :- body₁ and f and body₂

  That is, explicit existential quantification can be replaced in this case with implicit quantification.

The above transformations are inspired by (but are not derived from, due to a significant difference between naf and neg!) the classical tautologies (f ==> g) <==> (neg f or g)   and   forall X (f) <==> neg exist neg X (f), and by the fact mentioned in section The NAF Layer that naf p(X), when X does not occur anywhere else in the rule, is interpreted as forall X (naf p(X)).

2.7 The Courteous Rules Layer

The courteous layer introduces prioritized conflict handling. Four new features are introduced into the syntax:

• rule labels, which declare names used for prioritization between rules;
• classical negation of atoms;
• a syntactically reserved prioritization predicate, which is used to specify the prioritization ordering between rules;
• mutual exclusion (mutex) statements, which specify the scope of what constitutes conflict.

The theory behind the courteous logic programs is described in [Grosof2004a, Grosof99a].

The courteous layer builds upon the NAF layer of SWSL.

Rule Labels: Each rule has an optional label, which is used for specifying prioritization in conjunction with the prioritization predicate (below). The syntactic form of a rule label is a term enclosed by a pair of braces: { ... }. Thus, a labeled rule has the following form:

A label is a term, which may have variables. If so, these variables are interpreted as having the same scope as the implicitly quantified variables appearing in the rule expression. E.g., in the rule

the label specialoffer(?X) names the instance of the rule corresponding to the instance ?X. However, the label term may not itself be a variable, so the following is illegal syntax:

In general, labels are not unique; two or more rules (or instances of rules) may have the same label term. However, often it is convenient to specify rule labels uniquely within a particular given rulebase.

Classical Negation: The classical negation connective, neg, is permitted to appear within the head and/or the body of a rule. Its scope is restricted to be an atomic formula, however. Thus classical negation is restricted to appearing within a classical literal. For example:

However, the following example is illegal syntax because neg negates a non-atomic formula.

Note that the classical negation connective (neg) is also used in SWSL-FOL, the first-order subset of SWSL-Language. However, the semantics of classical negation in Courteous LP (and thus SWSL-Rules) is somewhat weaker than in FOL (and thus SWSL-FOL).

Prioritization Predicate: The prioritization predicate _"http://www.ruleml.org/spec/vocab/#overrides" specifies the prioritization ordering between rule labels, and thus between the rules labeled by those rule labels. The name of the prioritization predicate is syntactically reserved. In this document we will use the following prefix declaration

and abbreviate the prioritization predicate using the sQName r#overrides. In the future, we might adopt a different prefix, such as "http://www.swsi.org/swsl/reserved/#".

A statement r#overrides(label1,label2) indicates that the first argument, label1, has higher priority than the second argument, label2. For example, consider the following rulebase RBC1:

Here, the prioritization atom r#overrides(rep,qua) specifies that rep has higher priority than qua. Continuing that example, suppose the rulebase RBC1 also includes the facts:

Then, under the courteous semantics, the literal neg pacifist(nixon) is entailed as a conclusion, and the literal pacifist(nixon) is not entailed as a conclusion, because the rule labeled rep has higher priority than the rule labeled qua.

The prioritization predicate r#overrides, while its name is syntactically reserved, is otherwise an ordinary predicate -- it can appear freely in rules in the head and/or body. This is useful for reasoning about the prioritization ordering.

Mutual exclusion (mutex) statements: The scope of what constitutes conflict is specified by mutual exclusion (mutex) statements, which are part of the rule base and can be viewed as a kind of integrity constraint. Each such statement says that it is contradictory for a particular pair of literals (known as the "opposers") to be inferred, if an optional condition (known as the "given") holds true. The courteous LP semantics enforce that the set of sanctioned conclusions respects (i.e., is consistent with) all the mutexes within the given rulebase. Common uses for mutexes include specifying that two unary predicates are disjoint, or that a relation is functional; examples of these uses are given below.

A mutex without a given condition has the following syntactic form:

where lit1 and lit2 are classical literals. Intuitively, this statement means that it is a contradiction to derive both lit1 and lit2. For example:

says that it is a contradiction to conclude that the discount offered to the same customer ?CUST is both fivepercent and tenpercent. As another example,

specifies that it is a contradiction to conclude that the same individual is both a lion and an elephant.

A mutex with a condition has the following syntactic form:

Here condition is syntactically similar to a rule body, and lit1 and lit2 are classical literals. The symbol "|" is a language keyword, which separates the oposing literals from the condition. For example:

says that it is a contradiction to conclude that the discount offered to the same customer, ?CUST, is both ?Y and ?Z if ?Y and ?Z are distinct values. This means that the relation pricediscount is functional.

Courteous LP also assumes that there is an implicit mutex between each atom A and its classical negation neg A. This implicit mutex is also known as a "classical" mutex.

2.8 The HiLog Layer

HiLog [Chen93] extends the first-order syntax with higher-order features. In particular, it allows variables to range over function symbols, predicate symbols, and even atomic formulas. These features are useful for supporting reification and in cases when an agent needs to explore the structure of an unknown piece of knowledge. HiLog further supports parameterized predicates, which are useful for generic definitions (illustrated below).

• HiLog term (abbr., H-term): A HiLog term is either a first-order term or an expression of the following form: t(t1,...,tn), where t, t1, ..., tn are HiLog terms.

This definition may seem quite similar to the definition of complex first-order terms, but, in fact, it defines a vastly larger set of expressions. In first-order terms, t must be a constant, while in HiLog it can be any HiLog term. In particular, it can be a variable or even another first-order term. For instance, the following are legal HiLog terms:

• Regular first-order terms:   c, f(a,?X), ?X
• Variables over function symbols:   ?X(a,?Y), ?X(a,?Y(?X))
• Parameterized function symbols:   f(?X,a)(b,?X(c)), ?Z(?X,a)(b,?X(?Y)(d)), ?Z(f)(g,a)(p,?X)

We will see soon how such terms can be useful in knowledge representation.

• HiLog atomic formula: Any HiLog term is also a HiLog atomic formula.

Thus, expressions like ?X(a,?Y(?X)) are atomic formulas and thus can have truth values (when the variables are instantiated or quantified). What is less obvious is that ?X is also an atomic formula. What all this means is that atomic formulas are automatically reified and can be passed around by binding them to variables and evaluated. For instance, the following HiLog query

succeeds with the above database and ?X gets bound to p(a).

Another interesting example of a HiLog rule is

This can be viewed as a logical definition of the meta-predicate call/1 in Prolog. Such a definition does not make sense in first-order logic (and is, in fact, illegal), but it is legal in HiLog and provides the expected semantics for call/1.

We will now illustrate one use of the parameterized predicates of the form p(...)(...). The example shows a pair of rules that defines a generic transitive closure of a binary predicate. Depending on the actual predicate passed in as a parameter, we can get different transitive closures.

For instance, for the parent predicate, closure(parent) is defined by the above rules to be the ancestor relation; for the edge relation that represents edges in a graph, closure(edge) will become the transitive closure of the graph.

2.9 The Equality Layer

This layer introduces the full equality predicate, :=:. The equality predicate obeys the usual congruence axioms for equality. In particular, it is transitive, symmetric, reflexive, and the logical entailment relation is invariant with respect to the substitution of equals by equals. For instance, if we are told that bob :=: father(tom) (bob is the same individual as the one denoted by the term father(tom)) then if p(bob) is known to be true then we should be able to derive p(father(tom)). If we are also told that bob :=: uncle(mary) is true then we can derive father(tom):=: uncle(mary).

Equality in a Semantic Web language is important to be able to state that two different identifiers represent the same resource. For that reason, equality was part of OWL [OWL Reference]. Although equality drastically increases the computational complexity, some forms of equality, such as ground equality, can be handled efficiently in a rule-based language.

The equality predicate :=: is different from the unification operator = in several respects. First, for variable free terms, term₁ = term₂ if and only if the two terms are identical. In contrast, as we have just seen, two distinct terms can be equal with respect to :=:. Since :=: is reflective, it follows that the interpretation of :=: always contains the interpretation of =. Second, the unification operator = cannot appear in a rule head, while the equality predicate :=: can. When :=: occurs in the rule head (or as a fact), it is an assertion (maybe conditional) that two terms are equal. For instance, given the above definitions,

entails the following equalities between distinct terms: f(a,1):=:g(2,b) and f(a,2):=:g(3,b).

When term₁ :=: term₂ occurs in the body of a rule and term₁ and term₂ have variables, this predicate is interpreted as a test that there is a substitution that makes the two terms equal with respect to :=: (note: equal, not identical!). For instance, in the query

one answer substitution is ?X/1,?Y/2 and the other is ?X/2,?Y/3.

2.10 The Frames Layer

The Frames layer introduces object-oriented syntax modeled after F-logic [Kifer95] and its subsequent enhancements [Yang02, Yang03]. The main syntactic additions of this layer include

• Frame syntax. Frames are called molecules here (following the F-logic terminology).
• Path expressions.
• Notation for class membership and subclasses.
• Notation for type specification, which is given by signature molecules.

The object-oriented extensions introduced by the Frames layer are orthogonal to the other layers described so far and can be combined with them within the SWSL-Rules language.

As in most object-oriented languages, the three main concepts in the Frames layer of SWSL-Rules are objects, classes, and methods. (We are borrowing from the object-oriented terminology here rather than AI terminology, so we are refer to methods rather than slots.) Any class is also an object, and the same expression can denote an object or a class represented by this object in different contexts.

A method is a function that takes arguments and executes in the context of a particular object. When invoked, a method returns a result and can possibly alter the state of the knowledge base. A method that does not take arguments and does not change the knowledge base is called an attribute. An object is represented by its object Id, the values of its attributes, and by the definitions of its methods. Method and attribute names are represented as objects, so one can reason about them in the same language.

An object Id is syntactically represented by a ground term. Terms that do have variables are viewed as templates for collections of object Ids—one Id per ground instantiation of all the variables in the term. By term we mean any expression that can bind a variable. What constitutes a legal term depends on the layer. In the basic case, by term we mean just a first-order term. If the Frames layer is combined with HiLog, then terms are meant to be HiLog terms. Later, when we introduce reification, reification terms will also be considered.

Molecules. Molecules play the role of atomic formulas. We first describe atomic molecules and then introduce complex molecules. Although both atomic and complex molecules play the role of atomic formulas, complex molecules are not indivisible. This is why they are called molecules and not atoms. Molecules come in several different forms:

• Value molecule. If t, m, v are terms then t[m -> v] is a value molecule.

  Here t denotes an object, m denotes a method invocation in the scope of the object t, and v denotes a value that belongs to a set returned by this invocation. We call m ``a method invocation'' because if m = s(t1,...,tn), i.e., has arguments, then t[s(t1,...,tn) -> v] is interpreted as an invocation of method s on arguments t1,...,tn in the context of the object t, which returns a set of values that contains v.

  The syntax t[m -> {v1,...,vk}] is also supported; it means that if m is invoked in the context of the object t then it returns a set that contains v1,...,vk. Thus, semantically, such a term is equivalent to a conjunction of t[m -> v1], ..., t[m -> vk], so the expressions t[m -> {v1,...,vk}] is just a syntactic sugar.

• Boolean valued molecule. These molecules have the form t[m] where t and m are terms.

  Boolean molecules are useful to specify things like mary[female]. The same could be alternatively written as mary[female -> true], but this is less natural.

• Class membership molecule. If t and s are terms then t:s is a membership molecule.

  If t and s are variable free, then such a molecule states that the object t is a member of class s. If these terms contain variables, then such a molecule can be viewed as many class membership statements, one per ground instantiation of the variables.

• Subclass molecule: If t and s are terms then t::s is a subclass molecule.

  If t and s are variable free, then such a molecule states that the object t is a subclass of s. As in the case of class membership molecules, subclass molecules that have variables can be viewed as statements about many subclass relationships.

• Signature molecule: If t, m, v are terms then t[m => v] is a signature molecule.

  If t, m, and v are variable-free terms then the informal meaning of the above signature molecule is that t represents a class, which has a method invocation m which returns a set of objects of type v (i.e., each object in the set belongs to class v). If these terms are non-ground then the signature represents a collection of statements—one statement per ground instantiation of the terms.

  When m itself has arguments, for instance m = s(t1,...,tn), then the arguments are interpreted as types. Thus, t[s(t1,...,tn) => v] states that when the n-ary method s is invoked on object of class t with arguments that belong to classes t1, ..., tn, the method returns a set of objects of class v.

• Boolean signature molecules: A Boolean signature molecule has the form t[m=>]. Its purpose is to provide type information for Boolean valued molecules. Namely, if m=s(t1,...,tn), then when the method s is invoked on an object of class t, the method arguments must belong to classes t1, ..., tn.

• Cardinality constraints: Signature molecules can have associated cardinality constraints. Such molecules have the form

        t[s(t1,...,tn) {min : max} => v]

  where min and max are non-negative integers such that min ≤ max. Max can also be *, which means positive infinity.

  Such a signature states not only that the invocation of the method s with arguments of type t1,...,tn on an object of class t returns objects of class v, but also that the number of such objects in the result is no less than min and no more than max.

  The semantics of constraints in SWSL-Rules is similar to constraints in databases and is unlike the cardinality restrictions in OWL [OWL Reference]. For instance, if a cardinality constraint says that an attribute should have at least two values and the rule base derives only one then the constraint is violated. In contrast, OWL would infer that there is another, yet unknown, value. Likewise, if a cardinality constraint says that the number of elements is at most three while the rule base derives four unequal elements then the constraint is, again, violated. This should be compared to the OWL semantics, which will infer that some pair of derived values in fact consists of equal elements.

Signatures and type checking: Signatures are assertions about the expected types of the method arguments and method results. They typically do not have direct effect on the inference (unless signatures appear in rule bodies). The signature information is optional.

The semantics of signatures is defined as follows. First, the intended model of the knowledge base is computed (which in SWSL-Rules is taken to be the well-founded model). Then, if typing needs to be checked, we must verify that this intended model is well-typed. A well-typed model is one where the value molecules conform to their signatures. For the precise definition of well-typed models see [Kifer95]. (There can be several different notions of well-typed models. For instance, one for semi-structured data and another for completely structured data.)

A type-checker can be written in SWSL-Rules using just a few rules. Such a type checker is a query, which returns "No", if the model is well-typed and a counterexample otherwise. In particular, type-checking has the same complexity as querying. An example of such type checker can be found in the FLORA-2 manual [Yang04].

It is important to be aware of the fact that the semantics of the cardinality constraints in signature molecules is inspired by database theory and practice and it is different from the semantics of such constraints in OWL [OWL Reference]. In SWSL-Rules, cardinality constraints are restrictions on the intended models of the knowledge base, but they are not part of the axioms of the knowledge base. Therefore, the intended models of the knowledge base are determined without taking the cardinality constraints into the account. Intended models that do not satisfy these restrictions are discarded. In contrast, in OWL cardinality constraints are represented as logical statements in the knowledge base and all models are computed by taking the constraints into the account. Therefore, in OWL it is not possible to talk about knowledge base updates that violate constraints. For instance, the following signature married[spouse {1:1} => married] states that every married person has exactly one spouse. If john:married is true but there is no information about John's spouse then OWL will assume that john has some unknown spouse, while SWSL-Rules will reject the knowledge base as inconsistent. If, instead, we know that john[spouse -> mary] and john[spouse -> sally] then OWL will conclude that mary and sally are the same object, while SWSL-Rules will again rule the knowledge base to be inconsistent (because, in the absence of the information to the contrary — for example, if no :=:-statements have been given — mary and sally will be deemed to be distinct objects).

Inheritance in SWSL-Rules: Inheritance is an optional feature, which is expressed by means of the syntactic features described below. In SWSL-Rules, methods and attributes can be inheritable and non-inheritable. Non-inheritable methods/attributes correspond to class methods in Java, while inheritable methods and attributes correspond to instance methods.

The value- and signature-molecules considered so far involve non-inheritable attributes and methods. Inheritable methods are defined using the *-> and *=> arrow types, i.e., t[m *-> v] and t[m *=> v]. For Boolean methods we use t[*m] and t[m*=>].

Signatures obey the laws of monotonic inheritance, which are as follows:

• t:s and s[m *=> v] entails t[m *=> v]
• t::s and s[m *=> v] entails t[m => v]

These laws state that type declarations for inheritable methods are inherited to subclasses in an inheritable form, i.e., they can be further inherited. However, to the members of a class such declarations are inherited in a non-inheritable form. Thus, inheritance of signatures is propagated through subclasses, but stops once it hits class members.

Inheritance of value molecules is more involved. This type of inheritance is nonmonotonic and it can be overridden if the same method or attribute is defined for a more specific class. More precisely,

• t:s and s[m *-> v] entails t[m *-> v]   unless overridden or in conflict
• t::s and s[m *-> v] entails t[m -> v]   unless overridden or in conflict

Similarly to signatures, value molecules are inherited to subclasses in the inheritable form and to members of the classes in the non-inheritable form. However, the key difference is the phrase "unless overridden or in conflict." Intuitively, this means that if, for example, there is a class w in-between t and s such that the inheritable method m is defined there then the inheritance from s is blocked and m should be inherited from w instead. Another situation when inheritance might be blocked arises due to multiple inheritance conflicts. For instance, if t is a subclass of both s and u, and if both s and u define the method m, then inheritance of m does not take place at all (either from s or from u; this policy can be modified by specifying appropriate rules, however). The precise model-theoretic semantics of inheritance with overriding is based on an extended form of the Well-Founded Semantics. Details can be found in [Yang02].

Note that signature inheritance is not subject to overriding, so every inheritable molecule is inherited to subclasses and class instances. If multiple molecules are inherited to a class member or a subclass, then all of them are considered to be true.

Inheritance of Boolean methods is similar to the inheritance of methods and attributes that return non-Boolean values. Namely,

• t:s and s[m*=>] entails t[m*=>]
• t::s and s[m*=>] entails t[m =>]
• t:s and s[*m] entails t[*m]   unless overridden
• t::s and s[*m] entails t[m]   unless overridden

Complex molecules: SWSL-Rules molecules can be combined into complex molecules in two ways:

• By grouping.
• By nesting.

Grouping applies to molecules that describe the same object. For instance,

is, by definition, equivalent to

Molecules connected by the or connective can also be combined using the usual precedence rules:

becomes

The and connective inside a complex molecule can also be replaced with a comma, for brevity. For example,

Nesting applies to molecules in the following ``chaining'' situation, which is a common idiom in object-oriented databases:

is by definition equivalent to

Nesting can also be used to combine membership and subclass molecules with value and signature molecules in the following situations:

are equivalent to

respectively.

Molecules can also be nested inside predicates and terms with a semantics similar to nesting inside other molecules. For instance, p[a->c] is considered to be equivalent to p(a) and a[b->c]. Deep nesting and, in fact, nesting in any part of another molecule or predicate is also allowed. Thus, the formulas

are considered to be equivalent to

respectively. Note that molecule nesting leads to a completely compositional syntax, which in our case means that molecules are allowed in any place where terms are allowed. (Not all of these nestings might look particularly natural, e.g., a[b -> c](q,r) or p(a[b -> c](?X)), but there is no good reason to reject these nestings and thus complicate the syntax either.)

Path expressions: Path expressions are useful shorthands that are widely used in object-oriented and Web languages. In a logic-based language, a path expression sometimes allows writing formulas more concisely by eliminating multiple nested molecules and explicit variables. SWSL-Rules defines path expressions only as replacements for value molecules, since this is where this shorthand is most useful in practice.

A path expression has the form

or

The former corresponds to non-inheritable molecules and the latter to inheritable ones. In fact, "." and "!" can be mixed within the same path expression.

A path expression can occur anywhere where a term is allowed to occur. For instance, a[b -> c.d], a.b.c[e -> d], p(a.b), and X=a.b are all legal formulas. The semantics of path expressions in the body of a rule and in its head are similar, but slightly different. This difference is explained next.

In the body of a rule, an occurrence of the first path expression above is treated as follows. The conjunction

is added to the body and the occurrence of the path expression is replaced with the variable ?Var_n. In this conjunction, the variables ?Var1, ..., ?Varn are new and are used to represent intermediate values. The second path expression is treated similarly, except that the conjunction

is used. For instance, mary.father.mother = sally in a rule body is replaced with

In the head of a rule, the semantics of path expressions is reduced to the case of a body occurrence as follows.. If a path expression, ρ, occurs in the head of a rule, it is replaced with a new variable, ?V, and the predicate ?V=ρ is conjoined to the body of the rule. For instance,

is understood as

Note that since molecules can appear wherever terms can, path expressions of the form a.b[c -> d].e.f[g -> h].k are permitted. They are conceptually similar to XPath expressions with predicates that control the selection of intermediate nodes in XML documents. Formally, such a path expression will be replaced with the variable ?V and will result in the addition of the following conjunction:

It is instructive to compare SWSL-Rules path expressions with XPath. SWSL-Rules path expressions were originally proposed for F-logic [Kifer95] several years before XPath. The purpose was to extend the familiar notation in object-oriented programming languages and to adapt it to a logic-based language. It is easy to see that the ``*'' idiom of XPath can be captured with the use of a variable. For instance, b/*/c applied to object e is expressed as e.b.?X.c. The ``..'' idiom of XPath is also easy to express. For instance, a//submissions/2005/b/c applied to object d is expressed as ?_[?_ -> d.a].b.c. On the other hand, there is no counterpart for the // idiom of XPath. The reason is that this idiom is not well-defined when there are cycles in the data (for instance, a[b -> a]). However, recursive descent into the object graph can be defined via recursive rules.

2.11 Reification

The reification layer allows SWSL-Rules to treat certain kinds of formulas as terms and therefore to manipulate them, pass them as parameters, and perform various kinds of reasoning with them. In fact, the HiLog layer already allows certain formulas to be reified. Indeed, since any HiLog term is also a HiLog atomic formula, such atomic formulas are already reifiable. However, the reification layer goes several steps further by supporting reification of arbitrary rule or formula that can occur in the rule head or rule body. (Provided that it does not contain explicit quantifiers -- see below.)

Formally, if F is a formula that has the syntactic form of a rule head, a rule body, or of a rule then F is also considered to be a term. This means that such a formula can be used wherever a term can occur.

Note that a reified formula represents an objectification of the corresponding formulas. This is useful for specifying ontologies where objects represent theories that can be true in some worlds, but are not true in the present world (and thus those theories cannot be asserted in the present world). Examples include the effects of actions: effects of an action might be true in the world that will result after the execution of an action, but they are not necessarily true now.

In general, reification of formulas can lead to logical paradoxes [Perlis85]. The form of reification used in SWSL-Rules does not cause paradoxes, but other unpleasantries can occur. For instance, the presences of a truth axiom (true(?X) <--> ?X) can render innocently looking rule-bases inconsistent. However, as shown in [Yang03], the form of reification in SWSL-Rules does not cause paradoxes as long as

• rule heads do not contain classical negation; and
• a rule head cannot be a variable, i.e., as long as the rules of the form  ?X :- body  (which are legal in HiLog) are disallowed.

We therefore adopt the above restrictions for all layers of SWSL-Rules (but not for SWSL-FOL).

As presented above, reification introduces syntactic ambiguity, which arises due to the nesting conventions for molecules. For instance, consider the following molecule:

Suppose that t is a reification of another molecule, c[d -> e]. Since we have earlier said that any formula suitable to appear in the rule body can also be viewed as a term, we can expand the above formula into

But this is ambiguous, since earlier we defined the above as a commonly used object-oriented idiom, a syntactic sugar for

Similarly, if we want to write something like t[b -> c] where t is a reification of f[g -> h] then we cannot write f[g -> h][b -> c] because this nested molecule is a syntactic sugar for f[g -> h] and f[b -> c]. To resolve this ambiguity, we introduce the reification operator, ${...}, whose only role is to tell the parser that a particular occurrence of a nested molecule is to be treated as a term that represents a reified formula rather than as syntactic sugar for the object-oriented idiom.

Note that the explicit reification operator is not required for HiLog predicates because there is no ambiguity. For instance, we do not need to write ${p(?X)} below (although it is permitted and is considered the same as p(?X)):

This is because a[b -> p(?X)] does not mean   a[b -> p(?X)] and p(?X), since the sugar is used only for nested molecules.

In contrast, explicit reification is needed below, if we want to reify p(?X[foo -> bar]):

Otherwise p(?X[foo -> bar]) would be treated as syntactic sugar for sugar for

Therefore, to reify p(?X[foo -> bar]) in the above molecule one must write this instead:

Example. Reification in SWSL-Rules is very powerful and yet it doesn't add to the complexity of the language. The following fragment of a knowledge base models an agent who believes in the modus ponens rule:

Since the agent believes in p(a) and in the modus ponens rule, it can infer q(a). Note that in the above we did not need explicit reification of p(a), since no ambiguity can arise. However, we used the explicit reification anyway, for clarity.

Syntactic rules. Currently SWSL-Rules does not permit explicit quantifiers under the scope of the reification operator, because the semantics for reification given in [Yang03, Kifer04] does not cover this case. So not every formula can be reified. More specifically, the formulas that are allowed under the scope of the reification operator are:

• The formulas that are allowed in the rule head or quantifier-free formulas in the rule body.
• Quantifier-free rules.

The implication of these restrictions is that every term that represents a reification of a SWSL-Rules formula has only free variables, which can be bound outside of the term. Each such term can therefore be viewed as a (possibly infinite) set of reifications of the ground instances of that formula.

2.12 Skolemization in SWSL-Rules

It is often necessary to specify existential information in the head of a rule or in a fact. Due to the limitations of the logic programming paradigm, which trades the expressive power for executional efficiency, such information cannot be specified directly. However, existential variables in the rule heads can be approximated through the technique known as Skolemization [Chang73]. The idea of Skolemization is that in a formula of the form ∀ Y1...Yn∃ X ... φ the existential variable X can be removed and replaced everywhere in φ with the function term f(Y1...Yn), where f is a new function symbol that does not occur anywhere else in the specification. The rationale for such a substitution is that, for any query, the original rule base is unsatisfiable if and only if the transformed rule base is unsatisfiable [Chang73]. This implies that the query to the original rule base can be answered if and only if it can be answered when posed against the Skolemized rule base. However, from the point of view of logical entailment, the Skolemized rule base is stronger than the original one, and this is why we say that Skolemization only approximates existential quantification, but is not equivalent to it.

Skolemization is defined for formulas in prenex normal form, i.e., formulas where all the quantifiers are collected in a prefix to the formula and apply to the entire formula. A formula that is not in the prenex normal form can be converted to one in the prenex normal form by a series of equivalence transformations [Chang73].

SWSL-Rules supports Skolemization by providing special constants _# and _#1, _#2, _#3, and so on. As with other constants in SWSL, these symbols can be used both in argument positions and in the position of a function. For instance, _#(a,_#,_#2(c,_#2)) is a legal function term.

Each occurrence of the symbol _# denotes a new constant. Generation of such a constant is the responsibility of the SWSL-Rules compiler. For instance, in _#(a,_#,_#2(c,_#2)), the two occurrences of _# denote two different constants that do not appear anywhere else. In the first case, the constant is in the position of a function symbol. The numbered Skolem constants, such as _#2 in our example, also denote a new constant that does not occur anywhere else in the rule base. However, the different occurrences of the same numbered symbol in the same rule denote the same new constant. Thus, in the above example the two occurrences of _#2 denote the same new symbol. Here is a more complete example:

In the first line, the two occurrences of _#1 denote the same new Skolem constant, since they occur in the scope of the same rule. In the second line, the occurrence of _# denotes a new Skolem function symbol. Since we used _# here, this symbol is distinct from any other constant. Note, however, that even if we used _#1 in the second rule, that symbol would have denoted a distinct new function symbol, since it occurs in a separate rule and there is no other occurrence of _#1 in that rule.

The Skolem constants in SWSL-Rules are in some ways analogous to the blank nodes in RDF. However, they have the semantics suitable for a rule-based language and it has been argued in [Yang03] that the Skolem semantics is superior to RDF, which relies on existential variables in the rule heads [Hayes04].

2.13 SWSL-Rules and XML Schema Data Types

SWSL-Rules supports the primitive XML Schema data types. However, since SWSL-Rules is quite different from XML, it adapts the lexical representation for XML data types to the form that is more suitable for a logic-based language. The translation from the XML lexical representation of primitive data types to SWSL-Rules is straightforward.

The general rule is that each primitive value is represented by a function term whose functor symbol is the name of the primitive data type prefixed with an underscore (_). The arguments of the term represent the various components of the primitive data type. For instance, _string("abc"), _date(2005,7,18), _decimal(123.56), _integer(321), _float(23e5), and so on.

The string, decimal, integer, and float data types have a shorthand notation (some of which had been seen before). Thus, _string("abc") is abbreviated to "abc", _decimal(123.56) to 123.56, _integer(321) to 321, and _float(23e5) to 23e5.

Other primitive data types are represented using a similar notation. For instance, the duration of 1 year, 2 months, 3 days, 10 hours, and 30 minutes is represented as _duration(1,2,3,10,30,0) where the first argument of _duration represents years and the last seconds. The same negative duration is represented as -_duration(1,2,3,10,30,0). For another example, the values of the dateTime type are represented as _dateTime(2005,10,29,15,55,40).

It is often necessary to exchange values of primitive data types between applications. Since the internal representations of the data types vary from language to language, serialization into a commonly agreed representation has been used for this purpose. SWSL-Rules supports serialization of primitive data types via the built-in predicate _serialize. It takes three arguments: a SWSL-Rules value of a SWSL-Rules data type, a URI that denotes the target of serialization, and a result, which is a string that contains the serialized value. Currently, the only target is http://www.w3.org/2001/XMLSchema, which refers to XML Schema 1.0. Other targets will be added as necessary (for example, for XML Schema 1.1 when it is released). Example: _serialize(_date(2005,1,1),_"http://www.w3.org/2001/XMLSchema",?Result) binds ?Result to "2005-01-01".

The predicate _serialize is intended to work both ways: for serialization and deserialization. Deserialization occurs when the last argument is bound to a string representation of a data type and the first argument is unbound. For instance, _serialize(?Result,_"http://www.w3.org/2001/XMLSchema","2005-01-01") binds ?Result to _date(2005,1,1).

2.14 Semantics of SWSL-Rules

A single point of reference for the model-theoretic semantics of SWSL-Rules will be given in a separate document. Here we will only give an overview and point to the papers where the semantics of the different layers were defined separately.

First, we note that the semantics of the Lloyd-Topor leyers -- both monotonic and nonmonotonic -- is transformational and was given in Sections 2.4 and 2.6. Similarly, the Courteous layer is defined transformationally and is described in [Grosof2004a].

The model theory of NAF is given by the well-founded semantics as described in [VanGelder91]. The model theory behind HiLog is described in [Chen93] and F-logic is described in [Kifer95]. The semantics of inheritance that is used in SWSL-Rules is defined in [Yang02]. The model theory of reification is given in [Yang03] and was further extended to reification of rules in [Kifer04].

The semantics of the Equality layer is based on the standard semantics (for instance, [Chang73]) but is modified by the unique name assumption, which states that syntactically distinct terms are unequal. This modification is described in [Kifer95], and we summarize it here. First, without equality, SWSL-Rules makes the unique name assumption. With equality, the unique name assumption is modified to say that terms that cannot be proved equal with respect to :=: are assumed to be unequal. In other words, SWSL-Rules makes a closed world assumption about explicit equality.

Other than that, the semantics of :=: is standard. The interpretation of this predicate is assumed to be an equivalence relation with congruence properties. A layman's term for this is "substitution of equals by equals." This means that if, for example, t:=:s is derived for some terms t and s then, for any formula φ, it is true if and only if ψ is true, where ψ is obtained from φ by replacing some occurrences of t with s.

Overall, the semantics of SWSL-Rules has nonmonotonic flavor even without NAF and its extension layers. This is manifested by the use of the unique name assumption (modified appropriately in the presence of equality) and the treatment of constraints. To explain the semantics of constraints, we first need to explain the idea of canonic models.

In classical logic, all models of a set of formulas are created equal and are given equal consideration. Nonmonotonic logics, on the other hand, carefully define a subset of models, which are declared to be canonical and logical entailment is considered only with respect to this subset of models. Normally, the canonical models are so-called minimal models, but not all minimal models are canonical.

Any rule set that does not use the features of the NAF layer and its extensions is known to have a unique minimal model, which is also its canonical model. This is an extension of the well-known fact for Horn clauses in classical logic programming [Lloyd87]. With NAF, a rule set may have multiple incomparable minimal models, and it is well-known that not all of these models appropriately capture the intended meaning of rules. However, it turns out that one such model can be distinguished, and it is called the well-founded model [VanGelder91]. A formula is considered to be true according to the SWSL-Rules semantics if and only if it is true in that one single model, and the formula is false if and only if it is false in that model.

Now, in the presence of constraints, the semantics of SWSL-Rules is defined as follows. Given a rulebase, first its canonical model is determined. In this process, all constraints are ignored. Next, the constraints are checked in the canonical model. If all of them are true, the rulebase is said to be consistent. If at least one constraint is false in the canonical model, the constraint is said to be violated and the rulebase is said to be inconsistent.

2.15 SWSL-FOL: The First-order Subset of SWSL

The SWSL language includes all the connectives used in first-order logic and, therefore, syntactically first-order logic is a subset of SWSL. When the semantics of first-order connectives differs from their nonmonotonic interpretation, new nonmonotonic connectives are introduced. For instance, first-order negation, neg, has a nonmonotonic counterpart naf and first-order implications <== and ==> have a nonmonotonic counterpart :-.

It follows from the above that SWSL-Rules and SWSL-FOL share significant portions of their syntax. In particular, every connective used in SWSL-FOL can also be used in SWSL-Rules. However, not every first-order formula in SWSL-FOL is a rule and the rules in SWSL-Rules are not first-order formulas (because of ":-"). Therefore, neither SWSL-FOL is a subset of SWSL-Rules nor the other way around. Furthermore, even though the classical connectives neg and ==>/<== can occur in SWSL-Rules, they are embedded into an overall nonmonotonic language and their semantics cannot be said to be exactly first-order.

Formally, SWSL-FOL consists of the following formulas:

• First-order atomic formulas
• If φ and ψ are SWSL-FOL formulas then so are   φ and ψ,   φ or ψ,   neg φ,   φ ==> ψ,   φ <== ψ,   and   φ <==> ψ.
• If φ is a SWSL-FOL formula and X is a variable, then the following are also SWSL-FOL formulas:   exist ?X (φ)   and   forall ?X (φ).   SWSL-FOL allows to combine quantifiers of the same sort, so   exist ?X,?Y (φ)   is the same as   exist ?X exist ?Y (φ).

As in the case of SWSL-Rules, we will ise the period (".") to designate the end of a SWSL-FOL formula.

SWSL defines three extensions of SWSL-FOL. The first extension adds the equality operator, :=:, the second incorporates the object-oriented syntax from the Frames layer of SWSL-Rules, the third does the same for the HiLog layer.

Formally, SWSL-FOL+Equality has the same syntax as SWSL-FOL, but, in addition, the following atomic formulas are allowed:

• term :=: term

SWSL-FOL+Frames has the same syntax as SWSL-FOL except that, in addition, the following is allowed:

• SWSL-Rules molecules, as defined in the Frames layer are valid SWSL-FOL formulas.
• The path expressions defined of the SWSL-Rules Frames syntax are not used in SWSL-FOL. In SWSL-Rules, path expressions are interpreted differently in the rule head and body. Since SWSL-FOL does not distinguish the head of a rule from its body, the path expression syntax is not well-defined in this context.

SWSL-FOL+HiLog extends SWSL-FOL by allowing HiLog terms and HiLog atomic formulas instead of first-order terms and first-order atomic formulas.

Each of these extensions is not only a syntactic extension of SWSL-FOL but also a semantic extension. This means that if φ and ψ are formulas in SWSL-FOL then φ |= ψ in SWSL-FOL if and only if the same holds in SWSL-FOL+Equality, SWSL-FOL+Frames, and SWSL-FOL+HiLog. We will say that SWSL-FOL+Equality, SWSL-FOL+Frames, and SWSL-FOL+HiLog are conservative semantic extensions of SWSL-FOL.

SWSL-FOL+HiLog and SWSL-FOL+Frames can be combined both syntactically and semantically. The resulting language is a conservative semantic extension of both SWSL-FOL+HiLog and SWSL-FOL+Frames. Similarly, SWSL-FOL+Equality and SWSL-FOL+Frames can be combined and the resulting language is a conservative extension of both. Interestingly, combining SWSL-FOL+Equality with SWSL-FOL+HiLog leads to a conservative extension of SWSL-FOL+HiLog, but not of SWSL-FOL+Equality! More precisely, if φ and ψ are formulas in SWSL-FOL+Equality and φ |= ψ then the same holds in SWSL-FOL+HiLog. However, there are formulas such that φ |= ψ holds in SWSL-FOL+HiLog but not in SWSL-FOL+Equality [Chen93].

2.16 Semantics of SWSL-FOL

The semantics of the first-order sublanguage of SWSL is based on the standard first-order model theory and is monotonic. The only new elements here are the higher-order extension that is based on HiLog [Chen93] and the frame-based extension based on F-logic [Kifer95]. The respective references provide a complete model theory for these extensions, which extends the standard model theory for first-order logic.

2.17 Future Extensions

To enhance the power of the SWSL-Rules language, a number of extensions are being planned, as described below.

• If-then-else. The if test then test1 is sometimes more convenient and familiar than the ==> operator. More important, however, is the fact that the more complete idiom, if test then test1 else test2, is known to be very useful and common in rule-based languages. Although the else-part can be expressed with negation as failure, this is not natural and most well-developed languages support the if-then-else idiom directly. This idiom may be added to SWSL-Rules later.

• Aggregate operators. Aggregate operators, such as sum, average, etc., are important database operations. XML languages such as XPath, XSLT, and XQuery all have support for aggregation. Of these, only XQuery permits aggregation over general set comprehension. A future extension of SWSL-Rules will allow aggregation in the style of FLORA-2, which supports explicit set comprehension and nested aggregation. The general syntax of such aggregation is:

        ?Result = aggregate{?Var [GroupingVarList] | Query }

  where aggregate can be max, min, avg, count, sum, collectset, collectbag. The last two aggregates return lists of the instantiations of ?Var that satisfy Query without the duplicates (collectset) and with possible duplicates (collectbag).

  The grouping variables provide the functionality similar to GROUP BY of SQL. They have the effect that the aggregation produces one list of results per every instantiation of the variables in GroupingVarList for which Query has a solution. The variable ?Result gets successively bound to each such list (one list at a time).

• Constraints. Constraints play a very important role in database and knowledge base applications. As a future extension, SWSL-Rules will have database-style constraints. Database constraints are different in nature from restrictions used in Description Logic. Whereas restrictions in Description Logic are part of the same logical theory as the rest of the statements and are used to derive new statements, constraints in databases are not used to derive new information. Instead, they serve as tests of correctness for the canonical models of the knowledge base. In this framework, canonical models (e.g., the well-founded model [VanGelder91]) are first computed without taking constraints into account. These models are then checked against the constraints. The models that do not satisfy the constraints are discarded. In the case of the well-founded semantics, which always yields a single model, testing satisfaction of the constraints validates whether the knowledge base is in a consistent state.

• Procedural attachments, state changes à la Transaction Logic, situated logic programs. A procedural attachment is a predicate or a method that is implemented by an external procedure (e.g., in Java or Python). Such a procedure can have a side effect on the real world (e.g., sending an email or activating a device) or it can receive information from the outside world. First formalizations of these ideas in the context of database and rule based languages appeared in [Maier81, Chimenti89]. These ideas were recently explored in [Grosof2004a] in the context of e-commerce. Transaction Logic [Bonner98] provides a seamless integration of these concept into the logic.

  An attached procedure can be specified by a link statement, which associates a predicate or a method with an external program. The exact details of the syntax have not been finalized, but the following is a possibility:

        attachment relation/Arity name-of-java-procedure(integer,string,...)

  This syntax can be generalized to include object-oriented methods.

  Another necessary extension involves update primitives - primitives for changing the underlying state of the knowledge. These primitives can add or delete facts, and even add or delete rules. A declarative account of such update operations in the context of a rule-based language is given by Transaction Logic [Bonner98]. This logic also can also be used to represent triggers (also known as ECA rules) [Bonner93].

• Predicates with named arguments. For predicates with ordered arguments, named attributes are essentially supported by the current syntax. For instance, if -> is viewed as an infix binary function symbol, then p(foo -> 1, bar -> 2) is a valid term in SWSL-Rules. Predicates with unordered arguments can make unification exponential and are unlikely to be supported in the future.

• The "rest"-variables. The ``rest'' notation à la SCL can be useful in metaprogramming. A rest-variable binds to a list of variables or terms and it always occurs as the last variable of a term. During unification with another term, such a variable binds to a list of arguments of that term beginning with argument corresponding to the variable till the rest of the term (whence the name of such variables). For instance, in the following term, ?R is a rest-variable:

        p(?X,?Y | ?R)

  If this term is unified with p(?Z,f,?Z,q), then ?X binds to ?Z, ?Y to f, and ?R to the list [?Z,q].

• Non-ground identity relation, ==. This predicate is true if the arguments are identical up to variable renaming. This predicate is not declarative but can be very useful, as demonstrated by the extensive practice of logic programming.

3 Combining SWSL-Rules and SWSL-FOL

SWSL includes two fundamentally distinct knowledge representation languages:

1. SWSL-Rules -- a declarative rule-based language based on the logic programmin/deductive database paradigm; and
2. SWSL-FOL -- a classical first order logic based language

In this section, we discuss how -- and also why -- to combine knowledge expressed in SWSL-Rules with knowledge expressed in SWSL-FOL.

First, it is worthwhile to review the motivations for having the two distinct knowledge representation languages.

SWSL-Rules is especially well suited to represent available knowledge and desired patterns of reasoning for several tasks in semantic Web services:

• authorization policies (for security, access control, confidentiality, privacy, and other kinds of trust);
• contracts (partial or complete, proposed or finalized);
• monitoring of processes to recognize and handle exceptions or other dynamic conditions (e.g., monitoring of performance of contracts to detect and respond to violations of contract provisions such as late delivery or non-payment);
• advertising, discovery, and matchmaking (e.g., advertisements and requests for quotation or requests for proposals can be regarded as partial contract proposals);
• semantic mediation, especially translation mappings that mediate between different ontologies or contexts and thus between knowledge expressed in those different ontologies or contexts (e.g., to translate from the output of one service to the input expected by another service); and
• object-oriented ontologies that use default inheritance with priorities and/or cancellation (e.g., in the manner of the Process Handbook [Process Handbook] [Bernstein2003] [Grosof2004d]).

In particular, the capabilities of SWSL-Rules for logical nonmonotonicity (negation-as-failure and/or Courteous prioritized conflict handling) is used heavily in many use case scenarios for each of the above tasks and the associated kinds of knowledge.

SWSL-FOL is especially well suited to represent available knowledge and desired patterns of reasoning for several other tasks in semantic Web services, especially revolving around the process model:

• Composition of services, and associated planning using process models;
• Analysis, verification, and validation of services in terms of their process models; and
• Ontologies expressed in first order classical logic, e.g., in Description Logic (for example, in OWL-DL).

In particular, the capabilities of SWSL-FOL for disjunction, reasoning by cases, contrapositive reasoning, and/or existentials are used heavily in many use case scenarios for each of the above tasks and its associated kinds of knowledge.

SWSL-Rules and SWSL-FOL overlap largely in syntax, and SWSL-Rules includes almost all of the connectives of SWSL-FOL. The deeper issue, however, is the semantic relationship between SWSL-Rules and SWSL-FOL.

For several purposes it is desirable to combine knowledge expressed in the SWSL-Rules form with knowledge expressed in the SWSL-FOL form. One important such purpose is:

• LP rules "on top of" FOL ontologies. "On top of" here means that some of the predicates mentioned in the set of rules are defined via ontological knowledge expressed in FOL. Such FOL ontologies can often be viewed as "background" knowledge.

For example, the predicates might be classes or properties defined via OWL-DL axioms, i.e., expressed in the Description Logic fragment of FOL.

In terms of semantics, it is desirable to have reasoning in SWSL-Rules respect as much as possible the information contained in such background FOL ontologies. In particular, it is desirable to enable sufficient completeness in the semantic combination to ensure that the conclusions drawn in SWSL-Rules will be (classically) not inconsistent with the SWSL-FOL ontologies.

Ideally, there would be one well-understood overall knowledge representation formalism that subsumes both SWSL-Rules and SWSL-FOL. This would provide the general theoretical basis for combining arbitrary SWSL-Rules knowledge with arbitrary SWSL-FOL knowledge. Unfortunately, finding such an umbrella formalism is still an open issue for basic research. Instead, the current scientific understanding provides only a limited theoretical basis for combining SWSL-Rules knowledge with SWSL-FOL knowledge. On the bright side, there are limited expressive cases for which it is well-understood theoretically how to do such combination.

The Venn diagram of relationships between the different formalisms, given in Figure 2.1 illustrates the most salient aspects of the current scientific understanding.

Figure 2.1: The relationships among different formalisms

The shield shape represents first-order logic-based formalisms. The (diagonally-rotated) bread-slice shape shows the expressivity of the logic programming based paradigms. These overlap partially -- in the Horn rules subset. FOL includes expressiveness beyond the overlap, notably: positive disjunctions; existentials; and entailment of non-ground and non-atomic conclusions. Likewise, LP includes expressiveness beyond the overlap, such as negation-as-failure, which is logically nonmonotonic. Description Logic (cf. OWL-DL), depicted as an oval shape, is a fragment of FOL.

Horn FOL is another fragment of FOL. Horn LP is a slight weakening of Horn FOL. "Weakening" here means that the conclusions from a given set of Horn premises that are entailed according to the Horn LP formalism are a subset of the conclusions entailed (from that same set of premises) according to the Horn FOL formalism. However, the set of ground atomic conclusions is the same in the Horn LP as in the Horn FOL. For most practical purposes (e.g., relational database query answering), Horn LP is thus essentially similar in its power to the Horn FOL.

Horn LP is a fragment of both FOL and nonmonotonic LP -- i.e., of both SWSL-Rules and SWSL-FOL. Horn LP is thus a limited "bridge" that provides a way to pass information -- either premises, or ground-atomic conclusions -- from FOL to LP, or vice versa. Knowledge from FOL that is in the Horn LP subset of expressiveness can be easily combined with general LP knowledge. Vice versa, knowledge from LP that is in the Horn LP subset of expressiveness can be easily combined with general FOL knowledge. Description Logic Programs (DLP) [Grosof2003a] represent a fragment of Horn LP. It likewise acts as a "bridge" between Description Logic (i.e., OWL-DL) and LP.

Note that, technically, LP uses a different logical connective for implication (":-" in SWSL syntax) than FOL uses. When we speak of Horn LP as a fragment of FOL, we are viewing this LP implication connective as mapped into the FOL implication connective (also known as material implication).

Horn LP as "bridge". To summarize, there is some initial good news about semantic combination:

• The Horn LP case is a "bridge" between SWSL-Rules and SWSL-FOL.
• The DLP case is a "bridge" between SWSL-Rules and OWL-DL.

Builtin predicates. Another case of well behaved semantic combination is for builtin predicates that are purely informational, e.g., that represent arithmetic comparisons or operations such as less-than or multiplication. Technically, in LP these can be viewed as procedural attachments. But alternatively, they can be viewed as predicates that have fixed extensions. Their semantics in both FOL and LP can thus be viewed essentially as virtual knowledge base consisting of a set of ground facts. This thus falls into the Horn LP fragment.

Hypermonotonic reasoning as "bridge". Recently, a new theoretical approach called hypermonotonic reasoning [Grosof2004c] has been developed to enable a case of "bridging" between (nonmon) LP and FOL that is considerably more expressive than Horn LP.

We will now describe in more detail some preliminary results about this hypermonotonic reasoning approach that bear upon the relationship of LP to FOL and thus upon how to combine LP knowledge with FOL knowledge.

Courteous LP (including its fragment: LP with negation-as-failure) can be viewed as a weakening of FOL, under a simple mapping of Courteous LP rules/conclusions into FOL. "Weakening" here means that for a given set of premises, the set of conclusions entailed in the Courteous LP formalism is in general a subset of the set of conclusions entailed by the FOL formalism. In other words:

• (Courteous) LP is sound but incomplete relative to FOL.

This fundamental relationship between the formalisms provides an augmentation to the theoretical basis for combining knowledge in LP (i.e., SWSL-Rules) with knowledge in FOL.

Consider a set of rules S in LP and a set of formulas B in FOL. Let T be a translation mapping from the language of S to the language of B. S is said to be hypermonotonic with respect to B and T when S is sound but incomplete relative to B, under the mapping T. That is, when the conclusions entailed in S from a given set of premises P are in general always a subset of the conclusions entailed in B from the translated premises of S.

Define CLP2 to be the fragment of the Courteous LP formalism in which explicit negation-as-failure is omitted (i.e., prohibited). Each rule and mutex in CLP2 can be mapped quite straightforwardly and intuitively to a clause in FOL: simply replace the LP implication connective (":-" in SWSL-Rules syntax) by the FOL implication connective. Observe that this is the same mapping/translation that was considered in relating the Horn LP to FOL. Each ground-literal conclusion in CLP2 can also be mapped, in the same fashion, into a ground-literal in FOL.

The restriction on Courteous LP to avoid explicit negation-as-failure is not very onerous essentially, since the great majority of use cases in which explicit negation-as-failure is employed can be reformulated during manual authoring of rules so as to avoid it as a construct. More generally, the mapping can be extended, by complicating it a bit, to permit explicit negation-as-failure.

Going in the reverse direction, every clause in FOL can also be mapped into CLP2, in such a way that the resulting CLP information is a weakening of the FOL clause that nevertheless preserves much of the strength of the FOL clause. This reverse-translation mapping from FOL to CLP is complicated somewhat by the directional nature of the LP implication connective. "Directional" here means having a direction from body towards head. Each LP rule can be viewed as a directed clause. Consider a FOL clause C that consists of a disjunction of m literals:

• (universal closure of:) L1 or ... or Lm.

Here, each Li is an atom or a classically-negated atom. When mapping c to CLP2, there are m possible choices of one for each possible choice of which literal is to be made head of the LP rule. Each possible choice corresponds to a different rule -- the LP rule in which literal Li is chosen as head has the form:

• Li :- neg L1, ..., neg Li-1, neg Li+1, ..., neg Lm .

Altogether, the FOL clause C is mapped into a set of m LP rules:

• L1 :- neg L2, neg L3, ..., neg Lm .
• L2 :- neg L1, neg L3, ..., neg Lm .
• ...
• Lm :- neg L1, neg L2, ..., neg Lm-1 .

where neg (neg A) is replaced equivalently by A. This set of rules is called the "omni-directional" set of rules for that clause -- or, more briefly, the "omni rules" for that clause.

In general, FOL axioms need not be clausal since they may include existential quantifiers. However, often skolemization can be performed to represent such existentials in a manner that preserves soundness (as is usual for skolemization). A refinement of the reverse translation mapping above is to exploit such skolemization in order to relax the requirement of clausal form. We use such skolemization particularly for head existentials.

Automatic weakened translation of FOL ontologies into SWSL-Rules. In the ontologies aspect of SWSL, it is desirable to have a "bridging" technique to automatically translate FOL ontologies into SWSL-Rules in such a manner as to preserve soundness (from an FOL viewpoint) but to be nevertheless fairly strong (i.e., capture much of the strength/content of the original FOL axioms). We have adopted, as an experimental "bridging" approach, the reverse translation mapping technique described above in order to map FOL ontologies into SWSL-Rules (heavily using the Courteous feature). In particular, we have applied this technique to map the axioms of PSL Core and Outer Core into SWSL-Rules so as to create a weakened version of that ontology that can be utilized within SWSL-Rules. Because some of these PSL axioms include existentials, we utilize the skolemization refinement described above, particularly for head existentials. The mapping from the PSL axioms to SWSL-Rules is given in appendix PSL in SWSL-FOL and SWSL-Rules.

The precise algorithm used to obtain the SWSL-Rules translation for a given axiom in SWSL-FOL is as follows:

Input: a formula F in SWSL-FOL.
Output: a set of rules R, expressed in SWSL-Rules.

1) Translate F into formula F1 in Prenex Normal Form.

2) Skolemize F1 to get F2, which is in Skolem Normal Form.

3) Write F2 as a set S of clauses.

4) For each clause C in S, produce the omnidirectional set of rules for C (as defined above).

R then is the union of all the omnidirectional sets of rules produced by (4). 

4 Serialization of SWSL in RuleML

SWSL is serialized in XML using RuleML. RuleML-style serialization of SWSL enables interoperation with other XML applications for rules and provides an encoding for transporting SWSL-Rules via the SOAP infrastructure of Web services.

RuleML integrates various rule paradigms via common set of concepts and defines a family of rule-based, Web-enabled sublanguages with various degrees of expressiveness. This section applies the RuleML approach to serialization of SWSL. This is done mostly by reusing and sometimes extending the existing RuleML sublanguages. In addition, a new sublanguage for the serialization of HiLog is developed.

Serialization of the presentation syntax of SWSL-Rules amounts to construction of explicit parse trees and then representing these trees linearly as XML markup that is compliant with XML Schema of the appropriate RuleML sublanguages. Starting with Version 0.89, the XML Schema specification of RuleML supports SWSL-Rules.

Serialization of SWSL-FOL does not require any new constructs, and it is done by repurposing existing RuleML features. Serialization of SWSL-FOL is discussed at the end of this section, in Section 4.5.

Conceptually, RuleML models XML trees as objects and thus divides all XML tags into class descriptors, called type tags, and property descriptors, called role tags. This conceptual object-oriented model implies that type tags and role tags must alternate, which is known as striped XML syntax. For instance, in F-logic and RDF, classes can have properties, which point to classes, which have properties that point to classes, etc. Similarly, in the striped XML syntax, a type tag has role tags as subelements, whose children are again type tags, etc. When the role of a subelement is clear from the context, its tag may be skipped for brevity, as in RDF's StripeSkipping.

4.1 Serialization of the HiLog Layer

HiLog terms. The HiLog serialization uses the type tag Hterm for HiLog terms, Con for constants, and Var for variables. Since HiLog allows arbitrary terms to be used in the position of predicate and function symbols, the RuleML serialization allows not only constants but also variables and Hterms under the op role tag . The following illustrates the main aspects of the HiLog serialization.

• Regular first-order terms. For instance, the HiLog terms c, f(a,?X), ?X are represented by the following three XML fragments, respectively:

  	    <Con>c</Con>
  	  

  	    <Hterm>
  	       <op><Con>f</Con></op>
  	       <Con>a</Con>
  	       <Var>X</Var>
  	    </Hterm>
  	  

  	    <Var>X</Var>
  	  

• Variables over function symbols. For instance, the terms ?X(a,?Y), ?X(a,?Y(?X)) are serialized as follows:

  	    <Hterm>
  	       <op><Var>X</Var></op>
  	       <Con>a</Con>
  	       <Var>Y</Var>
  	    </Hterm>
  	  

  	    <Hterm>
  	       <op><Var>X</Var></op>
  	       <Con>a</Con>
  	       <Hterm>
  	          <op><Var>Y</Var></op>
  	          <Var>X</Var>
  	       </Hterm>
  	    </Hterm>
  	  

• Parameterized function symbols. For instance, the HiLog terms f(?X,a)(b,?X(c)), ?Z(?X,a)(b,?X(?Y)(d)), ?Z(f)(g,a)(p,?X) will be serialized as shown below:

  	    <Hterm>
  	       <op>
  	          <Hterm>
  	             <op><Con>f</Con></op>
  	             <Var>X</Var>
  	             <Con>a</Con>
  	          </Hterm>
  	       </op>
  	       <Con>b</Con>
  	       <Hterm>
  	          <op><Var>X</Var></op>
  	          <Con>c</Con>
  	       </Hterm>
  	    </Hterm>
  	  

  	    <Hterm>
  	       <op>
  	          <Hterm>
  	             <op><Var>Z</Var></op>
  	             <Var>X</Var>
  	             <Con>a</Con>
  	          </Hterm>
  	       </op>
  	       <Con>b</Con>
  	       <Hterm>
  	          <op>
  	             <Hterm>
                          <op><Var>X</Var></op>
                          <Var>Y</Var>
  	             </Hterm>
  	          </op>
  	          <Con>d</Con>
  	       </Hterm>
  	    </Hterm>
  	  

  	    <Hterm>
  	       <op>
  	          <Hterm>
  	             <op>
                          <Hterm>
                             <op><Var>Z</Var></op>
                             <Con>f</Con>
                          </Hterm>
  	             </op>
  	             <Con>g</Con>
  	             <Con>a</Con>
  	          </Hterm>
  	       </op>
  	       <Con>p</Con>
  	       <Var>X</Var>
  	    </Hterm>
  	  

HiLog atomic formulas. Since any HiLog term is also a HiLog atomic formula, the RuleML serialization for these formulas is the same as for HiLog terms. The following example shows an encoding of a query, which uses the Query element of RuleML:

	?- q(?X) and ?X.
      

	<Query>
	   <And>
	      <Hterm>
	         <op><Con>q</Con></op>
	         <Var>X</Var>
	      </Hterm>
	      <Var>X</Var>
	   </And>
	<Query>
      

Another interesting example is a HiLog rule

	call(?X) :- ?X.
      

which is a logical definition of the meta-predicate call/1 in Prolog. This is translated using the RuleML tags Implies, head, and body, as follows:

	<Implies>
	   <head>
	      <Hterm>
	         <op><Con>call</Con></op>
	         <Var>X</Var>
	      </Hterm>
	   </head>
	   <body>
	      <Var>X</Var>
	   </body>
	</Implies>
      

4.2 Serialization of Explicit Equality

The explicit equality predicate :=: is serialized using the RuleML's element Equal. For example,

	f(a,?X):=:g(?Y,b) :- p(?X,?Y).
      

is serialized as

	<Implies>
	   <head>
	      <Equal>
	         <Hterm>
	            <op><Con>f</Con></op>
	            <Con>a</Con>
	            <Var>X</Var>
	         </Hterm>
	         <Hterm>
	            <op><Con>g</Con></op>
	            <Var>Y</Var>
	            <Con>b</Con>
	         </Hterm>
	      </Equal>
	   </head>
	   <body>
	      <Hterm>
	         <op><Con>p</Con></op>
	         <Var>X</Var>
	         <Var>Y</Var>
	      </Hterm>
	   </body>
	</Implies>
      

4.3 Serialization of the Frames Layer

To serialize the Frames layer of SWSL-Rules we need to show the serialization of the various molecules and path expressions introduced by F-logic.

Molecules. The serialization of molecules uses slotted atoms, which have an oid but often do not have an op. The overall structure of F-logic molecules (except for class membership and subclassing) is as follows:

	Atom ::= oid op? slot*
      

• Value molecules. If t, m, v are terms then the value molecule t[m -> v] is serialized as follows:

  	    <Atom><oid>t'</oid><slot>m' v'</slot></Atom>
  	  

  Here and elsewhere we use primes to represent recursive RuleML serialization. For instance, t', m', and v' denote RuleML serializations of t, m, and v, respectively. For instance, o[f(a,b) -> 3] would be represented by the following fragment:

  	    <Atom>
  	       <oid><Con>o</Con></oid>
  	       <slot>
  	          <Hterm><Con>f</Con><Con>a</Con><Con>b</Con></Hterm>
  	          <Con>3</Con>
  	       </slot>
  	    </Atom>
  	  

  The syntax t[m -> {v1,...,vk}] is also supported: the set-valued result is serialized using the Set tag:

  	    <Atom>
  	       <oid>t'</oid>
  	       <slot>
  	          m'
  	          <Set>v1',...,vk'</Set>
  	       </slot>
  	    </Atom>
  	  

• Boolean molecules. These molecules have the form t[m] where t and m are terms. They are serialized using singleton slot elements. For instance, mary[female] is represented as follows:

  	    <Atom>
  	       <oid><Con>mary</Con></oid>
  	       <slot>
  	          <Con>female</Con>
  	       </slot>
  	    </Atom>
  	  

• Class membership molecule. Class membership molecules of the form t:s are serialized using the InstanceOf element:

  	    <InstanceOf>t' s'</InstanceOf>
  	  

  where t' and s' represent RuleML serializations of t and s.

• Subclass molecule. The subclass molecules of the form t::s are represented using the SubclassOf element as follows:

  	    <SubclassOf>t' s'</SubclassOf>
  	  

  As before, t' and s' represent RuleML serializations of t and s, respectively.

• Signature molecule. Signature molecules of the form t[m => v] are represented using the Signature element, where the prime represents RuleML serialization of the corresponding term:

  	    <Signature><oid>t'</oid><slot>m' v'</slot></Signature>
  	  

• Boolean signature molecules. A Boolean signature molecule has the form t[=>m]. Its RuleML serialization uses singleton slot elements within a Signature element:

  	    <Signature><oid>t'</oid><slot>m'</slot></Signature>
  	  

• Cardinality constraints. Signature molecules can have associated cardinality constraints. Such molecules have the form

  t[s(t1,...,tn) {min : max} => v]

  In RuleML this becomes:

  	    <Signature>
  	       <oid>t'</oid>
  	       <slot mincard="min" maxcard="max">
  	          <Hterm><Con>s'</Con>t1'...tn'</Hterm>
  	          v'
  	       </slot>
  	    </Signature>
  	  

Nested molecules. Direct serialization of nested molecules is not currently supported. Instead, they must first be broken into conjunctions of non-nested molecules and then serialized.

Slot access and path expressions. Serialization of slot access uses the RuleML Get primitive. Serialization of path expressions is supported via the polyadic RuleML SlotProd element. For example, room.ceiling.color becomes the following:

        <Get>
           <oid><Con>room</Con></oid>
           <SlotProd><Con>ceiling</Con><Con>color</Con></SlotProd>
        </Get> 
      

4.4 Serialization of Reification

SWSL-Rules supports reification of F-logic molecules, formulas that can occur in the head or the body of a rule, and of the rules themselves. The only restriction is that explicit quantifiers cannot occur under the scope of the reification operator. The main idea behind RuleML serialization of such statements is that the corresponding serialized statement must be embedded within a Reify element.

To illustrate, consider the following molecule:

	a[b -> ${p(X[foo -> bar])}] 
      

Since the reified statement (p(X[foo -> bar]) is an Hterm, this tag becomes the child of the Reify element.

	<Hterm>
	   <oid><Con>a</Con></oid>
	   <slot>
	      <Con>b</Con>
	      <Reify>
	         <Hterm>
	            <op><Con>p</Con></op>
	            <Hterm>
	               <oid><Var>X</Var></oid>
	               <slot><Con>foo</Con><Con>bar</Con></slot>
	            </Hterm>
	         </Hterm>
	      </Reify>
	   </slot>
	</Hterm>
      

The following example illustrates serialization of a reified rule.

	john[believes -> ${p(?X) implies q(?X)}].
      

The corresponding serialization is shown below. Since the top-level tag of a rule is Implies, this tag becomes the child of the Reify element.

	<Hterm>
	   <oid>john</oid>
	   <slot>
	      <Con>believes</Con>
	      <Reify>
	         <Implies>
	            <body>
	               <Hterm>
	                  <op><Con>p</Con></op>
	                  <Var>X</Var>
	               </Hterm>
	            </body>
	            <head>
	               <Hterm>
	                  <op><Con>q</Con></op>
	                  <Var>X</Var>
	               </Hterm>
	            </head>
	         </Implies>
	      </Reify>
	   </slot>
	</Hterm>
      

4.5 Serialization of SWSL-FOL

Serialization of SWSL-FOL reuses the existing FOL RuleML sublanguage. The serialization is accomplished through the following rules:

• First-order atomic formulas are serialized as <Atom>...</Atom>. What actually goes between the Atom tags depends on the type of the atomic formula (i.e., whether it is a predicate formula or a F-logic frame).
• If φ and ψ are serialized SWSL-FOL formulas then so are <And> φ ψ </And>, <Or> φ ψ </Or>, <Neg> φ </Neg>, <Implies> φ ψ </Implies> (SWSL-FOL's φ impliedBy ψ must be first replaced with ψ implies φ), and <Equivalent> φ ψ </Equivalent> (for SWSL-FOL's iff).
• If X is a variable and φ is a serialized SWSL-FOL formula, then the following are also SWSL-FOL serialized formulas: <Exists> <Var>X</Var> φ </Exists> and <Forall> <Var>X</Var> φ </Forall>. Serialized SWSL-FOL also allows to combine quantifiers of the same sort and reduce repetitiveness. For instance, <Exists> <Var>X</Var> <Var>Y</Var> φ </Exists> is a shorthand for <Exists> <Var>X</Var> <Exists> <Var>Y</Var> φ </Exists> </Exists>.

5 Glossary

Activity

Activity. In the formal PSL ontology, the notion of activity is a basic construct, which corresponds intuitively to a kind of (manufacturing or processing) activity. In PSL, an activity may have associated occurrences, which correspond intuitively to individual instances or executions of the activity. (We note that in PSL an activity is not a class or type with occurrences as members; rather, an activity is an object, and occurrences are related to this object by the binary predicate occurrence_of.) The occurrences of an activity may impact fluents (which provide an abstract representation of the "real world"). In FLOWS, with each service there is an associated activity (called the "service activity" of that service). The service activity may specify aspects of the internal process flow of the service, and also aspects of the messaging interface of that service to other services.

Channel

Channel. In FLOWS, a channel is a formal conceptual object, which corresponds intuitively to a repository and conduit for messages. The FLOWS notion of channel is quite primitive, and under various restrictions can be used to model the form of channel or message-passing as found in web services standards, including WSDL, BPEL, WS-Choreography, WSMO, and also as found in several research investigations, including process algrebras.

FLOWS

First-order Logic Ontology for Web Services. FLOWS, also known as SWSO-FOL, is the first-order logic version of the Semantic Web Services Ontology. FLOWS is an extension of the PSL-OuterCore ontology, to incorporate the fundamental aspects of (web and other electronic) services, including service descriptors, the service activity, and the service grounding.

Fluent

Fluent. In FLOWS, following PSL and the situation calculii, a fluent is a first-order logic term or predicate whose value may vary over time. In a first-order model of a FLOWS theory, this being a model of PSL-OuterCore, time is represented as a discrete linear sequence of timees, and fluents has a value for each time in this sequence.

Grounding

Grounding. The SWSO concepts for describing service activities, and the instantiations of these concepts that describe a particular service activity, are abstract specifications, in the sense that they do not specify the details of particular message formats, transport protocols, and network addresses by which a Web service is accessed. The role of the grounding is to provide these more concrete details. A substantial portion of the grounding can be acheived by mapping SWSO concepts into corresponding WSDL constructs. (Additional grounding, e.g., of some process-related aspects of SWSO, might be acheived using other standards, such as BPEL.)

Message

Message. In FLOWS, a message is a formal conceptual object, which corresponds intuitively to a single message that is created by a service occurrence, and read by zero or more service occurrences. The FLOWS notion of message is quite primitive, and under various restrictions can be used to model the form of messages as found in web services standards, including WSDL (1.0 and 2.0), BPEL, WS-Choreography, WSMO, and also as found in several research investigations. A message has a payload, which corresponds intuitively to the body or contents of the message. In FLOWS emphasis is placed on the knowledge that is gained by a service occurrence when reading a message with a given payload (and the knowledge needed to create that message.

Occurrence

Occurence (of a service). In FLOWS, a service S has an associated FLOWS activity A (which generalizes the notion of PSL activity). An occurrence of S is formally a PSL occurrence of the activity A. Intuitively, this occurrence corresponds to an instance or execution (from start to finish) of the activity A, i.e., of the process associated with service S. As in PSL, an occurrence has a starting time time and an ending time.

PSL

Process Specification Language. The Process Specification Language (PSL) is a formally axiomatized ontology [Gruninger03a, Gruninger03b] that has been standardized as ISO 18629. PSL provides a layered, extensible ontology for specifying properties of processes. The most basic PSL constructs are embodied in PSL-Core; and PSL-OuterCore incorporates several extensions of PSL-Core that includes several useful constructs. (An overview of concepts in PSL that are relevant to FLOWS is given in Section 6 of the Semantic Web Services Ontology document.)

QName

Qualified name. A pair (URI, local-name). The URI represents a namespace and local-name represents a name used in an XML document, such as a tag name or an attribute name. In XML, QNames are syntactically represented as prefix:local-name, where prefix is a macro that expands into a concrete URI. See Namespaces in XML for more details.

ROWS

Rules Ontology for Web Services. ROWS, also known as SWSO-Rules, is the rules-based version of the Semantic Web Services Ontology. ROWS is created by a relatively straight-forward, almost faithful, transformation of FLOWS, the First-order Logic Ontology for Web Services. As with FLOWS, ROWS incorporates fundamental aspects of (web and other electronic) services, including service descriptors, the service activity, and the service grounding. ROWS enables a rules-based specification of a family of services, including both the underlying ontology and the domain-specific aspects.

Service

(Formal) Service. In FLOWS, a service is a conceptual object, that corresponds intuitively to a web service (or other electronically accessible service). Through binary predicates a service is associated with various service descriptors (a.k.a. non-functional properties) such as Service Name, Service Author, Service URL, etc.; an activity (in the sense of PSL) which specifies intuitively the process model associated with the service; and a grounding.

Service contract

Describes an agreement between the service requester and service provider, detailing requirements on a service occurrence or family of service occurrences.

Service descriptor

Service Descriptor. This is one of several non-functional properties associated with services. The Service Descriptors include Service Name, Service Author, Service Contract Information, Service Contributor, Service Description, Service URL, Service Identifier, Service Version, Service Release Date, Service Language, Service Trust, Service Subject, Service Reliability, and Service Cost.

Service offer description

Describes an abstract service (i.e. not a concrete instance of the service) provided by a service provider agent.

Service requirement description

Describes an abstract service required by a service requester agent, in the context of service discovery, service brokering, or negotiation.

sQName

Serialized QName. A serialized QName is a shorthand representation of a URI. It is a macro that expands into a full-blown URI. sQNames are not QNames: the former are URIs, while the latter are pairs (URI, local-name). Serialized QNames were originally introduced in RDF as a notation for shortening URI representation. Unfortunately, RDF introduced confusion by adopting the term QName for something that is different from QNames used in XML. To add to the confusion, RDF uses the syntax for sQNames that is identical to XML's syntax for QNames. SWSL distinguishes between QNames and sQNames, and uses the syntax prefix#local-name for the latter. Such an sQName expands into a full URI by concatenating the value of prefix with local-name.

URI

Universal Resource Identifier. A symbol used to locate resources on the Web. URIs are defined by IETF. See Uniform Resource Identifiers (URI): Generic Syntax for more details. Within the IETF standards the notion of URI is an extension and refinement of the notions of Uniform Resource Locator (URL) and Relative Uniform Resource Locators.

6 References

[Berardi03]

Automatic composition of e-services that export their behavior. D. Berardi, D. Calvanese, G. De Giacomo, M. Lenzerini, and M. Mecella. In Proc. 1st Int. Conf. on Service Oriented Computing (ICSOC), volume 2910 of LNCS, pages 43--58, 2003.

[Bernstein2000]

How can cooperative work tools support dynamic group processes? Bridging the specificity frontier. A. Bernstein. In Proc. Computer Supported Cooperative Work (CSCW'2000), 2000.

[Bernstein2002]

Towards High-Precision Service Retrieval. A. Bernstein, and M. Klein. In Proc. of the first International Semantic Web Conference (ISWC'2002), 2002.

[Bernstein2003]

Beyond Monotonic Inheritance: Towards Semantic Web Process Ontologies. A. Bernstein and B.N. Grosof (NB: authorship sequence is alphabetic). Working Paper, Aug. 2003. Available at: http://ebusiness.mit.edu/bgrosof/#beyond-mon-inh-basic.

[Bonner93]

Database Programming in Transaction Logic. A.J. Bonner, M. Kifer, M. Consens. Proceedings of the 4-th Intl.~Workshop on Database Programming Languages, C. Beeri, A. Ohori and D.E. Shasha (eds.), 1993. In Springer-Verlag Workshops in Computing Series, Feb. 1994: 309-337.

[Bonner98]

A Logic for Programming Database Transactions. A.J. Bonner, M. Kifer. Logics for Databases and Information Systems, J. Chomicki and G. Saake (eds.). Kluwer Academic Publishers, 1998: 117-166.

[Bruijn05]

Web Service Modeling Ontology (WSMO). J. de Bruijn, C. Bussler, J. Domingue, D. Fensel, M. Hepp, M. Kifer, B. Kaenig-Ries, J. Kopecky, R. Lara, E. Oren, A. Polleres, J. Scicluna, M. Stollberg. DERI Technical Report.

[BPML 1.0]

A. Arkin. Business Process Modeling Language. BPMI.org, 2002

[BPEL 1.1]

Business Process Execution Language for Web Services, Version 1.1 . S. Thatte, editor. OASIS Standards Specification, May 5, 2003.

[Bultan03]

Conversation specification: A new approach to design and analysis of e-service composition. T. Bultan, X. Fu, R. Hull, and J. Su. In Proc. Int. World Wide Web Conf. (WWW), May 2003.

[Chang73]

Symbolic Logic and Mechanical Theorem Proving. C.L. Chang and R.C.T. Lee. Academic Press, 1973.

[Chen93]

HiLog: A Foundation for Higher-Order Logic Programming. W. Chen, M. Kifer, D.S. Warren. Journal of Logic Programming, 15:3, February 1993, 187-230.

[Chimenti89]

Towards an Open Architecture for LDL. D. Chimeti, R. Gamboa, R. Krishnamurthy, VLDB Conference, 1989: 195-203.

[deGiacomo00]

ConGolog, A Concurrent Programming Language Based on the Situation Calculus. G. de Giacomo, Y. Lesperance, and H. Levesque. Artificial Intelligence, 121(1--2):109--169, 2000.

[Fu04]

WSAT: A Tool for Formal Analysis of Web Services. X. Fu, T. Bultan, and J. Su. 16th International Conference on Computer Aided Verification (CAV), July 2004.

[Frohn94]

Access to Objects by Path Expressions and Rules. J. Frohn, G. Lausen, H. Uphoff. Intl. Conference on Very Large Databases, 1994, pp. 273-284.

[Gosling96]

The Java language specification.Gosling, James, Bill Joy, and Guy L. Steele. 1996. Reading, Mass.: Addison-Wesley.

[Grosof99a]

A Courteous Compiler From Generalized Courteous Logic Programs To Ordinary Logic Programs. B.N. Grosof. IBM Report included as part of documentation in the IBM CommonRules 1.0 software toolkit and documentation, released on http://alphaworks.ibm.com. July 1999. Also available at: http://ebusiness.mit.edu/bgrosof/#gclp-rr-99k.

[Grosof99b]

A Declarative Approach to Business Rules in Contracts. B.N. Grosof, J.K. Labrou, and H.Y. Chan. Proceedings of the 1st ACM Conference on Electronic Commerce (EC-99). Also available at: http://ebusiness.mit.edu/bgrosof/#econtracts+rules-ec99.

[Grosof99c]

DIPLOMAT: Compiling Prioritized Default Rules Into Ordinary Logic Programs (Extended Abstract of Intelligent Systems Demonstration). B.N. Grosof. IBM Research Report RC 21473, May 1999. Extended version of 2-page refereed conference paper appearing in Proceedings of the National Conference on Artificial Intelligence (AAAI-99), 1999. Also available at: http://ebusiness.mit.edu/bgrosof/#cr-ec-demo-rr-99b.

[Grosof2003a]

Description Logic Programs: Combining Logic Programs with Description Logic. B.N. Grosof, I. Horrocks, R. Volz, and S. Decker. Proceedings of the 12th International Conference on the World Wide Web (WWW-2003). Also available at: http://ebusiness.mit.edu/bgrosof/#dlp-www2003.

[Grosof2004a]

Representing E-Commerce Rules Via Situated Courteous Logic Programs in RuleML. B.N. Grosof. Electronic Commerce Research and Applications, 3:1, 2004, 2-20. Preprint version is also available at: http://ebusiness.mit.edu/bgrosof/#.

[Grosof2004b]

SweetRules: Tools for Semantic Web Rules and Ontologies, including Translation, Inferencing, Analysis, and Authoring. B.N. Grosof, M. Dean, S. Ganjugunte, S. Tabet, C. Neogy, and D. Kolas. http://sweetrules.projects.semwebcentral.org. Software toolkit and documentation. Version 2.0, Dec. 2004.

[Grosof2004c]

Hypermonotonic Reasoning: Unifying Nonmonotonic Logic Programs with First Order Logic. B.N. Grosof. http://ebusiness.mit.edu/bgrosof/#HypermonFromPPSWR04InvitedTalk. Slides from Invited Talk at Workshop on Principles and Practice of Semantic Web Reasoning (PPWSR04), Sep. 2004; revised Oct. 2004. Paper in preparation.

[Grosof2004d]

SweetPH: Using the Process Handbook for Semantic Web Services. B.N. Grosof and A. Bernstein. http://ebusiness.mit.edu/bgrosof/#SweetPHSWSLF2F1204Talk. Slides from Presentation at SWSL Meeting, Dec. 9-10, 2004. Note: Updates the design in the 2003 Working Paper "Beyond Monotonic Inheritance: Towards Semantic Web Process Ontologies" and describes implementation.

[Grosof2004e]

SweetDeal: Representing Agent Contracts with Exceptions using Semantic Web Rules, Ontologies, and Process Descriptions. B.N. Grosof and T.C. Poon. International Journal of Electronic Commerce (IJEC), 8(4):61-98, Summer 2004 Also available at: http://ebusiness.mit.edu/bgrosof/#sweetdeal-exceptions-ijec.

[Grosof2004f]

Semantic Web Rules with Ontologies, and their E-Business Applications. B.N. Grosof and M. Dean. Slides of Conference Tutorial (3.5-hour) at the 3rd International Semantic Web Conference (ISWC-2004). Available at: http://ebusiness.mit.edu/bgrosof/#ISWC2004RulesTutorial.

[Gruninger03a]

A Guide to the Ontology of the Process Specification Language. M. Gruninger. Handbook on Ontologies in Information Systems. R. Studer and S. Staab (eds.). Springer Verlag, 2003.

[Gruninger03b]

Process Specification Language: Principles and Applications. M. Gruninger and C. Menzel. AI Magazine, 24:63-74, 2003.

[Gruninger03c]

Applications of PSL to Semantic Web Services. M. Gruninger. Workshop on Semantic Web and Databases. Very Large Databases Conference, Berlin.

[Hayes04]

RDF Model Theory. Hayes, P. W3C, February 2004.

[Helland05]

Data on the Outside Versus Data on the Inside. P. Helland. Proc. 2005 Conf. on Innovative Database Research (CIDR), January, 2005.

[Hull03]

E-Services: A Look Behind the Curtain. R. Hull, M. Benedikt, V. Christophides, J. Su. Proc. of the ACM Symp. on Principles of Database Systems (PODS), San Diego, June, 2003.

[Kifer95]

Logical Foundations of Object-Oriented and Frame-Based Languages, M. Kifer, G. Lausen, J. Wu. Journal of ACM, 1995, 42, 741-843.

[Kifer04]

A Logical Framework for Web Service Discovery, M. Kifer, R. Lara, A. Polleres, C. Zhao. Semantic Web Services Workshop, November 2004, Hiroshima, Japan.

[Klein00a]

Towards a Systematic Repository of Knowledge About Managing Collaborative Design Conflicts. Klein, Mark. 2000.  Proceedings of the Conference on Artificial Intelligence in Design. Boston, MA, USA.

[Klein00b]

A Knowledge-Based Approach to Handling Exceptions in Workflow Systems. Klein, Mark, and C. Dellarocas. 2000.  Computer Supported Cooperative Work: The Journal of Collaborative Computing 9:399-412.

[Lloyd87]

Foundations of logic programming (second, extended edition). J. W. Lloyd. Springer series in symbolic computation. Springer-Verlag, New York, 1987.

[Lindenstrauss97]

Automatic Termination Analysis of Logic Programs. N. Lindenstrauss and Y. Sagiv. International Conference on Logic Programming (ICLP), 1997.

[Maier81]

Incorporating Computed Relations in Relational Databases. D. Maier, D.S. Warren. SIGMOD Conference, 1981: 176-187.

[Malone99]

Tools for inventing organizations: Toward a handbook of organizational processes. T. W. Malone, K. Crowston, J. Lee, B. Pentland, C. Dellarocas, G. Wyner, J. Quimby, C. Osborne, A. Bernstein, G. Herman, M. Klein, E. O'Donnell. Management Science, 45(3), pages 425--443, 1999.

[McIlraith01]

Semantic Web Services. IEEE Intelligent Systems, Special Issue on the Semantic Web, S. McIlraith, T.Son and H. Zeng. 16(2):46--53, March/April, 2001.

[Milner99]

Communicating and Mobile Systems: The π-Calculus. R. Milner. Cambridge University Press, 1999.

[Narayanan02]

Simulation, Verification and Automated Composition of Web Services. S. Narayanan and S. McIlraith. In Proceedings of the Eleventh International World Wide Web Conference (WWW-11), May, 2002.

[Ontobroker]

Ontobroker 3.8. Ontoprise, GmbH.

[OWL Reference]

OWL Web Ontology Language 1.0 Reference. Mike Dean, Dan Connolly, Frank van Harmelen, James Hendler, Ian Horrocks, Deborah L. McGuinness, Peter F. Patel-Schneider, and Lynn Andrea Stein. W3C Working Draft 12 November 2002. Latest version is available at http://www.w3.org/TR/owl-ref/.

[OWL-S 1.1]

OWL-S: Semantic Markup for Web Services. David Martin, editor. Technical Overview (associated with OWL-S Release 1.1).

[Papazoglou03]

Service-Oriented Computing: Concepts, Characteristics and Directions. M.P. Papazoglou. Keynote for the 4th International Conference on Web Information Systems Engineering (WISE 2003), December 10-12, 2003.

[Perlis85]

Languages with Self-Reference I: Foundations. D. Perlis. Artificial Intelligence, 25, 1985, 301-322.

[Preist04]

A Conceptual Architecture for Semantic Web Services, C. Preist, 1993. In Proceedings of Third International Semantic Web Conference, Nov. 2004: 395-409.

[Reiter01]

Knowledge in Action: Logical Foundations for Specifying and Implementing Dynamical Systems. Raymond Reiter. MIT Press. 2001

[Scherl03]

Knowledge, Action, and the Frame Problem. R. B. Scherl and H. J. Levesque. Artificial Intelligence, Vol. 144, 2003, pp. 1-39.

[Singh04]

Protocols for Processes: Programming in the Large for Open Systems. M. P. Singh, A. K. Chopra, N. V. Desai, and A. U. Mallya. Proc. of the 19th Annual ACM Conf. on Object-Oriented Programming, Systems, Languages, and Applications (OOPSLA), Vancouver, October 2004.

[SWSL Requirements]

Semantic Web Services Language Requirements. B. Grosof, M. Gruninger, et al, editors. White paper of the Semantic Web Services Language Committee.

[UDDI v3.02]

Universal Description, Discovery and Integration (UDDI) protocol. S. Thatte, editor. OASIS Standards Specification, February 2005.

[VanGelder91]

The Well-Founded Semantics for General Logic Programs. A. Van Gelder, K.A. Ross, J.S. Schlipf. Journal of ACM, 38:3, 1991, 620-650.

[WSCL 1.0]

Web Services Conversation Language (WSCL) 1.0. A. Banerji et al. W3C Note, March 14, 2002.

[WSDL 1.1]

Web Services Description Language (WSDL) 1.1. E. Christensen, F. Curbera, G. Meredith, and S. Weerawarana. W3C Note, March 15, 2001.

[WSDL 2.0]

Web Services Description Language (WSDL) 2.0 -- Part 1: Core Language. R. Chinnici, M. Gudgin, J.-J. Moreau, J. Schlimmer, and S. Weerawarana. W3C Working Draft, August 3, 2004.

[WSDL 2.0 Primer]

Web Services Description Language (WSDL) Version 2.0 -- Part 0: Primer. D. Booth, C. Liu, editors. W3C Working Draft, 21 December 2004.

[WS-Choreography]

Web Services Choreography Description Language Version 1.0. N. Kavantzas, D. Burdett, et. al., editors. W3C Working Draft, December 17, 2004.

[XSLT]

XSL Transformations (XSLT) Version 1.0. J. Clark, editor. W3C Recommendation, 16 November 1999.

[XQuery 1.0]

XQuery 1.0: An XML Query Language. S. Boag, D. Chamberlin, et al, editors. W3C Working Draft 04 April 2005.

[Yang02]

Well-Founded Optimism: Inheritance in Frame-Based Knowledge Bases. G. Yang, M. Kifer. Intl. Conference on Ontologies, DataBases, and Applications of Semantics for Large Scale Information Systems (ODBASE), October 2002.

[Yang03]

Reasoning about Anonymous Resources and Meta Statements on the Semantic Web. G. Yang, M. Kifer. Journal on Data Semantics, Lecture Notes in Computer Science 2800, Springer Verlag, September 2003, 69-98.

[Yang04]

FLORA-2 User's Manual. G. Yang, M. Kifer, C. Zhao, V. Chowdhary. 2004.