Proposals/Better CTM Computation
Introduction
The precision of coordinates of SVG is a fundamental theme for the maps. When realizing the global scale level of details without massive javascript apps, required effective digits are at least eight based on most simple implementations.
For such a map, at least 1 meters precision is required toward the range of the earth ( earth circumferences = 40,000Km = 40000,000m ). Therefore required effective digit required is Eight.
It exceeds the effective digit of single floating point. (7.225 digits) By the way, the precision of a 0.1mm order is needed toward the range of a 100m order for technical drawings of airplanes, ships and spaceships. The effective digits in this case are 7 or more.
However, a proposal to recommend double floating point on computing did not obtain consensus at past F2F. The reason is that the single precision floating point is mainly used for the numerical operation on the current GPUs. Therefore, the issue of precision on very large maps and technical drawings has not been solved yet.
In order to solve this issue, I investigated the solution in consideration of restrictions of GPU. That method is a kind of tiling.
Note
This proposal was discussed. As a result, description of the computation method of CTM based on this proposal was added to the Conforming SVG Viewers chapter of SVG2 draft.
Improving Significant Figures by Transformation and Tiling
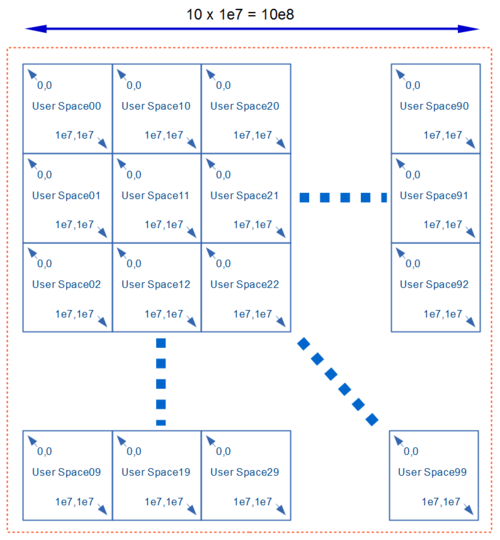
By providing a user coordinate system with an appropriate origin to each tile, the number of significant figures increases one digit in case of 10x10 tiling.
The following figure is expressing improvement of significant figures to eight digits by 10x10 tiling, assuming that significant figures of eache tiles are seven digits.
However, these tiles must be precisely pasted on the user coordinate system of the root which unifies them. It is expressed as this coordinate transformation. Red arrows show such transformations.
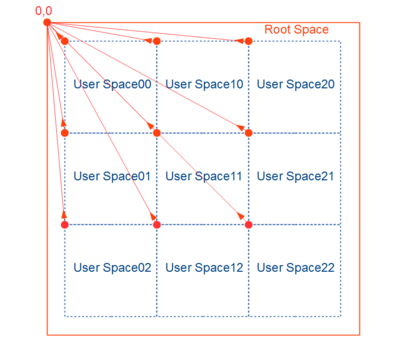
Besides, there is no graphics element on the root coordinate system. (Actual graphics are in individual tiles.) And an actual rendering is performed on the viewport space. Accordingly, a rendering is performed through the coordinate transformation to the viewport space.
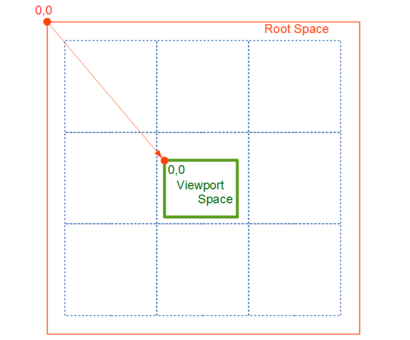
However, objects actually to be rendered are tiles which the viewport intersects only. Thick red arrow shows the coordinate transformation from the user space 11 to viewport space (3) (namely CTM) on such a tile. It is composition of the transformation from user space 11 to root space (1) and the transformation from root space to viewport space (2).
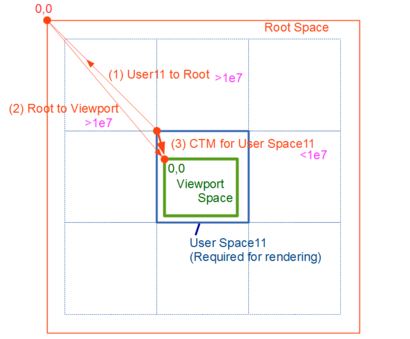
Such coordinate transformation is specified in Chapter 7.5 of SVG2 (Nested transformation). And the matrix for the composed coordinate transformation is defined as CTM.
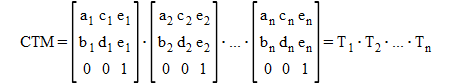
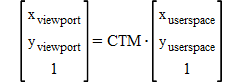
So, it is necessary for tiling to perform this coordinate transformation precisely. As this figure shows, both the matrix from user 11 to root and the matrix from root to viewport need long effective digits. However, the effective digits of CTM which is just needed for actual rendering is short. It is because user space 11 and viewport space are surely going near.
PROPOSAL
From above, double precision computation should be performed for the calculation of CTM by nested transformation to suppress errors.
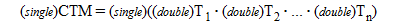
On the other hand, single precision is enough as CTM and the coordinate transformation computation. Therefore, single precision computation by GPU is possible.
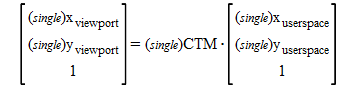
However, this may make it hard to implement multiply operation of nested matrixes by GPU.
Moreover, when there is nested viewport coordinate system, the transformation matrix to viewport coordinate system of a root should be computed by double. However, single is enough also for the translation computation to viewport space of the root by such a transformation matrix.
I think that this should be specified as one of the requirements since all the present viewers have this error amplification issue as the following chapter shows.
Supplement
- A bigger object than a tile must be divided for each tile.
- When a viewport is larger than a tile, a rounding error arises after all. However, in almost every cases, it will not become an issue. Because, a view port space is a coordinate system of a display device. It has a small effective digit number of about at most four digit.

Implementation status of browsers
| Chrome 48.0.2564.82 | No |
| Safari 9.0.2 | No |
| Internety Explorer 11 | No |
| Firefox 43.0.4(32bit) | No |
| Firefox 43.0.4(64bit) | YES! |
Tests
The test for checking behavior of CTM computation was prepared. [1] It also contains polyfill which emulates desirable computation.
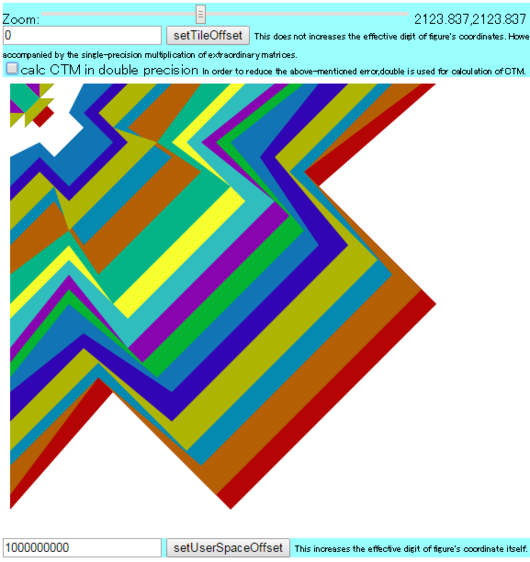
The slider of this test changes the zoom of viewport by changing svg element's viewBox property. Nested arrow graphics belong to the tile user space. Those arrows point out the origin of a tile user space. And a viewport is set up so that the origin of that tile may become an upper left corner of a screen. Therefore arrows point out the upper left corner of a screen.
If the number of the item setTileOffset is increased, the origin of a tile's user space toward root space will be shifted. (As a result, the required effective digit of viewBox (in root space) increases.) Provided that, viewport is still set up so that the origin of a tile may become an upper left corner of a screen by changing svg element's viewBox property. This is the coordinate transformation operation equivalent to this proposal.
Accordingly, if there are no transformation errors, regardless changing of zoom and setTileOffset, an arrow will always point out the upper left corner of a screen.
So, it should be displayed in this way.

In the above figure, since zero is set as setTileOffset and the required effective digit (of viewBox) has become a min, there is no error.
However, on the browser which has notable transformation rounding errors, when a big value is set as setTileOffset (e.g. 1000000000), you will recognize that the error of the origin of a graphic increasees along with zoom-in.
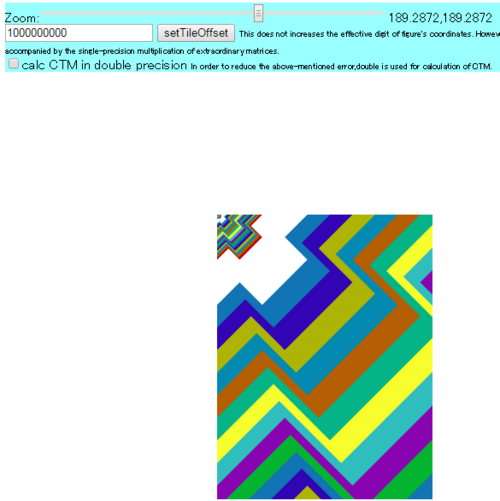
It may be a reason that nested poor precision transformation for CTM made the error amplify.
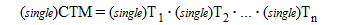
Polyfill
polyfill which this test has performs computation of CTM by double. A check box (named calc CTM in double precision) enables the polyfill. You will recognize that poyfill eliminates errors on any browsers.

Remarks
By the way, If the number of the item 'setUserSpaceOffset' is increased, the required effective digits of tile itself's user space will increase. Along with zoom-in, you could recognize that graphics collapses. This issue can not be canceled by this proposal. Only extension of the effective digits of user space solves this issue. Therefore, solution of this issue is out of scope in this proposal.
Revision of Conforming SVG Viewers
From above, I propose that this computation method is described as one of the requirements for Conforming SVG Viewer in Appendix D.8 instead of Conforming High Quality Viewer.
If SVG supports only a rendition of the coordinate system of each tile, the scalable global mapping system by unifying those tiles needs to be built as massive Web Apps. Tiling and Layering and Levels of Details are the standardization work for realizing such mapping system without massive Web Apps. Therefore, I want such a high precision tiling to be secured by all the viewers.
Incidentally
The current 4.3. Real number precision chapter does not specifically show the requirements for computation. On the other hand, Conforming SVG Viewers Appendix has made reference about precision at two part. One is a comparatively abstract description about computation.
- All visual rendering must be accurate to within one device pixel (px unit) to the mathematically correct result at the initial 1:1 zoom ratio. It is suggested that viewers attempt to keep a high degree of accuracy when zooming.
Another is described as requirements for the restrictive high quality viewer.
This shows that all the computations should be performed by double.
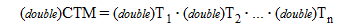
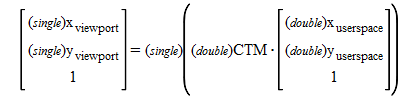
It is the method which I proposed before and the computation by GPU is difficult. On the other hand, this proppsal is a more easy method for viewer implementation, because it can apply single precision except for computation of CTM.