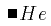 .[Cajori, 1928/1929]
.[Cajori, 1928/1929]| Up: Table of Contents | Working Draft 6-Jan-98 |
As has been noted in the introductory section of this report, mathematics can be distinguished by its use of a (relatively) formal language, mathematical notation. However, mathematics and its presentation should not be viewed as one and the same thing. Mathematical sums or products exist and are meaningful to many applications completely without regard to how they are rendered aurally or visually. The intent of the content markup in Mathematical Markup Language is to provide an explicit encoding of the underlying mathematical structure of an expression, rather than any particular rendering for the expression.
There are many reasons for providing a specific encoding for content. Even a disciplined and systematic use of presentation tags cannot properly capture this semantic information. This is because without additional information it is impossible to decide if a particular presentation was chosen deliberately to encode the mathematical structure or simply to achieve a particular visual or aural effect. Furthermore, an author using the same encoding to deal with both the presentation and mathematical structure might find a particular presentation encoding unavailable simply because convention had reserved it for a different semantic meaning.
The difficulties stem from the fact that there are many to one mappings from presentation to semantics and vice versa. For example the mathematical construct "H multiplied by e" is often encoded using an explicit operator as in H * e. In different presentational contexts, the multiplication operator might be invisible "H e" , or rendered as the spoken word "times". Generally, many different presentations are possible depending on the context and style preferences of the author or reader. Thus, given "H e" out of context it may be impossible to decide if this is the name of a chemical or a mathematical product of two variables H and e.
Mathematical presentation also changes with culture and time:
some expressions in combinatorial mathematics today have one
meaning to an English mathematician, and quite another to a French
mathematician. Notations may lose currency, for example the use of
musical sharp and flat symbols to denote maxima and minima. [Chaudry 1954] A notation in use
in 1644 for the multiplication mentioned above was 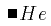 .[Cajori, 1928/1929]
.[Cajori, 1928/1929]
When we encode the underlying mathematical structure explicitly, without regard to how it is presented aurally or visually, we are able to interchange information more precisely with those systems which are able to manipulate the mathematics. In the trivial example above, such a system could substitute values for the variables H and e and evaluate the result. Further interesting application areas include interactive textbooks and other teaching aids.
The base set of content elements are chosen to be adequate for simple coding of most of the formulas used from kindergarten to the end of high school in the United States, and probably beyond through the first two years of college, that is up to A-Level or Baccalaureat level in Europe. Subject areas covered to some extent in MathML are:
The primary goal of the content encoding is to establish explicit connections between mathematical structures and their mathematical meanings. The content elements correspond directly to parts of the underlying mathematical expression tree. Each structure has an associated default semantics and there is a mechanism for associating new mathematical definitions with new constructs.
Significant advantages to the introduction of content specific tags include:
Expressions described in terms of content elements must still be rendered. For common expressions, default visual presentations are usually clear. "Take care of the sense and the sounds will take care of themselves" wrote Lewis Carroll [Carroll 1871]. Default presentations are included in the detailed description of each element occurring in section 4.4.
To accomplish these goals, the MathML content encoding is based on the concept of an expression tree. A content expression tree is constructed from a collection of more primitive objects, referred to herein as containers and operators. MathML possesses a rich set of predefined container and operator objects. As a general rule, operators are represented by empty MathML content elements and encode mathematical operators and functions. Containers encode mathematical objects, and are represented by non-empty MathML elements, which themselves may contain other containers and/or operators. MathML also provides several constructs for combining containers and operators in mathematically meaningful ways.
At the lowest level of a content expression tree, all tokens, or "leaf nodes," are encapsulated in non-empty elements that define their type. This notion applies to numbers, symbols and the more elaborate (compound) constructs such as sets, vectors and matrices. Elements are used in order to clearly identify the underlying items as objects. In this way, standard XML parsing can be used and attributes can be used to specify global properties of the objects.
The containers such as <cn>12345</cn> and <ci>x</ci>, represent actual mathematical objects such as numbers and variables, while operators such as <plus/> or <sin/> provide access to the basic mathematical operations and functions applicable to those objects. Additional containers such as <set>...</set> for sets, and <matrix>...</matrix> for matrices are provided for representing a variety of common compound objects.
For example, the number 12345 is encoded as
<cn>12345</cn>The attributes and CDATA content together provide the data necessary for an application to parse the number. For example, a default base of 10 is assumed, but to communicate that the underlying data was actually written in base 8, simply set the "base" attribute to 8 as in
<cn base="8">12345 </cn>while complex number 3 + 4 i can be indicated as
<cn type="complex">3 <sep/>4</cn>Such information makes it possible for another application to easily parse this into the correct number.
As another example, the scalar symbol v is encoded as
<ci>v</ci>By default ci elements represent elements from a commutative field. If a vector is intended then this fact can be encoded as
<ci type="vector">v </ci>
This invokes default semantics associated with the vector element, namely an arbitrary element of a finite dimensional vector space.
By using the ci element we have made clear that we are referring to a mathematical symbol but this does not say much about how it is rendered. By default a symbol is rendered as if the ci element were actually the presentation element mi (see section 3.2.2)). The actual rendering of a mathematical symbol can be made as elaborate as necessary simply by using the more elaborate presentational constructs (as described in chapter 3) in the body of the ci element.
The default rendering of a simple cn-tagged object is the same as for the presentation tag mn with some provision for overriding the presentation of the CDATA by providing explicit mn tags. This is described in detail in section 4.4 .
The issues for compound objects such as sets, vectors and matrices are all similar to those outlined above for numbers and symbols. Each such object has global properties as a mathematical object that impact how they are to be parsed. This may affect everything from the interpretation of operations that are applied to them through to how to render the symbols representing them. These mathematical properties are captured by setting attribute values.
The notion of constructing a general expression tree is essentially that of applying an operator to sub-objects. For example, the sum a + b can be thought of as an application of the <plus/> operator to two arguments a and b. Elements are used for operators for much the same reason that elements are used to contain objects. They are recognized at the XML parse level and their attributes can be used to record or modify the intended semantics. For example, setting the plus type attribute to vector as in <plus type="vector"/> can communicate that the intended operation is vector based.
Another important class of expressions is that of general function applications. There is a crucial semantic distinction between the function itself and the expression resulting from applying that function to zero or more arguments which must be captured. This is addressed by making the functions self-contained objects with their own properties and providing an explicit apply construct corresponding to function application.
The basic building block of a mathematical expression in MathML content markup is the apply element. An apply element corresponds to a complete mathematical expression. Roughly speaking, this means a piece of mathematics which could be surrounded by parentheses or "logical brackets" without changing its meaning.
For example, (x + y) might be encoded as
<apply><plus/> <ci> x </ci> <ci> y </ci> </apply>The opening and closing tags of apply specify exactly the scope of any operator or function. The content model of apply is simple and recursive. Symbolically, the content model can the described as:
apply => op a bwhere the operands a and b are containers or other content-based elements themselves, and op is any operator or function. Note that this allows apply constructs to be nested to arbitrary depth.
An apply may in principle have any number of operands:
apply => op a b [ c ... ]For example, (x + y + z) can be encoded as
<apply><plus/> <ci> a </ci> <ci> b </ci> <ci> c </ci> </apply>
Mathematical expressions involving a mixture of operations result in nested occurences of apply. For example, ax + b would be encoded as
<apply><plus/>
<apply><times/>
<ci> a </ci>
<ci> x </ci>
</apply>
<ci> b </ci>
</apply>
There is no need to introduce parentheses or to resort to operator precedence in order to parse the expression correctly. The apply tags provide the proper grouping for the re-use of the expressions within other constructs. Any expression enclosed by an apply element is viewed as a single coherent object.
An expression such as (F + G)(x) be just a product, as in
<apply><times/>
<apply><plus/>
<ci> F </ci>
<ci> G </ci>
</apply>
<ci> x </ci>
</apply>
or it might indicate the application of the function
F + G to the argument x. This is
indicated by constructing the sum
<apply><plus/> <ci> F </ci> <ci> G </ci> </apply>and applying it to the argument<ci> x </ci> as in
<apply>
<apply><plus/>
<ci> F </ci>
<ci> G </ci>
</apply>
<ci> x </ci>
</apply>
Both the function and the arguments may be simple identifiers or
more complicated expressions.
The most common operations and functions such as <plus/> and <sin/> have been predefined explicitly as empty elements (see section section 4.4). They have type and definition attributes, and by changing these attributes, the author can record that a different sort of algebraic operation is intended. This allows essentially the same notation to be re-used for a discussion taking place in a different algebraic domain.
Due to the nature of mathematics the notation must be extendable. The key to extendability is the ability of the user to define new functions.
It is always possible to apply arbitrary expressions as if they were functions and to infer their functional properties directly from that usage as was done in the previous section. However such an approach would preclude being able to encode the fact that the construct was a function or to record its mathematical properties except by actually using it. The fn element is used as a container to construct an actual function object in much the same way that ci is used to constuct a symbol.
To record the fact that F+G is being used semantically as if it were a function, encode it as:
<fn>
<apply><plus/>
<ci>F</ci>
<ci>G</ci>
</apply>
</fn>
Its intended semantic role (as a function) has now been indicated. Furthermore, the "definition" attribute of the fn can now be used to point to a written definition of such a function as in
<fn definition="Sums My Favourite Function Space">
<apply><plus/>
<ci>F</ci>
<ci>G</ci>
</apply>
</fn>
This would be important information to any application wanting to evaluate or simplify such an expression according to systematic rules provided for an algebra of functions.
To indicate that a matrix as an operator encode it as
<fn>
<matrix>
<matrixrow>
<ci> a </ci>
<ci> b </ci>
</matrixrow>
<matrixrow>
<ci> c </ci>
<ci> d </ci>
</matrixrow>
</matrix>
</fn>
A common usage of fn is to describe a completely new function. The definition attribute can then be used to refer explicitly to the mathematical definition. An example of such a construct is:
<fn definition="Definition_Of_NewG"> <ci>NewG</ci> </fn>The definition attribute can be given as a string, and would typically refer to a URL which provides a written definition for the NewG. Two functions would behave the same if they refer to the same definition. The role of the definition attribute is very similar to the role of definitions included at the beginning many mathematical papers, and which often just refer to a definition used by a particular book.
Consider a document discussing the vectors A = (a,b,c) and B = (d,e,f) and later including the expression V = A + B. It is important to be able communicate the fact that wherever A and B are used they represent a particular vector. The properties of that vector may determine aspects of operators such as plus.
The simple fact that A is a vector can be communicated by using the tagging
<ci type=vector>A </ci>but this still does not communicate, for example, which vector is involved or its dimensions.
The declare construct is used to associate specific properties or meanings with an object. The actual declaration itsself is not rendered visually (or in any other form). However, it indirectly impacts the semantics of all affected uses of the declared object.
The scope of a declare is local to the object in which it is declared, unless it has the attribute scope="global" in which case the scope is global to the document.
Its uses range all the way from resetting default attribute values through to associating an expression with a particular instance of of a more elaborate structure. Subsequent uses of the original expression (within the scope of the declare) play the same semantic role as would the paired object.
For example, the declaration
<declare>
<ci> A </ci>
<vector>
<ci> a </ci>
<ci> b </ci>
<ci> c </ci>
</vector>
</declare>
specifies that A stands for the particular vector (a,b,c) so
that subsequent uses of A as in V = A +
B can take this into account. When declare is used in
this way, the actual encoding
<apply><eq/>
<ci> V </ci>
<apply><plus/>
<ci> A </ci>
<ci> B </ci>
</apply>
</apply>
remains unchanged but the expression can be interpreted properly as
vector addition.
There is no requirement to declare an expression to stand for a specific object. For example, the declaration
specifies that A is a vector without indicating the number of components or the values of specific components. The possible values for the type attribute include all the predefined container element names names such as vector, matrix or set.<declare type="vector"> <ci> A </ci> </declare>
The lambda calculus allows a user to construct a function from a variable and an expression. For example, the lambda construct underlies the common mathematical idiom illustrated here:
Let f be a function such that f(x) = x2 + 2
There are various notations for this concept in mathematical literature, such as lambda(x, F(x) ) = F or lambda(x, [F] ) = F, where x is a free variable in F.
This concept is implemented in MathML with the lambda element. A lambda construct with n internal variables is encoded by a lambda element with n + 1 children. All but the last child must be ci elements containing the identifiers of the internal variables. The last is an expression defining the function. This is typically an apply, but can also be any content container element.
The following constructs lambda(x, sin (x+1)):
<lambda>
<ci> x </ci>
<apply> <sin/>
<apply><plus/>
<ci> x </ci>
<cn> 1 </cn>
</apply>
</apply>
</lambda>
To use declare and lambda to construct the function f for which f(x) = x2 + x + 3 use:
<declare type="fn">
<ci> f </ci>
<lambda> <ci> x </ci>
<apply><plus/>
<apply><power/>
<ci> x </ci>
<cn> 2 </cn>
</apply>
<ci> x </ci>
<cn> 3 </cn>
</apply>
</lambda>
</declare>
The following declares and constructs the function J such
that J(x,y) = the integral from x to y of
t4 with respect to t.
<declare type="fn">
<ci> J </ci>
<lambda>
<ci> x </ci>
<ci> y </ci>
<apply> <int/>
<apply> <power/>
<ci>t</ci>
<cn>4</cn>
</apply>
<lowlimit>
<ci> x </ci>
</lowlimit>
<uplimit>
<ci> y </ci>
</uplimit>
<bvar>
<ci> t </ci>
</bvar>
</apply>
</lambda>
</declare>
The function J can then in turn be applied to an argument
pair.
Given functions, it is natural to have functional inverses. This is handled by the inverse element.
Functional inverses can be problematic from a mathematical point of view in that it implicitly involves the definition of an inverse for an arbitrary function F. Even at the K through 12 level the concept of an inverse F-1 of many common functions F is not used in a uniform way. For example, the definitions used for the inverse trigonometric functions may differ slightly depending on the choice of domain and/or branch cuts.
MathML adopts the view:
If F is a function from a domain D to D', then the inverse G of F is a function over D' such that G(F(x)) = x for x in D.This definition does not assert that such an inverse exists for all or indeed any x in D, or that it is single-valued anywhere. Also, depending on the functions involved, additional properties such as F(G(y)) = y for y in D' may hold.
The inverse element is applied to a function whenever an inverse is required. For example, application of the inverse sine function to x (i.e., sin (-1) (x)) is encoded as:
<apply>
<apply><inverse/>
<sin/>
</apply>
<ci> x </ci>
</apply>
While arcsin is one of the predefined MathML functions, and
explicit reference to sin (-1) (x)) might
occur in a document discussing possible definitions of
arcsin.
While the primary role of the MathML content element set is to directly encode the mathematical structure of expressions independent of the notation used to present the objects, rendering issues cannot be ignored. Each content element has a default rendering, given in section 4.4. and several mechanisms (including style attributes, declarations and semantics elements) are provided for associating a particular rendering with an object.
The intent of MathML content markup is to encode mathematical expressions in such a way that the mathematical structure of the expression is clear. There must be no doubt when, for example, an actual sum, product or function application is intended and if specific numbers are present there must be enough information present to reconstruct the correct number for purposes of computation. It is still up to any MathML-compliant processor to decide what is to be done with such a content based expression. A renderer or a structured editor might simply use the data and its own built-in knowledge of mathematical structure to render the object. Alternatively, it might manipulate the object to build a new mathematical object. A more computationally oriented system might attempt carry out the indicated operation or function evaluation.
To achieve this goal of recording mathematical structure the MathML content elements must be used consistently by authors. The purpose of this section is describe the intended, consistent usage. The requirements involve more than just satisfying the syntactic structure specified by an XML DTD. Failure to conform to the usage as described below will result in a MathML error, even though the expression may be syntactically valid according to the DTD.
A listing of content elements giving more detailed information about their attributes, syntax, and suggested default semantics and renderings is given in section 4.4. An EBNF grammar for the content element markup is given in appendix E.
Containers provide a means for the construction of mathematical objects of a given type.
| Tokens | ci, cn |
| Constructors | interval, list, matrix, matrixrow, set, vector, apply, e, lambda, fn |
| Specials | declare |
Token elements are typically the leaves of the MathML expression tree. Token elements are used to indicate numbers and symbols.
It is also possible for the canonically empty operator elements such as <exp/>, <sin/> and <cos/> to be leaves in an expression tree. The usage of of operator elements is described in Section 4.2.3.
<ci> <msub> <mi>c</mi> <mn>1</mn> </msub> </ci>
encodes an atomic symbol which displays visually as c 1 which, for purposes of content, is treated as a single symbol representing a real number. The detailed structure and specifications is provided in section 4.4.1.2.
MathML provides a number of elements for combining elements into familiar compound objects. The compound objects include things like lists, sets. Each constructor produces a new type of object.
respresents the open-closed interval often written (a,b].<interval closure="open-closed> <ci> a </ci> <ci> b </ci> </interval>
Typically, the child elements of a possibly empty list element are the actual components of an ordered list. For example an ordered list of the three symbols a, b, and c is encoded as
<list> <ci> a </ci> <ci> b </ci> <ci> c </ci> </list>Alternatively, a condition element can be used to define lists where membership depends on satisfying certain conditions.
An order attribute which is used to specify what ordering is to be used. When the nature of the child elements permits, the ordering defaults to a numeric or lexicographic ordering.
Sets are structured much the same as lists except that there is no implied ordering and the type of set may be "normal" or "multiset" with "multiset" indicating that repetitions are allowed.
For both sets and lists, the child elements must be valid MathML content elements, but the type of the components of a list is not restricted. For example, it might be a list of equations, or inequalities.
<matrix> <matrixrow> <cn> 1 </cn> <cn> 2 </cn> </matrixrow> <matrixrow> <cn> 3 </cn> <cn> 4 </cn> </matrixrow> </matrix>
The matrixrow elements must always be contained inside of a matrix and all matrixrows in a given matrix must have the same number of elements.
Note that the behaviour of the matrix and
matrixrow elements is substantially different from the
mtable and mtr presentation elements.
<vector>
<apply><plus/>
<ci> x </ci>
<ci> y </ci>
</apply>
<cn> 3 </cn>
<cn> 7 </cn>
</vector>
through to using the sine function to construct sin(x) as in<apply><plus/> <ci> a </ci> <ci> b </ci> </apply>
or constructing integrals. Its usage in any particular setting is determined largely by the properties of the function (the first child element) and as such its detailed usage is covered together with the functions and operators in section 4.2.3 Functions, Operators and Qualifiers<apply><sin/> <ci> a </ci> </apply>
Such expressions could in principle be regarded as applications of a boolean function, and as such could be constructed using apply. They have treated as a special class of expressions in order to better reflect traditional usage.
The actual structure of expressions constructed using relation is similar to that for the apply element. The use of relation is described in 4.2.4 Relations
<lambda>
<ci> x </ci>
<apply>
<sin/>
<ci> x </ci>
</apply>
</lambda>
The following constructs the constant function lambda(x, 3)
<lambda> <ci> x </ci> <cn> 3 </cn> </lambda>
The declare construct is described in detail in section 4.4.2.8. It is special in that its entire purpose is to modify the semantics of other objects. It is not rendered visually or aurally.
The need for declarations arises any time a symbol (including more general presentations) is being used to represent an instance of an object of a particular type. For example, you may wish to declare that the symbolic identifier V represents a vector.
The declaration <declare type="vector"><ci>V</ci></declare> resets the default type attribute of <ci>V</ci> to vector for all affected occurrences of <ci>V</ci>. This avoids having to write <ci type="vector">V</ci> every time you use the symbol.
More generally, declare can be used to associate expressions with specific content. For example, the declaration
<declare>
<ci>F</ci>
<lambda>
<ci> U </ci>
<ci> x </ci>
<apply><int/>
<ci> U </ci>
<bvar> <ci> x
</ci> <bvar>
<lowlimit> <cn> 0
</cn> <lowlimit>
<uplimit> <ci> a
</ci> <uplimit>
</apply>
</lambda>
</declare>
associates the symbol F with a new function defined by the
lambda construct. While the declaration is in effect the
expression
stands for the integral of U from 0 to a.<apply><ci>F</ci> <ci> U </ci> <ci> x </ci> </apply>
The declare element can also be used to change the definition of a function or operator. For example, if the URL "HTTP://.../MATHML:NONCOMMUTPLUS" described a non-commutative plus operation then the declaration
would indictate that all affected uses of plus are to be interpreted as having that definition of plus.<declare definition="HTTP://.../MATHML:NONCOMMUTPLUS"> <plus/> </declare>
| unary arithmetic | exp , factorial |
| unary logical | not |
| unary functional | inverse |
| unary trigonometric | sin , cos , tan , sec , cosec , cotan , sinh , cosh , tanh , sech , cosech , cotanh , arcsin , arccos , arctan |
| unary linear algebra | determinant, transpose |
| unary calculus | ln, log, totaldiff |
| binary arithmetic | quotient, divide, minus, power, rem |
| binary logical | implies |
| binary set operators | setdiff |
| nary arithmetic | plus, times, max, min, gcd |
| nary statistical | mean, sdev, var, median, mode |
| nary logical | and, or, xor |
| nary linear algebra | select |
| nary set operator | union, intersect |
| nary functional | fn |
| integral, sum, product operator | integral, sum, product |
| differential operator | diff, partialdiff |
From the point of view of usage, MathML regards functions (eg. sin, cos) and operators (eg. plus, times) in the same way. MathML predefined functions and operators are all canonically empty elements
Note: The fn element can be used to construct a user-defined function or operator. fn is discussed in more detail below.
denotes a real number, namely sin(5).<apply><sin/><cn>5</cn></apply>
MathML functions can also be used as arguments to other operators, for example
denotes a function, namely the result of adding the sine and cosine functions in some function space. (The default semantic definition of plus is such that it infers what kind of operation is intended from the type of its arguments.)<apply><plus/><sin/><cos/></apply>
The number of child elements in the apply is defined by the element in the first (ie. operator) position.
Unary operators are followed by exactly one other child element within the apply.
Binary operators are followed by exactly two child elements.
Nary operators are followed by zero or more child elements.
The one exception to these rules is that declare elements may be inserted in any position except the first. declare elements are not counted when satisfying the child element count for an apply containing a unary or binary operator element.
Integral, sum, product and differential operators are discussed below in section 4.2.3.4 Operators taking Qualifiers.
In MathML, only functions and operators can be applied to arguments. In order to provide a way of applying functions constructed out of other functions, or functions other than the functions provided by the content elements, MathML provides the fn element. The fn element accepts any valid MathML expression as content, and allows it to be used as a content function. It is an error for the fn element to have no content.
One typical way of using the fn element is with author-named functions, such as f(5), encoded as:
Another common use is to designate the result of combining several functions as a function again: (sin + cos)(z):<apply> <fn><ci>f</ci></fn> <cn> 5 </cn> </apply>
<apply>
<fn>
<apply>
<plus/>
<sin/>
<cos/>
</apply>
</fn>
<ci>z</ci>
</apply>
| qualifiers | lowlimit, uplimit, bvar, degree, logbase |
| operators | int, sum, prod, diff, partialdiff, limit, log, moment |
Operators taking qualifiers are canonically empty functions which differ from ordinary empty functions only in that they support the use of special "qualifier" elements to specify their meaning more fully. They are used in exactly the same way as ordinary operators, except that when they are used as operators, certain qualifier elements are also permitted to be in the enclosing apply. Qualifier schemata are always optional. They always follow the argument if it is present. If more than one qualifier is present, they appear in the order lowlimit uplimit bvar degree logbase. A typical example is:
<apply>
<int/>
<apply>
<power/>
<ci>x</ci>
<cn>2</cn>
<apply>
<lowlimit><cn>0</cn></lowlimit>
<uplimit><cn>1</cn></uplimit>
<bvar><ci>x</ci></bvar>
</apply>
It is also valid to use qualifier schema with a function not applied to an argument. For example, a function acting on integrable functions on the interval [0,1] might be denoted:
<fn>
<apply>
<int/>
<lowlimit><cn>0</cn></lowlimit>
<uplimit><cn>1</cn></uplimit>
<bvar><ci>x</ci></bvar>
</apply>
</fn>
The meaning and usage of qualifier schema varies from function to
function. The following list summarizes the usage of qualifier
schema with the MathML functions taking qualifiers.
denote the mixed partial (d2 / dx dy) f.<apply> <partialdiff/> <fn><ci>f</ci></fn> <bvar><ci>x</ci></bvar> <bvar><ci>y</ci></bvar> </apply>
<apply>
<sum/>
<apply>
<power/>
<ci>x</ci>
<ci>i</ci>
</apply>
<lowlimit><cn>0</cn></lowlimit>
<uplimit><cn>100</cn></uplimit>
<bvar><ci>i</ci></bvar>
</apply>
When used with sum or product, each qualifier schema
is expected to contain a singleq child schema; otherwise an error
is generated.| binary relation | neq |
| binary logical relation | implies |
| binary set relation | in, notin, notsubset, notprsubset |
| binary series relation | tendsto |
| nary relation | eq, leq, lt, geq, gt |
| nary set relation | subset, prsubset |
The MathML content tags include a number of canonically empty elements which denote arithmetic and logical relations. Relations are characterised by the fact that, if a external application were to evaluate them (MathML does not specify how to evaluate expressions), they would typically return a truth value. By contrast, operators generally return a value of the same type as the operands. For example, the result of evaluating a < b is either true or false (by contrast, 1 + 2 is again a number).
Relations are bracketed with their arguments using the relation element in much the same way that other functions are bracketed with apply. The relation element is the first child element of the relation. Thus, the example from the preceding paragraph is properly marked up as:
It is an error to enclose a relation in an element other than relation.<relation> <lt/> <ci>a</ci> <ci>b</ci> </relation>
The number of child elements in the relation is defined by the element in the first (ie. relation) position.
Unary relations are followed by exactly one other child element within the relation.
Binary relations are followed by exactly two child elements.
Nary relations are followed by zero or more child elements.
The one exception to these rules is that declare elements may be inserted in any position except the first. declare elements are not counted when satisfying the child element count for an relation containing a unary or binary relation element.
| condition | condition |
The condition element is used to define the "such that" constrcut in mathematical expressions.
The child elements of condition are:
Examples:
<condition>
<ci>x</ci>
<relation><lt/>
<apply><power/>
<ci>x</ci>
<cn>5</cn>
</apply>
<cn>3</cn>
</relation>
</condition>
This encodes " x such that x5 < 3 "
<condition>
<ci>x</ci>
<ci>y</ci>
<relation>
<lt/>
<apply><power/>
<ci>x</ci>
<ci>y</ci>
</apply>
<cn>1</cn>
</relation>
<relation>
<lt/>
<apply><power/>
<ci>y</ci>
<ci>x</ci>
</apply>
<apply><plus/>
<ci>y</ci>
<ci>x</ci>
</apply>
</relation>
</condition>
This encodes " x,y such that xy < 1 and yx < x + y "
| mappings | semantics, annotation, xml-annotation |
The use of content rather than presentation tagging for mathematics is sometimes referred to as "semantic tagging" [Buswell 1996]. The parse-tree of a fully bracketed MathML content tagged element structure corresponds directly to the expression-tree of the underlying mathematical expression. We therefore regard the content tagging itself as encoding the syntax of the mathematical expression. This is, in general, sufficient to obtain some rendering and even some symbolic manipulation (e.g., polynomial factorization).
However, even in such apparently simple expressions as X + Y, some additional information may be required for applications such as computer algebra. Are X and Y integers,or functions, etc.? 'Plus' represents addition over which field? This additional information is referred to as Semantic Mapping. In MathML, this mapping is provided by the semantics, annotation and xml-annotation elements.
The semantics element is the container element for the MathML expression together with its semantic mapping. semantics expects a variable number of child elements. The first is the element (which may itself be a complex element structure) for which this additional semantic information is being defined. The second and subsequent children, if any, are instances of the elements annotation and/or xml-annotation.
The semantics tags also accepts a definition attribute for use by external processing applications. One use might be a URL for a semantic context dictionary, for example. Since the semantic mapping information might in some cases be provided entirely by the definition attribute, the annotation or xml-annotation elements are optional.
The annotation element is a container for arbitrary data. This data may be in the form of text, computer algebra encodings, C programs, or whatever a processing application expects. annotation has an attribute encoding defining the form in use. Note that the content model of annotation is #PCDATA, so care must be taken that the particular encoding does not conflict with XML parsing rules.
The xml-annotation element is a container for semantic information in well-formed XML. For example, an XML form of the OpenMath semantics could be given. Another possible use here is to embed, for example, the presentation tag form of a construct given in content tag form in the first child element of semantics (or vice versa). xml-annotation has an attribute encoding defining the form in use.
For Example:
<semantics>
<apply> <divide/> <cn>123</cn>
<cn>456</cn>
</apply>
<annotation encoding="Mathematica">
N[123/456, 39]
</annotation>
<annotation encoding="TeX">
$0.269736842105263157894736842105263157894\ldots$
</annotation>
<annotation encoding="Maple">
evalf(123/456, 39);
</annotation>
<xml-annotation encoding="MathML-Presentation">
<mrow>
<mn> 0.269736842105263157894 </mn>
<mover accent='true'>
<mn> 736842105263157894 </mn>
<mo> &obar; </mo>
</mover>
</mrow>
</xml-annotation>
<xml-annotation encoding="OpenMath">
<OM_APP>..</OM_APP>
</xml-annotation>
</semantics>
where <OM_APP>..</OM_APP> are the elements defining the
additional semantic information.
Of course, providing an explicit semantic mapping at all is optional, and in general would only be provided where there is some requirement to process or manipulate the underlying mathematics.
Although semantic mappings can easily be provided by various proprietary, or highly specialized encodings, there are no widely available, non-proprietary standard semantic mapping schemes. In part to address this need, the goal of the OpenMath effort is to provide a platform-independent, vendor-neutral standard for the exchange of mathematical objects between applications. Such mathematical objects include semantic mapping information. The OpenMath group has defined an SGML syntax for the encoding of this information [OpenMath, 1996]. This element set could provide the basis of one XML-ANNOTATION element set.
An attraction of this mechanism is that the OpenMath syntax is specified in SGML, so that the whole expression is checkable by a DTD-based parser.
MathML functions, operators, and relations can all be thought of as mathematical functions if viewed in a sufficiently abstract way. For example, the standard addition operator can be regarded as a function mapping pairs of real numbers to real numbers. Similarly, a relation can be thought of as a function from some space of ordered pairs into the set of values {true, false}. To be mathematically meaningful, the domain and range of a function must be precisely specified. In practical terms, this means that functions only make sense when applied to certain kinds of operands. For example, thinking of the standard addition operator, it makes no sense to speak of "adding" a set to a function. Since MathML content markup seeks to encode mathematical expressions in a way that can be unambiguously evaluated, it is no surprise that the types of operands is an issue.
MathML specifies the types of arguments in two ways. The first way is by providing precise instructions for processing applications about the kinds of arguments expected by the MathML content elements denoting functions, operators and relations. These operand types are defined in terms of an OpenMath based content dictionary. For example, the MathML Content dictionary specifies that for real scalar arguments the <plus/> operator is the standard commutative addition operator over a field. Elements such as cn and ci have type arguments default values of "real". Thus some processors will be able to use this information to verify the validity of the indicated operations.
Although MathML specifies the types of argumentsfor functions, operators and relations, and provides a mechanism for typing arguments, a MathML compliant processor is not required to do any type checking. In other words, a MathML processor will not generate errors if argument types are incorrect. If the processor is a computer algebra system, it may be unable to evaluate an expression, but no error is generated.
Content element attributes are all of the type CDATA, that is any character string will be accepted as valid. In addition, each attribute has a list of predefined values, which a content processor is expected to recognise and process. The reason that the attribute values are not formally restricted to the list of predefined values is to allow for extension. A processor encountering a value (not in the predefined list) which it does not recognise may validly process it as the default value for that attribute.
Default = "10"
Default = "closed"
Default = "", ie. the semantics are defined within the MathML fragment, and/or by the MathML default semantics.
Default = "", ie. unspecified.
Default = "1"
Default = "function-model"
Default = "numeric"
Default = "local"
To affect the entire document , place a top level math element contining the "global-document" declarations at the beginning of the document. It is anticipated that the proper implementation of the "global-document" scoping will require further work integrating the MathML requirements with those for Cascading Style Sheets ( CSS1)
indicates type of the number. Predefined values: integer, rational, real, float, complex, complex-polar, complex-cartesian, constant.
Default = "real"
Default = "" , ie. unspecified
Default = "ci" , ie. a generic identifier
indicates the direction from which the limiting value is approached. Predefined values: above, below, two-sided.
Default = "above"
The type attribute, in addition to conveying semantic information, can be interpreted to provide rendering information. For example in
<ci type="vector">V</ci>a renderer could display a bold V for the vector.
All Content elements support the following general atttributes which can be used to modify the rendering of the markup.
The class and style attribute are intended for compatibility with Cascading Style Sheets, as described in 2.3.4.
Content or semantic tagging goes along with the (frequently implicit) premise that, if you know the semantics, you can always work out a presentation form. When an author's main goal is to mark up re-usable, evaluatable mathematical expressions, the exact rendering of the expression is probably not critical, provided that it is easily understandable. However, when an author's goal is more along the lines of providing enough additional semantic information to make a document more accessible by facilitating better visual rendering, voice rendering, or specialized processing, controlling the exact notation used becomes more of an issue.
MathML elements accept an attribute other (see 7.2.3)which can be used to specify things not specifically documented in MathML. On content tags, this attribute can be used by an author to express a preference between equivalent forms for a particular content element construct, where the selection of the presentation has nothing to do with the semantics. Examples might be
Thus, if a particular renderer recognized a display attribute to select between script style and display style fractions, an author might write
to indicate that the rendering 1/x is preferred.<apply other='display="scriptstyle"'> <divide/> <mn> 1 </mn> <mi> x </mi> </apply>
The information provided in the other attribute is intended for use by specific renderers or processors, and therefore, the permitted values are determined by the renderer being used. It is legal for a renderer to ignore this information. This might be intentional, in the case of a publisher imposing a house style, or simply because the renderer does not understand them, or is unable to carry them out.