The OWL 2 Web Ontology Language, informally OWL 2, is an ontology language for the Semantic Web with formally defined meaning. OWL 2 ontologies provide classes, properties, individuals, and data values and are stored as Semantic Web documents. OWL 2 ontologies can be used along with information written in RDF, and OWL 2 ontologies themselves are primarily exchanged as RDF documents. The OWL 2
Document Overview describes the overall state of OWL 2, and should be read before other OWL 2 documents.
This document defines the RDF-compatible model-theoretic semantics of OWL 2.
May Be Superseded
This section describes the status of this document at the time of its publication. Other documents may supersede this document. A list of current W3C publications and the latest revision of this technical report can be found in the W3C technical reports index at http://www.w3.org/TR/.
Summary of Changes
This Last Call Working Draft provides several significantdocument has undergone some small changes since the
previous version as an Ordinary Working Draftof 02 December 2008.21st April, 2009.
- The
following list provides only a high level overviewrange of owl:predicate was adjusted to remove undesirable
inferences.
- The
performed changes. See Section 10RDF vocabulary for a more detailed list of changes. The document has been restructured in several placesannotations was changed: owl:subject,
owl:predicate and owl:object became, respectively,
owl:annotatedSource, owl:annotatedProperty and
owl:annotatedTarget.
- The
presentationname of tablesrdf:text was changed to rdf:PlainLiteral.
- Some minor errors and
formulae has been improved. There is now a clear distinction betweeninfelicities were corrected.
- Some minor editorial changes were made.
Please Comment By 30 July 2009
The specified semantics called "OWL 2 RDF-Based Semantics", andOWL Working Group seeks
to gather experience from implementations in order to
increase confidence in the wholelanguage called "OWL 2 Full" as RDF graphs being interpreted using this semantics. The "Introduction" sectionand the texts describing the semantic conditions have been extended. The "Ontologies" section has been rewrittenmeet specific exit criteria. This document will remain a Candidate Recommendation until at least 30 July 2009. After that date, when
and now talks primarily about the RDF graph syntax forif the OWL 2 RDF-Based Semantics.exit criteria are met, the definitiongroup intends to request Proposed
Recommendation status.
Please send reports of datatypes with facetsimplementation experience, and the semantic conditions for datatype restrictions have been better alignedother
feedback, to public-owl-comments@w3.org
(public
archive). Reports of any success or difficulty with the Direct Semantics. The correspondence theorem has been revised andtest cases are encouraged. Open discussion among developers is welcome at public-owl-dev@w3.org (public archive).
No longer dependents on the comprehension conditions.Endorsement
Publication as a proof sketch for the theorem has been constructed, and an elaborate example exists that motivatesCandidate Recommendation does not imply endorsement by the theorem and its proof. Several WG resolutions have been implemented (see also the list of OWL 2 changes ). A few errors have been corrected. Last Call The Working Group believes it has completed its design work for the technologies specified this document, so this is a "Last Call" draft. The design is not expected to change significantly, going forward, and now is the key time for external review, before the implementation phase. Please Comment By 12 May 2009 The OWL Working Group seeks public feedback on this Working Draft. Please send your comments to public-owl-comments@w3.org ( public archive ). If possible, please offer specific changes to the text that would address your concern. You may also wish to check the Wiki Version of this document and see if the relevant text has already been updated. No Endorsement Publication as a Working Draft does not imply endorsement by the W3C Membership. This is a draft documentW3C Membership. This is a draft document and may be updated, replaced or obsoleted by other documents at any time. It is inappropriate to cite this document as other than work in progress.
Patents
This document was produced by a group operating under the 5 February 2004 W3C Patent Policy. W3C maintains a public list of any patent disclosures made in connection with the deliverables of the group; that page also includes instructions for disclosing a patent. An individual who has actual knowledge of a patent which the individual believes contains Essential Claim(s) must disclose the information in accordance with section 6 of the W3C Patent Policy.
Editor's Note: Outstanding Editorial Work: Some editorial work has been deferred to the time right before publication as a Proposed Recommendation
working draft,(PR), when the content of the document can be considered stable:
- The proof of the correspondence theorem
in Section 7.3(Section 7.3) might still need some further refinement.
- There are several item lists with both item bullets and numbers or letters. This will be changed into numbers/letters only after the proof of the correspondence theorem has been refined.
- Non-breakable whitespace will be put in formulae where appropriate.
1 Introduction (Informative)
This document defines the RDF-compatible model-theoretic semantics of OWL 2,
referred to as the "OWL 2 RDF-Based Semantics".
The OWL 2 RDF-Based Semantics gives a formal meaning
to every RDF graph
[RDF Concepts]
and is fully compatible with the
RDF Semantics specification
[RDF Semantics].
The specification provided here
is the successor to
the original OWL 1 RDF-Compatible Semantics specification
[OWL 1 RDF-Compatible Semantics].
Technically,
the OWL 2 RDF-Based Semantics
is defined as a
semantic extension
of
RDFS"D-Entailment"
(RDFS with datatype support ( "D-Entailment" ),support),
as specified in
[RDF Semantics].
In other words,
the meaning given to an RDF graph by the OWL 2 RDF-Based Semantics
includes the meaning given to the graph by the semantics of RDFS with datatypes,
and additional meaning is given to all the language constructs of OWL 2,
such as boolean connectives,
sub property chains
and qualified cardinality restrictions
(see the OWL 2 Structural Specification
[OWL 2 Specification]
for further information
on all the language constructs of OWL 2).
The definition of the semantics for the extra constructs
follows the same design principles
that have been applied to the RDF Semantics.
The content of this document is not meant to be self-contained,
but builds on top of the RDF Semantics document
[RDF Semantics]
by adding onlythose aspects
that are specific to OWL 2.
Hence,
the complete definition of the OWL 2 RDF-Based Semantics
is given by
the combination of both
the RDF Semantics document
and the OWL 2 RDF-Based Semantics document.document at hand.
In particular,
the terminology used in the RDF Semantics
is reused in the document at hand,here,
except for cases
where a conflict exists with the rest of the OWL 2 specification.
The following paragraphs
outline thisthe document's structure and content,
and provide an overview of
some of the distinguishing features of the OWL 2 RDF-Based Semantics.
According to Section 2,
the syntax
forover which the OWL 2 RDF-Based Semantics is defined
is the set of all RDF graphs
[RDF Concepts].
Every such RDF graph
is given a precise formal meaning
by the OWL 2 RDF-Based Semantics.
The language
that is determined
by RDF graphs
being interpreted using the OWL 2 RDF-Based Semantics
is called
"OWL 2 Full".
In this document,
RDF graphs are also called
"OWL 2 Full ontologies",
or simply "ontologies",
unless there is any risk of confusion.
The OWL 2 RDF-Based Semantics
interprets the
RDF and RDFS vocabularies
[RDF Semantics]
and the OWL 2 RDF-Based vocabulary (see Section 3 ). Also treated are,
together with an extended set of datatypes
and their constraining facets
for datatype restrictions.(see Section 3).
OWL 2 RDF-Based interpretations
(Section 4)
are defined on a universe
that is divided into parts,
namely individuals, classes, and properties,
which are identified with their RDF counterparts
(see Figure 1).
In particular,
the part of individuals equals the whole universe.
This means
that all classes and properties are also
individuals in their own right.
Further,
every name interpreted by an OWL 2 RDF-Based interpretation
denotes an individual.
The three basic parts are further divided into subparts as follows.
The part of individuals subsumes the part of data values,
which comprises the denotations of all literals.
Also subsumed by the individuals is the part of ontologies.
The part of classes subsumes the part of datatypes,
which are classes entirely consisting of data values.
Finally,
the part of properties subsumes the parts of
object properties,
data properties,
annotationontology properties
and ontologyannotation properties.
In particular,
the part of object properties equals the whole part of properties,
and all other kinds of properties are therefore also object properties.
For the particular case ofannotations properties
it is important tonote that annotations cannot reallybe regarded as "semantic-free comments"considered "semantic-free"
under the OWL 2 RDF-Based Semantics.
Just like every other triple or set of triples occurring in an RDF graph,
an annotation is actually an interpreted assertion that denotesassigned a truth value under theby any given OWL 2 RDF-Based Semantics. This means thatinterpretation.
Hence,
although annotations are meant to be "semantically weak",
i.e. their formal meaning does not significantly exceed
that coming from the RDF Semantics specification,
adding an annotation
may still change the meaning of an ontology.
An analogA similar discussion holds for statements
that are built from ontology properties.properties,
such as owl:imports,
which are used to define relationships between two ontologies.
Every class represents a specific set of individuals,
called the class extension of the class:class,
written as "ICEXT(C)".
An individual a is an instance of a given class C
exactly if a is a member of the class extension of C , written as "ICEXT( C )"..
Since a class is itself an individual under the OWL 2 RDF-Based Semantics,
classes are distinguished from their respective class extensions.
This distinction allows,
for example,
for a class to be an instance of itself
by being a member of its own class extension.
Also,
two classes may be equivalent
by sharing the same class extension,
though still being different individuals (i.e.,individuals,
i.e., they do not need to share the same properties).properties.
Similarly,
every property has a property extension,
written as "IEXT(p)",
associated with it, consistingit
that consists of pairs of individuals:individuals.
An individual a1 has a relationship to another individual a2
based on a given property p,
exactly if the pair ⟨ a1 , a2 ⟩
is a member of the property extension of p , written as "IEXT( p )"..
Again, properties are distinguished from their property extensions.
Individuals may play different roles.
For example,
an individual can be
both a data property and an annotation property,
since the different parts of the universe
of an OWL 2 RDF-Based interpretation
are not required to be mutually disjoint.
Or an individual can be
both a class and a property,
since
a class extension and a property extension
may independently be associated with the same individual.
The main part of the OWL 2 RDF-Based Semantics is Section 5,
which specifies
a formal meaning for all the actual semantic features in termsOWL 2 language constructs
by means of the
OWL 2 RDF-Based semantic conditions.
These semantic conditions extend all the semantic conditions
given in [RDF Semantics].
The OWL 2 RDF-Based semantic conditions effectively determine
which sets of RDF triples are assigned a specific meaning,
and what this meaning is.
For example,
there exist semantic conditions
that allow to interpret the RDF triple
"C owl:disjointWith D"
to mean that the denotations of the IRIs
"C "and "D
"have disjoint class extensions.
There is usually no need to provide localizing information
(e.g. by means of "typing triples")
for the IRIs occurring in an ontology.
As for the RDF Semantics,
the OWL 2 RDF-Based semantic conditions have been designed
to ensure that the denotation of any IRI
will actually be in the appropriate part of the universe.
For example,
the RDF triple
"C owl:disjointWith D"
is sufficient to deduce that
the denotations of the IRIs
"C "and "D
"are actually classes.
It is not necessary to explicitly add additional typing triples
"C rdf:type rdfs:Class"
and
"D rdf:type rdfs:Class"
to the ontology.
In the RDF Semantics,
this kind of "automatic localization"
was to some extent achieved by so called
"axiomatic triples" [RDF Semantics],
such as
"rdfs:subClassOf rdf:type rdf:Property"
or
"rdfs:subClassOf rdfs:domain rdfs:Class".
However, there is no explicit collection of additional axiomatic triples
for the OWL 2 RDF-Based Semantics
but, instead,
the specific axiomatic aspects of the OWL 2 RDF-Based Semantics
are determined by a subset of the OWL 2 RDF-Based semantic conditions.
Section 6
discusses axiomatic triples in general,
and provides
an example set of axiomatic triples
that is compatible with the OWL 2 RDF-Based Semantics.
Section 7 compares
the OWL 2 RDF-Based Semantics
with the OWL 2 Direct Semantics
[OWL 2 Direct Semantics].
While
the OWL 2 RDF-Based Semantics is based on the RDF Semantics specification
[RDF Semantics],
the OWL 2 Direct Semantics
is a description logic style semantics.
Several fundamental differences
exist between the two semantics,
but
there is also a strong relationship
basically stating that the OWL 2 RDF-Based Semantics
is able to reflect all logical conclusions
of the OWL 2 Direct Semantics.
This means that the OWL 2 Direct Semantics
can
in a sense
be regarded as a sub semantics of the OWL 2 RDF-Based Semantics.
The precise relationship is given by the
OWL 2 correspondence theorem.
Significant effort has been spent
in keeping the design of the OWL 2 RDF-Based Semantics
as close as possible
to that of the original specification of the OWL 1 RDF-Compatible Semantics
[OWL 1 RDF-Compatible Semantics].
The OWL 2 RDF-Based Semantics actually deviates from the OWL 1 RDF-Compatible Semanticsits predecessor in several aspects,
in most cases due to serious technical problems
that would have arisen
from a conservative semantic extension.
One important change is that,
while there still exist
so called "comprehension conditions"
for the OWL 2 RDF-Based Semantics
(see Section 8),
these are not part of the
normative set of semantic conditions anymore.
The OWL 2 RDF-Based Semantics also corrects several errors of theOWL 1 RDF-Compatible Semantics.1.
A list of differences between the two languages is given in
Section 9.
The italicized keywords MUST, MUST NOT, SHOULD, SHOULD NOT, and MAY are used to specify normative features of OWL 2 documents and tools, and are interpreted as specified in RFC 2119 [RFC 2119].
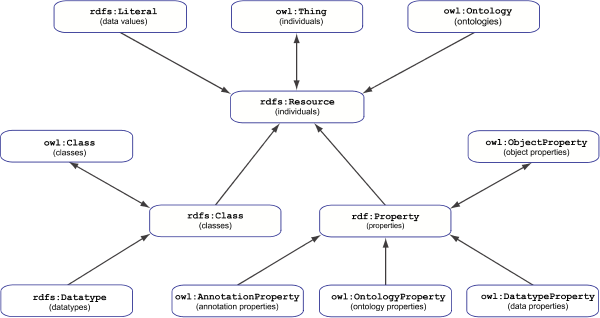
Figure 1: "Parts Hierarchy" of the OWL 2 RDF-Based Semantics
2 Ontologies
This section determines the syntax
for the OWL 2 RDF-Based Semantics.Semantics,
and gives an overview on typical content of ontologies
for ontology management tasks.
2.1 Syntax
Following Sections 0.2 and 0.3 of the RDF Semantics specification
[RDF Semantics],
the OWL 2 RDF-Based Semantics
is defined on every RDF graph
(Section 6.2 of [RDF Concepts]),
i.e. on every set of RDF triples
(Section 6.1 of [RDF Concepts]).
In accordance with the rest of the OWL 2 specification
(see Section 2.3 of
[OWL 2 Specification]),
this document
uses an extended notion of an RDF graph
by allowing the RDF triples in an RDF graph
to contain arbitrary IRIs
("Internationalized Resource Identifiers")
according to
[RFC 3987].
In contrast,
the RDF Semantics specification
[RDF Semantics]
is defined on RDF graphs containing URIs
[RFC 2396].
This change
is backwards compatible
with the RDF specification.specification,
since URIs are also IRIs.
Terminological note:
The document at hand
uses the term "IRI"
in accordance with the rest of the OWL 2 specification
(see Section 2.4 of [OWL 2 Specification]),
whereas the RDF Semantics specification
[RDF Semantics]
uses the term "URI reference" instead.reference".
According to [RFC 3987],
the term "IRI"
stands for an absolute resource identifier with optional fragment,
which is what is being used throughout this document.
In contrast,
the term "IRI reference" additionally covers relative references,
which are never used in this document.
Convention:
In this document,
IRIs are abbreviated
in the way defined by
Section 2.4 of [OWL 2 Specification],
i.e., the abbreviations consist of a prefix name and a local part,
such as
"prefix:localpart".
The definition of an RDF triple
inaccording to Section 6.1 of [RDF Concepts]
is restricted to cases
where the subject of an RDF triple is
an IRI
or a
blank node
(Section 6.6 of [RDF Concepts]),
and where the predicate of an RDF triple is
an IRI.
As a consequence,
the definition does not treat cases,
where,
for example,
the subject of a triple is a literal
(Section 6.5 of [RDF Concepts]),
as in
"s" ex:p ex:o,
or where the predicate of a triple is a blank node,
as in
ex:s _:p ex:o.
In order to allow for interoperability
with other existing orand future technologies and tools,
the document at hand
does not explicitly forbid the use of
generalized RDF graphs to containconsisting of generalized RDF triples,
which are defined to allow for
IRIs, literals and blank nodes
to occur in the subject, predicate and object position.
Thus,
an RDF graph
MAY
contain generalized RDF triples.triples,
but an implementation is not required to support generalized RDF graphs.
Note that every RDF graph consisting entirely of RDF triples according to
Section 6.1 of [RDF Concepts]
is also a generalized RDF graph.
Terminological notes:
The term
"OWL 2 Full"
refers to the language
that is determined
by the set of all RDF graphs
being interpreted using the OWL 2 RDF-Based Semantics.
Further,
in this document
the term
"OWL 2 Full ontology"
(or simply "ontology",
unless there is any risk of confusion)
will be used interchangeably
with the term "RDF graph".
2.2 Content of Ontologies (Informative)
While there do not exist any syntactic restrictions
on the set of RDF graphs
that can be interpreted by the OWL 2 RDF-Based Semantics,
in practice
an ontology will often contain certain kinds of componentsconstructs
that are aimed to support ontology management tasks.
Examples are
ontology headers
and
ontology IRIs,
as well as componentsconstructs that are about
versioning,
importing
and
annotating of ontologies,
including the concept of incompatibility between ontologies.
These topics are outside the scope of this semantics specification.
Section 3 of [OWL 2 Specification]
deals with these topics in greaterdetail,
and can therefore be used as a guide
on how to apply these componentsconstructs in OWL 2 Full ontologies accordingly.
The mappings of all these componentsconstructs to their respective RDF encodings
are defined in
[OWL 2 RDF Mapping].
3 Vocabulary
This section specifies the OWL 2 RDF-Based vocabulary,
and lists the names of the datatypes and facets
used under the OWL 2 RDF-Based Semantics.
3.1 Standard Prefixes
Table 3.1
lists the standard prefix names
and their prefix IRIs
used in this document.
Table 3.1: Standard Prefixes
|
| Prefix Name
| Prefix IRI
|
| OWL
| owl
| http://www.w3.org/2002/07/owl#
|
| RDF
| rdf
| http://www.w3.org/1999/02/22-rdf-syntax-ns#
|
| RDFS
| rdfs
| http://www.w3.org/2000/01/rdf-schema#
|
| XML Schema
| xsd
| http://www.w3.org/2001/XMLSchema#
|
3.2 Vocabulary Terms
Table 3.2
lists the IRIs of the OWL 2 RDF-Based vocabulary,
which is the set of vocabulary IRIs (or "vocabulary terms")terms
that are specific for the OWL 2 RDF-Based Semantics.
This vocabulary
extends the RDF and RDFS vocabularies
as specified by Sections 3.1 and 4.1 of
[RDF Semantics],
respectively.
Table 3.2
excludes those IRIs
that arewill be mentioned in
eitherSection 3.3 on datatype names
or
Section 3.4 on facet names.
Implementations are not required
to support the IRI owl:onProperties,
but
MAY
support it
in order to realize
n-ary dataranges with arity ≥ 2
(see Section 7 of
[OWL 2 Specification]
for further information).
Note:
The use of the IRI owl:DataRange has been deprecated as of OWL 2.
The IRI rdfs:Datatype
SHOULD
be used instead.
Table 3.2: OWL 2 RDF-Based vocabulary
owl:AllDifferent owl:AllDisjointClasses owl:AllDisjointProperties owl:allValuesFrom owl:annotatedProperty owl:annotatedSource owl:annotatedTarget owl:Annotation owl:AnnotationProperty owl:assertionProperty owl:AsymmetricProperty owl:Axiom owl:backwardCompatibleWith owl:bottomDataProperty owl:bottomObjectProperty owl:cardinality owl:Class owl:complementOf owl:DataRange owl:datatypeComplementOf owl:DatatypeProperty owl:deprecated owl:DeprecatedClass owl:DeprecatedProperty owl:differentFrom owl:disjointUnionOf owl:disjointWith owl:distinctMembers owl:equivalentClass owl:equivalentProperty owl:FunctionalProperty owl:hasKey owl:hasSelf owl:hasValue owl:imports owl:incompatibleWith owl:intersectionOf owl:InverseFunctionalProperty owl:inverseOf owl:IrreflexiveProperty owl:maxCardinality owl:maxQualifiedCardinality owl:members owl:minCardinality owl:minQualifiedCardinality owl:NamedIndividual owl:NegativePropertyAssertion owl:Nothing owl:objectowl:ObjectProperty owl:onClass owl:onDataRange owl:onDatatype owl:oneOf owl:onProperty owl:onProperties owl:Ontology owl:OntologyProperty owl:predicateowl:priorVersion owl:propertyChainAxiom owl:propertyDisjointWith owl:qualifiedCardinality owl:ReflexiveProperty owl:Restriction owl:sameAs owl:someValuesFrom owl:sourceIndividual owl:subjectowl:SymmetricProperty owl:targetIndividual owl:targetValue owl:Thing owl:topDataProperty owl:topObjectProperty owl:TransitiveProperty owl:unionOf owl:versionInfo owl:versionIRI owl:withRestrictions
|
3.3 Datatype Names
Table 3.3
lists the IRIs of the datatypes used in the OWL 2 RDF-Based Semantics.
The normative set of datatypes for the OWL 2 RDF-Based Semantics equals the set of datatypesdatatype rdf:XMLLiteral is described in
Section 3.1 of
[RDF Semantics].
All other datatypes are described in
Section 4 of [OWL 2 Specification].
The meaningnormative set of rdf:XMLLiteral is described in Section 3.1datatypes of [ RDFthe OWL 2 RDF-Based Semantics ]. All otherequals the set of datatypes
are asdescribed in Section 4 of
[OWL 2 Specification].
Table 3.3: Datatypes of the OWL 2 RDF-Based Semantics
xsd:anyURI xsd:base64Binary xsd:boolean xsd:byte xsd:dateTime xsd:dateTimeStamp xsd:decimal xsd:double xsd:float xsd:hexBinary xsd:int xsd:integer xsd:language xsd:long xsd:Name xsd:NCName xsd:negativeInteger xsd:NMTOKEN xsd:nonNegativeInteger xsd:nonPositiveInteger xsd:normalizedString rdf:PlainLiteral xsd:positiveInteger owl:rational owl:real xsd:short xsd:string rdf:textxsd:token xsd:unsignedByte xsd:unsignedInt xsd:unsignedLong xsd:unsignedShort rdf:XMLLiteral
|
Feature At Risk #1: owl:rational support
Note: This feature is "at risk" and may be removed from this specification based on feedback. Please send feedback to public-owl-comments@w3.org. For the current status see features "at risk" in OWL 2
The owl:rational datatype might be removed from OWL 2 if implementation experience reveals problems with supporting this datatype.
3.4 Facet Names
Table 3.4
lists the IRIs of the facets used underin the OWL 2 RDF-Based Semantics.
Each datatype listed in Section 3.3
has a (possibly empty) set of constraining facets.
All facets are described in
Section 4 of [OWL 2 Specification]
in the context of their respective datatypes.
The normative set of facets forof the OWL 2 RDF-Based Semantics equals the set of facets
described in Section 4 of
[OWL 2 Specification].
In this specification,
facets can beare used to restrict datatypes.for defining datatype restrictions
(see Section 5.7).
For example,
to refer to the set of all strings of length 5,5
one can restrict
the datatype xsd:string
(Section 3.3)
by the facet xsd:length
and the value 5.
In this specification, facets are used for defining datatype restrictions , see Section 5.7 . The meaning of each facet, to which datatypes it can be applied, and which values it can take for a given datatype is described in Section 4 of [ OWL 2 Specification ].Table 3.4: Datatype Facets of the OWL 2 RDF-Based Semantics
rdf:langPatternrdf:langRange xsd:length xsd:maxExclusive xsd:maxInclusive xsd:maxLength xsd:minExclusive xsd:minInclusive xsd:minLength xsd:pattern
|
4 Interpretations
The OWL 2 RDF-Based Semantics provides
vocabulary interpretations and vocabulary entailment
(see Section 2.1 of [RDF Semantics])
for the RDF and RDFS vocabularies
and for the OWL 2 RDF-Based vocabulary.
This section defines
the concepts of an
OWL 2 RDF-Based datatype map
and an
OWL 2 RDF-Based interpretation,
and specifies what
satisfaction of ontologies,
consistency and entailment
meanmeans under the OWL 2 RDF-Based Semantics.
In addition,
the so called "parts" of the universe
of an OWL 2 RDF-Based interpretation
are defined.
4.1 Datatype Maps
According to Section 5.1 of the RDF semantics specification
[RDF Semantics],
a datatype d has the following components:
- LS(d), the lexical space of d, which is a set of lexical forms;
- VS(d), the value space of d, which is a set of data values;
- L2V(d), the lexical-to-value mapping of d, which maps lexical forms in
the lexical spaceLS(d) to data values in the value spaceVS(d).
Terminological notes:
The document at hand uses the term
"data value"
in accordance with the rest of the OWL 2 specification
(see Section 4 of [OWL 2 Specification]),
whereas the RDF Semantics specification
[RDF Semantics]
uses the term
"datatype value" instead.
Further, the names "LS" and "VS",
which stand for the lexical space and the value space of a datatype,
respectively,
are not used in the RDF Semantics specification,
but have been introduced here for easier reference.
In this document,
the basic definition of a datatype
is extended to take facets into account.
For information and an example on facets, seefacets
(see Section 3.4 .).
Note that
Section 5.1 of the RDF Semantics specification
[RDF Semantics]
explicitly permits
that semantic extensions
may impose more elaborate datatyping conditions
than those listed above.
A datatype with facets ,d
,is a datatype that has the following additional components:
- FS(d), the facet space of d, which is a set of pairs of the form ⟨ F , v ⟩, where F is an IRI called the constraining facet and v is an arbitrary data value called the constraining value;
- F2V(d), the facet-to-value mapping of d, which maps each facet-value pair ⟨ F , v ⟩ in
the facet spaceFS(d) to a subset of the value spaceVS(d).
Note that
it is not further specified
ofwhat kindthe denotationnature of a facet IRIIRI's denotation is,
i.e. it is only known that a facet IRI denotes some individual.
The definition of datatypes with facets does not suggest a certain kind of object.Semantic extensions
MAY
impose further restrictions on the denotations of facets.
In fact,
Section 5.3
will define additional restrictions on facets.
Also note
that for a datatype d
and a facet-value pair ⟨ F , v ⟩ in FS(d)
the value v
is not required
to be included in the value space VS(d) of d itself.
For example,
the datatype xsd:string
(Section 3.3)
has the facet xsd:length
(Section 3.4),
which takes non-negative integers as its values,
rather than strings.
In this document,
it will always be assumed from now on that
every datatype d is a datatype with facets.
If the facet space FS(d) of a datatype d
has not been explicitly defined,
or if it is not derived from another datatype's facet space
according to some well defined condition,
then FS(d) is the empty set.
Unless there is any risk of confusion,
the term "datatype"
will always refer to a datatype with facets.
Section 5.1 of the RDF Semantics specification
[RDF Semantics]
further
defines a datatype map D to be
a set of name-datatype pairs
⟨ u , d ⟩
consisting of an IRI u and a datatype d,
such that no IRI appears twice in the set.
According toAs a previous comment,consequence of what has said before,
in this document
every datatype map D will entirely consist of datatypes with facets.
The following definition specifies what an OWL 2 RDF-Based datatype map is.
Definition 4.1 (OWL 2 RDF-Based Datatype Map):
A datatype map D
is an OWL 2 RDF-Based datatype map,
if and only if
for every datatype name u listed in Section 3.3
and its respective set of constraining facets (Section 3.4)
there is
a name-datatype pair ⟨ u, d ⟩ in D
,with the respectivespecified
lexical space LS(d),
value space VS(d),
lexical-to-value mapping L2V(d),
facet space FS(d) and
facet-to-value mapping F2V(d ) specified according).
Note that Definition 4.1
does not prevent additional datatypes
to the definitionsbe in Section 4 of [an OWL 2 Specification ] (for the facets listed in Section 3.4 ). NoteRDF-Based datatype map.
For the special case of
an OWL 2 RDF-Based datatype map D
that exclusively contains no otherthe datatypes than thoselisted in
Section 3.3,
it is ensured that
there are datatypes available for all the facet values,
i.e.,
for every name-datatype pair ⟨ u , d ⟩ in D
and for every facet-value pair
⟨ F , v ⟩
in the facet spaceFS(d)
there exists a name-datatype pair ⟨ u* , d* ⟩ in D
such that v is in the value spaceVS(d*).
4.2 Vocabulary Interpretations
From the RDF Semantics specification
[RDF Semantics],
let V be a set of IRIs andliterals and IRIs
containing the RDF and RDFS vocabularies,
and let D be a datatype map according to Section 5.1 of
[RDF Semantics]
(and accordingly Section 4.1).
A D-interpretation I of V with respect to D is a tuple
I = ⟨ IR , IP , IEXT , IS , IL , LV ⟩ .
IR is the universe of I,
i.e., a nonempty set
that contains at least
the denotations of IRIs andliterals and IRIs in V.
IP is a subset of IR,
the properties of I.
LV,
the data values of I,
is a subset of IR
that contains at least the set of plain literals
(see Section 6.5 of [RDF Concepts]),
and
the value spaces forof each datatype of D.
IEXT is used to associate properties with their property extension,
and is a mapping from IP to the powerset of IR × IR.
IS is a mapping from IRIs in V to their denotations in IR.
In particular,
IS(u) = d
for any name-datatype pair ⟨ u , d ⟩ in D.
IL is a mapping from typed literals
"s"^^u
in V
to their denotations in IR,
where IL("s"^^u) = L2V(d)(s),
provided that d is a datatype of D,
IS(u) = d, and
s is in the lexical space LS(d);
otherwise
IL("s"^^u)
is not in LV.
Convention:
Following the practice,
as also introduced in
Section 1.4 of [RDF Semantics],
for a given interpretation I of a vocabulary V
the notation
"I(x)"
will be used to
denote "IS("IL(x)" and "IL("IS(x)"
for the IRIs x in V and thetyped literals and IRIs x in V,
respectively.
As detailed in [RDF Semantics],
a D-interpretation has to meet all the semantic conditions
for ground graphs
and blank nodes,
those for RDF interpretations and
RDFS interpretations,
and the
"general semantic conditions for datatypes".
In this document,
the basic definition of a D-interpretation
is extended to take facets into account.
A D-interpretation with facets ,I
,is a D-interpretation for a datatype map D
consisting entirely of datatypes with facets
(Section 4.1),
where I meets the following additional semantic conditions:
for each name-datatype pair ⟨ u , d ⟩ in D
and each facet-value pair ⟨ F , v ⟩ in the facet space FS(d)
- F is in the vocabulary V of I;
- a name-datatype pair ⟨ u* , d* ⟩ exists in D, such that v is in the value space VS(d*).
In this document,
it will always be assumed from now on that
every D-interpretation I
is a D-interpretation with facets.
Unless there is any risk of confusion,
the term "D-interpretation"
will always refer to a D-interpretation with facets.
The following definition specifies what an OWL 2 RDF-Based interpretation is.
Definition 4.2 (OWL 2 RDF-Based Interpretation):
Let D be an OWL 2 RDF-Based datatype map,
and let V be a vocabulary
that includes
the RDF and RDFS vocabularies
and the OWL 2 RDF-Based vocabulary
together with all the datatype and facet names
listed in Section 3.
An OWL 2 RDF-Based interpretation,
I = ⟨ IR , IP , IEXT , IS , IL , LV ⟩,
of V with respect to D
,is a D-interpretation of V with respect to D
that meets all the extra semantic conditions
given in Section 5.
4.3 Satisfaction, Consistency and Entailment
The following definitions specify
what it means thatfor an RDF graph isto be satisfied
by a given OWL 2 RDF-Based interpretation,
what it means that an RDF graph isto be consistent
under the OWL 2 RDF-Based Semantics,
and what it means that an RDF graph entailsto entail another RDF graph under the OWL 2 RDF-Based Semantics.graph.
The notion of satisfaction under the OWL 2 RDF-Based Semantics
is based on the notion of satisfaction for D-interpretations and Simple interpretations,
as defined in [RDF Semantics].
In essence,
in order to satisfy an RDF graph,
an interpretation I has to satisfy all the triples in the graph,
i.e.,
for a triple of the form "s p o"
it is necessary that the relationship
⟨ I(s) , I(o) ⟩ ∈ IEXT(I(p))
holds
(special treatment is necessaryexists for blank nodes,
as detailed in
Section 1.5 of [RDF Semantics]).
In other words,
the given graph has to be compatible with
the specific form of the IEXT mapping of the interpretationI.
The maindistinguishing aspect of OWL 2 RDF-Based satisfaction is
that an interpretation I needs to meet
all the OWL 2 RDF-Based semantic conditions
((see Section 5),
which actually constrainhave the effect of constraining the possible forms
the mappingan IEXT of Imapping can have.
Definition 4.3 (OWL 2 RDF-Based Satisfaction):
Let G be an RDF graph,
let D be an OWL 2 RDF-Based datatype map,
let V be a vocabulary
that includes
the RDF and RDFS vocabularies
and the OWL 2 RDF-Based vocabulary
together with all the datatype and facet names listed in Section 3,
and let I be a D-interpretation of V with respect to D.
I OWL 2 RDF-Based satisfies G with respect to V and D
if and only if
I is an OWL 2 RDF-Based interpretation of V with respect to D
that
satisfies G
as a D-interpretation of V with respect to D
according to
[RDF Semantics].
Definition 4.4 (OWL 2 RDF-Based Consistency):
Let S be a collection of RDF graphs,
and let D be an OWL 2 RDF-Based datatype map.
S is OWL 2 RDF-Based consistent with respect to D
if and only if
there is some OWL 2 RDF-Based interpretation I with respect to D
(ofof some vocabulary V
that includes
the RDF and RDFS vocabularies
and the OWL 2 RDF-Based vocabulary
together with all the datatype and facet names listed in Section 3 )),
such that I OWL 2 RDF-Based satisfies all the RDF graphs in S
with respect to V and D.
Definition 4.5 (OWL 2 RDF-Based Entailment):
Let S1 and S2 be collections of RDF graphs,
and let D be an OWL 2 RDF-Based datatype map.
S1 OWL 2 RDF-Based entails S2 with respect to D
if and only if
for every OWL 2 RDF-Based interpretation I with respect to D
(ofof any vocabulary V that includes
the RDF and RDFS vocabularies
and the OWL 2 RDF-Based vocabulary
together with all the datatype and facet names listed in Section 3
) thatthe following holds:
If I
OWL 2 RDF-Based satisfies all the RDF graphs in S1
with respect to V and D also,
then I
OWL 2 RDF-Based satisfies all the RDF graphs in S2
with respect to V and D.
4.4 Parts of the Universe
Table 4.1
defines the "parts" of the universe
of a given OWL 2 RDF-Based interpretation I.
The firstsecond column tells the name of the part.
The secondthird column gives a definition of the part
in terms of the mapping IEXT of I,
and by referring to particular terms of
the RDF, RDFS and OWL 2 RDF-Based vocabularies.
The third column notes what the defined part is meant to be.As an example,
the part of all datatypes is named "IDC",
and it is defined as the set of all individuals x
for which the relationship
"⟨ x , I(rdfs:Datatype) ⟩
∈
IEXT(I(rdf:type))"
holds.
According to the semantics of rdf:type,
as defined in
Section 4.1 of [RDF Semantics],
this actuallymeans that the name "IDC"
denotes the set of all members of theclass extension
(see Section 4.5)
of I(rdfs:Datatype .).
Table 4.1: Parts of the Universe
|
| Name of
Part S
| Definition of S as
{ x ∈ IR | ⟨ x , I(E) ⟩ ∈ IEXT(I(rdf:type)) }
where IRI E is
|
Noteindividuals
| IR
| rdfs:Resource
|
individuals LV rdfs:Literaldata values
| LV
| rdfs:Literal
|
| ontologies
| IX
| owl:Ontology
|
ontologiesclasses
| IC
| rdfs:Class
|
classesdatatypes
| IDC
| rdfs:Datatype
|
datatypesproperties
| IP
| rdf:Property
|
| data properties
| IODP
| owl:DatatypeProperty
|
data properties IOAP owl:AnnotationProperty annotationontology properties
| IOXP
| owl:OntologyProperty
|
ontologyannotation properties
| IOAP
| owl:AnnotationProperty
|
4.5 Class Extensions
The mapping ICEXT from IC to P(IR) (where P isthe power set),powerset of IR,
which associates classes with their class extension,
is defined
for every c ∈ IC
as
ICEXT(c) = { x ∈ IR | ⟨ x , c ⟩ ∈ IEXT(I(rdf:type)) } for every c ∈ IC..
5 Semantic Conditions
This section defines the semantic conditions of the OWL 2 RDF-Based Semantics.
The semantic conditions presented here are basically only those for the specific constructs of OWL 2.
The complete set of semantic conditions for the OWL 2 RDF-Based Semantics
is the combination of the semantic conditions presented here
and the semantic conditions
for Simple Entailment, RDF, RDFS and D-Entailment,
as specified in
the RDF Semantics specification
[RDF Semantics].
Section 5.1
specifies semantic conditions for the different parts of the universe
(defined(as defined in Section 4.4)
of the OWL 2 RDF-Based interpretation being considered.
Section 5.2
and
Section 5.3
list semantic conditions for the classes and the properties of the OWL 2 RDF-Based vocabulary.
In the rest of this section,
the OWL 2 RDF-Based semantic conditions
for the different language constructs of OWL 2
are specified.
Conventions used in this Section
iff:
Throughout this section
the term "iff" is used as a shorthandshortform for "if and only if".
Conjunctive commas:
A comma
(",")
that separatesseparating two assertions in a semantic condition, as in
"c ∈ IC , p ∈ IP",
is read as a logical "and".
Further,
a comma separating two variables,
as in
an expression such as"c, d ∈ IC",
is used for abbreviating two comma separated assertions,
"c ∈ IC , d ∈ IC"
in this example.
Unscoped variables:
If no explicit scope is explicitlygiven for a variable "x" ,"x",
as in "∀ x : …" or "{ x | … }",
then "x" is unconstrained,
which means thatx ∈ IR,
i.e. "x""x" denotes an arbitrary individual in the universe.
Set cardinality:
For a set S,
an expression of the form "#S" means the number of elements in S.
Sequence expressions:
An expression of the form
"s sequence of a1 , … , an ∈ S"
means that "s" represents a list of n ≥ 0
elements,individuals a1 , … , an,
all of them being members of the set S.
Precisely,
s = I(rdf:nil) for n = 0,0;
and for n > 0
there exist
z1 ∈ IR , … , zn ∈ IR,
such that
s = z1 ,
a1 ∈ S ,
⟨ z1 , a1 ⟩ ∈ IEXT(I(rdf:first)) ,
⟨ z1 , z2 ⟩ ∈ IEXT(I(rdf:rest)) ,
… ,
an ∈ S,
⟨ zn , an ⟩ ∈ IEXT(I(rdf:first)) ,
⟨ zn , I(rdf:nil) ⟩ ∈ IEXT(I(rdf:rest)) .
Note,
as mentioned in Section 3.3.3 of [RDF Semantics],
there are no semantic constraints that enforce "well-formed" sequence structures.
So, for example,
it is possible for a sequence head s to refer to more than one sequence.
Set names:
The following names for certain setsare used as convenient abbreviations:abbreviations for certain sets:
- ISEQ: The set of all sequences. This set equals the class extension of rdf:List, i.e., ISEQ := ICEXT(I(rdf:List)).
- INNI: The set of all non-negative integers. This set equals the value space of the datatype xsd:nonNegativeInteger, i.e., INNI := ICEXT(I(xsd:nonNegativeInteger)), but is also subsumed by the value spaces of other numerical datatypes, such as xsd:integer.
Notes on the Form of Semantic Conditions (Informative)
One design goal of OWL 2
was to ensure an appropriate degree of alignment
between the OWL 2 RDF-Based Semantics and
the OWL 2 Direct Semantics
[OWL 2 Direct Semantics]
withinunder the different constraints the two semantics have to adhere to.meet.
The way this semantic alignment is actuallydescribed
is via the OWL 2 Correspondence Theorem
in Section 7.2.
For this theorem to hold,
the semantic conditions
that treat the RDF encodings
of OWL 2 axioms
(Section(compare Section 3.2.5 of [OWL 2 RDF Mapping]
and
Section 9 of [OWL 2 Specification]),
such as
inverse property axioms,
must have the form of "iff" ("if-and-only-if") conditions.
This means that these semantic conditions
completely determine the semantics of these construct encodings.
On the other hand,
the RDF encodings
of OWL 2 expressions
(Section(compare Section 3.2.4 of [OWL 2 RDF Mapping]
and
Sections 6 – 8 of [OWL 2 Specification]),
such as
property restrictions,
are treated by "if-then" conditions.
These weaker semantic conditions for expressions
are sufficient for the correspondence theorem to hold,
so there is no necessity to define stronger "iff" conditions under the OWL 2 RDF-Based Semantics
for these language constructs.
Special cases are
the semantic conditions for
boolean connectives
of classes
and
enumerations
of individuals.
These language constructs actuallybuild OWL 2 expressions.
However,But for backwards compatibility reasons
there are also RDF encodings of axioms
based on the vocabulary for these language constructs
(see Table 18 in Section 3.2.5 of
[OWL 2 RDF Mapping]).
For example, an RDF expression of the form
ex:c1 owl:unionOf ( ex:c2 ex:c3 ) .
is mapped by the reverse RDF mapping
intoto an OWL 2 axiom
that states the equivalence of the class denoted by
ex:c1
with the union of the classes denoted by
ex:c2
and
ex:c3.
So,In order to ensure that the
correspondence theorem
holds,
and in accordance with the original OWL 1 RDF-Compatible Semantics specification
[OWL 1 RDF-Compatible Semantics],
the semantic conditions for the mentioned language constructs are therefore
"iff" conditions.
Further,
special treatment exists for OWL 2 axioms
that have amulti-triple representationrepresentations in RDF,
where the different triples share a common "root node",
such as the blank node
"_:x"
in the examplefollowing example:
_:x rdf:type owl:AllDisjointClasses .
_:x owl:members ( ex:c1 ex:c2 ) .
In essence,
the semantic conditions for the encodings of these language constructs
are "iff" conditions,
as usual for axioms.
However,
in order to cope with the specific syntactic aspect of a "root node",
the "iff" conditions of these language constructs have been split into two "if-then" conditions,
where the "if-then" condition representing the right-to-left direction
contains an additional premise of the form
"∃ z ∈ IR".
The singlepurpose of this premise is to ensure the existence of an individual
that is needed to satisfy the root node
under the OWL 2 RDF-Based semantics.
The language constructs in question are
n-ary disjointness axioms
in Section 5.115.10,
and
negative property assertions
in Section 5.15.
The "if-then" semantic conditions in this section
sometimes do not explicitly list all typing statements in their consequent
that one might expect.
For example,
the semantic condition for
owl:allValuesFromowl:someValuesFrom restrictions in
Section 5.6
does not list the statement
"x ∈ ICEXT(I(owl:Restriction))"
on its right hand side.
Consequences are generally not mentioned,
if they can already be deduced by other means.
Often,
these redundant consequences follow from the
semantic conditions for classes and properties
in
Section 5.2
and
Section 5.3,
respectively,
occasionally in connection with the semantic conditions
for the parts of the universe
in
Section 5.1.
In the example above,
the omitted consequence can be obtained
from the third column of the entry for
owl:allValuesFromowl:someValuesFrom
in the table in
Section 5.3,
which determines that
IEXT(I( owl:allValuesFromowl:someValuesFrom))
⊆
ICEXT(I(owl:Restriction)) × IC.
5.1 Semantic Conditions for the Parts of the Universe
Table 5.1
lists the semantic conditions
for the parts of the universe
of the OWL 2 RDF-Based interpretation being considered, as definedconsidered.
Additional semantic conditions affecting the parts
are given in Section 4.45.2.
The first column tells the name of the part.part,
as defined in
Section 4.4.
The second column defines
certain conditions on the part .part.
In most cases,
it is specifiedthe column specifies for the part
by which other part it is subsumed,
and by thisthus the position of the part
in the "parts hierarchy" of the universe
is narrowed down.
The third column provides further
information about the instances
of those parts
that consist of classes or properties.
In general,
if the part consists of classes,
then it is specifiedfor the class extensions of the member classes
it is specified by which part of the universe they are subsumed.
If the part consists of properties,
then the domains and ranges of the member properties are determined.
Table 5.1: Semantic Conditions for the Parts of the Universe
Name of
Part S
| Conditions on S
| Conditions on
Instances x of S
|
| IR
| S ≠ ∅
|
|
| LV
| S ⊆ IR
|
|
| IX
| S ⊆ IR
|
|
| IC
| S ⊆ IR
| ICEXT(x) ⊆ IR
|
| IDC
| S ⊆ IC
| ICEXT(x) ⊆ LV
|
| IP
| S ⊆ IR
| IEXT(x) ⊆ IR × IR
|
| IODP
| S ⊆ IP
| IEXT(x) ⊆ IR × LV
|
IOAPIOXP
| S ⊆ IP
| IEXT(x) ⊆ IRIX × IR IOXPIX
|
| IOAP
| S ⊆ IP
| IEXT(x) ⊆ IXIR × IXIR
|
5.2 Semantic Conditions for the Vocabulary Classes
Table 5.2
lists the semantic conditions for the classes
that have IRIs in the OWL 2 RDF-Based vocabulary.
In addition,
the table contains all thethose classes
with IRIs in the RDF and RDFS vocabularies
that represent
parts of the universe
of the OWL 2 RDF-Based interpretation being considered
(Section 4.4).
The semantic conditions for the remaining classes
with names in the RDF and RDFS vocabularies
can be found in the RDF Semantics specification
[RDF Semantics].
The first column tells the name of the class.
The second column defines
of what particular kind a class is,
i.e. whether it is a general class (a member of the part IC)
or a datatype (a member of IDC).
The third column specifies
for the class extension of the class
by which part of the universe
(Section 4.4)
it is subsumed . Thus,:
from an entry of the form
"ICEXT(I(C )) ⊆S",)) ⊆ S",
for a class name C
and a set S,S,
and given an RDF triple of the form
"u rdf:type C",
one can deduce
that the relationship
given by"I(u ) ∈ S") ∈ S"
holds.
Note that some entries are of the form
"ICEXT(I(C)) = S",
which means that the class extension is exactly specified to be that set.
See Section 5.1
for further semantic conditions
on those classes that represent parts.
Not included in this table are the datatypes of the OWL 2 RDF-Based Semantics
with IRIs listed in Section 3.3.
For each such datatype IRI E,
the following semantic conditions hold
(as a consequence of
the fact that E is a member of the datatype map
of every OWL 2 RDF-Based interpretation
according to
Definition 4.2,
and by the "General semantic conditions for datatypes"
givenlisted in Section 5.1 of [RDF Semantics]):
- I(E) ∈ IDC
- ICEXT(I(E)) ⊆ LV
Table 5.2: Semantic Conditions for the Vocabulary Classes
| IRI E
| I(E)
| ICEXT(I(E))
|
| owl:AllDifferent
| ∈ IC
| ⊆ IR
|
| owl:AllDisjointClasses
| ∈ IC
| ⊆ IR
|
| owl:AllDisjointProperties
| ∈ IC
| ⊆ IR
|
| owl:Annotation
| ∈ IC
| ⊆ IR
|
| owl:AnnotationProperty
| ∈ IC
| = IOAP
|
| owl:AsymmetricProperty
| ∈ IC
| ⊆ IP
|
| owl:Axiom
| ∈ IC
| ⊆ IR
|
| rdfs:Class
| ∈ IC
| = IC
|
| owl:Class
| ∈ IC
| = IC
|
| owl:DataRange
| ∈ IC
| = IDC
|
| rdfs:Datatype
| ∈ IC
| = IDC
|
| owl:DatatypeProperty
| ∈ IC
| = IODP
|
| owl:DeprecatedClass
| ∈ IC
| ⊆ IC
|
| owl:DeprecatedProperty
| ∈ IC
| ⊆ IP
|
| owl:FunctionalProperty
| ∈ IC
| ⊆ IP
|
| owl:InverseFunctionalProperty
| ∈ IC
| ⊆ IP
|
| owl:IrreflexiveProperty
| ∈ IC
| ⊆ IP
|
| rdfs:Literal
| ∈ IDC
| = LV
|
| owl:NamedIndividual
| ∈ IC
| ⊆ IR
|
| owl:NegativePropertyAssertion
| ∈ IC
| ⊆ IR
|
| owl:Nothing
| ∈ IC
| = ∅
|
| owl:ObjectProperty
| ∈ IC
| = IP
|
| owl:Ontology
| ∈ IC
| = IX
|
| owl:OntologyProperty
| ∈ IC
| = IOXP
|
| rdf:Property
| ∈ IC
| = IP
|
| owl:ReflexiveProperty
| ∈ IC
| ⊆ IP
|
| rdfs:Resource
| ∈ IC
| = IR
|
| owl:Restriction
| ∈ IC
| ⊆ IC
|
| owl:SymmetricProperty
| ∈ IC
| ⊆ IP
|
| owl:Thing
| ∈ IC
| = IR
|
| owl:TransitiveProperty
| ∈ IC
| ⊆ IP
|
5.3 Semantic Conditions for the Vocabulary Properties
Table 5.3
lists the semantic conditions for the properties
that have IRIs in the OWL 2 RDF-Based vocabulary.
In addition,
the table contains all thethose properties
with IRIs in the RDF andRDFS vocabulariesvocabulary
that are specified to be annotation properties
under the OWL 2 RDF-Based Semantics.
The semantic conditions for the remaining properties
with names in the RDF andRDFS vocabulariesvocabulary
can be found in the RDF Semantics specification
[RDF Semantics].
The first column tells the name of the property.
The second column defines
of what particular kind a property is,
i.e. whether it is a general property (a member of the part IP),
a datatype property (a member of IODP),
an ontology property (a member of IOXP) or
an annotation property (a member of IOAP).
The third column specifies
the domain and range of the property. Thus,property:
from an entry of the form
"IEXT(I(p )) ⊆ S)) ⊆ S1 × S × S2",
for a property name p
and sets S1 and S2,
and given an RDF triple of the form
"s p o",
one can deduce
that the relationships
given by"I(s ) ∈ S) ∈ S1"
and
"I(o ) ∈ S) ∈ S2"
hold.
Note that some entries are of the form
"IEXT(I(p)) = S1 × S2",
which means that the property extension is exactly specified
to be the Cartesian product of the two sets.
Not included in this table are the datatype facets of the OWL 2 RDF-Based Semantics
with IRIs
listed in Section 3.4,
which are used to specify datatype restrictions
(see Section 5.7).
For each such datatype facet IRI E,
the following semantic conditions
extend
the basic semantics specification
that has been given for
datatypes with facets
in Section 4.1:
- I(E) ∈ IP
- IEXT(I(E)) ⊆ IR × LV
Implementations are not required
to support the semantic condition for
owl:onProperties,
but
MAY
support it
in order to realize
n-ary dataranges with arity ≥ 2
(see Section 7 of
[OWL 2 Specification]
for further information).
Informative notes:
owl:topObjectProperty
relates every two individuals in the universe towith each other.
Likewise, owl:topDataProperty
relates every individual towith every data value.
Further,
owl:bottomObjectProperty
and
owl:bottomDataProperty
stand both for the empty relationship.
The ranges of the properties
owl:deprecated and owl:hasSelf
are not restricted in any form,
and, in particular,
they are not restricted to be boolean values.
The actual object values of these properties
do not have any intended meaning,
but could as well have been defined to be of any other value.
Therefore, the semantics given here are of a form
that the values can be arbitrarily chosen
without leading to any non-trivial semantic conclusions.
It is, however, recommended to still use an object literal of the form
"true"^^xsd:boolean
in ontologies,
in order to not get in conflict
with the required usage of these properties
in scenarios that ask for applying the reverse RDF mapping
(compare Table 13 in Section 3.2.4 of [OWL 2 RDF Mapping]
for owl:hasSelf,
and Section 5.5 of [OWL 2 Specification]
for owl:deprecated).
The range of the property
owl:annotatedProperty
is unrestricted
in order to avoid undesired semantic side effects from an annotation,
when the annotated axiom or annotation is not contained in the ontology.
Table 5.3: Semantic Conditions for the Vocabulary Properties
| IRI E
| I(E)
| IEXT(I(E))
|
| owl:allValuesFrom
| ∈ IP
| ⊆ ICEXT(I(owl:Restriction)) × IC
|
owl:assertionPropertyowl:annotatedProperty
| ∈ IP
| ⊆ ICEXT( I ( owl:NegativePropertyAssertion ))IR × IP owl:backwardCompatibleWithIR
|
| owl:annotatedSource
| ∈ IOXPIP
| ⊆ IXIR × IXIR
|
| owl:annotatedTarget
| ∈ IP
| ⊆ IR × IR
|
| owl:assertionProperty
| ∈ IP
| ⊆ ICEXT(I(owl:NegativePropertyAssertion)) × IP
|
| owl:backwardCompatibleWith
| ∈ IOXP
| ⊆ IX × IX
|
| owl:bottomDataProperty
| ∈ IODP
| = ∅
|
| owl:bottomObjectProperty
| ∈ IP
| = ∅
|
| owl:cardinality
| ∈ IP
| ⊆ ICEXT(I(owl:Restriction)) × INNI
|
| rdfs:comment
| ∈ IOAP
| ⊆ IR × LV
|
| owl:complementOf
| ∈ IP
| ⊆ IC × IC
|
| owl:datatypeComplementOf
| ∈ IP
| ⊆ IDC × IDC
|
| owl:deprecated
| ∈ IOAP
| ⊆ IR × IR
|
| owl:differentFrom
| ∈ IP
| ⊆ IR × IR
|
| owl:disjointUnionOf
| ∈ IP
| ⊆ IC × ISEQ
|
| owl:disjointWith
| ∈ IP
| ⊆ IC × IC
|
| owl:distinctMembers
| ∈ IP
| ⊆ ICEXT(I(owl:AllDifferent)) × ISEQ
|
| owl:equivalentClass
| ∈ IP
| ⊆ IC × IC
|
| owl:equivalentProperty
| ∈ IP
| ⊆ IP × IP
|
| owl:hasKey
| ∈ IP
| ⊆ IC × ISEQ
|
| owl:hasSelf
| ∈ IP
| ⊆ ICEXT(I(owl:Restriction)) × IR
|
| owl:hasValue
| ∈ IP
| ⊆ ICEXT(I(owl:Restriction)) × IR
|
| owl:imports
| ∈ IOXP
| ⊆ IX × IX
|
| owl:incompatibleWith
| ∈ IOXP
| ⊆ IX × IX
|
| owl:intersectionOf
| ∈ IP
| ⊆ IC × ISEQ
|
| owl:inverseOf
| ∈ IP
| ⊆ IP × IP
|
| rdfs:isDefinedBy
| ∈ IOAP
| ⊆ IR × IR
|
| rdfs:label
| ∈ IOAP
| ⊆ IR × LV
|
| owl:maxCardinality
| ∈ IP
| ⊆ ICEXT(I(owl:Restriction)) × INNI
|
| owl:maxQualifiedCardinality
| ∈ IP
| ⊆ ICEXT(I(owl:Restriction)) × INNI
|
| owl:members
| ∈ IP
| ⊆ IR × ISEQ
|
| owl:minCardinality
| ∈ IP
| ⊆ ICEXT(I(owl:Restriction)) × INNI
|
| owl:minQualifiedCardinality
| ∈ IP
| ⊆ ICEXT(I(owl:Restriction)) × INNI
|
owl:object ∈ IP ⊆ IR × IRowl:onClass
| ∈ IP
| ⊆ ICEXT(I(owl:Restriction)) × IC
|
| owl:onDataRange
| ∈ IP
| ⊆ ICEXT(I(owl:Restriction)) × IDC
|
| owl:onDatatype
| ∈ IP
| ⊆ IDC × IDC
|
| owl:oneOf
| ∈ IP
| ⊆ IC × ISEQ
|
| owl:onProperty
| ∈ IP
| ⊆ ICEXT(I(owl:Restriction)) × IP
|
| owl:onProperties
| ∈ IP
| ⊆ ICEXT(I(owl:Restriction)) × ISEQ
|
owl:predicate ∈ IP ⊆ IR × IPowl:priorVersion
| ∈ IOXP
| ⊆ IX × IX
|
| owl:propertyChainAxiom
| ∈ IP
| ⊆ IP × ISEQ
|
| owl:propertyDisjointWith
| ∈ IP
| ⊆ IP × IP
|
| owl:qualifiedCardinality
| ∈ IP
| ⊆ ICEXT(I(owl:Restriction)) × INNI
|
| owl:sameAs
| ∈ IP
| ⊆ IR × IR
|
| rdfs:seeAlso
| ∈ IOAP
| ⊆ IR × IR
|
| owl:someValuesFrom
| ∈ IP
| ⊆ ICEXT(I(owl:Restriction)) × IC
|
| owl:sourceIndividual
| ∈ IP
| ⊆ ICEXT(I(owl:NegativePropertyAssertion)) × IR
|
owl:subject ∈ IP ⊆ IR × IRowl:targetIndividual
| ∈ IP
| ⊆ ICEXT(I(owl:NegativePropertyAssertion)) × IR
|
| owl:targetValue
| ∈ IP
| ⊆ ICEXT(I(owl:NegativePropertyAssertion)) × LV
|
| owl:topDataProperty
| ∈ IODP
| = IR × LV
|
| owl:topObjectProperty
| ∈ IP
| = IR × IR
|
| owl:unionOf
| ∈ IP
| ⊆ IC × ISEQ
|
| owl:versionInfo
| ∈ IOAP
| ⊆ IR × IR
|
| owl:versionIRI
| ∈ IOXP
| ⊆ IX × IX
|
| owl:withRestrictions
| ∈ IP
| ⊆ IDC × ISEQ
|
5.4 Semantic Conditions for Boolean Connectives
Table 5.4
lists the semantic conditions for boolean connectives,
including
intersections, unions and complements
of classes and datatypes.
An intersection or a union of a collection of datatypes
or a complement of a datatype
is itself a datatype.
While a complement of a class is created w.r.t. the whole universe,
a datatype complement is created for a datatype w.r.t. the set of data values only.
Informative notes:
Every first semantic condition of the three condition pairs in the table is an "iff" condition,
since the treatedcorresponding OWL 2 language constructs
have the status ofare both
class expressions and axioms of OWL 2.axioms.
In contrast,
the firstsemantic condition on datatype complements
is an "if-then" condition,
since it only has the status ofcorresponds to a datarange expression.
See the
notes on the form of semantic conditions
for further information on this topic.information.
For the remaining semantic conditions
that treat the cases of intersections and unions of datatypes
it is sufficient to have "if-then" conditions,
since stronger "iff" conditions would be obsoleted byredundant
due to the more general "iff" conditions
that already exist for classes.
Note that the datatype related semantic conditions
do not apply to empty sets,
but one can still receive a datatype from an empty set
by explicitly asserting the resulting class
to be an instance of class rdfs:Datatype.
Table 5.4: Semantic Conditions for Boolean Connectives
| if s sequence of c1 , … , cn ∈ IR then
|
| ⟨ z , s ⟩ ∈ IEXT(I(owl:intersectionOf))
| iff
| z , c1 , … , cn ∈ IC ,
ICEXT(z) = ICEXT(c1) ∩ … ∩ ICEXT(cn)
|
|
|
| if
| then
|
s sequence of d1 , … , dn ∈ IDC , n ≥ 1 ,
⟨ z , s ⟩ ∈ IEXT(I(owl:intersectionOf))
| z ∈ IDC
|
|
|
| if s sequence of c1 , … , cn ∈ IR then
|
| ⟨ z , s ⟩ ∈ IEXT(I(owl:unionOf))
| iff
| z , c1 , … , cn ∈ IC ,
ICEXT(z) = ICEXT(c1) ∪ … ∪ ICEXT(cn)
|
|
|
| if
| then
|
s sequence of d1 , … , dn ∈ IDC , n ≥ 1 ,
⟨ z , s ⟩ ∈ IEXT(I(owl:unionOf))
| z ∈ IDC
|
|
|
| ⟨ z , c ⟩ ∈ IEXT(I(owl:complementOf))
| iff
| z , c ∈ IC ,
ICEXT(z) = IR \ ICEXT(c)
|
|
|
| if
| then
|
| ⟨ z , d ⟩ ∈ IEXT(I(owl:datatypeComplementOf))
| ICEXT(z) = LV \ ICEXT(d)
|
5.5 Semantic Conditions for Enumerations
Table 5.5
lists the semantic conditions for enumerations,
i.e. classes that consist of an explicitly given finite set of instances.
In particular, an enumeration entirely consisting of data values is a datatype.
Informative notes:
The first semantic condition is an "iff" condition,
since the treatedcorresponding OWL 2 language construct
has the status ofis both a class expression and an axiom of OWL 2.axiom.
See the
notes on the form of semantic conditions
for further information on this topic.information.
For the remaining semantic condition
that treats the case of enumerations of data values
it is sufficient to have an "if-then" condition,
since a stronger "iff" condition would be obsoleted byredundant
due to the more general "iff" condition
that already exists for individuals.
Note that the data value related semantic condition
does not apply to empty sets,
but one can still receive a datatype from an empty set
by explicitly asserting the resulting class
to be an instance of class rdfs:Datatype.
Table 5.5: Semantic Conditions for Enumerations
| if s sequence of a1 , … , an ∈ IR then
|
| ⟨ z , s ⟩ ∈ IEXT(I(owl:oneOf))
| iff
| z ∈ IC ,
ICEXT(z) = { a1 , … , an }
|
|
|
| if
| then
|
s sequence of v1 , … , vn ∈ LV , n ≥ 1 ,
⟨ z , s ⟩ ∈ IEXT(I(owl:oneOf))
| z ∈ IDC
|
5.6 Semantic Conditions for Property Restrictions
Table 5.6
lists the semantic conditions for property restrictions.
Value restrictions require that
some or all of the values of a certain property
must be instances of a given class,
or that the property has a specifically defined value.
By placing a self restriction on some given property
one only regardsconsiders those individuals
that are reflexively related to themselves via this property.
Cardinality restrictions determine
how often a certain property is allowed
to be applied to a given individual.
Qualified cardinality restrictions
are more specific than cardinality restrictions
in that they determine the quantity of a property application
with respect to a particular class
from which the property values are taken.
Implementations are not required
to support the semantic conditions for
owl:onProperties,
but
MAY
support them
in order to realize
n-ary dataranges with arity ≥ 2
(see Section 7 of
[OWL 2 Specification]
for further information).
Informative notes:
All the semantic conditions are "if-then" conditions,
since the treatedcorresponding OWL 2 language constructs
have the status ofare class expressions of OWL 2.expressions.
The "if-then" conditions generally only list those consequences
on their right hand side
that are specific for the respective condition,
i.e. consequences that do not already follow by other means.
See the
notes on the form of semantic conditions
for further information on these topics.information.
Note that the semantic condition for self restrictions
does not constrain the right hand side of
a owl:hasSelf assertion
to be the boolean value "true"^^xsd:boolean.
See Section 5.3 for an explanation.
Table 5.6: Semantic Conditions for Property Restrictions
| if
| then
|
⟨ z , c ⟩ ∈ IEXT(I(owl:someValuesFrom)) ,
⟨ z , p ⟩ ∈ IEXT(I(owl:onProperty))
| ICEXT(z) = { x | ∃ y : ⟨ x , y ⟩ ∈ IEXT(p) and y ∈ ICEXT(c) }
|
s sequence of p1 , … , pn ∈ IR , n ≥ 1 ,
⟨ z , c ⟩ ∈ IEXT(I(owl:someValuesFrom)) ,
⟨ z , s ⟩ ∈ IEXT(I(owl:onProperties))
| p1 , … , pn ∈ IP ,
ICEXT(z) = { x | ∃ y1 , … , yn : ⟨ x , yk ⟩ ∈ IEXT(pk) for each 1 ≤ k ≤ n and ⟨ y1 , … , yn ⟩ ∈ ICEXT(c) }
|
⟨ z , c ⟩ ∈ IEXT(I(owl:allValuesFrom)) ,
⟨ z , p ⟩ ∈ IEXT(I(owl:onProperty))
| ICEXT(z) = { x | ∀ y : ⟨ x , y ⟩ ∈ IEXT(p) implies y ∈ ICEXT(c) }
|
s sequence of p1 , … , pn ∈ IR , n ≥ 1 ,
⟨ z , c ⟩ ∈ IEXT(I(owl:allValuesFrom)) ,
⟨ z , s ⟩ ∈ IEXT(I(owl:onProperties))
| p1 , … , pn ∈ IP ,
ICEXT(z) = { x | ∀ y1 , … , yn : ⟨ x , yk ⟩ ∈ IEXT(pk) for each 1 ≤ k ≤ n implies ⟨ y1 , … , yn ⟩ ∈ ICEXT(c) }
|
⟨ z , a ⟩ ∈ IEXT(I(owl:hasValue)) ,
⟨ z , p ⟩ ∈ IEXT(I(owl:onProperty))
| ICEXT(z) = { x | ⟨ x , a ⟩ ∈ IEXT(p) }
|
⟨ z , v ⟩ ∈ IEXT(I(owl:hasSelf)) ,
⟨ z , p ⟩ ∈ IEXT(I(owl:onProperty))
| ICEXT(z) = { x | ⟨ x , x ⟩ ∈ IEXT(p) }
|
⟨ z , n ⟩ ∈ IEXT(I(owl:minCardinality)) ,
⟨ z , p ⟩ ∈ IEXT(I(owl:onProperty))
| ICEXT(z) = { x | #{ y | ⟨ x , y ⟩ ∈ IEXT(p) } ≥ n }
|
⟨ z , n ⟩ ∈ IEXT(I(owl:maxCardinality)) ,
⟨ z , p ⟩ ∈ IEXT(I(owl:onProperty))
| ICEXT(z) = { x | #{ y | ⟨ x , y ⟩ ∈ IEXT(p) } ≤ n }
|
⟨ z , n ⟩ ∈ IEXT(I(owl:cardinality)) ,
⟨ z , p ⟩ ∈ IEXT(I(owl:onProperty))
| ICEXT(z) = { x | #{ y | ⟨ x , y ⟩ ∈ IEXT(p) } = n }
|
⟨ z , n ⟩ ∈ IEXT(I(owl:minQualifiedCardinality)) ,
⟨ z , p ⟩ ∈ IEXT(I(owl:onProperty)) ,
⟨ z , c ⟩ ∈ IEXT(I(owl:onClass))
| ICEXT(z) = { x | #{ y | ⟨ x , y ⟩ ∈ IEXT(p) and y ∈ ICEXT(c) } ≥ n }
|
⟨ z , n ⟩ ∈ IEXT(I(owl:minQualifiedCardinality)) ,
⟨ z , p ⟩ ∈ IEXT(I(owl:onProperty)) ,
⟨ z , d ⟩ ∈ IEXT(I(owl:onDataRange))
| p ∈ IODP ,
ICEXT(z) = { x | #{ y ∈ LV | ⟨ x , y ⟩ ∈ IEXT(p) and y ∈ ICEXT(d) } ≥ n }
|
⟨ z , n ⟩ ∈ IEXT(I(owl:maxQualifiedCardinality)) ,
⟨ z , p ⟩ ∈ IEXT(I(owl:onProperty)) ,
⟨ z , c ⟩ ∈ IEXT(I(owl:onClass))
| ICEXT(z) = { x | #{ y | ⟨ x , y ⟩ ∈ IEXT(p) and y ∈ ICEXT(c) } ≤ n }
|
⟨ z , n ⟩ ∈ IEXT(I(owl:maxQualifiedCardinality)) ,
⟨ z , p ⟩ ∈ IEXT(I(owl:onProperty)) ,
⟨ z , d ⟩ ∈ IEXT(I(owl:onDataRange))
| p ∈ IODP ,
ICEXT(z) = { x | #{ y ∈ LV | ⟨ x , y ⟩ ∈ IEXT(p) and y ∈ ICEXT(d) } ≤ n }
|
⟨ z , n ⟩ ∈ IEXT(I(owl:qualifiedCardinality)) ,
⟨ z , p ⟩ ∈ IEXT(I(owl:onProperty)) ,
⟨ z , c ⟩ ∈ IEXT(I(owl:onClass))
| ICEXT(z) = { x | #{ y | ⟨ x , y ⟩ ∈ IEXT(p) and y ∈ ICEXT(c) } = n }
|
⟨ z , n ⟩ ∈ IEXT(I(owl:qualifiedCardinality)) ,
⟨ z , p ⟩ ∈ IEXT(I(owl:onProperty)) ,
⟨ z , d ⟩ ∈ IEXT(I(owl:onDataRange))
| p ∈ IODP ,
ICEXT(z) = { x | #{ y ∈ LV | ⟨ x , y ⟩ ∈ IEXT(p) and y ∈ ICEXT(d) } = n }
|
5.7 Semantic Conditions for Datatype Restrictions
Table 5.7
lists the semantic conditions for datatype restrictions,
which are used to define sub datatypes of existing datatypes
by restricting the original datatype
viaby means of a set of facet-value pairs.
For information and an example on facets, seefacets
(see Section 3.4 . Note that).
Certain special cases exist:
If no facet-value pair is applied to a given datatype at all,
then the resulting datatype will be equivalent to the original datatype.
Note further that,Further,
if a facet-value pair is applied to a datatype
without being a member of the datatype's facet space,
then the ontology cannot be satisfied
and will therefore be inconsistent.
In particular,
a datatype restriction with one or more specified facet-value pairs
will result in an inconsistent ontology,
if applied to a datatype havingwith an empty facet space (usually,space.
The set IFS(d)
for a non-empty facet space only exists for those datatypes belonging to thedatatype map). The set IFSd
is defined by
IFS(d) := { ⟨ I(F) , v ⟩ | ⟨ F , v ⟩ ∈ FS(d) } ,
where
d is a datatype,F is the IRI of a facet,
and v is a value of the facet.
This set corresponds to the facet space, FS, ofspace FS(d ,),
as defined in Section 4.1,
but rather consists of
pairs of the denotation of a facet and its value.
The mapping IF2VIF2V(d)
for a datatype d
is defined by
IF2V(d)(⟨ I(F) , v ⟩) := F2V(d)(⟨ F , v ⟩) ,
where
d is a datatype,F is the IRI of a facet,
and v is a value of the facet.
This mapping corresponds to the facet-to-value mapping, F2V, ofmapping F2V(d ,),
as defined in Section 4.1,
resulting in the same subsets of the value space VS(d),
but rather applies to
pairs of the denotation of a facet and its value.
Informative notes:
The semantic condition is an "if-then" condition,
since the treatedcorresponding OWL 2 language construct
has the status ofis a datarange expression of OWL 2.expression.
The "if-then" condition only lists those consequences
on its right hand side
that are specific for the condition,
i.e. consequences that do not already follow by other means.
See the
notes on the form of semantic conditions
for further information on these topics.information.
Table 5.7: Semantic Conditions for Datatype Restrictions
| if
| then
|
s sequence of z1 , … , zn ∈ IR ,
f1 , … , fn ∈ IP ,
⟨ z , d ⟩ ∈ IEXT(I(owl:onDatatype)) ,
⟨ z , s ⟩ ∈ IEXT(I(owl:withRestrictions)) ,
⟨ z1 , v1 ⟩ ∈ IEXT(f1) , … , ⟨ zn , vn ⟩ ∈ IEXT(fn)
| z , d ∈ IDC ,
f1 , … , fn ∈ IODP ,
v1 , … , vn ∈ LV ,
⟨ f1 , v1 ⟩ , … , ⟨ fn , vn ⟩ ∈ IFS(d) ,
ICEXT(z) = ICEXT(d) ∩ IF2V(d)(⟨ f1 , v1 ⟩) ∩ … ∩ IF2V(d)(⟨ fn , vn ⟩)
|
5.8 Semantic Conditions for the RDFS Vocabulary
Table 5.8
extends the RDFS semantic conditions
for parts of the RDFS vocabulary, includingsubclass axioms, subproperty axioms, domain axioms and range axioms,axioms.
The semantic conditions provided here are "iff" conditions,
while the original semantic conditions,
as originally definedspecified in
Section 4.1 of [RDF Semantics ].],
were weaker "if-then" conditions.
Only the additional semantic conditions are given here
and the other conditions on theof RDF and RDFS
vocabulariesare retained.
Informative notes:
All the semantic conditions are "iff" conditions,
since the treatedcorresponding OWL 2 language constructs
have the status of axioms of OWL 2.are axioms.
See the
notes on the form of semantic conditions
for further information on this topic. Note that the original semantics for these RDFS axioms only provide for weaker "if-then" semantic conditions.information.
Table 5.8: Semantic Conditions for the RDFS Vocabulary
| ⟨ c1 , c2 ⟩ ∈ IEXT(I(rdfs:subClassOf))
| iff
| c1 , c2 ∈ IC ,
ICEXT(c1) ⊆ ICEXT(c2)
|
| ⟨ p1 , p2 ⟩ ∈ IEXT(I(rdfs:subPropertyOf))
| p1 , p2 ∈ IP ,
IEXT(p1) ⊆ IEXT(p2)
|
| ⟨ p , c ⟩ ∈ IEXT(I(rdfs:domain))
| p ∈ IP , c ∈ IC ,
∀ x , y : ⟨ x , y ⟩ ∈ IEXT(p) implies x ∈ ICEXT(c)
|
| ⟨ p , c ⟩ ∈ IEXT(I(rdfs:range))
| p ∈ IP , c ∈ IC ,
∀ x , y : ⟨ x , y ⟩ ∈ IEXT(p) implies y ∈ ICEXT(c)
|
5.9 Semantic Conditions for Sub Property ChainsEquivalence and Disjointness
Table 5.9
lists the semantic conditions for sub property chains, which allow forspecifying
complex property subsumption axioms. As an example, one can define a sub property chain axiom, for which the chain consisting of the extensions of the properties ex:hasFatherthat two individuals are equal or different from each other,
and ex:hasBrother is covered by the extension of the property ex:hasUncle .that either two classes or two properties
are equivalent or disjoint with each other,
respectively.
Also treated here are disjoint union axioms.
Informative notes:
All the semantic condition is anconditions are "iff" condition,conditions,
since the treated language construct has the status of an axiom ofcorresponding OWL 2.2 language constructs
are axioms.
See the
notes on the form of semantic conditions
for further information on this topic.information.
Also note that the
semantics has been specified in a way to allow for a sub property chain axiomIRI owl:equivalentClass
is used to be satisfiable without requiring the existence of a property that represents the property chain. Table 5.9: Semantic Conditions for Sub Property Chains if s sequence of p 1 , … , p n ∈ IR then ⟨ p , s ⟩ ∈ IEXT( I ( owl:propertyChainAxiom )) iff p ∈ IP , p 1 , … , p n ∈ IP , ∀ y 0 , … , y n : ⟨ y 0 , y 1 ⟩ ∈ IEXT( p 1 ) and … and ⟨ y n-1 , y n ⟩ ∈ IEXT( p n ) implies ⟨ y 0 , y n ⟩ ∈ IEXT( p ) 5.10 Semantic Conditions for Equivalence and Disjointness Axioms Table 5.10 lists the semantic conditions for specifying that two individuals are equal or different from each other, and that either two classes or two properties are equivalent or disjoint with each other. Also treated here are disjoint union axioms that allow for stating that a given class is equivalent to the union of a given collection of mutually disjoint classes. Informative notes: All the semantic conditions are "iff" conditions, since the treated language constructs have the status of axiomsformulate datatype definitions
(see Section 9.4 of
[OWL 2. See the notes on the form of semantic conditions2 Specification]
for furtherinformation on this topic.about datatype definitions).
Table 5.10:5.9: Semantic Conditions for Equivalence and Disjointness
Axioms⟨ a1 , a2 ⟩ ∈ IEXT(I(owl:sameAs))
| iff
| a1 = a2
|
| ⟨ a1 , a2 ⟩ ∈ IEXT(I(owl:differentFrom))
| a1 ≠ a2
|
| ⟨ c1 , c2 ⟩ ∈ IEXT(I(owl:equivalentClass))
| c1 , c2 ∈ IC ,
ICEXT(c1) = ICEXT(c2)
|
| ⟨ c1 , c2 ⟩ ∈ IEXT(I(owl:disjointWith))
| c1 , c2 ∈ IC ,
ICEXT(c1) ∩ ICEXT(c2) = ∅
|
| ⟨ p1 , p2 ⟩ ∈ IEXT(I(owl:equivalentProperty))
| p1 , p2 ∈ IP ,
IEXT(p1) = IEXT(p2)
|
| ⟨ p1 , p2 ⟩ ∈ IEXT(I(owl:propertyDisjointWith))
| p1 , p2 ∈ IP ,
IEXT(p1) ∩ IEXT(p2) = ∅
|
|
|
| if s sequence of c1 , … , cn ∈ IR then
|
| ⟨ c , s ⟩ ∈ IEXT(I(owl:disjointUnionOf))
| iff
| c , c1 , … , cn ∈ IC ,
ICEXT(c) = ICEXT(c1) ∪ … ∪ ICEXT(cn) ,
ICEXT(cj) ∩ ICEXT(ck) = ∅ for each 1 ≤ j ≤ n and each 1 ≤ k ≤ n such that j ≠ k
|
5.115.10 Semantic Conditions for N-ary AxiomsDisjointness
Table 5.115.10
lists the semantic conditions for specifying
n-ary diversity and disjointness axioms,
i.e. that several given individuals
are mutually different from each other,
and that eitherseveral given classes or severalproperties
are mutually disjoint with each other.other,
respectively.
Note that there are two alternative ways
to specify owl:AllDifferent axioms,
by using either the property
owl:members
that is used for all other constructs, too,
or by applying the legacy property
owl:distinctMembers.
There is no difference in theBoth variants have an equivalent formal meaning of these two variants.meaning.
Informative notes:
The semantic conditions essentially represent "iff" conditions,
since the treated language constructs have the status of axioms ofcorresponding OWL 2.2 language constructs
are axioms.
However,
there are actually two suchsemantic conditions for each language construct,construct
due to the multi-triple RDF encoding of these language constructs.
The actual"if-then" conditions only list those consequences
on their right hand side
that are specific for the respective condition,
i.e. consequences that do not already follow by other means.
See the
notes on the form of semantic conditions
for further information on these topics.information.
Table 5.11:5.10: Semantic Conditions for N-ary AxiomsDisjointness
| if
| then
|
s sequence of a1 , … , an ∈ IR ,
z ∈ ICEXT(I(owl:AllDifferent)) ,
⟨ z , s ⟩ ∈ IEXT(I( owl:distinctMembersowl:members))
| aj ≠ ak for each 1 ≤ j ≤ n and each 1 ≤ k ≤ n such that j ≠ k
|
|
|
| if
| then exists z ∈ IR
|
s sequence of a1 , … , an ∈ IR ,
aj ≠ ak for each 1 ≤ j ≤ n and each 1 ≤ k ≤ n such that j ≠ k
| z ∈ ICEXT(I(owl:AllDifferent)) ,
⟨ z , s ⟩ ∈ IEXT(I( owl:distinctMembersowl:members))
|
|
|
| if
| then
|
s sequence of a1 , … , an ∈ IR ,
z ∈ ICEXT(I(owl:AllDifferent)) ,
⟨ z , s ⟩ ∈ IEXT(I( owl:membersowl:distinctMembers))
| aj ≠ ak for each 1 ≤ j ≤ n and each 1 ≤ k ≤ n such that j ≠ k
|
|
|
| if
| then exists z ∈ IR
|
s sequence of a1 , … , an ∈ IR ,
aj ≠ ak for each 1 ≤ j ≤ n and each 1 ≤ k ≤ n such that j ≠ k
| z ∈ ICEXT(I(owl:AllDifferent)) ,
⟨ z , s ⟩ ∈ IEXT(I( owl:membersowl:distinctMembers))
|
|
|
| if
| then
|
s sequence of c1 , … , cn ∈ IR ,
z ∈ ICEXT(I(owl:AllDisjointClasses)) ,
⟨ z , s ⟩ ∈ IEXT(I(owl:members))
| c1 , … , cn ∈ IC ,
ICEXT(cj) ∩ ICEXT(ck) = ∅ for each 1 ≤ j ≤ n and each 1 ≤ k ≤ n such that j ≠ k
|
|
|
| if
| then exists z ∈ IR
|
s sequence of c1 , … , cn ∈ IC ,
ICEXT(cj) ∩ ICEXT(ck) = ∅ for each 1 ≤ j ≤ n and each 1 ≤ k ≤ n such that j ≠ k
| z ∈ ICEXT(I(owl:AllDisjointClasses)) ,
⟨ z , s ⟩ ∈ IEXT(I(owl:members))
|
|
|
| if
| then
|
s sequence of p1 , … , pn ∈ IR ,
z ∈ ICEXT(I(owl:AllDisjointProperties)) ,
⟨ z , s ⟩ ∈ IEXT(I(owl:members))
| p1 , … , pn ∈ IP ,
IEXT(pj) ∩ IEXT(pk) = ∅ for each 1 ≤ j ≤ n and each 1 ≤ k ≤ n such that j ≠ k
|
|
|
| if
| then exists z ∈ IR
|
s sequence of p1 , … , pn ∈ IP ,
IEXT(pj) ∩ IEXT(pk) = ∅ for each 1 ≤ j ≤ n and each 1 ≤ k ≤ n such that j ≠ k
| z ∈ ICEXT(I(owl:AllDisjointProperties)) ,
⟨ z , s ⟩ ∈ IEXT(I(owl:members))
|
5.125.11 Semantic Conditions for InverseSub Property AxiomsChains
Table 5.125.11
lists the semantic conditions for inversesub property chains,
which allow for specifying complex property subsumption axioms.
The inverse ofAs an example,
one can define a givensub property ischain axiom
that specifies
the corresponding property with subjectchain consisting of the extensions of the properties
ex:hasFather
and
object swapped for eachex:hasBrother
to be a sub relation of
the extension of the property
assertion built from it.ex:hasUncle.
Informative notes:
The semantic condition is an "iff" condition,
since the treatedcorresponding OWL 2 language construct
has the status ofis an axiom of OWL 2.axiom.
See the
notes on the form of semantic conditions
for further information on this topic.information.
The semantics has been specified in a way
that allows a sub property chain axiom to be satisfiable
without requiring the existence of a property
that represents the property chain.
Table 5.12:5.11: Semantic Conditions for InverseSub Property Axioms ⟨Chains
if s sequence of p1 , … , p 2n ∈ IR then
|
⟨ p , s ⟩ ∈ IEXT(I( owl:inverseOfowl:propertyChainAxiom))
| iff
| p ∈ IP ,
p1 , … , p 2n ∈ IP ,
∀ y0 , … , yn : ⟨ y0 , y1 ⟩ ∈ IEXT(p1) = {and … and ⟨ xyn-1 , yn ⟩ |∈ IEXT(pn) implies ⟨ y0 , xyn ⟩ ∈ IEXT(p 2)
|
} 5.135.12 Semantic Conditions for Property CharacteristicsInverse Properties
Table 5.135.12
lists the semantic conditions for inverse property characteristics. Ifaxioms.
The inverse of a given property
is functional , then at most one distinct value can be assigned to any given individual via this property. An inverse functionalthe corresponding property
with subject and object swapped
for each property assertion built from it.
Informative notes:
The semantic condition is an "iff" condition,
since the corresponding OWL 2 language construct
is an axiom.
See the
notes on the form of semantic conditions
for further information.
Table 5.12: Semantic Conditions for Inverse Properties
| ⟨ p1 , p2 ⟩ ∈ IEXT(I(owl:inverseOf))
| iff
| p1 , p2 ∈ IP ,
IEXT(p1) = { ⟨ x , y ⟩ | ⟨ y , x ⟩ ∈ IEXT(p2) }
|
5.13 Semantic Conditions for Property Characteristics
Table 5.13
lists the semantic conditions for property characteristics.
If a property is functional,
then at most one distinct value can be assigned
to any given individual
via this property.
An inverse functional property can be regarded as a "key" property,
i.e. no two different individuals
can be assigned the same value
via this property.
A reflexive property relates every individual in the universe to itself,
whereas an irreflexive property does not relate any individual with itself at all.
If two individuals are related by a symmetric property,
then this property also relates them by the reverse relationship,reversely,
while this is never the case for an asymmetric property.
A transitive property
that relates an individual a with an individual b,
and the latter with an individual c,
also relates a with c.
Informative notes:
All the semantic conditions are "iff" conditions,
since the treatedcorresponding OWL 2 language constructs
have the status of axioms of OWL 2.are axioms.
See the
notes on the form of semantic conditions
for further information on this topic.information.
Table 5.13: Semantic Conditions for Property Characteristics
| p ∈ ICEXT(I(owl:FunctionalProperty))
| iff
| p ∈ IP ,
∀ x , y1 , y2 : ⟨ x , y1 ⟩ ∈ IEXT(p) and ⟨ x , y2 ⟩ ∈ IEXT(p) implies y1 = y2
|
| p ∈ ICEXT(I(owl:InverseFunctionalProperty))
| p ∈ IP ,
∀ x1 , x2 , y : ⟨ x1 , y ⟩ ∈ IEXT(p) and ⟨ x2 , y ⟩ ∈ IEXT(p) implies x1 = x2
|
| p ∈ ICEXT(I(owl:ReflexiveProperty))
| p ∈ IP ,
∀ x : ⟨ x , x ⟩ ∈ IEXT(p)
|
| p ∈ ICEXT(I(owl:IrreflexiveProperty))
| p ∈ IP ,
∀ x : ⟨ x , x ⟩ ∉ IEXT(p)
|
| p ∈ ICEXT(I(owl:SymmetricProperty))
| p ∈ IP ,
∀ x , y : ⟨ x , y ⟩ ∈ IEXT(p) implies ⟨ y , x ⟩ ∈ IEXT(p)
|
| p ∈ ICEXT(I(owl:AsymmetricProperty))
| p ∈ IP ,
∀ x , y : ⟨ x , y ⟩ ∈ IEXT(p) implies ⟨ y , x ⟩ ∉ IEXT(p)
|
| p ∈ ICEXT(I(owl:TransitiveProperty))
| p ∈ IP ,
∀ x , y , z : ⟨ x , y ⟩ ∈ IEXT(p) and ⟨ y , z ⟩ ∈ IEXT(p) implies ⟨ x , z ⟩ ∈ IEXT(p)
|
5.14 Semantic Conditions for Keys
Table 5.14
lists the semantic conditions for Keys.
Keys provide an alternative to inverse functional properties
(see Section 5.13).
They allow for defining a property as a key local to a given class:
the specified property
will have the features of a key
only for individuals withinbeing instances of the class,
and no assumption is made
about individuals
external to the class, orfor which it is unknown whether they are instancesmembership of the class.class cannot be entailed.
Further,
it is possible to define "compound keys",
i.e. several properties can be combined into a single key
applicable to composite values.
PleaseNote that
keys are not functional by default
under the OWL 2 RDF-Based Semantics.
Informative notes:
The semantic condition is an "iff" condition,
since the treatedcorresponding OWL 2 language construct
has the status ofis an axiom of OWL 2.axiom.
See the
notes on the form of semantic conditions
for further information on this topic.information.
Table 5.14: Semantic Conditions for Keys
| if s sequence of p1 , … , pn ∈ IR then
|
| ⟨ c , s ⟩ ∈ IEXT(I(owl:hasKey))
| iff
| c ∈ IC ,
p1 , … , pn ∈ IP ,
∀ x , y , z1 , … , zn :
if x ∈ ICEXT(c) and y ∈ ICEXT(c) and
⟨ x , zk ⟩ ∈ IEXT(pk) and ⟨ y , zk ⟩ ∈ IEXT(pk) for each 1 ≤ k ≤ n
then x = y
|
5.15 Semantic Conditions for Negative Property Assertions
Table 5.15
lists the semantic conditions for negative property assertions.
They allow to state that
an individual a 1 doestwo given individuals are not stand in a relationship p with another individualrelated by a 2 .given property.
The second form based on owl:targetValue
is more specific than the first form based on owl:targetIndividual
,in that it is restricted to the case of negative data property assertions.
Note that the second form
will coerce the target individual of a negative property assertion
into a data value,
due to the range defined for the property
owl:targetValue
in
Section 5.3.
Informative notes:
The semantic conditions essentially represent "iff" conditions,
since the treatedcorresponding OWL 2 language constructs
have the status of axioms of OWL 2.are axioms.
However,
there are actually two suchsemantic conditions for each language construct,
due to the multi-triple RDF encoding of these language constructs.
The actual"if-then" conditions only list those consequences
on their right hand side
that are specific for the respective condition,
i.e. consequences that do not already follow by other means.
See the
notes on the form of semantic conditions
for further information on these topics.information.
Table 5.15: Semantic Conditions for Negative Property Assertions
| if
| then
|
⟨ z , a1 ⟩ ∈ IEXT(I(owl:sourceIndividual)) ,
⟨ z , p ⟩ ∈ IEXT(I(owl:assertionProperty)) ,
⟨ z , a2 ⟩ ∈ IEXT(I(owl:targetIndividual))
| ⟨ a1 , a2 ⟩ ∉ IEXT(p)
|
|
|
| if
| then exists z ∈ IR
|
a1 ∈ IR ,
p ∈ IP ,
a2 ∈ IR ,
⟨ a1 , a2 ⟩ ∉ IEXT(p)
| ⟨ z , a1 ⟩ ∈ IEXT(I(owl:sourceIndividual)) ,
⟨ z , p ⟩ ∈ IEXT(I(owl:assertionProperty)) ,
⟨ z , a2 ⟩ ∈ IEXT(I(owl:targetIndividual))
|
|
|
| if
| then
|
⟨ z , a ⟩ ∈ IEXT(I(owl:sourceIndividual)) ,
⟨ z , p ⟩ ∈ IEXT(I(owl:assertionProperty)) ,
⟨ z , v ⟩ ∈ IEXT(I(owl:targetValue))
| p ∈ IODP ,
⟨ a , v ⟩ ∉ IEXT(p)
|
|
|
| if
| then exists z ∈ IR
|
a ∈ IR ,
p ∈ IODP ,
v ∈ LV ,
⟨ a , v ⟩ ∉ IEXT(p)
| ⟨ z , a ⟩ ∈ IEXT(I(owl:sourceIndividual)) ,
⟨ z , p ⟩ ∈ IEXT(I(owl:assertionProperty)) ,
⟨ z , v ⟩ ∈ IEXT(I(owl:targetValue))
|
6 Appendix: Axiomatic Triples (Informative)
The RDF Semantics specification
[RDF Semantics]
defines so called "axiomatic triples"
as part of the semantics of RDF and RDFS.
Unlike the RDF Semantics,
the OWL 2 RDF-Based Semantics does not providenormatively specify any axiomatic triples.
It might not be possible to give a set of RDF triples
that captures all "axiomatic aspects"
of the OWL 2 RDF-Based Semantics,
just as one cannot expect
to define the whole OWL 2 RDF-Based Semantics specification
in terms of RDF entailment rules only.
Furthermore,
axiomatic triples for the OWL 2 RDF-Based Semantics could,
in principle,
contain arbitrarily complex class or propertyexpressions,
e.g. the union of several classes,
and by this it becomes non-obvious
which oneof several possible inequivalentnon-equivalent sets of axiomatic triples
should be selected.
However,
the OWL 2 RDF-Based Semantics includes many semantic conditions
that can in a sense be regarded to beas being "axiomatic",
and thus can be considered a replacement for the missing axiomatic triples.
After an overview on axiomatic triples for RDF and RDFS
in Section 6.1,
the Sections 6.2
and
6.3
will discuss how the "axiomatic" semantic conditions
of the OWL 2 RDF-Based Semantics
relate to axiomatic triples,
resulting in
an example set of axiomatic triples
that is compatible with the OWL 2 RDF-Based Semantics.
6.1 Axiomatic Triples in RDF
In RDF and RDFS
[RDF Semantics],
axiomatic triples are used
to provide basic meaning
tofor all the vocabulary terms
of the respective language.two languages.
This formal meaning is independent of any given RDF graph,
and it even holds for vocabulary terms,
which do not occur in a graph
that is interpreted by an RDF or RDFS interpretation.
As a consequence,
all the axiomatic triples of RDF and RDFS
are entailed by the empty graph,
when being interpreted under the semantics of RDF or RDFS,
respectively.
Examples of RDF and RDFS axiomatic triples are:
(1) rdf:type rdf:type rdf:Property .
(2) rdf:type rdfs:domain rdfs:Resource .
(3) rdf:type rdfs:range rdfs:Class .
(4) rdfs:Datatype rdfs:subClassOf rdfs:Class .
(5) rdfs:isDefinedBy rdfs:subPropertyOf rdfs:seeAlso .
As shown by these examples,
axiomatic triples are typically used by the RDF Semantics specification
to determine the part of the universe
the denotation of a vocabulary term belongs to (1).
In the case of a property,
the domain (2) and range (3) is specified as well.
Also, in some cases,
hierarchical relationships
between classes (4) or properties (5) of the vocabulary
are determined by axiomatic triples.determined.
Under the OWL 2 RDF-Based Semantics,
all the axiomatic triples of RDF and RDFS
could, in principle, be replaced by
"axiomatic" semantic conditions
that have neither premises nor bound variables.
By specifically applying the
RDFS semantic conditions
for the RDFS vocabularygiven in Section 5.8,
the example axiomatic triples (1) – (5)
can be equivalently restated as:
I(rdf:type) ∈ ICEXT(I(rdf:Property)) ,
IEXT(I(rdf:type)) ⊆ ICEXT(I(rdfs:Resource)) × ICEXT(I(rdfs:Class)) ,
ICEXT(I(rdfs:Datatype)) ⊆ ICEXT(I(rdfs:Class)) ,
IEXT(I(rdfs:isDefinedBy)) ⊆ IEXT(I(rdfs:seeAlso)) .
All the axiomatic triples of RDF and RDFS
can be considered "simple"
in the sense that
they have in their object position
only single terms
from the RDF and RDFS vocabularies,
and no complex class or property expressions
canappear there.
6.2 Axiomatic Triples for the Vocabulary Classes
of the RDF-Based SemanticsThe semantic conditions for vocabulary classes
in Table 5.2
of Section 5.2
can be considered as corresponding to
a set of axiomatic triples
for the classes in the vocabulary of the OWL 2 RDF-Based Semantics.
First,
for each IRI E
occurring in the first column of Table 5.2,
which specifies the semantic conditions for classes,if the second column contains an entry
of the form
"I(E) ∈ S"
for some set S,
then this entry corresponds to some RDF triple of the form "E rdf:type C",
where C is the IRI of some class with ICEXT(I(C)) = S.
In the table, S will always be either
the part IC of all classes,
or some sub part of IC.
Hence, in a corresponding RDF triple the IRI C will typically be
one of
"rdfs:Class",
"owl:Class"
(S=IC in both cases)
or "rdfs:Datatype" (S=IDC).
For example,
the semantic condition for the IRI "owl:FunctionalProperty",
given by
I(owl:FunctionalProperty) ∈ IC ,
would have the corresponding axiomatic triple
owl:FunctionalProperty rdf:type rdfs:Class .
Further,
for each IRI E in the first column of the table,
if the third column contains an entry
of the form
"ICEXT(I(E)) ⊆ S"
(or "ICEXT(I(E)) = S")
for some set S,
then this entry corresponds to some RDF triple of the form
"E rdfs:subClassOf C"
(or "E owl:equivalentClass C"),
where C is the IRI of some class with ICEXT(I(C)) = S.
In every case,
S will be either one of
the parts of the universe of I
or the empty set.
For example,
the semantic condition
ICEXT(I(owl:FunctionalProperty)) ⊆ IP
would have the corresponding axiomatic triple
owl:FunctionalProperty rdfs:subClassOf rdf:Property .
In addition,
the semantic conditions for the
parts of the universe
in Table 5.1
of Section 5.1
have to be taken into account.
In particular,
if an entry in the second column of Table 5.1
, which specifies the semantic conditions for the parts of the universe,is of the form
"S1 ⊆ S2"
for some sets S1 and S2,
then this corresponds to some RDF triple
of the form
"C1 owl:subClassOf C2",
where C1 and C2 are the IRIs
of some classes with
ICEXT(I(C1)) = S1
and
ICEXT(I(C2)) = S2,
respectively,
according to
Section 5.2.
JustAs stated in
Section 6.1
for the RDF axiomatic triples,
all the axiomatic triples for classes
can be considered "simple"
in the sense that
they will have in their object position
only single terms
from the RDF, RDFS and OWL 2 RDF-Based vocabularies
(Section 3.2).
Note that some of the axiomatic triples obtained in this way
already follow from the semantics of RDF and RDFS,
as defined in
[RDF Semantics].
6.3 Axiomatic Triples for the Vocabulary Properties
of the RDF-Based SemanticsThe semantic conditions for vocabulary properties
in Table 5.3
of Section 5.3
can be considered as corresponding to
a set of axiomatic triples
for the properties in the vocabulary of the OWL 2 RDF-Based Semantics.
First,
for each IRI E
occurring in the first column of Table 5.3,
which specifies the semantic conditions for properties,if the second column contains an entry
of the form
"I(E) ∈ S" for some set S,
then this entry corresponds to some RDF triple of the form
"E rdf:type C",
where C is the IRI of some class with ICEXT(I(C)) = S.
In the table,
S will always be either
the part IP of all properties,
or some sub part of IP.
Hence, in a corresponding RDF triple the IRI C will typically be
one of
"rdf:Property",
"owl:ObjectProperty",
(S=IP in both cases),
"owl:DatatypeProperty" (S=IODP),
" owl:AnnotationPropertyowl:OntologyProperty" (S =IOAP)=IOXP)
or " owl:OntologyPropertyowl:AnnotationProperty" (S =IOXP).=IOAP).
For example,
the semantic condition for the IRI "owl:disjointWith",
given by
I(owl:disjointWith) ∈ IP ,
would have the corresponding axiomatic triple
owl:disjointWith rdf:type rdf:Property .
Further,
for each IRI E in the first column of the table,
if the third column contains an entry
of the form
"IEXT(I(E)) ⊆ S1 × S2"
for some sets S1 and S2,
then this entry corresponds to some RDF triples of the forms
"E rdfs:domain C1"
and
"E rdfs:range C2",
where C1 and C2
are the IRIs of some classes with
ICEXT(I(C1)) = S1
and
ICEXT(I(C2)) = S2,
respectively.
Note that the sets S1 and S2
do not always correspond
to any of the parts of the universe of I.
For example,
the semantic condition
IEXT(I(owl:disjointWith)) ⊆ IC × IC
would have the corresponding axiomatic triples
owl:disjointWith rdfs:domain rdfs:Classowl:Class .
owl:disjointWith rdfs:range rdfs:Classowl:Class .
Exceptions are the semantic conditions
"IEXT(I(owl:topObjectProperty)) = IR × IR"
and
"IEXT(I(owl:topDataProperty)) = IR × LV",
since the exactly specified property extensions of these properties
cannot be expressed solely by domain and range axiomatic triples.
For example,
the domain and range axiomatic triples for
owl:sameAs
are equal to those for
owl:topObjectProperty,
but the property extension of
owl:sameAs
is different from
that of
owl:topObjectProperty.
JustAs stated in
Section 6.1
for the RDF axiomatic triples,
all the axiomatic triples for properties
can be considered "simple"
in the sense that
they will have in their object position
only single terms
from the RDF, RDFS and OWL 2 RDF-Based vocabularies
(Section 3.2).
7 Appendix: Relationship to the Direct Semantics (Informative)
This section compares
the OWL 2 RDF-Based Semantics
with the
OWL 2 Direct Semantics
[OWL 2 Direct Semantics].
While
the OWL 2 RDF-Based Semantics is based on the RDF Semantics specification
[RDF Semantics],
the OWL 2 Direct Semantics
is a description logic style semantics.
Several fundamental differences
exist between the two semantics,
but
there is also a strong relationship
basically stating that the OWL 2 RDF-Based Semantics is able
to reflect all logical conclusions
of the OWL 2 Direct Semantics.
This means that the OWL 2 Direct Semantics
can
in a sense
be regarded as a sub semantics of the OWL 2 RDF-Based Semantics.
Technically,
the comparison will be performed
by comparing the sets of entailments
that hold for each of the two semantics,
respectively.
The definition of an OWL 2 RDF-Based entailment
was given in
Section 4.3
of this document,
while the definition of an OWL 2 Direct entailment
is provided in
Section 2.5 of [OWL 2 Direct Semantics].
In both cases,
entailments are defined for pairs of ontologies,
and such an ordered pair of two ontologies will be called an
entailment query
in this section.
Comparing the two semantics by means of entailments
will only be meaningful
if the entailment queries
allow for applying
both
the OWL 2 RDF-Based Semantics
and the
OWL 2 Direct Semantics
to them.
In order to ensure this,
the comparison will be restricted to entailment queries,
for which the left-hand side and right-hand side ontologies
are both
OWL 2 DL ontologies in RDF graph form.
These are RDF graphs
that can be transformed
by applying
the reverse OWL 2 RDF mapping
[OWL 2 RDF Mapping]
into corresponding
OWL 2 DL ontologies in Functional Syntax form
according to the Functional style syntax defined in
[OWL 2 FunctionalSpecification],
and which must further meet
all the restrictions on OWL 2 DL ontologies
that are specified in
Section 3 of [OWL 2 FunctionalSpecification].
In fact,
these restrictions must be mutually met by
both ontologies that occur in an entailment query,
i.e.
all these restrictions need to be satisfied
as if the two ontologies would be part of a single ontology.
Any entailment query that adheres to the conditions defined here
will be called an
OWL 2 DL entailment query.
Ideally,
the relationship between
the OWL 2 RDF-Based Semantics and the OWL 2 Direct Semantics
would be of the form that
every OWL 2 DL entailment query
that is an OWL 2 Direct entailment
is also an OWL 2 RDF-Based entailment.
However,
this desirable relationship
cannot hold in general
due to a variety of differences
that exist between
the OWL 2 RDF-Based Semantics
and the OWL 2 Direct Semantics,
as demonstrated in
Section 7.1.
Fortunately,
the problems resulting from these semantic differences
can be overcome
in a way that
for every OWL 2 DL entailment query
there is another one
for which
the desired entailment relationship indeed holds,
and the new entailment query is
semantically equivalent to the original entailment query
under the OWL 2 Direct Semantics.
This is the gist of the
theOWL 2 Correspondence Theorem,
which will be presented in
Section 7.2.
The
proof of this theorem,
given in Section 7.3,
will further demonstrate
that such a substitute OWL 2 DL entailment query
can always be algorithmically constructed
by means of simple syntactic transformations.
7.1 Example on Semantic Differences
This section will show
that differences exist
between
the OWL 2 RDF-Based Semantics and the OWL 2 Direct Semantics,
and it will be demonstrated
how these semantic differences
complicate a comparison
of the two semantics
in terms of entailments.
An example OWL 2 DL entailment query will be given,
which will happen to be an OWL 2 Direct entailment
without being an OWL 2 RDF-Based entailment.
The section will explain
the different reasons
and will provide a resolution
of each of them.
It will turn out
that the example entailment query
can be syntactically transformed
into another
OWL 2 DL entailment query
that is both
an OWL 2 Direct entailment
and
an OWL 2 RDF-Based entailment,
while being semantically unchanged
compared to the original entailment query
under the OWL 2 Direct Semantics.
This example will motivate
the OWL 2 Correspondence Theorem
in Section 7.2
and its proof
in Section 7.3.
The example entailment query consists of the following
pair
of RDF graphs⟨ G1* , G2* ⟩:⟩
of RDF graphs:
G1* :
(1) ex:o1 rdf:type owl:Ontology .
(2) ex:c1 rdf:type owl:Class .
(3) ex:c2 rdf:type owl:Class .
(4) ex:c1 rdfs:subClassOf ex:c2 .
G2* :
(1) ex:o2 rdf:type owl:Ontology .
(2) ex:c1 rdf:type owl:Class .
(3) ex:c2 rdf:type owl:Class .
(4) ex:c3 rdf:type owl:Class .
(5) ex:c1 rdfs:subClassOf _:x .
(6) _:x rdf:type owl:Class .
(7) _:x owl:unionOf ( ex:c2 ex:c3 ) .
(8) ex:c3 rdfs:comment "an annotation"rdfs:label "c3" .
Both G1* and G2*
are
OWL 2 DL ontologies in RDF graph form
and can therefore be mapped by the reverse RDF mapping
[OWL 2 RDF Mapping]
intoto the following two OWL 2 DL ontologies in Functional Syntax form
F(G1*) and F(G2*):
F(G1*) :
(1) Ontology( ex:o1
(2) Declaration( Class( ex:c1 ) )
(3) Declaration( Class( ex:c2 ) )
(4) SubClassOf( ex:c1 ex:c2 )
(5) )
F(G2*) :
(1) Ontology( ex:o2
(2) Declaration( Class( ex:c1 ) )
(3) Declaration( Class( ex:c2 ) )
(4) Declaration( Class( ex:c3 ) )
(5) SubClassOf( ex:c1 ObjectUnionOf( ex:c2 ex:c3 ) )
(6) AnnotationAssertion( rdfs:commentrdfs:label ex:c3 "an annotation""c3" )
(7) )
It follows that
F(G1*) OWL 2 Direct entails F(G2*).
To show this,
only the axioms
(4) of F(G1*)
and
(5) of F(G2*)
have to be considered.
None of the other statements in the two ontologies
are relevant for this OWL 2 Direct entailment to hold,
since they do not have a formal meaning
under the OWL 2 Direct Semantics.
However,
it turns out that the RDF graph
G1*
does not OWL 2 RDF-Based entail
G2*,
for reasons discussed in detail now.
Reason 1: An annotation in F(G2*).
The ontology F(G2*)
contains an annotation (6).
The OWL 2 Direct Semantics
does not give a formal meaning to
annotations.
In contrast,
under the OWL 2 RDF-Based Semantics
every RDF triple occurring in an RDF graph
has a formal meaning,
including
the corresponding annotation triple (8) in G2*.
Since this annotation triple
only occurs in G2*
but not in G1*,
there will exist OWL 2 RDF-Based interpretations
that satisfy G1*
without satisfying triple (8) of G2*.
Hence,
G1*
does not OWL 2 RDF-Based entail G2*.
Resolution of Reason 1.
The annotation triple (8) in G2*
will be removed,
which will avoid requiring
OWL 2 RDF-Based interpretations to interpret this triple.
The changed RDF graphs will still be
OWL 2 DL ontologies in RDF graph form,
since annotations are strictly optional in OWL 2 DL ontologies.
Also, this operation will not change the formal meaning of the ontologies
under the OWL 2 Direct Semantics,
since annotations do not have a formal meaning under this semantics.
Reason 2: An entity declaration exclusively in F(G2*).
The ontology F(G2*)
contains an entity declaration for the class IRI
ex:c3 (4),
for which there is no corresponding entity declaration
in F(G1*).
The OWL 2 Direct Semantics does not give a formal meaning to
entity declarations,
while the OWL 2 RDF-Based Semantics gives a formal meaning
to the corresponding declaration triple (4) in G2*.
The consequences are analog to those described for reason 1.
Resolution of Reason 2.
The declaration triple (4) in G2*
will be copied to G1*.
An OWL 2 RDF-Based interpretation
that satisfies the modified graph G1*
will then also satisfy the declaration triple.
The changed RDF graphs will still be
OWL 2 DL ontologies in RDF graph form,
since adding the entity declaration
does not hurt any of the
restrictions on OWL 2 DL ontologies.
Also, this operation will not change the formal meaning of the ontologies
under the OWL 2 Direct Semantics,
since entity declarations do not have a formal meaning under this semantics.
Reason 3: Different ontology IRIs in F(G1*) and F(G2*).
The ontology IRIs for the two ontologies,
given by (1) in F(G1*)
and by (1) in F(G2*),
differ from each other.
The OWL 2 Direct Semantics does not give a formal meaning to
ontology headers,
while the OWL 2 RDF-Based Semantics gives a formal meaning
to the corresponding header triples
(1) in G1*
and
(1) in G2*.
Since these header triples differ from each other,
the consequences are analog to those described for reason 1.
Resolution of Reason 3.
The IRI
in the subject position of the header triple (1)
in G2*
is changed into a blank node.
Due to the existential semantics of blank nodes under the OWL 2 RDF-Based Semantics
this new triple will then be entailed
by triple (1)
in G1*.
The changed RDF graphs will still be
OWL 2 DL ontologies in RDF graph form,
since an ontology IRI is optional for an OWL 2 DL ontology.
(Note, however, that it would have been an error to simply remove
triple (1) from G2*,
since an OWL 2 DL ontology is required to contain an ontology header.)
Also, this operation will not change the formal meaning of the ontologies
under the OWL 2 Direct Semantics,
since ontology headers do not have a formal meaning under this semantics.
Reason 4: A class expression in F(G2*).
Axiom (5) of F(G2*)
contains a class expression
that represents the union of the two classes
denoted by
ex:c2
and
ex:c3.
Within G2*,
this class expression is represented
by the triples (6) and (7),
both having the blank node
"_:x"
in their respective subject position.
The way the OWL 2 RDF-Based Semantics interprets these two triples
differs from the way
the OWL 2 Direct Semantics treats the class expression
in axiom (5) of F(G2*).
The OWL 2 Direct Semantics treats classes as sets,
i.e. subsets of the universe.
Thus,
the IRIs
ex:c2
and
ex:c3
in F(G2*)
denote two sets,
and the class expression
in axiom (5) of F(G2*)
therefore represents the set
that consists of the union of these two sets.
In general, the union of two arbitrary sets is always ensured to exist as a set as well, since it is an element of the powerset of the universe. Hence the class denoted by the class expression in axiom (5) of F( G 2 * ) is warranted to exist with respect to the OWL 2 Direct Semantics.The OWL 2 RDF-Based Semantics,
on the other hand,
treats classes as individuals,
i.e. members of the universe.
While every class under the OWL 2 RDF-Based Semantics
represents a certain subset of the universe,
namely its class extension,
this set is actually distinguished from the class itself.
For two given classes
it is ensured under the OWL 2 RDF-Based Semantics,
just as for the OWL 2 Direct Semantics,
that the union of their class extensions will always exist
as a subset of the universe.
However,
there is no generalguarantee
that there will also alwaysexist
an individual in the universe
that has this set union as its class extension, i.e. it cannot be guaranteed that there will always be a union class for every union set.extension.
Under the OWL 2 RDF-Based Semantics,
triple (7) of G2*
claims that
there isa class exists being
the union of two other classes.
But since
the existence of such a union class
is not alreadyensured by G1*,
there will existbe OWL 2 RDF-Based interpretations
that satisfy G1*
without satisfying
triple (7) of G2*.
Hence,
G1*
does not
OWL 2 RDF-Based entail
G2*.
Resolution of Reason 4.
The triples (6) and (7) of G2*
are copied to G1*
together with the new triple
"_:x owl:equivalentClass _:x".
If an OWL 2 RDF-Based interpretation satisfies the modified graph G1*,
then the triples (6) and (7) of G2*
will also be satisfied.
The changed RDF graphs will still be
OWL 2 DL ontologies in RDF graph form,
since the whole set of added triples
encodes a proper OWL 2 DL axiom.
Further,
for the IRI
ex:c3,
which occurs in the union class expression
but not in G1*,
an entity declaration has already beenis added
to G1*
by the resolution of reason 2.
Also, this operation will not change
the formal meaning of the ontologies
under the OWL 2 Direct Semantics,
since the added equivalence axiom
is actuallya tautology under this semantics.
Note that it would have been an error
to simply copy the
triples (6) and (7) of G2*
to G1*,
without also adding the new triple
"_:x owl:equivalentClass _:x".
This would have produced a class expression
that has no connection to any axiom in the ontology.
An OWL 2 DL ontology is basically a set of axioms
and does not allow for the occurrence of
"dangling" class expressions.
This is the reason for actually "embedding" the class expression
in an axiom.
It would have also been wrong
to use an arbitrary axiom for such an embedding,
since it has to be ensured
that the formal meaning of the original ontology does not change
under the OWL 2 Direct Semantics.
However,
any tautological axiom
that contains the original class expression
would have been sufficient for this purpose as well.
Complete Resolution: The transformed entailment query.
Combining the resolutions of all the above reasons
leads to the following new pair of RDF graphs
⟨ G1 , G2 ⟩:
G1 :
(1) ex:o1 rdf:type owl:Ontology .
(2) ex:c1 rdf:type owl:Class .
(3) ex:c2 rdf:type owl:Class .
(4) ex:c3 rdf:type owl:Class .
(5) ex:c1 rdfs:subClassOf ex:c2 .
(6) _:x owl:equivalentClass _:x .
(7) _:x rdf:type owl:Class .
(8) _:x owl:unionOf ( ex:c2 ex:c3 ) .
G2 :
(1) _:o rdf:type owl:Ontology .
(2) ex:c1 rdf:type owl:Class .
(3) ex:c2 rdf:type owl:Class .
(4) ex:c3 rdf:type owl:Class .
(5) ex:c1 rdfs:subClassOf _:x .
(6) _:x rdf:type owl:Class .
(7) _:x owl:unionOf ( ex:c2 ex:c3 ) .
The following list reiterates the changes compared to the original RDF graphs
G1* and G2*:
- Resolution of Reason 1 (annotation): Triple (8) in G2* has been removed, i.e. there is no corresponding annotation triple in G2.
- Resolution of Reason 2 (entity declaration): Triple (4) in G2* has been copied to G1*, becoming triple (4) in G1.
- Resolution of Reason 3 (ontology IRIs): The IRI in the subject position of triple (1) in G2* has been changed into a blank node, becoming triple (1) in G2.
- Resolution of Reason 4 (class expression): Triples (6) and (7) in G2* have been copied to G1* together with the new triple "_:x owl:equivalentClass _:x", becoming triples (6), (7) and (8) in G1.
G1 and G2
are again
OWL 2 DL ontologies in RDF graph form
and can be mapped by the reverse RDF mapping
to the following
OWL 2 DL ontologies in Functional Syntax form
F(G1) and F(G2):
F(G1) :
(1) Ontology( ex:o1
(2) Declaration( Class( ex:c1 ) )
(3) Declaration( Class( ex:c2 ) )
(4) Declaration( Class( ex:c3 ) )
(5) SubClassOf( ex:c1 ex:c2 )
(6) EquivalentClasses( ObjectUnionOf( ex:c2 ex:c3 ) ObjectUnionOf( ex:c2 ex:c3 ) )
(7) )
F(G2) :
(1) Ontology(
(2) Declaration( Class( ex:c1 ) )
(3) Declaration( Class( ex:c2 ) )
(4) Declaration( Class( ex:c3 ) )
(5) SubClassOf( ex:c1 ObjectUnionOf( ex:c2 ex:c3 ) )
(6) )
As said earlier,
all the applied changes
preserve the formal meaning
of the original OWL 2 DL ontologies
under the OWL 2 Direct Semantics.
In particular,Hence,
it is still the case
that
F(G1)
OWL 2 Direct entails
F(G2).
However,
due to the syntactic transformation
the situation has changed for the OWL 2 RDF-Based Semantics.
It is now possible to show,
by following the lines of argumentation
for the resolutions of the different reasons given above,
that G1 OWL 2 RDF-Based entails G2
.as well.
7.2 Correspondence Theorem
This section presents the OWL 2 Correspondence Theorem,
which compares the semantic expressivity of
the OWL 2 RDF-Based Semantics
with that of
the OWL 2 Direct Semantics.
The theorem basically claimsstates that
the OWL 2 RDF-Based Semantics is able to reflect all the semantic conclusions
of the OWL 2 Direct Semantics,
where the notion of a "semantic conclusion"
is technically expressed in terms of an entailment.entailment.
However,
as discussed in
Section 7.1,
there exist semantic differences
between the OWL 2 RDF-Based Semantics and the OWL 2 Direct Semantics thatSemantics,
which do not allow for stating
that any OWL 2 DL entailment query
that is an OWL 2 Direct entailment
will always also be an
OWL 2 RDF-Based entailment.
Nevertheless,
it can still be ensured that
any given OWL 2 DL entailment query
can be substituted
by another OWL 2 DL entailment query
in a way
that for the substitute entailment query
the desired relationship will really hold,
without changingwhile preserving the formal meaning
compared to the original entailment query
under the OWL 2 Direct Semantics.
In fact,
the theorem only makes the seemingly weak assertion
that such a substitute entailment query
will always exist.
But the actual
proof of the theorem
in Section 7.3
will be more concrete
in that it will substitute each given OWL 2 DL entailment query
bywith a variant
that can be algorithmically constructed
by applying a set of simple syntactic transformations
to the original entailment query.
One can get an idea of how this works
from Section 7.1.
Technical note on corresponding datatype maps:
A distinction exists
between the format of
an OWL 2 RDF-Based datatype map,
as defined by Definition 4.1,
and the format of an OWL 2 Direct datatype map,
as defined in
Section 2.1 of [OWL 2 Direct Semantics].
It is, however, possible to translate
between
an OWL 2 RDF-Based datatype map D
and
the corresponding OWL 2 Direct datatype map F(D)
in the following way:
Let D be an OWL 2 RDF-Based datatype map
according to
Definition 4.1.
The corresponding OWL 2 Direct datatype map
[ OWL 2 Direct Semantics ]F(D) := (
NDT ,
NLS ,
NFS ,
⋅ DT ,
⋅ LS ,
⋅ FS
)
[OWL 2 Direct Semantics]
is given by
- Datatype Names: NDT is defined as the set of all IRIs u, for which there is a datatype d, such that ⟨ u , d ⟩ ∈ D.
- Lexical Space: For each datatype name u ∈ NDT, set NLS(u) := LS(d), where ⟨ u , d ⟩ ∈ D.
- Facet Space: For each datatype name u ∈ NDT, set NFS(u) := FS(d), where ⟨ u , d ⟩ ∈ D.
- Value Space: For each datatype name u ∈ NDT, set (u) DT := VS(d), where ⟨ u , d ⟩ ∈ D.
- Lexical-to-Value Mapping: For each datatype name u ∈ NDT and each lexical form a ∈ NLS(u),
(⟨set ⟨ a , u ⟩) ⟩ LS := L2V(d)(a), where ⟨ u , d ⟩ ∈ D.
- Facet-to-Value Mapping: For each datatype name u ∈ NDT and each pair ⟨ F , v ⟩ ∈ NFS(u),
(⟨set ⟨ F , v ⟩) ⟩ FS := F2V(d)(⟨ F , v ⟩), where ⟨ u , d ⟩ ∈ D.
Theorem 7.1 (OWL 2 Correspondence Theorem):
Let D be an OWL 2 RDF-Based datatype map
according to Definition 4.1,
with F(D)
being the
OWL 2 Direct datatype map
according to
Section 2.1 of [OWL 2 Direct Semantics]
that corresponds to D w.r.t.according to the
technical note on corresponding datatype maps.
Let
G1* and G2*
be RDF graphs
that are
OWL 2 DL ontologies in RDF graph form,
with
F(G1*) and F(G2*)
being the
OWL 2 DL ontologies in Functional Syntax form
[OWL 2 Specification]
that result from applying the reverse OWL 2 RDF mapping
[OWL 2 RDF Mapping]
to
G1* and G2*,
respectively.
Let
F(G1*) and F(G2*)
mutually meet
the restrictions on OWL 2 DL ontologies
as specified in Section 3 of [OWL 2 Specification].
Then,
there exist RDF graphs
G1 and G2
that are
OWL 2 DL ontologies in RDF graph form,
such that all the following conditions hold,
with
F(G1) and F(G2)
being the
OWL 2 DL ontologies in Functional Syntax form
that result from applying the reverse OWL 2 RDF mapping
to
G1 and G2,
respectively:
- (1) F(G1) and F(G2) mutually meet the restrictions on OWL 2 DL ontologies;
- (2) F(G1) OWL 2 Direct entails F(G1*) with respect to F(D), if and only if F(G1*) OWL 2 Direct entails F(G1) with respect to F(D);
- (3) F(G2) OWL 2 Direct entails F(G2*) with respect to F(D), if and only if F(G2*) OWL 2 Direct entails F(G2) with respect to F(D);
- (4) if F(G1) OWL 2 Direct entails F(G2) with respect to F(D), then G1 OWL 2 RDF-Based entails G2 with respect to D.
7.3 AProof for the Correspondence Theorem
This is a sketch of a proof for
Theorem 7.1 (OWL 2 Correspondence Theorem),
stated in
Section 7.2.
The proof sketch provides
the basic line of argumentation for showing the theorem.
However,
for complexity reasons,
some technical aspects of the theorem are only coarsely treated,
and the proof sketch also refrains
from taking the full amount of language constructs of OWL 2 into account.
A complete proof can make use of the observation
that the definitions of the OWL 2 Direct Semantics
and the OWL 2 RDF-Based Semantics
are actually closely aligned
for all the different language constructs of OWL 2.
The proof sketch will make use of an approach
that will be called "balancing" throughout this appendix,
and which will now be introduced.
A concrete example for how this approach can be applied
is given in Section 7.1.
Definition (Balanced):
A pair of RDF graphs
⟨ G1 , G2 ⟩
is called
balanced,
if and only if
G1 and G2
are OWL 2 DL ontologies in RDF graph form,
such that all the following additional conditions hold,
with
F(G1) and F(G2)
being the
OWL 2 DL ontologies in Functional Syntax form
[OWL 2 Specification]
that result from applying the reverse OWL 2 RDF mapping
[OWL 2 RDF Mapping]
to
G1 and G2,
respectively:
- (1) F(G1) and F(G2) mutually meet the restrictions on OWL 2 DL ontologies as specified in Section 3 of [OWL 2 Specification];
- (2) for every IRI or blank node x occurring in G1 or G2, there is a declaration triple (Table 7 in [OWL 2 RDF Mapping]) in the graph for every entity type (Section 5.8 of [OWL 2 Specification]) of x (there are no missing entity declarations);
- G2 does not contain
- (5) G2 contains exactly one ontology header (Table 4 in [OWL 2 RDF Mapping]) consisting of a single RDF triple of the form "b rdf:type owl:Ontology", where b is a blank node;
- any subgraph g of G2 that is the RDF encoding of one of the following OWL 2 constructs is also a subgraph of G1:
Balancing Lemma:
An algorithm exists
that terminates on every input
and that has the following input/output behavior:
Let the input of the algorithm be
a pair of RDF graphs
⟨ G1* , G2* ⟩,
where
G1* and G2*
are OWL 2 DL ontologies in RDF graph form,
with
F(G1*) and F(G2*)
being the
OWL 2 DL ontologies in Functional Syntax form
[OWL 2 Specification]
that result from applying the reverse OWL 2 RDF mapping
[OWL 2 RDF Mapping]
to
G1* and G2*,
respectively.
Let
F(G1*) and F(G2*)
mutually meet
the restrictions on OWL 2 DL ontologies
as specified in Section 3 of [OWL 2 Specification].
Then the output of the algorithm
will be a pair of RDF graphs
⟨ G1 , G2 ⟩,
where
G1 and G2
are OWL 2 DL ontologies in RDF graph form,
such that
for any OWL 2 RDF-Based datatype map D
according to Definition 4.1
all the following conditions hold,
with
F(G1) and F(G2)
being the
OWL 2 DL ontologies in Functional Syntax form
that result from applying the reverse OWL 2 RDF mapping
to
G1 and G2,
respectively,
and
with F(D)
being the
OWL 2 Direct datatype map
according to
Section 2.1 of [OWL 2 Direct Semantics]
that corresponds to D w.r.t.according to the
technical note on corresponding datatype maps
in Section 7.2:
- (1) the pair ⟨ G1 , G2 ⟩ is balanced;
- (2) F(G1) OWL 2 Direct entails F(G1*) with respect to F(D), and F(G1*) OWL 2 Direct entails F(G1) with respect to F(D);
- (3) F(G2) OWL 2 Direct entails F(G2*) with respect to F(D), and F(G2*) OWL 2 Direct entails F(G2) with respect to F(D).
Proof of the Balancing Lemma:
Let
G1* and G2*
be OWL 2 DL ontologies in RDF graph form,
with
F(G1*) and F(G2*)
being the corresponding
OWL 2 DL ontologies in Functional Syntax form
that result from applying the reverse OWL 2 RDF mapping
to
G1* and G2*,
respectively,
such that
F(G1*) and F(G2*)
mutually meet
the restrictions on OWL 2 DL ontologies.
The resulting RDF graphs G1 and G2
are constructed as follows.
The initial versions of G1 and G2
are copies of G1* and G2*,
respectively.
A preprocessing step
will substitute all blank nodes in G1
for fresh blank nodes that do not occur in G2.
One can therefore assume from now on
that G1 and G2 have no common blank nodes.
Since G1 and G2
are OWL 2 DL ontologies in RDF graph form,
the canonical parsing process for computing the reverse OWL 2 RDF mapping,
as described in
Section 3 of [OWL 2 RDF Mapping],
can be applied
to map the graphs G1 and G2
to corresponding OWL 2 DL ontologies in Functional Syntax form.
For the resulting ontologies
it is then algorithmically possible
to determine for every occurring IRI and anonymous individual
all the entity types.
By this,
all missing declaration triples
are added to G1 and G2.
Further,
since G1 and G2
are OWL 2 DL ontologies in RDF graph form,
the canonical parsing process
can also be applied
to safely identify all subgraphs
of G1 and G2
that correspond to language constructs
described in
[OWL 2 Specification],
including all the language constructs considered in the theorem.
Based on these observations, the following steps are performed on every subgraph g ⊆ G2 that has been identified by the canonical parsing process:
- (a) If g is the RDF encoding of an annotation, then g will be removed from G2.
- (b) If g is a deprecation triple, then g will be removed from G2.
- (c) If g is an ontology header (which may include ontology properties, such as import directives), then g is substituted in G2 by a triple of the form "x rdf:type owl:Ontology", where x is a fresh blank node. At the end of the process, all but one of these triples will be removed from G2.
- (d) If g is the RDF encoding of an entity declaration, then g is copied to G1.
- (e) If g is the RDF encoding of a property expression with root blank node x, then g together with the RDF triple "x owl:equivalentProperty x" is added to G1.
- (f) If g is the RDF encoding of a class expression with root blank node x, then g together with the RDF triple "x owl:equivalentClass x" is added to G1.
- (g) If g is the RDF encoding of a data range expression with root blank node x, then:
- if g is part of a data property restriction expression, then nothing needs to be done, since this case is covered by the treatment of class expressions in (f);
- if g is part of a datatype definition, then G2 contains a triple "u owl:equivalentClass x" with some IRI u that is declared as a datatype, and then the triple and g are copied to G1;
- otherwise, g is part of at least one data property range axiom. One such property p is chosen randomly, and the RDF encoding r of a universal property restriction expression on property p is created for the datarange expression rooted by node x. Let the RDF graph r have fresh root blank node y. r together with the RDF triple "y owl:equivalentClass y" is added to G1.
In the following it is shown that all the claims of the theorem hold.
A: Existence of a terminating algorithm.
An algorithm exists
for mapping
the input pair
⟨ G1* , G2* ⟩
to the output pair
⟨ G1 , G2 ⟩,
since
the canonical parsing process
for the determination of the missing entity declarations
and for the identification of the language construct subgraphs
is described in the form of an algorithm
in [OWL 2 RDF Mapping].
All other operations described above
can obviously be performed algorithmically.
The algorithm terminates,
since the canonical parsing process terminates
(including termination on invalid input),
and since all other operations described above
are executed by a finite number of steps,
respectively.
B: The resulting RDF graphs are OWL 2 DL ontologies.
Since the original RDF graphs
G1* and G2*
are OWL 2 DL ontologies in RDF graph form,
this is also the case for
G1 and G2,
since each of the steps above
transforms a pair of OWL 2 DL ontologies in RDF graph form
again into a pair of OWL 2 DL ontologies in RDF graph form,
for the following reasons:
- The substitution of existing blank nodes by fresh blank nodes does not change the structure of an OWL 2 DL ontology in RDF graph form.
- If an entity has some entity type but the corresponding entity declaration is omitted, then it may be added without harm.
- Annotations and deprecation statements can always be removed from an OWL 2 DL ontology, as done by (a) and (b), since they are non-required language constructs.
- Any OWL 2 DL ontology requires the existence of an ontology header, but does not require the existence of an ontology IRI, so it is sufficient to replace an ontology header by (c).
- G1 contains entity declarations for every IRI occurring in G1, since by (d) all entity declarations from G2* have been copied to G1, and only IRIs from both G1* and G2* can occur in G1 via (e), (f) and (g). It is not a problem to have entity declarations for IRIs that are not further used in an OWL 2 DL ontology.
- Adding a datatype definition to an OWL 2 DL ontology, as done by (g), will lead to a new OWL 2 DL ontology (note that the corresponding datatype declaration from G2* has been copied to G1 as well).
- Adding syntactically valid OWL 2 DL axioms to an OWL 2 DL ontology, as done by (e), (f) and (g), will lead to a new OWL 2 DL ontology.
C: The resulting pair of RDF graphs is balanced.
Property (1) of the theorem requires that
the pair
⟨ G1 , G2 ⟩
is balanced.
The following list checks that all the properties of the definition are satisfied.
- Property (1): F(G1) and F(G2) mutually meet the restrictions on OWL 2 DL ontologies, since the restrictions are mutually met by the original ontologies, and since only declarations and expressions that already existed in G2* are added to G1 by (d), (e), (f) and (g). The removal of annotations by (a) and deprecation triples by (b) from G2*, as well as the replacement of the ontology header of G2* by (c) do not hurt any syntactic restrictions either.
- Property (2): All missing entity declaration triples have been added to G1 and G2.
- Properties (3) and (4): G2 does not contain any RDF encodings of annotations nor deprecation triples due to their removal by (a) and (b), respectively.
- Property (5): G2 contains exactly one ontology header consisting of a single triple of the form "b rdf:type owl:Ontology", where b is a blank node, due to the replacement of the existing ontology headers by (c).
- Property (6): Each RDF encoding of an entity declaration in G1 also occurs in G2, due to their copying by (d).
- Properties (7), (8) and (9): Each RDF encoding of a property, class or data range expression in G1 also occurs in G2, due to their adding by (e), (f) and (g), respectively.
D: The resulting ontologies are semantically equivalent with the original ontologies.
Property (2) of the theorem requires that
F(G1) is semantically equivalent with F(G1*).
This is the case,
since F(G1) differs from F(G1*) only by
- additional entity declarations (due to the addition of all missing entity declarations and due to (d)), which have no formal meaning under the OWL 2 Direct Semantics;
- datatype definitions (due to (g)), which only introduce a new name for a data range expression;
- additional OWL 2 DL axioms (due to (e), (f) and (g)), which are all, by construction, tautologies under the OWL 2 Direct Semantics.
Further,
property (3) of the theorem requires that
F(G2) is semantically equivalent with F(G2*).
This is the case,
since F(G2) differs from F(G2*) only by
additional entity declarations,
and missing annotations
including deprecation annotations
(due to (a) and (b)),
which all have no formal meaning under the OWL 2 Direct Semantics.
End of the Proof of the Balancing Lemma.
In the following,
the correspondence theorem will be proven.
Assume that the premises of the correspondence theorem hold
for given RDF graphs
G1* and G2*.
This allows for applying the
balancing lemma,
which provides the existence of certain RDF graphs
G1 and G2
that are OWL 2 DL ontologies in RDF graph form.
Hence,
it is possible to build
OWL 2 DL ontologies in Functional Syntax form
F(G1) and F(G2)
by applying the reverse OWL 2 RDF mapping
to
G1 and G2,
respectively.
The balancing lemma
further provides that the pair
⟨ G1 , G2 ⟩
is balanced.
The claimed property (1) of the correspondence theorem
follows directly from property (1) of the balancing lemma
and from property (1) of the "Balanced"-definition.
The claimed properties (2) and (3) of the correspondence theorem
follow directly from properties (2) and (3) of the balancing lemma,
respectively.
The rest of this proof will treat
the claimed property (4) of the correspondence theorem,
which states that
if F(G1) OWL 2 Direct entails F(G2)
with respect to F(D),
then G1 OWL 2 RDF-Based entails G2
with respect to D.
Let I be an OWL 2 RDF-Based interpretation
w.r.t. an OWL 2 RDF-Based datatype map D
of a vocabulary VI
that covers all the names
(IRIs and literals)
occurring in the RDF graphs G1 and G2,
and let I OWL 2 RDF-Based satisfy G1.
It will be shown that I OWL 2 RDF-Based satisfies G2.
As a first step,
an OWL 2 Direct interpretation J
w.r.t. the corresponding OWL 2 Direct datatype map F(D)
will be constructed
for a vocabulary VJ
that covers all the names
(IRIs and literals)
occurring in the OWL 2 DL ontologies in Functional Syntax form
F(G1) and F(G2).
J will be defined in a way
such that it closely corresponds to I
on those parts of the vocabularies VI and VJ
that cover
G1 and G2,
and
F(G1) and F(G2),
respectively.
G1 and G2
are OWL 2 DL ontologies in RDF graph form
that are mapped by the reverse RDF mapping
to F(G1) and F(G2),
respectively.
This means that the same literals are used
in both G1 and F(G1),
and in both G2 and F(G2),
respectively.
Further,
since the pair
⟨ G1 , G2 ⟩
is balanced,
according to property (2) of the "Balanced"-definition
there are entity declarations
in F(G1) and F(G2)
for all the entity types
of every non-built-in IRI occurring in
G1 and G2,
respectively.
For each entity declaration
of the form
Declaration(T(u))
in F(G1) and F(G2),
where T is the entity type for some IRI u,
a typing triple
of the form
u rdf:type t
exists in G1 or G2,
respectively,
where t denotes the class
representing the part of the universe
that corresponds to T;
and vice versa.
Since the pair
⟨ G1 , G2 ⟩
is balanced,
all the entity declarations of F(G2) are also contained in F(G1),
and therefore
all the typing triples of G2
that correspond to some entity declaration in F(G2)
are also contained in G1.
Since I OWL 2 RDF-Based satisfies G1,
all these "declaring" typing triples are OWL 2 RDF-Based satisfied by I,
and thus all non-built-in IRIs
in G1 and G2
are actually instances of their declared parts of the universe.
Based on these observations,
the OWL 2 Direct interpretation
J and its vocabulary VJ
for the datatype map F(D)
can now be defined.
The vocabulary
VJ := (
VC ,
VOP ,
VDP ,
VI ,
VDT ,
VLT ,
VFA
)
is defined as follows.
- The set VC of class names contains all IRIs that are declared as classes in F(G1).
- The set VOP of object property names contains all IRIs that are declared as object properties in F(G1).
- The set VDP of data property names contains all IRIs that are declared as data properties in F(G1).
- The set VI of individual names contains all IRIs that are declared as named individuals in F(G1).
The sets
VDT of datatype names,
VLT of literals, and
VFA of facet-literal pairs
are defined according to
Section 2.1 of [OWL 2 Direct Semantics]
w.r.t. the datatype map F(D).
Specifically,
VDT includes
all IRIs that are declared as datatypes in F(G1).
The interpretation
J := (
ΔI ,
ΔD ,
⋅ C ,
⋅ OP ,
⋅ DP ,
⋅ I ,
⋅ DT ,
⋅ LT ,
⋅ FA
)
is defined as follows.
The object and data domains of J are identified
with the universe IR and the set of data values LV of I,
respectively,
i.e.,
ΔI := IR and
ΔD := LV.
The datatype interpretation function ⋅ DT,
the literal interpretation function ⋅ LT, and
the facet interpretation function ⋅ FA
are defined according to
Section 2.2 of [OWL 2 Direct Semantics].
Specifically,
⋅ DT interprets
all IRIs that are declared as datatypes in F(G1)
according the following definition.
For every non-built-in IRI u
occurring in F(G1):
- If u is declared as a named individual, then set uI := I(u), since the graph contains the triple "u rdf:type owl:NamedIndividual", i.e., I(u) ∈ IR.
- If u is declared as a class, then set uC := ICEXT(I(u)), since the graph contains the triple "u rdf:type owl:Class", i.e., I(u) ∈ IC.
- If u is declared as a datatype, then set uDT := ICEXT(I(u)), since the graph contains the triple "u rdf:type rdfs:Datatype", i.e., I(u) ∈ IDC.
- If u is declared as an object property, then set uOP := IEXT(I(u)), since the graph contains the triple "u rdf:type owl:ObjectProperty", i.e., I(u) ∈ IP.
- If u is declared as a data property, then set uDP := IEXT(I(u)), since the graph contains the triple "u rdf:type owl:DatatypeProperty", i.e., I(u) ∈ IODP.
Note that G1 may also contain declarations of annotation properties,
but they will not be interpreted by the OWL 2 Direct Semantics
and are therefore ignored here.
This will not lead to problems,
since the pair
⟨ G1 , G2 ⟩
is balanced,
and therefore G2 does not contain any annotations.
Further, note that the definition of J
is compatible with the concept of a non-separated vocabulary in OWL 2 DL
(also called "punning",
see Section 5.9 of [OWL 2 Specification]).
Since G1 and G2 are OWL 2 DL ontologies in RDF graph form,
it is allowed that the same IRI u is declared to be all of
an individual name, and
a class name, and
either an object property name or a data property name.
According to I,
the IRI u will always denote the same individual in the universe IR,
where I(u) will be both a class and a property.
Under J, however,
the individual name u will denote an individual,
the class name u will denote a subset of ΔI,
and the property name u will denote a subset of ΔI × ΔI.
Literals occurring in G1 and G2
are mapped by the OWL 2 RDF mapping
to the same literals
in the corresponding interpreted language constructs
of F(G1) and F(G2),
which comprise
data enumerations,
has-value restrictions with a data value,
cardinality restrictions,
datatype restrictions,
data property assertions, and
negative data property assertions.
Also, the semantics of literals
is strictly analog for both
the OWL 2 RDF-Based Semantics and the OWL 2 Direct Semantics.
Therefore, literals need no further treatment in this proof.
Based on the premise that I OWL 2 RDF-Based satisfies G1,
it has to be shown that J OWL 2 Direct satisfies F(G1).
For this to hold
it will be sufficient to show that
J OWL 2 Direct satisfies every axiom occurring in F(G1).
Let A be an axiom occurring in F(G1),
and let gA be the subgraph of G1
that is mapped to A by the reverse OWL 2 RDF mapping.
It is possible to prove that
J OWL 2 Direct satisfies A
by showing that
the meaning,
which is given to A by the OWL 2 Direct Semantics,
is compatible with the semantic relationship
that,
according to J,
holds between the denotations of the names occurring in A.
The basic idea is as follows:
Since I OWL 2 RDF-Based satisfies G1,
all the triples occurring in gA are OWL 2 RDF-Based satisfied by I.
Also, since I is an OWL 2 RDF-Based interpretation,
all the OWL 2 RDF-Based semantic conditions are met by I.
Hence, the left-to-right directions
of all the semantic conditions
that are "matched" by the triples in gA will apply.
This will reveal certain semantic relationships
that,
according to I,
hold between the denotations of the names occurring in gA.
These semantic relationships are,
roughly speaking,
the semantic consequences of the axiom
that is encoded by the triples in gA.
Since the denotations w.r.t. J of all the names occurring in A
have been defined in terms of
the denotations and class and property extensions w.r.t. I
of the same names occurring in gA,
and since the meaning of the axiom A
w.r.t. the OWL 2 Direct Semantics
turns out to be fully covered
by the semantic consequences of the subgraph gA
w.r.t. the OWL 2 RDF-Based Semantics,
one can eventually show that J OWL 2 Direct satisfies A.
A special note is necessary for anonymous individuals occurring in an assertion A.
These have the form of the same blank node b
both in A and in gA.
Both the OWL 2 RDF-Based Semantics and the OWL 2 Direct Semantics
treat blank nodes as existential variables in an ontology.
Since I satisfies gA,
b can be mapped to an individual x in IR such that
gA becomes true under I
(see Section 1.5 in [RDF Semantics]
for the precise definition
on how blank nodes are treated in RDF based languages).
The same mapping from b to x can also be used for J
in order to OWL 2 Direct satisfy A.
This basic idea is now demonstrated in more detail
for a single example axiom A in F(G1),
which can be taken as a hint on
how a complete proof could be constructed in principle.
A complete proof
would need to take every language construct of OWL 2 into account,
as well as additional aspects such as datatype maps and facets.
As in the example below,
such a proof can make use of the observation
that the definitions of the OWL 2 Direct Semantics and the OWL 2 RDF-Based Semantics
are actually closely aligned
for all the different language constructs of OWL 2.
Let A = SubClassOf(ex:c1 ObjectUnionOf(ex:c2 ex:c3))
for IRIs ex:c1, ex:c2 and ex:c3
that are declared to be classes
elsewhere in F(G1).
Due to the reverse OWL 2 RDF mapping,
gA has the form
gA :
ex:c1 rdfs:subClassOf _:x .
_:x rdf:type owl:Class .
_:x owl:unionOf ( ex:c2 ex:c3 ) .
Since I is an OWL 2 RDF-Based interpretation,
it meets all the OWL 2 RDF-Based semantic conditions.
Since I OWL 2 RDF-Based satisfies G1,
all the triples in gA are OWL 2 RDF-Based satisfied,
and this triggers the left-to-right directions of the semantic conditions
for subclass axioms
(rdfs:subClassOf)
and union class expressions
(owl:unionOf).
This reveals that the denotations of the names in gA
are actually classes
I(ex:c1) ∈ IC ,
I(ex:c2) ∈ IC ,
I(ex:c3) ∈ IC ,
and that the following semantic relationship
holds between the extensions of these classes:
ICEXT(I(ex:c1))
⊆
ICEXT(I(ex:c2))
∪
ICEXT(I(ex:c3)) .
From applying the definition of J follows that
the following semantic relationship,
w.r.t. J,
holds between the denotations of the class names occurring in A:
(ex:c1) C
⊆
(ex:c2) C
∪
(ex:c3) C .
This semantic relationship equals the meaning of the
axiom A = SubClassOf(ex:c1 ObjectUnionOf(ex:c2 ex:c3))
w.r.t. the OWL 2 Direct Semantics.
Hence, J OWL 2 Direct satisfies A.
Since J OWL 2 Direct satisfies F(G1),
and since
F(G1) OWL 2 Direct entails F(G2),
it follows that
J OWL 2 Direct satisfies F(G2).
The next step will be
to show that I OWL 2 RDF-Based satisfies G2.
For this to hold,
I needs to OWL 2 RDF-Based satisfy all the triples occurring in G2,
taking into account the premise that an OWL 2 RDF-Based interpretation
is required to meet all the OWL 2 RDF-Based semantic conditions.
Since the pair
⟨ G1 , G2 ⟩
is balanced,
G2
contains a single ontology header
consisting of a single triple
"b rdf:type owl:Ontology"
with a blank node b,
and it does neither contain
annotations nor deprecation statements.
Hence,
F(G2) only consists of entity declarations and axioms,
and does not have any ontology IRI
and no ontology version, annotations or import directives.
Further,
since G2 is an OWL 2 DL ontology in RDF graph form,
every triple occurring in G2,
which is not the ontology header triple,
belongs to some subgraph of G2
that is mapped by the reverse OWL 2 RDF mapping
to one of the entity declarations or axioms
contained in F(G2).
For the ontology header triple
"b rdf:type owl:Ontology"
in G2:
Since G1 is an OWL 2 DL ontology in RDF graph form,
G1 contains an ontology header
containing a triple
"x rdf:type owl:Ontology",
where x is either an IRI or a blank node.
Since I OWL 2 RDF-Based satisfies G1,
this particular triple is satisfied by I.
From the semantic conditions of "Simple Entailment",
as defined in
[RDF Semantics],
follows that
the triple
"b rdf:type owl:Ontology"
with the existentially interpreted blank node b
is satisfied by I, too.
For entity declarations,
let A be an entity declaration in F(G2),
and let gA be the corresponding subgraph of G2.
Since the pair
⟨ G1 , G2 ⟩
is balanced,
A occurs in F(G1),
and hence gA is a subgraph of G1.
Since I OWL 2 RDF-Based satisfies G1,
I in particular OWL 2 RDF-Based satisfies gA.
For axioms,
let A be an axiom in F(G2),
and let gA be the corresponding subgraph of G2.
It is possible to prove
that I OWL 2 RDF-Based satisfies gA,
by showing that
all the premises for the right-to-left hand side
of the particular semantic conditions,
which are associated with the sort of axiom represented by gA,
are met.
This will allow to apply the semantic condition,
from which will follow that
all the triples in gA are OWL 2 RDF-Based satisfied by I.
The premises of the semantic condition
generally require
that the denotations of all the non-built-in names in gA
are contained in the appropriate part of the universe,
and that the semantic relationship
that is expressed on the right hand side of the semantic condition
actually holds between the denotations of all these names w.r.t. I.
Special care has to be taken
regarding the blank nodes occurring in gA.
The basic idea is as follows:
For every non-built-in IRI u occurring in gA,
u also occurs in A.
Since the pair
⟨ G1 , G2 ⟩
is balanced,
property (2) of the "Balanced"-definition provides that
there are entity declarations in F(G2)
for all the entity types of u,
each being of the form
E := "Declaration(T(u))"
for some entity type T.
From the reverse RDF mapping follows
that for each such declaration E
a typing triple e exists in G2,
being of the form e := "u rdf:type t",
where t is the name of a class
representing the part of the universe corresponding to the entity type T.
It has already been shown that
for E being an entity declaration in F(G2),
and e being the corresponding subgraph in G2,
I OWL 2 RDF-Based satisfies e.
Hence, I(u) is an individual contained in the appropriate part of the universe.
Further,
since J OWL 2 Direct satisfies F(G2),
J OWL 2 Direct satisfies A.
Therefore, the semantic relationship
that is represented by A according to the OWL 2 Direct Semantics
actually holds
between the denotations of the names occurring in A
w.r.t. J.
Since the denotations of these names w.r.t. J
have been defined in terms of
the denotations and class and property extensions w.r.t. I
of the same names in G2,
by applying the definition of J it will turn out
that the analog relationship also holds
between the denotations of the same names occurring in gA.
Finally,
for the blank nodes occurring in gA,
it becomes clear from the fact that
G2 is an OWL 2 DL ontology in RDF graph form
that only certain kinds of subgraphs of gA
can occur having blank nodes.
- Case 1: A blank node corresponds to some anonymous individual in A (for A being one of a class assertion, object property assertion or data property assertion, according to Sections 5.6, 9.5 and 11.2 in [OWL 2 Specification]). The same blank node is used in A, and J interprets it as an existential variable. This renders the semantic relationship that is expressed by A into an existential assertion. After applying the definition of J, the analog existential assertion holds w.r.t. I, with the same blank node as the same existential variable in gA.
- Case 2: A blank node is the "root" node of the multi-triple RDF encoding gA of A (for gA being an n-ary disjointness axiom from Section
5.115.10, or a negative property assertion from Section 5.15). The right-to-left direction of the semantic condition for this kind of axiom is of a form that the triples in gA containing the blank node will be OWL 2 RDF-Based satisfied after all the premises of the semantic condition are met.
- Case 3: A blank node is the "root" node of the multi-triple RDF encoding gE of an expression in A (for gE being either a sequence, or one of a boolean connective from Section 5.4, an enumeration from Section 5.5, a property restriction from Section 5.6, or a datatype restriction from Section 5.7). Since the pair ⟨ G1 , G2 ⟩ is balanced, gE also occurs in G1. Since I OWL 2 RDF-Based satisfies G1, gE is OWL 2 RDF-Based satisfied, either, taking into account that blank nodes are existential variables. Hence, the left-to-right direction of the respective semantic condition for the particular sort of expression can be applied. This can be done for all the expressions occurring in gA, and gA can be seen as a directed acyclic graph with the triples encoding the actual axiom on top, and the different component expressions being connected via blank nodes. Eventually, one can see that all the premises of the right-to-left direction of the semantic condition for the axiom encoded by gA hold.
This basic idea is now demonstrated in more detail
for a single example axiom A in F(G2),
which can be taken as a hint on
how a complete proof could be constructed in principle.
A complete proof
would need to take every language construct of OWL 2 into account,
as well as additional aspects such as datatype maps and facets.
As in the example below,
such a proof can make use of the observation
that the definitions of the OWL 2 Direct Semantics and the OWL 2 RDF-Based Semantics
are actually closely aligned
for all the different language constructs of OWL 2.
Let A = SubClassOf(ex:c1 ObjectUnionOf(ex:c2 ex:c3))
for IRIs
ex:c1,
ex:c2 and
ex:c3
that are declared to be classes
elsewhere in F(G2).
Due to the reverse OWL 2 RDF mapping,
gA has the form
gA :
ex:c1 rdfs:subClassOf _:x .
_:x rdf:type owl:Class .
_:x owl:unionOf ( ex:c2 ex:c3 ) .
The entity declarations for the class names
ex:c1,
ex:c2 and
ex:c3
occurring in both A and gA
correspond to the typing triples
ex:c1 rdf:type owl:Class .
ex:c2 rdf:type owl:Class .
ex:c3 rdf:type owl:Class .
in G2,
respectively.
Based on the premise that the pair
⟨ G1 , G2 ⟩
is balanced,
all these typing triples are OWL 2 RDF-Based satisfied by I.
Hence, all of the IRIs denote classes:
I(ex:c1) ∈ IC ,
I(ex:c2) ∈ IC and
I(ex:c3) ∈ IC .
Since J OWL 2 Direct satisfies A,
the following semantic relationship
holds between the denotations of the class names in A w.r.t. J:
(ex:c1) C
⊆
(ex:c2) C
∪
(ex:c3) C .
Applying the definition of J
results in the following semantic relationship w.r.t. I
that holds between the denotations of the names in gA:
ICEXT(I(ex:c1))
⊆
ICEXT(I(ex:c2))
∪
ICEXT(I(ex:c3)) .
The subgraph gE of gA,
given by
gE :
_:x rdf:type owl:Class .
_:x owl:unionOf ( c2 c3 ) .
corresponds to a union class expression in A.
Since the pair
⟨ G1 , G2 ⟩
is balanced,
gE is also a subgraph of G1
(it will be assumed that
the same blank nodes are used
in both instances of gE
in order to simplify the argument).
Since both G1 and G2
are OWL 2 DL ontologies in RDF graph form,
the blank nodes occurring in gE
do not occur outside of gE,
neither in G1 nor in G2.
Since I OWL 2 RDF-Based satisfies G1,
according to the semantic conditions for RDF graphs with blank nodes
(see Section 1.5 of [RDF Semantics]),
a mapping B from blank(gE) to IR exists,
where blank(gE) is the set of all blank nodes in gE,
such that the extended interpretation I+B OWL 2 RDF-Based satisfies all the triples in gE.
An analog argument holds for all the blank nodes
occurring in the sequence expression ( c2 c3 ).
This allows to apply the left-to-right direction
of the semantic condition for union class expressions
(owl:unionOf),
providing:
[I+B](_:x) ∈ IC ,
ICEXT([I+B](_:x))
=
ICEXT(I(ex:c2))
∪
ICEXT(I(ex:c3)) .
Together with the intermediate results from above,
it follows:
I(ex:c1) ∈ IC ,
[I+B](_:x) ∈ IC ,
ICEXT(I(ex:c1))
⊆
ICEXT([I+B](_:x)) .
Therefore, all the premises are met
to apply the right-to-left direction of the semantic condition of subclass axioms
(rdfs:subClassOf),
which results in
⟨ I(ex:cl) , [I+B](_:x) ⟩
∈
IEXT(I(rdfs:subClassOf)) .
So,
the triple
ex:c1 rdfs:subClassOf _:x .
is OWL 2 RDF-Based satisfied by I+B,
where "_:x" is the same blank node
as the root blank node of the union class expression in gA.
Hence,
w.r.t. existential blank node semantics,
I OWL 2 RDF-Based satisfies all the triples in gA.
To conclude,
for every OWL 2 RDF-Based interpretation I
that OWL 2 RDF-Based satisfies G1
it turns out that I also OWL 2 RDF-Based satisfies G2.
Hence,
G1 OWL 2 RDF-Based entails G2.
Q.E.D.
8 Appendix: Comprehension Conditions (Informative)
The correspondence theorem
in Section 7.2
shows
that it is possible for the OWL 2 RDF-Based Semantics
to reflect all the entailments of the OWL 2 Direct Semantics
[OWL 2 Direct Semantics],
provided that one allows for certain "harmless" syntactic transformations
on the RDF graphs being considered.
This makes numerous potentially desirable and useful entailments available
that would otherwise be outside the scope of the OWL 2 RDF-Based Semantics,
for the technical reasons discussed in
Section 7.1.
It seems natural to ask for similar entailments
even
when an entailment query
does not formallyconsist of OWL 2 DL ontologies in RDF graph form.
However,
the correspondence theorem does not apply to such cases,
and thus the OWL 2 Direct Semantics cannot be taken
as a reference frame
for "desirable" orand "useful" entailments,
or for what it means thatwhen a givengraph transformation
iscan be considered "harmless" or not.
As discussed in
Section 7.1,
a core obstacle for the correspondence theorem to hold
waswere RDF encodings of OWL 2 expressions,
such as union class expressions,
whichwhen they appear on the right hand side of an entailment query.
Under the OWL 2 RDF-Based Semantics,
it is not generally ensured that an individual exists thatexists,
which represents the denotation of such an expression.
The "comprehension principles"conditions" defined in this section
are additional semantic conditions
that provide forthe necessary individuals
for every possible list,sequence, class and property expression.
By this,
the combination
of the normative semantic conditions of the OWL 2 RDF-Based Semantics
(Section 5)
and the comprehension conditions
can be regarded to "simulate" the semantic expressivity
of the OWL 2 Direct Semantics
on OWL 2 DLentailment queries, while at the same time allowing for the interpretationqueries consisting of arbitrary entailment queries.RDF graphs.
The combined semantics is,
however,
not primarily intended for use in actual implementations.
The comprehension conditions add significantly
to the complexity and expressivity
of the basic semantics
and,
in fact,
have proven to
lead to formal inconsistency.
But
the combined semantics
can still be seen as a generalized reference frame
for "desirable" and "useful" entailments,
and this can be used,
for example,
to evaluate methods that syntactically transform unrestricted entailment queries
in order to receive additional entailments under the OWL 2 RDF-Based Semantics.
Such a concrete method is, however,
outside the scope of this specification.
Note:
The conventions
in the introduction of
Section 5 ("Semantic Conditions")
apply to the current section as well.
8.1 Comprehension Conditions for Sequences
Table 8.1
lists the comprehension conditions for sequences,
i.e. RDF lists.
These comprehension conditions provide the existence
of sequences
built from any possiblefinite combination of individuals
contained in the universe.
Table 8.1: Comprehension Conditions for Sequences
| if
| then exists z1 , … , zn ∈ IR
|
| a1 , … , an ∈ IR
| ⟨ z1 , a1 ⟩ ∈ IEXT(I(rdf:first)) , ⟨ z1 , z2 ⟩ ∈ IEXT(I(rdf:rest)) , … ,
⟨ zn , an ⟩ ∈ IEXT(I(rdf:first)) , ⟨ zn , I(rdf:nil) ⟩ ∈ IEXT(I(rdf:rest))
|
8.2 Comprehension Conditions for Boolean Connectives
Table 8.2
lists the comprehension conditions for
boolean connectives
(see Section 5.4
for the corresponding semantic conditions).
These comprehension conditions provide the existence
of complement classes for any class,
and of unions andintersections and unions
built from any possiblefinite set of classes
contained in the universe.
Table 8.2: Comprehension Conditions for Boolean Connectives
| if
| then exists z ∈ IR
|
s sequence of c ∈ IC ⟨ z1 , … , c ⟩ ∈ IEXT( I ( owl:complementOf )) dn ∈ IDCIC
| ⟨ z , ds ⟩ ∈ IEXT(I( owl:datatypeComplementOfowl:intersectionOf))
|
| s sequence of c1 , … , cn ∈ IC
| ⟨ z , s ⟩ ∈ IEXT(I( owl:intersectionOfowl:unionOf))
|
s sequence ofc 1 , …∈ IC
| ⟨ z , c n⟩ ∈ ICIEXT(I(owl:complementOf))
|
| d ∈ IDC
| ⟨ z , sd ⟩ ∈ IEXT(I( owl:unionOfowl:datatypeComplementOf))
|
8.3 Comprehension Conditions for Enumerations
Table 8.3
lists the comprehension conditions for
enumerations
(see Section 5.5
for the corresponding semantic conditions).
These comprehension conditions provide the existence
of enumeration classes
built from any possiblefinite set of individuals
contained in the universe.
Table 8.3: Comprehension Conditions for Enumerations
| if
| then exists z ∈ IR
|
| s sequence of a1 , … , an ∈ IR
| ⟨ z , s ⟩ ∈ IEXT(I(owl:oneOf))
|
8.4 Comprehension Conditions for Property Restrictions
Table 8.4
lists the comprehension conditions for
property restrictions
(see Section 5.6
for the corresponding semantic conditions).
These comprehension conditions provide the existence
of cardinality restriction classesrestrictions
on any property and for any non-negative integer,
as well as value restriction classesrestrictions
on any property and on any class
contained in the universe.
Note that the comprehension conditions for self restrictions
constrains the right hand side of
the produced owl:hasSelf assertions
to be the boolean value
"true"^^xsd:boolean.
This is in accordance with
Table 13 in Section 3.2.4 of [OWL 2 RDF Mapping].
Implementations are not required
to support the comprehension conditions for
owl:onProperties,
but
MAY
support them
in order to realize
n-ary dataranges with arity ≥ 2
(see Section 7 of
[OWL 2 Specification]
for further information).
Table 8.4: Comprehension Conditions for Property Restrictions
| if
| then exists z ∈ IR
|
p ∈ IP ⟨ z , I ( "true"^^xsd:boolean ) ⟩ ∈ IEXT( I ( owl:hasSelf )) , ⟨ z , p ⟩ ∈ IEXT( I ( owl:onProperty ))c ∈ IC ,
p ∈ IP
| ⟨ z , c ⟩ ∈ IEXT(I( owl:allValuesFromowl:someValuesFrom)) ,
⟨ z , p ⟩ ∈ IEXT(I(owl:onProperty))
|
c ∈ IC ,
s sequence of p1 , … , pn ∈ IP , n ≥ 1
| ⟨ z , c ⟩ ∈ IEXT(I( owl:allValuesFromowl:someValuesFrom)) ,
⟨ z , s ⟩ ∈ IEXT(I(owl:onProperties))
|
c ∈ IC ,
p ∈ IP
| ⟨ z , c ⟩ ∈ IEXT(I( owl:someValuesFromowl:allValuesFrom)) ,
⟨ z , p ⟩ ∈ IEXT(I(owl:onProperty))
|
c ∈ IC ,
s sequence of p1 , … , pn ∈ IP , n ≥ 1
| ⟨ z , c ⟩ ∈ IEXT(I( owl:someValuesFromowl:allValuesFrom)) ,
⟨ z , s ⟩ ∈ IEXT(I(owl:onProperties))
|
a ∈ IR ,
p ∈ IP
| ⟨ z , a ⟩ ∈ IEXT(I(owl:hasValue)) ,
⟨ z , p ⟩ ∈ IEXT(I(owl:onProperty))
|
| p ∈ IP
| ⟨ z , I("true"^^xsd:boolean) ⟩ ∈ IEXT(I(owl:hasSelf)) ,
⟨ z , p ⟩ ∈ IEXT(I(owl:onProperty))
|
n ∈ INNI ,
p ∈ IP
| ⟨ z , n ⟩ ∈ IEXT(I( owl:cardinalityowl:minCardinality)) ,
⟨ z , p ⟩ ∈ IEXT(I(owl:onProperty))
|
n ∈ INNI ,
p ∈ IP
| ⟨ z , n ⟩ ∈ IEXT(I( owl:minCardinalityowl:maxCardinality)) ,
⟨ z , p ⟩ ∈ IEXT(I(owl:onProperty))
|
n ∈ INNI ,
p ∈ IP
| ⟨ z , n ⟩ ∈ IEXT(I( owl:maxCardinalityowl:cardinality)) ,
⟨ z , p ⟩ ∈ IEXT(I(owl:onProperty))
|
n ∈ INNI ,
c ∈ IC ,
p ∈ IP
| ⟨ z , n ⟩ ∈ IEXT(I( owl:qualifiedCardinalityowl:minQualifiedCardinality)) ,
⟨ z , c ⟩ ∈ IEXT(I(owl:onClass)) ,
⟨ z , p ⟩ ∈ IEXT(I(owl:onProperty))
|
n ∈ INNI ,
d ∈ IDC ,
p ∈ IODP
| ⟨ z , n ⟩ ∈ IEXT(I( owl:qualifiedCardinalityowl:minQualifiedCardinality)) ,
⟨ z , d ⟩ ∈ IEXT(I(owl:onDataRange)) ,
⟨ z , p ⟩ ∈ IEXT(I(owl:onProperty))
|
n ∈ INNI ,
c ∈ IC ,
p ∈ IP
| ⟨ z , n ⟩ ∈ IEXT(I( owl:minQualifiedCardinalityowl:maxQualifiedCardinality)) ,
⟨ z , c ⟩ ∈ IEXT(I(owl:onClass)) ,
⟨ z , p ⟩ ∈ IEXT(I(owl:onProperty))
|
n ∈ INNI ,
d ∈ IDC ,
p ∈ IODP
| ⟨ z , n ⟩ ∈ IEXT(I( owl:minQualifiedCardinalityowl:maxQualifiedCardinality)) ,
⟨ z , d ⟩ ∈ IEXT(I(owl:onDataRange)) ,
⟨ z , p ⟩ ∈ IEXT(I(owl:onProperty))
|
n ∈ INNI ,
c ∈ IC ,
p ∈ IP
| ⟨ z , n ⟩ ∈ IEXT(I( owl:maxQualifiedCardinalityowl:qualifiedCardinality)) ,
⟨ z , c ⟩ ∈ IEXT(I(owl:onClass)) ,
⟨ z , p ⟩ ∈ IEXT(I(owl:onProperty))
|
n ∈ INNI ,
d ∈ IDC ,
p ∈ IODP
| ⟨ z , n ⟩ ∈ IEXT(I( owl:maxQualifiedCardinalityowl:qualifiedCardinality)) ,
⟨ z , d ⟩ ∈ IEXT(I(owl:onDataRange)) ,
⟨ z , p ⟩ ∈ IEXT(I(owl:onProperty))
|
8.5 Comprehension Conditions for Datatype Restrictions
Table 8.5
lists the comprehension conditions for
datatype restrictions
(see Section 5.7
for the corresponding semantic conditions).
These comprehension conditions provide the existence
of datatypes
built from restricting any datatype
contained in the universe
by any possiblefinite set of facet-value pairs
contained in the facet space
(see Section 4.1)
of the original datatype.
The set IFS is defined in
Section 5.7.
Table 8.5: Comprehension Conditions for Datatype Restrictions
| if
| then exists z ∈ IR , s sequence of z1 , … , zn ∈ IR
|
d ∈ IDC ,
f1 , … , fn ∈ IODP ,
v1 , … , vn ∈ LV ,
⟨ f1 , v1 ⟩ , … , ⟨ fn , vn ⟩ ∈ IFS(d)
| ⟨ z , d ⟩ ∈ IEXT(I(owl:onDatatype)) ,
⟨ z , s ⟩ ∈ IEXT(I(owl:withRestrictions)) ,
⟨ z1 , v1 ⟩ ∈ IEXT(f1) , … , ⟨ zn , vn ⟩ ∈ IEXT(fn)
|
8.6 Comprehension Conditions for Inverse Property ExpressionsProperties
Table 8.6
lists the comprehension conditions for
inverse property expressions.
These comprehension conditions provide the existence
of an inverse property for any property
contained in the universe.
Inverse property expressions can be used
to build axioms with anonymous inverse properties,
such as in the graph
_:x owl:inverseOf ex:p .
_:x rdfs:subPropertyOf owl:topObjectProperty .
Note that,
to some extent,
the OWL 2 RDF-Based Semantics already covers the use of inverse property expressions
by means of the semantic conditions of inverse property axioms
(see Section 5.12),
since these semantic conditions also apply to an existential variablesvariable
on the left hand side of an inverse property axioms. However,axiom.
Nevertheless,
not all relevant cases are covered by this semantic condition.
For example,
one might expect the above example graph
to be generally true.
ButHowever,
the OWL 2 RDF-Based Semantics doesnormative semantic conditions
do not permit this conclusion,
since it is not ensured that
for every property p
there is an individual in the universe
that happens to be the inverse property of p.
Table 8.6: Comprehension Conditions for Inverse Property ExpressionsProperties
| if
| then exists z ∈ IR
|
| p ∈ IP
| ⟨ z , p ⟩ ∈ IEXT(I(owl:inverseOf))
|
9 Appendix: Changes from theOWL 1 RDF-Compatible Semantics(Informative)
This section lists relevant differences
between the OWL 2 RDF-Based Semantics and the original specification of the OWL 1 RDF-Compatible Semantics
[OWL 1 RDF-Compatible Semantics].
Significant effort has been spent
in keeping the design of the OWL 2 RDF-Based Semantics
as close as possible
to that of the OWL 1 RDF-Compatible Semantics.
While this aim was achieved to a large degree,
the OWL 2 RDF-Based Semantics actually deviates from the OWL 1 RDF-Compatible Semanticsits predecessor in several aspects,
in most cases due to serious technical problems
that would arisehave arisen
from a conservative semantic extension.
Not listed are
the new language constructs and the new datatypes of OWL 2.
The following markers are used:
- [DEV]: A deviation from the OWL 1 RDF-Compatible Semantics that formally breaks backwards compatibility.
- [EXT]: An extension to the OWL 1 RDF-Compatible Semantics that is backwards compatible.
- [NOM]: A change of the nomenclature
used incompared to that being used in the OWL 1 RDF-Compatible Semantics.
Generalized Graph Syntax [EXT]:
The OWL 2 RDF-Based Semantics
allows RDF graphs to contain
IRIs [RFC 3987]
(see Section 2.1),
whereas the OWL 1 RDF-Compatible Semantics was restricted to RDF graphs with
URIs [RFC 2396].
This change is in accordance with the rest of the OWL 2 specification, seespecification
(see Section 2.4 of [OWL 2 Specification ].]).
In addition,
the OWL 2 RDF-Based Semantics
MAYis now explicitly allowed to
be applied to RDF graphs containing
"generalized" RDF triples,
i.e. triples that can consist of
IRIs, literals or blank nodes
in all three positions
(Section 2.1 ).),
although implementations are not required to support this.
In contrast,
the OWL 1 RDF-Compatible Semantics was restricted to RDF graphs
conforming to the RDF Concepts specification
[RDF Concepts].
These limitations of the OWL 1 RDF-Compatible Semantics
were actually inherited from the
RDF Semantics specification
[RDF Semantics].
The relaxations are intended to warrant interoperability
with existing and future technologies and tools.
Both changes are compatible with theOWL 1 RDF-Compatible Semantics,1,
since all RDF graphs that were legal forunder the OWL 1 RDF-Compatible Semantics
are still legal under the OWL 2 RDF-Based Semantics.
Datatype Facets [EXT]:
The basic definitions of a datatype and a D-interpretation,
as defined by the RDF Semantics specification
and as applied by the OWL 1 RDF-Compatible Semantics,
have been extended
in Section 4 of the OWL 2 RDF-Based Semanticsto take datatypeconstraining facets into account. Facets are appliedaccount
(see Section 4),
in connection with a new language construct of OWL 2, called "datatype restrictions"order to allow for datatype restrictions
as specified in Section 5.7.
This change is compatible with theOWL 1 RDF-Compatible Semantics,1,
since Section 5.1
of the RDF Semantics specification
explicitly allows for extending the minimal datatype definition provided there.
Correspondence Theorem and Comprehension Conditions [DEV]:
The comprehensionsemantic conditions of the OWL 1 RDF-Compatible Semantics included
a set of so called
"comprehension conditions" .,
which allowed to show the original
"correspondence theorem"
stating that every entailment of OWL 2 RDF-Based Semantics extends this set by semantic1 DL was also an entailment of OWL 1 Full.
The document at hand adds comprehension conditions
for the new language constructs of OWL 2, see2
(see Section 8 .).
However,
the comprehension conditions
are not a normative aspect of the OWL 2 RDF-Based Semantics
anymore.
It has turned out
that combining the comprehension conditions
with the normative set of semantic conditions in
Section 5
would lead to formal inconsistency of the resulting languagesemantics
(Issue 119).
Further,In the OWL 1 RDF-Compatible Semantics specification, the comprehension conditions were primarily used to ensure the correctness of the so called "correspondence theorem" . However,addition,
it became clear that
a correspondence theorem along the lines of the original theorem
would not work for the relationship between the
OWL 2 RDF-Based Semantics and the
OWL 2 Direct Semantics [OWL 2 Direct Semantics],
since it is not possible to "balance" the differences between
the two semantics
solely by means of additional semantic conditions
(see Section 7.1).
Consequently,
the correspondence theorem
of the OWL 2 RDF-Based Semantics
(Section 7.2)
follows an alternative approach
that replaces the use of the comprehension conditions,conditions
and whichcan be seen as a technical refinement
of an idea
originally discussed by the WebOnt Working Group
(email).
This change is an incompatible deviation from theOWL 1 RDF-Compatible Semantics,1,
since certain aspects of the originally normative definition of the semantics
have been removed.
Flawed Semantics of Language Constructs with Argument Lists [DEV]:
In the OWL 1 RDF-Compatible Semantics,
the semantic conditions for
unions, intersections and enumerations of classes
hadwere defined in a flawed definitions thatform,
which lead to formal inconsistency of the OWL 1 RDF-Compatiblesemantics
(Issue 120;
see also an unofficial
problem description).
TheseThe affected semantic conditions have been corrected for the OWL 2 RDF-Based Semantics by changing the form of the semantic conditions,revised;
see
Section 5.4
and
Section 5.5.
This change is an incompatible deviation from theOWL 1 RDF-Compatible Semantics,1,
since the semantics has formally been weakened
by eliminatingin order to eliminate a source of inconsistency.
Incomplete Semantics of owl:AllDifferent [EXT]:
The OWL 1 RDF-Compatible Semantics missed a certain semantic condition
for axioms based on the vocabulary term "owl:AllDifferent"
(see also an unofficial
problem description).
The missing semantic condition
has been added to the OWL 2 RDF-Based Semantics
in(see Section 5.11 .5.10).
This change is compatible with theOWL 1 RDF-Compatible Semantics,1,
since the semantics has been conservatively extended.
Aligned Semantics of owl:DataRange and rdfs:Datatype [EXT]:
The class
owl:DataRange
has been made an equivalent class
to rdfs:Datatype
in the OWL 2 RDF-Based Semantics(see Section 5.2).
The main purpose for this change was
to allow for the deprecation of the term
owl:DataRange
in favor of rdfs:Datatype.
This change is compatible with OWL 1
according to an analysis
of the relationship between the two classes
ofin the OWL 1 RDF-Compatible Semantics
has been analyzed in(email).
This change is compatible with the OWL 1 RDF-Compatible Semantics according to this analysis. Weakened Semantics ofNon-Empty Data Value Enumerations [DEV]:
The application of thesemantic condition for enumerations of data values
in Section 5.5
is now restricted to non-empty sets of data values only.values.
This prevents the class owl:Nothing
from unintentionally becoming an instance
of the class rdfs:Datatype,
as analyzed in
(email).
This weakeningrestriction of the semantics
is an incompatible deviation from theOWL 1 RDF-Compatible Semantics. Note1.
Note, however,
that this change doesit is still permit the definition ofpossible
to define an empty enumeration with an explicitly given type rdfs:Datatypeof data values,
as explained in Section 5.5.
Terminological Clarifications [NOM]:
TheThis document uses the term "OWL 2 RDF-Based Semantics"
to refer to the specified semantics only.
According to Section 2.1,
the term "OWL 2 Full"
refers to the whole language
that is determined
by the set of RDF graphs
(also called "OWL 2 Full ontologies")
being interpreted using the OWL 2 RDF-Based Semantics.
OWL 1 has not been particularly clear on this distinction.
Where the OWL 1 RDF-Compatible Semantics specification talked about
"OWL Full interpretations",
"OWL Full satisfaction",
"OWL Full consistency"
and
"OWL Full entailment",
the OWL 2 RDF-Based Semantics Specification talks
in Section 4
about
"OWL 2 RDF-Based interpretations",
"OWL 2 RDF-Based satisfaction",
"OWL 2 RDF-Based consistency"
and
"OWL 2 RDF-Based entailment",
respectively,
since these terms are primarily meant to be related to
the OWL 2 RDF-Based Semantics.semantics
rather than the whole language.
Modified Abbreviations [NOM]:
The names
"RI", "PI", "CI",
"EXTI", "CEXTI",
"SI", "LI" and "LVI"
have been changed toreplaced by the corresponding names
defined in the RDF Semantics document [RDF Semantics],
namely "IR", "IP", "IC", "IEXT", "ICEXT", "IS", "IL" and "LV", respectively.
Furthermore,
all uses of the IRI mapping "IS"
have been replaced by the more general interpretation mapping "I",
following the conventions in the RDF Semantics document.
These changes are intended to support
the use of the OWL 2 RDF-Based Semantics document
as an incremental editorialextension
of the RDF Semantics document.
Names for the "parts of the universe"
that were exclusively used in the OWL 1 RDF-Compatible Semantics document,
such as "IX" or "IODP",
have not been changed.
Additional names for class extensions,Other abbreviations,
such as "IAD" for the class extension of owl:AllDifferent,
have in general not been reused in the document at hand,
but the explicit non-abbreviated form,
such as
"IEXT(I(owl:AllDifferent))",
is used instead.
Deprecated Vocabulary Terms [NOM]:
The following vocabulary terms have been deprecated as of OWL 2
by the Working Group,
and SHOULD NOT be used
in new ontologies anymore:
10 Appendix: Post Last-Call Changes from the Last Public Working Draft(Informative)
This section lists significantChanges sincefrom the
Second PublicLast Call Working Draft
of 02 December 2008. Section 1 "Introduction": Better clarifies the document's purpose at the beginning of the section. Reflects the chronology of the document21 April 2009:
- Renamed annotation vocabulary terms "owl:subject", "owl:predicate" and
explains each section. A diagram has been added showing the parts hierarchy. Many clarifications, partially due to feedback. Section 2 "Ontologies" (was Section 3): Now mainly talks about the graph syntax. No normative treatment of non-semantic aspects of OWL 2 anymore. In particular, no separate definition of an "imports closure" anymore. Section 3 "Vocabulary" (was Section 2): Section restructured into subsections. A table of standard prefixes has been added to the section. Section 4 "Interpretations": Restructured into subsections. Better alignment with the treatment of facets of datatypes with the treatment in the Direct Semantics. The definition of "satisfaction" has been made more explicit. Section 5 "Semantic Conditions": The introduction part has been cleaned up"owl:object" to better distinguish between a "conventions" part and an informative "notes" part. The "notes" part now explains the distinction between "if-and-only-if""owl:annotatedSource", "owl:annotatedProperty" and "if-then" semantic conditions. The preceding texts of all tables have been revised, partially based on feedback. Section 6 "Axiomatic Triples" (was Section 7): Section restructured into sub sections. Whole section revised for better understandability. Section 7 "Comparison with the Direct Semantics" (was Section 6): The formulation of"owl:annotatedTarget", respectively (per WG resolution).
- Replaced the
correspondence theorem does not takedatatype "rdf:text" by "rdf:PlainLiteral" (per WG resolution).
- Replaced the
comprehension conditions into account anymore, but follows a different approach. A proof sketch forfacet "rdf:langPattern" by "rdf:langRange", following the correspondence theorem has been constructed.same replacement in the example on the differences between the two semantics has been rewritten, to address both feedback and the changed correspondence theorem. The whole section has been marked as "informative". Section 8 "Comprehension Conditions" (was Section 6.2): The comprehension conditions have been moved into their own section, since they are not directly related to the relationship between the two semantics anymore. Added a comprehension condition for inverse property expressions. Section 9 "Changes from the OWL 1 RDF-Compatible Semantics" (was Section 9.2): Now completed. Implementation of WG resolutions and WG-internal reviews: Changed RDF encoding of sub property chain axioms to single triple form according to WG Resolution with addendum on LC Comment 34 (TQ / "Property chain inclusion axioms"). Updated document to new notion of datatype definitions (per WG resolution ). Removed datatype owl:realPlus from the language (per WG resolution ). There are now two time related datatypes, xsd:dateTime and the new xsd:dateTimeStamp (per WG resolution at TC of 1st April 2009). Added ontology property owl:versionIRI to language (per WG resolution at TC of 8th April 2009). Updated all occurrences of Functional Syntax expressions to follow changes to "strongly typed" syntax (per WG resolution ). All references to the term "URI" have been replaced by the term "IRI" [ RFC 3987 ], in accordance with the rest of the OWL 2 documents. All inlined RDF statements are written in Turtle-style syntax (per WG resolution ). Changed use of term "lexical value" to "lexical form" according to WG Resolution on LC Comment 16 ("lexical value"). Changed "arbitrary object" to "arbitrary data value" in the definition of a facet space (per LC response on LC comment 8 ). Citing [ OWL 2 Specification ] for abbreviation method of IRIs (per WG Resolution : "OWL will not rely on CURIEs spec but will define it's own IRI abbreviation mechanism compatible with the one used by SPARQL"). Clearly distinguished between the term "OWL 2 RDF-Based Semantics" for the specified semantics and the term "OWL 2 Full" for the language resulting from interpreting RDF graphs by using the OWL 2 RDF-Based Semantics, as a result of WG discussion based on several LC comments. Other names have been adjusted accordingly. The class extension of owl:NamedIndividual has been weakened to only be a subset of the domain, instead of being equal to the domain (per WG-internal review comment). Other non-editorial changes: The semantic condition and the comprehension condition for datatype restrictions have been revised, mainly due to the alignment of the treatment of facets to the treatment in the Direct Semantics. Changed semantic condition for owl:datatypeComplementOf from an "if-and-only-if" condition into an "if-then" condition, since this is sufficient for proving the correspondence theorem, and better matches the general strategy when to have "if-then" conditions. The semantic conditions on n-aryoriginal "rdf:PlainLiteral" specification.
- Changed range of property
restrictions have been extended"owl:annotatedProperty" from IP to treat general classes and properties,IR in order to be better in line with the unary value restrictions, and toavoid backwards compatibility problem in future versionsundesired semantic side effects from annotations. This was an oversight when the original semantic conditions for annotations of OWL. Other editorial changes: Renamed "comprehension principles" into "comprehension conditions" as inaxioms and annotations were removed from the OWL 1 RDF-Compatible Semantics. Changed terminology: "boolean class expressions" are now called "boolean connectives" to better matchdocument.
- Explained the
restoptional status of the OWL 2 specification.semantic conditions concerned with the RDF Semantics term "datatype value" has been substituted by "data value",IRI "owl:onProperties", in accordance with the rest of the OWL 2 spec.specification.
- The
rendering ofsemantic conditions and comprehension conditions for the formulae is now more similarn-ary property restrictions have been changed to that in the OWL 2 Direct Semantics [ OWL 2 Direct Semantics ]. Better alignmentonly cover property sequences of length greater than 0, since the orderingmeaning of semantic conditionsan expression with an empty property set is not clear.
- Shortened and clarified some section titles, moved the
Direct Semantics document. Revision of the layout of complex tables. Other corrections of errors: Sequence expressions are now also definedsection on semantic conditions for zero elements (as in the OWL 1 RDF-Compatible Semantics). Explicit mentioning that plain literals are also contained insub property chains within Section 5, and aligned the set LVentry order of a D-interpretation (asall tables in the OWL 1 RDF-Compatible Semantics).Section 8 with those in Section 5.
- Several editorial clarifications, minor corrections and cosmetic changes.
11 Acknowledgments
The starting point for the development of OWL 2 was the OWL1.1 member submission, itself a result of user and developer feedback, and in particular of information gathered during the OWL Experiences and Directions (OWLED) Workshop series. The working group also considered postponed issues from the WebOnt Working Group.
This document has been produced by the OWL Working Group (see below), and its contents reflect extensive discussions within the Working Group as a whole.
The editors extend special thanks to
Jie Bao (RPI),
Ivan Herman (W3C/ERCIM),
Peter F. Patel-Schneider (Bell Labs Research, Alcatel-Lucent) and
Zhe Wu (Oracle Corporation)
for their thorough reviews.
The regular attendees at meetings of the OWL Working Group at the time of publication of this document were:
Jie Bao (RPI),
Diego Calvanese (Free University of Bozen-Bolzano),
Bernardo Cuenca Grau (Oxford University),
Martin Dzbor (Open University),
Achille Fokoue (IBM Corporation),
Christine Golbreich (Université de Versailles St-Quentin and LIRMM),
Sandro Hawke (W3C/MIT),
Ivan Herman (W3C/ERCIM),
Rinke Hoekstra (University of Amsterdam),
Ian Horrocks (Oxford University),
Elisa Kendall (Sandpiper Software),
Markus Krötzsch (FZI),
Carsten Lutz (Universität Bremen),
Deborah L. McGuinness (RPI),
Boris Motik (Oxford University),
Jeff Pan (University of Aberdeen),
Bijan Parsia (University of Manchester),
Peter F. Patel-Schneider (Bell Labs Research, Alcatel-Lucent),
Sebastian Rudolph (FZI),
Alan Ruttenberg (Science Commons),
Uli Sattler (University of Manchester),
Michael Schneider (FZI),
Mike Smith (Clark & Parsia),
Evan Wallace (NIST),
andZhe Wu (Oracle Corporation).Corporation), and
Antoine Zimmermann (DERI Galway).
We would also like to thank past members of the working group:
Jeremy Carroll,
Jim Hendler,
Vipul Kashyap.
12 References
- [OWL 2 Direct Semantics]
- OWL 2 Web Ontology Language: Direct Semantics Boris Motik, Peter F. Patel-Schneider, Bernardo Cuenca Grau, eds. W3C
Working Draft, 21 AprilCandidate Recommendation, 11 June 2009, http://www.w3.org/TR/2009/WD-owl2-semantics-20090421/http://www.w3.org/TR/2009/CR-owl2-direct-semantics-20090611/. Latest version available at http://www.w3.org/TR/owl2-semantics/http://www.w3.org/TR/owl2-direct-semantics/. - [OWL 2 RDF Mapping]
- OWL 2 Web Ontology Language: Mapping to RDF Graphs Peter F. Patel-Schneider, Boris Motik, eds. W3C
Working Draft, 21 AprilCandidate Recommendation, 11 June 2009, http://www.w3.org/TR/2009/WD-owl2-mapping-to-rdf-20090421/http://www.w3.org/TR/2009/CR-owl2-mapping-to-rdf-20090611/. Latest version available at http://www.w3.org/TR/owl2-mapping-to-rdf/. - [OWL 2 Specification]
- OWL 2 Web Ontology Language: Structural Specification and Functional-Style Syntax Boris Motik, Peter F. Patel-Schneider, Bijan Parsia, eds. W3C
Working Draft, 21 AprilCandidate Recommendation, 11 June 2009, http://www.w3.org/TR/2009/WD-owl2-syntax-20090421/http://www.w3.org/TR/2009/CR-owl2-syntax-20090611/. Latest version available at http://www.w3.org/TR/owl2-syntax/. - [OWL 1 RDF-Compatible Semantics]
- OWL Web Ontology Language: Semantics and Abstract Syntax, Section 5. RDF-Compatible Model-Theoretic Semantics. Peter F. Patel-Schneider, Patrick Hayes, and Ian Horrocks, eds., W3C Recommendation, 10 February 2004.
- [RDF Concepts]
- Resource Description Framework (RDF): Concepts and Abstract Syntax. Graham Klyne and Jeremy J. Carroll,
eds.,eds. W3C Recommendation, 10 February 2004.2004, http://www.w3.org/TR/2004/REC-rdf-concepts-20040210/. Latest version available as http://www.w3.org/TR/rdf-concepts/.
- [RDF Semantics]
- RDF Semantics. Patrick Hayes, ed., W3C Recommendation, 10 February
2004.2004, http://www.w3.org/TR/2004/REC-rdf-mt-20040210/. Latest version available as http://www.w3.org/TR/rdf-mt/.
- [RFC 2119]
- RFC 2119: Key words for use in RFCs to Indicate Requirement Levels. Network Working Group, S. Bradner.
Internet Best Current Practice,IETF, March 1997.1997, http://www.ietf.org/rfc/rfc2119.txt
- [RFC 2396]
- RFC 2396 - Uniform Resource Identifiers (URI): Generic Syntax. T. Berners-Lee, R. Fielding, U.C. Irvine and L. Masinter. IETF, August 1998.
- [RFC 3987]
- RFC
3987 -3987: Internationalized Resource Identifiers (IRIs). M. Duerst and M. Suignard. IETF, January 2005, http://www.ietf.org/rfc/rfc3987.txt
