Abstract
This is a specification of a precise semantics for RDF and RDFS,
and of corresponding entailment and inference rules which are sanctioned by the
semantics.
Status of this Document
This is a W3C
Last Call Working Draft of the RDF Core Working
Group and has been produced as part of the W3C Semantic Web Activity (Activity
Statement).
This document is in the Last Call review period, which ends on
21 February 2003. This document has been endorsed by the RDF Core
Working Group.
This document is being released for review by W3C Members and
other interested parties to encourage feedback and comments,
especially with regard to how the changes made affect existing
implementations and content.
The Working Group notes that this Last Call Working Draft
completes the group's design of the formal Semantics for RDF,
however it may still need some editorial polishing and
clarification following Last Call.
In conformance with W3C
policy requirements, known patent and IPR constraints
associated with this Working Draft are detailed on the RDF Core Working Group Patent Disclosure
page.
Comments on this document are invited and should be sent to the
public mailing list www-rdf-comments@w3.org.
An archive of comments is available at http://lists.w3.org/Archives/Public/www-rdf-comments/.
This is a public W3C Last Call Working Draft for review by W3C
Members and other interested parties. This section describes the
status of this document at the time of its publication. It is a
draft document and may be updated, replaced, or obsoleted by other
documents at any time. It is inappropriate to use W3C Working
Drafts as reference material or to cite as other than "work in
progress". A list of current W3C Recommendations and other
technical documents can be found at http://www.w3.org/TR/.
Table of Contents
0. Introduction
0.1 Specifying a formal semantics:
scope and limitations
0.2 Graph
Syntax
0.3 Graph
Definitions
1. Interpretations
1.1 Technical
notes
1.2 Urirefs,
resources and literals
1.3
Interpretations
1.4 Denotations of
ground graphs
1.5 Blank nodes as
existential assertions
2. Simple entailment between RDF
graphs
2.1 Criteria
for non-entailment
3. Interpreting the RDF(S)
vocabulary
3.1 RDF
interpretations
3.2 Reification,
containers, collections and rdf:value
3.2.1
Reification
3.2.2 RDF containers
3.2.3 RDF collections
3.2.4 rdf:value
3.3 RDFS
Interpretations
3.3.1 A note on rdfs:Literal
3.4 Datatyped
interpretations
4. Vocabulary entailment and closure
rules
4.1. Rdf-entailment
and rdf closures(informative)
4.2.
Rdfs-entailment and rdfs closures(informative)
4.3 Datatyped
entailments (informative)
Appendix A. Translation into
Lbase(informative)
Appendix B. Proofs of lemmas
Appendix C. Glossary.
Appendix D. Acknowledgements
References
RDF is an assertional language intended to be used to express propositions using
precise formal vocabularies, particularly those specified using
RDFS [RDF-VOCABULARY], and as a
basic foundation for more advanced assertional languages. Exactly
what is considered to be the 'meaning' of an assertion in RDF/S in
some broad sense may depend on many factors, including social
conventions, comments in natural language or links to other
content-bearing documents. Much of this meaning will be
inaccessible to machine processing and is mentioned here only to
emphasize that the formal semantics described here is not intended to
provide an analysis of 'meaning' in this broad sense. The semantics
given here restricts itself to a formal notion of meaning which could be
characterized as the part that is common to all other accounts of
meaning, and can be captured in mechanical inference rules. For
@@check link@@further
discussion of notions of meaning in RDF , see [RDF-CONCEPTS]
We use a basic technique called model theory for specifying the semantics of a
formal language. Readers unfamiliar with model theory may find the
glossary in appendix C helpful; uses of terms
in a technical sense are linked to their definitions. Model theory assumes
that the language refers to a 'world', and describes the minimal conditions
that a world must satisfy in order to assign an appropriate meaning
for every expression in the language. A particular world is called an interpretation,
so that model
theory might be better called 'interpretation theory'. The idea
is to provide an abstract, mathematical account of the properties
that any such interpretation must have, making as few assumptions
as possible about its actual nature or intrinsic structure. Model
theory tries to be metaphysically and ontologically neutral. It is typically couched
in the language of set theory simply because that is the normal
language of mathematics - for example, this semantics assumes that
names denote things in a set IR called the 'universe' - but the use
of set-theoretic language here is not supposed to imply that the
things in the universe are set-theoretic in nature. Model theory is
usually most relevant to implementation via the notion of entailment, described
later, which makes it possible to define valid inference rules.
The chief utility of a formal semantic theory is not to provide
any deep analysis of the nature of the things being described by
the language or to suggest any particular processing model, but
rather to provide a technical way to determine when inference
processes are valid, i.e. when they preserve truth.
In this document we give two versions of the same semantic
theory: directly, and also (in an informative appendix) an
'axiomatic semantics' in the form of a translation from RDF and
RDFS into another formal language, Lbase [LBASE] which has a pre-defined
model-theoretic semantics. The translation technique offers some
advantages for machine processing and may be more readable, so is
described here as a convenience. We believe that both of these
descriptions, and also the closure rules described in section 4,
are all in exact correspondence, but only the directly described
model theory in sections 1- 3 should be taken as normative.
There are several aspects of meaning in RDF which are ignored by
this semantics; in particular, it treats URI references as simple
names, ignoring aspects of meaning encoded in particular URI forms
[RFC 2396] and does not provide any
analysis of time-varying data or of changes to URI references. It
does not provide any analysis of indexical uses of URI references, for example
to mean 'this document'. Some parts of the RDF and RDFS
vocabularies are not assigned any formal meaning, and in some
cases, notably the reification and container vocabularies, it
assigns less meaning than one might expect. These cases are noted
in the text and the limitations discussed in more detail.
RDF is an assertional logic, in which each triple expresses a simple
proposition. This
imposes a fairly strict monotonic discipline on the language, so that
it cannot express closed-world assumptions, local default
preferences, and several other commonly used non-monotonic
constructs.
Particular uses of RDF, including as a basis for more expressive
languages such as DAML [DAML] and OWL [OWL], may impose further semantic conditions in
addition to those described here, and such extra semantic
conditions can also be imposed on the meanings of terms in
particular RDF vocabularies. Extensions or dialects of RDF which
are obtained by imposing such extra semantic conditions may be
referred to as semantic extensions of RDF. Semantic
extensions of RDF are constrained in this recommendation using the
language of [RFC 2119]. Semantic extensions
of RDF MUST conform to the semantic conditions for simple and RDF
entailment described in sections 1 and 3.1 of this document. Any
name for entailment in a semantic extension SHOULD be indicated by
the use of a vocabulary entailment
term. The semantic conditions imposed on an RDF semantic extension
MUST define a notion of vocabulary
entailment which is valid according to the model-theoretic
semantics described in the normative parts of this document; except
that if the semantic extension is defined on some syntactically
restricted subset of RDF graphs, then the semantic conditions need
only apply to this subset. Specifications of such syntactically
restricted semantic extensions MUST include a specification of
their syntactic conditions which are sufficient to enable software
to distinguish unambiguously those RDF graphs to which the extended
semantic conditions apply. Applications based on such syntactically
restricted semantic extensions MAY treat RDF graphs which do not
conform to the required syntactic restrictions as errors.
An example of a semantic extension of RDF is RDF Schema, the
semantics of which are defined in later parts of this document. RDF
Schema imposes no extra syntactic restrictions.
Any semantic theory must be attached to a syntax. This semantics
is defined as a mapping on the abstract
syntax of RDF [RDF-CONCEPTS].
We use the following terminology defined there: uriref,
literal, plain
literal, typed
literal,
blank node and triple.
The convention that relates a set of triples to a picture of an
RDF graph can be stated as follows. Draw one oval for each blank
node and uriref which occur in either the S or O position in any
triple in the set, and one rectangle for each literal, and write
each uriref or literal as the label of its shape. Shapes
corresponding to blank nodes have no label. Then for each triple
<S,P,O>, draw an arrowed line from the shape produced from S
to the shape produced from O, and label it with P. Technically,
this is a picture of a mathematical structure which can be
described as a partially labeled directed pseudograph with unique
node labels, but we will simply refer to a set of triples as an
RDF graph. Graphs with isomorphic pictures in this sense
are considered to be identical; this means that we do not
distinguish sets of triples which differ only in the identity of
their blank nodes. This slight abuse of terminology allows us to
simplify the presentation by ignoring questions of re-naming of
bound variables.
In this document we will use the N-triples
syntax described in [RDF-TESTS] to
describe RDF graphs. This notation uses a nodeID convention to
indicate blank nodes in the triples of a graph. Note that while node
identifiers such as _:xxx serve to identify blank
nodes in the surface syntax, these expressions are not
considered to be the label of the graph node they identify; they
are not names, and do not occur in the actual graph. In particular,
two N-triples
documents which differ only by re-naming their node identifiers
will be understood to describe identical RDF graphs.
The N-triples syntax requires that urirefs be given in full,
enclosed in angle brackets. In the interests of brevity, we use the
imaginary URI scheme 'ex:' to provide illustrative examples. To
obtain a more realistic view of the normal appearance of the
N-triples syntax, the reader should imagine this replaced with
something like 'http://www.example.org/rdf/mt/artificial-example/'.
We will also make extensive use of the Qname prefixes
rdf:, rdfs: and xsd: defined
as follows:
Prefix rdf: namespace URI:
http://www.w3.org/1999/02/22-rdf-syntax-ns#
Prefix rdfs: namespace URI:
http://www.w3.org/2000/01/rdf-schema#
Prefix xsd: namespace URI:
http://www.w3.org/2001/XMLSchema#
Since Qname syntax is not legal N-triples syntax, and in the
interests of brevity and readability, we will use the convention
whereby a Qname is used without surrounding angle brackets to
indicate the corresponding uriref enclosed in angle brackets, eg
the triple
<ex:a> rdf:type rdfs:Property .
should be read as an abbreviation for the N-triples syntax
<ex:a>
<http://www.w3.org/1999/02/22-rdf-syntax-ns#type>
<http://www.w3.org/2000/01/rdf-schema#Property> .
In stating rules and giving general semantic conditions we will
use single characters or character sequences without a colon to
indicate an arbitrary name or blank node in a triple.
Several definitions will be important in what follows.They are
stated together here for reference.
A subgraph of an RDF graph
is simply a subset of the triples in the graph. We will
identify each triple with the singleton set containing it, so that
each triple in a graph is considered to be a subgraph.
Consider a set S of graphs which
share no blank nodes. The graph consisting of all the triples in
all the graphs in S is another graph, which we will call the
merge of S. Each of the original graphs is a subgraph of
the merged graph. Notice that when forming a merged graph, two
occurrences of a given uriref or literal as nodes in two different
graphs become a single node in the union graph (since by definition
they are the same uriref or literal), but blank nodes are not
'merged' in this way. If the members of the set S share some blank
nodes, then we will define the merge of S to be the merge of a set
obtained by replacing blank nodes in some members of S by distinct
blank nodes to obtain another set S' of graphs which are isomorphic
to those in S.
Notice that one does not, in general, obtain the merge of a set
of graphs by concatenating their corresponding N-triples documents
and constructing the graph described by the merged document, since
if some of the documents use the same node identifiers, the merged
document will describe a graph in which some of the blank nodes
have been 'accidentally' merged. To merge Ntriples documents it is
necessary to check if the same nodeID is used in two or more
documents, and to replace it with a distinct nodeID in each of
them, before merging the documents. Similar cautions apply to
merging graphs described by RDF/XML documents which contain
nodeIDs, see [RDF-SYNTAX].
An RDF graph will be said to be
ground if it has no blank nodes.
We will refer to a set of
urirefs as a vocabulary. The vocabulary of a graph is the
set of urirefs that it contains (either as nodes, on arcs or in
typed literals). A
name is a uriref or a typed literal. A name is
from a vocabulary V if it is in V or is a typed literal
containing a uriref in V. The names of a graph are all the
names which occur in the graph. This is the set of expressions that
need to be assigned a meaning by an interpretation. We do not think of plain
literals as names because their interpretation is fixed by the RDF
semantic rules. When giving examples, we will sometimes use a
string of characters with no intervening colon to indicate 'some
name'.
An instance of an RDF
graph is, intuitively, a similar graph in which some blank nodes
may have been replaced by urirefs or literals, so that for example
"Jocasta married Oedipus" is an instance of "Jocasta married
somebody". However, it is technically convenient to also allow
blank nodes to be replaced by other blank nodes, so we need to
state this rather more precisely. Suppose that M is a mapping from
a set of blank nodes to some set of literals, blank nodes and
urirefs; then any graph obtained from a graph G by replacing some
or all of the blank nodes N in G by M(N) is an instance of
G. Note that any graph is an instance of itself, and if H is an
instance of G then every triple in H is an instance of some triple
in G.
This allows blank nodes in the second graph to be replaced by
names in the instance (which might cause some nodes to be
identified that were previously distinct) but it also allows them
to be replaced by other blank nodes. For example, the graph:
_:xxx <ex:b> _:xxx .
is an instance of
_:xxx <ex:b> _:yyy .
In particular, any graph obtained by replacing all blank nodes
by new blank nodes not in the original graph is an instance of the
original and also, by inverting the mapping, has it as an instance.
By our convention, such isomorphic graphs are considered to be
identical.
A proper instance
of a graph is an instance in which at least one blank node has been
replaced by a name. The above example is not a proper
instance.
An instance with respect
to a vocabulary V is an instance in which all the names in the
instance that were substituted for blank nodes in the original are
names from V.
We do not impose any logical restrictions on the domains and
ranges of properties; in particular, a property may be applied to
itself. When classes are
introduced in RDFS, we will allow them to contain themselves. This
might seem to violate one of the axioms of standard
(Zermelo-Fraenkel) set theory, the axiom of foundation, which
forbids infinitely descending chains of membership. However, the
semantic model given here distinguishes properties and classes
considered as objects from their extensions - the sets of object-value pairs
which satisfy the property, or things that are 'in' the class -
thereby allowing the extension of a property or class to contain
the property or class itself without violating the axiom of
foundation. In particular, this use of a class extension mapping
allows classes to contain themselves. For example, it is quite OK
for (the extension of) a 'universal' class to contain the class
itself as a member, a convention that is often adopted at the top
of a classification hierarchy. (If an extension contained itself
then the axiom would be violated, but that case never arises.) The
technique is described more fully in [Hayes&Menzel].
In this respect, RDFS differs from many conventional ontology
frameworks such as UML which assume a more structured system of
'layers', or which draw a sharp distinction between data and
meta-data. However, while RDFS does not assume the existence of
such structure, it does not prohibit it. RDF allows such loops, but
it does not mandate their use for all parts of a user vocabulary.
If this aspect of RDFS is found worrying, then it is possible to
restrict oneself to a subset of RDF graphs which do not contain any
such 'loops' of class membership or property application, and still
retain much of the expressive power of RDFS for many practical
purposes.
The use of the explicit extension mapping also makes it possible
for two properties to have exactly the same values, or two classes
to contain the same instances, and still be distinct entities. This
means that RDFS classes can be considered to be rather more than
simple sets; they can be thought of as 'classifications' or
'concepts' which have a robust notion of identity which goes beyond
a simple extensional correspondence. This property of
the model theory
has significant consequences in more expressive languages built on
top of RDF, such as OWL, which are capable
of expressing identity between properties and classes directly.
This 'intensional'
nature of classes and properties is sometimes claimed to be a
useful property of a descriptive language, but a full discussion of
this issue is beyond the scope of this document.
Notice that the question of whether or not a class contains
itself as a member is quite different from the question of whether
or not it is a subclass of itself. All classes are subclasses of
themselves.
RDF uses two kinds of referring expression, urirefs and
literals. We make very simple and basic assumptions about these.
Urirefs are treated as logical constants, i.e. as names which
denote things (the things are called 'resources', following [RFC 2396], but no assumptions are made here
about the nature of resources; we treat 'resource' here as
synonymous with 'entity'.) The meaning of a literal is principally
determined by its character string: it either refers to the value
mapped from the string by the associated datatype, or if no
datatype is provided then it refers to the literal itself, which is
either a unicode character string or a pair of a string with a
language tag.
We do not take any position here on the way that urirefs may be
composed from other expressions, e.g. from relative URIs or Qnames;
the semantics simply assumes that such lexical issues have been
resolved in some way that is globally coherent, so that a single
uriref can be taken to have the same meaning wherever it occurs.
Similarly, the semantics has no special provision for tracking
temporal changes. It assumes, implicitly, that urirefs have the
same meaning whenever they occur. To provide an adequate
semantics which would be sensitive to temporal changes is a
research problem which is beyond the scope of this document.
The semantics does not assume any particular relationship
between the denotation of a uriref and a document or network
resource which can be obtained by using that uriref in an HTTP
transfer protocol, or any entity which is considered to be the
source of such documents. Such a requirement could be added as a
semantic extension, but the formal semantics described here makes
no assumptions about any connection between the denotations of
urirefs and the uses of those urirefs in other protocols.
The basic intuition of model-theoretic semantics is that
asserting a sentence makes a claim about the world: it is another way of saying that the
world is, in fact, so arranged as to be an interpretation
which makes the sentence true. In other words, an assertion amounts
to stating a constraint on the possible ways the
world might be. Notice that there is no presumption here that any
assertion contains enough information to specify a single unique
interpretation. It is usually impossible to assert enough in any
language to completely constrain the interpretations to a single
possible world, so there is no such thing as 'the' unique RDF
interpretation. In general, the larger an RDF graph is - the more
it says about the world - then the smaller the set of
interpretations that an assertion of the graph allows to be true - the
fewer the ways the world could be, while making the asserted graph
true of it.
The following definition of an interpretation is couched in
mathematical language, but what it amounts to intuitively is that
an interpretation provides just enough information about a possible
way the world might be - a 'possible world' - in order to fix the
truth-value (true or false) of any ground RDF triple. It does this
by specifying for each uriref, what it is supposed to be a name of;
and also, if it is used to indicate a property, what values that
property has for each thing in the universe; and if it used to indicate a
datatype, we assume that the datatype defines a mapping between
lexical forms and datatype values. This is just enough information
to fix the truth-value of any ground triple, and hence any ground RDF
graph.(We will show how to determine the truth-values of non-ground
graphs in the following section.) Notice that if we left any of
this information out, it would be possible for some well-formed triple to
be left without a determinate value; and also that any other
information - such as the exact nature of the things in the universe - would,
regardless of its intrinsic interest, be irrelevant to the actual
truth-values of any triple.
All interpretations will be relative to a set of urirefs, called
the vocabulary of the interpretation; so that one should speak,
strictly, of an interpretation of an RDF vocabulary, rather than of
RDF itself. Some interpretations may assign special meanings to the
symbols in a particular vocabulary. Interpretations which share the
special meaning of a particular vocabulary will be named for that
vocabulary, so that we will speak of 'rdf-interpretations' ,
'rdfs-interpretations', etc.. An interpretation with no particular
extra conditions on a vocabulary will be called a simple
interpretation, or simply an interpretation. A simple
interpretation can be viewed as having an empty vocabulary.
RDF uses several forms of literal. The chief semantic
characteristic of literals is that their meaning is largely
determined by the form of the string they contain. In the case of
typed literals, however, the full specification of the meaning
depends on being able to access datatype information which is
external to RDF itself; for this reason we postpone a full
discussion of the meaning of typed literals until later sections,
where we introduce a special notion of datatype interpretation. For
now, we will assume that each interpretation defines a mapping IL
from typed literals to their interpretations, and will impose
stronger conditions on IL as the notion of 'interpretation' is
extended in later sections. Simple literals, without embedded
datatypes, are always interpreted as referring to themselves:
either a character string or a pair consisting of two character
strings, the second of which is a language tag.
The set of all possible values of all literals is assumed to be
a set called LV. Since the set of datatypes is not restricted by
RDF syntax, it is impossible to give a sharp definition of LV, but
it is required to contain all literal strings, all pairs consisting
of a literal string and a language tag, and all well-formed
canonical XML documents.
A simple interpretation I of a vocabulary V is
defined by:
1. A non-empty set IR of resources, called the domain or
universe of I, which is a superset of LV.
2. A distinguished subset IP of IR.
3. A mapping IEXT from IP into the powerset of IR x IR i.e. the
set of sets of pairs <x,y> with x and y in IR .
4. A mapping IS from V into IR
5. A mapping IL from typed literals into IR.
IEXT(x) is a set of pairs which identify the arguments for which
the property is true, i.e. a binary relational extension, called
the extension of x.
This trick of distinguishing a relation as an object from its
relational extension allows a property to occur in its own
extension, as noted earlier.
The assumption that IR is a superset of LV amounts to saying
that literal values are thought of as real entities that 'exist'.
This assumption may seem controversial, since it amounts to saying
that literal values are resources. We note however that this does
not imply that literals should be identified with urirefs.
There is a technical reason why the range of IL is IR rather
than being restricted to LV. When we consider interpretations which
take account of datatype information, it is syntactically possible
for a typed literal to be internally inconsistent, and we will
require such badly typed literals to denote a non-literal
value.
In the next sections we give the exact rules for how an
interpretation of a vocabulary determines the truth-values of any
RDF graph, by a recursive definition of the denotation - the
semantic "value" - of any RDF expression in terms of those of its
immediate subexpressions. RDF has two kinds of denotation: names
denote things in the universe, and sets of triples denote
truth-values.These rules apply to all subsequent semantic
extensions.
The denotation of a ground RDF graph in I is given recursively
by the following rules, which extend the interpretation mapping I
from labels to ground graphs. These rules (and extensions of them
given later) work by defining the denotation of any piece of RDF
syntax E in terms of the denotations of the immediate syntactic
constitutents of E, hence allowing the denotation of any piece of
RDF to be determined by a kind of syntactic recursion.
| if E is a plain literal then I(E) = E |
| if E is a typed literal than I(E) = IL(E) |
| if E is a uriref then I(E) = IS(E) |
| if E is a triple s p o . then I(E) = true if
<I(s),I(o)> is in IEXT(I(p)), otherwise I(E)=
false. |
| if E is a ground RDF graph then I(E) = false if I(E') =
false for some triple E' in E, otherwise I(E) =true. |
Note that the denotation of plain literals is always in LV.
If the vocabulary of an RDF graph contains urirefs that are not
in the vocabulary of an interpretation I - that is, if I simply
does not give a semantic value to some name that is used in the
graph - then these truth-conditions will always yield the value
false for some triple in the graph, and hence for the graph itself.
Turned around, this means that any assertion of a graph implicitly
asserts that all the names in the graph actually refer to something
in the world. The final condition implies that an empty graph (an
empty set of triples) is trivially true.
As an illustrative example, the following is a small
interpretation for the artificial vocabulary {ex:a, ex:b,
ex:c}. We use integers to indicate the non-literal 'things'
in the universe. This is not meant to imply that RDF
interpretations should be interpreted as being about arithmetic,
but more to emphasize that the exact nature of the things in the
universe is irrelevant.(In this and subsequent examples we use the
greater-than and less-than symbols in several ways: following
mathematical usage to indicate abstract pairs and n-tuples;
following Ntriples syntax to enclose urirefs, and also as
arrowheads when indicating mappings. We apologize for any
confusion.)
IR = LV union{1, 2};
IEXT: 1->{<1,2>,<2,1>}
IS: ex:a->1, ex:b->1,
ex:c->2
IL: any typed literal -> 2
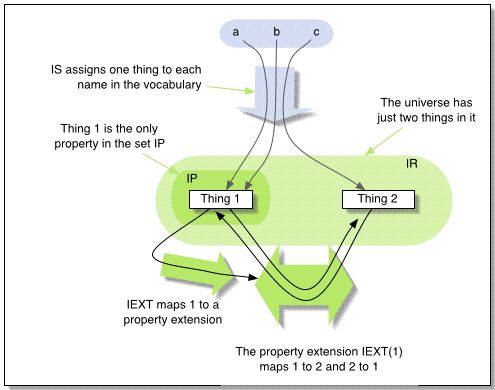
Figure 1: An example of an interpretation. Note, this is
not a picture of an RDF graph.
The figure does not show the infinite number of members of
LV.
This interpretation makes these triples true:
<ex:a> <ex:b> <ex:c>
.
<ex:c> <ex:a> <ex:a>
.
<ex:c> <ex:b> <ex:a>
.
<ex:a> <ex:b>
"whatever"^^<ex:b> .
For example, I(<ex:a> <ex:b> <ex:c>
.) = true if
<I(ex:a),I(ex:c)> is in
IEXT(I(<ex:b>)), i.e. if <1,2> is in
IEXT(1), which is {<1,2>,<2,1>} and so does contain
<1,2> and so I(<ex:a <ex:b> ex:c>)
is true.
The truth of the fourth literal is a consequence of the rather
idiosyncratic interpretation chosen here for typed literals; this
kind of oddity will be ruled out when we consider datatyped
intepretations.
It makes these triples false:
<ex:a> <ex:c> <ex:b>
.
<ex:a> <ex:b> <ex:b>
.
<ex:c> <ex:a> <ex:c>
.
<ex:a> <ex:b> "whatever"
.
For example, I(<ex:a> <ex:c> <ex:b>
.) = true if
<I(ex:a),I(<ex:b>)>,
i.e.<1,1>, is in IEXT(I(ex:c)); but
I(ex:c)=2 and IEXT is not defined on 2, so the
condition fails and I(<ex:a> <ex:c> <ex:b>
.) = false.
It makes all triples containing a plain literal false, since the
property extension does not have any pairs containing a character
string.
To emphasize; this is only one possible interpretation of this
vocabulary; there are (infinitely) many others. For example, if we
modified this interpretation by attaching the property extension to
2 instead of 1, none of the above triples would be true.
Blank nodes are treated as simply indicating the existence of a
thing, without using, or saying anything about, the name of that
thing. (This is not the same as assuming that the blank node
indicates an 'unknown' uriref; for example, it does not assume that
there is any uriref which refers to the thing. The discussion of skolemization in the
proof appendix is relevant to this point.)
We now show how an interpretation can specify the truth-value of
a graph containing blank nodes. This will require some definitions,
as the theory so far provides no meaning for blank nodes. Suppose I
is an interpretation and A is a mapping from some set of blank
nodes to the universe IR of I, and define I+A to be an extended
interpretation which is like I except that it uses A to give the
interpretation of blank nodes. Define blank(E) to be the set of
blank nodes in E. Then we can extend the above rules to include the
two new cases that are introduced when blank nodes occur in the
graph:
| If E is a blank node then [I+A](E) = A(E) |
| If E is an RDF graph then I(E) = true if [I+A'](E) =
true for some mapping A' from blank(E) to IR, otherwise
I(E)= false. |
Notice that we have not changed the definition of an
interpretation; it still consists of the same values IR, IP, IEXT,
IS and IL. We have simply extended the rules for defining
denotations under an interpretation, so that the same
interpretation that provides a truth-value for ground graphs also
assigns truth-values to graphs with blank nodes, even though it
provides no denotation for the blank nodes themselves. Notice also
that the blank nodes themselves are perfectly well-defined
entities; they differ from other nodes only in not being assigned a
denotation by an interpretation, reflecting the intuition that they
have no 'global' meaning (i.e. outside the graph in which they
occur).
This effectively treats all blank nodes as having the same
meaning as existentially quantified variables in the RDF graph in
which they occur. However, there is no need to specify the scope of
the quantifier within a graph, and no need to use any explicit
quantifier syntax.( If we were to apply the semantics directly to
N-triples syntax, we would need to indicate the quantifier
scope, since in this lexicalization syntax the same node identifier
may occur several times corresponding to a single blank node in the
graph. The above rule amounts to the convention that would place
the quantifiers just outside, or at the outer edge of, the
N-triples document corresponding to the graph.)
For example, with this convention, the graph defined by the
following triples is false in the interpretation shown in figure
1:
_:xxx <ex:a> <ex:b> .
<ex:c> <ex:b> _:xxx .
since if A' maps the blank node to 1 then the first triple is
false in I+A', and if it maps it to 2 then the second triple is
false.
Note that each of these triples, if thought of as a single
graph, would be true in I, but the whole graph is not; and that if
a different nodeID were used in the two triples, indicating that
the RDF graph had two blank nodes instead of one, then A' could map
one node to 2 and the other to 1, and the resulting graph would be
true under the interpretation I.
Following conventional terminology, we say that I satisfies E if I(E)=true,
and that a set S of expressions (simply) entails E if every interpretation
which satisfies every member of S also satisfies E. In later
sections these notions will be adapted to classes of
interpretations with particular vocabularies, but throughout this
section 'entailment' should be interpreted as meaning simple
entailment.
Entailment is the key idea which connects model-theoretic
semantics to real-world applications. As noted earlier, making an
assertion amounts to claiming that the world is an interpretation
which assigns the value true to the assertion. If A entails B, then
any interpretation that makes A true also makes B true, so that an
assertion of A already contains the same "meaning" as an assertion
of B; we could say that the meaning of B is somehow contained in,
or subsumed by, that of A. If A and B entail each other, then they
both "mean" the same thing, in the sense that asserting either of
them makes the same claim about the world. The interest of this
observation arises most vividly when A and B are different
expressions, since then the relation of entailment is exactly the
appropriate semantic licence to justify an application inferring or
generating one of them from the other. Through the notions of
satisfaction, entailment and validity, formal semantics gives a
rigorous definition to a notion of "meaning" that can be related
directly to computable methods of determining whether or not
meaning is preserved by some transformation on a representation of
knowledge.
Any process which constructs a
graph E from some other graph(s) S is said to be (simply)
valid if S entails E, otherwise invalid. Note
that being an invalid process does not mean that the conclusion is
false, and being valid does not guarantee truth. However, validity
represents the best guarantee that any assertional language can
offer: if given true inputs, it will never draw a false conclusion
from them.
In this section we give a few basic results about simple
entailment and valid inference. Simple entailment can be recognized
by relatively simple syntactic comparisons. The two basic forms of
simply valid inference in RDF are, in logical terms, the inference
from (P and Q) to P, and the inference from (foo baz) to (exists
(?x) foo(?x)).
These results apply only to simple entailment, not to the
extended notions of entailment introduced in later sections.
Proofs, all of which are straightforward, are given in the appendix, which also describes some other
properties of entailment which may be of interest.
Subgraph
Lemma. A graph entails all its subgraphs .
Instance
Lemma. A graph is entailed by any of its instances.
The relationship between merging and entailment is simple, and
obvious from the definitions:
Merging
lemma. The merge of a set S of RDF graphs is entailed
by S, and entails every member of S.
This means that a set of graphs can be treated as equivalent to its
merge, i.e. a single graph, as far as the model theory is
concerned. In what follows, therefore, we will often not bother to
distinguish between a set of graphs and a single graph. This can be
used to simplify the terminology somewhat: for example, we can
paraphrase the definition of S entails E, above, by saying that S
entails E when every interpretation which satisfies S also
satisfies E.
The main result for simple RDF inference is:
Interpolation
Lemma. S entails a graph E if and only if a subgraph of
the merge of S is an instance of E.
The interpolation lemma completely characterizes simple RDF
entailment in syntactic terms. To tell whether a set of RDF graphs
entails another, find a subgraph of their merge and replace names
by blank nodes to get the second. Of course, there is no need to
actually construct the merge. If working backwards from the consequent E, the most
efficient technique would be to treat blank nodes as variables in a
process of subgraph-matching, allowing them to bind to 'matching'
names in the antecedent graph(s) in S, i.e. those which may
entail the consequent graph. The interpolation lemma shows
that this process is valid, and is also complete if the subgraph-matching algorithm is.
The existence of complete subgraph-checking algorithms also
shows that RDF entailment is decidable, i.e. there is a terminating
algorithm which will determine for any finite set S and any graph
E, whether or not S entails E.
Notice however that such a variable-binding process would only
be appropriate when applied to the conclusion of a
proposed entailment. This corresponds to using the document as a
goal or a query, in contrast to asserting it, i.e. claiming it to
be true. If an RDF document is asserted, then it would be invalid
to bind new values to any of its blank nodes, since the resulting
graph would not be entailed by the assertion, as explained in the
next section.
Finally, the following is a trival but important consequence of
the definition of entailment:
Monotonicity Lemma. Suppose S is a subgraph of
S' and S entails E. Then S' entails E.
In contrast to names, which have a global identity which carries
across all graphs, blank nodes should not be identified with other
nodes or replaced with urirefs, in order to ensure that the
resulting graph is entailed by what one starts with. To state this
condition precisely, we need to first exclude a counterexample. It
is possible for a graph to contain two triples one of which is an
instance of the other, for example:
<ex:a> <ex:b> _:xxx .
<ex:a> <ex:b> <ex:c> .
Such an internally redundant graph is equivalent to one of its own instances, since
replacing the blank node by <ex:c> would result
in a single-triple graph which is a subgraph of the original. To
rule out such cases of internal redundancy, we will say that an RDF graph is lean if none
of its triples is an instance of any other. Then the above
principle is made precise in the following two lemmas concerning
criteria for non-entailment:
Anonymity lemma
1. Suppose E is a lean graph and E' is a proper instance of E.
Then E does not entail E'.
Anonymity lemma
2. Suppose that E is a lean graph and that E' is like E except that
two distinct blank nodes in E have been identified in E'. Then E
does not entail E'.
This means that there is no valid RDF inference process which
can produce an RDF graph in which a single blank node occurs in
triples originating from several different graphs. (Of course, such
a graph can be constructed, but it will not be entailed by the original
documents. An assertion of such a graph would reflect the addition
of new information about identity.)
We emphasise again that these results apply only to simple
entailment, not to the vocabulary entailment relationships defined
in rest of the document.
So far we have considered only the model theory of what might be
called the logical form of the RDF graph itself, without imposing
any special interpretations on any vocabulary. In the rest of the
document we will extend the model theory to describe the semantic
conditions reflecting the intended meanings of the
rdf: and rdfs: namespaces.
Although we will do this in stages, the same general technique
is used throughout. First we describe a special vocabulary, i.e. a
set of urirefs which will be given a special meaning; then we give
the extra conditions on an interpretation which capture those
meanings; then we restrict the notions of satisfiability and
entailment to apply to these interpretations only. This essentially
imposes an a priori restriction on the world being described
that it satisfy the extra conditions. The new semantic conditions
are automatically assumed to be true; an interpretation which would
violate them is simply not allowed to count as a possible world.
Since there are now several distinct notions of interpretation,
entailment and satisfiability, we use the Qname namespace prefix
conventions to identify the various distinctions, eg an
rdf-interpretation is an interpretation satisfying the rdf semantic
conditions, rdf-entailment means entailment relative to such
interpretations, and so on. We call this general idea vocabulary
entailment, i.e. entailment relative to a set of
interpretations which satisfy extra semantic conditions on a
vocabulary. Vocabulary entailment is more powerful than simple
entailment, in the sense that a given set of premises entails more
consequences. In general, as the vocabulary is increased and extra
semantic conditions imposed, the class of satisfying interpretations is restricted, and
hence the corresponding notion of entailment becomes more powerful.
For example, if S simply entails E then it also rdf-entails E,
since every rdf-interpretation is also a simple interpretation; but
S may rdf-entail E even though it does not simply entail it.
Intuitively, a conclusion may depend on some of the extra
assumptions incorporated in the semantic conditions imposed on the
vocabulary.
Another way of expressing this is that any restriction on
interpretations decreases the number of possible ways that
an interpretation might be a counterexample to E's following
from S.
Simple entailment is the vocabulary entailment of the empty
vocabulary. It is therefore the weakest form of RDF entailment,
which holds for any vocabulary; it is the entailment which depends
only on the basic logical form of RDF graphs, without making any
further assumptions about the meaning of any urirefs.
We will consider syntactic criteria for recognizing vocabulary
entailment in the next section.
RDF imposes some extra semantic conditions on the following
(rather small) vocabulary, which we will call rdfRV:
| RDF vocabulary |
rdf:type
rdf:Property rdf:nil rdf:List
rdf:XMLLiteral |
An
rdf-interpretation of a vocabulary V is an interpretation I
on (V union rdfV) which satisfies the following extra
conditions:
IP contains I(rdf:type) |
x is in IP if and only if <x,
I(rdf:Property)> is in
IEXT(I(rdf:type)) |
<I(rdf:nil),
I(rdf:List)> is in
IEXT(I(rdf:type)) |
|
if xxx is a well-formed XML document, then
IL("xxx"^^rdf:XMLLiteral) is
the XML canonical form of
xxx;
and if yyy is a language identifier then
IL("xxx"@yyy^^rdf:XMLLiteral)
is the XML canonical form of xxx
with the language tag yyy
|
The first condition forces every rdf interpretation to contain a
thing denoted by rdf:type; which will be used as a property to
associate 'type' values with resources. The second condition could
be regarded as defining IP to be the set of resources in the
universe of the interpretation which have the value
I(rdf:Property) of the property
I(rdf:type). Such subsets of the universe will be
central in interpretations of RDFS. The third condition says that
the empty list object is classified as being a list: this is the
only formal condition the RDF semantics places on the collection
vocabulary, described later. The fourth condition defines the
built-in RDF datatype; here 'canonical form' is understood in the
sense of [XML-C14N]. For an exact
statement of the precise conditions for attaching language tags
to XML documents see [RDF-CONCEPTS].
For example, the following rdf-interpretation extends the simple
interpretation in figure 1:
IR = {1, 2, T , P}; IP = {1, T}
IEXT: 1->{<1,2>,<2,1>},
T->{<1,P>,<T,P>}
IS: ex:a -> 1, ex:b ->1,
ex:c -> 2, rdf:type->T,
rdf:Property->P, rdf:nil ->1,
rdf:List ->P
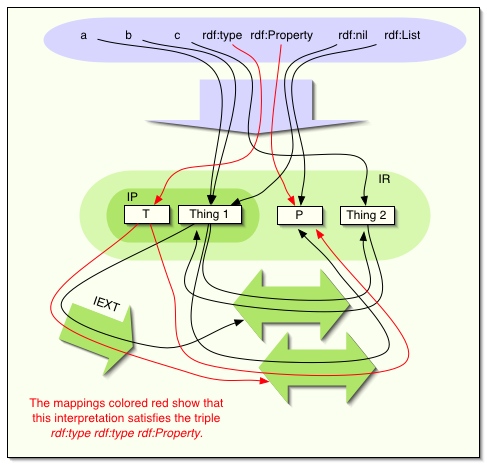
Figure 2: An example of an rdf-interpretation.
This is not the smallest rdf-interpretation which extends the
earlier example, since we could have made
I(rdf:Property) be 2 and IEXT(T) be
{<1,2>,<T,2>}, and managed without having P in the
universe. In general, a given entity in an interpretation may play
several 'roles' at the same time, as long as this can be done
without violating any of the required semantic conditions. The
above interpretation identifies properties with lists, for example;
of course, other interpretations might not make such an
identification.
It is important to note that every rdf-interpretation is also a
simple interpretation.The 'extra' structure does not prevent it
acting in the simpler role.
The RDF vocabulary contains several other items. Some of these
are omitted because they have no formal semantic meaning, or have a
meaning which can only be described using the RDFS vocabulary.
RDF provides vocabularies which are intended for use in
describing containers and bounded collections, and a reification
vocabulary to enable an RDF graph to describe, as well as exhibit,
triples. Although these vocabularies have reasonably clear
informally intended conventional meanings, we do not impose any
further formal semantic conditions on them, so the notions of
rdf-entailment and rdf-interpretation apply to them without further
change. They are discussed here in order to explain both the
intuitive meanings intended, and also to note the intuitive
consequences which are not supported by the formal model theory.
Constraints are imposed on the meanings of these vocabularies in
semantic extensions. The RDFS assigns range and domain conditions
for some of the properties used in this vocabulary.We will refer to
the complete set of all rdf urirefs, consisting of the RDF
vocabulary and all of the reification, container and collection
vocabularies and the uriref rdf:value , as the RDF
vocabulary, rdfV.
The lack of a formal semantics for these vocabularies does not
reflect any technical semantic problems, but rather is a design
decision to make it easier to implement processes to check formal
RDF entailment. Since no extra formal semantic conditions are
imposed on them, they are not considered to be restricted
vocabularies in RDF. In RDFS, however, the entire RDF vocabulary is
considered to be a restricted vocabulary.
The RDF reification vocabulary consists of a class name and
three property names.
| RDF reification vocabulary |
rdf:Statement rdf:subject rdf:predicate
rdf:object |
Semantic extensions MAY limit the interpretation of these so
that a triple of the form
aaa rdf:type rdf:Statement .
is true in I just when I(aaa) is a token of an RDF triple in some RDF document,
and the three properties, when applied to such a denoted triple,
have the same values as the respective components of that
triple.
This may be illustrated by considering the following two RDF
graphs, the first of which consists of a single triple.
<ex:a> <ex:b> <ex:c> .
and
_:xxx rdf:type rdf:Statement .
_:xxx rdf:subject <ex:a> .
_:xxx rdf:predicate <ex:b> .
_:xxx rdf:object <ex:c> .
The second graph is called a reification of the triple in the first
graph, and the node which is intended to refer to the first triple
- the blank node in the second graph - is called, rather
confusingly, a reified triple. (This can be a blank node
or a uriref.) In the intended interpretation of the reification
vocabulary, the second graph would be made true in an
interpretation I by interpreting the reified triple to refer to a
token of the triple in the first graph in some concrete RDF
document, considering that token to be valid RDF syntax, and then
using I to interpret the syntactic triple which the token
instantiates, so that the subject, predicate and object of that
triple are interpreted in the same way in the reification as in the
triple described by the reification. This could be stated formally
as follows: <x,y> is in IEXT(I(rdf:subject))
just when x is a token of an RDF triple of the form
aaa bbb ccc .
and y is I(aaa); similarly for predicate and object. Notice that
the value of the rdf:subject property is not the
subject uriref itself but its interpretation, and so this condition
involves a two-stage interpretation process: we have to interpret
the reified node - the subject of the triples in the reification -
to refer to another triple, then treat that triple as RDF syntax
and apply the interpretation mapping again to get to the referent
of its subject. This requires triple tokens to exist as first-class
entities in the universe IR of an interpretation. In sum: the
meaning of the reification is that a document exists containing a
triple token which means whatever the first graph means.
We emphasize that the semantic extension described here requires
the reified triple that the reification describes -
I(_:xxx) in the above example - to be a
particular token or instance of a triple in a (real
or notional) RDF document, rather than an 'abstract' triple
considered as a grammatical form. There could be several such
entities which have the same subject, predicate and object
properties. Although a graph is defined as a set of triples,
several such tokens with the same triple structure might occur in
different documents. Thus, it would be meaningful to claim that the
blank node in the second graph above does not refer to the triple
in the first graph, but to some other triple with the same
structure. This particular interpretation of reification was chosen
on the basis of use cases where properties such as dates of
composition or provenance information have been applied to the
reified triple, which are meaningful only when thought of as
referring to a particular instance or token of a triple.
Although RDF applications may use reification to refer to triple
tokens in RDF documents, the connection between the document and
its reification must be maintained by some means external to RDF.
RDF syntax provides no means to 'connect' an RDF triple to its
reification. Since an assertion of a reification of a triple does
not implicitly assert the triple itself, this means that there are
no entailment relationships which hold between a triple
and a reification of it. Thus the reification vocabulary has no
effective semantic constraints on it, other than those that apply
to an RDF interpretation. The chief facts that are worthy of note
about RDF reification, in fact, are examples of
non-entailments.
A reification of a triple does not entail the triple, and is not
entailed by it. (The reason for first is clear, since the
reification only asserts that the triple token exists, not that it
is true. The second non-entailment is a consequence of the fact
that asserting a triple does not automatically assert that any
triple tokens exist in the universe being described by the triple.
For example, the triple might be part of an ontology describing
animals, which could be satisfied by an interpretation in which the
universe contained only animals.)
Since the relation between triples and reifications of triples
in any RDF graph or graphs need not be one-to-one, asserting a
property about some entity described by a reification need not
entail that the same property holds of another such entity, even if
it has the same components. For example,
_:xxx rdf:type rdf:Statement .
_:xxx rdf:subject <ex:subject> .
_:xxx rdf:predicate <ex:predicate> .
_:xxx rdf:object <ex:object> .
_:yyy rdf:type rdf:Statement .
_:yyy rdf:subject <ex:subject> .
_:yyy rdf:predicate <ex:predicate> .
_:yyy rdf:object <ex:object> .
_:xxx <ex:property> <ex:foo> .
does not entail
_:yyy <ex:property> <ex:foo> .
RDF provides vocabularies for describing three classes of
containers. Containers have a type, and their members can
be listed by using a fixed set of container membership
properties. These properties are indexed by integers to
provide a way to distinguish the members from each other, but these
indices should not necessarily be thought of as defining an
ordering of the container itself.
The rdfs vocabulary, described below, adds a generic membership
property which holds regardless of position, and classes containing
all the containers and all the membership properties.
| RDF Container Vocabulary |
rdf:Seq rdf:Bag rdf:Alt rdf:_1 rdf:_2
... |
One should understand this RDF vocabulary as describing
containers, rather than as a vocabulary for constructing them, as
would typically be supplied by a programming language. On this
view, the actual containers are entities in the semantic universe,
and RDF graphs which use the vocabulary simply provide very basic
information about these entities, enabling an RDF graph to
characterize the container type and give partial information about
the members of a container. Since the RDF container vocabulary is
so limited, many 'natural' assumptions concerning RDF containers
are not formally sanctioned by the RDF model theory. This should not be taken as
meaning that these assumptions are false, but only that RDF does
not formally entail that they must be true.
There are no special semantic conditions on the container
vocabulary: the only 'structure' which RDF presumes its containers
to have is what can be inferred from the use of this vocabulary and
the semantic conditions on the rest of the RDF vocabulary. The
intended mode of use is that things of type rdf:Bag
are considered to be unordered but to allow duplicates; things of
type rdf:Seq are considered to be ordered, and things
of type rdf:Alt are considered to represent a
collection of alternatives, possibly with a preference ordering.
The ordering of items in an ordered container is intended to be
indicated by the numerical ordering of the container membership
properties. However, these informal interpretations are not
reflected in any formal RDF entailments.
RDF does not support any entailments which could arise from
re-ordering the elements of an rdf:Bag. For example,
_:xxx rdf:type rdf:Bag .
_:xxx rdf:_1 <ex:a> .
_:xxx rdf:_2 <ex:b> .
does not entail
_:xxx rdf:_1 <ex:b> .
_:xxx rdf:_2 <ex:a> .
Notice that if this conclusion were valid, then the result of
conjoining it to the original graph would also be a valid
entailment, which would assert that both elements were in both
positions. (This is a consequence of the fact that RDF is a purely
assertional language.)
There is no assumption that a property of a container applies to
any of the elements of the container, or that if a property applies
to a container then the property applies to any of the members of
the container, or vice versa. There is no formal requirement that
the three container classes are disjoint, so that for example
something can be asserted to be both an rdf:Bag and an
rdf:Seq. There is no assumption that containers are
gap-free, so that for example
_:xxx rdf:type rdf:Seq.
_:xxx rdf:_1 <ex:a> .
_:xxx rdf:_3 <ex:c> .
does not entail
_:xxx rdf:_2 _:yyy .
There is no way in RDF to 'close' a container, i.e. to assert
that it contains only a fixed number of members. This is a
reflection of the fact that it is always consistent to add a triple
to a graph asserting a membership property of any container. And
finally, there is no built-in assumption that an RDF container has
only finitely many members.
3.2.3 RDF
collections
RDF provides a vocabulary for describing collections, ie.'list
structures' in terms of head-tail links. Collections differ from
containers in allowing branching structure and in having an
explicit terminator, allowing applications to determine the exact
set of items in the collection.
| RDF Collection Vocabulary |
rdf:List rdf:first rdf:rest rdf:nil |
As with containers, no special semantic conditions are imposed
on this vocabulary other than the type of nil being List. It is
intended for use typically in a context where a container is
described using blank nodes to connect a 'well-formed' sequence of
items, each described by three triples of the form
_:c1 rdf:type rdf:List .
_:c1 rdf:first aaa .
_:c1 rdf:rest _:c2
where the final item is indicated by the use of
rdf:nil as the value of the property
rdf:rest. In a familiar convention,
rdf:nil can be thought of as the empty collection.
Clearly, any such graph amounts to an assertion that the
collection, and all its sub-collections, exist, and since the
members of the collection can be determined by inspection, this is
often sufficient to enable applications to determine what is meant.
Note however that the semantics does not require any collections to
exist other than those mentioned explicitly in a graph (and the
empty collection). For example, the existence of a collection
containing two items does not automatically guarantee that the
similar collection with the items permuted also exists:
_:c1 rdf:type rdf:List .
_:c1 rdf:first <ex:aaa> .
_:c1 rdf:rest _:c2 .
_:c2 rdf:type rdf:List .
<ex:bbb> .
_:c2 rdf:rest rdf:nil .
does not entail
_:c3 rdf:type rdf:List .
_:c3 rdf:first <ex:bbb> .
_:c3 rdf:rest _:c4 .
_:c4 rdf:type rdf:List .
<ex:aaa> .
_:c4 rdf:rest rdf:nil .
Also, RDF imposes no 'wellformedness' conditions on the use of this
vocabulary, so that it is possible to write RDF graphs which assert
the existence of highly peculiar objects such as lists with forked
or non-list tails, or multiple heads:
_:666 rdf:type rdf:List .
_:666 rdf:first <ex:aaa> .
_:666 rdf:first <ex:bbb> .
_:666 rdf:rest <ex:ccc> .
_:666 rdf:rest _:777 .
_:666 rdf:rest rdf:nil .
As this example shows, it is also possible to write a set of
triples which underspecify a collection by failing to specify its
rdf:rest property value.
Semantic extensions MAY place extra syntactic well-formedness
restrictions on the use of this vocabulary in order to rule out
such graphs, and MAY exclude interpretations of the collection
vocabulary which violate the convention that the subject of a
'linked' collection of three-triple items of the form described
above, ending with an item ending with rdf:nil,
denotes a totally ordered sequence whose members are the
denotations of the rdf:first values of the items, in
the order got by tracing the rdf:rest properties from
the subject to rdf:nil. This permits sequences which
contain other sequences.
3.2.4 rdf:value
The intended use for rdf:value is
explained
intuitively in [RDF-PRIMER]. It
is typically used to identify a 'primary' or 'main' value of a
property which has several values, or has as its value a complex
entity with several facets or properties of its own.
Since the range of possible uses for
rdf:value is so wide, it is impossible to give a
precise model-theoretic statement which covers all the intended
meanings or use cases. Users are cautioned, therefore, that the use
of rdf:value is somewhat risky, and that it should be
treated as a 'blank' piece of RDF syntax whose meaning in any
particular case should be defined by the user, and may vary from
application to application. In practice, the intended meaning is
often clear from the context, but may be lost when graphs are
merged or when conclusions are inferred.
RDFSchema extends RDF to
include a larger vocabulary rdfsV with more complex semantic
constraints:
| RDFS vocabulary |
rdfs:domain rdfs:range rdfs:Resource rdfs:Literal
rdfs:Datatype rdfs:Class rdfs:subClassOf rdfs:subPropertyOf
rdfs:member rdfs:Container rdfs:ContainerMembershipProperty
rdfs:comment rdfs:seeAlso, rdfs:isDefinedBy
rdfs:label |
(rdfs:comment, rdfs:seeAlso,
rdfs:isDefinedBy and rdfs:label are
included here because some constraints which apply to their use can
be stated using rdfs:domain, rdfs:range and
rdfs:subPropertyOf. Other than this, the formal
semantics does not assign them any particular meanings.)
Although not strictly necessary, it is convenient to state the
RDFS semantics in terms of a new semantic construct, a 'class', i.e. a resource
which represents a set of things in the universe which all have
that class as the value of their rdf:type property.
Classes are defined to be things of type rdfs:Class.
We will assume that there is a mapping ICEXT (for the Class
Extension in I) from classes to their extensions; the first
semantic condition in the table below amounts to the following
definition of this mapping in terms of the relational extension of
rdf:type:
ICEXT(x) = {y | <y,x> is in IEXT(I(rdf:type))
}
Notice that a class may have an empty class extension; that (as
noted earlier) two different class entities could have the same
class extension; and that given the above definition, the class
extension of rdfs:Class contains the class
rdfs:Class.
An
rdfs-interpretation of V is an rdf-interpretation I of (V
union rdfV union rdfsV) which satisfies the following semantic
conditions and all the triples in the subsequent table, which we
will call axiomatic triples. The first condition can be
understood as a definition of ICEXT and hence of IC, the set of
classes. Since I is an rdf-interpretation, this means that IP =
ICEXT(I(rdf:Property))
|
x is in ICEXT(y) iff <x,y> is in
IEXT(I(rdf:type))
IC = ICEXT(I(rdfs:Class))
IR = ICEXT(I(rdfs:Resource))
ICEXT(I(rdfs:Literal)) is a subset of
LV
|
|
If <x,y> is in IEXT(I(rdfs:range))
and <u,v> is in IEXT(x) then v is in ICEXT(y)
|
|
If <x,y> is in IEXT(I(rdfs:domain))
and <u,v> is in IEXT(x) then u is in ICEXT(y)
|
|
<x,y> is in
IEXT(I(rdfs:subClassOf)) if and only if x
and y are in IC and ICEXT(x) is a subset of ICEXT(y)
|
|
<x,y> is in
IEXT(I(rdfs:subPropertyOf)) if and only if x
and y are in IP and IEXT(x) is a subset of IEXT(y)
|
If x is in
ICEXT(I(rdfs:ContainerMembershipProperty))
then <x,I(rdfs:member)> is in
IEXT(I(rdfs:subPropertyOf)) |
ICEXT(I(rdf:XMLLiteral))
is the set of all canonical XML documents. |
|
IC contains:
I(rdfs:Resource),
I(rdf:Property), I(rdfs:Class),
I(rdfs:Literal),
I(rdfs:Datatype), I(rdf:Seq),
I(rdf:Bag), I(rdf:Alt),
I(rdfs:Container), I(rdf:List),
I(rdfs:ContainerMembershipProperty),
I(rdf:Statement)
|
|
IP contains:
I(rdf:type), I(rdfs:domain),
I(rdfs:range),
I(rdfs:subPropertyOf),
I(rdfs:subClassOf),
I(rdfs:comment), I(rdfs:label),
I(rdf:subject),
I(rdf:predicate),
I(rdf:object), I(rdfs:member),
I(rdf:_1), I(rdf:_2),
... , I(rdf:first),
I(rdf:rest), I(rdfs:seeAlso),
I(rdfs:isDefinedBy),
I(rdfs:comment), I(rdfs:label),
I(rdf:value)
|
|
rdfs:subPropertyOf rdfs:domain rdf:Property
.
rdfs:subClassOf rdfs:domain rdfs:Class
.
rdfs:domain rdfs:domain rdf:Property
.
rdfs:range rdfs:domain rdf:Property .
rdf:subject rdfs:domain rdf:Statement
.
rdf:predicate rdfs:domain rdf:Statement
.
rdf:object rdfs:domain rdf:Statement
.
rdf:first rdfs:domain rdf:List .
rdf:rest rdfs:domain rdf:List .
rdfs:subPropertyOf rdfs:range rdf:Property
.
rdfs:subClassOf rdfs:range rdfs:Class
.
rdfs:domain rdfs:range rdfs:Class .
rdfs:range rdfs:range rdfs:Class .
rdf:type rdfs:range rdfs:Class .
rdfs:comment rdfs:range rdfs:Literal
.
rdfs:label rdfs:range rdfs:Literal .
rdf:rest rdfs:range rdf:List .
rdf:Alt rdfs:subClassOf rdfs:Container
.
rdf:Bag rdfs:subClassOf rdfs:Container
.
rdf:Seq rdfs:subClassOf rdfs:Container
.
rdfs:ContainerMembershipProperty rdfs:subClassOf
rdfs:Property .
rdfs:isDefinedBy rdfs:subPropertyOf rdfs:seeAlso
.
rdf:XMLLiteral rdf:type rdfs:Datatype
.
rdfs:Datatype rdfs:subClassOf rdfs:Class
.
rdf:_1 rdf:type
rdfs:ContainerMembershipProperty .
rdf:_2 rdf:type rdfs:ContainerMembershipProperty
.
...
|
The truth of the axiomatic triples could be stated as conditions
on IEXT and ICEXT, but it is convenient to use the truth-of-triples
formulation. Similarly, the conditions on IC and IP in the first
table could be stated as axiomatic triples with property
rdf:type and objects rdfs:Class and
rdfs:Property respectively.
Since ICEXT(I(rdfs:Resource)) is
the universe, everything has rdfs:Resource as an
rdf:type value, and every class is a subclass of
rdfs:Resource.Such assertions would be redundant,
therefore.
Similarly, some domain and range assertions are omitted from the
above table; in those cases, the domain or range of the property
may be taken to be rdfs:Resource, i.e. the universe;
such range and domain assertions are essentially vacuous.
The semantics given here for rdfs:range and
rdfs:domain do not entail that superclasses of domains
or ranges of a property must also be domains and ranges of that
property. Semantic extensions MAY strengthen the domain and range
semantic conditions to the following:
|
<x,y> is in IEXT(I(rdfs:range)) if and
only if (if <u,v> is in IEXT(x) then v is in
ICEXT(y))
|
|
<x,y> is in IEXT(I(rdfs:domain)) if and
only if (if <u,v> is in IEXT(x) then u is in
ICEXT(y))
|
This stronger condition will not effect any class-membership
entailments on the elements of the domains and ranges of the
property. The semantics given here was chosen because it is
sufficient for all normal uses of these terms and allows some
subtleties in class reasoning.
Note that datatypes are considered to be
classes. As illustrated by the semantic condition on the class
extension of rdf:XMLLiteral, the members of a datatype
class are the values of the datatype. This is explained in more
detail in section 3.4 below.
We do not attempt to give a pictorial diagram of an
rdfs-interpretation.
Although the semantic conditions on rdfs-interpretations include
the intuitively sensible condition that
ICEXT(I(rdfs:Literal)) must be a subset of LV, there is no way to impose this condition
by any RDF assertion or syntactic closure rule. This limitation is
due to the fact that RDF does not allow literals to occur in the
subject position of a triple, so there are severe restrictions on
what can be said about literals in RDF. Similarly, while
properties may be asserted of the class rdfs:Literal,
none of these can be validly transferred to literals
themselves.
For example, a triple of the form
<ex:a> rdf:type rdfs:Literal .
is consistent even though 'ex:a' is a uriref rather
than a literal. What it says is that I(ex:a) is a
literal value, ie that the uriref 'ex:a'
denotes a literal value. It does not specify exactly which
literal value it denotes.
Note that the interpolation lemma guarantees that any triple
containing a simple literal object entails a similar triple with a
bnode as object:
<ex:a> <ex:b> "10" .
entails
<ex:a> <ex:b> _:xxx .
This means that literal denotes 'something', which could
therefore also be named, at least in principle, by a uriref.
3.4 Datatyped
interpretations
A datatype is an entity characterized by a set of character
strings called lexical forms and a mapping from that set
to a set of values. (The built-in datatype
rdf:XMLLiteral,
exceptionally, allows pairs in its lexical space.) Exactly how
these sets are defined is a matter external to RDF. Since the set
of possible datatypes is open-ended, we will assume that datatype
interpretations are defined relative to a particular set of
datatypes, and refer to D-interpretations where D is a set
of datatypes, which we will call recognized datatypes.
Urirefs which denote recognized datatypes are required to have the
same denotation in all D-interpretations, so recognizing a datatype
amounts to fixing the meaning of a uriref.
The set of recognized datatypes always includes
rdf:XMLLiteral and may include the XML Schema, part 2
built-in datatypes defined in [XML-SCHEMA2], which we will refer to as XSD
and use the Qname prefix xsd:. In any
XSD-interpretation, any uriref of the form
http://www.w3.org/2001/XMLSchema#sss will be
understood to denote the datatype named sss in [XML-SCHEMA2]
We will describe the semantic conditions in terms of a mapping
L2V from datatypes to their lexical-to-value mappings; the valid
lexical forms of a datatype d constitute the domain of L2V(d), and
the range of L2V(d) is the set of elements of the value space of d.
Recall that the set LV is required to include all members of all
datatype value spaces, so that the range of L2V(d) must be a subset
of LV.
A D-interpretation of a graph G is an
rdfs-interpretation I of V, where V contains the vocabulary of G,
which satisfies the following extra conditions on all datatypes
other than the built-in datatype:
ICEXT(I(rdfs:Datatype)) = D |
| For any typed literal "sss"^^ddd or "sss"@ttt^^ddd in G,
if I(ddd) is in D and 'sss' is a valid lexical form for
I(ddd) then IL("sss"^^ddd) = L2V(I(ddd))(sss) |
| For any typed literal "sss"^^ddd or "sss"@ttt^^ddd in G,
if I(ddd) is in D and 'sss' is not a valid lexical form for
I(ddd) then IL("sss"^^ddd) is not in LV |
| If x is in D, then ICEXT(x) is the value space of L2V(x)
and is a subset of ICEXT(I(rdfs:Literal)) |
The first condition says that membership in the class
rdfs:Datatype means the same as being a recognized
datatype. Thus, the inclusion of a triple of the form
<ex:somedatatype> rdf:type rdfs:Datatype
.
in an RDF graph can be understood as a claim that
ex:somedatatype identifies a recognized datatype. The
semantic conditions on rdfs-interpretations have the consequence
that the built-in datatype rdf:XMLLiteral is a
recognized datatype in all RDFS interpretations, and therefore in
all D-interpretations for any D.
The second condition says that the meaning of any typed literal
which uses a recognized datatype is the value of the literal
character string under that datatype, and that the language tag, if
present, is ignored. For example, if I is an XSD-interpretation
then I("15"^^xsd:decimal) must be the number fifteen.
Notice that this applies only to datatypes in D; typed literals
whose type is not a recognized datatype are treated as before, i.e.
as denoting some unknown thing. This means that their meanings can
be further restricted by adding a suitable extra datatype to the
set of recognized datatypes.
The third condition requires that an 'ill-formed' typed literal,
i.e. one where the literal string is not in the lexical space of
the datatype, not denote any literal value. Intuitively, such a
name does not denote any value, but in order to avoid the semantic
complexities which arise from empty names, we require such a typed
literal to denote an 'arbitrary' value. Thus for example, if D
contains the XML schema datatypes, then all that can be concluded
about I("arthur"^^xsd:decimal) is that it is
not in ICEXT(I(rdfs:Literal)). Any graph in
which a typed literal denotes a non-literal value is a datatype
violation.
The semantic conditions for the built-in datatype
rdf:XMLLiteral have been described in previous
sections; but in a datatyped interpretation, in addition, a graph
which contains a literal with a non-well-formed XML string or an
illegal language tag, and which is typed with
rdf:XMLLiteral is always considered a datatype
violation. These semantic conditions are exactly similar to the
above if one defines the lexical space of
rdf:XMLLiteral as the set of all XML documents and all
pairs of XML documents and language tags, and
L2V(I(rdf:XMLLiteral)) as XML canonicalization. The
possible inclusion of language tags makes this a special case,
however: in all other cases, RDF ignores any language tags which
occur in typed literals.
The final condition indicates that RDF treats
datatypes as classes, i.e. they are assumed to have a class
extension, which is required to be the set of items in the value
space of the datatype. All the members of all such datatype classes
are required to be literal values.
ICEXT(I(rdf:XMLLiteral)) is the set of all well-formed
canonical XML documents in any D-interpretation I.
RDF does not itself impose any identity conditions on elements
in value spaces, nor assume any subclass relationships between
datatype value classes. Information about such relationships should
be obtained from the specifications of the datatypes
themselves.
The treatment of unknown types provides a trivial proof of the
following lemma:
Datatype monotonicity lemma. If D is a subset
of D' and S D-entails E, then S D'-entails E.
It is possible for an RDF graph to have no D-interpretation
which satisfies it. For example, XML Schema requires that the value
spaces of xsd:string and xsd:decimal to
be disjoint, so it is impossible to construct a XSD-interpretation
satisfying the
graph
<ex:a> <ex:b> "25"^^xsd:decimal .
<ex:b> rdfs:range xsd:string .
This situation could be characterized by saying that the graph
is XSD-inconsistent, or more generally as a datatype
clash. Note that it is possible to construct a satisfying
rdfs-interpretation for this graph, but any such interpretation,
when extended to an XSD-interpretation, would violate the XSD
conditions, since the class extensions of
I(xsd:decimal) and I(xsd:string) would
have a nonempty intersection.
Datatype clashes are the only inconsistencies recognized by this model theory. The definition of entailment means that a
D-inconsistent graph D-entails any RDF graph; however, it will
usually not be appropriate to consider such 'trivial' entailments
as useful consequences, since they are not valid rdf- or rdfs-
entailments.
This semantics for datatypes is minimal. It makes no provision
for associating a datatype with a property
so that it applies to all values of the property, for example, and
does not provide any way of explicitly asserting that a blank node
denotes a particular value under a datatype mapping. We expect that
semantic extensions and future versions of RDF will impose more
elaborate datatyping conditions. Semantic extensions may also refer
to other kinds of information about a datatype, such as orderings
of the value space.
We will say that S rdf-entails E (S rdfs-entails
E, S D-entails E) when every rdf-interpretation (every
rdfs-interpretation, every interpretation datatyped with respect to
D) which satisfies every member of S also satisfies E. This follows
the wording of the definition of simple
entailment in section 2, but refers only to rdf- , rdfs- or
D-interpretations instead of all simple interpretations. These are
examples of vocabulary entailment,
i.e. entailment relative to a set of interpretations which satisfy
extra semantic conditions on a vocabulary.
It is easy to see that the lemmas in section 2 do not hold for
vocabulary entailment. For example, the triple
rdf:type rdf:type rdf:Property .
is true in every rdf-interpretation, and hence rdf-entailed by
the empty graph, which immediately contradicts the interpolation
lemma for rdf-entailment.
Rather than develop a separate theory of the syntactic
conditions for recognizing entailment for each special vocabulary,
we will use a general technique for reducing these broader notions
of entailment to simple entailment, by defining the closure
of an RDF graph relative to a set of semantic conditions. The basic
idea is to rewrite the semantic conditions as a set of syntactic
inference rules, and define the closure to be the result of
applying those rules to exhaustion. The resulting graphs will
contain RDF triples which explicitly state all the special meanings
embodied in the extra semantic conditions, in effect axiomatizing
them in RDF itself. A graph rdf-entails (rdfs-entails) another just
when its rdf-closure (rdfs-closure) simply entails it. It is not
possible to provide such a tight result for D-entailment closures
since the relevant semantic conditions require identities which
cannot be stated in RDF.
The notion of closure used here is purely a formal device to
relate two notions of entailment. We do not mean to suggest that
closure rules should be used as a computational technique, or that
actually generating the full closure would be the best process to
use in order to determine vocabulary entailment.
Closure rules correspond to implication axioms in the
Lbase translation given in the appendix.
The rdf-closure of
an RDF graph E is the graph got by adding triples to E according to
the following (very simple) rules:
1. Add the following triple (which is true in any
rdf-interpretation):
rdf:nil rdf:type rdf:List .
2. Apply the following rules recursively to generate all legal
RDF triples (i.e. until none of the rules apply or the graph is
unchanged.) Here xxx and yyy stand for any uriref, bNode or
literal, aaa for any uriref.
|
if E contains |
then add |
| rdf1 |
xxx aaa yyy . |
aaa rdf:type rdf:Property . |
| rdf2a |
xxx aaa "yyy"^^rdf:XMLLiteral
.
where yyy is a well-formed XML document
|
xxx aaa "zzz"^^rdf:XMLLiteral
.
where zzz is a well-formed XML document with the same
XML canonical form as yyy.
|
| rdf2b |
xxx aaa
"yyy"@ttt^^rdf:XMLLiteral
.
where yyy is a well-formed XML document and ttt is a
language tag
|
xxx aaa
"zzz"@ttt^^rdf:XMLLiteral
.
where zzz is any well-formed XML document such that the
canonical form of the XML document yyy with the language
tag ttt is the same as the canonical form of zzz with
language tag ttt.
|
Notice that rdf1 immediately generates the triple
rdf:type rdf:type rdf:Property .
which expresses a central semantic property of rdf
interpretations.
The following lemma is the basic result on rdf-entailment, and
illustrates a general pattern of how to characterize vocabulary
entailment syntactically.
RDF entailment
lemma. S rdf-entails E if and only if the rdf-closure of
the merge of S simply entails E.
The result is rather obvious, but a complete proof is given in
the appendix to illustrate the proof method.
The rather awkward statement of rules rdf2a and b is necessary
to ensure that the entailment lemma holds when the conclusion E
contains a non-canonicalized XML literal. In practice, it would be
sufficient to apply a canonicalization operation to both S and E,
taking appropriate account of language tags, and then ignore these
rules.
RDFS closures require more complex rules to reflect the
consequences of the more elaborate semantic constraints on the rdfs
vocabulary.
The rdfs-closure
of an RDF graph E is the graph got by adding triples to E according
to the RDF closure rules together with the following rules:
1. Add the RDFS axiomatic triples from the table in section 3.3, and
all the following triples. There are many other triples which are
true in every rdfs-interpretation, but they will be generated from
these by the closure rules.
rdf:type rdfs:range rdfs:Class .
rdfs:Resource rdf:type rdfs:Class .
rdfs:Literal rdf:type rdfs:Class .
rdf:Statement rdf:type rdfs:Class .
rdf:nil rdf:type rdf:List .
rdf:XMLLiteral rdf:type rdfs:Datatype .
rdf:subject rdf:type rdf:Property .
rdf:predicate rdf:type rdf:Property .
rdf:object rdf:type rdf:Property .
rdf:first rdf:type rdf:Property .
rdf:rest rdf:type rdf:Property .
2. Add all triples of the following forms. This is an infinite
set because the RDF container vocabulary is infinite. However,
since none of these triples entail any of the others, it is only
necessary, in practice, to add the triples which use those
container properties which actually occur in any particular graph
or set of graphs in order to check the rdfs-entailment relation
between those graphs.
rdf:_1 rdf:type rdfs:ContainerMembershipProperty .
rdf:_2 rdf:type rdfs:ContainerMembershipProperty .
...
3. Apply the following rules recursively to generate all legal
RDF triples (i.e. until none of the rules apply or the graph is
unchanged.) Here, xxx, yyy and zzz stand for any uriref, bNode or
literal, aaa for any uriref, and uuu for any uriref or bNode (but
not a literal).
| |
If E contains: |
then add: |
| rdf1 |
xxx aaa yyy .
|
aaa rdf:type rdf:Property . |
| rdfs2 |
xxx aaa yyy .
aaa rdfs:domain zzz .
|
xxx rdf:type zzz . |
| rdfs3 |
xxx aaa uuu .
aaa rdfs:range zzz .
|
uuu rdf:type zzz . |
| rdfs4a |
xxx aaa yyy . |
xxx rdf:type rdfs:Resource . |
| rdfs4b |
xxx aaa uuu . |
uuu rdf:type rdfs:Resource . |
| rdfs5a |
aaa rdfs:subPropertyOf bbb
.
bbb rdfs:subPropertyOf ccc .
|
aaa rdfs:subPropertyOf ccc
. |
| rdfs5b |
xxx rdf:type rdf:Property . |
xxx rdfs:subPropertyOf xxx
. |
| rdfs6 |
xxx aaa yyy .
aaa rdfs:subPropertyOf bbb .
|
xxx bbb yyy . |
| rdfs7a |
xxx rdf:type rdfs:Class .
|
xxx rdfs:subClassOf rdfs:Resource . |
| rdfs7b |
xxx rdf:type rdfs:Class . |
xxx rdfs:subClassOf xxx . |
| rdfs8 |
xxx rdfs:subClassOf yyy
.
yyy rdfs:subClassOf zzz .
|
xxx rdfs:subClassOf zzz . |
| rdfs9 |
xxx rdfs:subClassOf yyy
.
aaa rdf:type xxx .
|
aaa rdf:type yyy . |
| rdfs10 |
xxx rdf:type rdfs:ContainerMembershipProperty
. |
xxx rdfs:subPropertyOf rdfs:member . |
The outputs of these rules will often trigger others. For
example, these rules will generate the complete transitive closures
of all subclass and subproperty heirarchies, together with all of
the resulting type information about everything which can be
inferred to be a member of any of the classes, and will propagate
all assertions in the graph up the subproperty heirarchy,
re-asserting them for all super-properties. rdfs1 will generate
type assertions for all the property names used in the graph, and
rdfs3 together with the first triple in the above list will add all
the types for all the class names used. Any subproperty or subclass
assertion will generate appropriate type assertions for its subject
and object via rdfs 2 and 3 and the domain and range assertions in
the RDFS axiomatic triple set. The rules will generate all
assertions of the form
xxx rdf:type rdfs:Resource .
for every xxx in V, and of the form
xxx rdfs:subClassOf rdfs:Resource .
for every class name; and several more 'universal' facts, such
as
rdf:Property rdf:type rdfs:Class .
However, it is easy to see that (with the restriction noted of
the infinite sets to those membership properties which occur in the
graph) the rules will indeed terminate on any finite RDF graph,
since there are only finitely many triples that can be formed from
a given finite vocabulary.
A similar result applies here as in the case of rdf-entailment,
though it takes considerably more work to prove:
RDFS
Entailment Lemma. S rdfs-entails a graph E if and only if
the rdfs-closure of the merge of S simply entails E.
We note in passing that the stronger 'iff' semantic conditions
on rdfs:domain and rdfs:range mentioned
in section 3.3 would be captured by removing rules rdfs4a and
rdfs4b, and adding the additional rules
| rdfs 2a |
xxx rdfs:domain yyy .
yyy rdfs:subClassOf zzz
.
|
xxx rdfs:domain zzz . |
| rdfs 3a |
xxx rdfs:range yyy .
yyy rdfs:subClassOf zzz
.
|
xxx rdfs:range zzz . |
| rdfs 4a' |
xxx aaa yyy . |
aaa rdfs:domain rdfs:Resource . |
| rdfs 4b' |
xxx aaa yyy . |
aaa rdfs:range rdfs:Resource . |
and that these would provide a redundant inference path to the
conclusions of rdfs 2 and 3.
4.3 Datatype
entailments (Informative)
In order to capture datatype entailment in terms of assertions
and closure rules, the rules need to refer to information supplied
by the datatypes themselves; and to state the rules it is necessary
to assume syntactic conditions which can only be checked by
consulting the datatype sources. Since such questions are beyond
the scope of RDF, it is impossible to prove an entailment lemma for
datatype closures analogous to those for RDF and RDFS.
Since language tags play no role in the meaning of a typed
literal, they can in practice be ignored, and any literal of the
form "sss"@ttt^^ddd, where ddd is not rdf:XMLLiteral,
treated as identical to the same literal without the language tag,
"sss"@ddd. We can capture this convention by special rules which
allow language tags to be inserted or removed:
| rdfD 0a |
aaa ppp "sss"@ttt^^ddd . |
aaa ppp "sss"^^ddd . |
| rdfD 0b |
aaa ppp "sss"^^ddd . |
aaa ppp "sss"@uuu^^ddd . |
Here, ttt and uuu are any legal language tags and ddd is
anything other than rdf:XMLLiteral. Clearly, these
rules together can replace any language tag by any other.We also
have a rule applying to all recognized datatypes, which requires
their elements to be recognized as elements of
rdfs:Literal:
| rdfD 0c |
xxx rdf:type rdfs:Datatype . |
xxx rdfs:subClassOf rdfs:Literal . |
For each kind of information which is available about a
datatype, we can give inference rules for information of that kind,
which can be thought of as extending the table of RDFS closure
rules. These should be understood as applying to datatypes other
than the built-in datatype, the rules for which are part of the RDF
closure rules.
The basic information specifies, for each literal string,
whether or not it is a legal lexical form for the dataype. This
corresponds to the following rule, for each string sss that is a
legal lexical form for the datatype ddd. Here _:xxx is a new blank
node, i.e. one that does not appear elsewhere in the graph:
| rdfD 1 |
ddd rdf:type rdfs:Datatype .
aaa ppp "sss"^^ddd .
|
aaa ppp _:xxx .
_:xxx rdf:type ddd .
|
Suppose it is known that two lexical forms sss and ttt map to
the same value under the datatype ddd; then the following rule
applies:
| rdfD 2 |
ddd rdf:type rdfs:Datatype .
aaa ppp "sss"^^ddd .
|
aaa ppp "ttt"^^ddd . |
Suppose it is known that the lexical form sss of the datatype
ddd and the lexical form ttt of the datatype eee map to the same
value. Then the following rule applies:
| rdfD 3 |
ddd rdf:type rdfs:Datatype .
eee rdf:type rdfs:Datatype .
aaa ppp "sss"^^ddd .
|
aaa ppp "ttt"^^eee . |
Suppose that it is known that the value space of the datatype
ddd is a subset of that of the datatype eee. Then the following
rule applies:
| rdfD 4 |
ddd rdf:type rdfs:Datatype .
eee rdf:type rdfs:Datatype .
|
ddd rdfs:subClassOf eee . |
The rules rdfD2 and 3 are essentially
substitutions by virtue of equations between lexical forms. Such
equations may be capable of generating infinitely many conclusions,
e.g. it is valid to add any number of leading zeros to any numeral
and still be a correct lexical form for xsd:integer.
To avoid such correct but
unhelpful inferences, it is sufficient to restrict rdfD2 to cases
which replace a lexical form with the canonical form for the
datatype in question, when such a canonical form is defined. In
order for the rules to be complete, however, such canonicalization rules
would need to be applied to the conclusions as well as the
antecedents of any proposed entailments, and the corresponding
rules of type rdfD3 would need to reflect knowledge of identities
between canonical forms of the distinct datatype.
In particular cases other information might be available, which
could be expressed using a particular RDFS vocabulary. Semantic
extensions MAY define further such datatype-specific meanings.
Note that the rule rdfD 0c allows us to conclude that any
well-formed typed literal of a recognized datatype must denote
something in the class rdfs:Literal.
aaa ppp "sss"^^ddd .
ddd rdf:type rdfs:Datatype .
aaa ppp _:xxx .
_:xxx rdf:type ddd . (by rule rdfD 1)
ddd rdfs:subClassOf rdfs:Literal .
_:xxx rdf:type rdfs:Literal .
The rule rdfD1 is sufficient to expose a datatype clash, by a
chain of reasoning of the following form:
ppp rdfs:range ddd .
aaa ppp "sss"^^eee .
aaa ppp _:xxx .
_:xxx rdf:type eee . (by rule rdfD 1)
_:xxx rdf:type ddd . (by rule rdfs 3)
It may be useful to incorporate the assumption that any uriref
appearing in a typed literal is presumed to be a datatype, which
would be captured by the following rule. Note however that this is
not strictly valid, so represents a (small) semantic extension.
| rdfD -1 |
aaa ppp "sss"^^ddd .
|
ddd rdf:type rdfs:Datatype .
|
Datatype clashes and violations may be considered to be error
conditions. However, we note that such graphs are not strictly
ill-formed, and can be used to support valid RDFS entailments which
might be meaningful in certain contexts.
As noted in the introduction, an alternative way to specify RDF
interpretations is to give a translation from RDF into a formal
logic with a model
theory already attached, as it were. This 'axiomatic semantics'
approach has been suggested and used previously with various
alternative versions of the target logical language [Conen&Klapsing] [Marchiori&Saarela] [McGuinness&al]. Here we use a
version of first-order logic which was designed to provide a
semantic reference for such translations from web-based languages,
called Lbase [LBASE], which
uses a particularly efficient syntax.
To translate an RDF graph into the semantic reference language
Lbase, apply the following rules to each expression
noted. Each rule gives a translation TR[E] for the
expression E, to be applied recursively. To achieve a translation
which reflects a vocabulary entailment, add the axioms specified.
Each vocabulary includes all axioms and rules for preceding
vocabularies, so that the RDFS translation of a graph should
include the RDF translation as well as the RDFS axioms, and so
on.
This translation uses the Lbase logical expressions
Lbase:String and
Lbase:XMLthing, which are true respectively
of unicode character strings, and anything that is denoted by a
piece of well-formed XML syntax; and it introduces some terminology
in order to give a logical account of the meanings implicit in the
various literal constructions. The axioms given are sufficient to
define the intended meanings of the vocabulary used.
Lbase translation rules
| RDF expression E |
Lbase expression
TR[E] |
| a plain literal "sss" |
'sss', with all occurrences of the symbols
',\,(,),<,> prefixed with \ |
| a plain literal "sss"@tag |
the term pair(TR["sss"],
'tag') |
| a typed literal "sss"(@tag)^^ddd |
the term
L2V(TR["sss"],TR[ddd]) |
the uriref rdfs:Resource |
T |
a uriref of the form rdf:_nnn |
rdf-member(nnn) |
| any other uriref aaa |
aaa |
| a blank node |
a variable (one distinct variable per blank node) |
| a triple aaa rdf:type bbb . |
TR[bbb](TR[aaa])
and rdfs:Class(TR[bbb]) |
| any other triple aaa bbb ccc . |
TR[bbb](TR[aaa],
TR[ccc]) and
rdf:Property(TR[bbb]) |
| an RDF graph |
The existential closure of the conjunction of the
translations of all the triples in the graph. |
| a set of RDF graphs |
The conjunction of the translations of all the graphs. |
L2V(?y,?x) is a term denoting the value of the
lexical form ?y under the L2V mapping of the datatype ?x. Datatype
specifications in Lbase must include sufficient axioms
to define the appropriate values of L2V. This can be simply a
countably infinite set of equations stating the value for each
legal lexical string, eg all equations of the form
L2V('345',xsd:decimal)=345,
but other axiomatic theories can be used in some cases.
RDF axioms
|
rdf:type(?x,?y) implies ?y(?x)
rdf:Property(rdf:type)
rdf:List(rdf:nil)
pair(?x,?y)=pair(?u,?v) iff (?x=?u and ?y=?v) ;;
uniqueness for pairs, required by graph syntax rules.
Lbase:XMLThing(?x) implies
L2V(?x,rdf:XMLLiteral)=XMLCanonical(?x)
(Lbase:XMLThing(?x) and LanguageTag(?y)) implies
L2V(pair(?x,?y),rdf:XMLLiteral)=XMLCanonical(withLang(?x,?y))
|
The RDF treatment of XML special forms does not lend itself to
axiomatic description. The special function
XMLCanonical is intended to map well-formed XML
strings to their canonical forms. The meaning of this can be
expressed by a countable set of Lbaseequations, but is
probably more usefully encoded in practice by an XML
canonicalization algorithm. Similarly, the function
withLang maps an XML document and a language tag to
the similar document with that language tag attached; again, this
would be more usefully specified by an algorithm than by the
infinite collection of corresponding axioms, in practice. The
predicate LanguageTag is intended to be true of
syntactically correct XML language tags. Such axioms could be given
as a list of atomic assertions, one for each of the valid language
tags, and an assertion that all language tags were in the list.
RDFS axioms
|
T(?x)
rdfs:Class(?y) implies (?y(?x) iff rdf:type(?x,?y))
(rdfs:range(?x,?y) and ?x(?u,?v)) implies ?y(?v)
(rdfs:domain(?x,?y) and ?x(?u,?v)) implies ?y(?u)
(rdfs:subClassOf(?x ?y) iff
(rdfs:Class(?x) and rdfs:Class(?y) and (forall
(?u)(?x(?u) implies ?y(?u)))
)
(rdfs:subPropertyOf(?x,?y) iff
(rdf:Property(?x) and rdf:Property(?y) and
(forall (?u ?v)(?x(?u,?v) implies ?y(?u,?v)))
)
rdfs:ContainerMembershipProperty(?x) implies
rdfs:subPropertyOf(?x,rdfs:member)
rdf:XMLLiteral(?x) implies rdfs:Literal(?x)
Lbase:String(?y) implies
rdfs:Literal(?y)
LanguageTag(?x) implies
Lbase:String(?x)
(Lbase:String(?x) and LanguageTag(?y))
implies rdfs:Literal(pair(?x,?y))
rdfs:Datatype(rdf:XMLLiteral)
Lbase:NatNumber(?x) implies
rdfs:ContainerMembershipProperty(rdf-member(?x))
rdfs:Class(T)
rdfs:Class(rdf:Property)
rdfs:Class(rdfs:Class)
rdfs:Class(rdfs:Datatype)
rdfs:Class(rdf:Seq)
rdfs:Class(rdf:Bag)
rdfs:Class(rdf:Alt)
rdfs:Class(rdfs:Container)
rdfs:Class(rdf:List)
rdfs:Class(rdfs:ContainerMembershipProperty)
rdfs:Class(rdf:Statement)
rdf:Property(rdfs:domain)
rdf:Property(rdfs:range)
rdf:Property(rdfs:subClassOf)
rdf:Property(rdfs:subPropertyOf)
rdf:Property(rdfs:comment)
rdf:Property(rdf:predicate)
rdf:Property(rdf:subject)
rdf:Property(rdf:object)
rdf:Property(rdf:first)
rdf:Property(rdf:rest)
rdf:Property(rdfs:seeAlso)
rdf:Property(rdfs:isDefinedBy)
rdf:Property(rdfs:label)
rdf:Property(rdf:value)
;; the rest of the axioms are direct transcriptions of the
RDFS axiomatic triples listed earlier, using the RDF to
Lbase transcription rules.
rdfs:domain(rdfs:subPropertyOf,rdf:Property)
rdfs:domain(rdfs:subClassOf,rdfs:Class)
rdfs:domain(rdfs:domain,rdf:Property)
rdfs:domain(rdfs:range,rdf:Property)
rdfs:domain(rdf:subject,rdf:Statement)
rdfs:domain(rdf:predicate,rdf:Statement)
rdfs:domain(rdf:object,rdf:Statement)
rdfs:domain(rdf:first,rdf:List)
rdfs:domain(rdf:rest,rdf:List)
rdfs:range(rdfs:subPropertyOf,rdf:Property)
rdfs:range(rdfs:subClassOf,rdfs:Class)
rdfs:range(rdfs:domain,rdfs:Class)
rdfs:range(rdfs:range,rdfs:Class)
rdfs:range(rdf:type,rdfs:Class)
rdfs:range(rdfs:comment,rdfs:Literal)
rdfs:range(rdfs:label,rdfs:Literal)
rdfs:range(rdf:rest,rdf:List)
rdfs:subClassOf(rdfs:Datatype,rdfs:Literal)
rdfs:subClassOf(rdf:Alt,rdfs:Container)
rdfs:subClassOf(rdf:Bag,rdfs:Container)
rdfs:subClassOf(rdf:Seq, rdfs:Container)
rdfs:subClassOf(rdfs:ContainerMembershipProperty,rdf:Property)
rdfs:subPropertyOf(rdfs:isDefinedBy,rdfs:seeAlso)
|
The third and fourth axioms for domain and range can be changed
to 'if and only if' as suggested in section 3; these would then
have the consequence
rdfs:Property(?x) implies (rdfs:domain(?x,T) and
rdfs:range(?x,T))
RDF-D axioms
|
rdfs:Datatype(?x) implies ( LegalLexicalForm(?y,?x))
iff ?x(L2V(?y,?x)) )
( rdfs:Datatype(?x) and LegalLexicalForm(?y,?x) and ?x(?y))
implies rdfs:Literal(?y)
Lbase:XMLThing(?x) iff
LegalLexicalForm(?x,rdf:XMLLiteral)
|
Here, LegalLexicalForm(?y,?x) is true when ?y is a
character string which is a legal lexical for for the datatype ?x.
As with L2V, the corresponding axiomatic theory
depends on the particular datatype, but in the limit can be two
countably infinite sets of atomic sentences asserting for each
string whether or not it is a legal form for that datatype. Usually
these will conform to some regular pattern; for example, the
lexical forms for the datatype xsd:decimal can be
defined by infinitely many axioms of the form
LegalLexicalForm('345',xsd:decimal)
Subgraph
Lemma. A graph entails all its subgraphs.
Proof. Obvious, from definitions of subgraph and entailment. If the graph is true in I then
for some A, all its triples are true in I+A, so every subset of
triples is true in I. QED
Instance
Lemma. A graph is entailed by all its instances.
Proof. Suppose I satisfies E' and E' is an instance of E. Then for some mapping A on the
blank nodes of E', I+A satisfies every triple in E'. For each
blank node b in E, define B(b)=I+A(c), where c is the blank node
or name that is substituted for b in E', or c=b if nothing was
substituted for it. Then I+B(E)=I+A(E')=true, so I satisfies E.
But I was arbitrary; so E' entails E.
QED.
Merging
lemma. The merge of a set S of
RDF graphs is entailed by S, and entails every member of S.
Proof. Obvious, from definitions of entailment and merge. All members of S are
true iff all triples in the merge of S are true.
QED.
This means that, as noted in the text, we can treat a set of
graphs as a single graph when discussing satisfaction and
entailment. We will do this from now on, and refer to an
interpretation of a set of graphs, a set of graphs entailing a
graph, and so on, meaning in each case to refer to the merge of the
set of graphs, and references to 'graph' in the following can be
taken to refer to graphs or to sets of graphs.
For ground graphs, the subgraph lemma can
be strengthened to provide simple necessary and sufficient
conditions for entailment.
Conjunction
Lemma.If E is ground, then I satisfies E if and only if it satisfies every
triple in E.
Proof. Obvious, from definition of denotation for ground graphs.
QED
Plain Subgraph
Lemma. If E and E' are ground, then E entails E' if
and only if E' is a subgraph of E.
Proof. 'If' follows directly from subgraph
lemma; 'only if' follows from previous lemma and definition of entailment. QED
To prove the subsequent lemmas we introduce a way of
constructing an interpretation of a graph by using the lexical
items in the graph itself. (This was
Herbrand's idea.) Given a graph G, the Herbrand
interpretation of G , Herb(G), is the interpretation I defined
as follows. The universe IR of I is the set of names and blank
nodes in G; IS is the identity mapping on the vocabulary of G, IL
maps XML documents to their canonical forms, and is otherwise is
the identity mapping on typed literals, IEXT is defined by:
<s,o> is in IEXT(p) just when there is a triple in the graph
of the form s p o ., and IP is defined to be the set of urirefs
which occur either as arc labels in the graph, or as subjects of
triples of the form s rdf:type rdf:Property .
(This follows the standard definition of Herbrand interpretation
but has some special features for RDF. The first part of the IP
condition ensures that Herb(G) is an interpretation, and the second
is a technical requirement for some of the later proofs. The XML
condition is needed to make sure that Herbrand interpretations
satisfy the built-in datatype rules.)
It is easy to see that Herb(G) is an interpretation which
satisfies G. Clearly it satisfies all the ground triples in G; and
if A is the identity mapping on blank nodes of G, then Herb(G)+A
satisfies the entire graph; so Herb(G) satisfies G.
Herbrand interpretations treat urirefs and non-XML typed
literals in the same way as simple literals, i.e. as denoting their
own syntactic forms. Of course this may not be what was intended by
the writer of the RDF, but the lemma shows that any graph
can be interpreted in this way. This therefore establishes
the
Satisfaction
Lemma. Any RDF graph has a satisfying interpretation.
QED
Herbrand interpretations have some very useful properties. The
Herbrand interpretation of a graph is a 'minimal' interpretation,
which is 'just enough' to make the graph true; and so any
interpretation which satisfies the graph must in a sense agree with
the Herbrand interpretation; and of course any interpretation which
does agree with the Herbrand interpretation will satisfy the graph.
Taken together and made precise, these observations provide a way
to characterize entailment between graphs in terms of Herbrand
interpretations.
Herb(G) satisfies G, but only just. Anything that goes beyond
what is said by the graph itself is not satisfied by the Herbrand
interpretation. This sense of 'going beyond' can be characterized
both semantically and syntactically.
The semantic version refers to subinterpretations and
isomorphisms between interpretations. Given two interpretations I
and J, say that I is a subinterpretation of J , and write
I << J, if the vocabulary of I is a subset of the vocabulary
of J and there is a projection mapping from IR into JR, IS into JS,
IL into JL and IEXT into JEXT such that any triple is true in J if
it is true in I; and that I and J are isomorphic if each
is a subinterpretation of the other. Obviously if I << J and
I satisfies E then J satisfies E, so if I and J are isomorphic then
they satisfy the same graphs. The key property of Herbrand
interpretations, proved below, is that I satisfies E just when
Herb(E) << I.
The syntactic version can be described in terms of instances and
subgraphs. Say that a graph E' is
separable from a graph E if no instance of E' is a subgraph
of E. In particular, a ground graph is separable from E just
when it is not a subgraph of E, and a ground triple is separable
just in case it isn't in the graph. Graphs which are not separable
from E are entailed by E, by the subgraph and instance lemmas; but
for all others, there is a way to arrange the world so that they
are false and E true.
In particular, if E' is separable from E then Herb(E) does not
satisfy E'; for suppose that it did, then for some mapping B from
the blank nodes of E' to the blank nodes and vocabulary of E,
Herb(E)+B satisfies E', which means that for every triple
s p o .
in E', the triple
[Herb(E)+B](s) p [Herb(E)+B](o) .
occurs in E, by definition of Herb(E). But the set of these
triples is an instance of E', by construction; so E' is not
separable from E.
This means that we can state an exact correspondence between
separability and Herbrand interpretations:
Herbrand separation lemma. Herb(E) satisfies E'
if and only if E' is not separable from E. QED
Probably the most useful property of Herbrand interpretations is
the following. The version of this lemma for first-order logic,
called Herbrand's theorem, is the basis of all the logical
completeness
results.
Herbrand lemma. I satisfies E if and only if
Herb(E) << I.
Proof. Suppose I satisfies E. The
interpretation mapping I itself defines a projection mapping from
Herb(E) into I, and if I satisfies E then I makes true all the
triples that Herb(E) makes true, so Herb(E) << I.
Suppose Herb(E) << I. Since Herb(E) satisfies E, there
is a mapping A from the blank nodes of E so that I+A satisfies
all the triples from E, so I satisfies E
QED
The following is an immediate consequence:
Herbrand entailment lemma. S entails E if and
only if Herb(S) satisfies E.
Proof. Suppose S entails E. Herb(S) satisfies
S, so Herb(S) satisfies E.
Now suppose Herb(S) satisfies E. If I satisfies S then Herb(S)
<< I; so I satisfies E. But I was arbitrary; so S entails
E.
QED
Putting the separation and entailment results together, it is
obvious that S entails E if and only if E is not separable from S.
This is simply a restatement of the:
Interpolation Lemma. S entails
E if and only if a subgraph of S is an instance of E.
QED.
The following are direct consequences of the interpolation
lemma:
Anonymity lemma
1. Suppose E is a lean graph and E' is a proper
instance of E. Then E does not entail E'.
Proof. Since E' is a proper instance and E is lean, E' is separable from E. Therefore E
does not entail E' QED
Anonymity lemma
2. Suppose that E is a lean graph and that E' is like E
except that two distinct blank nodes in E have been identified in
E'. Then E does not entail E'.
Proof. We have to show that E' is separable
from E.
First we assume that the blank nodes occur in two distinct
triples in E. Suppose that E contains the triples
S1 P1 _:x1 .
S2 P2 _:x2 .
where E' contains the subgraph consisting of the triples
S1 P1 _:x .
S2 P2 _:x .
Since E is lean, it contains no other triples of the form S1
P1 O' or S2 P2 O'. Therefore, this subgraph has no instances in
E, so E' is separable from E. The arguments for the cases where
the blank nodes occur in other positions in the triples are
similar.
The only remaining case is where E contains a single triple
with two blank nodes which are identified in E':
_:x1 P _:x2 .
where E' contains
_:x P _:x .
The argument here is similar; there is no substitution for the
blank node in the second graph which can produce the first
graph.
Since E' is separable from E, E does not entail E'.
QED.
Skolemization is a
syntactic transformation routinely used in automatic inference
systems in which existential variables are replaced by 'new'
functions - function names not used elsewhere - applied to any
enclosing universal variables. While not itself strictly a valid
operation, skolemization adds no new content to an expression, in
the sense that a skolemized expression has the same entailments as
the original expression provided they do not contain the new skolem
functions.
In RDF, skolemization simplifies to the special case where an
existential variable is replaced by a 'new' name, i.e. a uriref
which is guaranteed to not occur anywhere else.(Using a literal
would not do. Literals are never 'new' in the required sense, since
their meaning is fixed.) To be precise, a skolemization of
E (with respect to V) is a ground instance of E with respect to a
vocabulary V which is disjoint from the vocabulary of E.
The following lemma shows that skolemization has the same
properties in RDF as it has in conventional logics. Intuitively,
this lemma shows that asserting a skolemization expresses a similar
content to asserting the original graph, in many respects. In
effect, it simply gives 'arbitrary' names to the anonymous entities
whose existence was asserted by the use of blank nodes. However,
care is needed, since these 'arbitrary' names have the same status
as any other urirefs once published. Also, skolemization would not
be an appropriate operation when applied to anything other than the
antecendent of an entailment. A skolemization of a query would
represent a completely different query.
Skolemization
Lemma. Suppose sk(E) is a skolemization of E with respect
to V. Then sk(E) entails E; and if sk(E) entails F and the
vocabulary of F is disjoint from V, then E entails F .
Proof. sk(E) entails E by the interpolation
lemma.
Now, suppose that sk(E) entails F where F shares no vocabulary
with V; and suppose I is some interpretation satisfying E. Then
for some mapping A from the blank nodes of E, I+A satisfies E.
Define an interpretation I' of the vocabulary of sk(E) by:
IR'=IR, IEXT'=IEXT, I'(x)=I(x) for x in the vocabulary of E, and
I'(x)=[I+A](y) for x in V, where y is the blank node in E that is
replaced by x in sk(E).Clearly I' satisfies sk(E), so I'
satisfies F. But I'(F)=[I+A](F) since the vocabulary of F is
disjoint from that of V; so I satisfies F. So E entails F.
QED.
RDF
closure lemma. The Herbrand interpretation of the
rdf-closure of E is an rdf-interpretation of E.
Proof. This follows from a comparison of the
rdf closure rules with the semantic conditions on an
rdf-interpretation. Although the argument is very simple in
this case, we give it here in full to illustrate the general
technique. Basically, one can 'read off' the semantic conditions
from the triples in the closure graph itself, taking into account
the minimality of the Herbrand interpretation. We will refer to
the rdf-closure of E as rdfclos(E), and for orthographic
convenience we refer to Herb(rdfclos(E)) as H in the rest of the
proof, and write IPH to indicate the IP mapping of the
interpretation H.
Clearly, H satisfies the triples
rdf:nil rdf:type rdf:List .
rdf:type rdf:type rdf:Property .
so IPH contains rdf:type, which is
H(rdf:type), so it satisfies the first condition.
The third condition is then an obvious consequence of the
definition of property extensions in Herbrand
interpretations.
The second closure rules implies that if rdfclos(E) contains
the triple s p o ., then it also contains the triple
p rdf:type rdf:Property .
so by the definition of Herbrand interpretation, HP contains
p. This establishes that the 'if' part of the second
condition.
To show the 'only if' part, suppose x is in IPH.
Then either x rdf:type rdf:Property. is in
rdfclos(E) or s x o. is in rdfclos(E) for certain s and o. In the
latter case, the closure rules show that again,
x rdf:type rdf:Property.
is in rdfclos(E). So in all cases, <x, H(rdf:Property)>
is in HEXT(H(rdf:type)). QED.
RDF
entailment lemma. S rdf-entails E if and only if the
rdf-closure of S simply entails E.
Proof. The 'if' case follows from the fact
that the rdf closure rules are all rdf-valid, which can be
checked case by case; since S rdf-entails rdfclos(S), if
rdfclos(S) entails E then S rdf-entails E.
Now suppose S rdf-entails E and I is a simple interpretation
of rdfclos(S). Herb(rdfclos(S)) satisfies rdfclos(S) by
construction. Since rdfclos(S) contains S, Herb(rdfclos(S))
satisfies S and, by the RDF closure lemma, is an RDF
interpretation; so, since S rdf-entails E, Herb(rdfclos(S))
satisfies E. But Herb(rdfclos(S)) << I by the Herbrand
lemma; so I satisfies E. But I was arbitrary, so S entails E.
QED.
RDFS
Closure Lemma. The Herbrand interpretation of the
rdfs-closure of E is an rdfs-interpretation of E.
Proof.(Sketch) As in the proof of the RDF
closure lemma, this follows from a point-by-point comparison of
the rdfs closure rules with the semantic conditions on an
rdfs-interpretation, and uses the minimality of the Herbrand
interpretation to establish the necessary conditions on the
interpretation. A full proof would be long but tedious. We will
illustrate the form of the argument by considering some typical
cases in detail.
In some cases the clearest way to argue this is to show the
converse, by demonstrating that a simple interpretation of
rdfs-clos(E) that violates any of the semantic conditions for an
rdfs-interpretation of E would thereby make some triple in
rdfs-clos(E) false, so could not be the Herbrand
interpretation.
For example, if I violates the condition on
IEXT(I(rdfs:range)), then there exist x, y, u and v
in IR with <x,y> in IEXT(I(rdfs:range)),
<u,v> in IEXT(x) but v not in ICEXT(y). Projecting these
entities into the Herbrand interpretation with the identity map
for blank nodes will identify two triples
aaa rdfs:range bbb .
ccc aaa ddd .
where I(aaa)=x, I(bbb)=y, I(ccc)=u and I(ddd)=v; but I makes
the triple
ddd rdf:type bbb .
false, since I(ddd) is not in ICEXT(I(bbb)); and by the
closure rule rdfs3, this triple is in rdfsclos(E); so I fails to
satisfy the rdfs closure.
(sketch) QED.
RDFS
Entailment Lemma. S rdfs-entails E iff the rdfs-closure of
S simply entails E.
Proof. Exactly similar to proof of RDF
entailment lemma. QED.
Appendix C: Glossary of terms
(informative).
Antecedent (n.) In an inference, the
expression(s) from which the conclusion is derived. In an entailment relation, the
entailer. Also assumption.
Assertion (n.) (i) Any expression
which is claimed to be true. (ii) The act of claiming something to
be true.
Class
(n.) A general concept, category or classification. Something used primarily to
classify or categorize other things. Formally, a resource of type
rdfs:Class with an associated set of resources all of which
have the class as a value of the rdf:type property.
Classes are often called 'predicates' in the formal logical
literature.
(RDF distinguishes class from set, although the two are often
identified. Distinguishing classes from sets allows RDF more
freedom in constructing class heirachies, as explained earlier.)
Complete (adj., of an inference
system). Able to draw all valid inferences. See Inference. Also used with a qualifier:
able to draw all valid inferences in a certain limited form or kind
(e.g.between expressions in a certain normal form, or meeting
certain syntactic conditions.)
Consequent (n.) In an inference,
the expression constructed from the antecedent. In an entailment relation, the
entailee. Also conclusion.
Correct (adj., of an inference
system). Unable to draw any invalid inferences. See
Inference.
Entail (v.),
entailment(n.). A semantic relationship between
expressions which holds whenever the truth of the first guarantees
the truth of the second. Equivalently, whenever it is logically
impossible for the first expression to be true and the second one
false. Equivalently, when any interpretation which satisfies the first also satisfies the second.
(Also used between a set of expressions and an expression.)
Equivalent (prep., with
to) True under exactly the same conditions; making
identical claims about the world, when asserted. Entails and is entailed
by.
Extensional (adj., of a logic) A
set-based theory or logic of classes, in which classes are
considered to be sets, properties considered to be sets of
<object, value> pairs, and so on. A theory which admits no
distinction between entities with the same extension. See Intensional.
Formal (adj.) Couched in language
sufficiently precise as to enable results to be established using
conventional mathematical techniques.
Iff
(conj.) Conventional abbreviation for 'if and only if'. Used to
express necessary and sufficient conditions.
Inconsistent (adj.),
false under all interpretations; impossible to satisfy.
Inconsistency (n.), any inconsistent expression or
graph.
Indexical (adj., of a logic
expression) having a meaning which implicitly refers to the context
of use. Examples from English include words like 'here', 'now',
'this'.
Inference (n.) An
act or process of constructing new expressions from existing
expressions, or the result of such an act or process. Inferences
corresponding to entailments are described as correct
or valid. Inference rule, formal
description of a type of inference; inference
system, set of inference rules; also, software which
generates inferences or checks inferences for validity.
Intensional (adj., of a logic)
Not extensional. A
logic which allows distinct entities with the same extension.
(The merits and demerits of intensionality have been extensively
debated in the philosophical logic literature. Extensional semantic
theories are simpler, and conventional semantics for formal logics
usually assume an extensional view, but conceptual analysis of
ordinary language often suggests that intensional thinking is more
natural. Examples often cited are that an extensional logic is
obliged to treat all 'empty' extensions as identical, so must
identify 'round square' with 'santa clause', and is unable to
distinguish concepts that 'accidentally' have the same instances,
such as human beings and bipedal hominids without body hair. RDFS
model theory is
basically intensional but has some extensional aspects, most
notably in the 'if and only if' conditions in the definitions of
rdfs:subClassOf and rdfs:subPropertyOf,
which force these properties to take account only of the class and
property extensions.)
Interpretation
(of) (n.) A minimal formal description of those
aspects of a world which
is just sufficient to establish the truth or falsity of any
expression of a logic.
(Some logic texts distinguish between a interpretation
structure, which is a 'possible world' considered as something
independent of any particular vocabulary, and an interpretation
mapping from a vocabulary into the structure. The RDF
semantics takes the simpler route of merging these into a single
concept.)
Logic
(n.) A formal language which expresses propositions.
Metaphysical (adj.).
Concerned with the true nature of things in some absolute or
fundamental sense.
Model Theory (n.) A
formal semantic theory which relates expressions to
interpretations.
(The name 'model theory' arises from the usage, traditional in
logical semantics, in which a satisfying interpretation is called a
"model". This usage is often found confusing, however, as it is
almost exactly the inverse of the meaning implied by terms like
"computational modelling", so we have avoided it in this
document.)
Monotonic (adj., of a logic or
inference system) Satisfying the condition that if S entails E then
(S + T) entails E, i.e. adding information to some antecedents
cannot invalidate a valid entailment.
(All logics based on a conventional model theory and a standard notion of
entailment are monotonic. Monotonic logics have the property that
entailments remain valid outside of the context in which they were
generated. This is why RDF is designed to be monotonic.)
Nonmonotonic (adj.,of a logic
or inference system) Not monotonic. Non-monotonic formalisms have been
proposed and used in AI and various applications. Examples of
nonmonotonic inferences include default reasoning, where
one assumes a 'normal' general truth unless it is contradicted by
more particular information (eg birds usually fly, but penguins
don't fly); negation-by-failure, commonly assumed in logic
programming systems, where one concludes, from a failure to prove a
proposition, that the proposition is false; and implicit
closed-world assumptions, often assumed in database
applications, where one concludes from a lack of information about
an entity in some corpus that the information is false (e.g. that
if someone is not listed in an employee database, that hse is not
an employee.)
(The relationship between monotonic and nonmonotonic inferences
is often subtle. For example, if a closed-world assumption is made
explicit, e.g. by asserting explicitly that the corpus is complete
and providing explicit provenance information in the conclusion,
then closed-world reasoning is monotonic; it is the implicitness
that makes the reasoning nonmonotonic. Nonmonotonic conclusions can
be said to be valid only in some kind of 'context', and are liable
to be incorrect or misleading when used outside that context.
Making the context explicit in the reasoning and visible in the
conclusion is a way to map them into a monotonic framework.)
Ontological (adj.) (Philosophy)
Concerned with what kinds of things really exist. (Applied)
Concerned with the details of a formal description of some topic or
domain.
Proposition (n.) Something that
has a truth-value; a statement or expression that is true or
false.
(Philosophical analyses of language traditionally distinguish
propositions from the expressions which are used to state them, but
model theory does not require this distinction.)
Reify
(v.), reification (n.) To categorize as an object;
to describe as an entity. Often used to describe a convention
whereby a syntactic expression is treated as a semantic object and
itself described using another syntax. In RDF, a reified triple is
a description of a triple-token using other RDF triples.
Resource (n.)(as used in RDF)(i) An
entity; anything in the universe. (ii) As a class name: the class
of everything; the most inclusive category possible.
Satisfy (v.t.),
satisfaction,(n.) satisfying
(adj., of an interpretation). To make true. The basic semantic
relationship between an interpretation and an expression. X
satisfies Y means that if the
world conforms to the conditions described by X, then Y must be
true.
Semantic (adj.) ,
semantics (n.). Concerned with the specification
of meanings. Often contrasted with syntactic to emphasise
the distinction between expressions and what they denote.
Skolemization (n.) A
syntactic transformation in which blank nodes are replaced by 'new'
names.
(Although not strictly valid, Skolemization retains the
essential meaning of an expression and is often used in mechanical
inference systems. The full logical form is more complex. It is
named after the logician
A. T. Skolem)
Token
(n.) A particular physical inscription of a symbol or expression in
a document. Usually contrasted with type, the abstract
grammatical form of an expression.
Universe (n., also Universe of
discourse) The universal classification, or the set of all
things that an interpretation considers to exist. In RDF/S, this is
identical to the set of resources.
Use (v.)
contrasted with mention; to use a piece of syntax to
denote or refer to something else. The normal way that language is
used.
("Whenever, in a sentence, we wish to say something about a
certain thing, we have to use, in this sentence, not the thing
itself but its name or designation." - Alfred
Tarski)
Valid
(adj., of an inference or inference process) Corresponding to an entailment, i.e. the
conclusion of the inference is entailed by the antecedent of the
inference. Also correct.
Well-formed (adj., of an
expression). Syntactically legal.
World
(n.) (with the:) (i) The actual world. (with
a:)(ii) A way that the actual world might be arranged.
(iii) An interpretation (iv) A possible world.
(The metaphysical status of '
possible worlds' is highly controversial. Fortunately, one does
not need to commit oneself to a belief in parallel universes in
order to use the concept in its second and third senses, which are
sufficient for semantic purposes.)
Appendix D: Acknowledgements
This document reflects the joint effort of the members of the RDF Core Working
Group. Particular contributions were made by D. Connolly, J.
Carroll, J. Grant, R. V. Guha, G. Klyne, O. Lassilla, B. McBride,
S. Melnick, J. deRoo and P. Stickler.
The basic idea of using an explicit extension mapping to allow
self-application without violating the axiom of foundation was
suggested by Christopher Menzel.
Several people found errors in earlier drafts. Herman ter Horst
suggested improvements to the proofs. Peter Patel-Schneider found
several major problems in earlier drafts, and suggested several
important technical improvements.
- [OWL]
- Web Ontology
Language (OWL) Reference Version 1.0, Dean, M.,Connolly,
D.,van Harmelen, F., Hendler, J.,Horrocks, I., McGuinness, D.,
Patel-Schneider, P.,Stein, L. (Editors), World Wide Web
Consortium Working Draft, 12 November 2002
- [RDF-CONCEPTS]
- Resource
Description Framework (RDF): Concepts and Abstract
Syntax, Klyne G., Carroll J. (Editors), World Wide Web
Consortium, November 2002 (work in progress).
- [RDF-SYNTAX]
- RDF/XML
Syntax Specification (Revised), Beckett D. (Editor),
World Wide Web Consortium, November 2002.
- [RDF-VOCABULARY]
- RDF
Vocabulary Description Language 1.0: RDF Schema, Brickley
D., Guha R.V. (Editors), World Wide Web Consortium, November
2002.
- [RDF-TESTS]
- RDF
Test Cases, Grant J., Beckett D. (Editors) World Wide
Web Consortium, November 2002.
- [RDFMS]
- Resource
Description Framework (RDF) Model and Syntax
Specification, Lassila O., Swick R. R.(Editors), World
Wide Web Consortium, 22 February 1999.
- [RFC 2119]
- RFC 2119
- Key Words for use in RFCs to Indicate Requirement
Levels Bradner, S., March 1997
- [RFC 2396]
- RFC
2396 - Uniform Resource Identifiers (URI): Generic
Syntax Berners-Lee,T., Fielding and Masinter,L.,
August 1998
- [XML-C14N]
- Canonical
XML, Boyer, J. W3C Recommendation, March 2001.
- [XSD]
- XML Schema
Part 2: Datatypes, Biron, P. V., Malhotra, A.
(Editors) World Wide Web Consortium Recommendation, 2 May
2001
- [Conen&Klapsing]
-
A Logical Interpretation of RDF, Conen, W., Klapsing,
R..circulated to
RDF Interest Group, August 2000.
- [DAML]
- Frank van Harmelen, Peter F. Patel-Schneider, Ian Horrocks
(editors), Reference
Description of the DAML+OIL (March 2001) ontology markup
language
- [Hayes&Menzel]
-
A Semantics for the Knowledge Interchange Format,
Hayes, P., Menzel, C., Proceedings of 2001 Workshop on the
IEEE Standard Upper Ontology, August 2001.
- [KIF]
- Michael R. Genesereth, Knowledge
Interchange Format, 1998 (draft American National
Standard).
- [Marchiori&Saarela]
- Query +
Metadata + Logic = Metalog, Marchiori, M., Saarela,
J.. 1998.
- [LBASE]
- Lbase:
Semantics for Languages of the Semantic Web, Guha, R.
V., Hayes, P., November 2002.
- [McGuinness&al]
-
DAML+OIL:An Ontology Language for the Semantic Web,
McGuinness,D. L., Fikes, R., Hendler J. and Stein, L.A., IEEE
Intelligent Systems, Vol. 17, No. 5, September/October 2002.
- [RDF-PRIMER]
- RDF
Primer, Manola F., Miller E. (Editors), World Wide Web
Consortium W3C Working Draft, November 2002.

