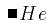Working Draft 10-Jul-1997

4. Content Markup

4.1 Introduction

4.1.1 The Intent of Content Markup

As has been noted in the introductory sections of this report, Mathematics can be distinguished by its use of a (relatively) formal language, mathematical notation. Mathematics and its notation should not be viewed as one and the same thing. The intent of content markup in Mathematical Markup Language is to support the encoding of underlying mathematical content of an expression, rather than any particular rendering for the expression.

For example the construct "H multiplied by e" is expressed using an explicit operator H<TIMES/>e. In different presentational contexts, the multiplication operator might be invisible (e.g. on paper), or rendered as the spoken word "times". Knowing the underlying mathematical construct, it is often possible to generate many different presentations according to the context and style preferences of the author or reader. For common expressions a default visual presentation is usually clear. "Take care of the sense and the sounds will take care of themselves" wrote Lewis Carroll [Carroll 1871]. Going in the reverse direction, that is from a presentation form to the underlying construct, is not necessarily easy: "He" could be interpreted as an atomic text string (or a chemical symbol). Context information may be required to decide between possible interpretations. Clues as to the interpretation are plainly important to speech rendering.

Mathematical presentation changes with culture and time: some expressions in combinatorial mathematics today would have one meaning to an English mathematician, and quite another to a French mathematician. Notations may lose currency, for example the use of musical sharp and flat symbols to denote maxima and minima. [Chaudry 1954] A notation in use in 1644 for the multiplication mentioned above was 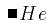square H e .[Cajori, 1928/1929]

Encoding the underlying mathematical constructs allows us to interchange information more precisely with systems which are able to manipulate the mathematics. In the trivial example above, such a system could substitute values for the variables H and e, evaluating the result. Further interesting application areas include CD-based textbooks and other interactive teaching aids.

4.1.2 The Scope of Content Markup

It is clear that the semantics of much mathematical notation is not yet a matter of consensus. In any case it would be an enormous job to codify most of mathematics, and indeed a task which could never be complete. Therefore this MathML proposal specifies a number of commonplace mathematical constructs which should be useful to a large number of potential users. The content tags set out below should be adequate for simple coding of most of the formulas used from kindergarten to the end of high school in the US, and probably beyond through the first two years of college, that is up to A-Level or Baccalaureat level.

The areas covered to some extent in this initial draft are:

It is not claimed, or even suggested, that the proposed element set is complete for these areas.

4.1.3 Basic Concepts of Content Markup

The guidelines governing the design of the MathML content elements are the following principles:

In order to accomplish these goals, MathML introduces two types of Content elements. The first type typically represents operators and functions, such as <SIN/> and <PLUS/>. These elements are canonically empty. Operators and functions are applied to arguments by using another empty element, the <APPLY/> element.

Elements of the second type can be seen as containers, and in general serve to mark the scope of the operators contained in them, or to define a context for the elements contained. Examples of this type are the mathematical expression construct <EXPR>, and <SET> .

MathML content tags directly encode the mathematical meaning of expressions, but this does not of itself define the notation used to present the meaning to a reader. Default visual renderings for the content elements are given in Section 4.2 . In addition, content tags , in common with all MathML tags, have a "STYLE" attribute (see Section 4.4), which can be used to pass rendering preference information on to a specific renderer which can make use of it.

The <EXPR> Construct

The basic building block of a mathematical expression in MathML content markup is the EXPR element. An EXPR corresponds to a complete mathematical expression. Roughly speaking, this means a piece of mathematics which could be surrounded by parentheses or "logical brackets" without changing its meaning.

For example, 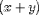$(x + y)$ might be encoded as

<EXPR> <MI>x</MI> <PLUS/> <MI>y</MI> </EXPR>.

Using EXPR, (as with braces in traditional mathematics notation), it is possible to specify exactly the scope of any operator or function. The content model of EXPR is simple and recursive. Symbolically, the content model can the described as:

EXPR => a op b
where a and b are simple identifiers, or EXPR constructs themselves, and op is any operator or function. Note that this allows EXPR constructs to be nested to arbitrary depth.

An EXPR may also optionally contain more than one operator:

EXPR => a op b [op c ...]
For example,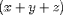$(x + y + z)$ can be encoded as
<EXPR> <MI>x</MI> <PLUS/> <MI>y</MI> <PLUS/> <MI>z</MI> </EXPR>.

When an EXPR is used in this way, it is important to keep in mind the issue of operator precedence. In cases where several operators are enclosed in a single EXPR, operator association or precedence must be resolved by an external processing application, if it wishes to evaluate the EXPR. Therefore, in most situations, it is probably preferable to fully bracket expressions, particularly when several different operators are involved. For example, 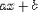$ax + b$ is better encoded as 

<EXPR>
  <EXPR><MI>a</MI><TIMES/><MI>x</MI></EXPR>
  <PLUS/>
  <MI>b</MI>
</EXPR>
although it is also valid to encode it as
<EXPR><MI>a</MI><TIMES/><MI>x</MI><PLUS/><MI>b</MI></EXPR>.

In addition to determining the scope of operators and functions, the <EXPR> container plays an important role in grouping expressions within other constructs. For example, by default a <VECTOR> element expects to have its components separated by an explicit separator, the <SEP/> tag. However, an expression enclosed by an EXPR is viewed as a single coherent molecule, so that the <SEP/> tag is not needed to separate it from its neighbors.

Since the bracketing is logical, it need not necessarily be rendered. Default rendering.

The APPLY construct

One reason for using MathML content markup is to make the mathematical expressions easily available to external processing applications such as computer algebra systems, and intelligent renderers. Therefore, a key requirement of functional representation in content markup is that it must be possible to perform symbolic algebra on mathematical functions as first class objects, and apply the result to an argument. That is, in addition to 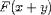$F (x + y)$ we must be able to encode $(F + G)(x)$ .

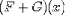To understand the MathML approach to applying a function to an argument, consider f(x). This can be encoded as

<EXPR> <MI>f</MI> <APPLY/> <MI>x</MI> </EXPR>
Note that f and x may be simple identifiers, or more complex constructs built from EXPRs and other function elements. For example, one can construct 'new' functions which can then be applied to an argument using the APPLY element. Thus, the expression (F + G)-1(x) can be encoded as 
<EXPR>
   <EXPR>
     <INVERSE/>
     <APPLY/>
     <EXPR><MI>F</MI><PLUS/><MI>G</MI></EXPR>
   </EXPR>
   <APPLY/>
   <MI>x</MI>
</EXPR>

Functions supported explicitly in MathML are all canonically empty elements and can be used as first class objects in symbolic manipulation. Examples are <PLUS/>, <SIN/>. User defined functions such as <FN>functionname</FN> can also be used in this way. Although, it is probably best to always use the APPLY element, just as it is prudent to fully bracket expressions with EXPRs, the APPLY element is optional and may be omitted in unambiguous situations. The only such situation which commonly arises is when a function named in MathML appears alone with an argument in an EXPR. For example, we can write sin (x) as

<EXPR><SIN/> <MI>x</MI> </EXPR>
as there is no other operator within the EXPR.

Default rendering of APPLY.

The INVERSE construct

The INVERSE construct is problematic from a mathematical point of view in that it implicitly involves the definition of an inverse for an arbitrary function F. Even at the K through 12 level the concept of an inverse F-1 of many common functions F is not used in a uniform way. For example, inverse trigonometric functions are inverses in a slightly different way from the way in which log function is the inverse of the exponential.

In an effort to be as inclusive as possible, MathML adopts the view that

"If F is a function from a domain D to D', then the inverse G of F is a function over D' such that G(F(x)) = x for x in D."
This definition does not assert that such an inverse exists for all or indeed any x in D, or that it is single-valued anywhere. Authors writing pedagogical material that may be evaluated by other applications may therefore wish to address the issue of the existence of a particular inverse function.

4.1.4 Leaf Tokens in Content Markup

In order to simplify processing of MathML by rendering applications, MathML includes a concept called "leaf-tagging". This means that, at the lowest level, any PCDATA token is encapsulated in an element defining its presentation type. For reasons of simplicity, Content Markup uses the token tags from the Presentation Tagset: MI and MN are used to encapsulate identifiers and numbers. MF and MTEXT may also be used to encapsulate fences and embedded text. This type information is intended for renderers and may be ignored by mathematical processing applications.

This is the simplest form of embedded presentation markup. Presentation constructs of arbitrary complexity may be embedded in place of the simple tokens MI, MN etc. This is discussed in more detail in section 5.

4.2 The Content Markup Elements

The MathML content tags are given in tables below. They are grouped in categories which roughly reflect the area of mathematics from which they come, and also the grouping in the MathML DTD.

There is no linguistic difference in MathML between operators and functions. The separation here and in the DTD is for reasons of clarity. Some functions in this list may not ever be used in symbolic manipulations.

4.2.1 Basic Content Elements

TagDescription Default Rendering
<APPLY/> makes explicit application of a function to its argument By default, the APPLY element renders as a thin space between the function and its argument, or as the spoken word "of". Note that this does not automatically create the parentheses around the function argument. Rendering Notes
<E> equation or relation (see notes) $a = b$
<EXPR> "scoping" or "bracketing" element Since the bracketing is logical, it need not necessarily be rendered visually. By default, an EXPR is rendered in the same manner as the MROW presentation schema. Rendering Notes
<FN> user-defined function; (see notes)
<FN><MI>functionname </MI> </FN>
<INTERVAL> interval constructor; (see notes)
<INTERVAL CLOSURE="Open-Closed">
  <MI>a</MI><SEP/><MI>b</MI>
</INTERVAL>
$(a , b]$
<INVERSE/> generic inverse for functions
<SEP/> generic separator; (see notes) none Rendering Notes
<ST/> "such that" separator; (see notes)
<SET>
   <MI>i</MI> <ST/>
   <E>
     <MN>1</MN><LE/><
     MI>i</MI><LE/><MI>n</MI>
   </E>
</SET>
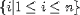
$\{i | 1\le i\le n\}$

Notes on Basic Content Elements:

E
The <E> construct is used not only for equalities but also for other relations. It is helpful to distinguish equations from expressions in general for reasons of clarity, for example in teaching, and also for some math processing applications, such as linear algebra systems solving a set of equations, grouped using the <SET> element .
<E> could also be used by an automatic equation numbering device, or for indexing, say.

ST and SEP
<ST/> is the "such that" between an equation and its quantifier, as in "x < 2 such that x in R" coded as 
<E>
  <MI>x</MI> <LT/> <MN>2</MN>
  <ST/>
  <E>
    <MI>x</MI> <IN/> <MI>R</MI>
  </E>
</E>
<SEP/> is a more generic separator for array-like containers, and elements such as the INTERVAL container.

INTERVAL
The INTERVAL element accepts an IMPLIED attribute "CLOSURE". The valid values are Open, Closed, Open-Closed or Closed-Open. The default is "Closed".

FN
The FN element is used for encoding author defined functions. The content of this element is the name of the function. This may be simple PCDATA token, or a more complex construct using presentation tags. In any situation where an explicitly defined MathML function can be used, the FN element may also be used.

4.2.2 Arithmetic and Algebra





TagDescription Default Rendering
<PLUS/> addition $a + b$
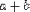
<MINUS/> subtraction $a - b$
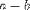
<TIMES/> multiplication $ a b $
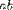
<OVER/> division $ a / b $
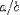
<EXP/> "exponentiation"
<EXPR><EXP/><APPLY/><MI>x</MI></EXPR>
$e^x$
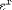
<POWER/> "to the power of"
<EXPR><MI>x</MI><POWER/><MN>3</MN></EXPR>
<DIV/> "division modulo base"
<EXPR><MI>a</MI><DIV/><MI>N</MI></EXPR>
<REM/> "remainder modulo base"
<EXPR><MI>a</MI><REM/><MN>N</MN></EXPR>
<FACTORIAL> factorial
<FACTORIAL><MI>n</MI></FACTORIAL>
 $ n!$
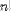
<MIN> minimum
<MIN><MI>A</MI></MIN>
 $ \min A$
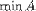
<MIN> minimum
<MIN>
   <MI>x</MI> <ST/><MI>x</MI> <IN/>
   <SET>
      <MI>x</MI> <ST/>
      <E>
        <EXPR><MI>x</MI><POWER><MN>3<MN></EXPR>
        <LT/>
        <MI>&Pi;</MI>
     </E>
   </SET>
</MIN>
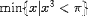
$\min\{x | x^3 < \pi\}$
<MAX> maximum
<MAX><MI>A</MI></MAX>
$ \max A$

4.2.3 Relations

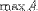
TagDescription Default Rendering
<EQ/> equals $ A = B $ 
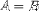
<E><MI>A</MI><EQ/><MI>B</MI></E>
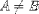
<NEQ/> not equal $ A \neq B $ 
<E><MI>A</MI><NEQ/><MI>B</MI></E>
<GT/> greater than $ A > B $ 
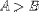
<E><MI>A</MI><GT/><MI>B</MI></E>
<LT/> less than $ A < B $ 
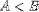
<E><MI>A</MI><LT/><MI>B</MI></E>
<GEQ/> greater than or equal $ A\ge B $ 
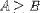
<E><MI>A</MI><GEQ/><MI>B</MI></E>
<LEQ/> less than or equal $ A \le B $ 
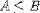
<E><MI>A</MI><LEQ/><MI>B</MI></E>

4.2.4 Calculus

TagDescription Default Rendering
<LN> natural logarithm $ \ln a $ 
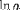
<LN><MI>a</MI></LN>
<LOG> logarithm; $ \log a $ 
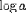
<LOG><MI>a</MI></LOG>
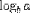
use <DEGREE> for base; (see notes) $ \log_b a $ 
<LOG>
  <MI>a</MI>
  <DEGREE><MI>b</MI></DEGREE>
</LOG>
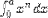
<INT/> one-dimensional definite integral (see notes) $ \int_0^a x^n \,dx $ 
<EXPR>
    <INT/>
    <LOWLIMIT><MN>0</MN></LOWLIMIT>
    <UPLIMIT><MI>a</MI></UPLIMIT>
    <EXPR>
      <MI>x</MI><POWER/><MI>n</MI>
    </EXPR>
    <BVAR><MI>x</MI></BVAR>
</EXPR>
By default, the upper and lower limits are rendered in their usual positions, and the bound variable is rendered with a small space and the letter "d" in front of it.
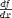
<DIFF/> derivative, differentiation $ \frac{d f}{d x} $ 
<EXPR>
  <DIFF/>
  <MI>f</MI>
  <BVAR><MI>x</MI></BVAR>
</EXPR>
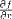
<PARTIALDIFF/> partial derivative $ \frac{\partial f}{\partial x} $ 
<EXPR>
    <PARTIALDIFF/>
    <MI>f</MI>
    <BVAR>x</BVAR>
</EXPR>
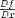
<TOTALDIFF/> total derivative $ \frac{D f}{D x} $ 
<EXPR>
    <TOTALDIFF/>
    <MI>f</MI>
    <BVAR><MI>x</MI></BVAR>
</EXPR>
<LOWLIMIT> lower limit of integral, see notes see <INT>
<UPLIMIT> upper limit of integral, see notes see <INT>
<BVAR> bound variable; (see notes)
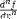
<DEGREE> holds the n in "nth derivative"; (see notes) $ \frac{d^n f}{{d x}^n} $ 
<EXPR>
    <DIFF/>
    <MI>f</MI>
    <BVAR><MI>x</MI></BVAR>
    <DEGREE><MI>n</MI></DEGREE>
</EXPR>

Notes on Calculus Elements

BVAR
The BVAR element specifies a "bound variable". In different contexts, this means different things. In an integral, it specifies what integral is being integrated. In a derivative, it indicates which variable is being differentiated. The BVAR element is also used with sums and products.

DEGREE
There are a number basic mathematical constructs which come in families, such as derivatives, moments, and logarithms to various bases. Rather than introduce special tags for each of these families, MathML uses a single general construct, the DEGREE element.

INT
The INT element uses the auxiliary qualifier elements UPLIMIT, LOWLIMIT, the limits of integration, and BVAR the variable of integration. These optional elements may appear at any position inside the EXPR element which contains the INT.

LOG
If DEGREE is not present, the base of the logarithm is 10. For natural logarithms base e, <LN> should be used.

LOWLIMIT and UPLIMIT
These elements specify lower and upper limits. The exact usage is context-specific. In an integral, they specify the limits of integration. These elements are also used to specify the limits of an index for sums and products, and also to specify a limiting value for a variable in a limit.

4.2.5 Theory of Sets

TagDescription Default Rendering
<SET> set $ \{z | F(z) =0 \} $ 
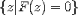
<SET>
  <MI>z</MI><ST/>
  <E>
    <EXPR>
      <FN><MI>F</MI></FN><APPLY/><MI>z</MI>
    </EXPR>
    <EQ/><MN>0</MN>
  </E>
</SET>
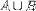
<UNION/> union (join) $A \cup B$ 
<EXPR>
  <MI>A </MI>
  <UNION/>
  <MI>B</MI>
</EXPR>
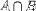
<INTERSECT/> intersection (meet) $A \cap B$ 
<EXPR>
  <MI>A</MI>
  <INTERSECTION/>
  <MI>B</MI>
</EXPR>
<IN/> is in, or is an element of a set $a \in A$ 
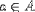
<EXPR>
  <MI>a</MI>
  <IN/>
  <MI>A</MI>
</EXPR>
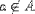
<NOTIN/> is not in $a \not\in A$ 
<EXPR>
  <MI>a</MI>
  <NOTIN/>
  <MI>A</MI>
</EXPR>
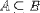
<SUBSET/> is a subset $A \subseteq B$ 
<EXPR>
  <MI>A</MI>
  <SUBSET/>
  <MI>B</MI>
</EXPR>
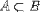
<PRSUBSET/> is a proper subset $A \subset B$ 
<EXPR>
  <MI>a</MI>
  <PRSUBSET/>
  <MI>A</MI>
</EXPR>
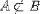
<NOTPRSUBSET/> is not a proper subset $A \not\subset B$ 
<EXPR>
  <MI>a</MI>
  <NOTPRSUBSET/>
  <MI>A</MI>
</EXPR>

4.2.6 Sequences and Series

TagDescription Default Rendering
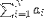
<SUM/> sum; (see notes) $\sum_{i=1}^N a_i$ 
<EXPR>
  <SUM/>
  <LOWLIMIT><MN>1</MN></LOWLIMIT>
  <UPLIMIT><MI>N</MI></UPLIMIT>
  <BVAR><MI>i</MI></BVAR>
  <EXPR>
    <MSUB>
      <MI>a</MI>
      <MI>i</MI>
    </MSUB>
  </EXPR>
</EXPR>
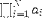
<PRODUCT/> product; (see notes) $\prod_{i=1}^N a_i$ 
<EXPR>
  <PRODUCT/>
  <LOWLIMIT><MN>1</MN></LOWLIMIT>
  <UPLIMIT><MI>N</MI></UPLIMIT>
  <BVAR><MI>i</MI></BVAR>
  <EXPR>
    <MSUB>
      <MI>a</MI>
      <MI>i</MI>
    </MSUB>
  </EXPR>
</EXPR>
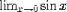
<LIMIT/> limit; (see notes) $\lim_{x\to0} \sin x$ 
<EXPR>
  <LIMIT/>
  <LOWLIMIT><MI>x</MI><TENDSTO/><MN>0</MN></LOWLIMIT>
  <EXPR><SIN/><MI>x</MI></EXPR>
</EXPR>
<TENDSTO/> tends to

Notes on Sequences and Series Content Elements:

LIMIT
The LIMIT element also accepts the auxiliary qualifier element LOWLIMIT.

PRODUCT and SUM
These elements, like the INT element, utilize the auxiliary qualifier elements UPLIMIT, LOWLIMIT and BVAR. These optional elements may appear at any position inside the EXPR element which immediately contains the SUM or PRODUCT element.

4.2.7 Trigonometry

We just list the names of the common functions provided: their interpretations should be clear.

<SIN/> <COS/> <TAN/>
<SEC/> <COSEC/> <COTAN/>
<SINH/> <COSH/> <TANH/>
<SECH/> <COSECH/> <COTANH/>
<ARCSIN/> <ARCCOS/> <ARCTAN/>

4.2.8 Statistics

TagDescription Default Rendering
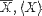
<MEAN> mean or average $\overline X, \langle X\rangle$ 
<MEAN><MI>X</MI></MEAN>
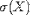
<SDEV> standard deviation $\sigma(X)$ 
<SDEV><MI>X</MI></SDEV>
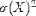
<VAR> variance $\sigma (X)^2$ 
<VAR><MI>X</MI></VAR>
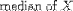
<MEDIAN> median median of $X$ 
<MEDIAN><MI>X</MI></MEDIAN>
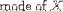
<MODE> mode mode of $X$ 
<MODE><MI>X</MI></MODE>
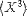
<MOMENT> use <DEGREE> for the n in "nth moment" $\langle X^3\rangle$ 
<MOMENT>
  <MI>X</MI>
  <DEGREE><MN>3</MN><DEGREE>
</MOMENT>

4.2.9 Linear Algebra

TagDescriptionDefault Rendering
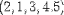
<VECTOR> vector; see notes $(2,1,3,4.5)$ 
<VECTOR>
  <MN>2</MN><SEP/><MN>1</MN>
  <SEP/><MN>3</MN><SEP/><MN>4.5</MN>
</VECTOR>
.. or.. 
<VECTOR>
  <MN>2</MN><MN>1</MN>
  <MN>3</MN><MN>4.5</MN>
</VECTOR>
<MATRIX> matrix
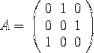
<MATRIXROW> matrix row; see notes $A = \begin{array}{ccc} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{array}$ 
<E>
  <MI>A</MI><EQ/>
  <MATRIX>
    <MATRIXROW>
      <MN>0</MN><SEP/>
      <MN>1</MN><SEP/><MN>0</MN>
    </MATRIXROW>
    <MATRIXROW>
      <MN>0</MN><SEP/>
      <MN>0</MN><SEP/><MN>1</MN>
    </MATRIXROW>
    <MATRIXROW>
      <MN>1</MN><SEP/>
      <MN>0</MN><SEP/><MN>0</MN>
    </MATRIXROW>
  </MATRIX>
</E>
.. or.. 
<E>
  <MI>A</MI><EQ/>
  <MATRIX>
    <MATRIXROW>
      <MN>0</MN><MN>1</MN><MN>0</MN>
    </MATRIXROW>
    <MATRIXROW>
      <MN>0</MN><MN>0</MN><MN>1</MN>
    </MATRIXROW>
    <MATRIXROW>
      <MN>1</MN><MN>0</MN><MN>0</MN>
    </MATRIXROW>
  </MATRIX>
</E>
<MATRIXINVERSE> matrix inverse $ A^{-1} $ 
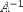
<MATRIXINVERSE><MI>A</MI></MATRIXINVERSE>
<DETERMINANT> determinant $ \det A $ 
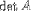
<DETERMINANT><MI>A</MI></DETERMINANT>

Notes on Linear Algebra Elements:
VECTOR and MATRIXROW
These elements both contain their entries as content. When the entries are ordinary data (#PCDATA) it is necessary to use a separator, in order to specify where one entry ends and another begins. In MathML, the SEP element is used. When the entries are actually valid MathML expressions, then no separator is needed. For example, if a MATRIXROW contains of a sequence of fully delimited EXPRS, the SEP elements may be omitted.

4.2.10 Semantic Mapping Elements

The use of the semantic mapping elements is explained in section 4.3.

TagDescription Default Rendering
<ANNOTATION> container element for a semantic annotation in a non-XML format None
<SEMANTICS> container element for a MathML construct together with its semantic mapping information None
<XML-ANNOTATION> container element for a semantic annotation in an XML format None

4.3 Syntax and Semantics

4.3.1 The Semantics of "Syntax" and the Syntax of <SEMANTICS>

The use of content rather than presentation tagging for mathematics is sometimes referred to as "semantic tagging" [Buswell 1996]. The parse-tree of a fully bracketed MathML content tagged element structure corresponds directly to the expression-tree of the underlying mathematical expression. We therefore regard the content tagging itself as encoding the syntax of the mathematical expression. This is, in general, sufficient to obtain some rendering and even some symbolic manipulation (e.g., polynomial factorization).

However, even in such apparently simple expressions as X + Y, some additional information may be required for applications such as computer algebra. Are X and Y integers,or functions, etc.? 'Plus' represents addition over which field? This additional information is referred to as Semantic Mapping. In MathML, this mapping is provided by the SEMANTICS, ANNOTATION and XML-ANNOTATION elements.

The SEMANTICS element is the container element for the MathML expression together with its semantic mapping. SEMANTICS expects a variable number three child elements. The first is the element (which may itself be a complex element structure) for which this additional semantic information is being defined. The second and subsequent children, if any, are instances of the elements ANNOTATION or XML-ANNOTATION.

The SEMANTICS tags also accepts a "SEMTYPE" attribute for use by external processing applications. One use might be a URL for a semantic context dictionary, for example. Since the semantic mapping information might in some cases be provided entirely by the "SEMTYPE" attribute, the ANNOTATION or XML-ANNOTATION elements are optional.

The ANNOTATION element is a container for arbitrary data. This data may be in the form of text, computer algebra encodings, C programs, or whatever a processing application expects. ANNOTATION has an attribute ENCODING defining the form in use. Note that the content model of ANNOTATION is #PCDATA, so care must be taken that the particular encoding does not conflict with XML parsing rules.

The XML-ANNOTATION element is a container for semantic information in well-formed XML. For example, an XML form of the OpenMath semantics could be given. Another possible use here is to embed, for example, the presentation tag form of a construct given in content tag form in the first child element of SEMANTICS (or vice versa). ANNOTATION has an attribute ENCODING defining the form in use.

For Example:

<SEMANTICS>
    <EXPR> <MN>123</MN> <OVER/>
<MN>456</MN> </EXPR>
    <ANNOTATION encoding="Mathematica">
        N[123/456, 39]
    </ANNOTATION>
    <ANNOTATION encoding="TeX">
        $0.269736842105263157894736842105263157894\ldots$
    </ANNOTATION>
    <XML-ANNOTATION encoding="MathML-Presentation">
        <MROW>
            <MN> 0.269736842105263157894 </MN>
            <MOVER>
            <MN> 736842105263157894 </MN>
            <MO> &horizontalLine; </MO>
        </MOVER>
        </MROW>
    </XML-ANNOTATION>
    <XML-ANNOTATION encoding="OpenMath">
        <OM_APP>..</OM_APP>
    </XML-ANNOTATION>
</SEMANTICS>
where <OM_APP>..</OM_APP> are the elements defining the additional semantic information.

Of course, providing an explicit semantic mapping at all is optional, and in general would only be provided where there is some requirement to process or manipulate the underlying mathematics.

4.3.2 Semantic Mappings

Although semantic mappings can easily be provided by various proprietary, or highly specialized encodings, there are no widely available, non-proprietary standard semantic mapping schemes. In part to address this need, the goal of the OpenMath effort is to provide a platform-independent, vendor-neutral standard for the exchange of mathematical objects between applications. Such mathematical objects include semantic mapping information. The OpenMath group has defined an SGML syntax for the encoding of this information [OpenMath, 1996]. This element set could provide the basis of one XML-ANNOTATION element set.

An attraction of this mechanism is that the OpenMath syntax is specified in SGML, so that the whole expression is checkable by a DTD-based parser.

4.4 Modifying Content Markup Rendering

In order to facilitate compatibility with Cascading Style Sheets (CSS1), all MathML elements accept CLASS and STYLE attributes. At present, many MathML properties that would be desirable to control via style sheets are not defined in CSS1. Conversely, CSS1 properties which are applicable to MathML may not be accessible to embedded MathML renderers in the immediate future. However, the CLASS and STYLE attributes provide some degree of compatibility now, and may provide much greater compatibility in the future.

There is a great deal of work underway on the problem of controlling the layout of XML extensions to HTML via style sheet mechanisms. The HTML-Math working group will be coordinating its efforts with other groups over the next year to insure that MathML will be compatible with emerging style sheet mechanisms.

Content or semantic tagging goes along with the (frequently implicit) premise that, if you know the semantics, you can always work out a presentation form. When an author's main goal is to mark up re-usable, evaluatable mathematical expressions, the exact rendering of the expression is probably not critical, provided that it is easily understandable. However, when an author's goal is more along the lines of providing enough additional semantic information to make a document more accessible by facilitating better visual rendering, voice rendering, or specialized processing, controlling the exact notation used becomes more of an issue.

MathML elementss accept an attribute OTHER (see 7.2.4) which can be used to specify things not specifically documented in MathML. On content tags, this attribute can be used by an author to express a preference between equivalent forms for a particular content element construct, where the selection of the presentation has nothing to do with the semantics. Examples might be

Thus, if a particular renderer recognized a display attribute to select between script style and display style fractions, an author might write 

<EXPR OTHER='display="scriptstyle"'><MN> 1 </MN><OVER/><MI> x </MI></EXPR>
to indicate that the rendering 1/x is preferred.

The information provided in the "OTHER" attribute is intended for use by specific renderers or processors, and therefore, the permitted values are determined by the renderer being used. It is legal for a renderer to ignore this information. This might be intentional, in the case of a publisher imposing a house style, or simply because the renderer does not understand them, or is unable to carry them out.

There will be a need for the construction of translators for the layout of material tagged with content tags according to the wishes of those wanting the output.

4.4.1 Notes on the Rendering of Content Elements

APPLY and EXPR
An author can control how an APPLY or EXPR is rendered by mixing presentation and content tags (for example adding parentheses), or by using the OTHER attribute with a specific renderer.

SEP
By default, SEP is not rendered, so that commas may have to be added explicitly if required, for example to separate the components of a vector. This can be done by inserting presentation elements containing the comma, or by use of the OTHER attribute to signal this preference to the renderer.