He [Cajori1928].
Mathematical Markup Language (MathML) Version 2.0
3 Presentation Markup
4 Content Markup
4.1 Introduction
4.1.1 The Intent of Content Markup
4.1.2 The Scope of Content Markup
4.1.3 Basic Concepts of Content Markup
4.2 Content Element Usage Guide
4.2.1 Overview of Syntax and Usage
4.2.2 Containers
4.2.3 Functions, Operators and Qualifiers
4.2.4 Relations
4.2.5 Conditions
4.2.6 Syntax and Semantics
4.2.7 Semantic Mappings
4.2.8 MathML element types
4.3 Content Element Attributes
4.3.1 Content Element Attribute Values
4.3.2 Attributes Modifying Content Markup Semantics
4.3.3 Attributes Modifying Content Markup Rendering
4.4 The Content Markup Elements
4.4.1 Token Elements
4.4.2 Basic Content Elements
4.4.3 Arithmetic, Algebra and Logic
4.4.4 Relations
4.4.5 Calculus and Vector Calculus
4.4.6 Theory of Sets
4.4.7 Sequences and Series
4.4.8 Elementary classical functions
4.4.9 Statistics
4.4.10 Linear Algebra
4.4.11 Semantic Mapping Elements
5 Combining Presentation and Content Markup
As has been noted in the introductory section of this recommendation, mathematics can be distinguished by its use of a (relatively) formal language, mathematical notation. However, mathematics and its presentation should not be viewed as one and the same thing. Mathematical sums or products exist and are meaningful to many applications completely without regard to how they are rendered aurally or visually. The intent of the content markup in the Mathematical Markup Language is to provide an explicit encoding of the underlying mathematical structure of an expression, rather than any particular rendering for the expression.
There are many reasons for providing a specific encoding for content. Even a disciplined and systematic use of presentation tags cannot properly capture this semantic information. This is because without additional information it is impossible to decide if a particular presentation was chosen deliberately to encode the mathematical structure or simply to achieve a particular visual or aural effect. Furthermore, an author using the same encoding to deal with both the presentation and mathematical structure might find a particular presentation encoding unavailable simply because convention had reserved it for a different semantic meaning.
The difficulties stem from the fact that there are many to one mappings from presentation to semantics and vice versa. For example the mathematical construct `H multiplied by e' is often encoded using an explicit operator as in H × e. In different presentational contexts, the multiplication operator might be invisible `H e', or rendered as the spoken word `times'. Generally, many different presentations are possible depending on the context and style preferences of the author or reader. Thus, given `H e' out of context it may be impossible to decide if this is the name of a chemical or a mathematical product of two variables H and e.
Mathematical presentation also changes with culture and time: some
expressions in combinatorial mathematics today have one meaning to an
Russian mathematician, and quite another to a French
mathematician; see section 5.4.1 [Notational Style Sheets] for an example.
Notations may lose currency, for example the use of musical sharp and flat
symbols to denote maxima and minima [Chaundy1954]. A notation
in use in 1644 for the multiplication mentioned above was He [Cajori1928].
When we encode the underlying mathematical structure explicitly, without regard to how it is presented aurally or visually, we are able to interchange information more precisely with those systems that are able to manipulate the mathematics. In the trivial example above, such a system could substitute values for the variables H and e and evaluate the result. Further interesting application areas include interactive textbooks and other teaching aids.
The semantics of general mathematical notation is not a matter of consensus. It would be an enormous job to systematically codify most of mathematics - a task that can never be complete. Instead, MathML makes explicit a relatively small number of commonplace mathematical constructs, chosen carefully to be sufficient in a large number of applications. In addition, it provides a mechanism for associating semantics with new notational constructs. In this way, mathematical concepts that are not in the base collection of elements can still be encoded (section 4.2.6 [Syntax and Semantics]).
The base set of content elements are chosen to be adequate for simple coding of most of the formulas used from kindergarten to the end of high school in the United States, and probably beyond through the first two years of college, that is up to A-Level or Baccalaureate level in Europe. Subject areas covered to some extent in MathML are:
It is not claimed, or even suggested, that the proposed set of elements is complete for these areas, but the provision for author extensibility greatly alleviates any problem omissions from this finite list might cause.
The design of the MathML content elements are driven by the following principles:
PCDATA
or on additional processing such as operator precedence parsing.
The primary goal of the content encoding is to establish explicit connections between mathematical structures and their mathematical meanings. The content elements correspond directly to parts of the underlying mathematical expression tree. Each structure has an associated default semantics and there is a mechanism for associating new mathematical definitions with new constructs.
Significant advantages to the introduction of content-specific tags include:
Expressions described in terms of content elements must still be rendered. For common expressions, default visual presentations are usually clear. `Take care of the sense and the sounds will take care of themselves' wrote Lewis Carroll [Carroll1871]. Default presentations are included in the detailed description of each element occurring in section 4.4 [The Content Markup Elements].
To accomplish these goals, the MathML content encoding is based on the concept of an expression tree. A content expression tree is constructed from a collection of more primitive objects, referred to herein as containers and operators. MathML possesses a rich set of predefined container and operator objects, as well as constructs for combining containers and operators in mathematically meaningful ways. The syntax and usage of these content elements and constructions is described in the next section.
Since the intent of MathML content markup is to encode mathematical expressions in such a way that the mathematical structure of the expression is clear, the syntax and usage of content markup must be consistent enough to facilitate automated semantic interpretation. There must be no doubt when, for example, an actual sum, product or function application is intended and if specific numbers are present, there must be enough information present to reconstruct the correct number for purposes of computation. Of course, it is still up to a MathML-compliant processor to decide what is to be done with such a content-based expression, and computation is only one of many options. A renderer or a structured editor might simply use the data and its own built-in knowledge of mathematical structure to render the object. Alternatively, it might manipulate the object to build a new mathematical object. A more computationally oriented system might attempt to carry out the indicated operation or function evaluation.
The purpose of this section is to describe the intended, consistent usage. The requirements involve more than just satisfying the syntactic structure specified by an XML DTD. Failure to conform to the usage as described below will result in a MathML error, even though the expression may be syntactically valid according to the DTD.
In addition to the usage information contained in this section, section 4.4 [The Content Markup Elements] gives a complete listing of each content element, providing reference information about their attributes, syntax, examples and suggested default semantics and renderings. The rules for using presentation markup within content markup are explained in section 5.2.3 [Presentation Markup Contained in Content Markup]. An informal EBNF grammar describing the syntax for the content markup is given in appendix B [Content Markup Validation Grammar].
MathML content encoding is based on the concept of an expression tree. As a general rule, the terminal nodes in the tree represent basic mathematical objects, such as numbers, variables, arithmetic operations and so on. The internal nodes in the tree generally represent some kind of function application or other mathematical construction that builds up a compound object. Function application provides the most important example; an internal node might represent the application of a function to several arguments, which are themselves represented by the terminal nodes underneath the internal node.
The MathML content elements can be grouped into the following categories based on their usage:
These are the building blocks out of which MathML content expressions are constructed. Each category is discussed in a separate section below. In the remainder of this section, we will briefly introduce some of the most common elements of each type, and consider the general constructions for combining them in mathematically meaningful ways.
Content expression trees are built up from basic mathematical
objects. At the lowest level, leaf nodes are encapsulated in
non-empty elements that define their type. Numbers and symbols are marked
by the token elements cn and ci. More elaborate constructs such as sets, vectors and
matrices are also marked using elements to denote their types, but rather
than containing data directly, these container elements are
constructed out of other elements. Elements are used in order to clearly
identify the underlying objects. In this way, standard XML parsing can be
used and attributes can be used to specify global properties of the
objects.
The containers such as
<cn>12345<cn/> ,
<ci>x</ci> and
<csymbol definitionURL="mySymbol.htm" encoding="text">S</csymbol>
represent mathematical numbers , identifiers and externally defined
symbols. Below, we will look at operator elements
such as plus or sin, which
provide access to the basic mathematical operations and functions
applicable to those objects. Additional containers such as set for sets, and matrix for
matrices are provided for representing a variety of common compound
objects.
For example, the number 12345 is encoded as
<cn>12345</cn>
The attributes and PCDATA content together provide the data
necessary for an application to parse the number. For example, a default
base of 10 is assumed, but to communicate that the underlying data was
actually written in base 8, simply set the
base attribute to 8 as in
<cn base="8">12345</cn>
while the complex number 3 + 4i can be encoded as
<cn type="complex">3<sep/>4</cn>
Such information makes it possible for another application to easily parse this into the correct number.
As another example, the scalar symbol v is encoded as
<ci>v</ci>
By default, ci elements represent elements from a
commutative field (see appendix C [Content Element Definitions]).
If a vector is intended then this fact can be encoded as
<ci type="vector">v</ci>
This invokes default semantics associated with the vector element, namely an arbitrary element of a
finite-dimensional vector space.
By using the ci and csymbol elements we have made clear that we are
referring to a mathematical identifier or symbol but this does not say
anything about how it should be rendered. By default a symbol is rendered
as if the ci or csymbol
element were actually the presentation element mi
(see section 3.2.2 [Identifier (mi)]). The actual rendering of a mathematical
symbol can be made as elaborate as necessary simply by using the more
elaborate presentational constructs (as described in chapter 3 [Presentation Markup]) in the body of the ci or csymbol element.
The default rendering of a simple cn-tagged
object is the same as for the presentation element mn with some provision for overriding the presentation
of the PCDATA by providing explicit mn
tags. This is described in detail in section 4.4 [The Content Markup Elements].
The issues for compound objects such as sets, vectors and matrices are all similar to those outlined above for numbers and symbols. Each such object has global properties as a mathematical object that impact how they are to be parsed. This may affect everything from the interpretation of operations that are applied to them through to how to render the symbols representing them. These mathematical properties are captured by setting attribute values.
The notion of constructing a general expression tree is essentially that
of applying an operator to sub-objects. For example, the sum a +
b can be thought of as an application of the addition operator to
two arguments a and b. In MathML, elements are used for
operators for much the same reason that elements are used to contain
objects. They are recognized at the level of XML parsing, and their
attributes can be used to record or modify the intended semantics. For
example, with the MathML plus element, setting the
definitionURL and encoding
attributes as in
<plus definitionURL="www.vnbooks.com/VectorCalculus.htm"
encoding="text"/>
can communicate that the intended operation is vector-based.
There is also another reason for using elements to denote operators.
There is a crucial semantic distinction between the function itself and the
expression resulting from applying that function to zero or more arguments
which must be captured. This is addressed by making the functions
self-contained objects with their own properties and providing an explicit
apply construct corresponding to function
application. We will consider the apply construct
in the next section.
MathML contains many pre-defined operator elements, covering a range of
mathematical subjects. However, an important class of expressions involve
unknown or user-defined functions and symbols. For these situations, MathML
provides a general csymbol element, which is
discussed below.
apply constructThe most fundamental way of building up a mathematical expression in
MathML content markup is the apply construct. An
apply element typically applies an operator to its
arguments. It corresponds to a complete mathematical expression. Roughly
speaking, this means a piece of mathematics that could be surrounded by
parentheses or `logical brackets' without changing its
meaning.
For example, (x + y) might be encoded as
<apply> <plus/> <ci> x </ci> <ci> y </ci> </apply>
The opening and closing tags of apply specify
exactly the scope of any operator or function. The most typical way of
using apply is simple and recursive. Symbolically,
the content model can the described as:
<apply> op a b </apply>
where the operands a and b are containers or other
content-based elements themselves, and op is an operator or
function. Note that since apply is a container,
this allows apply constructs to be nested to
arbitrary depth.
An apply may in principle have any number of operands:
<apply> op a b [c...] <apply>
For example, (x + y + z) can be encoded as
<apply> <plus/> <ci> a </ci> <ci> b </ci> <ci> c </ci> </apply>
Mathematical expressions involving a mixture of operations result in
nested occurrences of apply. For example,
ax + b would be encoded as
<apply>
<plus/>
<apply>
<times/>
<ci> a </ci>
<ci> x </ci>
</apply>
<ci> b </ci>
</apply>
There is no need to introduce parentheses or to resort to operator
precedence in order to parse the expression correctly. The apply tags provide the proper grouping for the re-use
of the expressions within other constructs. Any expression enclosed by an
apply element is viewed as a single coherent
object.
An expression such as (F + G)(x) might be a product, as in
<apply>
<times/>
<apply>
<plus/>
<ci> F </ci>
<ci> G </ci>
</apply>
<ci> x </ci>
</apply>
or it might indicate the application of the function F + G to the argument x. This is indicated by constructing the sum
<apply> <plus/> <ci> F </ci> <ci> G </ci> </apply>
and applying it to the argument x as in
<apply>
<apply>
<plus/>
<ci> F </ci>
<ci> G </ci>
</apply>
<ci> x </ci>
</apply>
Both the function and the arguments may be simple identifiers or more complicated expressions.
In MathML 1.0 , another construction closely related to the use of the
apply element with operators and arguments was the
reln element. The reln
element was used to denote that a mathematical relation holds between its
arguments, as opposed to applying an operator. Thus, the MathML markup for
the expression x < y was given in MathML 1.0 by:
<reln> <lt/> <ci> x </ci> <ci> y </ci> </reln>
In MathML 2.0, the apply construct is used with all
operators, including logical operators. The expression above becomes
<apply> <lt/> <ci> x </ci> <ci> y </ci> </apply>
in MathML 2.0. The use of reln with relational operators is supported for reasons
of backwards compatibility, but deprecated. Authors creating new content
are encouraged to use apply in all cases.
The most common operations and functions such as plus and sin have been
predefined explicitly as empty elements (see section 4.4 [The Content Markup Elements]).
They have type and definitionURL
attributes, and by changing these attributes, the author can record that a
different sort of algebraic operation is intended. This allows essentially
the same notation to be re-used for a discussion taking place in a
different algebraic domain.
Due to the nature of mathematics the notation must be extensible. The key to extensibility is the ability of the user to define new functions and other symbols to expand the terrain of mathematical discourse.
It is always possible to create arbitrary expressions, and then to use
them as symbols in the language. Their properties can then be inferred
directly from that usage as was done in the previous section. However, such
an approach would preclude being able to encode the fact that the construct
was a known symbol, or to record its mathematical properties except by
actually using it. The csymbol element is used as a
container to construct a new symbol in much the same way that ci is used to construct an identifier. (Note that
`symbol' is used here in the abstract sense and has no
connection with any presentation of the construct on screen or paper). The
difference in usage is that csymbol should refer to
some mathematically defined concept with an external definition referenced
via the definitionURL attribute, whereas ci is used for identifiers that are essentially
`local' to the MathML expression and do not use any external
definition mechanism. The target of the definitionURL
attribute on the csymbol element may encode the
definition in any format: the particular encoding in use is given by the
encoding attribute
To use csymbol to describe a completely new
function, we write for example
<csymbol definitionURL="www.vnbooks.com/VectorCalculus.htm"
encoding="text">
<ci>Christoffel</ci>
</csymbol>
The definitionURL attribute specifies a URI
that provides a written definition for the Christoffel symbol.
Suggested default definitions for the content elements of MathML
appear in appendix C [Content Element Definitions] in a format based on OpenMath, although
there is no requirement that a particular format be used. The role of the
definitionURL attribute is very similar to the role
of definitions included at the beginning of many mathematical papers, and
which often just refer to a definition used by a particular book.
MathML 1.0 supported the use of the fn to encode the fact that
a construct is explicitly being used as a function or operator. To record
the fact that F+ G is being used semantically as if it
were a function, it was encoded as:
<fn>
<apply>
<plus/>
<ci>F</ci>
<ci>G</ci>
</apply>
</fn>
This usage, although allowed in MathML 2.0 for reasons of backwards
compatibility, is now deprecated. The fact that a construct is being used
as an operator is clear from the position of the construct as the first
child of the apply. If it is required to add additional
information to the construct, it should be wrapped in a semantics
element, for example:
<semantics definitionURL="www.mathslib.com/vectorfuncs/plus.htm"
encoding="Mathematica 4.0">
<apply>
<plus/>
<ci>F</ci>
<ci>G</ci>
</apply>
</semantics>
MathML 1.0 supported the use of definitionURL with
fn to refer to external definitions for user-defined
functions. This usage, although allowed for reasons of backwards
compatibility, is deprecated in MathML 2.0 in favour of using csymbol
to define the function, and then apply to link the function
to its arguments. For example:
<apply>
<csymbol definitionURL="http://www.defs.org/function_spaces.html#my_def"
encoding="text">
<ci>BigK</ci>
</csymbol>
<ci>x</ci>
<ci>y</ci>
</apply>
Given functions, it is natural to have functional inverses. This is
handled by the inverse element.
Functional inverses can be problematic from a mathematical point of view in that it implicitly involves the definition of an inverse for an arbitrary function F. Even at the K-through-12 level the concept of an inverse F -1 of many common functions F is not used in a uniform way. For example, the definitions used for the inverse trigonometric functions may differ slightly depending on the choice of domain and/or branch cuts.
MathML adopts the view: if F is a function from a domain D to D', then the inverse G of F is a function over D' such that G(F(x)) = x for x in D. This definition does not assert that such an inverse exists for all or indeed any x in D, or that it is single-valued anywhere. Also, depending on the functions involved, additional properties such as F(G( y)) = y for y in D' may hold.
The inverse element is applied to a function
whenever an inverse is required. For example, application of the inverse
sine function to x, i.e. sin -1 (x),
is encoded as:
<apply> <apply> <inverse/> <sin/> </apply> <ci> x </ci> </apply>
While arcsin is one of the predefined MathML
functions, an explicit reference to sin -1(x) might
occur in a document discussing possible definitions of
arcsin.
Consider a document discussing the vectors
A = (a, b, c) and
B = (d, e, f),
and later including the expression
V = A + B.
It is important to be able to communicate the fact that wherever
A and B
are used they represent a particular vector. The properties of that vector
may determine aspects of operators such as plus.
The simple fact that A is a vector can be communicated by using the markup
<ci type="vector">A</ci>
but this still does not communicate, for example, which vector is involved or its dimensions.
The declare construct is used to associate
specific properties or meanings with an object. The actual declaration
itself is not rendered visually (or in any other form). However, it
indirectly impacts the semantics of all affected uses of the declared
object.
The scope of a declaration is, by default, local to the MathML element
in which the declaration is made. If the scope
attribute of the declare element is set to global, the declaration applies to the entire MathML
expression in which it appears.
The uses of the declare element range from
resetting default attribute values to associating an expression with a
particular instance of a more elaborate structure. Subsequent uses of the
original expression (within the scope of the
declare) play the same semantic role as would the
paired object.
For example, the declaration
<declare>
<ci> A </ci>
<vector>
<ci> a </ci>
<ci> b </ci>
<ci> c </ci>
</vector>
</declare>
specifies that
A stands for the particular vector (a, b, c)
so that subsequent uses of A as in
V = A + B can take this into account.
When declare is used in this way, the actual
encoding
<apply>
<eq/>
<ci> V </ci>
<apply>
<plus/>
<ci> A </ci>
<ci> B </ci>
</apply>
</apply>
remains unchanged but the expression can be interpreted properly as vector addition.
There is no requirement to declare an expression to stand for a specific object. For example, the declaration
<declare type="vector"> <ci> A </ci> </declare>
specifies that A is a vector without indicating the number of
components or the values of specific components. The possible values for
the type attribute include all the predefined
container element names such as vector, matrix or set
(see section 4.3.2.9 [type]).
The lambda calculus allows a user to construct a function from a variable and an expression. For example, the lambda construct underlies the common mathematical idiom illustrated here:
Let f be the function taking x to x2 + 2
There are various notations for this concept in mathematical literature,
such as
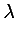(x, F(x)) = F or
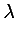(x, [F] ) = F,
where x is a free variable in F.
This concept is implemented in MathML with the lambda element. A lambda construct with n
internal variables is encoded by a lambda element
with n+1 children. All but the last child must be bvar elements containing the identifiers of the
internal variables. The last child is an expression defining the function. This
is typically an apply, but can also be any
container element.
The following constructs
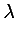(x, sin(x+1)):
<lambda>
<bvar><ci> x </ci></bvar>
<apply>
<sin/>
<apply>
<plus/>
<ci> x </ci>
<cn> 1 </cn>
</apply>
</apply>
</lambda>
To use declare and lambda to construct the function f for which
f( x) = x2 + x + 3 use:
<declare type="fn">
<ci> f </ci>
<lambda>
<bvar><ci> x </ci></bvar>
<apply>
<plus/>
<apply>
<power/>
<ci> x </ci>
<cn> 2 </cn>
</apply>
<ci> x </ci>
<cn> 3 </cn>
</apply>
</lambda>
</declare>
The following markup declares and constructs the function J such that J(x, y) is the integral from x to y of t 4 with respect to t.
<declare type="fn">
<ci> J </ci>
<lambda>
<bvar><ci> x </ci></bvar>
<bvar><ci> y </ci></bvar>
<apply> <int/>
<bvar>
<ci> t </ci>
</bvar>
<lowlimit>
<ci> x </ci>
</lowlimit>
<uplimit>
<ci> y </ci>
</uplimit>
<apply> <power/>
<ci>t</ci>
<cn>4</cn>
</apply>
</apply>
</lambda>
</declare>
The function J can then in turn be applied to an argument pair.
The last example of the preceding section illustrates the use of
qualifier elements lowlimit, uplimit, and bvar used in
conjunction with the int element. A number of
common mathematical constructions involve additional data that is either
implicit in conventional notation, such as a bound variable, or thought of
as part of the operator rather than an argument, as is the case with the
limits of a definite integral.
Content markup uses qualifier elements in conjunction with a number of
operators, including integrals, sums, series, and certain differential
operators. Qualifier elements appear in the same
apply element with one of these operators. In
general, they must appear in a certain order, and their precise meaning
depends on the operators being used. For details, see section 4.2.3.2 [Operators taking Qualifiers].
The qualifier element bvar is also used in
another important MathML construction. The condition element is used to place conditions on bound
variables in other expressions. This allows MathML to define sets by rule,
rather than enumeration, for example. The following markup, for instance,
encodes the set {x | x < 1}:
<set>
<bvar><ci> x </ci></bvar>
<condition>
<apply>
<lt/>
<ci> x </ci>
<cn> 1 </cn>
</apply>
</condition>
</set>
While the primary role of the MathML content element set is to directly encode the mathematical structure of expressions independent of the notation used to present the objects, rendering issues cannot be ignored. Each content element has a default rendering, given in section section 4.4 [The Content Markup Elements], and several mechanisms (including section 4.3.3.2 [General Attributes]) are provided for associating a particular rendering with an object.
Containers provide a means for the construction of mathematical objects of a given type.
| Tokens | ci,
cn,
csymbol |
| Constructors | interval,
list,
matrix,
matrixrow,
set,
vector,
apply,
reln,
fn,
lambda |
| Specials | declare |
Token elements are typically the leaves of the MathML expression tree. Token elements are used to indicate mathematical identifiers, numbers and symbols.
It is also possible for the canonically empty operator elements such as
exp, sin and cos to be leaves in an expression tree. The usage of
operator elements is described in section 4.2.3 [Functions, Operators and Qualifiers].
cn element is the MathML token element used
to represent numbers. The supported types of numbers include:
real,
integer,
rational,
complex-cartesian, and
complex-polar, with
real being
the default type. An attribute base (with default
value 10) is used to help specify how the content is
to be parsed. The content itself is essentially PCDATA, separated
by <sep/> when two parts are needed in order to fully
describe a number. For example, the real number 3 is constructed by
<cn type="real"> 3 </cn>,
while the rational number 3/4 is constructed as
<cn type="rational"> 3<sep/>4 </cn>.
The detailed structure and specifications are provided in
section 4.4.1.1 [Number (cn)].
ci element, or `content
identifier' is used to construct a variable, or an identifier. A type attribute indicates the type of object the symbol
represents. Typically, ci represents a real scalar,
but no default is
specified. The content is either PCDATA or a general presentation
construct (see section 3.1.5 [Summary of Presentation Elements]). For example,
<ci> <msub> <mi>c</mi> <mn>1</mn> </msub> </ci>encodes an atomic symbol that displays visually as c 1which, for purposes of content, is treated as a single symbol representing a real number. The detailed structure and specifications is provided in section 4.4.1.2 [Identifier (
ci)].
csymbol element, or `content
symbol' is used to construct a symbol whose semantics are not part
of the core content elements provided by MathML, but defined externally.
csymbol does not make any attempt
to describe how to map the arguments occurring in any application of the
function into a new MathML expression. Instead, it depends on its definitionURL attribute to point to a particular
meaning, and the encoding attribute to give the
syntax of this definition.
The content of a csymbol is either PCDATA
or a general presentation construct (see section 3.1.5 [Summary of Presentation Elements]).
For example,
<csymbol definitionURL="www.vnbooks.com/ContDiffFuncs.htm"
encoding="text">
<msup>
<mi>C</mi>
<mn>2</mn>
</msup>
</csymbol>
encodes an atomic symbol that displays visually as C
2 and that, for purposes of content, is treated as a single symbol
representing the space of twice-differentiable continuous functions.
The detailed structure and specifications is
provided in section 4.4.1.3 [Externally defined symbol
(csymbol)].
MathML provides a number of elements for combining elements into familiar compound objects. The compound objects include things like lists, sets. Each constructor produces a new type of object.
interval element is described in detail in
section 4.4.2.4 [Interval (interval)]. It denotes an interval on the
real line with the values represented by its children as end points. The
closure attribute is used to qualify the type of
interval being represented. For example,
<interval closure="open-closed"> <ci> a </ci> <ci> b </ci> </interval>represents the open-closed interval often written (a,b].
set and list
elements are described in detail in section 4.4.6.1 [Set (set)] and
section 4.4.6.2 [List (list)]. Typically, the child elements of a possibly
empty list element are the actual components of
an ordered list. For example, an ordered list of the three symbols
a, b, and c is encoded as
<list> <ci> a </ci> <ci> b </ci> <ci> c </ci> </list>Alternatively,
bvar and condition elements can be used to define lists where
membership depends on satisfying certain conditions.
An order attribute, which is used to specify what
ordering is to be used. When the nature of the child elements permits, the
ordering defaults to a numeric or lexicographic ordering.
Sets are structured much the same as lists except that there is no
implied ordering and the type of set may be normal or multiset with
multiset indicating that repetitions are allowed.
For both sets and lists, the child elements must be valid MathML content
elements. The type of the child elements is not restricted. For example,
one might construct a list of equations, or inequalities.
matrix element is used to represent
mathematical matrices. It is described in detail in section 4.4.10.2 [Matrix (matrix)]. It has zero or more child elements,
all of which are matrixrow elements. These in turn
expect zero or more child elements that evaluate to algebraic expressions
or numbers. These sub-elements are often real numbers, or symbols as in
<matrix> <matrixrow> <cn> 1 </cn> <cn> 2 </cn> </matrixrow> <matrixrow> <cn> 3 </cn> <cn> 4 </cn> </matrixrow> </matrix>The
matrixrow elements must always be contained
inside of a matrix, and all rows in a given matrix must have the same number
of elements.
Note that the behavior of the matrix and matrixrow elements is substantially different from the
mtable and mtr presentation
elements.
vector element is described in detail in
section 4.4.10.1 [Vector (vector)]. It constructs vectors from an
n-dimensional vector space so that its n child elements
typically represent real or complex valued scalars as in the three-element
vector
<vector>
<apply>
<plus/>
<ci> x </ci>
<ci> y </ci>
</apply>
<cn> 3 </cn>
<cn> 7 </cn>
</vector>
apply element is described in detail in
section 4.4.2.1 [Apply (apply)]. Its purpose is apply a
function or operator to its arguments to produce an an expression
representing an element of the range of the function. It is involved in
everything from forming sums such as a + b as in
<apply> <plus/> <ci> a </ci> <ci> b </ci> </apply>through to using the sine function to construct sin(a) as in
<apply> <sin/> <ci> a </ci> </apply>or constructing integrals. Its usage in any particular setting is determined largely by the properties of the function (the first child element) and as such its detailed usage is covered together with the functions and operators in section 4.2.3 [Functions, Operators and Qualifiers].
reln element is described in detail in
section 4.4.2.2 [Relation (reln)]. It was used in MathML 1.0 to
construct an expression such as a = b, as in
<reln><eq/> <ci> a </ci> <ci> b </ci> </reln>indicating an intended comparison between two mathematical values. MathML 2.0 takes the view that this should be regarded as the application of a boolean function, and as such could be constructed using
apply. The use of reln with logical operators
is supported for reasons of backwards compatibility, but deprecated in
favour of apply.
fn element was used in MathML 1.0 to
make explicit the fact that an expression is being used as a function
or operator. This is allowed in MathML 2.0 for backwards compatibility,
but is deprecated, as the use of an expression as a function or operator
is clear from its position as the first child of an
apply. fn is discussed
in detail in section 4.4.2.3 [Function (fn)].
lambda element is used to construct a
user-defined function from an expression and one or more free
variables. The lambda construct with n internal variables takes
n+1 children. The first (second, up to n) is a bvar containing the identifiers of the internal
variables. The last is an expression defining the function. This is
typically an apply, but can also be any container
element. The following constructs
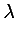(x, sin x)
<lambda>
<bvar><ci> x </ci></bvar>
<apply>
<sin/>
<ci> x </ci>
</apply>
</lambda>
The following constructs the constant function
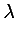(x, 3)
<lambda> <bvar><ci> x </ci></bvar> <cn> 3 </cn> </lambda>
The declare construct is described in detail in
section 4.4.2.8 [Declare (declare)]. It is special in that its
entire purpose is to modify the semantics of other objects. It is not
rendered visually or aurally.
The need for declarations arises any time a symbol (including more general presentations) is being used to represent an instance of an object of a particular type. For example, you may wish to declare that the symbolic identifier V represents a vector.
The declaration
<declare type="vector"><ci>V</ci></declare>
resets the default type attribute of <ci>V</ci> to
vector for all affected occurrences of
<ci>V</ci>. This avoids having to write
<ci type="vector">V</ci> every time you use the
symbol.
More generally, declare can be used to associate
expressions with specific content. For example, the declaration
<declare>
<ci>F</ci>
<lambda>
<bvar><ci> U </ci></bvar>
<apply>
<int/>
<bvar><ci> x </ci></bvar>
<lowlimit><cn> 0 </cn></lowlimit>
<uplimit><ci> a </ci></uplimit>
<ci> U </ci>
</apply>
</lambda>
</declare>
associates the symbol F with a new function defined by the lambda construct. Within the scope where the
declaration is in effect, the expression
<apply> <ci>F</ci> <ci> U </ci> </apply>
stands for the integral of U from 0 to a.
The declare element can also be used to change
the definition of a function or operator. For example, if the URL
http://.../MathML:noncommutplus described a non-commutative
plus operation encoded in Maple syntax, then the declaration
<declare definitionURL="http://.../MathML:noncommutplus"
encoding="Maple V">
<plus/>
</declare>
would indicate that all affected uses of plus are to
be interpreted as having that definition of plus.
The operators and functions defined by MathML can be divided into categories as shown in the table below.
| unary arithmetic | exp,
factorial,
minus,
abs,
conjugate,
arg,
real,
imaginary
|
| unary logical |
not
|
| unary functional | inverse,
ident |
| unary elementary classical functions | sin,
cos,
tan,
sec,
csc,
cot,
sinh,
cosh,
tanh,
sech,
csch,
coth,
arcsin,
arccos,
arctan,
arccosh,
arccot,
arccoth,
arccsc,
arccsch,
arcsec,
arcsech,
arcsinh,
arctanh,
exp,
ln,
log
|
| unary linear algebra | determinant,
transpose |
| unary calculus and vector calculus |
divergence,
grad,
curl,
laplacian
|
| unary set-theoretic |
card
|
| binary arithmetic | quotient,
divide,
minus,
power,
rem |
| binary logical |
implies,
equivalent,
approx
|
| binary set operators | setdiff |
| binary linear algebra |
vectorproduct,
scalarproduct,
outerproduct
|
| n-ary arithmetic | plus,
times,
max,
min,
gcd |
| n-ary statistical | mean,
sdev,
variance,
median,
mode |
| n-ary logical | and,
or,
xor |
| n-ary linear algebra | selector |
| n-ary set operator | union,
intersect |
| n-ary functional | fn,
compose |
| integral, sum, product operators | int,
sum,
product |
| differential operator | diff,
partialdiff |
| quantifier | forall,
exists |
From the point of view of usage, MathML regards functions (for example
sin and cos) and operators
(for example plus and times)
in the same way. MathML predefined functions and operators are all
canonically empty elements.
Note that the csymbol element can be used to
construct a user-defined symbol that can be used as a function or
operator.
MathML functions can be used in two ways. They can be used as the
operator within an apply element, in which case
they refer to a function evaluated at a specific value. For example,
<apply> <sin/> <cn>5</cn> </apply>
denotes a real number, namely sin(5).
MathML functions can also be used as arguments to other operators, for example
<apply> <plus/><sin/><cos/> </apply>
denotes a function, namely the result of adding the sine and cosine
functions in some function space. (The default semantic definition of plus is such that it infers what kind of operation is
intended from the type of its arguments.)
The number of child elements in the apply is
defined by the element in the first (i.e. operator) position.
Unary operators are followed by exactly one other child
element within the apply.
Binary operators are followed by exactly two child elements.
N-ary operators are followed by zero or more child elements.
The one exception to these rules is that declare elements may be inserted in any position except
the first. declare elements are not counted when
satisfying the child element count for an apply
containing a unary or binary operator element.
Integral, sum, product and differential operators are discussed below in section 4.2.3.2 [Operators taking Qualifiers].
The table below contains the qualifiers and the operators taking qualifiers in MathML.
| qualifiers | lowlimit,
uplimit,
bvar,
degree,
logbase,
interval,
condition |
| operators | int,
sum,
product,
root,
diff,
partialdiff,
limit,
log,
moment,
min,
max,
forall,
exists |
Operators taking qualifiers are canonically empty functions that differ
from ordinary empty functions only in that they support the use of special
qualifier elements to specify their meaning more fully. They
are used in exactly the same way as ordinary operators, except that when
they are used as operators, certain qualifier elements are also permitted
to be in the enclosing apply. They always precede
the argument if it is present. If more than one qualifier is present, they
appear in the order
bvar,
lowlimit,
uplimit,
interval,
condition,
degree,
logbase.
A typical example is:
<apply>
<int/>
<bvar><ci>x</ci></bvar>
<lowlimit><cn>0</cn></lowlimit>
<uplimit><cn>1</cn></uplimit>
<apply>
<power/>
<ci>x</ci>
<cn>2</cn>
</apply>
</apply>
It is also valid to use qualifier schema with a function not applied to an argument. For example, a function acting on integrable functions on the interval [0,1] might be denoted:
<fn>
<apply>
<int/>
<bvar><ci>x</ci></bvar>
<lowlimit><cn>0</cn></lowlimit>
<uplimit><cn>1</cn></uplimit>
</apply>
</fn>
The meaning and usage of qualifier schema varies from function to function. The following list summarizes the usage of qualifier schema with the MathML functions taking qualifiers.
int function accepts the
lowlimit,
uplimit,
bvar,
interval and
condition schemata. If both
lowlimit and
uplimit schema are present,
they denote the limits of a definite integral. The domain of integration
may alternatively be specified using interval or condition. The bvar schema signifies the variable of integration. When
used with int, each qualifier schema is expected to
contain a single child schema; otherwise an error is generated.
diff function accepts the
bvar schema. The
bvar schema specifies with respect to
which variable the derivative is being taken. The bvar may itself contain a degree schema that is used to specify the order of the
derivative, i.e. a first derivative, a second derivative, etc. For example,
the second derivative of f with respect to x is:
<apply>
<diff/>
<bvar>
<ci> x </ci>
<degree>
<cn> 2 </cn>
</degree>
</bvar>
<apply><fn><ci>f</ci></fn>
<ci> x </ci>
</apply>
</apply>
partialdiff function accepts zero or more
bvar schemata. The bvar
schema specify with respect to which variables the derivative is being
taken. The bvar elements may themselves contain degree schemata that are used to specify the order of
the derivative. Variables specified by multiple bvar elements will be used in order as the variable of
differentiation in mixed partials. When used with partialdiff, the degree schema
is expected to contain a single child schema. For example,
<apply> <partialdiff/> <bvar><ci>x</ci></bvar> <bvar><ci>y</ci></bvar> <fn><ci>f</ci></fn> </apply>denote the mixed partial (d2 / dxdy)f.
sum and product
functions accept the bvar, lowlimit, uplimit, interval and condition
schemata. If both lowlimit and uplimit schemata are present, they denote the limits of
the sum or product. The limits may alternatively be specified using the interval or condition
schema. The bvar schema signifies the index
variable in the sum or product. A typical example might be:
<apply>
<sum/>
<bvar><ci>i</ci></bvar>
<lowlimit><cn>0</cn></lowlimit>
<uplimit><cn>100</cn></uplimit>
<apply>
<power/>
<ci>x</ci>
<ci>i</ci>
</apply>
</apply>
When used with sum or product, each qualifier schema is expected to contain a
single child schema; otherwise an error is generated.
limit function accepts zero or more bvar schemata, and optional condition and lowlimit
schemata. A condition may be used to place
constraints on the bvar. The bvar schema denotes the variable with respect to which
the limit is being taken. The lowlimit schema
denotes the limit point. When used with limit, the
bvar and lowlimit schemata
are expected to contain a single child schema; otherwise an error is
generated.
log function accepts only the logbase schema. If present, the logbase schema denotes the base with respect to which
the logarithm is being taken. Otherwise, the log is assumed to be base
10. When used with log, the logbase schema is expected to contain a single child
schema; otherwise an error is generated.
moment function accepts only the degree schema. If present, the degree schema denotes the order of the
moment. Otherwise, the moment is assumed to be the first order moment. When
used with moment, the degree schema is expected to contain a single child
schema; otherwise an error is generated.
min and
maxfunctions accept a
bvar schema in cases where the maximum or minimum
is being taken over a set of values specified by a
condition schema together with an expression
to be evaluated on that set.
bvar element was optional when using a
condition; if a
condition element containing a single
variable was given by itself following a
min or
max operator, the variable was implicitly
assumed to be bound, and the expression to be maximized or minimized
(if absent) was assumed to be the single bound variable.
This usage is deprecated in MathML 2.0
in favour of explicitly stating the bound variable(s) and the expression
to be maximised in all cases.
The min and max elements
may also be applied to a list of values in which case no qualifier schemata
are used. For examples of all three usages, see section 4.4.3.4 [Maximum and minimum
(max, min)].
forall and exists are used
in conjuction with one or more bvar schemata to
represent simple logical assertions. There are two ways of using the
logical quantifier operators. The first usage is for representing a simple,
quantified assertion. For example, the statement `there exists
x< 9' would be represented as:
<apply>
<exists/>
<bvar><ci> x </ci></bvar>
<apply><lt/>
<ci> x </ci><cn> 9 </cn>
</apply>
</apply>
The second usage is for representing implications. Hypotheses are given by
a condition element following the bound variables.
For example the statement `for all x < 9, x <
10' would be represented as:
<apply>
<forall/>
<bvar><ci> x </ci></bvar>
<condition>
<apply><lt/>
<ci> x </ci><cn> 9 </cn>
</apply>
</condition>
<apply><lt/>
<ci> x </ci><cn> 10 </cn>
</apply>
</apply>
Note that in both usages one or more bvar qualifiers
are mandatory.
| binary relation |
neq,
equivalent,
approx
|
| binary logical relation | implies |
| binary set relation | in,
notin,
notsubset,
notprsubset |
| binary series relation | tendsto |
| n-ary relation | eq,
leq,
lt,
geq,
gt |
| n-ary set relation | subset,
prsubset |
The MathML content tags include a number of canonically empty elements which denote arithmetic and logical relations. Relations are characterized by the fact that, if an external application were to evaluate them (MathML does not specify how to evaluate expressions), they would typically return a truth value. By contrast, operators generally return a value of the same type as the operands. For example, the result of evaluating a < b is either true or false (by contrast, 1 + 2 is again a number).
Relations are bracketed with their arguments using the apply element in the same way as other functions. In
MathML 1.0, relational operators were bracketed using reln. This usage, although still supported, is now
deprecated in favour of apply. The element for the relational
operator is the first child element of the
apply. Thus, the example from the preceding
paragraph is properly marked up as:
<apply> <lt/> <ci>a</ci> <ci>b</ci> </apply>
It is an error to enclose a relation in an element other than
apply or reln.
The number of child elements in the apply is
defined by the element in the first (i.e. relation) position.
Unary relations are followed by exactly one other child
element within the apply.
Binary relations are followed by exactly two child elements.
N-ary relations are followed by zero or more child elements.
The one exception to these rules is that declare elements may be inserted in any position except
the first. declare elements are not counted when
satisfying the child element count for an apply
containing a unary or binary relation element.
| condition | condition |
The condition element is used to define the
`such that' construct in mathematical expressions. Condition
elements are used in a number of contexts in MathML. They are used to
construct objects like sets and lists by rule instead of by
enumeration. They can be used with the forall and
exists operators to form logical expressions. And
finally, they can be used in various ways in conjunction with certain
operators. For example, they can be used with and int element to specify domains of integration, or to
specify argument lists for operators like min and
max.
The condition element is always used together
with one or more bvar elements.
The exact interpretation depends on the context, but generally speaking,
the condition element is used to restrict the
permissible values of a bound variable appearing in another expression to
those that satisfy the relations contained in the condition. Similarly, when the condition element contains a set, the values of the bound variables are restricted
to that set.
A condition element contains a single child that is either a apply, or a reln element
(deprecated). Compound conditions are indicated by applying relations such
as and inside the child of the condition.
The following encodes `there exists x such that x 5 < 3'.
<apply>
<exists/>
<bvar><ci> x </ci></bvar>
<condition>
<apply><lt/>
<apply>
<power/>
<ci>x</ci>
<cn>5</cn>
</apply>
<cn>3</cn>
</apply>
</condition>
</apply>
The next example encodes `for all xin N there exists prime numbers p, q such that p+ q= 2x'.
<apply>
<forall/>
<bvar><ci>x</ci></bvar>
<condition>
<apply><in/>
<ci>x</ci>
<csymbol encoding="text" definitionURL="www.naturalnums.htm>N</csymbol>
</apply>
</condition>
<apply><exists/>
<bvar><ci>p</ci></bvar>
<bvar><ci>q</ci></bvar>
<condition>
<apply><and/>
<apply><in/><ci>p</ci>
<csymbol encoding="text" definitionURL="www.primes.htm>P</csymbol>
</apply>
<apply><in/><ci>q</ci>
<csymbol encoding="text" definitionURL="www.primes.htm>P</csymbol>
</apply>
<apply><eq/>
<apply><plus/><ci>p</ci><ci>q</ci></apply>
<apply><times/><cn>2</cn><ci>x</ci></apply>
</apply>
</condition>
</apply>
</apply>
A third example shows the use of quantifiers with condition. The following markup encodes `there exists
x < 3 such that x2 = 4'.
<apply>
<exists/>
<bvar><ci> x </ci></bvar>
<condition>
<apply><lt/><ci>x</ci><cn>3</cn></apply>
</condition>
<apply>
<eq/>
<apply>
<power/><ci>x</ci><cn>2</cn>
</apply>
<cn>4</cn>
</apply>
</apply>
| mappings | semantics,
annotation,
annotation-xml |
The use of content markup rather than presentation markup for mathematics is sometimes referred to as semantic tagging [Buswell1996]. The parse-tree of a valid element structure using MathML content elements corresponds directly to the expression tree of the underlying mathematical expression. We therefore regard the content tagging itself as encoding the syntax of the mathematical expression. This is, in general, sufficient to obtain some rendering and even some symbolic manipulation (e.g. polynomial factorization).
However, even in such apparently simple expressions as X +
Y, some additional information may be required for applications
such as computer algebra. Are X and Y integers, or
functions, etc.? `Plus' represents addition over which field?
This additional information is referred to as semantic
mapping. In MathML, this mapping is provided by the semantics, annotation and annotation-xml elements.
The semantics element is the container element
for the MathML expression together with its semantic mappings. semantics expects a variable number of child
elements. The first is the element (which may itself be a complex element
structure) for which this additional semantic information is being
defined. The second and subsequent children, if any, are instances of the
elements annotation and/or annotation-xml.
The semantics tags also accepts the
definitionURL and encoding
attributes for use by external processing
applications. One use might be a URI for a semantic content
dictionary, for example. Since the semantic mapping information might in
some cases be provided entirely by the definitionURL
attribute, the annotation or annotation-xml elements are optional.
The annotation element is a container for
arbitrary data. This data may be in the form of text, computer algebra
encodings, C programs, or whatever a processing application expects. annotation has an attribute encoding defining the form in use. Note that the content
model of annotation is PCDATA, so care must be
taken that the particular encoding does not conflict with XML parsing
rules.
The annotation-xml element is a container for
semantic information in well-formed XML. For example, an XML form of the
OpenMath semantics could be given. Another possible use here is to embed,
for example, the presentation tag form of a construct given in content tag
form in the first child element of semantics (or
vice versa). annotation-xml has an attribute encoding defining the form in use.
For example:
<semantics>
<apply>
<divide/>
<cn>123</cn>
<cn>456</cn>
</apply>
<annotation encoding="Mathematica">
N[123/456, 39]
</annotation>
<annotation encoding="TeX">
$0.269736842105263157894736842105263157894\ldots$
</annotation>
<annotation encoding="Maple">
evalf(123/456, 39);
</annotation>
<annotation-xml encoding="MathML-Presentation">
<mrow>
<mn> 0.269736842105263157894 </mn>
<mover accent='true'>
<mn> 736842105263157894 </mn>
<mo> ‾ </mo>
</mover>
</mrow>
</annotation-xml>
<annotation-xml encoding="OpenMath">
<OMA>...</OMA>
</annotation-xml>
</semantics>
where OMA is the element defining the additional
semantic information.
Of course, providing an explicit semantic mapping at all is optional, and in general would only be provided where there is some requirement to process or manipulate the underlying mathematics.
Although semantic mappings can easily be provided by various
proprietary, or highly specialized encodings, there are no widely
available, non-proprietary standard schemes for semantic mapping. In part
to address this need, the goal of the OpenMath effort is to provide a
platform-independent, vendor-neutral standard for the exchange of
mathematical objects between applications. Such mathematical objects
include semantic mapping information. The OpenMath group has defined an
SGML syntax for the encoding of this information [OpenMath1996]. This element set could provide the basis of
one annotation-xml element set.
An attractive side of this mechanism is that the OpenMath syntax is specified in XML, so that a MathML expression together with its semantic annotations can be validated using XML parsers.
MathML functions, operators and relations can all be thought of as mathematical functions if viewed in a sufficiently abstract way. For example, the standard addition operator can be regarded as a function mapping pairs of real numbers to real numbers. Similarly, a relation can be thought of as a function from some space of ordered pairs into the set of values {true, false}. To be mathematically meaningful, the domain and range of a function must be precisely specified. In practical terms, this means that functions only make sense when applied to certain kinds of operands. For example, thinking of the standard addition operator, it makes no sense to speak of `adding' a set to a function. Since MathML content markup seeks to encode mathematical expressions in a way that can be unambiguously evaluated, it is no surprise that the types of operands is an issue.
MathML specifies the types of arguments in two ways. The first way is by
providing precise instructions for processing applications about the kinds
of arguments expected by the MathML content elements denoting functions,
operators and relations. These operand types are defined in a dictionray of
default semantic bindings for content elements, which is given in
appendix C [Content Element Definitions]. For example, the MathML content dictionary
specifies that for real scalar arguments the plus operator is the standard
commutative addition operator over a field. The elements cn has a type attribute with a default value of real. Thus some processors will be able to use this
information to verify the validity of the indicated operations.
Issue (ci-default-type):Shouldn't
cihavenoneor `unspecified' as the default type?
Although MathML specifies the types of arguments for functions, operators and relations, and provides a mechanism for typing arguments, a MathML-compliant processor is not required to do any type checking. In other words, a MathML processor will not generate errors if argument types are incorrect. If the processor is a computer algebra system, it may be unable to evaluate an expression, but no MathML error is generated.
Content element attributes are all of the type CDATA, that is, any
character string will be accepted as valid. In addition, each attribute has
a list of predefined values, which a content processor is expected to
recognize and process. The reason that the attribute values are not
formally restricted to the list of predefined values is to allow for
extension. A processor encountering a value (not in the predefined list)
which it does not recognize may validly process it as the default value for
that attribute.
Each attribute is followed by the elements to which it can be applied.
base
10
closure
open,
closed,
open-closed,
closed-open.
The default value is closed
definitionURL
definitionURL attribute would be some standard,
machine-readable format. However, there are several reasons why MathML does
not require such a format.
First, no such format currently exists. There are several projects
underway to develop and implement standard semantic encoding formats, most
notably the OpenMath effort. But by nature, the development of a
comprehensive system of semantic encoding is a very large enterprise, and
while much work has been done, much additional work remains. Therefore,
even though the definitionURL is designed and
intended for use with a formal semantic encoding language such as OpenMath,
it is premature to require any one particular format.
Another reason for leaving the format of the definitionURL attribute unspecified is that there will
always be situations where some non-standard format is preferable. This is
particularly true in situations where authors are describing new ideas.
It is anticipated that in the near term, there will be a variety of
renderer-dependent implementations of the
definitionURL attribute. For example, a translation tool might
simply prompt the user with the specified definition in situations where
the proper semantics have been overridden, and in this case, human-readable
definitions will be most useful. Other software may utilize OpenMath
encodings. Still other software may use proprietary encodings, or look for
definitions in any of several formats.
As a consequence, authors need to be aware that there is no guarantee a
generic renderer will be able to take advantage of information pointed to
by the definitionURL attribute. Of course, when
widely-accepted standardized semantic encodings are available, the
definitions pointed to can be replaced without modifying the original
document. However, this is likely to be labor intensive.
There is no default value for the definitionURL
attribute, i.e. the semantics are defined within the MathML fragment,
and/or by the MathML default semantics.
encoding
csymbol , semantics and operator elements, the syntax of
the target referred to by
definitionURL. Predefined values are
MathML-Presentation,
MathML-Content.
Other typical values:
TeX,
OpenMath.
The default value is "", i.e. unspecified.
nargs
nary, or any numeric string.
The default value is 1
occurrence
prefix,
infix,
function-model.
The default value is function-model
order
lexicographic,
numeric.
The default value is numeric
scope
local,
global.
local means the containing MathML element.
global means the containing
math element.
local.
At present, declarations cannot affect anything outside of the
containing math element. Ideally, one would like
to make document-wide declarations by setting the value of the
scope attribute to be
global-document. However, the proper mechanism for
document-wide declarations very much depends on details of the way in which
XML will be embedded in HTML, future XML style sheet mechanisms, and the
underlying Document Object Model.
Since these supporting technologies are still in flux at present, the
MathML specification does not include
global-document as a pre-defined value of the
scope attribute. It is anticipated, however, that this issue
will be revisited in future revisions of MathML as supporting technologies
stabilize. In the near term, MathML implementors that wish to simulate the
effect of a document-wide declaration are encouraged to pre-process
documents in order to distribute document-wide declarations to each
individual math element in the document.
type
integer,
rational,
real,
float,
complex,
complex-polar,
complex-cartesian,
constant.
The default value is real.
Notes. Each data type implies that the data adheres to
certain formating conventions, detailed below. If the data fails to conform
to the expected format, an error is generated. Details of the individual
formats are:
base is specified, then the digits are interpreted as being
digits computed to that base.
A real number may also be presented in scientific notation. Such numbers
have two parts (a mantissa and an exponent) separated by
`e'. The first part is a real number, while the second part is
an integer exponent indicating a power of the base. For example, 12.3e5
represents 12.3 times 10^5.base
attribute. If base is present, it specifies the
base for the digit encoding, and it specifies it base ten. Thus
base='16' specifies a hex encoding. When
base > 10, letters are added in alphabetical order as
digits. The legitimate values for base are
therefore between 2 and 36.<sep/>.
If base is present, it specifies the base used for
the digit encoding of both integers.<sep/>.<sep/>.constant
type is used to denote named constants. For example, an instance of
<cn type="constant">π</cn>should be interpreted
as having the semantics of the mathematical constant Pi. The data for a
constant cn tag may be one of the following
common constants:
| Symbol | Value |
π |
The usual
π of trigonometry: approximately 3.141592653... |
ⅇ (or
ⅇ) |
The base for natural logarithms: approximately 2.718281828 ... |
ⅈ (or
ⅈ) |
Square root of -1 |
γ |
Euler's constant: approximately 0.5772156649... |
∞ (or
&infty;) |
Infinity. Proper interpretation varies with context |
&true; |
the logical constant true |
&false; |
the logical constant false |
&NotANumber; (or
&NaN;) |
represents the result of an ill-defined floating point division |
integer,
rational,
real,
float,
complex,
complex-polar,
complex-cartesian,
constant, or the name of any content element.
The meaning of the various attribute values is the same as that listed
above for the cn element.
The default value is "", i.e. unspecified.
ci , i.e. a generic identifier
normal, multiset.
multiset indicates that repetitions are allowed.
The default value is normal.
above,
below, two-sided.
The default value is above.
type
The type attribute, in addition to conveying
semantic information, can be interpreted to provide rendering
information. For example in
<ci type="vector">V</ci>
a renderer could display a bold V for the vector.
All content elements support the following general attributes that can be used to modify the rendering of the markup.
class
style
id
other
The class, style and id attributes are intended for compatibility with
Cascading Style Sheets (CSS), as described in section 2.3.4 [Attributes Shared by all MathML Elements].
Content or semantic tagging goes along with the (frequently implicit) premise that, if you know the semantics, you can always work out a presentation form. When an author's main goal is to mark up re-usable, evaluatable mathematical expressions, the exact rendering of the expression is probably not critical, provided that it is easily understandable. However, when an author's goal is more along the lines of providing enough additional semantic information to make a document more accessible by facilitating better visual rendering, voice rendering, or specialized processing, controlling the exact notation used becomes more of an issue.
MathML elements accept an attribute other (see
section 7.2.3 [Attribute for unspecified data]), which can be used to specify things
not specifically documented in MathML. On content tags, this attribute can
be used by an author to express a preference between
equivalent forms for a particular content element construct, where the
selection of the presentation has nothing to do with the
semantics. Examples might be
Thus, if a particular renderer recognized a display attribute to select between script-style and display-style fractions, an author might write
<apply other='display="scriptstyle"'> <divide/> <mn> 1 </mn> <mi> x </mi> </apply>
to indicate that the rendering 1/x is preferred.
The information provided in the other attribute
is intended for use by specific renderers or processors, and therefore, the
permitted values are determined by the renderer being used. It is legal for
a renderer to ignore this information. This might be intentional, in the
case of a publisher imposing a house style, or simply because the renderer
does not understand them, or is unable to carry them out.
This section provides detailed descriptions of the MathML content tags. They are grouped in categories that broadly reflect the area of mathematics from which they come, and also the grouping in the MathML DTD. There is no linguistic difference in MathML between operators and functions. Their separation here and in the DTD is for reasons of historical usage.
When working with the content elements, it can be useful to keep in mind the following.
The available content elements are:
cn
ci
csymbol (MathML 2.0)apply
reln (deprecated)fn (deprecated for externally defined functions)interval
inverse
sep
condition
declare
lambda
compose
ident
quotient
exp
factorial
divide
max and min
minus
plus
power
rem
times
root
gcd
and
or
xor
not
implies
forall
exists
abs
conjugate
arg (MathML 2.0)real (MathML 2.0)imaginary (MathML 2.0)eq
neq
gt
lt
geq
leq
equivalent (MathML 2.0)approx (MathML 2.0)int
diff
partialdiff
lowlimit
uplimit
bvar
degree
divergence (MathML 2.0)grad (MathML 2.0)curl (MathML 2.0)laplacian (MathML 2.0)set
list
union
intersect
in
notin
subset
prsubset
notsubset
notprsubset
setdiff
card (MathML 2.0)sum
product
limit
tendsto
exp
ln
log
sin
cos
tan
sec
csc
cot
sinh
cosh
tanh
sech
csch
coth
arcsin
arccos
arctan
arccosh
arccot
arccoth
arccsc
arccsch
arcsec
arcsech
arcsinh
arctanh
mean
sdev
variance
median
mode
moment
vector
matrix
matrixrow
determinant
transpose
selector
vectorproduct (MathML 2.0)scalarproduct (MathML 2.0)outerproduct (MathML 2.0)annotation
semantics
annotation-xml
cn)The cn element is used to specify actual
numerical constants. The content model must provide sufficient information
that a number may be entered as data into a computational system. By
default, it represents a signed real number in base 10. Thus, the content
normally consists of PCDATA restricted to a sign, a string of decimal
digits and possibly a decimal point, or alternatively one of the predefined
symbolic constants such as π.
The cn element uses the attribute type to represent other types of numbers such as,
for example, integer, rational, real or complex, and uses the
attribute base to specify the numerical base.
In addition to simple PCDATA, cn accepts as
content PCDATA separated by the (empty) element sep. This determines the different parts needed to
construct a rational or complex-cartesian number.
The cn element may also contain arbitrary presentation
markup in its content (see chapter 3 [Presentation Markup]) so that its presentation
can be very elaborate.
Alternative input notations for numbers are possible, but must be
explicitly defined by using the definitionURL and
encoding attributes, to refer to a written
specification of how a sequence of real numbers separated by <sep/> should be interpreted.
All attributes are CDATA:
real,
integer,
rational,
complex-cartesian,
complex-polar,
constant
CDATA for XML DTD) between 2 and 36.
<cn type="real"> 12345.7 </cn> <cn type="integer"> 12345 </cn> <cn type="integer" base="16"> AB3 </cn> <cn type="rational"> 12342 <sep/> 2342342 </cn> <cn type="complex-cartesian"> 12.3 <sep/> 5 </cn> <cn type="complex-polar"> 2 <sep/> 3.1415 </cn> <cn type="constant"> π </cn>
By default, contiguous blocks of PCDATA contained in cn elements should render as if it were wrapped in an
mn presentation element. Similarly, presentation
markup contained in a cn element should render as
it normally would. A mixture of PCDATA and presentation markup
should render as if it were contained wrapped in an mrow element, with contiguous blocks of PCDATA
wrapped in mn elements.
However, not all mathematical systems that encounter content based tagging do visual or aural rendering. The receiving applications are free to make use of a number in the manner it normally handles numerical data. Some systems might simplify the rational number 12342/2342342 to 6171/1171171 while pure floating point based systems might approximate this as 0.5269085385e-2. All numbers might be re-expressed in base 10. The role of MathML is simply to record enough information about the mathematical object and its structure so that it may be properly parsed.
The following renderings of the above MathML expressions are included both to help clarify the meaning of the corresponding MathML encoding and as suggestions for authors of rendering applications. In each case, no mathematical evaluation is intended or implied.
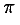
ci)The ci element is used to name an identifier in
a MathML expression (for example a variable). Such names are used to
identify mathematical objects. By default they are assumed to represent
complex scalars.
The ci element may contain arbitrary presentation
markup in its content (see chapter 3 [Presentation Markup]) so that its presentation
as a symbol can be very elaborate.
The ci element uses the
type attribute to specify the type of object
that it represents. Valid types include
integer,
rational,
real,
float,
complex,
constant, and more generally,
any of the names of the MathML container elements (e.g.
vector) or their type values. The
definitionURL and encoding
attributes can be used to extend the definition of
ci to include other types.
For example, a more advanced use might require a complex-vector.
1. <ci> x </ci>
2. <ci type="vector"> V </ci>
3. <ci>
<msub>
<mi>x</mi>
<mi>a</mi>
</msub>
</ci>
If the content of a ci element is tagged using
presentation tags, that presentation is used. If no such tagging is
supplied then the PCDATA content would typically be rendered as if it were
the content of an mi element. A renderer may wish
to make use of the value of the type attribute to improve on this. For
example, a symbol of type vector might be rendered
using a bold face. Typical renderings of the above symbols are:
csymbol)The csymbol element allows a writer to create an
element in MathML whose semantics are externally defined (i.e. not in the
core MathML content). The element can then be used in a MathML expression
as for example an operator or constant. Attributes are used to give the
syntax and location of the external definition of the symbol semantics.
Use of csymbol for referencing external semantics
can be contrasted with use of the semantics to
attach additional information in-line (ie. within the MathML fragment)
to a MathML construct. See section 4.2.6 [Syntax and Semantics]
All attributes are CDATA:
definitionURL. This syntax might be
text, or a formal syntax such as OpenMath.
<!-- reference to OpenMath formal syntax definition of Bessel function -->
<apply>
<csymbol encoding="OpenMath"
definitionURL="www.openmath.org/cds/BesselFunctions.ocd">
<msub><mi>J</mi><mn>0</mn></msub>
</csymbol>
<ci>y</ci>
</apply>
<!-- reference to human readable text description of Boltzmann's constant -->
<csymbol encoding="text"
definitionURL="www.uni.edu/universalconstants/Boltzmann.htm">
k
</csymbol>
By default, a contiguous block of PCDATA contained in a csymbol element should render as if it were wrapped in
an mo presentation element. Similarly, presentation
markup contained in a csymbol element should render
as it normally would. A mixture of PCDATA and presentation markup should
render as if it were contained wrapped in an mrow
element, with contiguous blocks of PCDATA wrapped in mo elements. The examples above would render by default
as
As csymbol is used to support reference to
externally defined semantics, it is a MathML error to have embedded content
MathML elements within the csymbol
element.
apply)The apply element allows a function or operator
to be applied to its arguments. Nearly all expression construction in
MathML content markup is carried out by applying operators or functions to
arguments. The first child of apply is the
operator, to be applied, with the other child elements as arguments.
The apply element is conceptually necessary in
order to distinguish between a function or operator, and an instance of its
use. The expression constructed by applying a function to 0 or more
arguments is always an element from the range of the function.
Proper usage depends on the operator that is being applied. For example,
the plus operator may have zero or more arguments.
while the minus operator requires one or two arguments
to be properly formed.
If the object being applied as a function is not already one of the
elements known to be a function (such as fn, sin or plus) then it is treated
as if it were the contents of an fn element.
Some operators such as diff and int make use of `named' arguments. These
special arguments are elements that appear as children of the apply element and identify `parameters'
such as the variable of differentiation or the domain of integration.
These elements are discussed further in section 4.2.3.2 [Operators taking Qualifiers].
1. <apply>
<factorial/>
<cn>3</cn>
</apply>
2. <apply>
<plus/>
<cn>3</cn>
<cn>4</cn>
</apply>
3. <apply>
<sin/>
<ci>x</ci>
</apply>
A mathematical system that has been passed an apply element is free to do with it whatever it
normally does with such mathematical data. It may be that no rendering is
involved (e.g. a syntax validator), or that the `function
application' is evaluated and that only the result is rendered (e.g.
sin(0) 
0).
When an unevaluated `function application' is rendered
there are a wide variety of appropriate renderings. The choice often
depends on the function or operator being applied. Applications of basic
operations such as plus are generally presented
using an infix notation while applications of sin
would use a more traditional functional notation such as
sin (x). Consult the default rendering for the
operator being applied.
Applications of user-defined functions (see csymbol, fn) that are not
evaluated by the receiving or rendering application would typically render
using a traditional functional notation unless an alternative presentation
is specified using the semantics tag.
reln)The reln element was used in MathML 1.0 to
construct an equation or relation. Relations were constructed in a manner
exactly analogous to the use of apply. This usage
is deprecated in MathML 2.0 in favour of the more generally usable apply.
The first child of reln is the relational
operator, to be applied, with the other child elements acting as arguments.
See section 4.2.4 [Relations] for further details.
<reln> <eq/> <ci> a </ci> <ci> b </ci> </reln> <reln> <lt/> <ci> a </ci> <ci> b </ci> </reln>
fn)The fn element makes explicit the fact that a
more general (possibly constructed) MathML object is being used in the same
manner as if it were a pre-defined function such as sin or plus.
fn has exactly one child element, used to
give the name (or presentation form) of the function. When
fn is used as the first child of an apply,
the number of following arguments is determined by the contents of
the fn.
In MathML 1.0, fn was also the primary mechanism
used to extend the collection of `known' mathematical
functions. This usage is now deprecated in favour of the more generally
applicable csymbol element. (New functions may also
be introduced by using declare in conjunction with
a lambda expression.)
1. <fn><ci> L </ci> </fn>
2. <apply>
<fn>
<apply>
<plus/>
<ci> f </ci>
<ci> g </ci>
</apply>
</fn>
<ci>z</ci>
</apply>
An fn object is rendered in the same way as its content.
A rendering application may add additional adornments such as
+parentheses to clarify the meaning.
interval)The interval element is used to represent simple
mathematical intervals of the real number line. It takes an attribute
closure, which can take on any of the values
open, closed,
open-closed, or
closed-open, with a default value of
closed.
More general domains are constructed by using the condition and bvar elements to
bind free variables to constraints.
The interval element expects either
two child elements that evaluate to real numbers or one child
element that is a condition defining the interval.
1. <interval>
<ci> a </ci>
<ci> b </ci>
</interval>
2. <interval closure="open-closed">
<ci> a </ci>
<ci> b </ci>
</interval>
inverse)The inverse element is applied to a function in
order to construct a generic expression for the functional inverse of that
function. (See also the discussion of inverse in
section 4.2.1.5 [The inverse construct]). As with other MathML functions, inverse may either be applied to arguments, or it may
appear alone, in which case it represents an abstract inversion operator
acting on other functions.
A typical use of the inverse element is in an
HTML document discussing a number of alternative definitions for a
particular function so that there is a need to write and define
f(-1)(x). To associate a particular definition with
f(-1), use the
definitionURL and encoding
attributes.
1. <apply>
<inverse/>
<ci> f </ci>
</apply>
2. <apply>
<inverse definitionURL="../MyDefinition.htm" encoding="text"/>
<ci> f </ci>
</apply>
3. <apply>
<apply><inverse/>
<ci type="matrix"> a </ci>
</apply>
<ci> A </ci>
</apply>
The default rendering for a functional inverse makes use of a parenthesized exponent as in f(-1)(x).
sep)The sep element is to separate PCDATA into
separate tokens for parsing the contents of the various specialized forms
of the cn elements. For example, sep is used when specifying the real and imaginary
parts of a complex number (see section 4.4.1 [Token Elements]). If it
occurs between MathML elements, it is a MathML error.
<cn type="complex"> 3 <sep/> 4 </cn>
The sep element is not directly rendered
(see section 4.4.1 [Token Elements]).
condition)The condition element is used to place a
condition on one or more free variables or identifiers. The conditions may
be specified in terms of relations that are to be satisfied by the
variables, including general relationships such as set membership.
It is used to define general sets and lists in situations where the
elements cannot be explicitly enumerated. Condition contains either a
single apply or reln
element; the apply element is used to construct
compound conditions. For example, it is used below to describe the set of
all x such that x < 5. See the discussion on sets in
section 4.4.6 [Theory of Sets].
See section 4.2.5 [Conditions] for further details.
1. <condition>
<apply><in/><ci> x </ci><ci type="set"> R </ci></apply>
</condition>
2. <condition>
<apply> <and/>
<apply><gt/><ci> x </ci><cn> 0 </cn></apply>
<apply><lt/><ci> x </ci><cn> 1 </cn></apply>
</apply>
</condition>
3. <apply>
<max/>
<bvar><ci> x </ci></bvar>
<condition>
<apply> <and/>
<apply><gt/><ci> x </ci><cn> 0 </cn></apply>
<apply><lt/><ci> x </ci><cn> 1 </cn></apply>
</apply>
</condition>
<apply>
<minus/>
<ci> x </ci>
<apply>
<sin/>
<ci> x </ci>
</apply>
</apply>
</apply>
1. 
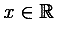
2. 
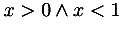
3. 
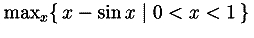
declare)The declare construct has two primary roles. The
first is to change or set the default attribute values for a specific
mathematical object. The second is to establish an association between a
`name' and an object. Once a declaration is in effect, the
`name' object acquires the new attribute settings, and (if the
second object is present) all the properties of the associated object.
The various attributes of the declare element
assign properties to the object being declared or determine where the
declaration is in effect.
By default, the scope of a declaration is `local' to the
surrounding container element. Setting the value of the scope attribute to global extends
the scope of the declaration to the enclosing math
element. As discussed in section 4.3.2.8 [scope], MathML
contains no provision for making document-wide declarations at present,
though it is anticipated that this capability will be added in future revisions
of MathML, when supporting technologies become available. declare takes one or two children. The first child,
which is mandatory, is a ci containing the identifier being
declared:
<declare type="vector"> <ci> V </ci> </declare>
The second child, which is optional, is a constructor initialising the variable:
<declare type="vector">
<ci> V </ci>
<vector>
<cn> 1 </cn><cn> 2 </cn><cn> 3 </cn>
</vector>
</declare>
The constructor type and the type of the element declared must
agree. For example, if the type attribute of the declaration is fn, the second child (constructor) must be an element
equivalent to an
fn element (This would include actual
fn elements,
lambda elements and any of the defined function in
the basic set of content tags.) If no type is specified in the declaration
then the type attribute of the declared name is set to the type of the
constructor (second child) of the declaration. The type attribute of the
declaration can be especially useful in the special case of the second
element being a semantic tag.
All attributes are CDATA:
type
scope
nargs
occurrence
prefix,
infix or function-model
indications.definitionURL
encoding
The declaration
<declare type="fn" nargs="2" scope="local">
<ci> f </ci>
<apply>
<plus/>
<ci> F </ci><ci> G </ci>
</apply>
</declare>
declares f to be a two-variable function with the property that f(x,y) = (F + G)(x,y).
The declaration
<declare type="fn">
<ci> J </ci>
<lambda>
<bvar><ci> x </ci></bvar>
<apply><ln/>
<ci> x </ci>
</apply>
</lambda>
</declare>
associates the name J with a one-variable function defined so that
J(x) = ln y. (Note that because of the type
attribute of the declare element, the second
argument must be something of type fn, namely a
known function like sin, an fn construct, or a lambda
construct.)
The type attribute on the declaration is only necessary if
if the type cannot be inferred from the type of the second argument.
Even when a declaration is in effect it is still possible to override
attributes values selectively as in <ci type="integer"> V
</ci>. This capability is needed in order to write statements of
the form `Let S be a member of S'.
Since the declare construct is not directly rendered, most
declarations are likely to be invisible to a reader. However,
declarations can produce quite different effects in an application
which evaluates or manipulates MathML content. While the declaration
<declare>
<ci> v </ci>
<vector>
<cn> 1 </cn>
<cn> 2 </cn>
<cn> 3 </cn>
</vector>
</declare>
is active the symbol v acquires all the properties of the vector, and even its dimension and components have meaningful values. This may affect how v is rendered by some applications, as well as how it is treated mathematically.
lambda)The lambda element is used to construct a
user-defined function from an expression and one or more free
variables. The lambda construct with n internal variables takes
n+1 children. The first n children identify the variables
that are used as placeholders in the last child for actual parameter
values. See section 4.2.2.2 [Constructors] for further details.
The following markup represents
(x, sin x+1).
<lambda>
<bvar><ci> x </ci></bvar>
<apply><sin/>
<apply>
<plus/>
<ci> x </ci>
<cn> 1 </cn>
</apply>
</apply>
</lambda>
The following examples constructs a one argument function in which the argument b specifies the upper bound of a specific definite integral.
<lambda>
<bvar><ci> b </ci></bvar>
<apply>
<int/>
<bvar>
<ci> x </ci>
</bvar>
<lowlimit>
<ci> a </ci>
</lowlimit>
<uplimit>
<ci> b </ci>
</uplimit>
<apply><fn><ci> f </ci></fn>
<ci> x </ci>
</apply>
</apply>
</lambda>
Such constructs are often used in conjunction with
declare to construct new functions.
compose)The compose element represents the function
composition operator. Note that MathML makes no assumption about the domain
and range of the constituent functions in a composition; the domain of the
resulting composition may be empty.
To override the default semantics for the compose element, or to associate a more specific
definition for function composition, use the definitionURL and encoding
attributes. See section 4.2.3 [Functions, Operators and Qualifiers] for further details.
The following markup represents
.
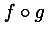<apply> <compose/> <fn><ci> f </ci></fn> <fn><ci> g </ci></fn> </apply>
The following markup represents
.
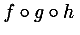<apply> <compose/> <ci type="fn"> f </ci> <ci type="fn"> g </ci> <ci type="fn"> h </ci> </apply>
The following examples both represent
.
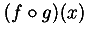<apply>
<apply><compose/>
<fn><ci> f </ci></fn>
<fn><ci> g </ci></fn>
</apply>
<ci> x </ci>
</apply>
<apply><fn><ci> f </ci></fn>
<apply>
<fn><ci> g </ci></fn>
<ci> x </ci>
</apply>
</apply>
ident)The ident element represents the identity
function. MathML makes no assumption about the function space in which the
identity function resides. That is, proper interpretation of the domain
(and hence range) of the identity function depends on the context in which
it is used.
To override the default semantics for the ident
element, or to associate a more specific definition, use the definitionURL and encoding
attributes (see section 4.2.3 [Functions, Operators and Qualifiers]).
The following markup encoded the expression
.
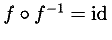<apply>
<eq/>
<apply><compose/>
<fn><ci> f </ci></fn>
<apply><inverse/>
<fn><ci> f </ci></fn>
</apply>
</apply>
<ident/>
</apply>
id
quotient)The quotient element is the operator used for
division modulo a particular base. When the quotient operator is applied to integer arguments
a and b, the result is the `quotient of a
divided by b'. That is, quotient
returns the unique integer, q such that a = q
b + r. (In common usage, q is called the
quotient and r is the remainder.)
The quotient element takes the attribute definitionURL and encoding
attributes, which can be used override the default semantics.
The quotient element is a binary arithmetic
operator (see section 4.2.3 [Functions, Operators and Qualifiers]).
<apply> <quotient/> <ci> a </ci> <ci> b </ci> </apply>
Various mathematical applications will use this data in different ways. Editing applications might choose an image such as shown below, while a computationally based application would evaluate it to 2 when a=13 and b=5.
There is no commonly used notation for this concept. Some possible renderings are
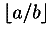
factorial)The factorial element is used to construct
factorials.
The factorial element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The factorial element is a unary
arithmetic operator (see section 4.2.3 [Functions, Operators and Qualifiers]).
<apply> <factorial/> <ci> n </ci> </apply>
If this were evaluated at n = 5 it would evaluate to 120.
n!
divide)The divide element is the division operator.
The divide element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The divide element is a binary arithmetic
operator (see section 4.2.3 [Functions, Operators and Qualifiers]).
<apply> <divide/> <ci> a </ci> <ci> b </ci> </apply>
As a MathML expression, this does not evaluate. However, on receiving such an expression, some applications may attempt to evaluate and simplify the value. For example, when a=5 and b=2 some mathematical applications may evaluate this to 2.5 while others will treat is as a rational number.
a/b
max, min)The elements max and min
are used to compare the values of their arguments. They return the maximum
and minimum of these values respectively.
The max and min elements
take the definitionURL and encoding attributes that can be used to override the
default semantics.
The max and min elements
are n-ary arithmetic operators (see section 4.2.3 [Functions, Operators and Qualifiers]).
When the objects are to be compared explicitly they are listed as arguments to the function as in:
<apply> <max/> <ci> a </ci> <ci> b </ci> </apply>
The elements to be compared may also be described using bound
variables with a condition element and an expression to be
maximised, as in:
<apply>
<min/>
<bvar><ci>x</ci></bvar>
<condition>
<apply><notin/><ci> x </ci><ci type="set"> B </ci></apply>
</condition>
<apply>
<power/>
<ci> x </ci>
<cn> 2 </cn>
</apply>
</apply>
Note that the bound variable must be stated even if it might be implicit in conventional notation. In MathML1.0, the bound variable and expression to be evaluated (x) could be omitted in the example below: this usage is deprecated in MathML2.0 in favour of explicitly stating the bound variable and expression in all cases:
<apply>
<bvar><ci>x</ci></bvar>
<max/>
<condition>
<apply><and/>
<apply><in/><ci>x</ci><ci type="set">B</ci></apply>
<apply><notin/><ci>x</ci><ci type="set">C</ci></apply>
</apply>
</condition>
<ci>x</ci>
</apply>
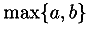
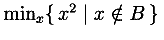
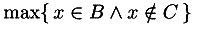
minus)The minus element is the subtraction operator.
The minus element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The minus element can be used as a unary
arithmetic operator (e.g. to represent -x), or as a
binary arithmetic operator (e.g. to represent
x-y).
<apply> <minus/> <ci> x </ci> <ci> y </ci> </apply>
If this were evaluated at x=5 and y=2 it would yield 3.
x - y
plus)The plus element is the addition operator.
The plus element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The plus element is an n-ary arithemtic
operator (see section 4.2.3 [Functions, Operators and Qualifiers]).
<apply> <plus/> <ci> x </ci> <ci> y </ci> <ci> z </ci> </apply>
If this were evaluated at x = 5, y = 2 and z = 1 it would yield 8.
x + y + z
power)The power element is a generic exponentiation
operator. That is, when applied to arguments a and b, it
returns the value the `a to the power of
b'.
The power element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The power element is an binary arithmetic
operator (see section 4.2.3 [Functions, Operators and Qualifiers]).
<apply> <power/> <ci> x </ci> <cn> 3 </cn> </apply>
If this were evaluated at x= 5 it would yield 125.
x3
rem)The rem element is the operator that returns
the `remainder' of a division modulo a particular base. When
the rem operator is applied to integer arguments
a and b, the result is the `remainder of a
divided by b'. That is, rem returns
the unique integer, r such that a = q b
+ r, where r < q. (In common usage,
q is called the quotient and r is the remainder.)
The rem element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The rem element is a binary arithmetic
operator (see section 4.2.3 [Functions, Operators and Qualifiers]).
<apply> <rem/> <ci> a </ci> <ci> b </ci> </apply>
If this were evaluated at a = 15 and b = 8 it would yield 7.
a mod b
times)The times element is the multiplication operator.
times takes the definitionURL and encoding
attributes which can be used to override the default semantics.
<apply> <times/> <ci> a </ci> <ci> b </ci> </apply>
If this were evaluated at a = 5.5 and b = 3 it would yield 16.5.
a b
root)The root element is used to construct roots. The
kind of root to be taken is specified by a degree
element, which should be given as the first child of the apply element enclosing the root element. Thus, square roots correspond to the case
where degree contains the value 2, cube roots
correspond to 3, and so on. If no degree is
present, a default value of 2 is used.
The root element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The root element is an operator taking
qualifiers (see section 4.2.3.2 [Operators taking Qualifiers]).
The nth root of a is is given by
<apply> <root/> <degree><ci type='integer'> n </ci></degree> <ci> a </ci> </apply>
![\sqrt[n]{a}](image/f4125.gif)
gcd)The gcd element is used to denote the greatest common
divisor of its arguments.
The gcd takes the definitionURL and encoding
attributes which can be used to override the default semantics.
The gcd element is an n-ary operator
(see section 4.2.3 [Functions, Operators and Qualifiers]).
<apply> <gcd/> <ci> a </ci> <ci> b </ci> <ci> c </ci> </apply>
If this were evaluated at a = 15, b = 21, c = 48 it would yield 3.
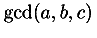
and)The and element is the boolean `and' operator.
The and element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The and element is an n-ary logical
operator (see section 4.2.3 [Functions, Operators and Qualifiers]).
<apply> <and/> <ci> a </ci> <ci> b </ci> </apply>
If this were evaluated and both a and b had truth values
of true, then the value would be true.
or)The or element is the boolean `or' operator.
The or element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The or element is an n-ary logical
operator (see section 4.2.3 [Functions, Operators and Qualifiers]).
<apply> <or/> <ci> a </ci> <ci> b </ci> </apply>
xor)The xor element is the boolean `exclusive or'
operator.
xor takes the definitionURL and encoding
attributes which can be used to override the default semantics.
The xor element is an n-ary logical
operator (see section 4.2.3 [Functions, Operators and Qualifiers]).
<apply> <xor/> <ci> a </ci> <ci> b </ci> </apply>
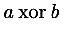
not)The not operator is the boolean
`not' operator.
The not element takes the attribute definitionURL and encoding
attributes, which can be used to override the default semantics.
The not element is a unary logical
operator (see section 4.2.3 [Functions, Operators and Qualifiers]).
<apply> <not/> <ci> a </ci> </apply>
implies)The implies element is the boolean relational
operator `implies'.
The implies element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The implies element is a binary logical
operator (see section 4.2.4 [Relations]).
<apply> <implies/> <ci> A </ci> <ci> B </ci> </apply>
Mathematical applications designed for the evaluation of such
expressions would evaluate this to true when a =
false and b = true.
forall)The forall element represents the universal quantifier
of logic. It must used in conjunction with one or more bound
variables, an optional condition element, and an
assertion, which may either take the form of an apply or
reln element.
The forall element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The forall element is an quantifier
(see section 4.2.3.2 [Operators taking Qualifiers]).
The first example encodes the sense of the expression `for all x, x - x = 0'.
<apply>
<forall/>
<bvar><ci> x </ci></bvar>
<apply><eq/>
<apply>
<minus/><ci> x </ci><ci> x </ci>
</apply>
<cn>0</cn>
</apply>
</apply>
A more involved example, making use of an optional condition
element encodes the sense of the expression: for all p,
q in 
such that p < q, p < q2.
<apply>
<forall/>
<bvar><ci> p </ci></bvar>
<bvar><ci> q </ci></bvar>
<condition>
<apply><and/>
<apply><in/><ci> p </ci><ci type="set"> Q </ci></apply>
<apply><in/><ci> q </ci><ci type="set"> Q </ci></apply>
<apply><lt/><ci> p </ci><ci> q </ci></apply>
</apply>
</condition>
<apply><lt/>
<ci> p </ci>
<apply>
<power/>
<ci> q </ci>
<cn> 2 </cn>
</apply>
</apply>
</apply>
A final example, utilizing both the forall and
exists quantifiers, encodes the sense of
the expression: for all n > 0, n in
, there
exist x, y, z in
such that xn +
yn = zn.
<apply>
<forall/>
<bvar><ci> n </ci></bvar>
<condition>
<apply><and/>
<apply><gt/><ci> n </ci><cn> 0 </cn></apply>
<apply><in/><ci> n </ci><ci type="set"> Z </ci></apply>
</apply>
</condition>
<apply>
<exists/>
<bvar><ci> x </ci></bvar>
<bvar><ci> y </ci></bvar>
<bvar><ci> z </ci></bvar>
<condition>
<apply><and/>
<apply><in/><ci> x </ci><ci type="set"> Z </ci></apply>
<apply><in/><ci> y </ci><ci type="set"> Z </ci></apply>
<apply><in/><ci> z </ci><ci type="set"> Z </ci></apply>
</apply>
</condition>
<apply>
<eq/>
<apply>
<plus/>
<apply><power/><ci> x </ci><ci> n </ci></apply>
<apply><power/><ci> y </ci><ci> n </ci></apply>
</apply>
<apply><power/><ci> z </ci><ci> n </ci></apply>
</apply>
</apply>
</apply>
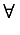
exists)The exists element represents the existential
quantifier of logic. It must used in conjuction with one or more bound
variables, an optional condition element, and an
assertion, which may either take the form of an apply or
reln element.
The exists element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The exists element is an quantifier
(see section 4.2.3.2 [Operators taking Qualifiers]).
The following example encodes the sense of the expression `there exists an x such that f(x) = 0'.
<apply>
<exists/>
<bvar><ci> x </ci></bvar>
<apply><eq/>
<apply>
<fn><ci> f </ci></fn>
<ci> x </ci>
</apply>
<cn>0</cn>
</apply>
</apply>
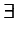
abs)The abs element represents the absolute value of a real
quantity or the modulus of a complex quantity.
The abs element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The abs element is a unary arithmetic
operator (see section 4.2.3 [Functions, Operators and Qualifiers]).
The following example encodes the absolute value of x.
<apply> <abs/> <ci> x </ci> </apply>
|x|
conjugate)The conjugate element represents the complex conjugate of a
complex quantity.
The conjugate element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The conjugate element is a unary arithmetic
operator (see section 4.2.3 [Functions, Operators and Qualifiers]).
The following example encodes the conjugate of x + iy.
<apply>
<conjugate/>
<apply>
<plus/>
<ci> x </ci>
<apply><times/>
<cn> ⅈ </cn>
<ci> y </ci>
</apply>
</apply>
</apply>
arg)The arg operator (introduced in MathML
2.0)) gives the `argument' of a complex number, which is
the angle (in radians) it makes with the positive real axis. Real negative
numbers have argument equal to
+.
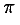The arg element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The arg element is a unary arithmetic
operator (see section 4.2.3 [Functions, Operators and Qualifiers]).
The following example encodes the argument operation on x + i y.
<apply>
<arg/>
<apply><plus/>
<ci> x </ci>
<apply><times/>
<cn> ⅈ </cn>
<ci> y </ci>
</apply>
</apply>
</apply>
real)The real operator (introduced in MathML 2.0)
gives the real part of a complex number, that is the x component in
x + i y
The real element takes the attributes encoding, definitionURL that can be used to override the
default semantics.
The real element is a unary arithmetic
operator (see section 4.2.3 [Functions, Operators and Qualifiers]).
The following example encodes the real operation on x + i y.
<apply>
<real/>
<apply><plus/>
<ci> x </ci>
<apply><times/>
<cn> ⅈ </cn>
<ci> y </ci>
</apply>
</apply>
</apply>
A MathML-aware evaluation system would return the x component, suitably encoded.
imaginary)The imaginary operator (introduced in
MathML 2.0) gives the imaginary part of a complex number, that
is the y component in x + i y
The imaginary element takes the attributes encoding, definitionURL that can be used to override the
default semantics.
The imaginary element is a unary
arithmetic operator (see section 4.2.3 [Functions, Operators and Qualifiers]).
The following example encodes the imaginary operation on x + iy.
<apply>
<imaginary/>
<apply><plus/>
<ci> x </ci>
<apply><times/>
<cn> ⅈ </cn>
<ci> y </ci>
</apply>
</apply>
</apply>
A MathML-aware evaluation system would return the y component, suitably encoded.
eq)The eq element is the relational operator
`equals'.
The eq element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The equals element is an n-ary
relation (see section 4.2.3.2 [Operators taking Qualifiers]).
<apply> <eq/> <ci> a </ci> <ci> b </ci> </apply>
If this were tested at a = 5.5 and b = 6
it would yield the truth value false.
a = b
neq)The neq element is the `not equal to' relational
operator.
neq takes the definitionURL and encoding
attributes which can be used to override the default semantics.
The neq element is an binary
relation (see section 4.2.4 [Relations]).
<apply> <neq/> <ci> a </ci> <ci> b </ci> </apply>
If this were tested at a = 5.5 and b = 6 it would yield
the truth value true.
gt)The gt element is the `greater than' relational
operator.
The gt element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The gt element is an n-ary relation
(see section 4.2.4 [Relations]).
<apply> <gt/> <ci> a </ci> <ci> b </ci> </apply>
If this were tested at a = 5.5 and b = 6 it would yield
the truth value false.
a > b
lt)The lt element is the `less than' relational
operator.
The lt element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The lt element is an n-ary relation
(see section 4.2.4 [Relations]).
<apply> <lt/> <ci> a </ci> <ci> b </ci> </apply>
If this were tested at a = 5.5 and b = 6 it would yield the truth value `true'.
a < b
geq)The geq element is the relational operator
`greater than or equal'.
The geq element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The geq element is an n-ary relation
(see section 4.2.4 [Relations]).
<apply> <geq/> <ci> a </ci> <ci> b </ci> </apply>
If this were tested for a = 5.5 and b = 5.5 it would
yield the truth value true.
leq)The leq element is the relational operator
`less than or equal'.
The leq element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The leq element is an n-ary relation
(see section 4.2.4 [Relations]).
<apply> <leq/> <ci> a </ci> <ci> b </ci> </apply>
If a = 5.4 and
b = 5.5 this will yield the truth value true.
equivalent)The equivalent element is the
`equivalence' relational operator.
The equivalent element takes the attributes encoding, definitionURL that can be used to override the
default semantics.
The equivalent element is an n-ary
relation (see section 4.2.3.2 [Operators taking Qualifiers]).
<apply>
<equivalent/>
<ci> a </ci>
<apply>
<not/>
<apply> <not/> <ci> a </ci> </apply>
</apply>
</apply>
This yields the truth value true for all values of a.
approx)The approx element is the relational operator
`approximately equal'.
The approx element takes the attributes encoding, definitionURL that can be used to override the
default semantics.
The approx element is a binary
relation (see section 4.2.3.2 [Operators taking Qualifiers]).
<apply> <approx/> <cn type="rational"> 22 <sep/> 7 </cn> <cn type="constant"> π </cn> </apply>
int)The int element is the operator element for an
integral. The lower limit, upper limit and bound variable are given by
(optional) child elements, lowlimit, uplimit and bvar in the
enclosing apply element. The integrand is also
specified as a child element of the enclosing apply element.
The domain of integration may alternatively be specified by using an interval element, or by a condition element. In such cases, if a bound variable
of integration is intended, it must be specified explicitly. (The
condition may involve more than one symbol.)
The int element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The int element is an operator taking
qualifiers (see section 4.2.3.2 [Operators taking Qualifiers]).
This example specifies a lowlimit,
uplimit, and bvar.
<apply>
<int/>
<bvar>
<ci> x </ci>
</bvar>
<lowlimit>
<cn> 0 </cn>
</lowlimit>
<uplimit>
<ci> a </ci>
</uplimit>
<apply>
<fn><ci> f </ci></fn>
<ci> x </ci>
</apply>
</apply>
This example specifies the domain of integration with an
interval element.
<apply>
<int/>
<bvar>
<ci> x </ci>
</bvar>
<interval>
<ci> a </ci>
<ci> b </ci>
</interval>
<apply><cos/>
<ci> x </ci>
</apply>
</apply>
The final example specifies the domain of integration with an
condition element.
<apply>
<int/>
<bvar>
<ci> x </ci>
</bvar>
<condition>
<apply><in/>
<ci> x </ci>
<ci type="set"> D </ci>
</apply>
</condition>
<apply><fn><ci> f </ci></fn>
<ci> x </ci>
</apply>
</apply>
diff)The diff element is the differentiation operator
element for functions of a single real variable. The bound variable is
given by a bvar element that is a child of the
containing apply element. The bvar elements
may also contain a degree element, which specifies the
order of the derivative to be taken.
The diff element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The diff element is an operator taking
qualifiers (see section 4.2.3.2 [Operators taking Qualifiers]).
<apply>
<diff/>
<bvar>
<ci> x </ci>
</bvar>
<apply><fn><ci> f </ci></fn>
<ci> x </ci>
</apply>
</apply>
partialdiff)The partialdiff element is the partial differentiation
operator element for functions of several real variables. The bound
variables are given by bvar elements, which are children
of the containing apply element. The bvar
elements may also contain a degree element, which
specifies the order of the partial derivative to be taken in that
variable.
The partialdiff element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The partialdiff element is an operator taking
qualifiers (see section 4.2.3.2 [Operators taking Qualifiers]).
<apply>
<partialdiff/>
<bvar>
<ci> x </ci>
<degree>
<cn> 2 </cn>
</degree>
</bvar>
<bvar>
<ci> y </ci>
</bvar>
<apply><fn><ci> f </ci></fn>
<ci> x </ci>
<ci> y </ci>
</apply>
</apply>
lowlimit)The lowlimit element is the container element used to
indicate the `lower limit' of an operator using qualifiers. For
example, in an integral, it can be used to specify the lower limit of
integration. Similarly, it is also used to specify the lower limit of
an index for sums and products.
The meaning of the lowlimit element depends on the
context it is being used in. For further details about how
qualifiers are used in conjunction with operators taking
qualifiers, consult section 4.2.3.2 [Operators taking Qualifiers].
<apply>
<int/>
<bvar>
<ci> x </ci>
</bvar>
<lowlimit>
<ci> a </ci>
</lowlimit>
<uplimit>
<ci> b </ci>
</uplimit>
<apply><fn><ci> f </ci></fn>
<ci> x </ci>
</apply>
</apply>
The default rendering of the lowlimit element and its
contents depends on the context. In the preceding example, it should
be rendered as a subscript to the integral sign:
Consult the descriptions of individual operators that make use of the
lowlimit construct for default renderings.
uplimit)The uplimit element is the container element used to
indicate the `upper limit' of an operator using qualifiers. For
example, in an integral, it can be used to specify the upper limit of
integration. Similarly, it is also used to specify the upper limit of
an index for sums and products.
The meaning of the uplimit element depends on the
context it is being used in. For further details about how
qualifiers are used in conjunction with operators taking
qualifiers, consult section 4.2.3.2 [Operators taking Qualifiers].
<apply>
<int/>
<bvar>
<ci> x </ci>
</bvar>
<lowlimit>
<ci> a </ci>
</lowlimit>
<uplimit>
<ci> b </ci>
</uplimit>
<apply><fn><ci> f </ci></fn>
<ci> x </ci>
</apply>
</apply>
The default rendering of the uplimit element and its
contents depends on the context. In the preceding example, it should
be rendered as a superscript to the integral sign:
Consult the descriptions of individual operators that make use of
the uplimit construct for default renderings.
bvar)The bvar element is the container element for the
`bound variable' of an operation. For example, in an integral it
specifies the variable of integration. In a derivative, it indicates
which variable with respect to which a function is being
differentiated. When the bvar element is used to
quantify a derivative, the bvar element may contain a
child degree element that specifies the order of the
derivative with respect to that variable. The bvar
element is also used for the internal variable in sums and products
and for the bound variable used with the universal and existential
quantifiers forall and exists.
The meaning of the bvar element depends on the context
it is being used in. For further details about how
qualifiers are used in conjunction with operators taking
qualifiers, consult section 4.2.3.2 [Operators taking Qualifiers].
<apply>
<diff/>
<bvar>
<ci> x </ci>
<degree>
<cn> 2 </cn>
</degree>
</bvar>
<apply>
<power/>
<ci> x </ci>
<cn> 4 </cn>
</apply>
</apply>
<apply>
<int/>
<bvar><ci> x </ci></bvar>
<condition>
<apply><in/><ci> x </ci><ci> D </ci></apply>
</condition>
<apply><fn><ci> f </ci></fn>
<ci> x </ci>
</apply>
</apply>
The default rendering of the bvar element and its
contents depends on the context. In the preceding examples, it should
be rendered as the x in the dx of the
integral, and as the x in the denominator of the
derivative symbol:
Note that in the case of the derivative, the default rendering of
the degree child of the bvar element is as
an exponent.
Consult the descriptions of individual operators that make use of the
bvar construct for default renderings.
degree)The degree element is the container element for the
`degree' or `order' of an operation. There are a number basic
mathematical constructs that come in families, such as derivatives
and moments. Rather than introduce special elements for each of these
families, MathML uses a single general construct, the
degree element for this concept of `order'.
The meaning of the degree element depends on the
context it is being used in. For further details about how
qualifiers are used in conjunction with operators taking
qualifiers, consult section 4.2.3.2 [Operators taking Qualifiers].
<apply>
<partialdiff/>
<bvar>
<ci> x </ci>
<degree>
<ci> n </ci>
</degree>
</bvar>
<bvar>
<ci> y </ci>
<degree>
<ci> m </ci>
</degree>
</bvar>
<apply><sin/>
<apply> <times/>
<ci> x </ci>
<ci> y </ci>
</apply>
</apply>
</apply>
The default rendering of the degree element and
its contents depends on the context. In the preceding example, the degree elements would be rendered as the exponents in
the differentiation symbols:
Consult the descriptions of individual operators that make use of the
degree construct for default renderings.
divergence)The divergence element is the vector calculus
divergence operator, often called div.
The divergence element takes the attributes encoding, definitionURL that can be used to override the
default semantics.
The divergence element is an unary
calculus operator (see section 4.2.3 [Functions, Operators and Qualifiers]).
<apply> <divergence/> <ci> a </ci> </apply>
If a is a vector field defined inside a closed surface S enclosing a volume V, then the divergence of a is given by
<apply>
<limit/>
<bvar>
<ci> V </ci>
</bvar>
<condition>
<apply>
<tendsto/>
<ci> V </ci>
<cn> 0 </cn>
</apply>
</condition>
<apply>
<divide/>
<apply><int encoding="text" definitionURL="SurfaceIntegrals.htm"/>
<bvar>
<ci> S</ci>
</bvar>
<ci> a </ci>
</apply>
<ci> V </ci>
</apply>
</apply>
grad)The grad element is the vector calculus gradient
operator, often called grad.
The grad element takes the attributes encoding, definitionURL that can be used to override the
default semantics.
The grad element is an unary calculus
operator (see section 4.2.3 [Functions, Operators and Qualifiers]).
<apply> <grad/> <ci> f</ci> </apply>
Where for example f is a scalar function and f(x,y,z) = k defines a surface S
curl)The curl element is the vector calculus curl
operator.
The curl element takes the attributes encoding, definitionURL that can be used to override the
default semantics.
The curl element is an unary calculus
operator (see section 4.2.3 [Functions, Operators and Qualifiers]).
<apply> <curl/> <ci> a </ci> </apply>
Where for example a is a vector.
laplacian)The laplacian element is the vector calculus
laplacian operator.
The laplacian element takes the attributes encoding, definitionURL that can be used to override the
default semantics.
The laplacian element is an unary calculus
operator (see section 4.2.3 [Functions, Operators and Qualifiers]).
<apply>
<eq/>
<apply><laplacian/>
<ci> f </ci>
</apply>
<apply>
<divergence/>
<apply><grad/>
<ci> f </ci>
</apply>
</apply>
</apply>
Where for example f is a vector
set)The set element is the container element that
constructs a set of elements. The elements of a set can be defined
either by explicitly listing the elements, or by using the
bvar and condition elements.
The set element is a constructor
element (see section 4.2.2.2 [Constructors]).
<set> <ci> b </ci> <ci> a </ci> <ci> c </ci> </set>
<set>
<bvar><ci> x </ci></bvar>
<condition>
<apply><lt/>
<ci> x </ci>
<cn> 5 </cn>
</apply>
</condition>
</set>
1. {a, b, c}
2. {x | x < 5 }
list)The list element is the container element that
constructs a list of elements. Elements can be defined either by
explicitly listing the elements, or by using the bvar and
condition elements.
Lists differ from sets in that there is an explicit order to the
elements. Two orders are supported: lexicographic and numeric. The
kind of ordering that should be used is specified by the
order attribute.
The list element is a constructor
element (see section 4.2.2.2 [Constructors]).
<list> <ci> a </ci> <ci> b </ci> <ci> c </ci> </list>
<list order="numeric">
<bvar><ci> x </ci></bvar>
<condition>
<apply><lt/>
<ci> x </ci>
<cn> 5 </cn>
</apply>
</condition>
</list>
1. [a, b, c]
2. [x | x < 5 ]
union)The union element is the operator for a
set-theoretic union or join of two (or more) sets.
The union attribute takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The union element is an n-ary set
operator (see section 4.2.3 [Functions, Operators and Qualifiers]).
<apply> <union/> <ci> A </ci> <ci> B </ci> </apply>
intersect)The intersect element is the operator for the
set-theoretic intersection or meet of two (or more) sets.
The intersect element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The intersect element is an n-ary set
operator (see section 4.2.3 [Functions, Operators and Qualifiers]).
<apply> <intersect/> <ci type="set"> A </ci> <ci type="set"> B </ci> </apply>
in)The in element is the relational operator used
for a set-theoretic inclusion (`is in' or `is a member
of').
The in element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The in element is a binary set
relation (see section 4.2.4 [Relations]).
<apply> <in/> <ci> a </ci> <ci type="set"> A </ci> </apply>
notin)The notin element is the relational operator
element used for set-theoretic exclusion (`is not in' or
`is not a member of').
The notin element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The notin element is a binary set
relation (see section 4.2.4 [Relations]).
<apply> <notin/> <ci> a </ci> <ci> A </ci> </apply>
subset)The subset element is the relational operator
element for a set-theoretic containment (`is a subset
of').
The subset element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The subset element is an n-ary set
relation (see section 4.2.4 [Relations]).
<apply> <subset/> <ci> A </ci> <ci> B </ci> </apply>
prsubset)The prsubset element is the relational operator
element for set-theoretic proper containment (`is a proper subset
of').
The prsubset element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The subset element is an n-ary set
relation (see section 4.2.4 [Relations]).
<apply> <prsubset/> <ci> A </ci> <ci> B </ci> </apply>
notsubset)The notsubset element is the relational operator
element for the set-theoretic relation `is not a subset
of'.
The notsubset element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The notsubset element is a binary set
relation (see section 4.2.4 [Relations]).
<apply> <notsubset/> <ci> A </ci> <ci> B </ci> </apply>
notprsubset)The notprsubset element is the operator element
for the set-theoretic relation `is not a proper subset
of'.
The notprsubset takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The notprsubset element is a binary set
relation (see section 4.2.4 [Relations]).
<apply> <notprsubset/> <ci> A </ci> <ci> B </ci> </apply>
setdiff)The setdiff element is the operator element for
a set-theoretic difference of two sets.
The setdiff element takes the definitionURL and encoding
attributes, which can be used to override the default semantics. setdiff is a binary operator.
The setdiff element is a binary set
operator (see section 4.2.3 [Functions, Operators and Qualifiers]).
<apply> <setdiff/> <ci> A </ci> <ci> B </ci> </apply>
card)The card element is the operator element for
deriving the size or cardinality of a set
The card element takes the attributes definitionURL, encoding that can be used to override the
default semantics.
The card element is a unary set
operator (see section 4.2.3 [Functions, Operators and Qualifiers]).
<apply>
<eq/>
<apply><card/>
<ci> A </ci>
</apply>
<ci> 5 </ci>
</apply>
where A is a set with 5 elements.
sum)The sum element denotes the summation
operator. Upper and lower limits for the sum, and more generally a domains
for the bound variables are specified using uplimit, lowlimit or a condition on the bound variables. The index for the
summation is specified by a bvar element.
The sum element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The sum element is an operator taking
qualifiers (see section 4.2.3.2 [Operators taking Qualifiers]).
<apply>
<sum/>
<bvar>
<ci> x </ci>
</bvar>
<lowlimit>
<ci> a </ci>
</lowlimit>
<uplimit>
<ci> b </ci>
</uplimit>
<apply><fn><ci> f </ci></fn>
<ci> x </ci>
</apply>
</apply>
<apply>
<sum/>
<bvar>
<ci> x </ci>
</bvar>
<condition>
<apply> <in/>
<ci> x </ci>
<ci type="set"> B </ci>
</apply>
</condition>
<apply><fn><ci> f </ci></fn>
<ci> x </ci>
</apply>
</apply>
product)The product element denotes the product
operator. Upper and lower limits for the product, and more generally a
domains for the bound variables are specified using uplimit, lowlimit or a condition on the bound variables. The index for the
product is specified by a bvar element.
The product element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The product element is an operator taking
qualifiers (see section 4.2.3.2 [Operators taking Qualifiers]).
<apply>
<product/>
<bvar>
<ci> x </ci>
</bvar>
<lowlimit>
<ci> a </ci>
</lowlimit>
<uplimit>
<ci> b </ci>
</uplimit>
<apply><fn><ci> f </ci></fn>
<ci> x </ci>
</apply>
</apply>
<apply>
<product/>
<bvar>
<ci> x </ci>
</bvar>
<condition>
<apply> <in/>
<ci> x </ci>
<ci type="set"> B </ci>
</apply>
</condition>
<apply><fn><ci> f </ci></fn>
<ci> x </ci>
</apply>
</apply>
limit)The limit element represents the operation of
taking a limit of a sequence. The limit point is expressed by specifying a
lowlimit and a bvar, or by
specifying a condition on one or more bound
variables.
The limit element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The limit element is an operator taking
qualifiers (see section 4.2.3.2 [Operators taking Qualifiers]).
<apply>
<limit/>
<bvar>
<ci> x </ci>
</bvar>
<lowlimit>
<cn> 0 </cn>
</lowlimit>
<apply><sin/>
<ci> x </ci>
</apply>
</apply>
<apply>
<limit/>
<bvar>
<ci> x </ci>
</bvar>
<condition>
<apply>
<tendsto type="above"/>
<ci> x </ci>
<ci> a </ci>
</apply>
</condition>
<apply><sin/>
<ci> x </ci>
</apply>
</apply>
tendsto)The tendsto element is used to express the relation
that a quantity is tending to a specified value.
The tendsto element takes the attributes type to set the direction from which the the limiting
value is approached and the definitionURL and encoding attributes, which can be used to override the
default semantics.
The tendsto element is a binary relational
operator (see section 4.2.4 [Relations]).
<apply>
<tendsto type="above"/>
<apply>
<power/>
<ci> x </ci>
<cn> 2 </cn>
</apply>
<apply>
<power/>
<ci> a </ci>
<cn> 2 </cn>
</apply>
</apply>
To express (x, y)
(f(x, y), g(x,y)),
one might use vectors, as in:
<apply>
<tendsto/>
<vector>
<ci> x </ci>
<ci> y </ci>
</vector>
<vector>
<apply><fn><ci> f </ci></fn>
<ci> x </ci>
<ci> y </ci>
</apply>
<apply><fn><ci> g </ci></fn>
<ci> x </ci>
<ci> y </ci>
</apply>
</vector>
</apply>
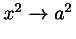
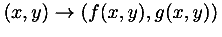
The names of the common trigonometric functions supported by MathML are listed below. Since their standard interpretations are widely known, they are discussed as a group.
sin |
cos |
tan |
sec |
csc |
cot |
sinh |
cosh |
tanh |
sech |
csch |
coth |
arcsin |
arccos |
arctan |
arccosh |
arccot |
arccoth |
arccsc |
arccsch |
arcsec |
arcsech |
arcsinh |
arctanh |
These operator elements denote the standard trigonometrical functions.
These elements all take the definitionURL and encoding attributes, which can be used to override the
default semantics.
They are all unary trigonometric operators. (see section 4.2.3 [Functions, Operators and Qualifiers]).
<apply>
<sin/>
<ci> x </ci>
</apply>
<apply>
<sin/>
<apply>
<plus/>
<apply><cos/>
<ci> x </ci>
</apply>
<apply>
<power/>
<ci> x </ci>
<cn> 3 </cn>
</apply>
</apply>
</apply>
sin x
sin(cos x + x3)
exp)The exp element represents the exponential function
associated with the inverse of the ln function. In
particular, exp(1) is approximately 2.718281828.
exp takes the definitionURL and encoding
attributes which may be used to override the default semantics.
The exp element is a unary arithmetic
operator (see section 4.2.3 [Functions, Operators and Qualifiers]).
<apply> <exp/> <ci> x </ci> </apply>
ln)The ln element is the natural logarithm operator.
The ln element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The ln element is an unary calculus
operator (see section 4.2.3 [Functions, Operators and Qualifiers]).
<apply> <ln/> <ci> a </ci> </apply>
If a = e this will yield the value 1.
ln a
log)The log element is the operator that returns a
logarithm to a given base. The base may be specified using a logbase element, which should be the first element
following log, i.e. the second child of the
containing apply element.
If the logbase element is not present, a default
base of 10 is assumed.
The log element takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
The log element can be used as either an
operator taking qualifiers or a unary calculus
operator (see section 4.2.3.2 [Operators taking Qualifiers]).
<apply>
<log/>
<logbase>
<cn> 3 </cn>
</logbase>
<ci> x </ci>
</apply>
This markup represents `the base 3 logarithm of x'. For natural
logarithms base e, the ln element should
be used instead.
log3 x
mean)
mean is the operator element for a mean or
average.
mean takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
mean is an n-ary operator
(see section 4.2.3 [Functions, Operators and Qualifiers]).
<apply> <mean/> <ci> X </ci> </apply>
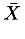or
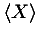
sdev)
sdev is the operator element for the standard deviation.
sdev takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
sdev is an n-ary operator
(see section 4.2.3 [Functions, Operators and Qualifiers]).
<apply> <sdev/> <ci> X </ci> </apply>
variance)
variance is the operator element for the statistical
variance.
variance takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
variance is an n-ary operator
(see section 4.2.3 [Functions, Operators and Qualifiers]).
<apply> <variance/> <ci> X </ci> </apply>
median)
median is the operator element for the median .
median takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
median is an n-ary operator
(see section 4.2.3 [Functions, Operators and Qualifiers]).
<apply> <median/> <ci> X </ci> </apply>
median(X)
mode)
mode is the operator for the statistical mode.
mode takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
mode is an n-ary operator
(see section 4.2.3 [Functions, Operators and Qualifiers]).
<apply> <mode/> <ci> X </ci> </apply>
mode(X)
moment)The moment element represents statistical
moments. Use degree for the n in
`n-th moment'.
moment takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
moment is an operator taking qualifiers
(see section 4.2.3.2 [Operators taking Qualifiers]).
<apply>
<moment/>
<degree>
<cn> 3 </cn>
</degree>
<ci> X </ci>
</apply>
vector)
vector is the container element for a vector. The
child elements form the components of the vector.
For purposes of interaction with matrices and matrix multiplication, vectors are regarded as equivalent to a matrix consisting of a single column, and the transpose of a vector behaves the same as a matrix consisting of a single row.
vector is a constructor element
(see section 4.2.2.2 [Constructors]).
<vector> <cn> 1 </cn> <cn> 2 </cn> <cn> 3 </cn> <ci> x </ci> </vector>
(1, 2, 3, x)
matrix)The matrix element is the container element for
matrix rows, which are represented by matrixrow.
The matrixrows contain the elements of a
matrix.
matrix is a constructor element
(see section 4.2.2.2 [Constructors]).
<matrix>
<matrixrow>
<cn> 0 </cn> <cn> 1 </cn> <cn> 0 </cn>
</matrixrow>
<matrixrow>
<cn> 0 </cn> <cn> 0 </cn> <cn> 1 </cn>
</matrixrow>
<matrixrow>
<cn> 1 </cn> <cn> 0 </cn> <cn> 0 </cn>
</matrixrow>
</matrix>
matrixrow)The matrixrow element is the container element for the
rows of a matrix.
matrixrow is a constructor element
(see section 4.2.2.2 [Constructors]).
<matrixrow> <cn> 1 </cn> <cn> 2 </cn> </matrixrow> <matrixrow> <cn> 3 </cn> <ci> x </ci> </matrixrow>
Matrix rows are not directly rendered by themselves outside of the context of a matrix.
determinant)The determinant element is the operator for
constructing the determinant of a matrix.
determinant takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
determinant is a unary operator
(see section 4.2.3 [Functions, Operators and Qualifiers]).
<apply> <determinant/> <ci type="matrix"> A </ci> </apply>
det A
transpose)The transpose element is the operator for constructing
the transpose of a matrix.
transpose takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
transpose is a unary operator
(see section 4.2.3 [Functions, Operators and Qualifiers]).
<apply> <transpose/> <ci type="matrix"> A </ci> </apply>
At
selector)The selector element is the operator for
indexing into vectors matrices and lists. It accepts one or more
arguments. The first argument identifies the vector, matrix or list from
which the selection is taking place, and the second and subsequent
arguments, if any, indicate the kind of selection taking place.
When selector is used with a single argument, it
should be interpreted as giving the sequence of all elements in the list,
vector or matrix given. The ordering of elements in the sequence for a
matrix is understood to be first by column, then by row. That is, for a
matrix (ai,j), where the indices
denote row and column, the ordering would be a1,1,
a1,2, ... a2,1,
a2,2 ... etcetera.
When three arguments are given, the last one is ignored for a list or vector, and in the case of a matrix, the second and third arguments specify the row and column of the selected element.
When two arguments are given, and the first is a vector or list, the second argument specifies an element in the list or vector. When a matrix and only one index i is specified as in
<apply>
<selector/>
<matrix>
<matrixrow>
<cn> 1 </cn> <cn> 2 </cn>
</matrixrow>
<matrixrow>
<cn> 3 </cn> <cn> 4 </cn>
</matrixrow>
</matrix>
<cn> 1 </cn>
</apply>
it refers to the i-th matrixrow. Thus, the preceding example selects the following row:
<matrixrow> <cn> 1 </cn> <cn> 2 </cn> </matrixrow>
selector takes the definitionURL and encoding
attributes, which can be used to override the default semantics.
selector is classified as an n-ary linear algebra
operator even though it can take only one, two, or three
arguments.
<apply> <selector/> <ci type="matrix"> A </ci> <cn> 3 </cn> <cn> 2 </cn> </apply>
The
selector construct renders the same as the expression
which it selects.
vectorproduct)The vectorproduct is the operator element for
deriving the vector product of two vectors
The vectorproduct element takes the attributes
definitionURL, encoding that can be used to override
the default semantics.
The vectorproduct element is a binary
vector operator (see section 4.2.3 [Functions, Operators and Qualifiers]).
<apply>
<eq/>
<apply><vectorproduct/>
<ci type="vector"> A </ci>
<ci type="vector"> B </ci>
</apply>
<apply><times/>
<ci> a </ci>
<ci> b </ci>
<apply><sin/>
<ci> θ </ci>
</apply>
</apply>
</apply>
where A and B are vectors,
a, b are the magnitudes of A, B and
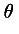is the angle between A and B.
scalarproduct)The scalarproduct is the operator element for
deriving the scalar product of two vectors
The scalarproduct element takes the attributes
definitionURL, encoding that can be used to override
the default semantics.
The scalarproduct element is a binary
vector operator (see section 4.2.3 [Functions, Operators and Qualifiers]).
<apply>
<eq/>
<apply><scalarproduct/>
<ci type="vector"> A </ci>
<ci type="vector">B </ci>
</apply>
<apply><times/>
<ci> a </ci>
<ci> b </ci>
<apply><cos/>
<ci> θ </ci>
</apply>
</apply>
</apply>
where A and B are vectors,
a, b are the magnitudes of A, B and
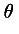is the angle between A and B.
outerproduct)The outerproduct is the operator element for
deriving the outer product of two vectors
The outerproduct element takes the attributes
definitionURL, encoding that can be used to override
the default semantics.
The outerproduct element is a binary
vector operator (see section 4.2.3 [Functions, Operators and Qualifiers]).
<apply> <outerproduct/> <ci type="vector">A</ci> <ci type="vector">B</ci> </apply>
where A and B are vectors.
This section explains the use of the semantic mapping elements
semantics,
annotation and
annotation-xml.
annotation)The annotation element is the container element
for a semantic annotation in a non-XML format.
The annotation element takes the attribute encoding to define the encoding being used.
The annotation element is a semantic mapping
element. It is always used with semantics.
<semantics>
<apply>
<plus/>
<apply><sin/>
<ci> x </ci>
</apply>
<cn> 5 </cn>
</apply>
<annotation encoding="TeX">
\sin x + 5
</annotation>
</semantics>
None. The information contained in annotations may optionally be used by a renderer able to process the kind of annotation given.
semantics)The semantics element is the container element
that associates additional representations with a given MathML
construct. The semantics element has as its first
child the expression being annotated, and the subsequent children are the
annotations. There is no restriction on the kind of annotation that can be
attached using the semantics element. For example, one might give a TEX
encoding, or computer algebra input in an annotation.
The representations that are XML based are enclosed in an annotation-xml element while those representations that
are to be parsed as PCDATA are enclosed in an annotation element.
The semantics element takes the definitionURL and encoding
attributes, which can be used to reference an external source for some or all
of the semantic information.
An important purpose of the semantics construct
is to associate specific semantics with a particular presentation, or
additional presentation information with a content construct. The default
rendering of a semantics element is the default
rendering of its first child. When a MathML-presentation annotation is
provided, a MathML renderer may optionally use this information to render
the MathML construct. This would typically be the case when the first child
is a MathML content construct and the annotation is provided to give a
preferred rendering differing from the default for the content
elements.
Use of semantics to
attach additional information in-line
to a MathML construct can be contrasted with use of the
csymbol for referencing external semantics.
See section 4.4.1.3 [Externally defined symbol
(csymbol)]
The semantics element is a semantic mapping element.
<semantics>
<apply>
<plus/>
<apply>
<sin/>
<ci> x </ci>
</apply>
<cn> 5 </cn>
</apply>
<annotation encoding="Maple">
sin(x) + 5
</annotation>
<annotation-xml encoding="MathML-Presentation">
...
...
</annotation-xml>
<annotation encoding="Mathematica">
Sin[x] + 5
</annotation>
<annotation encoding="TeX">
\sin x + 5
</annotation>
<annotation-xml encoding="OpenMath">
<OMA>...</OMA>
</annotation-xml>
</semantics>
The default rendering of a semantics element is
the default rendering of its first child.
annotation-xml)The annotation-xml container element is used to
contain representations that are XML based. It is always used together with
the semantics element, and takes the attribute encoding to define the encoding being used.
Issue (encoding):The various chapters use an interesting array of values for the
encodingattribute, namelyMaple V,Maple,MathML-Content,MathML-Presentation,Mathematica 4.0,Mathematica,OpenMath,TeX,mathml. We need some normative text here about what values this attribute can have, and we should have internal consistency among the chapters at the very least.
annotation-xml is a semantic mapping element.
<semantics>
<apply>
<plus/>
<apply><sin/>
<ci> x </ci>
</apply>
<cn> 5 </cn>
</apply>
<annotation-xml encoding="OpenMath">
<OMA><OMS name="plus" cd="arith1"/>
<OMA><OMS name="sin" cd="transc1"/>
<OMV name="x"/>
</OMA>
<OMI>5</OMI>
</OMA>
</annotation-xml>
</semantics>
See also the discussion of semantics above.
None. The information may optionally be used by a renderer able to process the kind of annotation given.