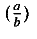 as opposed to the default rendering
as opposed to the default rendering
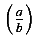 .
.
Mathematical Markup Language (MathML) Version 2.0
2 MathML Fundamentals
3 Presentation Markup
3.1 Introduction
3.1.1 What Presentation Elements Represent
3.1.2 Terminology Used In This Chapter
3.1.3 Required Arguments
3.1.4 Elements with Special Behaviors
3.1.5 Summary of Presentation Elements
3.2 Token Elements
3.2.1 Attributes common to token elements
3.2.2 Identifiers
3.2.3 Numbers
3.2.4 Operator, Fence, Separator or Accent
3.2.5 Text
3.2.6 Space
3.2.7 String Literal
3.3 General Layout Schemata
3.3.1 Horizontally Group Any Number of Subexpressions
3.3.2 Fractions
3.3.3 Radicals
3.3.4 Style Change
3.3.5 Error Message
3.3.6 Adjust Space Around Content
3.3.7 Making Content Invisible
3.3.8 Content Inside Pair of Fences
3.3.9 Enclose Content Inside Notation
3.4 Script and Limit Schemata
3.4.1 Subscript
3.4.2 Superscript
3.4.3 Subscript-superscript Pair
3.4.4 Underscript
3.4.5 Overscript
3.4.6 Underscript-overscript Pair
3.4.7 Prescripts and Tensor Indices
3.5 Tables and Matrices
3.5.1 Table or Matrix
3.5.2 Row in Table or Matrix
3.5.3 Entry in Table or Matrix
3.5.4 Alignment Markers
3.5.5 Equation Numbering
3.6 Enlivening Expressions
3.6.1 Bind Action to Subexpression
4 Content Markup
This chapter specifies the `presentation' elements of MathML, which can be used to describe the layout structure of mathematical notation. It is strongly recommended that, before reading the present chapter, one read section 2.3 [MathML Syntax and Grammar] on MathML syntax and grammar, which contains important information on MathML notations and conventions necessary for understanding some of the material in this chapter.
Presentation elements correspond to the `constructors' of traditional mathematical notation - that is, to the basic kinds of symbols and expression-building structures out of which any particular piece of traditional mathematical notation is built. They are designed to be medium-independent, in the sense that there are sensible ways to render them in audio, as well as in traditional visual media for mathematics. Because of the importance of traditional visual notation, the descriptions of which notational constructs the elements represent, and how they are typically rendered, is often given here in visual terms. However, the elements have been designed to contain enough information for good spoken renderings as well, provided the conventions described herein for their proper use are followed. Some attributes of these elements may make sense only for visual media, but most attributes can be treated in an analogous way in audio as well (for example, by a correspondence between time duration and horizontal extent).
One major anticipated use of MathML is to describe mathematical expressions within HTML documents, using multiple MathML expressions embedded in some manner in an HTML document. Note that HTML in general describes logical structures such as headings, paragraphs, etcetera. but only suggests (i.e. does not require) specific ways of rendering various logical parts of the document, in order to allow for medium-dependent rendering and for individual preferences of style; MathML presentation elements are fully compatible with this philosophy. This specification describes suggested visual rendering rules in some detail, but a particular MathML renderer is free to use its own rules as long as its renderings are intelligible.
The presentation elements are meant to express the syntactic
structure of mathematical notation in much the same way as titles, sections,
and paragraphs capture the higher level syntactic structure of a
textual document. Because of this, for example, a single row of
identifiers and operators, such as `x + a /
b', will often be represented not just by one
mrow element (which renders as a horizontal row
of its arguments), but by multiple nested mrow
elements corresponding to the nested subexpressions of which one
mathematical expression is composed - in this case,
<mrow>
<mi> x </mi>
<mo> + </mo>
<mrow>
<mi> a </mi>
<mo> / </mo>
<mi> b </mi>
</mrow>
</mrow>
Similarly, superscripts are attached not just to the preceding character, but to the full expression constituting their base. This structure allows for better-quality rendering of mathematics, especially when details of the rendering environment such as display widths are not known to the document author; it also greatly eases automatic interpretation of the mathematical structures being represented.
Certain extended characters, represented by entity references, are used
to name operators or identifiers which in traditional notation render the
same as other symbols, such as ⅆ, ⅇ, or ⅈ, or
operators which usually render invisibly, such as ⁢, ⁡, or
⁣. These are distinct notational
symbols or objects, as evidenced by their distinct spoken renderings and in
some cases by their effects on linebreaking and spacing in visual
rendering, and as such should be represented by the appropriate specific
entity references. For example, the expression represented visually as
`f(x)' would usually be spoken in English as
`f of x' rather than just
`f x'; this is expressible in MathML by
the use of the ⁡ operator after the
`f', which (in this case) can be aurally rendered as
`of'.
The complete list of MathML entities is described in chapter 6 [Entities, Characters and Fonts].
The MathML specification uses a number of technical terms to describe MathML-specific rules and conventions. The most notable example is the attribute value notations and conventions described in section 2.3.3 [MathML Attribute Values]. (See also the brief description of XML terminology in section 2.3.1 [An XML Syntax Primer].)
The remainder of this section introduces MathML-specific terminology and conventions used in this chapter.
The presentation elements are divided into two classes. Token
elements represent individual symbols, names, numbers, labels,
etcetera, and can have only characters and entity references (or the
vertical alignment element malignmark) as
content. Layout schemata build expressions out of parts,
and can have only elements as content (except for whitespace, which
they ignore). There are also a few empty elements used only in
conjunction with certain layout schemata.
All individual `symbols' in a mathematical expression should be
represented by MathML token elements. The primary MathML token element
types are identifiers (e.g. variables or function names), numbers, and
operators (including fences, such as parentheses, and separators, such
as commas). There are also token elements for representing text or
whitespace which has more aesthetic than mathematical significance,
and for representing `string literals' for compatibility with
computer algebra systems. Note that although a token element
represents a single meaningful `symbol' (name, number, label,
mathematical symbol, etcetera), such symbols may be comprised of more than
one character. For example sin and 24 are
represented by the single tokens <mi>sin</mi>
and <mn>24</mn> respectively.
In traditional mathematical notation, expressions are recursively constructed out of smaller expressions, and ultimately out of single symbols, with the parts grouped and positioned using one of a small set of notational structures, which can be thought of as `expression constructors'. In MathML, expressions are constructed in the same way, with the layout schemata playing the role of the expression constructors. The layout schemata specify the way in which subexpressions are built into larger expressions. The terminology derives from the fact that each layout schema corresponds to a different way of `laying out' its subexpressions to form a larger expression in traditional mathematical typesetting.
The terminology used in this chapter for special classes of elements, and for relationships between elements, is as follows: The presentation elements are the MathML elements defined in the chapter. These elements are listed in section 3.1.5 [Summary of Presentation Elements]. The content elements are the MathML elements defined in chapter 4 [Content Markup]. The content elements are listed in section 4.4 [The Content Markup Elements].
A MathML expression is a single instance of any of the
presentation elements with the exception of the empty elements
none or mprescripts, or is
a single instance of any of the content elements which are allowed as
content of presentation elements (listed in section 5.2.3 [Presentation Markup Contained in Content Markup]). A subexpression of an
expression E is any MathML expression which is part of
the content of E, whether directly or
indirectly, i.e. whether it is a `child' of
E or not.
A child of a layout schema is also called an argument
of that element. Token elements have no arguments, by definition, even
though they can contain the malignmark element;
this means that a malignmark element in a token
is not an argument, whereas in a layout schema it is one.
As a consequence of the above definitions, the content of a layout
schema consists exactly of a sequence of zero or more nonoverlapping
elements which are its arguments (possibly with intervening
whitespace, which is ignored in MathML). Note that an argument is
almost always a subexpression; the only exceptions are the empty
elements none and
mprescripts which are allowed only as special
arguments of the mmultiscripts element, but are
not subexpressions because they are not MathML expressions as defined
above.
Each MathML presentation element is described below in detail. The description starts with the information needed by authors of MathML (or of programs which generate MathML). The intended use of each element is described, along with the argument syntax it accepts. (There is also a table of argument count requirements and argument roles in section 3.1.3 [Required Arguments].) The valid attributes, along with their permissible and default values, are listed, and the effect of each attribute is discussed.
For certain elements, further information of interest mainly to those implementing MathML renderers is given in a subsection. This includes many details of one suggested set of rendering rules which can be used to render MathML expressions in a manner reminiscent of traditional visual notation.
Many of the elements described herein require a specific number of arguments (always 1, 2, or 3). Recall that MathML uses the term argument to describe a child element with additional MathML-specific requirements, usually related to which position it occupies in its parent.
In the detailed descriptions of element syntax given below, the number of required arguments is implicitly indicated by giving names for the arguments at various positions. The descriptions, interpreted according to the convention just stated, fully specify the allowed numbers of arguments for every element defined in this chapter. A few elements have additional requirements on the number or type of arguments, which are described with the individual element. For example, some elements accept sequences of zero or more arguments - that is, they are allowed to occur with no arguments at all.
Note that MathML elements encoding rendered space do count as arguments of the elements they appear in. See section 3.2.6 [Space] for a discussion of the proper use of such space-like elements.
mrowsThe elements listed in the following table as requiring exactly 1
argument (msqrt, mstyle,
merror, mpadded,
mphantom, and mtd) actually
accept any number of arguments, but if the number of arguments is 0,
or is more than 1, they treat their contents as a single
inferred mrow formed from all
their arguments.
For example,
<mtd> </mtd>
is treated as if it were
<mtd> <mrow> </mrow> </mtd>
and
<msqrt> <mo> - </mo> <mn> 1 </mn> </msqrt>
is treated as if it were
<msqrt>
<mrow>
<mo> - </mo>
<mn> 1 </mn>
</mrow>
</msqrt>
This feature allows MathML data not to contain (and its authors to
leave out) many mrow elements which would otherwise be
necessary.
In the descriptions in this chapter of the above-listed elements'
rendering behaviors, their content can be assumed to consist of
exactly one expression, which may be an mrow
element formed from their arguments in this manner. However, their
argument counts are shown in the following table as exactly 1, since
they are most naturally understood as acting on a single
expression.
For convenience, here is a table of each element's argument count
requirements, and the roles of individual arguments when these are
distinguished. Recall that a required argument count of 1 may indicate
an inferred mrow.
| Element | Required argument count | Argument roles (when these differ by position) |
mrow |
0 or more | |
mfrac |
2 | numerator denominator |
msqrt |
1 | |
mroot |
2 | base index |
mstyle |
1 | |
merror |
1 | |
mpadded |
1 | |
mphantom |
1 | |
mfenced |
0 or more | |
msub |
2 | base subscript |
msup |
2 | base superscript |
msubsup |
3 | base subscript superscript |
munder |
2 | base underscript |
mover |
2 | base overscript |
munderover |
3 | base underscript overscript |
mmultiscripts |
1 or more | base
(subscript superscript)*
[<mprescripts/>
(presubscript presuperscript)*] |
mtable |
0 or more rows | mtrs, inferred if necessary |
mtr |
0 or more table elements | mtds, inferred if necessary |
mtd |
1 | |
maction |
1 or more | depend on actiontype attribute |
Certain MathML presentation elements exhibit special behaviors in certain contexts. Such special behaviors are discussed in the detailed element descriptions below. However, for convenience, some of the most important classes of special behavior are listed here.
Certain elements are considered space-like; these are defined in
section 3.2.6 [Space]. This definition affects some of the suggested rendering
rules for mo elements (section 3.2.4 [Operator, Fence, Separator or Accent]).
Certain elements, e.g. msup, are able to
embellish operators which are their first argument. These elements are
listed in section 3.2.4 [Operator, Fence, Separator or Accent], which precisely defines an `embellished
operator' and explains how this affects the suggested rendering rules
for stretchy operators.
Certain elements treat their arguments as the arguments of an
`inferred mrow' if they are not given
exactly one argument, as explained in section 3.1.3 [Required Arguments].
The mtable element can infer
mtrs around its arguments, and the
mtr element can infer
mtds, as explained in the
sections about those elements.
mi |
identifier |
mn |
number |
mo |
operator, fence, or separator |
mtext |
text |
mspace |
space |
ms |
string literal |
mrow |
group any number of subexpressions horizontally |
mfrac |
form a fraction from two subexpressions |
msqrt |
form a square root sign (radical without an index) |
mroot |
form a radical with specified index |
mstyle |
style change |
merror |
enclose a syntax error message from a preprocessor |
mpadded |
adjust space around content |
mphantom |
make content invisible but preserve its size |
mfenced |
surround content with a pair of fences |
msub |
attach a subscript to a base |
msup |
attach a superscript to a base |
msubsup |
attach a subscript-superscript pair to a base |
munder |
attach an underscript to a base |
mover |
attach an overscript to a base |
munderover |
attach an underscript-overscript pair to a base |
mmultiscripts |
attach prescripts and tensor indices to a base |
mtable |
table or matrix |
mtr |
row in a table or matrix |
mtd |
one entry in a table or matrix |
maligngroup and malignmark |
alignment markers |
maction |
bind actions to a subexpression |
Token elements can contain any sequence of zero or more characters, or extended characters represented by entity references. In particular, tokens with empty content are allowed, and should typically render invisibly, with no width except for the normal extra spacing for that kind of token element. The allowed set of entity references for extended characters is given in chapter 6 [Entities, Characters and Fonts].
In MathML, characters and MathML entity references are only allowed to occur as part of the content of a token element. The only exception is whitespace between elements, which is ignored.
The malignmark element (see section 3.5.4 [Alignment Markers]) is the only element allowed in the content
of tokens. It marks a place which can be vertically aligned with other
objects, as explained in that section.
Several attributes related to text formatting
are provided on all token elements except mspace,
but on no other elements except mstyle.
These are:
| Name | values | default |
| fontsize | number v-unit | inherited |
| fontweight | normal | bold | inherited |
| fontstyle | normal | italic | normal (except on <mi>) |
| fontfamily | string | css-fontfamily | inherited |
| color | #rgb | #rrggbb | html-color-name | inherited |
(See section 2.3.3 [MathML Attribute Values] for terminology and notation used in attribute value descriptions.)
Token elements (other than mspace) should be
rendered as their content (i.e. in the visual case, as a
closely-spaced horizontal row of standard glyphs for the characters in
their content) using the attributes listed above, with surrounding
spacing modified by rules or attributes specific to each type of token
element. Some of the individual attributes are further discussed
below.
Issue (sheet-support): Now that XSL and CSS are available, the following text should be revised.
Recall that all MathML elements, including tokens, accept class, style, and id attributes for compatibility with style sheet
mechanisms, as described in section 2.3.4 [Attributes Shared by all MathML Elements]. In
principle, the font properties controlled by the attributes listed above
might be better handled using style sheets. When style sheet support
becomes available for XML, future revisions of MathML will likely revisit
the issue of font control.
MathML expressions are often embedded in a textual data format such as HTML, and their renderings are likewise embedded in a rendering of the surrounding text. The renderer of the surrounding text (e.g. a browser) should provide the MathML renderer with information about the rendering environment, including attributes of the surrounding text such as its font size, so that the MathML can be rendered in a compatible style. For this reason, most attribute values affecting text rendering are inherited from the rendering environment, as shown in the `default' column in the table above. (Note that it is also important for the rendering environment to provide the renderer with additional information, such as the baseline position of surrounding text, which is not specified by any MathML attributes.)
The exception to the general pattern of inheritance is the fontstyle attribute, whose default value is normal (non-slanted) for most tokens, but for mi depends on the content in a way described in the
section about mi, section 3.2.2 [Identifiers]. Note that fontstyle is not
inherited in MathML, even though the corresponding CSS1 property
`font-style' is inherited in CSS.
The fontsize attribute specifies the desired font
size. v-unit represents a unit of vertical length (see
section 2.3.3.3 [CSS-compatible attributes]). The most common unit for specifying font sizes in
typesetting is pt (points).
If the requested size of the current font is not available, the renderer should approximate it in the manner likely to lead to the most intelligible, highest quality rendering.
Many MathML elements automatically change fontsize in some
of their children; see the discussion of scriptlevel in the
section on mstyle, section 3.3.4 [Style Change].
The value of the fontfamily attribute should be the
name of a font which may be available to a MathML renderer, or
information which permits the renderer to select a font in some
manner; acceptable values and their meanings are dependent on the
specific renderer and rendering environment in use, and are not
specified by MathML (but see the note about
css-fontfamily below). (Note that the renderer's
mechanism for finding fonts by name may be case-sensitive.)
If the value of fontfamily is not recognized by a
particular MathML renderer, this should never be interpreted as a
MathML error; rather, the renderer should either use a font which it
considers to be a suitable substitute for the requested font, or
ignore the attribute and act as if no value had been given.
Note that any use of the fontfamily attribute is
unlikely to be portable across all MathML renderers. In particular, it
should never be used to try to achieve the effect of a reference to an
extended character (for example, by using a reference to a character
in some symbol font which maps ordinary characters to glyphs for
extended characters). As a corollary to this principle, MathML
renderers should attempt to always produce intelligible renderings for
the extended characters listed in chapter 6 [Entities, Characters and Fonts], even when these
characters are not available in the font family indicated. Such a
rendering is always possible - as a last resort, a character can be
rendered to appear as an XML-style entity reference using one of the
entity names given for the same character in chapter 6 [Entities, Characters and Fonts].
The symbol css-fontfamily refers to a legal value for
the font-family property in CSS1, which is a comma-separated list
of alternative font family names or generic font types in order of
preference, as documented in more detail in CSS1. MathML renderers are
encouraged to make use of the CSS syntax for specifying fonts when
this is practical in their rendering environment, even if they do not
otherwise support CSS. (See also the subsection CSS-compatible
attributes within section 2.3.3.3 [CSS-compatible attributes].
The syntax and meaning of the color attribute are as
described for the same attribute of <mstyle>
(section 3.3.4 [Style Change]).
An mi element represents a symbolic name or
arbitrary text which should be rendered as an identifier. Identifiers
can include variables, function names, and symbolic constants.
Not all `mathematical identifiers' are represented by
mi elements - for example, subscripted or primed
variables should be represented using msub or
msup respectively. Conversely, arbitrary text
playing the role of a `term' (such as an ellipsis in a summed series)
can be represented using an mi element, as shown
in an example in section 3.2.5.4 [Mixing text and mathematics]@@.
It should be stressed that mi is a
presentation element, and as such, it only indicates that its content
should be rendered as an identifier. In the majority of cases, the
contents of an mi will actually represent a
mathematical identifier such as a variable or function name. However,
as the preceding paragraph indicates, the correspondence between
notations which should render like identifiers and notations which are
actually intended to represent mathematical identifiers is not
perfect. For an element whose semantics is guaranteed to be that of an
identifier, see the description of ci in
chapter 4 [Content Markup].
mi
mi elements accept the attributes listed in
section 3.2.1 [Attributes common to token elements], but in one case with a different default value:
| Name | values | default |
| fontstyle | normal | italic | (depends on content; described below) |
A typical graphical renderer would render an
mi element as the characters in its content, with
no extra spacing around the characters (except spacing associated with
neighboring elements). The default fontstyle would
(typically) be normal (non-slanted) unless the content is a single
character, in which case it would be italic. Note that this rule
for fontstyle is specific to mi
elements; the default value for the fontstyle attribute
of other MathML token elements is normal.
mi
<mi> x </mi> <mi> D </mi> <mi> sin </mi> <mi></mi>
An mi element with no content is allowed;
<mi></mi> might, for example, be used by an
`expression editor' to represent a location in a MathML expression
which requires a `term' (according to conventional syntax for
mathematics) but does not yet contain one.
Identifiers include function names such as `sin'. Expressions such
as `sin x' should be written using the ⁡
operator (which also has the short name ⁡ as shown below;
see also the discussion of invisible operators in section 3.2.4 [Operator, Fence, Separator or Accent].
<mrow> <mi> sin </mi> <mo> ⁡ </mo> <mi> x </mi> </mrow>
Miscellaneous text that should be treated as a `term' can also be
represented by an mi element, as in:
<mrow> <mn> 1 </mn> <mo> + </mo> <mi> ... </mi> <mo> + </mo> <mi> n </mi> </mrow>
When an mi is used in such exceptional
situations, explicitly setting the fontstyle attribute
may give better results than the default behavior of some
renderers.
The names of symbolic constants should be represented as
mi elements:
<mi> π </mi> <mi> ⅈ </mi> <mi> ⅇ </mi>
Use of special entity references for such constants can simplify the interpretation of MathML presentation elements. See chapter 6 [Entities, Characters and Fonts] for a complete list of character entity references in MathML.
An mn element represents a `numeric
literal' or other data which should be rendered as a numeric
literal. Generally speaking, a numeric literal is a sequence of digits,
perhaps including a decimal point, representing an unsigned integer or real
number.
The concept of a mathematical `number' depends on the
context, and is not well-defined in the abstract. As a consequence, not all
mathematical numbers should be represented using mn; examples of mathematical numbers which should be
represented differently are shown below, and include negative numbers,
complex numbers, ratios of numbers shown as fractions, and names of numeric
constants.
Conversely, since mn is a presentation
element, there are a few situations where it may desirable to include
arbitrary text in the content of an mn which
should merely render as a numeric literal, even though that content
may not be unambiguously interpretable as a number according to any
particular standard encoding of numbers as character sequences. As a
general rule, however, the mn element should be
reserved for situations where its content is actually intended to
represent a numeric quantity in some fashion. For an element whose
semantics are guaranteed to be that of a particular kind of
mathematical number, see the description of cn in
chapter 4 [Content Markup].
<mn>
mn elements accept the attributes listed in
section 3.2.1 [Attributes common to token elements].
A typical graphical renderer would render an
mn element as the characters of its content, with
no extra spacing around them (except spacing from neighboring elements
such as mo). Unlike mi,
mn elements are (typically) rendered in an
unslanted font by default, regardless of their content.
mn
<mn> 2 </mn> <mn> 0.123 </mn> <mn> 1,000,000 </mn> <mn> 2.1e10 </mn> <mn> 0xFFEF </mn> <mn> MCMLXIX </mn> <mn> twenty one </mn>
mn aloneMany mathematical numbers should be represented using presentation
elements other than mn alone; this includes negative
numbers, complex numbers, ratios of numbers shown as fractions, and
names of numeric constants. Examples of MathML representations of
such numbers include:
<mrow> <mo> - </mo> <mn> 1 </mn> </mrow>
<mrow>
<mn> 2 </mn>
<mo> + </mo>
<mrow>
<mn> 3 </mn>
<mo> ⁢ </mo>
<mi> ⅈ </mi>
</mrow>
</mrow>
<mfrac> <mn> 1 </mn> <mn> 2 </mn> </mfrac>
<mi> π </mi>
<mi> ⅇ </mi>
An mo element represents an operator or
anything which should be rendered as an operator. In general, the
notational conventions for mathematical operators are quite
complicated, and therefore MathML provides a relatively sophisticated
mechanism for specifying the rendering behavior of an
mo element. As a consequence, in MathML the list
of things which should `render as an operator' includes a number of
notations which are not mathematical operators in the ordinary
sense. Besides ordinary operators with infix, prefix, or postfix
forms, these include fence characters such as braces, parentheses, and
`absolute value' bars, separators such as comma and semicolon, and
mathematical accents such as a bar or tilde over a symbol.
The term `operator' as used in the present chapter means
any symbol or notation which should render as an operator, and which is
therefore representable by an mo element. That is,
the term `operator' includes any ordinary operator, fence,
separator, or accent unless otherwise specified or clear from the
context.
All such symbols are represented in MathML with
mo elements since they are subject to essentially
the same rendering attributes and rules; subtle distinctions in the
rendering of these classes of symbols, when they exist, are supported
using the boolean attributes fence,
separator and accent which can be used to
distinguish these cases.
A key feature of the mo element is that its
default attribute values are set on a case-by-case basis from an
`operator dictionary' as explained below. In particular, default
values for fence, separator and
accent can usually be found in the operator dictionary
and therefore need not be specified on each mo
element.
Note that some mathematical operators are represented not by mo elements alone, but by mo
elements `embellished' with (for example) surrounding
superscripts; this is further described below. Conversely, as presentation
elements, mo elements can contain arbitrary text,
even when that text has no standard interpretation as an operator; for an
example, see the discussion `Mixing text and mathematics' in
section 3.2.5 [Text]. See also chapter 4 [Content Markup] for
definitions of MathML content elements which are guaranteed to have the
semantics of specific mathematical operators.
mo
mo elements accept the attributes listed in
section 3.2.1 [Attributes common to token elements], as described later in this
section. When a dictionary entry is not found for a given
mo element, the default value shown here in
parentheses is used.
| Name | values | default |
| form | prefix | infix | postfix | set by position of operator in an mrow (rule given below);
used with mo content to index operator dictionary |
| fence | true | false | set by dictionary (false) |
| separator | true | false | set by dictionary (false) |
| lspace | number h-unit | set by dictionary (0.27777em) |
| rspace | number h-unit | set by dictionary (0.27777em) |
| stretchy | true | false | set by dictionary (false) |
| symmetric | true | false | set by dictionary (true) |
| maxsize | number [ v-unit | h-unit ] | infinity | set by dictionary (infinity) |
| minsize | number [ v-unit | h-unit ] | set by dictionary (1) |
| largeop | true | false | set by dictionary (false) |
| movablelimits | true | false | set by dictionary (false) |
| accent | true | false | set by dictionary (false) |
h-unit represents a unit of horizontal length (see
section 2.3.3 [MathML Attribute Values]). v-unit represents a unit of vertical
length. If no unit is given with maxsize or
minsize, the number is a multiplier of the normal size of
the operator in the direction (or directions) in which it stretches.
These attributes are further explained below.
Typical graphical renderers show all mo
elements as the characters of their content, with additional spacing
around the element determined from the attributes listed
above. Detailed rules for determining operator spacing in visual
renderings are described in a subsection below. As always, MathML does
not require a specific rendering, and these rules are provided as
suggestions for the convenience of implementors.
Renderers without access to complete fonts for the MathML character
set may choose not to render an mo element as
precisely the characters in its content in some cases. For example,
<mo> ≤ </mo> might be rendered as
<= to a terminal. However, as a general rule,
renderers should attempt to render the content of an
mo element as literally as possible.
That is,
<mo> &le </mo> and
<mo> <= </mo> should render differently.
(The first one should render as a single extended character
representing a less-than-or-equal-to sign, and the second one as the
two-character sequence <=.)
mo elements representing
ordinary operators<mo> + </mo> <mo> < </mo> <mo> ≤ </mo> <mo> <= </mo> <mo> ++ </mo> <mo> ∑ </mo> <mo> .NOT. </mo> <mo> and </mo> <mo> ⁢ </mo>
mo elements
for fences and separatorsNote that the mo elements in these examples
don't need explicit fence or separator
attributes, since these can be found using the operator dictionary as
described below. Some of these examples could also be encoded using
the mfenced element described in section 3.3.8 [Content Inside Pair of Fences].
(a+b)
<mrow>
<mo> ( </mo>
<mrow>
<mi> a </mi>
<mo> + </mo>
<mi> b </mi>
</mrow>
<mo> ) </mo>
</mrow>
[0,1)
<mrow>
<mo> [ </mo>
<mrow>
<mn> 0 </mn>
<mo> , </mo>
<mn> 1 </mn>
</mrow>
<mo> ) </mo>
</mrow>
f(x,y)
<mrow>
<mi> f </mi>
<mo> ⁡ </mo>
<mrow>
<mo> ( </mo>
<mrow>
<mi> x </mi>
<mo> , </mo>
<mi> y </mi>
</mrow>
<mo> ) </mo>
</mrow>
</mrow>
Certain operators which are `invisible' in traditional
mathematical notation should be represented using specific entity
references within mo elements, rather than simply
by nothing. The entity references used for these `invisible
operators' are:
| Full name | Short name | Examples of use |
⁢ |
⁢ |
xy |
⁡ |
⁡ |
f(x) sin x |
⁣ |
⁣ |
m12 |
The MathML representations of the examples in the above table are:
<mrow>
<mi> x </mi>
<mo> ⁢ </mo>
<mi> y </mi>
</mrow>
<mrow>
<mi> f </mi>
<mo> ⁡ </mo>
<mrow>
<mo> ( </mo>
<mi> x </mi>
<mo> ) </mo>
</mrow>
</mrow>
<mrow>
<mi> sin </mi>
<mo> ⁡ </mo>
<mi> x </mi>
</mrow>
<msub>
<mi> m </mi>
<mrow>
<mn> 1 </mn>
<mo> ⁣ </mo>
<mn> 2 </mn>
</mrow>
</msub>
The reasons for using specific mo elements for
invisible operators include:
<mspace/> or mtext elements;
For example, an audio renderer might render f(x)
(represented as in the above examples) by speaking `f of x', but use
the word `times' in its rendering of xy.
Although its rendering must still be different depending on the structure
of neighboring elements (sometimes leaving out `of' or
`times' entirely), its task is made much easier by the use of
a different mo element for each invisible
operator.
For reasons like those for including special entities for invisible
operators, MathML also includes ⅆ for use in an
mo element representing the differential operator
symbol usually denoted by `d'.
mo elementsTypical visual rendering behaviors for mo
elements are more complex than for the other MathML token elements, so
the rules for rendering them are described in this separate
subsection.
Note that, like all rendering rules in MathML, these rules are suggestions rather than requirements. Furthermore, no attempt is made to specify the rendering completely; rather, enough information is given to make the intended effect of the various rendering attributes as clear as possible.
Many mathematical symbols, such as an integral sign, a plus sign,
or a parenthesis, have a well-established, predictable, traditional
notational usage. Typically, this usage amounts to certain default
attribute values for mo elements with specific
contents and a specific form attribute. Since these
defaults vary from symbol to symbol, MathML anticipates that renderers
will have an `operator dictionary' of default attributes for
mo elements (see Appendix C) indexed by each
mo element's content and form
attribute. If an mo element is not listed in the
dictionary, the default values shown in parentheses in the table of
attributes for mo should be used, since these
values are typically acceptable for a generic operator.
Some operators are `overloaded', in the sense that they can occur
in more than one form (prefix, infix, or postfix), with possibly
different rendering properties for each form. For example, `+' can be
either a prefix or an infix operator. Typically, a visual renderer
would add space around both sides of an infix operator, while only on
the left of a prefix operator. The form attribute allows
specification of which form to use, in case more than one form is
possible according to the operator dictionary and the default value
described below is not suitable.
form attributeThe form attribute does not usually have to be
specified explicitly, since there are effective heuristic rules for
inferring the value of the form attribute from the
context. If it is not specified, and there is more than one possible
form in the dictionary for an mo element with
given content, the renderer should choose which form to use as follows
(but see the exception for embellished operators, described later):
mrow of length (i.e. number of arguments) greater than
one (ignoring all space-like arguments (see section 3.2.6 [Space]) in the
determination of both the length and the first argument), the prefix form
is used;
mrow of length greater
than one (ignoring all space-like arguments), the postfix form is used;
mrow, the infix form is used.
Note that these rules make reference to the
mrow in which the mo
element lies. In some situations, this mrow
might be an inferred mrow implicitly present
around the arguments of an element such as
msqrt or mtd.
Opening (left) fences should have form="prefix",
and closing (right) fences should have form="postfix";
separators are usually `infix', but not always,
depending on their surroundings. As with ordinary operators,
these values do not usually need to be specified explicitly.
If the operator does not occur in the dictionary with the specified
form, the renderer should use one of the forms which is available
there, in the order of preference: infix, postfix, prefix; if no forms
are available for the given mo element content, the
renderer should use the defaults given in parentheses in the table of
attributes for mo.
There is one exception to the above rules for choosing an mo element's default form
attribute. An mo element which is
`embellished' by one or more nested subscripts, superscripts,
surrounding text or whitespace, or style changes behaves differently. It is
the embellished operator as a whole (this is defined precisely, below)
whose position in an mrow is examined by the above
rules and whose surrounding spacing is affected by its form, not the mo element at its core; however, the attributes
influencing this surrounding spacing are taken from the mo element at the core (or from that element's
dictionary entry).
For example, the `+4' in
a+4b
should be considered an infix operator as a whole, due to its position
in the middle of an mrow, but its rendering
attributes should be taken from the mo element
representing the `+', or when those are not specified explicitly,
from the operator dictionary entry for <mo form="infix"> +
</mo>.
The precise definition of an `embellished operator' is:
mo element;
msub,
msup,
msubsup,
munder,
mover,
munderover,
mmultiscripts,
mfrac, or
semantics
(section 4.2.7 [Syntax and Semantics]), whose first argument exists and is an embellished
operator;
mstyle,
mphantom, or
mpadded,
such that an mrow containing the same
arguments would be an embellished operator;
maction element whose selected
subexpression exists and is an embellished operator; mrow whose arguments consist (in any order)
of one embellished operator and zero or more space-like elements.
Note that this definition permits nested embellishment only when there are no intervening enclosing elements not in the above list.
The above rules for choosing operator forms and defining
embellished operators are chosen so that in all ordinary cases it will
not be necessary for the author to specify a form
attribute.
The following notes are included as a rationale for certain aspects of the above definitions, but should not be important for most users of MathML.
An mfrac is included as an `embellisher' because of
the common notation for a differential operator:
<mfrac>
<mo> ⅆ </mo>
<mrow>
<mo> ⅆ </mo>
<mi> x </mi>
</mrow>
</mfrac>
Since the definition of embellished operator affects the use of the
attributes related to stretching, it is important that it includes
embellished fences as well as ordinary operators; thus it applies to
any mo element.
Note that an mrow containing a single argument
is an embellished operator if and only if its argument is an
embellished operator. This is because an mrow
with a single argument must be equivalent in all respects to that
argument alone (as discussed in section 3.3.1 [Horizontally Group Any Number of Subexpressions]). This means that an
mo element which is the sole argument of an
mrow will determine its default form
attribute based on that mrow's position in a
surrounding, perhaps inferred, mrow (if there is
one), rather than based on its own position in the
mrow it is the sole argument of.
Note that the above definition defines every
mo element to be `embellished' - that is,
`embellished operator' can be considered (and implemented in
renderers) as a special class of MathML expressions, of which
mo is a specific case.
The amount of space added around an operator (or embellished
operator), when it occurs in an mrow, can be
directly specified by the lspace and rspace
attributes. These values are in ems if no units are given. By
convention, operators that tend to bind tightly to their arguments
have smaller values for spacing than operators that tend to bind less
tightly. This convention should be followed in the operator dictionary
included with a MathML renderer. In TEX, these values can only be
one of three values; typically they are 3/18em, 4/18em, and
5/18em. MathML does not impose this limit.
Some renderers may choose to use no space around most operators appearing within subscripts or superscripts, as is done in TEX.
Non-graphical renderers should treat spacing attributes, and other rendering attributes described here, in analogous ways for their rendering medium.
Four attributes govern whether and how an operator (perhaps
embellished) stretches so that it matches the size of other elements:
stretchy, symmetric, maxsize,
and minsize. If an operator has the attribute
stretchy=true, then it (that is, each character in its
content) obeys the stretching rules listed below, given the
constraints imposed by the fonts and font rendering system. In
practice, typical renderers will only be able to stretch a small set
of characters, and quite possibly will only be able to generate a
discrete set of character sizes.
There is no provision in MathML for specifying in which direction
(horizontal or vertical) to stretch a specific character or operator;
rather, when stretchy=true it should be stretched in
each direction for which stretching is possible. It is up to the
renderer to know in which directions it is able to stretch each
character. (Most characters can be stretched in at most one direction
by typical renderers, but some renderers may be able to stretch
certain characters, such as diagonal arrows, in both directions
independently.)
The minsize and maxsize attributes limit
the amount of stretching (in either direction). These two attributes
are given as multipliers of the operator's normal size in the
direction or directions of stretching, or as absolute sizes using
units. For example, if a character has maxsize="3", then
it can grow to be no more than three times its normal (unstretched)
size.
The symmetric attribute governs whether the height and
depth above and below the axis of the character are forced to be equal
(by forcing both height and depth to become the maximum of the two).
An example of a situation where one might set
symmetric=false arises with parentheses around a matrix
not aligned on the axis, which frequently occurs when multiplying
non-square matrices. In this case, one wants the parentheses to
stretch to cover the matrix, whereas stretching the parentheses
symmetrically would cause them to protrude beyond one edge of the
matrix. The symmetric attribute only applies to
characters that stretch vertically (otherwise it is ignored).
If a stretchy mo element is embellished (as defined
earlier in this section), the mo element at its core is
stretched to a size based on the context of the embellished operator
as a whole, i.e. to the same size as if the embellishments were not
present. For example, the parentheses in the following example (which
would typically be set to be stretchy by the operator dictionary) will be
stretched to the same size as each other, and the same size they would
have if they were not underlined and overlined, and furthermore will
cover the same vertical interval:
<mrow>
<munder>
<mo> ( </mo>
<mo> _ </mo>
</munder>
<mfrac>
<mi> a </mi>
<mi> b </mi>
</mfrac>
<mover>
<mo> ) </mo>
<mo> ‾ </mo>
</mover>
</mrow>
Note that this means that the stretching rules given below must
refer to the context of the embellished operator as a whole, not just
to the mo element itself.
This shows one way to set the maximum size of a parenthesis so that
it does not grow, even though its default value is
stretchy=true.
<mrow>
<mo maxsize="1"> ( </mo>
<mfrac>
<mi> a </mi> <mi> b </mi>
</mfrac>
<mo maxsize="1"> ) </mo>
</mrow>
The above should render as
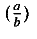 as opposed to the default rendering
as opposed to the default rendering
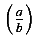 .
.
Note that each parenthesis is sized independently; if only one of
them had maxsize="1", they would render with different
sizes.
mrow element, or is the sole direct subexpression of an
mtd element in some row of a table, then it should
stretch to cover the height and depth (above and below the
axis) of the non-stretchy direct subexpressions in the
mrow element or table row, unless stretching is
constrained by minsize or maxsize attributes.
symmetric=true, then the maximum of the height and depth is
used to determine the size, before application of the minsize or
maxsize attributes.
mrow or mtd element is inferred
(see section 3.5.1 [Table or Matrix] for a discussion of inferred
mtd elements).
Most common opening and closing fences are defined in the operator
dictionary to stretch by default; and they stretch vertically. Also,
operators such as ∑, ∫, /, and vertical arrows stretch
vertically by default.
In the case of a stretchy operator in a table cell (i.e. within an
mtd element), the above rules assume each cell of
the table row containing the stretchy operator covers exactly one row.
(Equivalently, the value of the rowspan attribute is
assumed to be 1 for all the table cells in the table row, including
the cell containing the operator.) When this is not the case, the
operator should only be stretched vertically to cover those table
cells which are entirely within the set of table rows that the
operator's cell covers. Table cells which extend into rows not covered
by the stretchy operator's table cell should be ignored.
munder,
mover, or munderover element,
or if it is the sole direct subexpression of an mtd element (perhaps an inferred one) in some
column of a table (see mtable), then it, or the mo element at its core, should stretch to cover
the width of the other direct subexpressions in the given element (or
in the same table column), given the constraints mentioned above.
munder, mover, or
munderover element, or if it is the sole direct
subexpression of an mtd element in some column of a
table, then it should stretch to cover the width of the other direct
subexpressions in the given element (or in the same table column),
given the constraints mentioned above.
mtd element is inferred (see section 3.5.1 [Table or Matrix] for a discussion of inferred
mtd elements).
By default, most horizontal arrows and some accents stretch horizontally.
In the case of a stretchy operator in a table cell (i.e. within an
mtd element), the above rules assume each cell of
the table column containing the stretchy operator covers exactly one
column. (Equivalently, the value of the columnspan
attribute is assumed to be 1 for all the table cells in the table row,
including the cell containing the operator.) When this is not the
case, the operator should only be stretched horizontally to cover
those table cells which are entirely within the set of table columns
that the operator's cell covers. Table cells which extend into columns
not covered by the stretchy operator's table cell should be
ignored.
The rules for horizontal stretching include mtd
elements to allow arrows to stretch for use in commutative diagrams
laid out using mtable. The rules for the horizontal
stretchiness include scripts to make examples such as the following
work:
<mrow>
<mi> x </mi>
<munder>
<mo> → </mo>
<mtext> maps to </mtext>
</munder>
<mi> y </mi>
</mrow>
This displays as
 .
.
If a stretchy operator is not required to stretch (i.e. if it is not in one of the locations mentioned above, or if there are no other expressions whose size it should stretch to match), then it has the standard (unstretched) size determined by the font and current fontsize.
If a stretchy operator is required to stretch, but all other
expressions in the containing element or object (as described above)
are also stretchy, all elements that can stretch should grow to the
maximum of the normal unstretched sizes of all elements in the
containing object, if they can grow that large. If the value of
minsize or maxsize prevents this then that
(min or max) size is used.
For example, in an mrow containing nothing but
vertically stretchy operators, each of the operators should stretch to
the maximum of all of their normal unstretched sizes, provided no
other attributes are set which override this behavior. Of course,
limitations in fonts or font rendering may result in the final,
stretched sizes being only approximately the same.
mo
The largeop attribute specifies whether the
operator should be drawn larger than normal if displaystyle=true in the current
rendering environment. This roughly corresponds to TEX's
\displaystyle style setting. MathML uses two attributes, displaystyle and scriptlevel, to
control orthogonal presentation features that TEX encodes into one
`style' attribute with values \displaystyle,
\textstyle, \scriptstyle, and
\scriptscriptstyle. These attributes are discussed further in
section 3.3.4 [Style Change] describing the mstyle element. Note
that these attributes can be specified directly on an mstyle element's begin tag, but not on most other
elements. Examples of large operators include ∫
and ∏.
The movablelimits attribute specifies whether
underscripts and overscripts attached to this mo
element should be drawn as subscripts and superscripts when
displaystyle=false. movablelimits=false
means that underscripts and overscripts should never be drawn as
subscripts and superscripts. In general, displaystyle is
true for displayed mathematics and false for inline mathematics. Also,
displaystyle is false by default within tables,
scripts and fractions, and a few other exceptional situations detailed
in section 3.3.4 [Style Change]. Thus, operators with
movablelimits=true will display with limits (i.e.
underscripts and overscripts) in displayed mathematics, and with subscripts
and superscripts in inline mathematics, tables, scripts and so on. Examples
of operators that typically have movablelimits=true are
sum, prod, and
lim.
The accent attribute determines whether this operator
should be treated by default as an accent (diacritical mark) when used
as an underscript or overscript; see munder,
mover, and munderover
(sections 3.4.4-3.4.6).
The separator attribute may affect automatic
linebreaking in renderers which position ordinary infix operators at
the beginnings of broken lines rather than at the ends (that is, which
avoid linebreaking just after such operators), since linebreaking
should be avoided just before separators, but is acceptable just after
them.
The fence attribute has no effect in the suggested
visual rendering rules given here; it is not needed for properly
rendering traditional notation using these rules. It is provided so
that specific MathML renderers, especially non-visual renderers, have
the option of using this information.
An mtext element is used to represent
arbitrary text which should be rendered as itself. In general, the
mtext element is intended to denote commentary
text which is not central to the mathematical meaning or notational
structure of the expression it is contained in.
Note that some text with a clearly defined notational role might be
more appropriately marked up using mi or
mo; this is discussed further below.
An mtext element can be used to contain
`renderable whitespace', i.e. invisible characters which are intended
to alter the positioning of surrounding elements. In non-graphical
media, such characters are intended to have an analogous effect, such
as introducing positive or negative time delays or affecting rhythm in
an audio renderer. This is not related to any whitespace in the source
MathML consisting of blanks, newlines, tabs, or carriage returns;
whitespace present directly in the source is trimmed and collapsed, as
described in section 2.3.5 [Collapsing Whitespace in Input]. Whitespace which is
intended to be rendered as part of an element's content must be
represented by entity references (unless it consists only of single
blanks between non-whitespace characters).
Renderable whitespace can have a positive or negative width, as in
  and ​, or zero width, as
in ​. The complete list of such characters is
given in chapter 6 [Entities, Characters and Fonts]. Note that there is no formal distinction in MathML
between renderable whitespace characters and any other class of
characters, in mtext or in any other element.
Renderable whitespace can also include characters that affect alignment or linebreaking. Some of these characters are:
| Entity name | Purpose (rough description) |
| NewLine | start a new line and do not indent |
| IndentingNewLine | start a new line and do indent |
| NoBreak | do not allow a linebreak here |
| GoodBreak | if a linebreak is needed on the line, here is a good spot |
| BadBreak | if a linebreak is needed on the line, try to avoid breaking here |
For the complete list of MathML entities, consult chapter 6 [Entities, Characters and Fonts].
mtext
mtext elements accept the attributes listed in
section 3.2.1 [Attributes common to token elements].
See also the warnings about the legal grouping of `space-like elements' in section 3.2.6 [Space], and about the use of such elements for `tweaking' or conveying meaning in section 3.3.6 [Adjust Space Around Content].
mtext
<mtext> Theorem 1: </mtext> <mtext>   </mtext> <mtext>      </mtext> <mtext> /* a comment */ </mtext>
In some cases, text embedded in mathematics could be more appropriately
represented using mo or mi elements.
For example, the expression `there exists
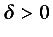 such that f(x) <1' is equivalent to
such that f(x) <1' is equivalent to
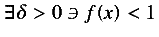 and could be represented as:
and could be represented as:
<mrow>
<mo> there exists </mo>
<mrow>
<mrow>
<mi> δ </mi>
<mo> > </mo>
<mn> 0 </mn>
</mrow>
<mo> such that </mo>
<mrow>
<mrow>
<mi> f </mi>
<mo> ⁡ </mo>
<mrow>
<mo> ( </mo>
<mi> x </mi>
<mo> ) </mo>
</mrow>
</mrow>
<mo> < </mo>
<mn> 1 </mn>
</mrow>
</mrow>
</mrow>
An example involving an mi element is:
x+x2+···+xn.
In this example, ellipsis should be represented using an mi element, since it takes the place of a term in the
sum (see section 3.2.2 [Identifiers], mi).
On the other hand, expository text within MathML is best
represented with an mtext element. An example of
this is:
Theorem 1: if x > 1, then x2 > x.
However, when MathML is embedded in HTML, the example is probably best rendered with only the two inequalities represented as MathML at all, letting the text be part of the surrounding HTML.
Another factor to consider in deciding how to mark up text is the
effect on rendering. Text enclosed in an mo
element is unlikely to be found in a renderer's operator dictionary,
so it will be rendered with the format and spacing appropriate for an
`unrecognized operator', which may or may not be better than the
format and spacing for `text' obtained by using an
mtext element. An ellipsis entity in an
mi element is apt to be spaced more appropriately
for taking the place of a term within a series than if it appeared in
an mtext element.
An mspace empty element represents a blank
space of any desired size, as set by its attributes. The default value
for each attribute is 0em or 0ex,
so it will not be useful without some attributes specified.
mspace
| Name | values | default |
| width | number h-unit | 0em |
| height | number v-unit | 0ex |
| depth | number v-unit | 0ex |
h-unit and v-unit represent units of
horizontal or vertical length, respectively (see section 2.3.3 [MathML Attribute Values]).
Note the warning about the legal grouping of `space-like elements'
given below, and the warning about the use of such elements for
`tweaking' or conveying meaning in section 3.3.6 [Adjust Space Around Content]. See also the other
elements which can render as whitespace, namely
mtext, mphantom, and
maligngroup.
A number of MathML presentation elements are `space-like' in the
sense that they typically render as whitespace, and do not affect the
mathematical meaning of the expressions in which they appear. As a
consequence, these elements often function in somewhat exceptional
ways in other MathML expressions. For example, space-like elements are
handled specially in the suggested rendering rules for
mo given in section 3.2.4 [Operator, Fence, Separator or Accent].
The following MathML elements are defined to be `space-like':
mtext, mspace,
maligngroup, or malignmark
element; mstyle, mphantom, or
mpadded element, all of whose direct subexpressions
are space-like; maction element whose selected
subexpression exists and is space-like; mrow all of whose direct subexpressions are space-like.
Note that an mphantom is not
automatically defined to be space-like, unless its content is
space-like. This is because operator spacing is affected by whether
adjacent elements are space-like. Since the
mphantom element is primarily intended as an aid
in aligning expressions, operators adjacent to an
mphantom should behave as if they were adjacent
to the contents of the mphantom,
rather than to an equivalently sized area of whitespace.
Authors who insert space-like elements or
mphantom elements into an existing MathML
expression should note that such elements are counted as
arguments, in elements which require a specific number of arguments,
or which interpret different argument positions differently.
Therefore, space-like elements inserted into such a MathML element
should be grouped with a neighboring argument of that element by
introducing an mrow for that purpose. For example, to allow for
vertical alignment on the right edge of the base of a superscript,
the expression
<msup> <mi> x </mi> <malignmark edge="right"/> <mn> 2 </mn> </msup>
is illegal, because msup must have exactly 2 arguments;
the correct expression would be:
<msup>
<mrow>
<mi> x </mi>
<malignmark edge="right"/>
</mrow>
<mn> 2 </mn>
</msup>
See also the warning about `tweaking' in section 3.3.6 [Adjust Space Around Content].
The ms element is used to represent
`string literals' in expressions meant to be interpreted by
computer algebra systems or other systems containing `programming
languages'. By default, string literals are displayed surrounded by
double quotes. As explained in section 3.2.5 [Text], ordinary text
embedded in a mathematical expression should be marked up with mtext, or in some cases mo or
mi, but never with ms.
Note that the string literals encoded by ms are
`Unicode strings' rather than `ASCII strings'. In
practice, non-ASCII characters will typically be represented by entity
references. For example, <ms>&</ms> represents a
string literal containing a single character, &, and
<ms>&</ms> represents a string literal containing 5
characters, the first one of which is &. (In fact,
MathML string literals are even more general than Unicode string literals,
since not all MathML entity references necessarily refer to existing
Unicode characters, as discussed in chapter 6 [Entities, Characters and Fonts].)
Like all token elements, ms does trim and
collapse whitespace in its content according to the rules of
section 2.3.5 [Collapsing Whitespace in Input], so whitespace intended to remain in the content should be
encoded as described in that section.
ms
ms elements accept the attributes listed in
section 3.2.1 [Attributes common to token elements], and additionally:
| Name | values | default |
| lquote | string | " |
| rquote | string | " |
In visual renderers, the content of an ms
element is typically rendered with no extra spacing added around the
string, and a quote character at the beginning and the end of the
string. By default, the left and right quote characters are both the
standard double quote character ". However,
these characters can be changed with the lquote and
rquote attributes respectively.
The content of ms elements should be rendered
with visible `escaping' of certain characters in the content,
including at least `double quote' itself, and preferably whitespace
other than individual blanks. The intent is for the viewer to see that
the expression is a string literal, and to see exactly which
characters form its content. For example, <ms>double quote is
"</ms> might be rendered as `double quote is
\"'.
Besides tokens there are several families of MathML presentation elements. One family of elements deals with various `scripting' notations, such as subscript and superscript. Another family is concerned with matrices and tables. The remainder of the elements, discussed in this section, describe other basic notations such as fractions and radicals, or deal with general functions such as setting style properties and error handling.
An mrow element is used to group together any
number of subexpressions, usually consisting of one or more mo elements acting as `operators' on one
or more other expressions which are their `operands'.
Several elements automatically treat their arguments as if they were
contained in an mrow element. See the discussion of
inferred mrows in section 3.1.3 [Required Arguments]. See also mfenced (section 3.3.8 [Content Inside Pair of Fences]), which can effectively form an mrow containing its arguments separated by commas.
mrow
None (except the attributes allowed for all MathML elements, listed in section 2.3.4 [Attributes Shared by all MathML Elements]).
mrow elements are typically rendered visually
as a horizontal row of their arguments, left to right in the order in
which the arguments occur, or audibly as a sequence of renderings of
the arguments. The description in section 3.2.4 [Operator, Fence, Separator or Accent] of suggested rendering
rules for mo elements assumes that all horizontal
spacing between operators and their operands is added by the rendering
of mo elements (or, more generally, embellished
operators), not by the rendering of the mrows
they are contained in.
MathML is designed to allow renderers to automatically linebreak expressions (that is, to break excessively long expressions into several lines), without requiring authors to specify explicitly how this should be done. This is because linebreaking positions can't be chosen well without knowing the width of the display device and the current font size, which for many uses of MathML will not be known except by the renderer at the time of each rendering.
Determining good positions for linebreaks is complex, and rules for
this are not described here; whether and how it is done is up to each
MathML renderer. Typically, linebreaking will involve selection of
`good' points for insertion of linebreaks between successive
arguments of mrow elements.
Although MathML does not require linebreaking or specify a
particular linebreaking algorithm, it has several features designed to
allow such algorithms to produce good results. These include the use
of special entities for certain operators, including invisible
operators (see section 3.2.4 [Operator, Fence, Separator or Accent]), or for providing hints related to
linebreaking when necessary (see section 3.2.5 [Text]), and the ability to
use nested mrows to describe subexpression
structure (see below).
mrow of one argumentMathML renderers are required to treat an mrow
element containing exactly one argument as equivalent in all ways to
the single argument occurring alone, provided there are no attributes
on the mrow element's begin tag. If there are
attributes on the mrow element's begin tag, no
requirement of equivalence is imposed. This equivalence condition is
intended to simplify the implementation of MathML-generating software
such as template-based authoring tools. It directly affects the
definitions of embellished operator and space-like element and the
rules for determining the default value of the form
attribute of an mo element; see sections 3.2.4
and 3.2.6. See also the discussion of equivalence of MathML
expressions in chapter 7 [The MathML Interface].
mrow
Subexpressions should be grouped by the document author in the same way
as they are grouped in the mathematical interpretation of the expression;
that is, according to the underlying `syntax tree' of the
expression. Specifically, operators and their mathematical arguments should
occur in a single mrow; more than one operator
should occur directly in one mrow only when they
can be considered (in a syntactic sense) to act together on the interleaved
arguments, e.g. for a single parenthesized term and its parentheses, for
chains of relational operators, or for sequences of terms separated by
+ and -. A precise rule is given below.
Proper grouping has several purposes: it improves display by possibly affecting spacing; it allows for more intelligent linebreaking and indentation; and it simplifies possible semantic interpretation of presentation elements by computer algebra systems, and audio renderers.
Although improper grouping will sometimes result in suboptimal
renderings, and will often make interpretation other than pure visual
rendering difficult or impossible, any grouping of expressions using
mrow is allowed in MathML syntax; that is,
renderers should not assume the rules for proper grouping will be
followed.
A precise rule for when and how to nest subexpressions using
mrow is especially desirable when generating
MathML automatically by conversion from other formats for displayed
mathematics, such as TEX, which don't always specify how subexpressions
nest. When a precise rule for grouping is desired, the following rule
should be used:
Two adjacent operators (i.e. mo elements,
possibly embellished), possibly separated by operands (i.e. anything
other than operators), should occur in the same
mrow only when the left operator has an infix or
prefix form (perhaps inferred), the right operator has an infix or
postfix form, and the operators are listed in the same group of
entries in the operator dictionary provided in Appendix C. In all
other cases, nested mrows should be used.
When forming a nested mrow (during generation
of MathML) which includes just one of two successive operators with
the forms mentioned above (which mean that either operator could in
principle act on the intervening operand or operands), it is necessary
to decide which operator acts on those operands directly (or would do
so, if they were present). Ideally, this should be determined from the
original expression; for example, in conversion from an
operator-precedence-based format, it would be the operator with the
higher precedence. If this cannot be determined directly from the
original expression, the operator which occurs later in the suggested
operator dictionary (Appendix C) can be assumed to have a higher
precedence for this purpose.
Note that the above rule has no effect on whether any MathML expression is valid, only on the recommended way of generating MathML from other formats for displayed mathematics or directly from written notation.
(Some of the terminology used in stating the above rule in defined in section 3.2.4 [Operator, Fence, Separator or Accent].)
mrow
As an example, 2x+y+x should be written as:
<mrow>
<mrow>
<mn> 2 </mn>
<mo> ⁢ </mo>
<mi> x </mi>
</mrow>
<mo> + </mo>
<mi> y </mi>
<mo> - </mo>
<mi> z </mi>
</mrow>
The proper encoding of (x, y) furnishes a less obvious
example of nesting mrows:
<mrow>
<mo> ( </mo>
<mrow>
<mi> x </mi>
<mo> , </mo>
<mi> y </mi>
</mrow>
<mo> ) </mo>
</mrow>
In this case, a nested mrow is required inside
the parentheses, since parentheses and commas, thought of as fence and
separator `operators', do not act together on their arguments.
The mfrac element is used for fractions. It
can also be used to mark up fraction-like objects such as binomial
coefficients and Legendre symbols. The syntax for
mfrac is
<mfrac> numerator denominator </mfrac>
mfrac
| Name | values | default |
| linethickness | number [ v-unit ] | thin | medium | thick | 1 (rule thickness) |
| numalign | left | center | right | center |
| denomalign | left | center | right | center |
| beveled | true | false | false |
The linethickness attribute indicates the thickness of
the horizontal `fraction bar', or `rule', typically used to render
fractions. A fraction with linethickness="0" renders
without the bar, and might be used within binomial coefficients. A
linethickness greater than one might be used with nested
fractions. These cases are shown below:
The numalign and
denomalign attributes control the horizontal
alignment of the numerator and denominator respectively. Typically,
numerators and denominators are centered, but a very long numerator or
denominator might be displayed on several lines and a left alignment
might be more appropriate for displaying them.
Issue (examples): Should there be examples of left and right alignment here?
The beveled attribute determines whether the
fraction is displayed with the numerator above the denominator
separated by a horizontal line or
whether a diagonal line is used to separate a slightly raised
numerator from a slightly lowered denominator. The later form
corresponds to the attribute value being true
and provides for a more compact form for simple numerator and
denominators
Issue (examples): Examples need to go here: 3/4 1/x^2
In general, the value of linethickness can be a
number, as a multiplier of the default thickness of the fraction bar
(the default thickness is not specified by MathML), or a number with a
unit of vertical length (see section 2.3.3 [MathML Attribute Values]), or one of the keywords
medium (same as 1), thin (thinner than 1,
otherwise up to the renderer), or thick (thicker than 1,
otherwise up to the renderer).
The mfrac element sets displaystyle to false, or if it
was already false increments scriptlevel by 1,
within numerator and denominator. These
attributes are inherited by every element from its rendering environment,
but can be set explicitly only on the mstyle
element. (See section 3.3.4 [Style Change].)
mfrac
The examples shown above can be represented in MathML as:
<mrow>
<mo> ( </mo>
<mfrac linethickness="0">
<mi> a </mi>
<mi> b </mi>
</mfrac>
<mo> ) </mo>
</mrow>
<mfrac linethickness="2">
<mfrac>
<mi> a </mi>
<mi> b </mi>
</mfrac>
<mfrac>
<mi> c </mi>
<mi> d </mi>
</mfrac>
</mfrac>
A more generic example is:
<mfrac>
<mrow>
<mn> 1 </mn>
<mo> + </mo>
<msqrt>
<mn> 5 </mn>
</msqrt>
</mrow>
<mn> 2 </mn>
</mfrac>
These elements construct radicals. The msqrt element is
used for square roots, while the mroot element is used
to draw radicals with indices, e.g. a cube root. The syntax for these
elements is
<msqrt> base </msqrt> <mroot> base index </mroot>
The mroot element requires exactly 2 arguments.
However, msqrt accepts any number of arguments; if
this number is not 1, its contents are treated as a single `inferred
mrow' containing its arguments, as described in
section 3.1.3 [Required Arguments].
msqrt and
mroot
None (except the attributes allowed for all MathML elements, listed in section 2.3.4 [Attributes Shared by all MathML Elements]).
The mroot element increments scriptlevel by 2, and sets displaystyle to false, within
index, but leaves both attributes unchanged within
base. The msqrt element leaves both
attributes unchanged within all its arguments. These attributes are
inherited by every element from its rendering environment, but can be set
explicitly only on mstyle. (See section 3.3.4 [Style Change].)
The mstyle element is used to make style
changes which affect the rendering of its
contents. mstyle can be given any attribute
accepted by any MathML presentation element; it can also be given
certain special attributes listed below.
The mstyle element accepts any number of
arguments. If this number is not 1, its contents are treated as a single
`inferred mrow' formed from all its
arguments, as described in section 3.1.3 [Required Arguments].
Loosely speaking, the effect of the mstyle element
is to change the default value of an attribute for the elements it
contains. Style changes work in one of two ways, depending on whether
an attribute's default value is documented as inherited.
The two cases are:
displaystyle or
scriptlevel (explained below), are inherited
from the surrounding context when they are not explicitly set. Specifying
such an attribute on an mstyle element sets the
value which will be inherited by its child elements. Unless a child element
overrides this inherited value, it will pass it on to its children, and
they will pass it to their children, and so on. But if a child element does
override it, either by an explicit attribute setting or automatically (as
is common for scriptlevel), the new (overriding)
value will be passed on to that element's children, and then to their
children, etc, until it is again overridden.
linethickness on
mfrac, have default values which are not normally
inherited. That is, if the linethickness attribute
is not set on the begin tag of an mfrac element,
it will normally use the default value of 1, even if it was
contained in a larger mfrac element which set this
attribute to a different value. For attributes like this, specifying a
value with an mstyle element has the effect of
changing the default value for all elements within its scope. The net
effect is that setting the attribute value with mstyle propagates the change to all the elements it
contains directly or indirectly, except for the individual elements on
which the value is overridden. Unlike in the case of inherited attributes,
elements which explicitly override this attribute have no effect on this
attribute's value in their children.
Note that attribute values inherited from an
mstyle, in either manner, affect a given element
in the mstyle's content only if that attribute is
not given a value in that element's begin tag. On any element for
which the attribute is set explicitly, the value specified on the
begin tag overrides the inherited value. The only exception to this
rule is when the value given on the begin tag is documented as
specifying an incremental change to the value inherited from that
element's context or rendering environment.
Note also that the difference between inherited and non-inherited
attributes set by mstyle, explained above, only
matters when the attribute is set on some element within the
mstyle's contents which has children which also
set it. Thus it never matters for attributes, such as
color, which can only be set on token elements (or on
mstyle itself).
There is one exceptional element, mpadded,
whose attributes cannot be set with mstyle. When
the attributes width, height and
depth are specified on an mstyle
element, they apply only to the mspace
element. Similarly, when lspace is set with
mstyle, it applies only to the
mo element.
mstyle
As stated above, mstyle accepts all attributes of all MathML
presentation elements. Additionally, mstyle can be given the
following special attributes which are implicitly inherited by every
MathML element as part of its rendering environment:
| Name | values | default |
| scriptlevel | ['+' | '-'] unsigned-integer | inherited |
| displaystyle | true | false | inherited |
| scriptsizemultiplier | number | 0.71 |
| scriptminsize | number v-unit | 8pt |
| color | #rgb | #rrggbb | html-color-name | inherited |
| background | #rgb | #rrggbb | transparent | html-color-name | transparent |
scriptlevel and displaystyle
MathML uses two attributes, displaystyle and
scriptlevel, to control orthogonal presentation features
that TEX encodes into one style attribute with values
\displaystyle, \textstyle, \scriptstyle, and \scriptscriptstyle. The
corresponding values of displaystyle and
scriptlevel for those TEX styles would be true and
0, false and
0, false and
1, and false and 2,
respectively.
The main effect of the displaystyle attribute is that
it determines the effect of other attributes such as the
largeop and movablescripts attributes of
mo. The main effect of the
scriptlevel attribute is to control the font
size. Typically, the higher the scriptlevel, the smaller
the font size. (Non-visual renderers can respond to the font size in
an analogous way for their medium.) More sophisticated renderers may
also choose to use these attributes in other ways, such as rendering
expressions with displaystyle=false in a more
vertically compressed manner.
These attributes are given initial values for the outermost expression of an instance of MathML based on its rendering environment. A short list of layout schemata described below modify these values for some of their subexpressions. Otherwise, values are determined by inheritance whenever they are not directly specified on a given element's start tag.
For an instance of MathML embedded in a textual data format (such
as HTML) in `display' mode, i.e. in place of a paragraph,
displaystyle = true and
scriptlevel = 0 for the
outermost expression of the embedded MathML; if the
MathML is embedded in `inline' mode, i.e. in place of a character,
displaystyle = false and
scriptlevel = 0 for
the outermost expression. See chapter 7 [The MathML Interface] for further
discussion of the distinction between `display' and `inline'
embedding of MathML and how this can be specified in particular
instances. In general, a MathML renderer may determine these initial
values in whatever manner is appropriate for the location and context
of the specific instance of MathML it is rendering, or if it has no
way to determine this, based on the way it is most likely to be used;
as a last resort it is suggested that it use the most generic values
displaystyle = "true" and
scriptlevel = "0".
The MathML layout schemata which typically display some of their
arguments in smaller type or with less vertical spacing, namely the
elements for scripts, fractions, radicals, and tables or matrices,
set displaystyle to false, and in some cases increase
scriptlevel, for those arguments. The new values are inherited
by all subexpressions within those arguments, unless they are
overridden.
The specific rules by which each element modifies
displaystyle and/or scriptlevel are given in the
specification for each element which does so; the complete list of
elements which modify either attribute are: the `scripting' elements
msub, msup, msubsup,
munder, mover,
munderover, and mmultiscripts; and the
elements mfrac, mroot, and
mtable.
When mstyle is given a
scriptlevel attribute with no sign, it sets the value of
scriptlevel within its contents to the value given, which
must be a nonnegative integer. When the attribute value consists of a
sign followed by an integer, the value of scriptlevel is
incremented (for '+') or decremented (for '-') by the amount
given. The incremental syntax for this attribute is an exception to
the general rules for setting inherited attributes using
mstyle, and is not allowed by any other attribute
on mstyle.
Whenever the scriptlevel is changed, either
automatically or by being explicitly incremented, decremented, or set,
the current font size is multiplied by the value of
scriptsizemultiplier to the power of the change in
scriptlevel. For example, if scriptlevel is
increased by 2, the font size is multiplied by
scriptsizemultiplier twice in succession; if
scriptlevel is explicitly set to 2 when it had been 3,
the font size is divided by scriptsizemultiplier.
The default value of scriptsizemultiplier is less than
one (in fact, it is approximately the square root of 1/2), resulting
in a smaller font size with increasing scriptlevel. To
prevent scripts from becoming unreadably small, the font size is never
allowed to go below the value of scriptminsize as a
result of a change to scriptlevel, though it can be set
to a lower value using the fontsize attribute (section 3.2.1 [Attributes common to token elements]) on mstyle or on token
elements. If a change to scriptlevel would cause the font
size to become lower than scriptminsize using the above
formula, the font size is instead set equal to
scriptminsize within the subexpression for which
scriptlevel was changed.
In the syntax for scriptminsize, v-unit represents a unit of vertical length (as
described in section 2.3.3 [MathML Attribute Values]). The most common unit for specifying font sizes
in typesetting is pt (points).
Explicit changes to the fontsize attribute have no
effect on the value of scriptlevel.
scriptlevel for renderersFor MathML renderers which support CSS1 style sheets, or some other
analogous style sheet mechanism, absolute or relative changes to
fontsize (or other attributes) may occur implicitly on
any element in response to a style sheet. Changes to
fontsize of this kind also have no effect on
scriptlevel. A style sheet-induced change to
fontsize overrides scriptminsize in the same
way as for an explicit change to fontsize in the
element's begin tag (discussed above), whether it is specified in the
style sheet as an absolute or a relative change. (However, any
subsequent scriptlevel-induced change to
fontsize will still be affected by it.) As is required
for inherited attributes in CSS1, the style sheet-modified
fontsize is inherited by child elements.
If the same element is subject to both a style sheet-induced and an
automatic (scriptlevel-related) change to its own
fontsize, the scriptlevel-related change is
done first - in fact, in the simplest implementation of the
element-specific rules for scriptlevel, this change would
be done by the element's parent as part of producing the rendering
properties it passes to the given element, since it is the parent
element which knows whether scriptlevel should be changed
for each of its child elements.
If the element's own fontsize is changed by a style
sheet and it also changes scriptlevel (and thus
fontsize) for one of its children, the style
sheet-induced change is done first, followed by the change inherited
by that child. If more than one child's scriptlevel is
changed, the change inherited by each child has no effect on the other
children. (As a mnemonic rule which applies to a `parse tree' of
elements and their children, style sheet-induced changes to
fontsize can be associated to nodes of the tree, i.e. to
MathML elements, and scriptlevel-related changes can be
associated to the edges between parent and child elements; then the
order of the associated changes corresponds to the order of nodes and
edges in each path down the tree.) For general information on the
relative order of processing of properties set by style sheets vs. by
attributes, see the appropriate subsection of CSS-compatible
attributes in section 2.3.3.3 [CSS-compatible attributes].
If scriptlevel is changed incrementally by an
mstyle element which also sets certain other
attributes, the overall effect of the changes may depend on the order
in which they are processed. In such cases, the attributes in the
following list should be processed in the following order, regardless
of the order in which they occur in the XML-format attribute list of
the mstyle begin tag:
scriptsizemultiplier, scriptminsize,
scriptlevel, fontsize.
Note that scriptlevel can, in principle, attain any
integral value by being decremented sufficiently, even though it can
only be explicitly set to nonnegative values. Negative values of
scriptlevel generated in this way are legal and should
work as described, generating font sizes larger than those of the
surrounding expression. Since scriptlevel is initially 0
and never decreases automatically, it will always be nonnegative
unless it is decremented past 0 using mstyle.
Explicit decrements of scriptlevel after the font size
has been limited by scriptminsize as described above
would produce undesirable results. This might occur, for example, in a
representation of a continued fraction, in which the scriptlevel was
decremented for part of the denominator back to its value for the
fraction as a whole, if the continued fraction itself was located in a
place which had a high scriptlevel. To prevent this
problem, MathML renderers should, when decrementing
scriptlevel, use as the initial font size the value the
font size would have had if it had never been limited by
scriptminsize. They should not, however, ignore the
effects of explicit settings of fontsize, even to values
below scriptminsize.
Since MathML renderers may be unable to make use of arbitrary font
sizes with good results, they may wish to modify the mapping from
scriptlevel to fontsize to produce better renderings in their
judgement. In particular, if fontsizes have to be rounded to available
values, or limited to values within a range, the details of how this
is done are up to the renderer. Renderers should, however, ensure that
a series of incremental changes to scriptlevel resulting in its
return to the same value for some subexpression that it had in a
surrounding expression results in the same fontsize for that
subexpression as for the surrounding expression.
The color attribute controls the color in which the
content of tokens is rendered. Additionally, when inherited from
mstyle or from a MathML expression's rendering
environment, it controls the color of all other drawing by MathML
elements, including the lines or radical signs that can be drawn by
mfrac, mtable, or
msqrt.
Note that the background attribute, though not
inherited, has the default value `transparent' (as in CSS1), which
effectively allows an element's parent to control its background.
The values of color and background can be specified as
a string consisting of '#' followed without intervening whitespace by
either 1-digit or 2-digit hexadecimal values for the red, green, and
blue components, respectively, of the desired color, with the same
number of digits used for each component (or as the keyword
`transparent' for background). The hexadecimal digits are not
case-sensitive. The possible 1-digit values range from 0 (component
not present) to F (component fully present), and the possible 2-digit
values range from 00 (component not present) to FF (component fully
present), with the 1-digit value x being equivalent to the
2-digit value xx (rather than x0).
% x0 would be a more strictly correct notation,
but renders terribly in some browsers.
These attributes can also be specified as an
html-color-name, which is defined in the following
subsection.
The color syntax described above is a subset of the syntax of the color and background-color
properties of CSS1. (The background-color syntax
is in turn a subset of the full CSS1 background
property syntax, which also permits specification of (for example)
background images with optional repeats. The more general attribute name
background is used in MathML to facilitate possible
extensions to the attribute's scope in future versions of MathML.)
Color values on either attribute can also be specified as an html-color-name, that is, as one of the color-name
keywords defined in [HTML40]. The list of allowed color names
includes most of the commonest English color words, though not orange, brown, or pink, and also includes
a number of less-common color words; see the reference for the complete
list and the equivalent RGB values. Note that the color name keywords are
not case-sensitive, unlike most keywords in MathML attribute values.
(The same color name keywords are defined for the CSS1
color property, but with unspecified RGB values.
See also section 2.3.3.3 [CSS-compatible attributes].)
The suggested MathML visual rendering rules do not define the
precise extent of the region whose background is affected by using the
background attribute on mstyle,
except that, when mstyle's content does not have
negative dimensions and its drawing region is not overlapped by other
drawing due to surrounding negative spacing, this region should lie
behind all the drawing done to render the content of the
mstyle, but should not lie behind any of the
drawing done to render surrounding expressions. The effect of overlap
of drawing regions caused by negative spacing on the extent of the
region affected by the background attribute is not
defined by these rules.
mstyle
The example of limiting the stretchiness of a parenthesis shown in the section on <mo>,
<mrow> <mo maxsize="1"> ( </mo> <mfrac> <mi> a </mi> <mi> b </mi> </mfrac> <mo maxsize="1"> ) </mo> </mrow>
can be rewritten using mstyle as:
<mstyle maxsize="1">
<mrow>
<mo> ( </mo>
<mfrac> <mi> a </mi> <mi> b </mi> </mfrac>
<mo> ) </mo>
</mrow>
</mstyle>
The merror element displays its contents as an
`error message'. This might be done, for example, by displaying the
contents in red, flashing the contents, or changing the background
color. The contents can be any expression or expression sequence.
merror accepts any number of arguments; if
this number is not 1, its contents are treated as a single `inferred
mrow' as described in section 3.1.3 [Required Arguments].
The intent of this element is to provide a standard way for programs that generate MathML from other input to report syntax errors in their input. Since it is anticipated that preprocessors that parse input syntaxes designed for easy hand entry will be developed to generate MathML, it is important that they have the ability to indicate that a syntax error occurred at a certain point. See section 7.2.2 [Handling of Errors].
The suggested use of merror for reporting
syntax errors is for a preprocessor to replace the erroneous part of
its input with an merror element containing a
description of the error, while processing the surrounding expressions
normally as far as possible. By this means, the error message will be
rendered where the erroneous input would have appeared, had it been
correct; this makes it easier for an author to determine from the
rendered output what portion of the input was in error.
No specific error message format is suggested here, but as with
error messages from any program, the format should be designed to make
as clear as possible (to a human viewer of the rendered error message)
what was wrong with the input and how it can be fixed. If the
erroneous input contains correctly formatted subsections, it may be
useful for these to be preprocessed normally and included in the error
message (within the contents of the merror
element), taking advantage of the ability of
merror to contain arbitrary MathML expressions
rather than only text.
merror
None (except the attributes allowed for all MathML elements, listed in section 2.3.4 [Attributes Shared by all MathML Elements]).
merror
If a MathML syntax-checking preprocessor received the input
<mfraction> <mrow> <mn> 1 </mn> <mo> + </mo> <msqrt> <mn> 5 </mn> </msqrt> </mrow> <mn> 2 </mn> </mfraction>
which contains the non-MathML element mfraction
(presumably in place of the MathML element mfrac),
it might generate the error message
<merror>
<mtext> Unrecognized element: <mfraction>;
arguments were: </mtext>
<mrow> <mn> 1 </mn> <mo> + </mo> <msqrt> <mn> 5 </mn> </msqrt> </mrow>
<mtext> and </mtext>
<mn> 2 </mn>
</merror>
Note that the preprocessor's input is not, in this case, valid MathML, but the error message it outputs is valid MathML.
An mpadded element renders the same as its
content, but with its overall size and other dimensions (such as
baseline position) modified according to its attributes. The
mpadded element does not rescale (stretch or
shrink) its content; its only effect is to modify the apparent size
and position of the `bounding box' around its content, so as to
affect the relative position of the content with respect to the
surrounding elements. The name of the element reflects the use of
mpadded to effectively add `padding', or extra
space, around its content. If the `padding' is negative, it is
possible for the content of mpadded to be
rendered outside the mpadded element's bounding
box; see below for warnings about several potential pitfalls of this
effect.
The mpadded element accepts any number of
arguments; if this number is not 1, its contents are treated as a single
`inferred mrow' as described in
section 3.1.3 [Required Arguments].
It is suggested that audio renderers add (or shorten) time delays
based on the attributes representing horizontal space
(width and lspace).
mpadded
| Name | values | default |
| width | [ + | - ] unsigned-number ( % [ pseudo-unit ] | pseudo-unit | h-unit ) | same as content |
| lspace | [ + | - ] unsigned-number ( % [ pseudo-unit ] | pseudo-unit | h-unit ) | 0 |
| height | [ + | - ] unsigned-number ( % [ pseudo-unit ] | pseudo-unit | v-unit ) | same as content |
| depth | [ + | - ] unsigned-number ( % [ pseudo-unit ] | pseudo-unit | v-unit ) | same as content |
(The pseudo-unit syntax symbol is described below.)
These attributes modify the dimensions of the `bounding
box' of the mpadded element. The dimensions
(which have the same names as the attributes) are defined in the next
subsection. Depending on the format of the attribute value, a dimension
may be set to a new value, or to an incremented or decremented version of
the content's corresponding dimension. Values may be specified as multiples
or percentages of any of the dimensions of the normal rendering of the
element's content (using so-called `pseudo-units'), or as
multiples of standard section 2.3.3.2 [Attributes with units].
If an attribute value begins with a + or
- sign, it specifies an increment or decrement of the
corresponding dimension by the following length value (interpreted as
explained below). Otherwise, the corresponding dimension is set
directly to the following length value. Note that the +
and - do not mean that the following value is positive or
negative, even when an explicit length unit (h-unit or
v-unit) is given. In particular, these attributes cannot
directly set a dimension to a negative value.
Length values (after the optional sign, which is not part of the
length value) can be specified in several formats. Each format begins
with an unsigned-number, which may be followed by a
% sign and an optional `pseudo-unit' (denoted by
pseudo-unit in the attribute syntaxes above), by a
pseudo-unit alone, or by one of the length units
(denoted by h-unit or v-unit) specified in
section 2.3.3.3 [CSS-compatible attributes], not including %. The possible
pseudo-units are the keywords width, lspace,
height, and depth; they each represent the
length of the same-named dimension of the mpadded
element's content (not of the mpadded element
itself). The lengths represented by h-unit or
v-unit are described in section 2.3.3.3 [CSS-compatible attributes].
In any of these formats, the length value specified is the product
of: the specified number; 0.01 if % is given; and the
length represented by the unit or pseudo-unit. If no pseudo-unit is
given after %, the one with the same name as the
attribute being specified is assumed.
Some examples of attribute formats using pseudo-units (explicit or
default) are as follows: depth="100% height" and
depth="1.0 height" both set the depth of the
mpadded element to the height of its content.
depth="105%" sets the depth to 1.05 times the content's
depth, and either depth="+100%" or
depth="200%" sets the depth to twice the content's
depth.
Dimensions that would be positive if the content was rendered
normally cannot be made negative using mpadded; a
positive dimension is set to 0 if it would otherwise become negative.
Dimensions which are initially 0 can be made negative, but this
should generally be avoided. See the warnings below on the use of
negative spacing for `tweaking' or conveying meaning.
The rules given above imply that all of the following attribute settings have the same effect, which is to leave the content's dimensions unchanged:
<mpadded width="+0em"> ... </mpadded> <mpadded width="+0%"> ... </mpadded> <mpadded width="-0em"> ... </mpadded> <mpadded width="- 0 height"> ... </mpadded> <mpadded width="100%"> ... </mpadded> <mpadded width="100% width"> ... </mpadded> <mpadded width="1 width"> ... </mpadded> <mpadded width="1.0 width"> ... </mpadded> <mpadded> ... </mpadded>
See appendix F [Glossary] for further information about some of the typesetting terms used here.
The width attribute refers to the overall horizontal
width of a bounding box. By default (i.e. when lspace is
not modified), the bounding box of the content of an
mpadded element should be rendered flush with the
left edge of the mpadded element's bounding
box. Thus, increasing width alone effectively adds space
on the right edge of the box.
The lspace attribute refers to the amount of space
between the left edge of a bounding box and where the rendering of its
contents' bounding box actually begins. Unlike the other dimensions,
lspace does not correspond to a real property of a
bounding box, but exists only transiently during the computations done
by each instance of mpadded. It is provided so
that there is a way to add space on the left edge of a bounding
box.
The rationale behind using width and
lspace to control horizontal padding instead of more
symmetric attributes, such as a hypothetical rspace and
lspace, is that it is desirable to have a `width' pseudo
unit, in part because `width' is an actual property of a bounding
box.
The height attribute refers to the amount of vertical
space between the baseline (the line along the bottom of most letter
glyphs in normal text rendering) and the top of the bounding box.
The depth attribute refers to the amount of vertical
space between the bottom of the bounding box and the baseline.
MathML renderers should ensure that, except for the effects of the
attributes, relative spacing between the contents of
mpadded and surrounding MathML elements is not
modified by replacing an mpadded element with an
mrow element with the same content. This holds
even if linebreaking occurs within the mpadded
element. However, if an mpadded element with
non-default attribute values is subjected to linebreaking, MathML does
not define how its attributes or rendering interact with the
linebreaking algorithm.
A likely temptation for the use of the mpadded
and mspace elements (and perhaps also mphantom and mtext) will be
for an author to improve the spacing generated by a specific renderer by
slightly modifying it in specific expressions, i.e. to
`tweak' the rendering.
Authors are strongly warned that different MathML renderers may use different spacing rules for computing the relative positions of rendered symbols in expressions which have no explicit modifications to their spacing; if renderer B improves upon renderer A's spacing rules, explicit spacing added to improve the output quality of renderer A may produce very poor results in renderer B, very likely worse than without any `tweaking' at all.
Even when a specific choice of renderer can be assumed, its spacing rules may be improved in successive versions, so that the effect of tweaking in a given MathML document may grow worse with time. Also, when style sheet mechanisms are extended to MathML, even one version of a renderer may use different spacing rules for users with different style sheets.
Therefore, it is suggested that MathML markup never use
mpadded or mspace elements
to tweak the rendering of specific expressions, unless the MathML is
generated solely to be viewed using one specific version of one MathML
renderer, using one specific style sheet (if style sheets are
available in that renderer).
In cases where the temptation to improve spacing proves too strong,
careful use of mpadded,
mphantom, or the alignment elements (section 3.5.4 [Alignment Markers]) may give more portable results than the
direct insertion of extra space using mspace or
mtext. Advice given to the implementors of MathML
renderers might be still more productive, in the long run.
MathML elements which permit `negative spacing', namely
mspace, mpadded, and
mtext, could in theory be used to simulate new
notations or `overstruck' characters by the visual overlap of the
renderings of more than one MathML subexpression.
This practice is strongly discouraged in all situations, for the following reasons:
More generally, any construct which uses spacing to convey mathematical meaning, rather than simply as an aid to viewing expression structure, is discouraged. That is, the constructs which are discouraged are those which would be interpreted differently by a human viewer of rendered MathML if all explicit spacing was removed.
If such constructs are used in spite of this warning, they should
be enclosed in a semantics element which also
provides an additional MathML expression which can be interpreted in a
standard way.
For example, the MathML expression
<mrow> <mpadded width="0"> <mi> C </mi> </mpadded> <mspace width="0.3em"/> <mtext> | </mtext> </mrow>
forms an overstruck symbol in violation of the policy stated above; it might be intended to represent the set of complex numbers for a MathML renderer which lacks support for the standard symbol used for this purpose. This kind of construct should always be avoided in MathML, for the reasons stated above; indeed, it should never be necessary for standard symbols, since a MathML renderer with no better method of rendering them is free to use overstriking internally, so that it can still support general MathML input.
However, if for whatever reason such a construct is used in MathML,
it should always be enclosed in a semantics element such as
<semantics>
<mrow>
<mpadded width="0"> <mi> C </mi> </mpadded>
<mspace width="0.3em"/>
<mtext> | </mtext>
</mrow>
<annotation-xml encoding="mathml">
<mi> &DoubleStruckCapitalC; </mi>
</annotation-xml>
</semantics>
which provides an alternative, standard encoding for the desired symbol, which is much more easily interpreted than the construct using negative spacing. (The alternative encoding in this example uses MathML presentation elements; the content elements described in chapter 4 [Content Markup] should also be considered.)
(The above warning also applies to most uses of rendering
attributes to alter the meaning conveyed by an expression, with the
exception of attributes on mi (such as
fontweight) used to distinguish one variable from
another.)
The mphantom element renders invisibly, but
with the same size and other dimensions, including baseline position,
that its contents would have if they were rendered
normally. mphantom can be used to align parts of
an expression by invisibly duplicating subexpressions.
The mphantom element accepts any number of
arguments; if this number is not 1, its contents are treated as a single
`inferred mrow' formed from all its
arguments, as described in section 3.1.3 [Required Arguments].
It is suggested that audio renderers render
mphantom elements in an analogous way for their
medium, by rendering them as silence of the same duration as the
normal rendering of their contents.
mphantom
None (except the attributes allowed for all MathML elements, listed in section 2.3.4 [Attributes Shared by all MathML Elements]).
Note that it is possible to wrap both an
mphantom and an mpadded
element around one MathML expression, as in
<mphantom><mpadded attribute-settings>
... </mpadded></mphantom>, to change its size and make it
invisible at the same time.
MathML renderers should ensure that the relative spacing between
the contents of an mphantom element and the
surrounding MathML elements is the same as it would be if the
mphantom element were replaced by an
mrow element with the same content. This holds
even if linebreaking occurs within the mphantom
element.
For the above reason, mphantom is
not considered space-like (section 3.2.6 [Space]) unless its
content is space-like, since the suggested rendering rules for
operators are affected by whether nearby elements are space-like. Even
so, the warning about the legal grouping of space-like elements may
apply to uses of mphantom.
There is one situation where the preceding rule for rendering an
mphantom may not give the desired effect. When an
mphantom is wrapped around a subsequence of the
arguments of an mrow, the default determination
of the form attribute for an mo
element within the subsequence can change. (See the default value of
the form attribute described in section 3.2.4 [Operator, Fence, Separator or Accent].) It may be
necessary to add an explicit form attribute to such an
mo in these cases. This is illustrated in the
following example.
mphantom
In this example, mphantom is used to ensure
alignment of corresponding parts of the numerator and denominator of a
fraction:
<mfrac>
<mrow>
<mi> x </mi>
<mo> + </mo>
<mi> y </mi>
<mo> + </mo>
<mi> z </mi>
</mrow>
<mrow>
<mi> x </mi>
<mphantom>
<mo form="infix"> + </mo>
<mi> y </mi>
</mphantom>
<mo> + </mo>
<mi> z </mi>
</mrow>
</mfrac>
This would render as something like
rather than as
The explicit attribute setting form="infix" on the
mo element inside the mphantom sets the
form attribute to what it would have been in the absence of the
surrounding mphantom. This is necessary since
otherwise, the + sign would be interpreted as a prefix
operator, which might have slightly different spacing.
Alternatively, this problem could be avoided without any explicit
attribute settings, by wrapping each of the arguments
<mo>+</mo> and <mi>y</mi> in its
own mphantom element, i.e.
<mfrac>
<mrow>
<mi> x </mi>
<mo> + </mo>
<mi> y </mi>
<mo> + </mo>
<mi> z </mi>
</mrow>
<mrow>
<mi> x </mi>
<mphantom>
<mo> + </mo>
</mphantom>
<mphantom>
<mi> y </mi>
</mphantom>
<mo> + </mo>
<mi> z </mi>
</mrow>
</mfrac>
The mfenced element provides a convenient form
in which to express common constructs involving fences (i.e. braces,
brackets, and parentheses), possibly including separators (such as
comma) between the arguments.
For example, <mfenced> <mi>x</mi> </mfenced>
renders as `(x)'and is equivalent to
<mrow> <mo> ( </mo> <mi>x</mi> <mo> ) </mo> </mrow>
and
<mfenced> <mi>x</mi> <mi>y</mi> </mfenced>
renders as `(x, y)'
and is equivalent to
<mrow> <mo> ( </mo> <mrow> <mi>x</mi> <mo>,</mo> <mi>y</mi> </mrow> <mo> ) </mo> </mrow>
Individual fences or separators are represented using
mo elements, as described in section 3.2.4 [Operator, Fence, Separator or Accent]. Thus, any mfenced
element is completely equivalent to an expanded form described below;
either form can be used in MathML, at the convenience of an author or
of a MathML-generating program. A MathML renderer is required to
render either of these forms in exactly the same way.
In general, an mfenced element can contain
zero or more arguments, and will enclose them between fences in an
mrow; if there is more than one argument, it will
insert separators between adjacent arguments, using an additional
nested mrow around the arguments and separators
for proper grouping (section 3.3.1 [Horizontally Group Any Number of Subexpressions]). The general expanded form is
shown below. The fences and separators will be parentheses and comma
by default, but can be changed using attributes, as shown in the
following table.
mfenced
| Name | values | default |
| open | string | ( |
| close | string | ) |
| separators | character * | , |
A generic mfenced element, with all attributes
explicit, looks as follows:
<mfenced open="opening-fence"
close="closing-fence"
separators="sep#1 sep#2 ... sep#(n-1)" >
arg#1
...
arg#n
</mfenced>
The opening-fence and closing-fence are
arbitrary strings. (Since they are used as the content of
mo elements, any whitespace they contain will be
trimmed and collapsed as described in section 2.3.5 [Collapsing Whitespace in Input].)
The value of separators is a sequence of zero or more
separator characters (or entity references), optionally separated by
whitespace. Each sep#i consists of exactly
one character or entity reference. Thus, separators=",;"
is equivalent to separators=" , ; ".
The general mfenced element shown above is
equivalent to the following expanded form:
<mrow>
<mo fence="true"> opening-fence </mo>
<mrow>
arg#1
<mo separator="true"> sep#1 </mo>
...
<mo separator="true"> sep#(n-1) </mo>
arg#n
</mrow>
<mo fence="true"> closing-fence </mo>
</mrow>
Each argument except the last is followed by a separator. The inner
mrow is added for proper grouping, as described in
section 3.3.1 [Horizontally Group Any Number of Subexpressions].
When there is only one argument, the above form has no separators;
since <mrow> arg#1 </mrow> is equivalent to
arg#1 (as described in section 3.3.1 [Horizontally Group Any Number of Subexpressions]), this case is also equivalent to:
<mrow> <mo fence="true"> opening-fence </mo> arg#1 <mo fence="true"> closing-fence </mo> </mrow>
If there are too many separator characters, the extra ones are
ignored. If separator characters are given, but there are too few, the
last one is repeated as necessary. Thus, the default value of
separators="," is equivalent to
separators=",,", separators=",,,", etcetera. If
there are no separator characters provided but some are needed, for
example if separators=" " or "" and there is more than
one argument, then no separator elements are inserted at all - that
is, the elements <mo separator="true"> sep#i
</mo> are left out entirely. Note that this is different
from inserting separators consisting of mo
elements with empty content.
Finally, for the case with no arguments, i.e.
<mfenced open="opening-fence"
close="closing-fence"
separators="anything" >
</mfenced>
the equivalent expanded form is defined to include just
the fences within an mrow:
<mrow> <mo fence="true"> opening-fence </mo> <mo fence="true"> closing-fence </mo> </mrow>
Note that not all `fenced expressions' can be encoded by an
mfenced element. Such exceptional expressions
include those with an `embellished' separator or fence or one
enclosed in an mstyle element, a missing or extra
separator or fence, or a separator with multiple content
characters. In these cases, it is necessary to encode the expression
using an appropriately modified version of an expanded form. As
discussed above, it is always permissible to use the expanded form
directly, even when it is not necessary. In particular, authors cannot
be guaranteed that MathML preprocessors won't replace occurrences of
mfenced with equivalent expanded forms.
Note that the equivalent expanded forms shown above include
attributes on the mo elements which identify them
as fences or separators. Since the most common choices of fences and
separators already occur in the operator dictionary with those
attributes, authors would not normally need to specify those
attributes explicitly when using the expanded form directly. Also, the
rules for the default form attribute (section 3.2.4 [Operator, Fence, Separator or Accent])
cause the opening and closing fences to be effectively given the
values form="prefix" and form="postfix"
respectively, and the separators to be given the value
form="infix".
Note that it would be incorrect to use mfenced
with a separator of, for instance, `+', as an abbreviation for an
expression using `+' as an ordinary operator, e.g.
<mrow> <mi>x</mi> <mo>+</mo> <mi>y</mi> <mo>+</mo> <mi>z</mi> </mrow>
This is because the + signs would be treated as separators,
not infix operators. That is, it would render as if they were marked up as
<mo separator="true">+</mo>, which might therefore
render inappropriately.
mfenced
(a+b)
<mfenced>
<mrow>
<mi> a </mi>
<mo> + </mo>
<mi> b </mi>
</mrow>
</mfenced>
Note that the above mrow is necessary so that
the mfenced has just one argument. Without it, this
would render incorrectly as `(a, +,
b)'.
[0,1)
<mfenced open="["> <mn> 0 </mn> <mn> 1 </mn> </mfenced>
f(x,y)
<mrow>
<mi> f </mi>
<mo> ⁡ </mo>
<mfenced>
<mi> x </mi>
<mi> y </mi>
</mfenced>
</mrow>
The menclose element renders its content
inside the enclosing notation specified by its notation attribute.
menclose accepts any number of arguments; if
this number is not 1, its contents are treated as a single `inferred
mrow' containing its arguments,
as described in section 3.1.3 [Required Arguments].
menclose
| Name | values | default |
| notation | longdiv | actuarial | radical | longdiv |
With notation has the value longdiv, the contents are drawn enclosed by a long
division symbol. A complete example of long division is accomplished
by also using mtable and malign. When notation is
specified as actuarial, the contents are drawn
enclosed by an actuarial symbol. The case of notation=radical is
equivalent to the msqrt schema.
The following markup might be used to encode an elementary US-style long division problem.
<mtable columnspacing='0' rowspacing='0'>
<mtr>
<mtd></mtd>
<mtd columnalign='right'><mn>10</mn></mtd>
</mtr>
<mtr>
<mtd columnalign='right'><mn>131</mn></mtd>
<mtd columnalign='right'>
<menclose notation='longdiv'><mn>1413</mn></menclose>
</mtd>
</mtr>
<mtr>
<mtd></mtd>
<mtd columnalign='right'>
<mrow>
<munder>
<mn>131</mn>
<mo>&bar;</mo>
</munder>
<mphantom><mn>3</mn></mphantom>
</mrow>
</mtd>
</mtr>
<mtr>
<mtd></mtd>
<mtd columnalign='right'><mn>103</mn></mtd>
</mtr>
</mtable>
This might render as:
Issue (graphic1): long division graphic needed
.
An example of using menclose for actuarial
notation is
<msub>
<mi>a</mi>
<mrow>
<menclose notation='actuarial'>
<mi>n</mi>
</menclose>
<mo>⁢</mo>
<mi>i</mi>
</mrow>
</msub>
which renders as
a_ n|i
Issue (graphic2): actuarial graphic needed
The elements described in this section position one or more scripts around a base. Attaching various kinds of scripts and embellishments to symbols is a very common notational device in mathematics. For purely visual layout, a single general-purpose element could suffice for positioning scripts and embellishments in any of the traditional script locations around a given base. However, in order to capture the abstract structure of common notation better, MathML provides several more specialized scripting elements.
In addition to sub/superscript elements, MathML has
over/underscript elements which place scripts above and below the
base. These elements can be used to place limits on large operators,
or for placing accents and lines above or below the base. The rules
for rendering accents differ from those for overscripts and
underscripts, and this difference can be controlled with the
accent and accentunder attributes, as
described in the appropriate sections below.
Rendering of scripts is affected by the scriptlevel
and displaystyle attributes, which are part of the
environment inherited by the rendering process of every MathML
expression, and are described under mstyle
(section 3.3.4 [Style Change]). These attributes cannot be given
explicitly on a scripting element, but can be specified on the start
tag of a surrounding mstyle element if
desired.
MathML also provides an element for attachment of tensor indices. Tensor indices are distinct from ordinary subscripts and superscripts in that they must align in vertical columns. Tensor indices can also occur in prescript positions.
Because presentation elements should be used to describe the abstract notational structure of expressions, it is important that the base expression in all `scripting' elements (i.e. the first argument expression) should be the entire expression that is being scripted, not just the rightmost character. For example, (x+y)2 should be written as:
<msup>
<mrow>
<mo> ( </mo>
<mrow>
<mi> x </mi>
<mo> + </mo>
<mi> y </mi>
</mrow>
<mo> ) </mo>
</mrow>
<mn> 2 </mn>
</msup>
The syntax for the msub element is <msub>
base subscript</msub>.
msub
| Name | values | default |
| subscriptshift | number v-unit | automatic (typical unit is ex) |
The subscriptshift attribute specifies the minimum
amount to shift the baseline of subscript down.
v-unit represents a unit of vertical length (see section 2.3.3 [MathML Attribute Values]).
The msub element increments
scriptlevel by 1, and sets displaystyle to
false, within subscript, but leaves both attributes
unchanged within base. (These attributes are inherited by
every element through its rendering environment, but can be set
explicitly only on mstyle; see section 3.3.4 [Style Change].)
The syntax for the msup element is
<msup> base superscript </msup>.
msup
| Name | values | default |
| superscriptshift | number v-unit | automatic (typical unit is ex) |
The superscriptshift attribute specifies the minimum
amount to shift the baseline of superscript up.
v-unit represents a unit of vertical length (see section 2.3.3 [MathML Attribute Values]).
The msup element increments
scriptlevel by 1, and sets displaystyle to
false, within superscript, but leaves both attributes
unchanged within base. (These attributes are inherited by
every element through its rendering environment, but can be set
explicitly only on mstyle; see section 3.3.4 [Style Change].)
The msubsup element is used so that the subscript and
superscript are both tight against the base, i.e. vertically aligned
as in the second case shown here:
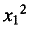 versus
versus
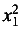 .
.
The syntax for the msubsup element is
<msubsup>base subscript superscript</msubsup>
msubsup
| Name | values | default |
| subscriptshift | number v-unit | automatic (typical unit is ex) |
| superscriptshift | number v-unit | automatic (typical unit is ex) |
The subscriptshift attribute specifies the minimum
amount to shift the baseline of subscript down. The
superscriptshift attribute specifies the minimum amount
to shift the baseline of superscript up.
v-unit represents a unit of vertical length (see section 2.3.3 [MathML Attribute Values]).
The msubsup element increments
scriptlevel by 1, and sets displaystyle to
false, within subscript and superscript,
but leaves both attributes unchanged within base. (These
attributes are inherited by every element through its rendering
environment, but can be set explicitly only on
mstyle; see section 3.3.4 [Style Change].)
msubsup
The msubsup is most commonly used for adding
sub/superscript pairs to identifiers as illustrated above. However,
another important use is placing limits on certain large operators
whose limits are traditionally displayed in the script positions even
when rendered in display style. The most common of these is the
integral. For example,
would be represented as
<mrow>
<msubsup>
<mo> ∫ </mo>
<mn> 0 </mn>
<mn> 1 </mn>
</msubsup>
<mrow>
<msup>
<mi> ⅇ </mi>
<mi> x </mi>
</msup>
<mo> ⁢ </mo>
<mrow>
<mo> ⅆ </mo>
<mi> x </mi>
</mrow>
</mrow>
</mrow>
The syntax for the munder element is
<munder> base underscript </munder>
munder
| Name | values | default |
| accentunder | true | false | automatic |
The accentunder attribute controls whether
underscript is drawn as an `accent' or as a limit. The
main difference between an accent and a limit is that the limit is
reduced in size whereas an accent is the same size as the base. A
second difference is that the accent is drawn closer to the base.
The default value of accentunder is false, unless
underscript is an mo element or an
embellished operator (see section 3.2.4 [Operator, Fence, Separator or Accent]). If
underscript is an mo element, the
value of its accent attribute is used as the default
value of accentunder. If underscript is an
embellished operator, the accent attribute of the
mo element at its core is used as the default
value. As with all attributes, an explicitly given value overrides
the default.
Here is an example (accent versus underscript):
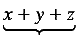 versus
versus
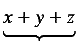 .
The MathML representation for this example is shown below.
.
The MathML representation for this example is shown below.
If the base is an operator with movablelimits=true (or an embellished operator whose mo element core has movablelimits=true), and displaystyle=false, then
underscript is drawn in a subscript position. In this case,
the accentunder attribute is ignored. This is often
used for limits on symbols such as ∑.
Within underscript, munder always
sets displaystyle to false, but increments
scriptlevel by 1 only when accentunder is
false. Within base, it always leaves both attributes
unchanged. (These attributes are inherited by every element through
its rendering environment, but can be set explicitly only on
mstyle; see section 3.3.4 [Style Change].)
munder
The MathML representation for the example shown above is:
<mrow>
<munder accentunder="true">
<mrow>
<mi> x </mi>
<mo> + </mo>
<mi> y </mi>
<mo> + </mo>
<mi> z </mi>
</mrow>
<mo> ⏟ </mo>
</munder>
<mtext> vs </mtext>
<munder accentunder="false">
<mrow>
<mi> x </mi>
<mo> + </mo>
<mi> y </mi>
<mo> + </mo>
<mi> z </mi>
</mrow>
<mo> ⏟ </mo>
</munder>
</mrow>
The syntax for the mover element is
<mover> base overscript> </mover>
.
mover
| Name | values | default |
| accent | true | false | automatic |
The accent attribute controls whether
overscript is drawn as an `accent' (diacritical mark) or
as a limit. The main difference between an accent and a limit is that
the limit is reduced in size whereas an accent is the same size as the
base. A second difference is that the accent is drawn closer to the
base. This is shown below (accent versus limit):
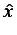 versus
versus
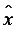 .
.
These differences also apply to `mathematical accents' such as
bars over expressions:
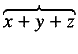 versus.
versus.
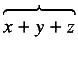 .
The MathML representation for each of these examples is shown below.
.
The MathML representation for each of these examples is shown below.
The default value of accent is false, unless
overscript is an mo element or an
embellished operator (see section 3.2.4 [Operator, Fence, Separator or Accent]). If
overscript is an mo element, the
value of its accent attribute is used as the default
value of accent for mover. If
overscript is an embellished operator, the
accent attribute of the mo element
at its core is used as the default value.
If the base is an operator with movablelimits=true
(or an embellished operator whose mo element core
has movablelimits=true), and
displaystyle=false, then overscript is
drawn in a superscript position. In this case, the accent
attribute is ignored. This is often used for limits on symbols such as
∑.
Within overscript, mover always
sets displaystyle to false, but increments
scriptlevel by 1 only when accent is
false. Within base, it always leaves both attributes
unchanged. (These attributes are inherited by every element through
its rendering environment, but can be set explicitly only on
mstyle; see section 3.3.4 [Style Change].)
mover
The MathML representation for the examples shown above is:
<mrow>
<mover accent="true">
<mi> x </mi>
<mo> &hat; </mo>
</mover>
<mtext> vs </mtext>
<mover accent="false">
<mi> x </mi>
<mo> &hat; </mo>
</mover>
</mrow>
<mrow>
<mover accent="true">
<mrow>
<mi> x </mi>
<mo> + </mo>
<mi> y </mi>
<mo> + </mo>
<mi> z </mi>
</mrow>
<mo> ‾ </mo>
</mover>
<mtext> vs </mtext>
<mover accent="false">
<mrow>
<mi> x </mi>
<mo> + </mo>
<mi> y </mi>
<mo> + </mo>
<mi> z </mi>
</mrow>
<mo> ‾ </mo>
</mover>
</mrow>
The syntax for the munderover element is
<munderover> base underscript overscript</munderover>
munderover
| Name | values | default |
| accent | true | false | automatic |
| accentunder | true | false | automatic |
The munderover element is used so that the
underscript and overscript are vertically spaced equally in relation
to the base and so that they follow the slant of the base as in the
second expression shown below:
versus
The MathML representation for this example is shown below.
The difference in the vertical spacing is too small to be noticed on a low resolution display at a normal font size, but is noticeable on a higher resolution device such as a printer and when using large font sizes. In addition to the visual differences, attaching both the underscript and overscript to the same base more accurately reflects the semantics of the expression.
The accent and accentunder attributes
have the same effect as the attributes with the same names on
mover (section 3.4.5 [Overscript]) and
munder (section 3.4.4 [Underscript]), respectively. Their
default values are also computed in the same manner as described for
those elements, with the default value of accent
depending on overscript and the default value of
accentunder depending on underscript.
If the base is an operator with movablelimits=true
(or an embellished operator whose mo element core
has movablelimits=true), and
displaystyle=false, then underscript and
overscript are drawn in a subscript and superscript
position, respectively. In this case, the accent and
accentunder attributes are ignored. This is often used
for limits on symbols such as ∑.
Within underscript, munderover
always sets displaystyle to false, but increments
scriptlevel by 1 only when accentunder is
false. Within overscript,
munderover always sets displaystyle
to false, but increments scriptlevel by 1 only when
accent is false. Within base, it always
leaves both attributes unchanged. (These attributes are inherited by
every element through its rendering environment, but can be set
explicitly only on mstyle; see section 3.3.4 [Style Change]).
munderover
The MathML representation for the example shown above with the left
expression made using separate munder and
mover elements, and the right one using an
munderover element, is:
<mrow>
<mover>
<munder>
<mo> ∫ </mo>
<mn> 0 </mn>
</munder>
<mi> &infinity; </mi>
</mover>
<mtext> vs </mtext>
<munderover>
<mo> ∫ </mo>
<mn> 0 </mn>
<mi> &infinity; </mi>
</munderover>
</mrow>
The syntax for the mmultiscripts element is
<mmultiscripts>
base
(subscript superscript)*
[ <mprescripts/> (presubscript presuperscript)* ]
</mmultiscripts>
Presubscripts and tensor notations are represented by a single
element, mmultiscripts. This element allows the
representation of any number of vertically-aligned pairs of subscripts
and superscripts, attached to one base expression. It supports both
postscripts (to the right of the base in visual notation) and
prescripts (to the left of the base in visual notation). Missing
scripts can be represented by the empty element
none.
The prescripts are optional, and when present are given after the postscripts, because prescripts are relatively rare compared to tensor notation.
The argument sequence consists of the base followed by zero or more
pairs of vertically-aligned subscripts and superscripts (in that
order) that represent all of the postscripts. This list is optionally
followed by an empty element mprescripts and a
list of zero or more pairs of vertically-aligned presubscripts and
presuperscripts that represent all of the prescripts. The pair lists
for postscripts and prescripts are given in a left-to-right order. If
no subscript or superscript should be rendered in a given position,
then the empty element none should be used in
that position.
The base, subscripts, superscripts, the optional separator element
mprescripts, the presubscripts, and the
presuperscripts, are all direct subexpressions of the
mmultiscripts element, i.e. they are all at the
same level of the expression tree. Whether a script argument is a
subscript or a superscript, or whether it is a presubscript or a
presuperscript is determined by whether it occurs in an even-numbered
or odd-numbered argument position, respectively, ignoring the empty
element mprescripts itself when determining the
position. The first argument, the base, is considered to be in
position 1. The total number of arguments must be odd, if
mprescripts is not given, or even, if it is.
The empty elements mprescripts and
none are only allowed as direct subexpressions
of mmultiscripts.
mmultiscripts
Same as attributes of msubsup.
The mmultiscripts element increments
scriptlevel by 1, and sets displaystyle to
false, within each of its arguments except base, but
leaves both attributes unchanged within base. (These
attributes are inherited by every element through its rendering
environment, but can be set explicitly only on
mstyle; see section 3.3.4 [Style Change].)
mmultiscripts
Two examples of the use of mmultiscripts are:
0F1(;a;z).
<mrow>
<mmultiscripts>
<mi> F </mi>
<mn> 1 </mn>
<none/>
<mprescripts/>
<mn> 0 </mn>
<none/>
</mmultiscripts>
<mo> ⁡ </mo>
<mrow>
<mo> ( </mo>
<mrow>
<mo> ; </mo>
<mi> a </mi>
<mo> ; </mo>
<mi> z </mi>
</mrow>
<mo> ) </mo>
</mrow>
</mrow>
 (where k and l are different indices)
(where k and l are different indices)
<mmultiscripts> <mi> R </mi> <mi> i </mi> <none/> <none/> <mi> j </mi> <mi> k </mi> <none/> <mi> l </mi> <none/> </mmultiscripts>
Matrices, arrays and other table-like mathematical notation are marked
up using mtable, mtr and
mtd elements. These elements are similar to the
TABLE, TR and TD elements of HTML, except that they provide
specialized attributes in order to provide the fine layout control
necessary for commutative diagrams, block matrices and so on.
A matrix or table is specified using the
mtable element. Inside of the
mtable element, mtr and
mtd elements can be given. If some argument to
mtable is not an mtr
element, renderers should assume a one-column row (i.e. the argument
is effectively wrapped with an inferred
mtr .../mtr
begin-end tag pair). Similarly, if some argument to a (possibly
inferred) mtr element is not an
mtd element, that argument is treated as a table
entry by effectively wrapping it with an inferred
mtd .../mtd
begin-end tag pair. The mtr or
mtd elements must be given explicitly if they
have attributes different from those they would inherit from the
enclosing mtable or mtr.
Note that the above rules imply that an mtable
whose arguments are expressions other than mtr or
mtd elements forms a single column of those
expressions.
Table rows that have fewer columns than other rows of the same
table (whether the other rows precede or follow them) are effectively
padded on the right with empty mtd elements so
that the number of columns in each row equals the maximum number of
columns in any row of the table. Note that the use of
mtd elements with non-default values of the
rowspan or columnspan attributes may affect
the number of mtd elements which should be given
in subsequent mtr elements to cover a given
number of columns.
Note that the usual representation of a matrix consists of an
mtable element surrounded by parentheses; see the
example below. This can be constructed using either
mrow or mfenced. The
parentheses are not rendered by the mtable
element itself.
mtable
| Name | values | default |
| align | (top | bottom | center | baseline | axis) [ rownumber ] | axis |
| rowalign | (top | bottom | center | baseline | axis) + | baseline |
| columnalign | (left | center | right) + | center |
| groupalign | group-alignment-list-list | {left} |
| alignmentscope | (true | false) + | true |
| columnwidth | ( auto | h-unit | fit ) + | auto |
| rowspacing | ( number v-unit ) + | 1.0ex |
| columnspacing | ( number h-unit ) + | 0.8em |
| rowlines | (none | solid | dashed) + | none |
| columnlines | (none | solid | dashed) + | none |
| frame | none | solid | dashed | none |
| framespacing | number h-unit number v-unit | 0.4em 0.5ex |
| equalrows | true | false | true |
| equalcolumns | true | false | true |
| displaystyle | true | false | false |
Note that the default value for each of rowlines,
columnlines and frame is the literal string
`none', meaning that the default is to render no lines, rather than
that there is no default.
As described in section 2.3.3 [MathML Attribute Values], the notation (x | y) +
means one or more occurrences of either x or
y, separated by whitespace. For example, possible values
for columnalign are left,
left left, and
left right center center.
If there are more entries than are necessary (e.g. more entries than
columns for columnalign), then only the first
entries will be used. If there are fewer entries, then the last entry is
repeated as often as necessary. For example, if columnalign="right center" and the table has three
columns, the first column will be right aligned and the second and third
columns will be centered.
The align attribute specifies where to align the
table with respect to its environment. `axis' means to align
the center of the table on the environment's axis. (The axis of an equation
is an alignment line used by typesetters. It is the line on which a minus
sign typically lies.) `center' and `baseline'
both mean to align the center of the table on the environment's
baseline. `top' or `bottom' aligns the top or
bottom of the table on the environment's baseline.
If the align attribute value ends with a rownumber between 1 and n (for a table with
n rows), the specified row is aligned in the way described above,
rather than the table as a whole; the top (first) row is numbered 1, and
the bottom (last) row is numbered n. The same is true if the rownumber is negative, between -1 and -n,
except that the bottom row is referred to as -1 and the top row as
-n. Other values of rownumber are
illegal.
The rowalign attribute specifies how the entries in
each row should be aligned. For example, `top' means that the tops of
each entry in each row should be aligned with the tops of the other
entries in that row. The columnalign attribute specifies
how the entries in each column should be aligned.
The groupalign and alignmentscope
attributes are described with the alignment elements,
maligngroup and
malignmark, in section 3.5.4 [Alignment Markers].
The columnwidth attribute specifies how wide
a column should be. The auto value means that
the column should be as wide as needed, which is the default. If an
explicit value is given, then the column is exactly that wide and the
contents of that column are made to fit in that width. The contents
are linewrapped or clipped at the discretion of the renderer. If fit is given as a value, the remaining pagewidth
after subtracting the widths for columns specified as auto and/or specific widths is divided equally
among the fit columns and this value is used
for the column width. If insufficient room remains to hold the
contents of the fit columns, renderers may
linewrap or clip the contents of the fit
columns.
The rowspacing and columnspacing
attributes specify how much space should be added between each row and
column. However, spacing before the first row and after the last row
(i.e. at the top and bottom of the table) is given by the second
number in the value of the framespacing attribute, and
spacing before the first column and after the last column (i.e. on the
left and on the right of the table) is given by the first number in
the value of the framespacing attribute.
In those attributes' syntaxes, h-unit or
v-unit represents a unit of horizontal or vertical
length, respectively (see section 2.3.3.3 [CSS-compatible attributes]). The units shown in the
attributes' default values (em or ex) are
typically used.
The rowlines and columnlines attributes
specify whether and what kind of lines should be added between each
row and column. Lines before the first row or column and after the
last row or column are given using the frame
attribute.
If a frame is desired around the table, the frame
attribute is used. If the attribute value is not `none', then
framespacing is used to add spacing between the lines of
the frame and the first and last rows and columns of the table. If
frame="none", then the framespacing
attribute is ignored. The frame and
framespacing attributes are not part of the
rowlines/columnlines,
rowspacing/columnspacing options because
having them be so would often require that rowlines and
columnlines would need to be fully specified instead of
just giving a single value. For example, if a table had five columns
and we wanted lines between the columns, but no frame, then we would
have to write columnlines="none solid solid solid solid
none". By separating the frame from the internal lines, we only need
to write columnlines="solid".
The equalrows attribute forces the rows all to be
the same total height when set to true. The equalcolumns attribute forces the columns all to be the
same width when set to true.
The displaystyle attribute specifies the value of
displaystyle (described under mstyle
in section 3.3.4 [Style Change]) within each cell
(mtd element, perhaps inferred) of the
table. Setting displaystyle=true can be useful for
tables whose elements are whole mathematical expressions; the default
value of false is appropriate when the table is part of an
expression, for example, when it represents a matrix. In either case,
scriptlevel (section 3.3.4 [Style Change]) is not changed for the table
cells.
mtable
A 3 by 3 identity matrix could be represented as follows:
<mrow>
<mo> ( </mo>
<mtable>
<mtr> <mn>1</mn> <mn>0</mn> <mn>0</mn> </mtr>
<mtr> <mn>0</mn> <mn>1</mn> <mn>0</mn> </mtr>
<mtr> <mn>0</mn> <mn>0</mn> <mn>1</mn> </mtr>
</mtable>
<mo> ) </mo>
</mrow>
This might be rendered as:
Note that the parentheses must be represented explicitly; they are not
part of the mtable element's rendering. This allows
use of other surrounding fences, such as brackets, or none at all.
An mtr element represents one row in a table
or matrix. An mtr element is only allowed as a
direct subexpression of an mtable element, and
specifies that its contents should form one row of the table. Each
argument of mtr is placed in a different column
of the table, starting at the leftmost column.
As described under mtable,
mtr elements can be inferred. Inferred
mtr elements necessarily have exactly one
argument.
If some argument to a (possibly inferred) mtr
element is not an mtd element, that argument is
treated as a table entry by effectively wrapping it with an inferred
mtd .../mtd
begin-end tag pair. Note that mtd elements must
be given explicitly if they have attributes different from those they
would inherit from the enclosing mtr or
mtable.
All mtr elements which cover fewer columns
than other rows of the same table (whether the other rows precede or
follow them) are effectively padded on the right with empty
mtd elements, as described under
mtable. The required number of arguments in some
mtr elements may be affected by the use of the
rowspan and columnspan attributes on
mtd elements.
mtr
| Name | values | default |
| rowalign | top | bottom | center | baseline | axis | inherited |
| columnalign | (left | center | right) + | inherited |
| groupalign | group-alignment-list-list | inherited |
The rowalign and columnalign attributes
allow a specific row to override the alignment specified by the same
attributes in the surrounding mtable element.
As with mtable, if there are more entries than
necessary in the value of columnalign (i.e. more entries
than columns in the row), then the extra entries will be ignored. If
there are fewer entries than columns, then the last entry will be
repeated as many times as needed.
The groupalign attribute is described with the alignment
elements, maligngroup and malignmark,
in section 3.5.4 [Alignment Markers].
An mtd element represents one entry in a table
or matrix. An mtd element is only allowed as a
direct subexpression of an mtr element (perhaps
an inferred one).
As described under mtr and
mtable, mtd elements can be
inferred. They must be given explicitly for table elements which have
attributes different than those of the enclosing
mtr or mtable.
The mtd element accepts any number of
arguments; if this number is not 1, its contents are treated as a single
`inferred mrow' formed from all its
arguments, as described in section 3.1.3 [Required Arguments].
mtd
| Name | values | default |
| rowspan | number | 1 |
| columnspan | number | 1 |
| rowalign | top | bottom | center | baseline | axis | inherited |
| columnalign | left | center | right | inherited |
| groupalign | group-alignment-list | inherited |
The rowspan and columnspan attributes
allow a specific matrix element to be treated as if it occupied the
number of rows or columns specified. The interpretation of how this
larger element affects specifying subsequent rows and columns is meant
to correspond with the similar attributes for HTML 3.2 tables.
The rowalign and columnalign attributes
allow a specific matrix element to override the alignment specified by
a surrounding mtable or mtr
element.
The groupalign attribute is described with the alignment
elements, maligngroup and malignmark,
in section 3.5.4 [Alignment Markers].
These are space-like elements (see section 3.2.6 [Space]) which can be used to vertically align specified points within a column of MathML expressions, by the automatic insertion of the necessary amount of horizontal space between specified subexpressions.
The discussion that follows will use the example of a set of simultaneous equations which should be rendered with vertical alignment of the coefficients and variables of each term, by inserting spacing somewhat like that shown here:
8.44x + 55 y = 0
3.1 x - 0.7y = -1.1
If the example expressions shown above were arranged in a column but not aligned, they would appear as:
8.44x + 55y = 0
3.1x - 0.7y = -1.1
(For audio renderers, it is suggested that the alignment elements produce the analogous behavior of altering the rhythm of pronunciation so that it is the same for several subexpressions in a column, by the insertion of the appropriate time delays in place of the extra horizontal spacing described here.)
The expressions whose parts are to be aligned (each equation, in the
example above) must be given as the table elements (i.e. as the mtd elements, perhaps inferred) of one column of an
mtable. To avoid confusion, the term `table
cell' rather than `table element' will be used in the
remainder of this section.
All interactions between alignment elements are limited to the
mtable column they arise in. That is, every
column of a table specified by an mtable element
acts as an `alignment scope' which contains within it all alignment
effects arising from its contents. It also excludes any interaction
between its own alignment elements and the alignment elements inside
any nested alignment scopes it might contain.
The reason mtable columns are used as
alignment scopes is that they are the only general way in MathML to
arrange expressions into vertical columns. Future versions of MathML
may provide an malignscope element which allows
an alignment scope to be created around any MathML element, but even
then, table columns would still sometimes need to act as alignment
scopes, and since they are not elements themselves, but rather are
made from corresponding parts of the content of several
mtr elements, they could not individually be the
content of an alignment scope element.
An mtable element can be given the attribute
alignmentscope=false to cause
its columns not to act as alignment scopes. This is discussed further at
the end of this section. Otherwise, the discussion in this section assumes
that this attribute has its default value of true.
To cause alignment, it is necessary to specify, within each
expression to be aligned, the points to be aligned with corresponding
points in other expressions, and the beginning of each alignment
group of subexpressions which can be horizontally shifted as a
unit to effect the alignment. Each alignment group must contain one
alignment point. It is also necessary to specify which expressions in
the column have no alignment groups at all, but are affected only by
the ordinary column alignment for that column of the table, i.e. by
the columnalign attribute, described elsewhere.
The alignment groups start at the locations of invisible
maligngroup elements, which are rendered with
zero width when they occur outside of an alignment scope, but within
an alignment scope are rendered with just enough horizontal space to
cause the desired alignment of the alignment group which follows
them. A simple algorithm by which a renderer can achieve this is given
later. In the example above, each equation would have one
maligngroup element before each coefficient,
variable, and operator on the left-hand side, one before the
= sign, and one before the constant on the right-hand
side.
In general, a table cell containing n
maligngroup elements contains n
alignment groups, with the ith group consisting of the
elements entirely after the ith
maligngroup element and before the
(i+1)-th; no element within the table cell's content
should occur entirely before its first
maligngroup element.
Note that the division into alignment groups does not
necessarily fit the nested expression structure of the MathML
expression containing the groups - that is, it is permissible for one
alignment group to consist of the end of one
mrow, all of another one, and the beginning of a
third one, for example. This can be seen in the MathML markup for the
present example, given at the end of this section.
The nested expression structure formed by
mrows and other layout schemata should reflect
the mathematical structure of the expression, not the alignment-group
structure, to make possible optimal renderings and better automatic
interpretations; see the discussion of proper grouping in section
3.3.1. Insertion of alignment elements (or other space-like elements)
should not alter the correspondence between the structure of a MathML
expression and the structure of the mathematical expression it
represents.
Although alignment groups need to coincide with the nested
expression structure of layout schemata, there are nonetheless
restrictions on where an maligngroup element is
allowed within a table cell. The maligngroup
element may only be contained within elements of the following types
(which are themselves contained in the table cell):
mrow element, including an inferred
mrow such as the one formed by a multi-argument
mtd element;
mstyle element;
mphantom element;
mfenced element;
maction element, though only its
selected subexpression is checked;
semantics element.
These restrictions are intended to ensure that alignment can be unambiguously specifed, while avoiding complexities involving things like overscripts, radical signs and fraction bars. They also ensure that a simple algorithm suffices to accomplish the desired alignment.
Note that some positions for an maligngroup
element, although legal, are not useful, such as for an
maligngroup element to be an argument of an
mfenced element. When inserting an
maligngroup element before a given element in
pre-existing MathML, it will often be necessary, and always
acceptable, to form a new mrow element to contain
just the maligngroup element and the element it
is inserted before. In general, this will be necessary except when the
maligngroup element is inserted directly into an
mrow or into an element which can form an
inferred mrow from its contents. See the warning
about the legal grouping of `space-like elements' in
section 3.2.6 [Space].
For the table cells which are divided into alignment groups, every
element in their content must be part of exactly one alignment group,
except the elements from the above list which contain
maligngroup elements inside them, and the
maligngroup elements themselves. This means
that, within any table cell containing alignment groups, the first
complete element must be an maligngroup element,
though this may be preceded by the begin tags of other elements.
This requirement removes a potential confusion about how to align
elements before the first maligngroup element,
and makes it easy to identify table cells which are left out of their
column's alignment process entirely.
Note that it is not required that the table cells in a column which are divided into alignment groups each contain the same number of groups. If they don't, zero-width alignment groups are effectively added on the right side of each table cell which has fewer groups than other table cells in the same column.
Expressions in a column which are to have no alignment groups
should contain no maligngroup
elements. Expressions with no alignment groups are aligned using only
the columnalign attribute which applies to the table
column as a whole, and are not affected by the groupalign
attribute described below. If such an expression is wider than the
column width needed for the table cells containing alignment groups,
all the table cells containing alignment groups will be shifted as a
unit within the column as described by the columnalign
attribute for that column. For example, a column heading with no
internal alignment could be added to the column of two equations given
above by preceding them with another table row containing an
mtext element for the heading, and using the
default columnalign="center" for the table, to
produce:
equations with aligned variables
8.44x + 55 y = 0
3.1 x - 0.7y = -1.1
or, with a shorter heading,
some equations 8.44x + 55 y = 0 3.1 x - 0.7y = -1.1
malignmark
Each alignment group's alignment point can either be specified by
an malignmark element anywhere within the
alignment group (except within another alignment scope wholly
contained inside it), or it is determined automatically from the
groupalign attribute. The groupalign
attribute can be specified on the group's preceding
maligngroup element or on its surrounding
mtd, mtr, or
mtable elements. In typical cases, using the
groupalign attribute is sufficient to describe the
desired alignment points, so no malignmark
elements need to be provided.
The malignmark element indicates that the
alignment point should occur on the right edge of the preceding
element, or the left edge of the following element or character,
depending on the edge attribute of
malignmark. Note that it may be necessary to
introduce an mrow to group an
malignmark element with a neighboring element,
in order not to alter the argument count of the containing
element. (See the warning about the legal grouping of `space-like
elements' in section 3.2.6 [Space]).
When an malignmark element is provided within an
alignment group, it can occur in an arbitrarily deeply nested element
within the group, as long as it is not within a nested alignment scope. It
is not subject to the same restrictions on location as maligngroup elements. However, its immediate
surroundings need to be such that the element to its immediate right or
left (depending on its edge attribute) can be
unambiguously identified. If no such element is present, renderers should
behave as if a zero-width element had been inserted there.
For the purposes of alignment, an element X is considered to be to the
immediate left of an element Y, and Y to the immediate right of X, whenever
X and Y are successive arguments of one (possibly inferred) mrow element, with X coming before Y. In the case of
mfenced elements, renderers should evaluate this
relation as if the mfenced element had been
replaced by the equivalent expanded form involving mrow. Similarly, an maction
element should be treated as if it were replaced by its currently selected
subexpression. In all other cases, no relation of `to the immediate
left or right' is defined for two elements X and Y. However, in the
case of content elements interspersed in presentation markup, renderers
should attempt to evaluate this relation in a sensible way. For example, if
a renderer maintains an internal presentation structure for rendering
content elements, the relation could be evaluated with respect to
that. (See chapter 4 [Content Markup] and chapter 5 [Combining Presentation and Content Markup] for further
details about mixing presentation and content markup.)
Unlike all other elements in MathML,
malignmark elements are allowed to occur within
the content of token elements, such as mn,
mi, or mtext. When this
occurs, the character immediately before or after the
malignmark element will carry the alignment
point; in all other cases, the element to its immediate left or right
will carry the alignment point. The rationale for this is that it is
sometimes desirable to align on the edges of specific characters
within multi-character token elements.
If there is more than one malignmark element
in an alignment group, all but the first one will be ignored. MathML
renderers may wish to provide a mode in which they will warn about
this situation, but it is not an error, and should trigger no warnings
by default. (Rationale: it would be inconvenient to have to remove all
unnecessary malignmark elements from
automatically generated data, in certain cases, such as when they are
used to specify alignment on `decimal points' other than the '.'
character.)
malignmark
| Name | values | default |
| edge | left | right | left |
malignmark has one attribute,
edge, which specifies whether the alignment point will be
found on the left or right edge of some element or character. The
precise location meant by `left edge' or `right edge' is discussed
below. If edge="right", the alignment point is the right
edge of the element or character to the immediate left of the
malignmark element. If edge="left",
the alignment point is the left edge of the element or character to
the immediate right of the malignmark
element. Note that the attribute refers to the choice of edge rather
than to the direction in which to look for the element whose edge will
be used.
For malignmark elements which occur within
the content of MathML token elements, the preceding or following
character in the token element's content is used; if there is no such
character, a zero-width character is effectively inserted for the
purpose of carrying the alignment point on its edge. For all other
malignmark elements, the preceding or following
element is used; if there is no such element, a zero-width element is
effectively inserted to carry the alignment point.
The precise definition of the `left edge' or `right edge' of a character or glyph (e.g. whether it should coincide with an edge of the character's bounding box) is not specified by MathML, but is at the discretion of the renderer; the renderer is allowed to let the edge position depend on the character's context as well as on the character itself.
For proper alignment of columns of numbers (using groupalign values of left, right, or decimalpoint), it is
likely to be desirable for the effective width (i.e. the distance between
the left and right edges) of decimal digits to be constant, even if their
bounding box widths are not constant (e.g. if `1' is narrower
than other digits). For other characters, such as letters and operators, it
may be desirable for the aligned edges to coincide with the bounding
box.
The `left edge' of a MathML element or alignment group
refers to the left edge of the leftmost glyph drawn to render the element
or group, except that explicit space represented by mspace or mtext elements
should also count as `glyphs' in this context, as should
glyphs which would be drawn if not for mphantom
elements around them. The `right edge' of an element or
alignment group is defined similarly.
maligngroup
| Name | values | default |
| groupalign | left | center | right | decimalpoint | inherited |
maligngroup has one attribute,
groupalign, which is used to determine the position of
its group's alignment point when no malignmark
element is present. The following discussion assumes that no
malignmark element is found within a group.
In the example given at the beginning of this section, there is one
column of 2 table cells, with 7 alignment groups in each table cell;
thus there are 7 columns of alignment groups, with 2 groups, one above
the other, in each column. These columns of alignment groups should be
given the 7 groupalign values `decimalpoint left left
decimalpoint left left decimalpoint', in that order. How to specify
this list of values for a table cell or table column as a whole, using
attributes on elements surrounding the
maligngroup element is described later.
If groupalign is `left',
`right', or `center', the alignment point is
defined to be at the group's left edge, at its right edge, or halfway
between these edges, respectively. The meanings of `left edge'
and `right edge' are as discussed above in relation to malignmark.
If groupalign is `decimalpoint',
the alignment point is the right edge of the last character before the
decimal point. The decimal point is the first `.' character
(ASCII 0x2e) in the first mn element found along
the alignment group's baseline. More precisely, the alignment group is
scanned recursively, depth-first, for the first mn
element, descending into all arguments of each element of the types
mrow (including inferred
mrows), mstyle,
mpadded, mphantom,
mfenced, or msqrt,
descending into only the first argument of each `scripting' element
(msub, msup,
msubsup, munder,
mover, munderover,
mmultiscripts) or of each
mroot or semantics element,
descending into only the selected subexpression of each
maction element, and skipping the content of all
other elements. The first mn so found always
contains the alignment point, which is the right edge of the last
character before the first decimal point in the content of the
mn element. If there is no decimal point in the
mn element, the alignment point is the right edge
of the last character in the content. If the decimal point is the
first character of the mn element's content, the
right edge of a zero-width character inserted before the decimal point
is used. If no mn element is found, the right
edge of the entire alignment group is used (as for
groupalign="right").
In order to permit alignment on decimal points in
cn elements, a MathML renderer can convert a
content expression into a presentation expression which renders the
same way before searching for decimal points as described above.
If characters other than `.' should be used as
`decimal points' for alignment, they should be preceded by malignmark elements within the mn token's content itself.
For any of the groupalign values, if an explicit
malignmark element is present anywhere within
the group, the position it specifies (described earlier) overrides the
automatic determination of alignment point from the
groupalign value.
groupalign valuesIt is not usually necessary to put a groupalign
attribute on every maligngroup element. Since
this attribute is usually the same for every group in a column of
alignment groups to be aligned, it can be inherited from an attribute
on the mtable which was used to set up the
alignment scope as a whole, or from the mtr or
mtd elements surrounding the alignment group. It
is inherited via an `inheritance path' which proceeds from
mtable through successively contained
mtr, mtd, and
maligngroup elements. There is exactly one
element of each of these kinds in this path from an
mtable to any alignment group inside it, though
the mtr and/or mtd elements
might be inferred ones, as described in the sections on those
elements. In general, the value of groupalign will be
inherited by any given alignment group from the innermost element
which surrounds the alignment group and which provides an explicit
setting for this attribute.
Note, however, that each mtd element needs, in
general, a list of groupalign values, one for each
maligngroup element inside it, rather than just
a single value. Furthermore, an mtr or
mtable element needs, in general, a list of lists
of groupalign values, since it spans multiple
mtable columns, each potentially acting as an
alignment scope. Such lists of group-alignment values are specified
using the following syntax rules:
group-alignment := left | right | center | decimalpoint
group-alignment-list := group-alignment +
>group-alignment-list-list := ( '{' group-alignment-list '}' ) +
As described in section 2.3.3 [MathML Attribute Values], | separates
alternatives; + represents optional repetition (i.e. 1 or
more copies of what precedes it), with extra values ignored and the
last value repeated if necessary to cover additional table columns or
alignment group columns; '{' and '}'
represent literal braces; and ( and ) are
used for grouping, but do not literally appear in the attribute
value.
The permissible values of the groupalign attribute of the
elements that have this attribute are specified using the above
syntax definitions as follows:
| Element type | groupalign attribute syntax | default value |
mtable |
group-alignment-list-list | {left} |
mtr |
group-alignment-list-list | inherited from mtable attribute |
mtd |
group-alignment-list | inherited from within mtr attribute |
maligngroup |
group-alignment | inherited from within mtd attribute |
In the example near the beginning of this section, the group
alignment values could be specified on every mtd
element using groupalign = `decimalpoint left left
decimalpoint left left decimalpoint', or on every
mtr element using groupalign =
`{decimalpoint left left decimalpoint left left decimalpoint}', or
(most conveniently) on the mtable as a whole
using groupalign = `{decimalpoint left left decimalpoint
left left decimalpoint}', which provides a single braced list of
group-alignment values for the single column of expressions to be
aligned.
The above rules are sufficient to explain the MathML representation of the example given near the start of this section. To repeat the example, the desired rendering is:
8.44x + 55 y = 0
3.1 x - 0.7y = -1.1
One way to represent that in MathML is:
<mtable groupalign="decimalpoint left left decimalpoint left left decimalpoint">
<mtd>
<mrow>
<mrow>
<maligngroup/>
<mn> 8.44 </mn>
<mo> ⁢ </mo>
<maligngroup/>
<mi> x </mi>
</mrow>
<maligngroup/>
<mo> + </mo>
<mrow>
<maligngroup/>
<mn> 55 </mn>
<mo> ⁢ </mo>
<maligngroup/>
<mi> y </mi>
</mrow>
</mrow>
<maligngroup/>
<mo> = </mo>
<maligngroup/>
<mn> 0 </mn>
</mtd>
<mtd>
<mrow>
<mrow>
<maligngroup/>
<mn> 3.1 </mn>
<mo> ⁢ </mo>
<maligngroup/>
<mi> x </mi>
</mrow>
<maligngroup/>
<mo> - </mo>
<mrow>
<maligngroup/>
<mn> 0.7 </mn>
<mo> ⁢ </mo>
<maligngroup/>
<mi> y </mi>
</mrow>
</mrow>
<maligngroup/>
<mo> = </mo>
<maligngroup/>
<mrow>
<mo> - </mo>
<mn> 1.1 </mn>
</mrow>
</mtd>
</mtable>
The alignment elements maligngroup and
malignmark can occur outside of alignment
scopes, where they are ignored. The rationale behind this is that in
situations in which MathML is generated, or copied from another
document, without knowing whether it will be placed inside an
alignment scope, it would be inconvenient for this to be an error.
An mtable element can be given the attribute
alignmentscope=false to cause its columns not to act as
alignment scopes. In general, this attribute has the syntax
(true | false) +; if its value is a list of boolean
values, each boolean value applies to one column, with the last value
repeated if necessary to cover additional columns, or with extra
values ignored. Columns which are not alignment scopes are part of the
alignment scope surrounding the mtable element,
if there is one. Use of alignmentscope=false allows
nested tables to contain malignmark elements for
aligning the inner table in the surrounding alignment scope.
As discussed above, processing of alignment for content elements is not well-defined, since MathML does not specify how content elements should be rendered. However, many renderers are likely to find it convenient to internally convert content elements to presentation elements which render the same way. Thus, as a general rule, even if a renderer does not perform such conversions internally, it is recommended that the alignment elements should be processed as if it did perform them.
A particularly important case for renderers to handle gracefully is
the interaction of alignment elements with the
matrix content element, since this element may or
may not be internally converted to an expression containing an
mtable element for rendering. To partially
resolve this ambiguity, it is suggested, but not required, that if the
matrix element is converted to an expression
involving an mtable element, that the
mtable element be given the attribute
alignmentscope=false, which will make the interaction
of the matrix element with the alignment elements
no different than that of a generic presentation element (in
particular, it will allow it to contain
malignmark elements which operate within the
alignment scopes created by the columns of an
mtable which contains the
matrix element in one of its table cells).
The effect of alignment elements within table cells which have
non-default values of the columnspan or
rowspan attributes is not specified, except that such use
of alignment elements is not an error. Future versions of MathML may
specify the behavior of alignment elements in such table cells.
The effect of possible linebreaking of an
mtable element on the alignment elements is not
specified.
A simple algorithm by which a MathML renderer can perform the
alignment specified in this section is given here. Since the alignment
specification is deterministic (except for the definition of the left
and right edges of a character), any correct MathML alignment
algorithm will have the same behavior as this one. Each
mtable column (alignment scope) can be treated
independently; the algorithm given here applies to one
mtable column, and takes into account the
alignment elements, the groupalign attribute described in
this section, and the columnalign attribute described
under mtable (section 3.5.1 [Table or Matrix]).
First, a rendering is computed for the contents of each table cell
in the column, using zero width for all
maligngroup and malignmark
elements. The final rendering will be identical except for horizontal
shifts applied to each alignment group and/or table cell. The
positions of alignment points specified by any
malignmark elements are noted, and the remaining
alignment points are determined using groupalign
values.
For each alignment group, the horizontal positions of the left edge, alignment point, and right edge are noted, allowing the width of the group on each side of the alignment point (left and right) to be determined. The sum of these two `side-widths', i.e. the sum of the widths to the left and right of the alignment point, will equal the width of the alignment group.
Second, each column of alignment groups, from left to right, is scanned. The ith scan covers the ith alignment group in each table cell containing any alignment groups. Table cells with no alignment groups, or with fewer than i alignment groups, are ignored. Each scan computes two maximums over the alignment groups scanned: the maximum width to the left of the alignment point, and the maximum width to the right of the alignment point, of any alignment group scanned.
The sum of all the maximum widths computed (two for each column of alignment groups) gives one total width, which will be the width of each table cell containing alignment groups. Call the maximum number of alignment groups in one cell n; each such cell's width is divided into 2n adjacent sections, called L(i) and R(i) for i from 1 to n, using the 2n maximum side-widths computed above; for each i, the width of all sections called L(i) is the maximum width of any cell's ith alignment group to the left of its alignment point, and the width of all sections called R(i) is the maximum width of any cell's ith alignment group to the right of its alignment point.
The alignment groups are then positioned in the unique way which places the part of each ith group to the left of its alignment point in a section called L(i), and places the part of each ith group to the right of its alignment point in a section called R(i). This results in the alignment point of each ith group being on the boundary between adjacent sections L(i) and R(i), so that all alignment points of ith groups have the same horizontal position.
The widths of the table cells which contain no alignment groups were computed as part of the initial rendering, and may be different for each cell, and different from the single width used for cells containing alignment groups. The maximum of all the cell widths (for both kinds of cells) gives the width of the table column as a whole.
The position of each cell in the column is determined by the
applicable part of the value of the columnalign attribute
of the innermost surrounding mtable,
mtr, or mtd element which
has an explicit value for it, as described in the sections on those
elements. This may mean that the cells containing alignment groups
will be shifted within their column, in addition to their alignment
groups having been shifted within the cells as described above, but
since each such cell has the same width, it will be shifted the same
amount within the column, thus maintaining the vertical alignment of
the alignment points of the corresponding alignment groups in each
cell.
MathML uses tables to allow for different styles of equation numbering.
Equation numbering is accomplished by using the columnwidth attribute
of mtable, and the meqno element.
The columnwidth attribute value fit allows equations to use up as much of a page as
possible, after accounting for any equation number. This allows for
styles of equation numbers that are left or right justified on a page.
In cases where only a few equations in a document are numbered,
using the columnwidth attribute alone is
probably sufficient.
<mtable columnalign='left right' columnwidth='fit auto'>
<mtr>
<mrow>
<mi>E</mi>
<mo>=</mo>
<mrow>
<mi>m</mi>
<mo>⁢</mo>
<msup>
<mi>c</mi>
<mn>2</mn>
</msup>
</mrow>
</mrow>
<mrow> <mo> ( </mo> <mn> 2.1 </mn> <mo> ) </mo> </mrow>
</mtr>
</mtable>
This should be rendered as:
| E = mc2 | (2.1) |
Issue (numbering-examples): rendering of equation numbering needed.
In larger documents with many numbered equations, automatic
numbering becomes important. While automatic equation numbering and
automatically resolving references to equation numbers is outside the
scope of MathML, these problems can be addressed by the use of XSL
style sheet or other means. The MathML meqno
construction provides support for both of these functions in a way
that is intended to facilitate XSL processing.
An equation number is indicated by the meqno
element. As noted above, the use of meqno to
indicate equation numbers is not required to do equation numbering, though
it is strongly recommended. The meqno element
simply renders its contents, which can be empty. The meqno element accepts any number of arguments; if this
number is not 1, its contents are treated as a single `inferred mrow' formed from all its arguments, as described in
section 3.1.3 [Required Arguments].
meqno is used to explicitly mark what is
an equation number so that transformation languages can match and
change the equation number or its style, such as whether the number is
surrounded by parentheses or whether the equation number appears on
the left or right side. In the later case, the transformation rule
would need to rewrite the row, not just the contents of the meqno element.
meqno
| Name | values | default |
| eqno | string | empty string |
The eqno attribute allows a numbered
equation to have a name that can be referenced elsewhere in the
document without refering to its number which may not be known at the
time the document is authored. For example, an XML application
containing embedded MathML might define a cite
element, with a eqno attribute. by looking for
matching eqno attributes, a tranformation
engine such as XSL could then replace all appropriate cite elements and the content of the
corresponding meqno element with an
automatically generated equation number.
Using the meqno construction, the example
given above might be coded as follows:
<mtable columnalign='left right' columnwidth='fit auto'>
<mtr>
<mrow>
<mi>E</mi>
<mo>=</mo>
<mrow>
<mi>m</mi>
<mo>⁢</mo>
<msup>
<mi>c</mi>
<mn>2</mn>
</msup>
</mrow>
</mrow>
<meqno eqno='famous formula'>
<mrow> <mo> ( </mo> <mn> 2.1 </mn> <mo> ) </mo> </mrow>
</meqno>
</mtr>
</mtable>
Authors can make links from MathML subexpressions by using the standard
simple link construction of XML, <name ... href="...">,
as described in section 7.1.5 [Mixing and Linking MathML and HTML]. However, links are only one
of many ways which specific renderers might provide authors for making
mathematical notation active. For example, in lengthy mathematical
expressions, the ability to `fold' expressions might be
provided, i.e. a renderer might allow a reader to toggle between an
ellipsis and a much longer expression which it represents.
To provide a mechanism for binding actions to expressions, MathML
provides the maction element. This element accepts any
number of subexpressions as arguments, and the following attributes:
| Name | values | default |
| actiontype | (described below) | (required attribute, no default value) |
| selection | positive-integer | 1 |
By default, renderers which do not recognize the specified
actiontype should render the selected subexpression as
defined below. If no selected subexpression exists, it is a MathML
error; the appropriate rendering in that case is as described in
section 7.2.2 [Handling of Errors] on the treatment of MathML errors.
Since a MathML-compliant renderer is not required to recognize any
particular actiontypes, a renderer can be fully MathML
compliant just by implementing the above-described default behavior.
The selection attribute is provided for those
actiontypes which permit someone viewing a document to select one of
several subexpressions for viewing. Its value should be a positive
integer which indicates one of the subexpressions of the
maction element, numbered from 1 to the number of
children of the element. When this is the case, the subexpression so
indicated is defined to be the `selected subexpression' of the
maction element; otherwise the `selected
subexpression' does not exist, which is an error. When the
selection attribute is not specified (including for
actiontypes for which it makes no sense), its default value is 1, so
the selected subexpression will be the first subexpression.
Note that the selection attribute of an
maction element affects not only the rendering of
the element itself, but potentially the rendering of elements
containing it; this can be due either to the reference to an
maction's selected subexpression in the
definition of embellished operator in section 3.2.4 [Operator, Fence, Separator or Accent], or to alignment
elements contained in the selected subexpression (section 3.5.4 [Alignment Markers]). This means that a change of the selection
by the viewer may require a rerendering of the surroundings, not just
their repositioning due to a change in size of the
maction element itself.
Furthermore, as described in chapter 7 [The MathML Interface], if a MathML renderer
responds to a user command to copy the currently selected MathML
subexpression to the environment's `clipboard', any
maction elements present in what is copied should
be given selection attributes which correspond to their selection
state in the MathML rendering at the time of the copy command.
A suggested list of actiontypes and their associated
actions is given below. Keep in mind, however, that this list is
mainly for illustration, and recognized values and behaviors will vary
from renderer to renderer. (Note that hyperlinks, which are part of
the actual MathML specification, are not included here, but are
described separately in chapter 7 [The MathML Interface].)
selection attribute value as described above.
Typical uses would be for exercises in education, ellipses in long
computer algebra output, or to illustrate alternate notations. Note
that the expressions may be of significantly different size, so that
size negotiation with the browser may be desirable. If size
negotiation is not available, scrolling, elision, panning, or some
other method may be necessary to allow full viewing.mtext element for the message in most circumstances.
For non-mtext messages, renderers might provide a
natural language translation of the markup, but this is not
required.mtext element for the message
in most circumstances. For non-mtext messages,
renderers may provide a natural language translation of the markup if
full MathML rendering is not practical, but this is not
required.