1. Introduction
1.1 Mathematics and its Notation
A distinguishing feature of mathematics is the use of a complex and highly
evolved system of two-dimensional symbolic notations. As J. R. Pierce has
written in his book on communication theory, mathematics and its notations
should not be viewed as one and the same thing
[Pierce
1961]. Mathematical ideas exist independently of the notations that
represent them. However, the relation between meaning and notation is subtle,
and part of the power of mathematics to describe and analyze derives from
its ability to represent and manipulate ideas in symbolic form. The challenge
in putting math on the Web is to capture both notation and content in such
a way that documents can utilize the highly-evolved notational practices
of print, and the potential for interconnectivity in electronic media.
Mathematical notations are constantly evolving as people continue
to discover innovative ways of approaching and expressing ideas. Even
the commonplace notations of arithmetic have gone through an amazing
variety of styles, including many defunct ones advocated by leading
mathematical figures of their day [Cajori 1928/1929]. Modern
mathematical notation is the product of centuries of refinement, and
the notational conventions for high-quality typesetting are quite
complicated. For example, variables, or letters which stand for
numbers, are usually typeset today in a special italic font subtly
distinct from the text italic. Spacing around symbols for operations
such as +, -, x and / is slightly different from that of text, to
reflect conventions about operator precedence. Entire books have been
devoted to the conventions of mathematical typesetting, from the
alignment of superscripts and subscripts, to rules for choosing
parenthesis sizes, to specialized notational practices for subfields
of mathematics [for instance, Chaudry,
Barret and Batey, 1954, Swanson
1979, Higham 1993,
or in the TeX literature
Knuth 1986, and Spivak 1986].
Notational conventions in mathematics, and printed text in general,
guide the eye and make printed expressions much easier to read and
understand. Though we usually take them for granted, we rely on
hundreds of conventions such as paragraphs, capital letters, font
families and cases, and even the device of decimal-like numbering of
sections such as we are using in this document (an invention due to
G. Peano, who is probably better known for his axioms for the natural
numbers). Such notational conventions are even more important for
electronic media, where one must contend with the difficulties of
on-screen reading.
However, there is more to putting math on the Web than
merely finding ways of displaying traditional mathematical
notation in a Web browser. The Web represents a fundamental
change in the underlying metaphor for knowledge storage, a
change in which interconnectivity plays a central
role. It is becoming increasingly important to find ways of
communicating mathematics which facilitate automatic
processing, searching and indexing, and reuse in other
mathematical applications and contexts. With this advance in
communication technology, there is an opportunity to expand
our ability to represent, encode, and ultimately to
communicate our mathematical insights and understanding with
each other. We believe that MathML is an important step in
developing Mathematics on the Web.
1.2 Origins and Goals
1.2.1 The History of MathML
The problem of encoding mathematics for computer processing or
electronic communication is much older than the Web. The
common practice among scientists before the Web was to write
papers in some encoded form based on the ASCII character set,
and e-mail them to each other. Several markup methods for
mathematics, in particular TeX [Knuth 1986], were already in
wide use in 1992, just before the Web rose to prominence, [Poppelier, van Herwijnen and
Rowley 1992].
Since its inception, the Web has demonstrated itself to be
a very effective method of making information available to
widely separated groups of individuals. However, even though
the World Wide Web was initially conceived and implemented by
scientists for scientists, the capability to include
mathematical expressions in HTML is very limited. At present,
most mathematics on the Web consists of text with GIF images
of scientific notation, which are difficult to read and to
author.
The World Wide Web Consortium (W3C) recognized that lack of
support for scientific communication was a serious problem.
Dave Raggett included a proposal for HTML Math in the HTML 3.0
working draft in 1994. A panel discussion on math markup was
held at the WWW Conference in Darmstadt in April 1995. In
November 1995, representatives from Wolfram Research presented
a proposal for doing math in HTML to the W3C team. In May
1996, the Digital Library Initiative meeting in
Champaign-Urbana played an important role in bringing together
many interested parties. Following the meeting, an HTML Math
Editorial Review Board was formed. In the intervening years,
this group has grown, and was formally reconstituted as the
W3C Math working group in March 1997.
The MathML proposal reflects the interests and expertise of a very
diverse group. Many contributions to the development of MathML deserve
special mention, some of which we touch on here. One such contribution
concerns the question of accessibility, especially for the visually
handicapped. T. V. Raman is particularly notable in this regard. Neil
Soiffer and Bruce Smith from Wolfram Research shared their
experience with the problems of representing mathematics in connection
with the design of Mathematica 3.0, which was an important influence in
the design of the presentation elements. Paul Topping from Design Science
also contributed his expertise in mathematical formatting and editing.
MathML has benefited from the participation of a number of working
group members involved in other math encoding efforts in the
SGML and
Nico Poppelier from Elsevier Science, Stéphane Dalmas from INRIA,
Sophia Antipolis,
Stan Devitt from Waterloo Maple, Angel Diaz and Robert S. Sutor from
IBM, and Stephen M. Watt from the University of Western Ontario. In
particular, MathML has been influenced by the OpenMath project, the
work of the ISO 12083 working group, and Stilo Technologies' work on a
'semantic' math DTD fragment. The American Mathematical Society has
played a key role in the development of MathML. Among other things, it
has provided two working group chairs: Ron Whitney led the group from
May 1996 to March 1997, and Patrick Ion, who has co-chaired the group
with Robert Miner from The Geometry Center, from March 1997 to the
present.
The working group has benefited from the help of many people. We
would like to particularly name Barbara Beeton, Chris Hamlin, John
Jenkins, Ira Polans, Arthur Smith, Robby Villegas and Joe Yurvati for
help and information in assembling the character tables in Chapter 6,
as well as Peter Flynn, Russel S. S. O'Connor, Andreas Strotmann, and
other contributors to the www-math mailing list for their careful
proofreading and constructive criticisms.
The demand for effective means of electronic scientific
communication is high. Increasingly, researchers, scientists,
engineers, educators, students and technicians find themselves
working remotely and relying on electronic communication. At
the same time, the image-based methods that are currently the
predominant means of transmitting scientific notation over the
Web are primitive and inadequate. Document quality is poor,
authoring is difficult, and mathematical information contained
in images is not available for searching, indexing, or reuse
in other applications.
The most obvious problems with HTML for mathematical communication are
of two types:
Display Problems. Consider the equation 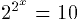 . This equation is sized to
match the surrounding line in 14pt type on the system where it
was authored. Of course, on other systems, or for other font
sizes, the equation is too small or too large. A second point
to observe is that the equation image was generated against a
white background. Thus, if a reader or browser resets the page
background to another color, the anti-aliasing in the image
results in white "halos." Next, consider the equation
. This equation is sized to
match the surrounding line in 14pt type on the system where it
was authored. Of course, on other systems, or for other font
sizes, the equation is too small or too large. A second point
to observe is that the equation image was generated against a
white background. Thus, if a reader or browser resets the page
background to another color, the anti-aliasing in the image
results in white "halos." Next, consider the equation 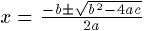 . This equation has a descender which
places the baseline for the equation at a point about a third
of the way from the bottom of the image. One can pad the image
like this:
. This equation has a descender which
places the baseline for the equation at a point about a third
of the way from the bottom of the image. One can pad the image
like this: 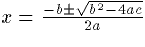 ,
so that the centerline of the image and the baseline of the
equation coincide, but this causes problems with the
inter-line spacing, which also makes the equation difficult to
read. Moreover, center alignment of images is handled in
slightly different ways by different browsers, making it
impossible to guarantee proper alignment for different
clients.
,
so that the centerline of the image and the baseline of the
equation coincide, but this causes problems with the
inter-line spacing, which also makes the equation difficult to
read. Moreover, center alignment of images is handled in
slightly different ways by different browsers, making it
impossible to guarantee proper alignment for different
clients.
Image-based equations are generally harder to see, read and comprehend
than the surrounding text in the browser window. Moreover, these problems
become worse when the document is printed. The resolution of the equations
will be around 70 dots per inch, while the surrounding text will typically
be 300 or more dots per inch. The disparity in quality is judged to be
unacceptable by most people.
Encoding Problems. Consider trying to search this page for part
of an equation, for example, the "=10" from the first equation above. In
a similar vein, consider trying to cut and paste an equation into another
application; even more demanding is to cut and paste a subexpression.
Using image based methods, neither of these common needs can
be adequately addressed. Although the use of ALT text in the document source
can help, it is clear that highly interactive Web documents must provide
a more sophisticated interface between browsers and mathematical notation.
Another problem with encoding mathematics as images is that it requires
more bandwidth. By using markup-based encoding, more of the rendering process
is moved to the client machine. Markup describing an equation is typically
smaller and more compressible than an image of the equation.
Some display problems associated with including math notation in
HTML documents as images could be addressed by improving browser image
handling. However, even if image handling were improved, the problem
of making the information contained in mathematical expressions
available to other applications would remain. Therefore, in planning
for the future, it is not sufficient to merely upgrade image-based
methods. To fully integrate mathematical material into Web documents,
a markup-based encoding of mathematical notation and content is
required.
In designing any markup language, it is essential to carefully
consider the needs of its potential users. In the case of MathML,
the needs of potential users cover a broad spectrum, from education to
research, and on to commerce:
The education community is a large and important group that must be
able to put scientific curriculum materials on the Web. At the same
time, educators often have limited resources of time and equipment,
and are severely hampered by the difficulty of authoring technical Web
documents. Students and teachers need to be able to create
mathematical content quickly and easily, using intuitive,
easy-to-learn, low-cost tools.
Electronic textbooks are another way of using the Web which will potentially
be very important in education. Management consultant Peter Drucker has
recently been prophesying the end of big-campus residential higher education
and its distribution over the Web [Drucker
1997]. Electronic textbooks will need to be active, allowing
intercommunication between the text and scientific software and graphics.
The academic research community generates large volumes of dense
scientific material. Increasingly, research publications are being
stored in databases, such as the highly successful physics preprint
server at Los Alamos National Laboratory. This is especially true in
some areas of physics and mathematics where academic journal prices
have been increasing at an unsustainable rate. In mathematics there
are large collections at
Duke,
MSRI
and
SISSA, and on the
AMS e-MATH
server. In addition, databases of information on mathematical
research, such as Mathematical Reviews and Zentralblatt für
Mathematik, offer on the Web millions of records containing math.
To accommodate the research community, a design for math markup
must facilitate the maintenance and operation of large document
collections, where automatic searching and indexing are
important. Because of the large collection of legacy data, especially
TeX documents, the ability to convert between existing formats and new
formats is also very important to the research community. Finally,
the ability to maintain information for archival purposes is vital to
academic research.
Corporate and academic scientists and engineers also use technical documents
in their work to collaborate, to record results of experiments and computer
simulations, and to verify calculations. For such uses, math on the Web
must provide a standard way of sharing information that can be easily read,
processed and generated using commonly available tools.
Another design requirement is the ability to render mathematical material
in other media such as speech or braille, which is extremely important
for the visually impaired.
Commercial publishers are also involved with math on the Web at all
levels from electronic versions of print books to interactive textbooks
to academic journals. Publishers require a method of putting math on the
Web that is capable of high-quality output, robust enough for large-scale
commercial use, and preferably compatible with their current, usually
SGML-based,
production systems.
1.2.4 Design Goals of
MathML
In order to meet the diverse needs of the scientific community,
MathML has been designed with the following ultimate goals in mind.
MathML should:
- encode mathematical material suitable for teaching
and scientific communication at all levels.
- encode both mathematical notation and
mathematical meaning.
- facilitate conversion to and from other math
formats, both presentational and semantic. Output formats should include:
- graphical displays
- speech synthesizers
- computer algebra systems' input
- other math layout languages, such as TeX
- plain text displays, e.g. VT100 emulators
- print media, including braille
It is recognized that conversion to and from other notational
systems or media may entail loss of information in the process.
- allow the passing of information intended for
specific renderers and applications.
- support efficient browsing for lengthy expressions.
- provide for extensibility.
- be well suited to template and other math editing
techniques.
- be human legible, and simple for software to generate and process.
No matter how successfully MathML might achieve its goals as a markup
language, it is clear that MathML will only be useful if it is
implemented well. To this end, the W3C Math working group has
identified a short list of additional implementation goals. These
goals attempt to describe concisely the minimal functionality MathML
rendering and processing software should try to provide.
-
MathML equations in HTML pages should render properly in popular Web browsers,
in accordance with reader and author viewing preferences, and at the highest
quality possible given the capabilities of the platform.
-
HTML documents containing MathML equations should print properly and at
high-quality printer resolutions.
-
MathML equations in Web pages should be able to react to mouse gestures,
and coordinate communication with other applications through the browser.
-
Equation editors and converters should be developed to facilitate the creation
of Web pages containing MathML equations.
These goals can probably be adequately addressed in the near term by
using embedded elements such as Java applets, plug-ins and ActiveX
controls to render MathML. However, the extent to which these goals
are ultimately met depends on the cooperation and support of browser
vendors, and other software developers. The W3C Math working group
will continue to work with the Document Object Model working group and
the proposed Extensible Style Language working group to ensure that
the needs of the scientific community will be met in the future.
1.3 The Role of MathML on the Web
The design goals of MathML require a system for encoding
mathematical material for the Web which is flexible and extensible,
suitable for interaction with external software, and capable of
producing high-quality rendering in several media. Any markup
language that encodes enough information to do all these tasks well
will of necessity involve some complexity.
At the same time, it is important for many groups, such as
students, to have simple ways to include math in Web pages by
hand. Similarly, other groups, such as the TeX community, would be
best served by a system which allowed the direct entry of markup
languages like TeX in Web pages. In general, specific user
groups are better served by more specialized kinds of input and output
tailored to their needs. Therefore, the ideal system for
communicating mathematics on the Web should provide both specialized
services for input and output, and general services for interchange
of information and rendering to multiple media.
In practical terms, the observation that math on the Web should
provide for both specialized and general need naturally leads to the
idea of a layered architecture. One layer consists of powerful,
general software tools exchanging, processing and rendering
suitably encoded mathematical data. A second layer consists of
specialized software tools aimed at specific user groups, and which
are capable of easily generating encoded mathematical data which can
then be shared with a general audience.
MathML is designed to provide the encoding of mathematical data for
the bottom, more general layer in a two-layer architecture. It is
intended to encode complex notational and semantic structure in an
explicit, regular, and easy to process way for renderers, searching
and indexing software, and other mathematical applications.
As a consequence, MathML is not primarily intended for direct
use by authors. While MathML is human-readable, in all but the
simplest cases it is too verbose and error-prone for hand generation.
Instead, it is anticipated that authors will use equation
editors, conversion programs, and other specialized software tools to
generate MathML. Alternatively, some renderers may convert other
kinds of input directly included in Web pages into MathML on the fly,
in response to a cut-and-paste operation, for example.
In some ways, MathML is analogous to other low-level, communication
formats such as Adobe's PostScript language. You can create a
PostScript file in a variety of ways, depending on your needs; experts
write and modify them by hand, authors create them with word
processors, graphic artists with illustration programs, and so on. Once you
have a PostScript file, however, you can share it with a very large
audience, since devices which render PostScript, such as printers and
screen previewers, are widely available.
Part of the reason for designing MathML as a markup language for a
low-level, general, communication layer is to stimulate mathematical
Web software development in the layers above. MathML provides a way
of coordinating the
development of modular authoring tools and rendering software. By
making it easier to develop a functional piece of a larger system,
MathML can stimulate a "critical mass" of software development,
greatly to the benefit of potential users of math on the Web.
One can envision a similar situation for mathematical data.
Authors are free to create MathML documents using the tools best suited
to their needs. For example, a student might prefer to use a
menu-driven equation editor that can write out MathML to an HTML
file. A researcher might use a computer algebra package that
automatically encodes the mathematical content of an expression, so
that it can be cut from a Web page and evaluated by a colleague. An
academic journal publisher might use a program that converts TeX
markup to HTML and MathML. Regardless of the method used to create a
MathML web page, once it exists, all the advantages of a powerful and
general communication layer become available. A variety of MathML
software could all be used with the same document to render it in
speech or print, to send it to a computer algebra system, or to manage
it as part of a large Web document collection. One may expect that
eventually MathML can be integrated into other arenas where
mathematical formulas occur, such as spreadsheets, statistical
packages and engineering tools.
The W3C Math working group is working with vendors to ensure that
a wide variety of MathML software will soon be available, including
both rendering and authoring tools. A current list of MathML software is
maintained at the World Wide Web Consortium.
The original conception of HTML Math was a simple, straightforward
extension to HTML that would be natively implemented in browsers.
However, very early on, the explosive growth of the Web made it clear
that a general extension mechanism was required, and that math was
only one of many kinds of structured data which would have to be
integrated into the Web using such a mechanism.
Given that MathML must integrate into the Web as an extension, it
is extremely important that MathML and MathML software can interact
well with the existing Web environment. In particular, MathML has
been designed with three kinds of interaction in mind. First, in
order to create mathematical Web content, it is important that
existing mathematical markup languages can be converted to MathML, and
that existing authoring tools can be modified to generate MathML.
Second, it must be possible to embed MathML markup seamlessly in HTML
markup in such a way that it will be accessible to future browsers,
search engines, and all kinds of Web applications which now manipulate
HTML. Finally, it must be possible to render MathML embedded in HTML in
today's web browsers in some fashion, even if it is less than ideal.
Existing Mathematical Markup Languages
Perhaps the most important influence on mathematical markup languages
of the last two decades is the TeX typesetting system developed by
Donald Knuth [Knuth 1986].
TeX is a de facto standard in the mathematical research
community, and it is pervasive in the scientific community at
large. TeX sets a standard for quality of visual rendering, and a
great deal of effort has gone into ensuring MathML can provide the
same visual rendering quality. Moreover, because of the many
legacy documents in TeX, and because of the large authoring community
versed in TeX, a priority in the design of MathML was the ability to
convert TeX math input into MathML format. The feasibility of such
conversion has been demonstrated by prototype software.
Extensive work on encoding mathematics has also been done in the
SGML community, and SGML-based encoding schemes are widely used by
commercial publishers. ISO 12083 is an important markup language which
contains a math DTD fragment primarily intended for describing the visual
presentation of mathematical notation. Because ISO 12083 math and its
derivatives share many presentational aspects with TeX, and because
SGML enforces structure and regularity more than TeX, much of the work
in ensuring MathML is compatible with TeX also applies well to
ISO12083.
MathML also pays particular attention to compatibility with other
mathematical software, and in particular, with computer algebra
systems. Many of the presentation elements of MathML are derived in
part from the mechanism of typesetting boxes. The MathML content
elements are heavily indebted to the OpenMath project and the Semantic
Maths DTD. The OpenMath project has close ties to both the SGML and
computer algebra communities, and has laid a foundation for an
SGML-based means of communication between mathematical software
packages, among other things. The feasibility of both generating and
interpreting MathML in computer algebra systems has been demonstrated
by prototype software.
HTML Extension Mechanisms
As noted above, the success of HTML has led to enormous pressure to
incorporate a wide variety of data types and software applications
into the Web. Each new format or application potentially places new
demands on HTML and on browser vendors. For some time, it has been
clear that a general extension mechanism is necessary to accommodate
new extensions to HTML. We began our work thinking of a plain extension
to HTML in the spirit of the first math support suggested for HTML 3.2.
But for various reasons, once we got into the details this proved to be
not so good an idea. Since work first began on MathML, XML has
emerged as the leading candidate for such a general extension mechanism.
XML stands for Extensible Markup Language. It is designed as a
simplified version of SGML, the meta-language used to define the
grammar and syntax of HTML. One of the goals of XML is to be suitable
for use on the Web, and in the context of this discussion it can be
viewed as a general mechanism for extending HTML. As its name implies,
extensibility is a key feature of XML; authors are free to declare and
use new tags and attributes. At the same time, XML grammar and syntax
rules carefully enforces document structure to facilitate automatic
processing and maintenance of large document collections.
Though details about how XML markup will ultimately be embedded in
HTML remain to be resolved, XML has garnered broad industry support
including major browser vendors. Devising a standard way of embedding
XML in HTML is also important with the W3C. Furthermore, other
applications of XML for all kinds of document publishing and
processing promise to become increasingly important. Consequently,
both on theoretical and pragmatic grounds, it makes a great deal of
sense to specify MathML as an XML application, and we have done so.
Browser Extension Mechanisms
While details of a general model for rendering and processing XML
extensions to HTML is still being being resolved, broad features of
the model are already fairly clear. Formatting Properties developed
by the Cascading Style Sheets and Formatting Properties Working Group
for CSS and made
available through the Document Object Model (DOM) will be applied to MathML
elements to obtain some stylistic control over the presentation of
MathML. Further development of these Formatting Properties falls
within the charter of both the CSS&FP and the XSL working groups. Thus, it
may soon be possible to write a style sheet which will largely
describe the correct display of MathML.
MathML was designed with the goal of style sheet-based rendering in
mind. It is the intention of the W3C Math Working Group to work
closely with W3C style sheet activities to ensure both that adequate
support for MathML is incorporated into future style sheet mechanisms,
and that MathML style sheets are developed. In particular, providing
for adequate follow-on activities beyond the scope of the W3C Math
working group charter is a high priority.
Until style sheet mechanisms are capable of delivering native browser
rendering of MathML, however, it is necessary to extend browser
capabilities by using embedded elements to render MathML. It may
soon be possible to instruct a browser to use a particular embedded
renderer to process embedded XML markup such as MathML, and coordinate
the resulting output with the surrounding Web page. Indeed, for
specialized processing, such as connecting to a computer algebra
system, this capability is likely to remain highly desirable.
However, for this kind of interaction to be really satisfactory, it
will be necessary to define a document object model rich enough to
facilitate complicated interactions between browsers and embedded
elements. For this reason, the W3C Math working group is coordinating
its efforts closely with the Document Object Model working group.
For processing by embedded elements, and for inter-communication
between scientific software generally, a style sheet-based layout
model is less than ideal in some ways. It can impose an additional
implementation burden in a setting where it may offer few advantages,
and it imposes implementation requirements for coordination between
browsers and embedded renderers that will likely be unavailable in the
immediate future.
For these reasons, the MathML specification defines an
attribute-based layout model, which has proven very effective for
high-quality rendering of complicated mathematical expressions in
several independent implementations. MathML presentation attributes
utilize W3C Formatting
Properties where possible. Also, MathML elements accept class,
style and id attributes to facilitate their use with CSS style sheets.
However, at present, there are few settings where CSS machinery is
currently available to MathML renderers.
When style sheet mechanisms become available to MathML,
it is anticipated their use will become the
dominant method of stylistic control of MathML presentation meant
for use in rendering environments which support those mechanisms.
Next: MathML Fundamentals
Up: Table of Contents
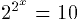 . This equation is sized to
match the surrounding line in 14pt type on the system where it
was authored. Of course, on other systems, or for other font
sizes, the equation is too small or too large. A second point
to observe is that the equation image was generated against a
white background. Thus, if a reader or browser resets the page
background to another color, the anti-aliasing in the image
results in white "halos." Next, consider the equation
. This equation is sized to
match the surrounding line in 14pt type on the system where it
was authored. Of course, on other systems, or for other font
sizes, the equation is too small or too large. A second point
to observe is that the equation image was generated against a
white background. Thus, if a reader or browser resets the page
background to another color, the anti-aliasing in the image
results in white "halos." Next, consider the equation 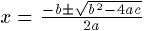 . This equation has a descender which
places the baseline for the equation at a point about a third
of the way from the bottom of the image. One can pad the image
like this:
. This equation has a descender which
places the baseline for the equation at a point about a third
of the way from the bottom of the image. One can pad the image
like this: 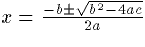 ,
so that the centerline of the image and the baseline of the
equation coincide, but this causes problems with the
inter-line spacing, which also makes the equation difficult to
read. Moreover, center alignment of images is handled in
slightly different ways by different browsers, making it
impossible to guarantee proper alignment for different
clients.
,
so that the centerline of the image and the baseline of the
equation coincide, but this causes problems with the
inter-line spacing, which also makes the equation difficult to
read. Moreover, center alignment of images is handled in
slightly different ways by different browsers, making it
impossible to guarantee proper alignment for different
clients.