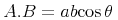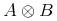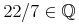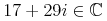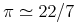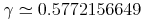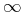4.1 Introduction
4.1.1 The Intent of Content Markup
The intent of Content Markup is to provide an explicit encoding of the underlying mathematical meaning of an expression, rather than any particular rendering for the expression. Mathematics is distinguished both by its use of rigorous formal logic to define and analyze mathematical concepts, and by the use of a (relatively) formal notational system to represent and communicate those concepts. However, mathematics and its presentation should not be viewed as one and the same thing. Mathematical notation, though more rigorous than natural language, is nonetheless at times ambiguous, context-dependent, and varies from community to community. In some cases, heuristics may adequately infer mathematical semantics from mathematical notation. But in many others cases, it is preferable to work directly with the underlying, formal, mathematical objects. Content Markup provides a rigorous, extensible semantic framework and a markup language for this purpose.
The difficulties in inferring semantics from a presentation stem
from the fact that there are many to one mappings from presentation to
semantics and vice versa. For example the mathematical construct
"H multiplied by e" is often
encoded using an explicit operator as in
H × e. In different
presentational contexts, the multiplication operator might be
invisible "H e", or rendered
as the spoken word "times". Generally, many different
presentations are possible depending on the context and style
preferences of the author or reader. Thus, given
"H e" out of context it may be
impossible to decide if this is the name of a chemical or a
mathematical product of two variables H and
e. Mathematical presentation also varies across cultures
and geographical regions. For example, many notations for long
division are in use in different parts of the world today. Notations
may lose currency, for example the use of musical sharp and flat
symbols to denote maxima and minima [Chaundy1954]. A
notation in use in 1644 for the multiplication mentioned above was
 He [Cajori1928].
He [Cajori1928].
By encoding the underlying mathematical structure explicitly, without regard to how it is presented aurally or visually, it is possible to interchange information more precisely between systems that semantically process mathematical objects. In the trivial example above, such a system could substitute values for the variables H and e and evaluate the result. Important application areas include computer algebra systems, automatic reasoning system, industrial and scientific applications, multi-lingual translation systems, mathematical search, and interactive textbooks.
The organization of this chapter is as follows. In Section 4.2 Content MathML Elements Encoding Expression Structure, a core collection of elements comprising Strict Content Markup are described. Strict Content Markup is sufficient to encode general expression trees in a semantically rigorous way. It is in one-to-one correspondence with OpenMath element set. OpenMath is a standard for representing formal mathematical objects and semantics through the use of extensible Content Dictionaries. Strict Content Markup defines a mechanism for associating precise mathematical semantics with expression trees by referencing OpenMath Content Dictionaries. The next two sections introduce markup that is more convenient than Strict markup for some purposes, somewhat less formal and verbose. In Section 4.3 Content MathML for Specific Structures, markup is introduced for representing a small number of mathematical idioms, such as limits on integrals, sums and product. These constructs may all be rewritten as Strict Content Markup expressions, and rules for doing so are given. In Section 4.4 Content MathML for Specific Operators and Constants, elements are introduced for many common function, operators and constants. This section contains many examples, including equivalent Strict Content expressions. In Section 4.5 Deprecated Content Elements, elements from MathML 1 and 2 whose use is now discouraged are listed. Finally, Section 4.6 The Strict Content MathML Transformation summarizes the algorithm for translating arbitrary Content Markup into Strict Content Markup. It collects together in sequence all the rewrite rules introduced throughout the rest of the chapter.
4.1.2 The Structure and Scope of Content MathML Expressions
Content MathML represents mathematical objects as expression trees. The notion of constructing a general expression tree is e.g. that of applying an operator to sub-objects. For example, the sum "x+y" can be thought of as an application of the addition operator to two arguments x and y. And the expression "cos(π)" as the application of the cosine function to the number π.
As a general rule, the terminal nodes in the tree represent basic mathematical objects such as numbers, variables, arithmetic operations and so on. The internal nodes in the tree represent function application or other mathematical constructions that build up a compound objects. Function application provides the most important example; an internal node might represent the application of a function to several arguments, which are themselves represented by the nodes underneath the internal node.
The semantics of general mathematical expressions is not a matter of consensus. It would be an enormous job to systematically codify most of mathematics – a task that can never be complete. Instead, MathML makes explicit a relatively small number of commonplace mathematical constructs, chosen carefully to be sufficient in a large number of applications. In addition, it provides a mechanism for referring to mathematical concepts outside of the base collection, allowing them to be represented, as well.
The base set of content elements is chosen to be adequate for simple coding of most of the formulas used from kindergarten to the end of high school in the United States, and probably beyond through the first two years of college, that is up to A-Level or Baccalaureate level in Europe.
While the primary role of the MathML content element set is to directly encode the mathematical structure of expressions independent of the notation used to present the objects, rendering issues cannot be ignored. There are different approaches for rendering Content MathML formulae, ranging from native implementations of the MathML elements to declarative notation definitions, to XSLT style sheets. Because rendering requirements for Content MathML vary widely, MathML 3 does not provide a normative specification for rendering. Instead, typical renderings are suggested by way of examples.
4.1.3 Strict Content MathML
In MathML 3, a subset, or profile, of Content MathML is defined: Strict Content MathML. This uses a minimal, but sufficient, set of elements to represent the meaning of a mathematical expression in a uniform structure, while the full Content MathML grammar is backward compatible with MathML 2.0, and generally tries to strike a more pragmatic balance between verbosity and formality.
Content MathML provides a large number of predefined functions
encoded as empty elements (e.g. sin, log, etc.)
and a variety of constructs for forming compound objects
(e.g. set, interval, etc.). By contrast, Strict
Content MathML uses a single element (csymbol) with an
attribute pointing to an external definition in extensible content
dictionaries to represent all functions, and uses only
apply and bind for building up compound
objects. The token elements such as ci and cn are
also considered part of Strict Content MathML, but with a more
restricted set of attributes and with content restricted to
text.
Strict Content MathML is designed to be compatible with OpenMath (in fact it is an XML encoding of OpenMath Objects in the sense of [OpenMath2004]). OpenMath is a standard for representing formal mathematical objects and semantics through the use of extensible Content Dictionaries. The table below gives an element-by-element correspondence between the OpenMath XML encoding of OpenMath objects and Strict Content MathML.
| Strict Content MathML | OpenMath |
|---|---|
cn |
OMI, OMF |
csymbol |
OMS |
ci |
OMV |
cs |
OMSTR |
apply |
OMA |
bind |
OMBIND |
bvar |
OMBVAR |
share |
OMR |
semantics |
OMATTR |
annotation,
annotation-xml |
OMATP, OMFOREIGN |
error |
OME |
cbytes |
OMB |
In MathML 3, formal semantics Content MathML expressions are given by specifying equivalent Strict Content MathML expressions. Since Strict Content MathML expressions all have carefully-defined semantics given in terms of OpenMath Content Dictionaries, all Content MathML expressions inherit well-defined semantics in this way. To make the correspondence exact, an algorithm is given in terms of transformation rules that are applied to rewrite non-Strict MathML constructs into a strict equivalents. The individual rules are introduced in context throughout the chapter. In Section 4.6 The Strict Content MathML Transformation, the algorithm as a whole is described.
As most transformation rules relate to classes of MathML elements that have similar argument structure, they are introduced in Section 4.3.4 Operator Classes where these classes are defined. Some special case rules for specific elements are given in Section Section 4.4 Content MathML for Specific Operators and Constants. Transformations in Section 4.2 Content MathML Elements Encoding Expression Structure concern non-Strict usages of the core Content MathML elements, those in Section 4.3 Content MathML for Specific Structures concern the rewriting of some additional structures not directly supported in Strict Content MathML.
The full algorithm described inSection 4.6 The Strict Content MathML Transformation is complete in the sense that it gives every Content MathML expression a specific meaning in terms of a Strict Content MathML expression. This means it has to give specific strict interpretations to some expressions whose meaning was insufficiently specified in MathML2. The intention of this algorithm is to be faithful to mathematical intuitions. However edge cases may remain where the normative interpretation of the algorithm may break earlier intuitions.
A conformant MathML processor need not implement this transformation. The existence of these transformation rules does not imply that a system must treat equivalent expressions identically. In particular systems may give different presentation renderings for expressions that the transformation rules imply are mathematically equivalent.
4.1.4 Content Dictionaries
Due to the nature of mathematics, any method for formalizing
the meaning of the mathematical expressions must be
extensible. The key to extensibility is the ability to define
new functions and other symbols to expand the terrain of
mathematical discourse. To do this, two things are required: a
mechanism for representing symbols not already defined by
Content MathML, and a means of associating a specific
mathematical meaning with them in an unambiguous way. In MathML
3, the csymbol element provides the means to represent
new symbols, while Content Dictionaries are the way
in which mathematical semantics are described. The association
is accomplished via attributes of the csymbol element
that point at a definition in a CD. The syntax and usage of
these attributes are described in detail in Section 4.2.3 Content Symbols <csymbol>.
Content Dictionaries are structured documents for the definition of mathematical concepts; see the OpenMath standard, [OpenMath2004]. To maximize modularity and reuse, a Content Dictionary typically contains a relatively small collection of definitions for closely related concepts. The OpenMath Society maintains a large set of public Content Dictionaries including the MathML CD group that including contains definitions for all pre-defined symbols in MathML. There is a process for contributing privately developed CDs to the OpenMath Society repository to facilitate discovery and reuse. MathML 3 does not require CDs be publicly available, though in most situations the goals of semantic markup will be best served by referencing public CDs available to all user agents.
In the text below, descriptions of semantics for predefined MathML symbols refer to the Content Dictionaries developed by the OpenMath Society in conjunction with the W3C Math Working Group. It is important to note, however, that this information is informative, and not normative. In general, the precise mathematical semantics of predefined symbols are not not fully specified by the MathML 3 Recommendation, and the only normative statements about symbol semantics are those present in the text of this chapter. The semantic definitions provided by the OpenMath Content CDs are intended to be sufficient for most applications, and are generally compatible with the semantics specified for analogous constructs in the MathML 2.0 Recommendation. However, in contexts where highly precise semantics are required (e.g. communication between computer algebra systems, within formal systems such as theorem provers, etc.) it is the responsibility of the relevant community of practice to verify, extend or replace definitions provided by OpenMath CDs as appropriate.
4.1.5 Content MathML Concepts
The basic building blocks of Content MathML expressions are numbers, identifiers and symbols. These building blocks are combined using function applications and binding operators. It is important to have a basic understanding of these key mathematical concepts, and how they are reflected in the design of Content MathML. For the convenience of the reader, these concepts are reviewed here.
In the expression "x+y",
x is a mathematical variable, meaning an identifier that
represents a quantity with no fixed value. It may have other
properties, such as being an integer, but its value is not a fixed
property. By contrast, the plus sign is an identifier that represents a
fixed and externally defined object, namely the addition function.
Such an identifier is termed a symbol, to distinguish it
from a variable. Common elementary functions and operators all have
fixed, external definitions, and are hence symbols. Content MathML
uses the ci element to represent variables, and the
csymbol to represent symbols.
The most fundamental way in which symbols and variables are
combined is function application. Content MathML makes a crucial
semantic distinction between a function itself (a symbol such as the
sine function, or a variable such as f) and the result of
applying the function to arguments. The apply element groups the function
with its arguments syntactically, and represents the expression
resulting from applying that function to its arguments.
Mathematically, variables are divided into bound and
free variables. Bound variables are variables that are
assigned a special role by a binding operator within a certain scope.
For example, the index variable within a summation is a bound
variable. They can be characterized as variables with the property
that they can be renamed consistently throughout the binding scope
without changing the underlying meaning of the expression. Variables
that are not bound are termed free variables.
Because the logical distinction between bound and free variables is
important for well-defined semantics, Content MathML differentiates
between the application of a function to a free variable,
e.g. f(x) and the operation of binding a
variable within a scope. The bind element is used the delineate
the binding scope, and group the binding operator with its bound
variables, which are indicated by the bvar element.
In Strict Content markup, the bind element is the only way
of performing variable binding. In non-Strict usage, however, markup
is provided that more closely resembles well-known idiomatic
notations, such as the "limit" notations for sums and
integrals. These constructs often implicitly bind variables, such as
the variable of integration, or the index variable in a sum. MathML
terms the elements used to represent the auxiliary data such as limits
required by these constructions qualifier elements.
Expressions involving qualifiers follow one of a small number of idiomatic patterns, each of which applies to class of similar binding operators. For example, sums and products are in the same class because they use index variables following the same pattern. The Content MathML operator classes are described in detail in Section 4.3.4 Operator Classes.
Each Content MathML element is described in a section below that
begins with a table summarizing the key information about the element.
For elements that have different Strict and non-Strict
usage, these syntax tables are divided to clearly separate the two cases. The element's content
model is given in the Content row, linked to the MathML
Schema in Appendix A Parsing MathML. The Attributes, and
Attribute Values rows similarly link to the schema. Where
applicable, the Class row specifies the operator class, which
indicate how many arguments the operator represented by this element
takes, and also in many cases determines the mapping to Strict Content
MathML, as described in Section 4.3.4 Operator Classes. Finally,
the Qualifiers row clarifies whether the operator takes
qualifiers and if so, which. Both specify how many siblings may follow
the operator element in an apply; see Section 4.2.5 Function Application <apply> and Section 4.3.3 Qualifiers for
details).
4.2 Content MathML Elements Encoding Expression Structure
In this section we will present the elements for encoding the structure of content MathML expressions. These elements are the only ones used for the Strict Content MathML encoding. Concretely, we have
-
basic expressions, i.e. Numbers, string literals, encoded bytes, Symbols, and Identifiers.
-
derived expressions, i.e. function applications and binding expressions, and
Full Content MathML allows further elements presented in Section 4.3 Content MathML for Specific Structures and Section 4.4 Content MathML for Specific Operators and Constants, and allows a richer content model presented in this section. Differences in Strict and non-Strict usage of are highlighted in the sections discussing each of the Strict element below.
4.2.1 Numbers <cn>
| Schema Fragment (Strict) | Schema Fragment (Full) | |||
|---|---|---|---|---|
| Class | Cn | Cn | ||
| Attributes | CommonAtt, type | CommonAtt, DefEncAtt, type?, base? | ||
type Attribute Values
|
"integer" | "real" | "double" | "hexdouble" | "integer" | "real" | "double" | "hexdouble" | "e-notation" | "rational" | "complex-cartesian" | "complex-polar" | "constant" | text | default is real | |
base Attribute Values
|
integer | default is 10 | ||
| Content | text | (text | mglyph | sep | PresentationExpression)* | ||
The cn element is the Content MathML element used to
represent numbers. Strict Content MathML supports integers, real numbers,
and double precision floating point numbers. In these types of numbers,
the content of cn is text. Additionally, cn
supports rational numbers and complex numbers in which the different
parts are separated by use of the sep element. Constructs
using sep may be rewritten in Strict Content MathML as
constructs using apply as described below.
The type attribute specifies which kind of number is
represented in the cn element. The default value is
"real". Each type implies that the content be of
a certain form, as detailed below.
4.2.1.1 Rendering <cn>-Represented Numbers
The default rendering of the text content of cn is the same as that of the Presentation element mn, with suggested variants in the
case of attributes or sep being used, as listed below.
4.2.1.2 Strict uses of <cn>
In Strict Content MathML, the type attribute is mandatory, and may only take the values
"integer", "real", "hexdouble" or
"double":
- integer
- An integer is represented by an optional sign followed by a string of one or more decimal "digits".
- real
- A real number is presented in radix notation. Radix notation consists of an optional sign ("+" or "-") followed by a string of digits possibly separated into an integer and a fractional part by a decimal point. Some examples are 0.3, 1, and -31.56.
- double
- This type is used to mark up those double-precision
floating point numbers that can be represented in the IEEE 754
standard format [IEEE754]. This includes a subset of the (mathematical) real
numbers, negative zero, positive and negative real infinity
and a set of "not a number" values. The lexical rules for
interpreting the text content of a
cnas an IEEE double are specified by Section 3.1.2.5 of XML Schema Part 2: Datatypes Second Edition [XMLSchemaDatatypes]. For example, -1E4, 1267.43233E12, 12.78e-2, 12 , -0, 0 and INF are all valid doubles in this format. - hexdouble
-
This type is used to directly represent the 64 bits of an IEEE 754 double-precision floating point number as a 16 digit hexadecimal number. Thus the number represents mantissa, exponent, and sign from lowest to highest bits using a least significant byte ordering. This consists of a string of 16 digits 0-9, A-F. The following example represents a NaN value. Note that certain IEEE doubles, such as the NaN in the example, cannot be represented in the lexical format for the "double" type.
<cn type="hexdouble">7F800000</cn>
Sample Presentation
<mn>0x7F800000</mn>
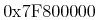
4.2.1.3 Non-Strict uses of <cn>
The base attribute is used to specify how the content is
to be parsed. The attribute value is a base 10 positive integer
giving the value of base in which the text content of the cn
is to be interpreted. The base attribute should only be
used on elements with type "integer" or
"real". Its use on cn elements of other type
is deprecated. The default value for base is
"10".
Additional values for the type attribute element for supporting
e-notations for real numbers, rational numbers, complex numbers and selected important
constants. As with the "integer", "real",
"double" and "hexdouble" types, each of these types
implies that the content be of a certain form. If the type attribute is
omitted, it defaults to "real".
- integer
-
Integers can be represented with respect to a base different from 10: If
baseis present, it specifies (in base 10) the base for the digit encoding. Thusbase='16' specifies a hexadecimal encoding. Whenbase> 10, Latin letters (A-Z, a-z) are used in alphabetical order as digits. The case of letters used as digits is not significant. The following example encodes the base 10 number 32736.<cn base="16">7FE0</cn>
Sample Presentation
<msub><mn>7FE0</mn><mn>16</mn></msub>
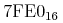
When
base> 36, some integers cannot be represented using numbers and letters alone. For example, while<cn base="1000">10F</cn>
arguably represents the number written in base 10 as 1,000,015, the number written in base 10 as 1,000,037 cannot be represented using letters and numbers alone when
baseis 1000. Consequently, support for additional characters (if any) that may be used for digits whenbase> 36 is application specific. - real
- Real numbers can be represented with respect to a base
different than 10. If a
baseattribute is present, then the digits are interpreted as being digits computed relative to that base (in the same way as described for type "integer"). - e-notation
-
A real number may be presented in scientific notation using this type. Such numbers have two parts (a significand and an exponent) separated by a
<sep/>element. The first part is a real number, while the second part is an integer exponent indicating a power of the base.For example,
<cn type="e-notation">12.3<sep/>5</cn>represents 12.3 times 105. The default presentation of this example is 12.3e5. Note that this type is primarily useful for backwards compatibility with MathML 2, and in most cases, it is preferable to use the "double" type, if the number to be represented is in the range of IEEE doubles: - rational
-
A rational number is given as two integers to be used as the numerator and denominator of a quotient. The numerator and denominator are separated by
<sep/>.<cn type="rational">22<sep/>7</cn>
Sample Presentation
<mrow><mn>22</mn><mo>/</mo><mn>7</mn></mrow>
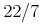
- complex-cartesian
-
A complex cartesian number is given as two numbers specifying the real and imaginary parts. The real and imaginary parts are separated by the
<sep/>element, and each part has the format of a real number as described above.<cn type="complex-cartesian"> 12.3 <sep/> 5 </cn>
Sample Presentation
<mrow> <mn>12.3</mn><mo>+</mo><mn>5</mn><mo>⁢</mo><mi>i</mi> </mrow>
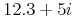
- complex-polar
-
A complex polar number is given as two numbers specifying the magnitude and angle. The magnitude and angle are separated by the
<sep/>element, and each part has the format of a real number as described above.<cn type="complex-polar"> 2 <sep/> 3.1415 </cn>
Sample Presentation
<mrow> <mn>2</mn> <mo>⁢</mo> <msup> <mi>e</mi> <mrow><mi>i</mi><mo>⁢</mo><mn>3.1415</mn></mrow> </msup> </mrow>
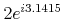
<mrow> <mi>Polar</mi> <mo>⁡</mo> <mfenced><mn>2</mn><mn>3.1415</mn></mfenced> </mrow>
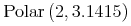
- constant
-
If the value
typeis "constant", then the content should be a Unicode representation of a well-known constant. Some important constants and their common Unicode representations are listed below.This
cntype is primarily for backward compatibility with MathML 1.0. MathML 2.0 introduced many empty elements, such as<pi/>to represent constants, and using these representations or a Strict csymbol representation is preferred.
In addition to the additional values of the type attribute, the
content of cn element can contain (in addition to the
sep element allowed in Strict Content MathML) mglyph
elements to refer to characters not currently available in Unicode, or
a general presentation construct (see Section 3.1.9 Summary of Presentation Elements),
which is used for rendering (see Section 4.1.2 The Structure and Scope of Content MathML Expressions).
Mapping to Strict Content MathML
If a base attribute is present, it specifies the base used for the digit
encoding of both integers. The use of base with
"rational" numbers is deprecated.
Rewrite: cn sep
If there are sep children of the cn,
then intervening text may be rewritten as cn
elements. If the cn element containing sep
also has a base attribute, this is copied to each
of the cn arguments of the resulting symbol, as
shown below.
<cn type="" base=""><sep/></cn>
is rewritten to
<apply><csymbol cd=""></csymbol> <cn type="integer" base=""></cn> <cn type="integer" base=""></cn> </apply>
The symbol used in the result depends on the type attribute according to the following table:
| type attribute | OpenMath Symbol |
|---|---|
| e-notation | bigfloat |
| rational | rational |
| complex-cartesian | complex_cartesian |
| complex-polar | complex_polar |
Note: In the case of bigfloat the symbol
takes three arguments, <cn type="integer">10</cn> should be inserted as the second argument, denoting the base of the exponent used.
If the type attribute has a different value, or if there is more than one <sep/> element, then the intervening expressions are converted as above, but a system-dependent choice of symbol for the head of
the application must be used.
If a base attribute has been used then the resulting expression is not Strict Content MathML, and each of the arguments needs to be recursively processed.
Rewrite: cn based_integer
A cn element with a base attribute other than 10 is rewritten as follows. (A base attribute with value 10 is simply removed) .
<cn type="" base=""></cn>
<apply><csymbol cd="nums1"></csymbol> <cn type="integer"></cn> <cs></cs> </apply>
If the original element specified type "integer" or if there is no type attribute, but the content of the element just consists of the characters [a-zA-Z0-9] and white space then the symbol used as the head in the resulting application should be based_integer as shown. Otherwise it should be should be based_float.
Rewrite: cn constant
In Strict Content MathML, constants should be represented using
csymbol elements. A number of important constants are defined in the
nums1 content dictionary. An expression of the form
<cn type="constant"></cn>has the Strict Content MathML equivalent
<csymbol cd="nums1"></csymbol>
where c2 corresponds to c as specified in the following table.
| Content | Description | OpenMath Symbol |
|---|---|---|
U+03C0 (π)
|
The usual π of trigonometry: approximately 3.141592653... | pi |
U+2147 (ⅇ or ⅇ)
|
The base for natural logarithms: approximately 2.718281828... | e |
U+2148 (ⅈ or ⅈ)
|
Square root of -1 | i |
U+03B3 (γ)
|
Euler's constant: approximately 0.5772156649... | gamma |
U+221E (∞ or &infty;)
|
Infinity. Proper interpretation varies with context | infinity |
Rewrite: cn presentation mathml
If the cn contains Presentation MathML markup, then it may
be rewritten to Strict MathML using variants of the rules above where
the arguments of the constructor are ci elements annotated
with the supplied Presentation MathML.
A cn expression with non-text content of the form
<cn type=""> <sep/> </cn>
is transformed to Strict Content MathML by rewriting it to
<apply><csymbol cd=""></csymbol> <semantics> <ci></ci> <annotation-xml encoding="MathML-Presentation"> </annotation-xml> </semantics> <semantics> <ci></ci> <annotation-xml encoding="MathML-Presentation"> </annotation-xml> </semantics> </apply>
Where the identifier names, p and q, (which have to be a text string) should be
determined from the presentation MathML content, in a system defined way, perhaps as
in the above example by taking the character data of the element ignoring any element
markup. Systems doing such rewriting should ensure that constructs using the same
Presentation MathML content are rewritten to semantics elements using the
same ci, and that conversely constructs that use different MathML should be
rewritten to different identifier names (even if the Presentation MathML has the same character data).
A related special case arises when a cn element
contains character data not permitted in Strict Content MathML
usage, e.g. non-digit, alphabetic characters. Conceptually, this is
analogous to a cn element containing a presentation
markup mtext element, and could be rewritten accordingly.
However, since the resulting annotation would contain no additional
rendering information, such instances should be rewritten directly
as ci elements, rather than as a semantics
construct.
4.2.2 Content Identifiers <ci>
| Schema Fragment (Strict) | Schema Fragment (Full) | |
|---|---|---|
| Class | Ci | Ci |
| Attributes | CommonAtt, type? | CommonAtt, DefEncAtt, type? |
type Attribute Values
|
"integer"| "rational"| "real"| "complex"| "complex-polar"| "complex-cartesian"| "constant"| "function"| "vector"| "list"| "set"| "matrix" | string |
| Qualifiers | BvarQ, DomainQ, degree, momentabout, logbase | |
| Content | text | text | mglyph | PresentationExpression |
Content MathML uses the ci element (mnemonic for "content
identifier") to construct a variable. Content identifiers
represent "mathematical variables" which have
properties, but no fixed value. For example, x and y are variables
in the expression "x+y", and the variable
x would be represented as
<ci>x</ci>
In MathML, variables are distinguished from symbols, which have fixed, external definitions, and are represented by the csymbol element.
After white space normalization the content of a ci element is interpreted as a
name that identifies it. Two variables are considered equal, if and only if their names
are identical and in the same scope (see Section 4.2.6 Bindings and Bound Variables <bind>
and <bvar> for a
discussion).
4.2.2.1 Strict uses of <ci>
The ci element uses the type attribute to specify the basic type of
object that it represents. In Strict Content MathML, the set of permissible values is
"integer", "rational", "real",
"complex", "complex-polar",
"complex-cartesian", "constant", "function",
vector, list, set, and matrix. These values correspond
to the symbols
integer_type,
rational_type,
real_type,
complex_polar_type,
complex_cartesian_type,
constant_type,
fn_type,
vector_type,
list_type,
set_type, and
matrix_type in the
mathmltypes Content Dictionary: In this sense the following two expressions are considered equivalent:
<ci type="integer">n</ci>
<semantics>
<ci>n</ci>
<annotation-xml cd="mathmltypes" name="type" encoding="MathML-Content">
<csymbol cd="mathmltypes">integer_type</csymbol>
</annotation-xml>
</semantics>4.2.2.2 Non-Strict uses of <ci>
The ci element allows any string value for the type
attribute, in particular any of the names of the MathML container elements or their type
values.
For a more advanced treatment of types, the type attribute is
inappropriate. Advanced types require significant structure of their own (for example,
vector(complex)) and are probably best constructed as mathematical objects and
then associated with a MathML expression through use of the semantics
element. See [MathMLTypes] for more examples.
Mapping to Strict Content MathML
Rewrite: ci type annotation
In Strict Content, type attributes are represented via semantic attribution. An expression of the form
<ci type=""></ci>
is rewritten to
<semantics> <ci></ci> <annotation-xml cd="mathmltypes" name="type" encoding="MathML-Content"> <ci></ci> </annotation-xml> </semantics>
The ci element can contain
mglyph elements to refer to characters not currently available in Unicode, or a
general presentation construct (see Section 3.1.9 Summary of Presentation Elements), which is used for
rendering (see Section 4.1.2 The Structure and Scope of Content MathML Expressions).
Rewrite: ci presentation mathml
A ci expression with non-text content of the form
<ci> </ci>is transformed to Strict Content MathML by rewriting it to
<semantics> <ci></ci> <annotation-xml encoding="MathML-Presentation"> </annotation-xml> </semantics>
Where the identifier name, p, (which has to be a text string) should be
determined from the presentation MathML content, in a system defined way, perhaps as
in the above example by taking the character data of the element ignoring any element
markup. Systems doing such rewriting should ensure that constructs using the same
Presentation MathML content are rewritten to semantics elements using the
same ci, and that conversely constructs that use different MathML should be
rewritten to different identifier names (even if the Presentation MathML has the same character data).
The following example encodes an atomic symbol that displays visually as C2 and that, for purposes of content, is treated as a single symbol
<ci> <msup><mi>C</mi><mn>2</mn></msup> </ci>
The Strict Content MathML equivalent is
<semantics>
<ci>C2</ci>
<annotation-xml encoding="MathML-Presentation">
<msup><mi>C</mi><mn>2</mn></msup>
</annotation-xml>
</semantics>Sample Presentation
<msup><mi>C</mi><mn>2</mn></msup>
4.2.2.3 Rendering Content Identifiers
If the content of a ci element consists of Presentation MathML, that
presentation is used. If no such tagging is supplied then the text
content is rendered as if it were the content of an mi element. If an
application supports bidirectional text rendering, then the rendering follows the
Unicode bidirectional rendering.
The type attribute can be interpreted to
provide rendering information. For example in
<ci type="vector">V</ci>
a renderer could display a bold V for the vector.
4.2.3 Content Symbols <csymbol>
| Schema Fragment (Strict) | Schema Fragment (Full) | |
|---|---|---|
| Class | Csymbol | Csymbol |
| Attributes | CommonAtt, cd | CommonAtt, DefEncAtt, type?, cd? |
| Content | SymbolName | text | mglyph | PresentationExpression |
| Qualifiers | BvarQ, DomainQ, degree, momentabout, logbase |
A csymbol is used to refer to a specific,
mathematically-defined concept with an external definition. In the
expression "x+y", the plus sign is
a symbol since it has a specific, external definition, namely the addition function.
MathML 3 calls such an identifier a
symbol. Elementary functions and common mathematical
operators are all examples of symbols. Note that the term
"symbol" is used here in an abstract sense and has no
connection with any particular presentation of the construct on screen
or paper.
4.2.3.1 Strict uses of <csymbol>
The csymbol identifies the specific mathematical concept
it represents by referencing its definition via attributes.
Conceptually, a reference to an external definition is merely a URI,
i.e. a label uniquely identifying the definition. However, to be
useful for communication between user agents, external definitions
must be shared.
For this reason, several longstanding efforts have been organized to develop systematic, public repositories of mathematical definitions. Most notable of these, the OpenMath Society repository of Content Dictionaries (CDs) is extensive, open and active. In MathML 3, OpenMath CDs are the preferred source of external definitions. In particular, the definitions of pre-defined MathML 3 operators and functions are given in terms of OpenMath CDs.
MathML 3 provides two mechanisms for referencing external definitions or content
dictionaries. The first, using the cd attribute, follows conventions
established by OpenMath specifically for referencing CDs. This is the
form required in Strict Content MathML. The second, using the
definitionURL attribute, is backward compatible with MathML 2, and can be used
to reference CDs or any other source of definitions that can be
identified by a URI. It is described in the following section
When referencing OpenMath CDs, the preferred method is to use the cd
attribute as follows. Abstractly, OpenMath symbol definitions are identified by a triple
of values: a symbol name, a CD name, and a CD base,
which is a URI that disambiguates CDs of the same name. To associate such a triple with a
csymbol, the content of the csymbol specifies the symbol name, and the
name of the Content Dictionary is given using the cd attribute. The CD base is
determined either from the document embedding the math element which contains the
csymbol by a mechanism given by the embedding document format, or by system
defaults, or by the cdgroup attribute , which is optionally specified on the
enclosing math element; see Section 2.2.1 Attributes. In the absence
of specific information http://www.openmath.org/cd is assumed as the CD base
for all csymbol elements annotation, and annotation-xml. This
is the CD base for the collection of standard CDs maintained by the OpenMath Society.
The cdgroup specifies a URL to an OpenMath CD Group file. For a detailed
description of the format of a CD Group file, see Section 4.4.2 (CDGroups)
in [OpenMath2004]. Conceptually, a CD group file is a list of
pairs consisting of a CD name, and a corresponding CD base. When a csymbol
references a CD name using the cd attribute, the name is looked up in the CD
Group file, and the associated CD base value is used for that csymbol. When a CD
Group file is specified, but a referenced CD name does not appear in the group file, or
there is an error in retrieving the group file, the referencing csymbol is not
defined. However, the handling of the resulting error is not defined, and is the
responsibility of the user agent.
While references to external definitions are URIs, it is strongly recommended that CD files be retrievable at the location obtained by interpreting the URI as a URL. In particular, other properties of the symbol being defined may be available by inspecting the Content Dictionary specified. These include not only the symbol definition, but also examples and other formal properties. Note, however, that there are multiple encodings for OpenMath Content Dictionaries, and it is up to the user agent to correctly determine the encoding when retrieving a CD.
4.2.3.2 Non-Strict uses of <csymbol>
In addition to the forms described above, the csymbol and element can contain
mglyph elements to refer to characters not currently available in Unicode, or a
general presentation construct (see Section 3.1.9 Summary of Presentation Elements), which is used for
rendering (see Section 4.1.2 The Structure and Scope of Content MathML Expressions). In this case, when
writing to Strict Content MathML, the csymbol should be treated as a
ci element, and rewritten using Rewrite: ci presentation mathml.
External definitions (in OpenMath CDs or elsewhere) may also be specified directly for
a csymbol using the definitionURL attribute. When used to reference
OpenMath symbol definitions, the abstract triple of (symbol name, CD name, CD base) is
mapped to a fully-qualified URI as follows:
URI =cdbase+ '/' +cd-name+ '#' +symbol-name
For example,
(plus, arith1, http://www.openmath.org/cd)
is mapped to
http://www.openmath.org/cd/arith1#plus
The resulting URI is specified as the value of the definitionURL attribute.
This form of reference is useful for backwards compatibility with MathML2 and to
facilitate the use of Content MathML within URI-based frameworks (such as RDF [rdf] in the Semantic Web or OMDoc [OMDoc1.2]). Another benefit is
that the symbol name in the CD does not need to correspond to the content of the
csymbol element. However, in general, this method results in much longer MathML
instances. Also, in situations where CDs are under development, the use of a CD Group
file allows the locations of CDs to change without a change to the markup. A third
drawback to definitionURL is that unlike the cd attribute, it is not
limited to referencing symbol definitions in OpenMath content dictionaries. Hence, it is
not in general possible for a user agent to automatically determine the proper
interpretation for definitionURL values without further information about the
context and community of practice in which the MathML instance occurs.
Both the cd and definitionURL mechanisms of external reference
may be used within a single MathML instance. However, when both a cd and a
definitionURL attribute are specified on a single csymbol, the
cd attribute takes precedence.
Mapping to Strict Content MathML
In non-Strict usage csymbol allows the use of
a type attribute.
Rewrite: csymbol type annotation
In Strict Content, type attributes are represented via semantic attribution. An expression of the form
<csymbol type="">symbolname</csymbol>is rewritten to
<semantics>
<csymbol>symbolname</csymbol>
<annotation-xml cd="mathmltypes" name="type" encoding="MathML-Content">
<ci></ci>
</annotation-xml>
</semantics>4.2.3.3 Rendering Symbols
If the content of a csymbol element is tagged using presentation tags,
that presentation is used. If no such tagging is supplied then the text
content is rendered as if it were the content of an mi element. In
particular if an application supports bidirectional text rendering, then the
rendering follows the Unicode bidirectional rendering.
4.2.4 String Literals <cs>
| Schema Fragment (Strict) | Schema Fragment (Full) | |
|---|---|---|
| Class | Cs | Cs |
| Attributes | CommonAtt | CommonAtt, DefEncAtt |
| Content | text | text |
The cs element encodes "string literals"
which may be used in Content MathML expressions.
The content of cs is text; no
Presentation MathML constructs are allowed even when used in
non-strict markup. Specifically, cs may not contain
mglyph elements, and the content does not undergo white space
normalization.
Content MathML
<set> <cs>A</cs><cs>B</cs><cs> </cs> </set>
Sample Presentation
<mrow>
<mo>{</mo>
<ms>A</ms>
<mo>,</mo>
<ms>B</ms>
<mo>,</mo>
<ms>  </ms>
<mo>}</mo>
</mrow>4.2.5 Function Application <apply>
| Schema Fragment (Strict) | Schema Fragment (Full) | |||
|---|---|---|---|---|
| Class | Apply | Apply | ||
| Attributes | CommonAtt | CommonAtt, DefEncAtt | ||
| Content | ContExp+ | ContExp+ | (ContExp, BvarQ, Qualifier?, ContExp*) | ||
The most fundamental way of building a compound object in mathematics is by applying a function or an operator to some arguments.
4.2.5.1 Strict Content MathML
In MathML, the apply element is used to build an expression tree that
represents the application a function or operator to its arguments. The
resulting tree corresponds to a complete mathematical expression. Roughly
speaking, this means a piece of mathematics that could be surrounded by
parentheses or "logical brackets" without changing its meaning.
For example, (x + y) might be encoded as
<apply><csymbol cd="arith1">plus</csymbol><ci>x</ci><ci>y</ci></apply>
The opening and closing tags of apply specify exactly the scope of any
operator or function. The most typical way of using apply is simple and
recursive. Symbolically, the content model can be described as:
<apply> op [ a b ...] </apply>
where the operands a, b, ... are MathML
expression trees themselves, and op is a MathML expression tree that
represents an operator or function. Note that apply constructs can be
nested to arbitrary depth.
An apply may in principle have any number of operands. For example,
(x + y + z) can be encoded as
<apply><csymbol cd="arith1">plus</csymbol> <ci>x</ci> <ci>y</ci> <ci>z</ci> </apply>
Note that MathML also allows applications without operands, e.g. to represent functions like random(), or current-date().
Mathematical expressions involving a mixture of operations result in nested
occurrences of apply. For example, a x + b
would be encoded as
<apply><csymbol cd="arith1">plus</csymbol>
<apply><csymbol cd="arith1">times</csymbol>
<ci>a</ci>
<ci>x</ci>
</apply>
<ci>b</ci>
</apply>There is no need to introduce parentheses or to resort to
operator precedence in order to parse expressions correctly. The
apply tags provide the proper grouping for the re-use
of the expressions within other constructs. Any expression
enclosed by an apply element is well-defined, coherent
object whose interpretation does not depend on the surrounding
context. This is in sharp contrast to presentation markup,
where the same expression may have very different meanings in
different contexts. For example, an expression with a visual
rendering such as (F+G)(x)
might be a product, as in
<apply><csymbol cd="arith1">times</csymbol>
<apply><csymbol cd="arith1">plus</csymbol>
<ci>F</ci>
<ci>G</ci>
</apply>
<ci>x</ci>
</apply>or it might indicate the application of the function F + G to the argument x. This is indicated by constructing the sum
<apply><csymbol cd="arith1">plus</csymbol><ci>F</ci><ci>G</ci></apply>
and applying it to the argument x as in
<apply>
<apply><csymbol cd="arith1">plus</csymbol>
<ci>F</ci>
<ci>G</ci>
</apply>
<ci>x</ci>
</apply>
In both cases, the interpretation of the outer apply is
explicit and unambiguous, and does not change regardless of
where the expression is used.
The preceding example also illustrates that in an
apply construct, both the function and the arguments
may be simple identifiers or more complicated expressions.
The apply element is conceptually necessary in order to distinguish
between a function or operator, and an instance of its use. The expression
constructed by applying a function to 0 or more arguments is always an element from
the codomain of the function. Proper usage depends on the operator that is being
applied. For example, the plus operator may have zero or more arguments,
while the minus operator requires one or two arguments in order to be properly
formed.
4.2.5.2 Rendering Applications
Strict Content MathML applications are rendered as mathematical
function applications. If
denotes the rendering of
and
the rendering of
, the the sample
rendering of a simple application is as follows:
Content MathML
<apply> </apply>
Sample Presentation
<mrow> <mo>⁡</mo> <mrow> <mo fence="true">(</mo> <mo separator="true">,</mo> <mo separator="true">,</mo> <mo separator="true">,</mo> <mo fence="true">)</mo> </mrow> </mrow>
Non-Strict MathML applications may also be used with qualifiers. In the absence of
any more specific rendering rules for well-known operators, rendering
should follow the sample presentation below, motivated by the typical
presentation for sum. Let
denote the rendering of
,
the rendering of
, and so on. Then:
Content MathML
<apply> <bvar> </bvar> <domainofapplication> </domainofapplication> </apply>
Sample Presentation
<mrow> <munder> <mrow> <mo>∈</mo><!--ELEMENT OF--> </mrow> </munder> <mo>⁡</mo><!--FUNCTION APPLICATION--> <mrow> <mo fence="true">(</mo> <mo fence="true">)</mo> </mrow> </mrow>
4.2.6 Bindings and Bound Variables <bind>
and <bvar>
Many complex mathematical expressions are constructed with the use of bound variables, and bound variables are an important concept of logic and formal languages. Variables become bound in the scope of an expression through the use of a quantifier. Informally, they can be thought of as the "dummy variables" in expressions such as integrals, sums, products, and the logical quantifiers "for all" and "there exists". A bound variable is characterized by the property that systematically renaming the variable (to a name not already appearing in the expression) does not change the meaning of the expression.
4.2.6.1 Bindings
| Schema Fragment (Strict) | Schema Fragment (Full) | |
|---|---|---|
| Class | Bind | Bind |
| Attributes | CommonAtt | CommonAtt, DefEncAtt |
| Content | ContExp, BvarQ*, ContExp | ContExp, BvarQ*, Qualifier*, ContExp+ |
Binding expressions are represented as MathML expression trees using the bind
element. Its first child is a MathML expression that represents a binding operator, for
example integral operator. This is followed by a non-empty list of bvar
elements denoting the bound variables, and then the final child which is a general
Content MathML expression, known as the body of the binding.
4.2.6.2 Bound Variables
| Schema Fragment (Strict) | Schema Fragment (Full) | |
|---|---|---|
| Class | BVar | BVar |
| Attributes | CommonAtt | CommonAtt, DefEncAtt |
| Content | ci | semantics-ci | (ci | semantics-ci), degree? | degree?, (ci | semantics-ci |
The bvar element is used to denote the bound variable of a binding
expression, e.g. in sums, products, and quantifiers or user defined functions.
The content of a bvar element is an annotated variable,
i.e. either a content identifier represented by a ci element or a
semantics element whose first child is an annotated variable. The
name of an annotated variable of the second kind is the name of its first
child. The name of a bound variable is that of the annotated variable
in the bvar element.
Bound variables are identified by comparing their names. Such
identification can be made explicit by placing an id on the ci
element in the bvar element and referring to it using the xref
attribute on all other instances. An example of this approach is
<bind><csymbol cd="quant1">forall</csymbol>
<bvar><ci id="var-x">x</ci></bvar>
<apply><csymbol cd="relation1">lt</csymbol>
<ci xref="var-x">x</ci>
<cn>1</cn>
</apply>
</bind>
This id based approach is especially helpful when constructions
involving bound variables are nested.
It is sometimes necessary to associate additional
information with a bound variable. The information might be
something like a detailed mathematical type, an alternative
presentation or encoding or a domain of application. Such
associations are accomplished in the standard way by replacing
a ci element (even inside the bvar element)
by a semantics element containing both the ci
and the additional information. Recognition of an instance of
the bound variable is still based on the actual ci
elements and not the semantics elements or anything
else they may contain. The id based-approach
outlined above may still be used.
The following example encodes forall x. x+y=y+x.
<bind><csymbol cd="quant1">forall</csymbol>
<bvar><ci>x</ci></bvar>
<apply><csymbol cd="relation1">eq</csymbol>
<apply><csymbol cd="arith1">plus</csymbol><ci>x</ci><ci>y</ci></apply>
<apply><csymbol cd="arith1">plus</csymbol><ci>y</ci><ci>x</ci></apply>
</apply>
</bind>In non-Strict Content markup, the bvar element is used in
a number of idiomatic constructs. These are described in Section 4.3.3 Qualifiers and Section 4.4 Content MathML for Specific Operators and Constants.
4.2.6.3 Renaming Bound Variables
It is a defining property of bound variables that they can be renamed
consistently in the scope of their parent bind element. This operation, sometimes known as α-conversion,
preserves the semantics of the expression.
A bound variable x may be renamed to say y so long as y does not occur free in the body of the binding, or in any annotations of the bound variable, x to be renamed, or later bound variables.
If a bound variable x is renamed, all free occurrences of x in annotations in its bvar element, any following bvar children of the bind and in the expression in the body of the bind should be renamed.
In the example in the previous section, note how renaming x to z produces the equivalent expression forall z. z+y=y+z, whereas x may not be renamed to y, as y is free in the body of the binding and would be captured, producing the expression forall y. y+y=y+y which is not equivalent to the original expression.
4.2.6.4 Rendering Binding Constructions
If
and
are Content MathML expressions
that render as the Presentation MathML expressions
and
then the sample rendering of a binding element is as follows:
Content MathML
<bind> <bvar> </bvar> <bvar> </bvar> <bvar> </bvar> </bind>
Sample Presentation
<mrow> <mrow> <mo separator="true">,</mo> <mo separator="true">,</mo> </mrow> <mo separator="true">.</mo> </mrow>
4.2.7 Structure Sharing <share>
To conserve space in the XML encoding, MathML expression trees can make use of structure sharing.
4.2.7.1 The share element
| Schema Fragment | ||
|---|---|---|
| Class | Share | |
| Attributes | CommonAtt, src | |
src Attribute Values
|
URI | |
| Content | Empty | |
The share element has an href attribute used to
to reference a MathML expression tree. The value of the
href attribute is a URI specifying the id
attribute of the root node of the expression tree. When building a
MathML expression tree, the share element is equivalent to a copy of the MathML
expression tree referenced by the href attribute. Note that this copy is
structurally equal, but not identical to the element referenced. The
values of the share will often be relative URI references, in which case they
are resolved using the base URI of the document containing the share element.
For instance, the mathematical object f(f(f(a,a),f(a,a)),f(f(a,a),f(a,a))) can be encoded as either one of the following representations (and some intermediate versions as well).
<apply><ci>f</ci>
<apply><ci>f</ci>
<apply><ci>f</ci>
<ci>a</ci>
<ci>a</ci>
</apply>
<apply><ci>f</ci>
<ci>a</ci>
<ci>a</ci>
</apply>
</apply>
<apply><ci>f</ci>
<apply><ci>f</ci>
<ci>a</ci>
<ci>a</ci>
</apply>
<apply><ci>f</ci>
<ci>a</ci>
<ci>a</ci>
</apply>
</apply>
</apply>
|
<apply><ci>f</ci>
<apply id="t1"><ci>f</ci>
<apply id="t11"><ci>f</ci>
<ci>a</ci>
<ci>a</ci>
</apply>
<share href="#t11"/>
</apply>
<share href="#t1"/>
</apply>
|
4.2.7.2 An Acyclicity Constraint
Say that an element dominates all its children and all
elements they dominate. Say also that a
share element dominates its target, i.e. the element that carries the
id attribute pointed to by the href attribute. For instance in the
representation on the right above, the apply element with id="t1" and also the
second share (with href="t11") both dominate the
apply element with id="t11".
The occurrences of the share element must obey the following global
acyclicity constraint: An element may not dominate itself. For example, the
following representation violates this constraint:
<apply id="badid1"><csymbol cd="arith1">divide</csymbol>
<cn>1</cn>
<apply><csymbol cd="arith1">plus</csymbol>
<cn>1</cn>
<share href="#badid1"/>
</apply>
</apply>Here, the apply element with id="foo" dominates its third child,
which dominates the share element, which dominates its target: the element with
id="foo". So by transitivity, this element dominates itself. By the
acyclicity constraint, the example is not a valid MathML expression tree. It
might be argued that such an expression could be given the interpretation of the continued fraction
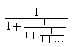 .
However, the procedure of building an expression tree by replacing
.
However, the procedure of building an expression tree by replacing
share element does not terminate for such an
expression, and hence such expressions are not allowed by Content MathML.
Note that the acyclicity constraints is not restricted to such simple cases, as the following example shows:
<apply id="bar"> <apply id="baz"> <csymbol cd="arith1">plus</csymbol> <csymbol cd="arith1">plus</csymbol> <cn>1</cn> <cn>1</cn> <share href="#baz"/> <share href="#bar"/> </apply> </apply>
Here, the apply with id="bar" dominates its third child, the
share with href="#baz". That element dominates its target apply
(with id="baz"), which in turn dominates its third child, the share
with href="#bar". Finally, the share with
href="#bar" dominates its target, the original
apply element with id="bar". So this pair of representations
ultimately violates the acyclicity constraint.
4.2.7.3 Structure Sharing and Binding
Note that the share element is a syntactic referencing mechanism:
a share element stands for the exact element it points to. In particular,
referencing does not interact with binding in a semantically intuitive way, since it
allows a phenomenon called variable capture to
occur. Consider an example:
<bind id="outer"><csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<apply><ci>f</ci>
<bind id="inner"><csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<share id="copy" href="#orig"/>
</bind>
<apply id="orig"><ci>g</ci><ci>x</ci></apply>
</apply>
</bind>
This represents a term
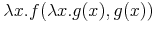 which has two sub-terms of the form
which has two sub-terms of the form
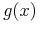 ,
one with
,
one with id="orig"
(the one explicitly represented) and one with id="copy",
represented by the share element.
In the original, explicitly-represented term,
the variable x is bound by the
outer bind element.
However, in the copy, the variable x is
bound by the inner bind element.
One says that the inner bind
has captured the variable x.
Using references that capture variables in this way can easily lead to representation
errors, and is not recommended. For instance, using
α-conversion to rename the inner occurrence of x
into, say, y leads to the semantically equivalent expression
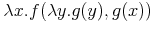 .
However, in this form, it is no longer possible to share the expression
.
However, in this form, it is no longer possible to share the expression
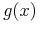 .
Replacing x with y in the inner
.
Replacing x with y in the inner
bvar without replacing the share element results in a change
in semantics.
4.2.8 Attribution via semantics
Content elements can be annotated with additional information via the
semantics element. MathML uses the
semantics element to wrap the annotated element and the
annotation-xml and annotation elements used for representing the
annotations themselves. The use of the semantics, annotation and
annotation-xml is described in detail Chapter 5 Mixing Markup Languages for Mathematical Expressions.
The semantics element is be considered part of both
presentation MathML and Content MathML. MathML considers a semantics element
(strict) Content MathML, if and only if its first child is (strict) Content MathML.
4.2.9 Error Markup <cerror>
| Schema Fragment (Strict) | Schema Fragment (Full) | |
|---|---|---|
| Class | Error | Error |
| Attributes | CommonAtt | CommonAtt, DefEncAtt |
| Content | csymbol, ContExp* | csymbol, ContExp* |
A content error expression is made up of a csymbol
followed by a sequence of zero or more MathML expressions. The
initial expression must be a csymbol indicating the kind of
error. Subsequent children, if present, indicate the context in
which the error occurred.
The cerror element has no direct mathematical meaning.
Errors occur as the result of some action performed on an expression
tree and are thus of real interest only when some sort of
communication is taking place. Errors may occur inside other objects
and also inside other errors.
As an example, to encode a division by zero error, one might
employ a hypothetical aritherror Content Dictionary
containing a DivisionByZero symbol, as in the following
expression:
<cerror> <csymbol cd="aritherror">DivisionByZero</csymbol> <apply><csymbol cd="arith1">divide</csymbol><ci>x</ci><cn>0</cn></apply> </cerror>
Note that error markup generally should enclose only the smallest
erroneous sub-expression. Thus a cerror will often be a sub-expression of
a bigger one, e.g.
<apply><csymbol cd="relation1">eq</csymbol>
<cerror>
<csymbol cd="aritherror">DivisionByZero</csymbol>
<apply><csymbol cd="arith1">divide</csymbol><ci>x</ci><cn>0</cn></apply>
</cerror>
<cn>0</cn>
</apply>The default presentation of a cerror element is an
merror expression whose first child is a presentation of the
error symbol, and whose subsequent children are the default
presentations of the remaining children of the cerror. In
particular, if one of the remaining children of the cerror is
a presentation MathML expression, it is used literally in the
corresponding merror.
<cerror> <csymbol cd="aritherror">DivisionByZero</csymbol> <apply><csymbol cd="arith1">divide</csymbol><ci>x</ci><cn>0</cn></apply> </cerror>
Sample Presentation
<merror> <mtext>DivisionByZero: </mtext> <mfrac><mi>x</mi><mn>0</mn></mfrac> </merror>
Note that when the context where an error occurs is so nonsensical that its default presentation would not be useful, an application may provide an alternative representation of the error context. For example:
<cerror> <csymbol cd="error">Illegal bound variable</csymbol> <cs> <bvar><plus/></bvar> </cs> </cerror>
4.2.10 Encoded Bytes <cbytes>
| Schema Fragment (Strict) | Schema Fragment (Full) | |
|---|---|---|
| Class | Cbytes | Cbytes |
| Attributes | CommonAtt | CommonAtt, DefEncAtt |
| Content | base64 | base64 |
The content of cbytes represents a stream of bytes as a
sequence of characters in Base64 encoding, that is it matches the
base64Binary data type defined in [XMLSchemaDatatypes]. All white space is ignored.
The cbytes element is mainly used for OpenMath
compatibility, but may be used, as in OpenMath, to encapsulate output
from a system that may be hard to encode in MathML, such as binary
data relating to the internal state of a system, or image data.
The rendering of cbytes is not expected to represent the
content and the proposed rendering is that of an empty
mrow. Typically cbytes is used in an
annotation-xml or is itself annotated with Presentation
MathML, so this default rendering should rarely be used.
4.3 Content MathML for Specific Structures
The elements of Strict Content MathML described in the previous section are sufficient to encode logical assertions and expression structure, and they do so in a way that closely models the standard constructions of mathematical logic that underlie the foundations of mathematics. As a consequence, Strict markup can be used to represent all of mathematics, and is ideal for providing consistent mathematical semantics for all Content MathML expressions.
At the same time, many notational idioms of mathematics are not straightforward to represent directly with Strict Content markup. For example, standard notations for sums, integrals, sets, piecewise functions and many other common constructions require non-obvious technical devices, such as the introduction of lambda functions, to rigorously encode them using Strict markup. Consequently, in order to make Content MathML easier to use, a range of additional elements have been provided for encoding such idiomatic constructs more directly. This section discusses the general approach for encoding such idiomatic constructs, and their Strict Content equivalents. Specific constructions are discussed in detail in Section 4.4 Content MathML for Specific Operators and Constants.
Most idiomatic constructions which Content markup addresses fall
into about a dozen classes. Some of these classes, such as container elements, have
their own syntax. Similarly, a small number of non-Strict
constructions involve a single element with an exceptional syntax,
for example partialdiff. These exceptional elements are
discussed on a case-by-case basis in Section 4.4 Content MathML for Specific Operators and Constants. However, the majority of constructs consist of
classes of operator elements which all share a particular usage of
qualifiers.
These classes of operators are described in Section 4.3.4 Operator Classes.
In all cases, non-Strict expressions may be rewritten using only Strict markup. In most cases, the transformation is completely algorithmic, and may be automated. Rewrite rules for classes of non-Strict constructions are introduced and discussed later in this section, and rewrite rules for exceptional constructs involving a single operator are given in Section 4.4 Content MathML for Specific Operators and Constants. The complete algorithm for rewriting arbitrary Content MathML as Strict Content markup is summarized at the end of the Chapter in Section 4.6 The Strict Content MathML Transformation.
4.3.1 Container Markup
Many mathematical structures are constructed from subparts or
parameters. The motivating example is a set. Informally, one
thinks of a set as a certain kind of mathematical object that
contains a collection of elements. Thus, it is intuitively natural
for the markup for a set to contain, in the XML sense, the markup
for its constituent elements. The markup may define the set
elements explicitly by enumerating them, or implicitly by rule,
using qualifier elements. However, in either case, the markup for
the elements is contained in the markup for the set, and
consequently this style of representation is termed
container markup in MathML. By contrast, Strict
markup represents an instance of a set as the result of applying a
function or constructor symbol to arguments. In this
style of markup, the markup for the set construction is a sibling
of the markup for the set elements in an enclosing apply
element.
While the two approaches are formally equivalent, container markup is generally more intuitive for non-expert authors to use, while Strict markup is preferable is contexts where semantic rigor is paramount. In addition, MathML 2 relied on container markup, and thus container markup is necessary in cases where backward compatibility is required.
MathML provides container markup for the following mathematical
constructs: sets, lists, intervals, vectors, matrices (two
elements), piecewise functions (three elements) and lambda
functions. There are corresponding constructor symbols in Strict
markup for each of these, with the exception of lambda functions,
which correspond to binding symbols in Strict markup. Note that in
MathML 2, the term "container markup" was also taken to include
token elements, and the deprecated declare, fn
and reln elements, but MathML 3 limits usage of the term
to the above constructs.
The rewrite rules for obtaining equivalent Strict Content markup from container markup depend on the operator class of the particular operator involved. For details about a specific container element, obtain its operator class (and any applicable special case information) by consulting the syntax table and discussion for that element in Section 4.4 Content MathML for Specific Operators and Constants. Then apply the rewrite rules for that specific operator class as described in Section 4.3.4 Operator Classes.
4.3.1.1 Container Markup for Constructor Symbols
The arguments to container elements corresponding to
constructors may either be explicitly given as a sequence of child
elements, or they may be specified by a rule using qualifiers. The
only exceptions are the piecewise, piece, and
otherwise elements used for representing functions with
piecewise definitions. The
arguments of these elements must always be specified
explicitly.
Here is an example of container markup with explicitly specified arguments:
<set><ci>a</ci><ci>b</ci><ci>c</ci></set>
This is equivalent to the following Strict Content MathML expression:
<apply><csymbol cd="set1">set</csymbol><ci>a</ci><ci>b</ci><ci>c</ci></apply>
Another example of container markup, where the list of arguments is given indirectly as an expression with a bound variable. The container markup for the set of even integers is:
<set> <bvar><ci>x</ci></bvar> <domainofapplication><integers/></domainofapplication> <apply><times/><cn>2</cn><ci>x</ci></apply> </set>
This may be written as follows in Strict Content MathML:
<apply><csymbol cd="set1">map</csymbol>
<bind><csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<apply><csymbol cd="arith1">times</csymbol>
<cn>2</cn>
<ci>x</ci>
</apply>
</bind>
<csymbol cd="setname1">Z</csymbol>
</apply>4.3.1.2 Container Markup for Binding Constructors
The lambda element is a container element
corresponding to the lambda symbol
in the fns1 Content Dictionary. However, unlike the
container elements of the preceding section, which purely
construct mathematical objects from arguments, the lambda
element performs variable binding as well. Therefore, the child
elements of lambda have distinguished roles. In
particular, a lambda element must have at least one
bvar child, optionally followed by qualifier elements, followed by a
Content MathML element. This basic difference between the
lambda container and the other constructor container
elements is also reflected in the OpenMath symbols to which they
correspond. The constructor symbols have an OpenMath role of
"application", while the lambda symbol has a role of "bind".
This example shows the use of lambda container element and the equivalent use of bind in Strict Content MathML
<lambda><bvar><ci>x</ci></bvar><ci>x</ci></lambda>
<bind><csymbol cd="fns1">lambda</csymbol> <bvar><ci>x</ci></bvar><ci>x</ci> </bind>
4.3.2 Bindings with <apply>
MathML allows the use of the apply element to perform
variable binding in non-Strict constructions instead of
the bind element. This usage conserves backwards
compatibility with MathML 2. It also simplifies the encoding of
several constructs involving bound variables with qualifiers as
described below.
Use of the apply element to bind variables is allowed
in two situations. First, when the operator to be applied is
itself a binding operator, the apply element merely
substitutes for the bind element. The logical quantifiers
<forall/>, <exists/> and the
container element lambda are the primary examples of this
type.
The second situation arises when the operator being applied allows the use of bound variables with qualifiers. The most common examples are sums and integrals. In most of these cases, the variable binding is to some extent implicit in the notation, and the equivalent Strict representation requires the introduction of auxiliary constructs such as lambda expressions for formal correctness.
Because expressions using bound variables with qualifiers are
idiomatic in nature, and do not always involve true variable
binding, one cannot expect systematic renaming (alpha-conversion)
of variables "bound" with apply to preserve meaning in
all cases. An example for this is the diff element where
the bvar term is technically not bound at all.
The following example illustrates the use of apply
with a binding operator. In these cases, the corresponding Strict
equivalent merely replaces the apply element with a
bind element:
<apply><forall/> <bvar><ci>x</ci></bvar> <apply><geq/><ci>x</ci><ci>x</ci></apply> </apply>
The equivalent Strict expression is:
<bind><csymbol cd="logic1">forall</csymbol> <bvar><ci>x</ci></bvar> <apply><csymbol cd="relation1">geq</csymbol><ci>x</ci><ci>x</ci></apply> </bind>
In this example, the sum operator is not itself a binding operator, but bound variables with qualifiers are implicit in the standard notation, which is reflected in the non-Strict markup. In the equivalent Strict representation, it is necessary to convert the summand into a lambda expression, and recast the qualifiers as an argument expression:
<apply><sum/> <bvar><ci>i</ci></bvar> <lowlimit><cn>0</cn></lowlimit> <uplimit><cn>100</cn></uplimit> <apply><power/><ci>x</ci><ci>i</ci></apply> </apply>
The equivalent Strict expression is:
<apply><csymbol cd="arith1">sum</csymbol>
<apply><csymbol cd="interval1">integer_interval</csymbol>
<cn>0</cn>
<cn>100</cn>
</apply>
<bind><csymbol cd="fns1">lambda</csymbol>
<bvar><ci>i</ci></bvar>
<apply><csymbol cd="arith1">power</csymbol>
<ci>x</ci>
<ci>i</ci>
</apply>
</bind>
</apply>4.3.3 Qualifiers
Many common mathematical constructs involve an operator together with some additional data. The additional data is either implicit in conventional notation, such as a bound variable, or thought of as part of the operator, as is the case with the limits of a definite integral. MathML 3 uses qualifier elements to represent the additional data in such cases.
Qualifier elements are always used in conjunction with operator or container
elements. Their meaning is idiomatic, and depends on the context in which they are
used. When used with an operator, qualifiers always follow the operator and precede
any arguments that are present. In all cases, if more than one qualifier is present,
they appear in the order bvar, lowlimit, uplimit,
interval, condition, domainofapplication, degree,
momentabout, logbase.
The precise function of qualifier elements depends on the operator or container that they modify. The majority of use cases fall into one of several categories, discussed below, and usage notes for specific operators and qualifiers are given in Section 4.4 Content MathML for Specific Operators and Constants.
4.3.3.1 Uses of
<domainofapplication>,
<interval>,
<condition>,
<lowlimit> and
<uplimit>
The primary use of domainofapplication, interval,
uplimit, lowlimit and condition is to
restrict the values of a bound variable. The most general qualifier
is domainofapplication. It is used to specify a set (perhaps
with additional structure, such as an ordering or metric) over which
an operation is to take place. The interval qualifier, and
the pair lowlimit and uplimit also restrict a bound
variable to a set in the special case where the set is an
interval. The condition qualifier, like
domainofapplication, is general, and can be used to restrict
bound variables to arbitrary sets. However, unlike the other
qualifiers, it restricts the bound variable by specifying a
Boolean-valued function of the bound variable. Thus,
condition qualifiers always contain instances of the bound
variable, and thus require a preceding bvar, while the other
qualifiers do not. The other qualifiers may even be used when no
variables are being bound, e.g. to indicate the restriction of a
function to a subdomain.
In most cases, any of the qualifiers capable of representing the
domain of interest can be used interchangeably. The most general
qualifier is domainofapplication, and therefore has a
privileged role. It is the preferred form, unless there are
particular idiomatic reasons to use one of the other qualifiers,
e.g. limits for an integral. In MathML 3, the other forms are treated
as shorthand notations for domainofapplication because they
may all be rewritten as equivalent domainofapplication
constructions. The rewrite rules to do this are given below. The other
qualifier elements are provided because they correspond to common
notations and map more easily to familiar presentations. Therefore,
in the situations where they naturally arise, they may be more
convenient and direct than domainofapplication.
To illustrate these ideas, consider the following examples showing alternative
representations of a definite integral. Let C denote the interval from 0 to 1,
and f(x) = x2. Then
domainofapplication could be used express the integral of a
function f over
C in this way:
<apply><int/>
<domainofapplication>
<ci type="set">C</ci>
</domainofapplication>
<ci type="function">f</ci>
</apply>Note that no explicit bound variable is identified in this
encoding, and the integrand is a function. Alternatively, the
interval qualifier could be used with an explicit bound variable:
<apply><int/> <bvar><ci>x</ci></bvar> <interval><cn>0</cn><cn>1</cn></interval> <apply><power/><ci>x</ci><cn>2</cn></apply> </apply>
The pair lowlimit and uplimit can also be used.
This is perhaps the most "standard" representation of this integral:
<apply><int/> <bvar><ci>x</ci></bvar> <lowlimit><cn>0</cn></lowlimit> <uplimit><cn>1</cn></uplimit> <apply><power/><ci>x</ci><cn>2</cn></apply> </apply>
Finally, here is the same integral, represented using
a condition on the bound variable:
<apply><int/>
<bvar><ci>x</ci></bvar>
<condition>
<apply><and/>
<apply><leq/><cn>0</cn><ci>x</ci></apply>
<apply><leq/><ci>x</ci><cn>1</cn></apply>
</apply>
</condition>
<apply><power/><ci>x</ci><cn>2</cn></apply>
</apply>
Note the use of the explicit bound variable within the
condition term. Note also that when a bound
variable is used, the integrand is an expression in the bound
variable, not a function.
The general technique of using a condition element
together with domainofapplication is quite powerful. For
example, to extend the previous example to a multivariate domain, one
may use an extra bound variable and a domain of application
corresponding to a cartesian product:
<apply><int/>
<bvar><ci>x</ci></bvar>
<bvar><ci>y</ci></bvar>
<domainofapplication>
<set>
<bvar><ci>t</ci></bvar>
<bvar><ci>u</ci></bvar>
<condition>
<apply><and/>
<apply><leq/><cn>0</cn><ci>t</ci></apply>
<apply><leq/><ci>t</ci><cn>1</cn></apply>
<apply><leq/><cn>0</cn><ci>u</ci></apply>
<apply><leq/><ci>u</ci><cn>1</cn></apply>
</apply>
</condition>
<list><ci>t</ci><ci>u</ci></list>
</set>
</domainofapplication>
<apply><times/>
<apply><power/><ci>x</ci><cn>2</cn></apply>
<apply><power/><ci>y</ci><cn>3</cn></apply>
</apply>
</apply>Note that the order of the inner and outer bound variables is significant.
Mappings to Strict Content MathML
When rewriting expressions to Strict Content MathML, qualifier
elements are removed via a series of rules described in this section.
The general algorithm for rewriting a MathML expression involving
qualifiers proceeds in two steps. First, constructs using the
interval, condition, uplimit and
lowlimit qualifiers are converted to constructs using only
domainofapplication. Second, domainofapplication
expressions are then rewritten as Strict Content markup.
Rewrite: interval qualifier
<apply> <bvar> </bvar> <lowlimit> </lowlimit> <uplimit> </uplimit> </apply>
<apply> <bvar> </bvar> <domainofapplication> <apply><csymbol cd="interval1"></csymbol> </apply> </domainofapplication> </apply>
The symbol used in this translation depends on the head of the
application, denoted by
here. By default interval should be
used, unless the semantics of the head term can be determined and
indicate a more specific interval symbols. In particular, several
predefined Content MathML element should be used with more specific
interval symbols. If the head is int then oriented_interval is used. When the head term
is sum or product, integer_interval should be used.
The above technique for replacing lowlimit and uplimit qualifiers
with a domainofapplication element is also used for replacing the
interval qualifier.
The condition qualifier restricts a bound variable by specifying a
Boolean-valued expression on a larger domain, specifying whether a given value is in the
restricted domain. The condition element contains a single child that represents
the truth condition. Compound conditions are formed by applying Boolean operators such as
and in the condition.
Rewrite: condition
To rewrite an expression using the condition
qualifier as one using domainofapplication,
<bvar> </bvar> <bvar> </bvar> <condition> </condition>
is rewritten to
<bvar> </bvar> <bvar> </bvar> <domainofapplication> <apply><csymbol cd="set1">suchthat</csymbol> <bind><csymbol cd="fns1">lambda</csymbol> <bvar> </bvar> <bvar> </bvar> </bind> </apply> </domainofapplication>
If the apply has a domainofapplication (perhaps originally expressed as
interval or an uplimit/lowlimit pair) then that is used for
. Otherwise is a set determined by the type attribute
of the bound variable as specified in Section 4.2.2.2 Non-Strict uses of <ci>, if that is
present. If the type is unspecified, the translation introduces an unspecified domain via
content identifier <ci>R</ci>.
By applying the rules above, expression using the
interval, condition, uplimit and
lowlimit can be rewritten using only
domainofapplication. Once a domainofapplication has
been obtained, the final mapping to Strict markup is accomplished
using the following rules:
Rewrite: restriction
An application of a function that is qualified by the
domainofapplication qualifier (expressed by an apply element without
bound variables) is converted to an application of a function term constructed with the
restriction symbol.
<apply> <domainofapplication> </domainofapplication> </apply>
may be written as:
<apply>
<apply><csymbol cd="fns1">restriction</csymbol>
</apply>
</apply>In general, an application involving bound variables and (possibly) domainofapplication is rewritten using the following rule, which makes the domain the first positional argument of the application, and uses
the lambda symbol to encode the variable bindings. Certain classes of operator have alternative rules, as described below.
Rewrite: apply bvar domainofapplication
A content MathML expression with bound variables and
domainofapplication
<apply> <bvar> </bvar> ... <bvar> </bvar> <domainofapplication> </domainofapplication> ... </apply>
is rewritten to
<apply> <bind><csymbol cd="fns1">lambda</csymbol> <bvar> </bvar> ... <bvar> </bvar> </bind> ... <bind><csymbol cd="fns1">lambda</csymbol> <bvar> </bvar> ... <bvar> </bvar> </bind> </apply>
If there is no domainofapplication qualifier the child is
omitted.
4.3.3.2 Uses of <degree>
The degree element is a qualifier used to specify the
"degree" or "order" of an operation. MathML uses the
degree element in this way in three contexts: to specify the degree of a
root, a moment, and in various derivatives. Rather than introduce special elements for
each of these families, MathML provides a single general construct, the
degree element in all three cases.
Note that the degree qualifier is not used to restrict a bound variable in
the same sense of the qualifiers discussed above. Indeed, with roots and moments, no
bound variable is involved at all, either explicitly or implicitly. In the case of
differentiation, the degree element is used in conjunction with a
bvar, but even in these cases, the variable may not be genuinely bound.
For the usage of degree with the root and moment operators, see the discussion of those
operators below. The usage of degree in differentiation is more complex. In
general, the degree element indicates the order of the derivative with
respect to that variable. The degree element is allowed as the second child of a
bvar element identifying a variable with respect to which the derivative is
being taken. Here is an example of a second derivative using the degree
qualifier:
<apply><diff/>
<bvar>
<ci>x</ci>
<degree><cn>2</cn></degree>
</bvar>
<apply><power/><ci>x</ci><cn>4</cn></apply>
</apply>For details see Section 4.4.4.2 Differentiation <diff/> and Section 4.4.4.3 Partial Differentiation <partialdiff/>.
4.3.4 Operator Classes
The Content MathML elements described in detail in the next section may be broadly separated into classes. The class of each element is shown in the syntax table that introduces the element in Section 4.4 Content MathML for Specific Operators and Constants. The class gives an indication of the general intended mathematical usage of the element, and also determines its usage as determined by the schema. The class also determines the applicable rewrite rules for mapping to Strict Content MathML. This section presents the rewrite rules for each of the operator classes.
The rules in this section cover the use cases applicable to
specific operator classes. Special-case rewrite rules for individual
elements are discussed in the sections below. However, the most
common usage pattern is generic, and is used by operators from almost all
operator classes. It consists of applying an operator to an explicit list
of arguments using an apply element. In these cases,
rewriting to Strict Content MathML is simply a matter of replacing the
empty element with an appropriate csymbol, as listed in the
syntax tables in Section 4.4 Content MathML for Specific Operators and Constants. This is summarized in
the following rule.
In MathML 2, the definitionURL attribute could be
used to redefine or modify the meaning of an operator element. When the definitionURL
attribute is present, the value for the cd attribute on the csymbol should be
determined by the definitionURL value if possible. The correspondence between cd and definitionURL values is described Section 4.2.3.2 Non-Strict uses of <csymbol>.
4.3.4.1 N-ary Operators (classes nary-arith, nary-functional, nary-logical, nary-linalg, nary-set, nary-constructor)
Many MathML operators may be used with an arbitrary number of
arguments. The corresponding OpenMath symbols for elements in these classes
also take an arbitrary number of arguments.
In all such cases, either the arguments my be given
explicitly as children of the apply or bind element, or
the list may be specified implicitly via the use of qualifier
elements.
4.3.4.1.1 Schema Patterns
The elements representing these n-ary operators are specified in the following schema patterns in Appendix A Parsing MathML: nary-arith.class, nary-functional.class, nary-logical.class, nary-linalg.class, nary-set.class, nary-constructor.class.
4.3.4.1.2 Rewriting to Strict Content MathML
If the argument list is given explicitly, the Rewrite: element rule applies.
Any use of qualifier elements is expressed in Strict Content
MathML, via explicitly applying the function to a list of arguments
using the apply_to_list symbol as shown
in the following rule. The rule only considers the
domainofapplication qualifier as other qualifiers may be
rewritten to domainofapplication as described earlier.
Rewrite: n-ary domainofapplication
An expression of the following form,
where represents any
element of the relevant class and
is an arbitrary expression involving the bound variable(s)
<apply> <bvar> </bvar> <domainofapplication> </domainofapplication> </apply>
is rewritten to
<apply><csymbol cd="fns2">apply_to_list</csymbol> <csymbol cd=""></csymbol> <apply><csymbol cd="list1">map</csymbol> <bind><csymbol cd="fns1">lambda</csymbol> <bvar> </bvar> </bind> </apply> </apply>
The above rule applies to all symbols in the listed classes.
In the case of nary-set.class the choice of Content
Dictionary to use depends on the type attribute on the
symbol, defaulting to set1, but multiset1
should be used if type="multiset".
Note that the members of the nary-constructor.class, such
as vector, use constructor syntax where the arguments and
qualifiers are given as children of the element rather than as
children of a containing apply. In this case, the above rules apply
with the analogous syntactic modifications.
4.3.4.2 N-ary Constructors for set and list (class nary-setlist-constructor)
The use of set and list follows the same format
as other n-ary constructors, however when rewriting to Strict
Content MathML a variant of the above rule is used. This is because the map
symbol implicitly constructs the required set or list, and apply_to_list is
not needed in this case.
4.3.4.2.1 Schema Patterns
The elements representing these n-ary operators are specified in the schema pattern nary-setlist-constructor.class.
4.3.4.2.2 Rewriting to Strict Content MathML
If the argument list is given explicitly, the Rewrite: element rule applies.
When qualifiers are used to specify the list of arguments, the following rule is used.
Rewrite: n-ary setlist domainofapplication
An expression of the following form,
where is either of the elements set or list and
is an arbitrary expression involving the bound variable(s)
<bvar> </bvar> <domainofapplication> </domainofapplication>
is rewritten to
<apply><csymbol cd="">map</csymbol> <bind><csymbol cd="fns1">lambda</csymbol> <bvar> </bvar> </bind> </apply>
Note that
when is already a set
or list of the appropriate type for the container element, and the lambda function created
from is
the identity, the entire container element should be rewritten
directly as .
In the case of set, the choice of Content
Dictionary and symbol depends on the value of its type attribute. When the
type attribute is "set", the set symbol is used. When the
type attribute is "multiset", the multiset symbol is used. For any other values of type
the set symbol should be used, annotated with the type
by rewriting the type attribute using the rule
Rewrite: attributes.
4.3.4.3 N-ary Relations (classes nary-reln, nary-set-reln)
MathML allows transitive relations to be used with multiple arguments, to give a natural expression to "chains" of relations such as a < b < c < d. However unlike the case of the arithmetic operators, the underlying symbols used in the Strict Content MathML are classed as binary, so it is not possible to use apply_to_list as in the previous section, but instead a similar function predicate_on_list is used, the semantics of which is essentially to take the conjunction of applying the predicate to elements of the domain two at a time.
4.3.4.3.1 Schema Patterns
The elements representing these n-ary operators are specified in the following schema patterns in Appendix A Parsing MathML: nary-reln.class, nary-set-reln.class.
4.3.4.3.2 Rewriting to Strict Content MathML
Rewrite: n-ary relations
An expression of the form
<apply> </apply>
rewrites to Strict Content MathML
<apply><csymbol cd="fns2">predicate_on_list</csymbol> <csymbol cd=""></csymbol> <apply><csymbol cd="list1">list</csymbol> </apply> </apply>
Rewrite: n-ary relations bvar
An expression of the form
<apply> <bvar> </bvar> <domainofapplication> </domainofapplication> </apply>
where
is an arbitrary expression involving the bound variable, rewrites to the Strict Content MathML
<apply><csymbol cd="fns2">predicate_on_list</csymbol> <csymbol cd=""></csymbol> <apply><csymbol cd="list1">map</csymbol> <bind><csymbol cd="fns1">lambda</csymbol> <bvar> </bvar> </bind> </apply> </apply>
The above rules apply to all symbols in classes nary-reln.class
and nary-set-reln.class. In the latter case the choice of Content
Dictionary to use depends on the type attribute on the
symbol, defaulting to set1, but multiset1
should be used if type="multiset".
4.3.4.4 N-ary/Unary Operators (classes nary-minmax, nary-stats)
The MathML elements, max, min and some statistical
elements such as mean may be used as a n-ary function as in
the above classes, however a special interpretation is given in the
case that a single argument is supplied. If a single argument is
supplied the function is applied to the elements represented by the
argument.
The underlying symbol used in Strict Content MathML for these elements is Unary and so if the MathML is used with 0 or more than 1 arguments, the function is applied to the set constructed from the explicitly supplied arguments according to the following rule.
4.3.4.4.1 Schema Patterns
The elements representing these n-ary operators are specified in the following schema patterns in Appendix A Parsing MathML: nary-minmax.class, nary-stats.class.
4.3.4.4.2 Rewriting to Strict Content MathML
Rewrite: n-ary unary set
When an element,
, of class nary-stats or nary-minmax
is applied to an explicit
list of 0 or 2 or more arguments,
<apply> </apply>
It is is translated to the unary application of the symbol
<csymbol cd="" name=""/>
as specified in the syntax table for the element to the set of
arguments, constructed using the
<csymbol cd="set1" name="set"/>
symbol.
<apply><csymbol cd=""></csymbol> <apply><csymbol cd="set1">set</csymbol> </apply> </apply>
Like all MathML n-ary operators, The list of arguments may be specified implicitly using qualifier elements. This is expressed in Strict Content MathML using the following rule, which is similar to the rule Rewrite: n-ary domainofapplication but differs in that the symbol can be directly applied to the constructed set of arguments and it is not necessary to use apply_to_list.
Rewrite: n-ary unary domainofapplication
An expression of the following form,
where represents any
element of the relevant class and
is an arbitrary expression involving the bound variable(s)
<apply> <bvar> </bvar> <domainofapplication> </domainofapplication> </apply>
is rewritten to
<apply><csymbol cd=""></csymbol> <apply><csymbol cd="set1">map</csymbol> <bind><csymbol cd="fns1">lambda</csymbol> <bvar> </bvar> </bind> </apply> </apply>
Note that
when is already a set
and the lambda function created from is
the identity, the domainofapplication term should should be
rewritten directly
as .
If the element is applied to a single argument the set symbol is not used and the symbol is applied directly to the argument.
Rewrite: n-ary unary single
When an element,
, of class nary-stats or nary-minmax
is applied to a single argument,
<apply> </apply>
It is is translated to the unary application of the symbol in the syntax table for the element.
<apply><csymbol cd=""></csymbol> </apply>
Note: Earlier versions of MathML were not explicit about the correct interpretation of elements in this class, and left it undefined as to whether an expression such as max(X) was a trivial application of max to a singleton, or whether it should be interpreted as meaning the maximum of values of the set X. Applications finding that the rule Rewrite: n-ary unary single can not be applied as the supplied argument is a scalar may wish to use the rule Rewrite: n-ary unary set as an error recovery. As a further complication, in the case of the statistical functions the Content Dictionary to use in this case depends on the desired interpretation of the argument as a set of explicit data or a random variable representing a distribution.
4.3.4.5 Binary Operators (classes binary-arith, binary-logical, binary-reln, binary-linalg, binary-set)
Binary operators take two arguments and simply map to OpenMath
symbols via Rewrite: element
without the need of any special rewrite rules. The binary
constructor interval is similar but uses constructor syntax
in which the arguments are children of the element, and the symbol
used depends on the type element as described in Section 4.4.1.1 Interval <interval>
4.3.4.5.1 Schema Patterns
The elements representing these binary operators are specified in the following schema patterns in Appendix A Parsing MathML: binary-arith.class, binary-logical.class, binary-reln.class, binary-linalg.class, binary-set.class.
4.3.4.6 Unary Operators (classes unary-arith, unary-functional, unary-set, unary-elementary, unary-veccalc)
Unary operators take a single arguments and map to OpenMath symbols via Rewrite: element without the need of any special rewrite rules.
4.3.4.6.1 Schema Patterns
The elements representing these unary operators are specified in the following schema patterns in Appendix A Parsing MathML: unary-arith.class, unary-functional.class, unary-set.class, unary-elementary.class, unary-veccalc.class.
4.3.4.7 Constants (classes constant-arith, constant-set)
Constant symbols relate to mathematical constants such as e and true and also to names of sets such as the Real Numbers, and Integers. In Strict Content MathML, they rewrite simply to the corresponding symbol listed in the syntax tables for these elements in Section 4.4.10 Constant and Symbol Elements.
4.3.4.7.1 Schema Patterns
The elements representing these constants are specified in the schema patterns constant-arith.class and constant-set.class.
4.3.4.8 Quantifiers (class quantifier)
The Quantifier class is used for the forall and exists quantifiers of predicate calculus.
4.3.4.8.1 Schema Patterns
The elements representing quantifiers are specified in the schema pattern quantifier.class.
4.3.4.8.2 Rewriting to Strict Content MathML
If used with bind and no qualifiers,
then the interpretation in Strict Content MathML is simple. In general
if used with apply or qualifiers, the interpretation in
Strict Content MathML is via the following rule.
Rewrite: quantifier
An expression of following form where
denotes an element of
class quantifier and
is an arbitrary expression involving the bound variable(s)
<apply> <bvar> </bvar> <domainofapplication> </domainofapplication> </apply>
is rewritten to an expression
<bind><csymbol cd=""></csymbol> <bvar> </bvar> <apply><csymbol cd=""></csymbol> <apply><csymbol cd="set1">in</csymbol> </apply> </apply> </bind>
where the symbols
<csymbol cd=""></csymbol>
and
<csymbol cd=""></csymbol>
are as specified in the syntax table of the element.
(The additional symbol being
and in the case of exists and
implies in the case of forall.) When no
domainofapplication is present, no logical conjunction is necessary, and the translation
is direct.
4.3.4.9 Other Operators (classes lambda, interval, int, diff partialdiff, sum, product, limit)
Special purpose classes, described in the sections for the appropriate elements
4.3.4.9.1 Schema Patterns
The elements are specified in the following schema patterns in Appendix A Parsing MathML: lambda.class, interval.class, int.class, partialdiff.class, sum.class, product.class, limit.class.
4.3.5 Non-strict Attributes
A number of content MathML elements such as cn and
interval allow attributes to specialize the semantics of the
objects they represent. For these cases, special rewrite rules are
given on a case-by-case basis in Section 4.4 Content MathML for Specific Operators and Constants. However,
content MathML elements also accept attributes shared all MathML elements, and
depending on the context, may also contain attributes from other XML
namespaces. Such attributes must be rewritten in alternative form in
Strict Content Markup.
Rewrite: attributes
For instance,
<ci class="" xmlns:other="" other:att=""></ci>
is rewritten to
<semantics> <ci></ci> <annotation cd="mathmlattr" name="class" encoding="text/plain"></annotation> <annotation-xml cd="mathmlattr" name="foreign" encoding="MathML-Content"> <apply><csymbol cd="mathmlattr">foreign_attribute</csymbol> <cs></cs> <cs></cs> <cs></cs> <cs></cs> </apply> </annotation-xml> </semantics>
For MathML attributes not allowed in Strict Content MathML the content dictionary mathmlattr is referenced, which provides symbols for all attributes allowed on content MathML elements.
4.4 Content MathML for Specific Operators and Constants
This section presents elements representing a core set of mathematical operators, functions and constants. Most are empty elements, covering the subject matter of standard mathematics curricula up to the level of calculus. The remaining elements are container elements for sets, intervals, vectors and so on. For brevity, all elements defined in this section are sometimes called operator elements.
Each subsection below discusses a specific operator element, beginning with a syntax table, giving the elements operator class. Special case rules for rewriting as Strict Markup are introduced as needed. However, in most cases, the generic rewrite rules for the appropriate operator class is sufficient. In particular, unless otherwise indicated, elements are to be rewritten using the default Rewrite: element rule. Note, however, that all elements in this section must be rewritten in some fashion, since they are not allowed in Strict Content markup.
In MathML 2, the definitionURL attribute could be
used to redefine or modify the meaning of an operator
element. This use of the definitionURL attribute is deprecated in MathML 3. Instead a
csymbol element should be used. In general, the value of
cd attribute on the csymbol will correspond to
the definitionURL value.
4.4.1 Functions and Inverses
4.4.1.1 Interval <interval>
| Class | interval |
|---|---|
| Attributes | CommonAtt, DefEncAtt,closure? |
| Content | ContExp,ContExp |
| OM Symbols | interval_cc, interval_oc, interval_co, interval_oo |
The interval element is a container element used to represent simple mathematical intervals of the
real number line. It takes an optional attribute closure, with a default value
of "closed".
Content MathML
<interval closure="open"><ci>x</ci><cn>1</cn></interval>
<interval closure="closed"><cn>0</cn><cn>1</cn></interval>
<interval closure="open-closed"><cn>0</cn><cn>1</cn></interval>
<interval closure="closed-open"><cn>0</cn><cn>1</cn></interval>
Sample Presentation
<mfenced><mi>x</mi><mn>1</mn></mfenced>
<mfenced open="[" close="]"><mn>0</mn><mn>1</mn></mfenced>
<mfenced open="(" close="]"><mn>0</mn><mn>1</mn></mfenced><mfenced open="[" close=")"><mn>0</mn><mn>1</mn></mfenced>
Mapping to Strict Content MathML
In Strict markup, the interval element corresponds to one
of four symbols from the interval1 content
dictionary. If closure has the value "open" then
interval corresponds to the
interval_oo.
With the value "closed"
interval corresponds to the symbol
interval_cc,
with value "open-closed" to
interval_oc, and with
"closed-open" to
interval_co.
4.4.1.2 Inverse <inverse>
| Class | unary-functional |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | inverse |
The inverse element is applied to a function in order to
construct a generic expression for the functional inverse of that
function. The inverse element may either be applied to
arguments, or it may appear alone, in which case it represents an
abstract inversion operator acting on other functions.
Content MathML
<apply><inverse/> <ci> f </ci> </apply>
Sample Presentation
<msup><mi>f</mi><mrow><mo>(</mo><mn>-1</mn><mo>)</mo></mrow></msup>
Content MathML
<apply> <apply><inverse/><ci type="matrix">A</ci></apply> <ci>a</ci> </apply>
Sample Presentation
<mrow> <msup><mi>A</mi><mrow><mo>(</mo><mn>-1</mn><mo>)</mo></mrow></msup> <mo>⁡</mo> <mfenced><mi>a</mi></mfenced> </mrow>
4.4.1.3 Lambda <lambda>
| Class | lambda |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | BvarQ, DomainQ, ContExp |
| Qualifiers | BvarQ,DomainQ |
| OM Symbols | lambda |
The lambda element is used to construct a user-defined
function from an expression, bound variables, and qualifiers. In a
lambda construct with n (possibly 0) bound variables, the
first n children are bvar elements that identify
the variables that are used as placeholders in the last child for
actual parameter values. The bound variables can be restricted by an
optional domainofapplication qualifier or one of its
shorthand
notations. The meaning of the lambda construct is an
n-ary function that returns the expression in the last
child where the bound variables are replaced with the respective
arguments.
The domainofapplication child restricts the possible
values of the arguments of the constructed function. For instance, the
following lambda construct represents a function on
the integers.
<lambda> <bvar><ci> x </ci></bvar> <domainofapplication><integers/></domainofapplication> <apply><sin/><ci> x </ci></apply> </lambda>
If a lambda construct does not contain bound variables, then
the lambda construct is superfluous and may be removed,
unless it also contains a domainofapplication construct.
In that case, if the last child of the lambda construct is
itself a function, then the domainofapplication restricts
its existing functional arguments, as in this example, which is
a variant representation for the function above.
<lambda> <domainofapplication><integers/></domainofapplication> <sin/> </lambda>
Otherwise, if the last child of the lambda construct is not a
function, say a number, then the lambda construct will not be
a function, but the same number, and any domainofapplication
is ignored.
Content MathML
<lambda>
<bvar><ci>x</ci></bvar>
<apply><sin/>
<apply><plus/><ci>x</ci><cn>1</cn></apply>
</apply>
</lambda>Sample Presentation
<mrow> <mi>λ</mi> <mi>x</mi> <mo>.</mo> <mfenced> <mrow> <mi>sin</mi> <mo>⁡</mo> <mrow><mo>(</mo><mi>x</mi><mo>+</mo><mn>1</mn><mo>)</mo></mrow> </mrow> </mfenced> </mrow>
<mrow> <mi>x</mi> <mo>↦</mo> <mrow> <mi>sin</mi> <mo>⁡</mo> <mrow><mo>(</mo><mi>x</mi><mo>+</mo><mn>1</mn><mo>)</mo></mrow> </mrow> </mrow>
Mapping to Strict Markup
Rewrite: lambda
If the lambda element does not contain qualifiers, the
lambda expression is directly translated into a bind
expression.
<lambda> <bvar> </bvar><bvar> </bvar> </lambda>
rewrites to the Strict Content MathML
<bind><csymbol cd="fns1">lambda</csymbol> <bvar> </bvar><bvar> </bvar> </bind>
Rewrite: lambda domainofapplication
If the lambda element does contain qualifiers, the
qualifier may be rewritten to domainofapplication
and then the lambda expression is translated to a
function term constructed with lambda
and restricted to the specified domain using
restriction.
<lambda> <bvar> </bvar><bvar> </bvar> <domainofapplication> </domainofapplication> </lambda>
rewrites to the Strict Content MathML
<apply><csymbol cd="fns1">restriction</csymbol>
<bind><csymbol cd="fns1">lambda</csymbol>
<bvar> </bvar><bvar> </bvar>
</bind>
</apply>4.4.1.4 Function composition <compose/>
| Class | nary-functional |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| Qualifiers | BvarQ,DomainQ |
| OM Symbols | left_compose |
The compose element represents the function
composition operator. Note that MathML makes no assumption about the domain
and codomain of the constituent functions in a composition; the domain of the
resulting composition may be empty.
The compose element is a commutative n-ary operator. Consequently, it may be
lifted to the induced operator defined on a collection of arguments indexed by a (possibly
infinite) set by using qualifier elements as described in Section 4.3.4.1 N-ary Operators (classes nary-arith, nary-functional, nary-logical,
nary-linalg, nary-set, nary-constructor).
Content MathML
<apply><compose/><ci>f</ci><ci>g</ci><ci>h</ci></apply>
Sample Presentation
<mrow><mi>f</mi><mo>∘</mo><mi>g</mi><mo>∘</mo><mi>h</mi></mrow>
Content MathML
<apply><eq/>
<apply>
<apply><compose/><ci>f</ci><ci>g</ci></apply>
<ci>x</ci>
</apply>
<apply><ci>f</ci><apply><ci>g</ci><ci>x</ci></apply></apply>
</apply>Sample Presentation
<mrow>
<mrow>
<mrow><mo>(</mo><mi>f</mi><mo>∘</mo><mi>g</mi><mo>)</mo></mrow>
<mo>⁡</mo>
<mfenced><mi>x</mi></mfenced>
</mrow>
<mo>=</mo>
<mrow>
<mi>f</mi>
<mo>⁡</mo>
<mfenced>
<mrow>
<mi>g</mi>
<mo>⁡</mo>
<mfenced><mi>x</mi></mfenced>
</mrow>
</mfenced>
</mrow>
</mrow>4.4.1.5 Identity function <ident/>
| Class | unary-functional |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | identity |
The ident element represents the
identity function. Note that MathML makes no assumption about the
domain and codomain of the represented identity function, which
depends on the context in which it is used.
Content MathML
<apply><eq/>
<apply><compose/>
<ci type="function">f</ci>
<apply><inverse/>
<ci type="function">f</ci>
</apply>
</apply>
<ident/>
</apply>Sample Presentation
<mrow> <mrow> <mi>f</mi> <mo>∘</mo> <msup><mi>f</mi><mrow><mo>(</mo><mn>-1</mn><mo>)</mo></mrow></msup> </mrow> <mo>=</mo> <mi>id</mi> </mrow>
4.4.1.6 Domain <domain/>
| Class | unary-functional |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | domain |
The domain element represents the domain of the
function to which it is applied. The domain is the set of values
over which the function is defined.
Content MathML
<apply><eq/> <apply><domain/><ci>f</ci></apply> <reals/> </apply>
Sample Presentation
<mrow> <mrow><mi>domain</mi><mo>⁡</mo><mfenced><mi>f</mi></mfenced></mrow> <mo>=</mo> <mi mathvariant="double-struck">R</mi> </mrow>
4.4.1.7 codomain <codomain/>
| Class | unary-functional |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | range |
The codomain represents the codomain, or range, of the function
to which is is applied. Note that the codomain is not necessarily
equal to the image of the function, it is merely required to contain
the image.
Content MathML
<apply><eq/> <apply><codomain/><ci>f</ci></apply> <rationals/> </apply>
Sample Presentation
<mrow> <mrow><mi>codomain</mi><mo>⁡</mo><mfenced><mi>f</mi></mfenced></mrow> <mo>=</mo> <mi mathvariant="double-struck">Q</mi> </mrow>
4.4.1.8 Image <image/>
| Class | unary-functional |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | image |
The image element represent the image of
the function to which it is applied. The image of a function is the
set of values taken by the function. Every point in the image is
generated by the function applied to some point of the domain.
Content MathML
<apply><eq/> <apply><image/><sin/></apply> <interval><cn>-1</cn><cn> 1</cn></interval> </apply>
Sample Presentation
<mrow> <mrow><mi>image</mi><mo>⁡</mo><mfenced><mi>sin</mi></mfenced></mrow> <mo>=</mo> <mfenced open="[" close="]"><mn>-1</mn><mn>1</mn></mfenced> </mrow>
4.4.1.9 Piecewise declaration (<piecewise>, <piece>, <otherwise>)
piecewise
|
piece
|
otherwise
|
The piecewise, piece, and otherwise elements are used to
represent "piecewise" function definitions of the form "
H(x) = 0 if x less than 0, H(x) = 1
otherwise".
The declaration is constructed using the piecewise element. This contains
zero or more piece elements, and optionally one otherwise element. Each
piece element contains exactly two children. The first child defines the value
taken by the piecewise expression when the condition specified in the associated
second child of the piece is true. The degenerate case of no piece
elements and no otherwise element is treated as undefined for all values of the
domain.
The otherwise element allows the specification of a value to be taken by the
piecewise function when none of the conditions (second child elements of the
piece elements) is true, i.e. a default value.
It should be noted that no "order of execution" is implied by the
ordering of the piece child elements within piecewise. It is the
responsibility of the author to ensure that the subsets of the function domain defined by
the second children of the piece elements are disjoint, or that, where they
overlap, the values of the corresponding first children of the piece elements
coincide. If this is not the case, the meaning of the expression is
undefined.
Here is an example:
Content MathML
<piecewise>
<piece>
<apply><minus/><ci>x</ci></apply>
<apply><lt/><ci>x</ci><cn>0</cn></apply>
</piece>
<piece>
<cn>0</cn>
<apply><eq/><ci>x</ci><cn>0</cn></apply>
</piece>
<piece>
<ci>x</ci>
<apply><gt/><ci>x</ci><cn>0</cn></apply>
</piece>
</piecewise>Sample Presentation
<mrow>
<mo>{</mo>
<mtable>
<mtr>
<mtd><mrow><mo>−</mo><mi>x</mi></mrow></mtd>
<mtd columnalign="left"><mtext>  if  </mtext></mtd>
<mtd><mrow><mi>x</mi><mo><</mo><mn>0</mn></mrow></mtd>
</mtr>
<mtr>
<mtd><mn>0</mn></mtd>
<mtd columnalign="left"><mtext>  if  </mtext></mtd>
<mtd><mrow><mi>x</mi><mo>=</mo><mn>0</mn></mrow></mtd>
</mtr>
<mtr>
<mtd><mi>x</mi></mtd>
<mtd columnalign="left"><mtext>  if  </mtext></mtd>
<mtd><mrow><mi>x</mi><mo>></mo><mn>0</mn></mrow></mtd>
</mtr>
</mtable>
</mrow>Mapping to Strict Markup
In Strict Content MathML, the container elements
piecewise, piece and otherwise are mapped
to applications of the constructor symbols of the same names in the
piece1 CD. Apart from the fact that these three
elements (respectively symbols) are used together, the mapping to
Strict markup is straightforward:
Content MathML
<piecewise>
<piece>
<apply><cn>0</cn></apply>
<apply><lt/><ci>x</ci><cn>0</cn></apply>
</piece>
<piece>
<cn>1</cn>
<apply><gt/><ci>x</ci><cn>1</cn></apply>
</piece>
<otherwise>
<ci>x</ci>
</otherwise>
</piecewise>Strict Content MathML equivalent
<apply><csymbol cd="piece1">piecewise</csymbol>
<apply><csymbol cd="piece1">piece</csymbol>
<cn>0</cn>
<apply><csymbol cd="relation1">lt</csymbol><ci>x</ci><cn>0</cn></apply>
</apply>
<apply><csymbol cd="piece1">piece</csymbol>
<cn>1</cn>
<apply><csymbol cd="relation1">gt</csymbol><ci>x</ci><cn>1</cn></apply>
</apply>
<apply><csymbol cd="piece1">otherwise</csymbol>
<ci>x</ci>
</apply>
</apply>4.4.2 Arithmetic, Algebra and Logic
4.4.2.1 Quotient <quotient/>
| Class | binary-arith |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | quotient |
The quotient element represents the integer division
operator. When the operator is applied to integer arguments
a and b, the result is the "quotient of
a divided by b". That is, the quotient
of integers a and b, is the integer
q such that a = b * q +
r, with |r| less than |b| and
a * r positive. In common usage, q
is called the quotient and r is the remainder.
Content MathML
<apply><quotient/><ci>a</ci><ci>b</ci></apply>
Sample Presentation
<mrow><mo>⌊</mo><mi>a</mi><mo>/</mo><mi>b</mi><mo>⌋</mo></mrow>
4.4.2.2 Factorial <factorial/>
| Class | unary-arith |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | factorial |
This element represents the unary factorial operator on non-negative integers.
The factorial of an integer n is given by n! = n*(n-1)* ... * 1
Content MathML
<apply><factorial/><ci>n</ci></apply>
Sample Presentation
<mrow><mi>n</mi><mo>!</mo></mrow>
4.4.2.3 Division <divide/>
| Class | binary-arith |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | divide |
The divide element represents the division operator in a
number field.
Content MathML
<apply><divide/> <ci>a</ci> <ci>b</ci> </apply>
Sample Presentation
<mrow><mi>a</mi><mo>/</mo><mi>b</mi></mrow>
4.4.2.4 Maximum <max/>
| Class | nary-minmax |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| Qualifiers | BvarQ, DomainQ |
| OM Symbols | max |
The max element denotes the maximum function, which
returns the largest of the arguments to which it is applied. Its
arguments may be explicitly specified in the enclosing
apply element, or specified using qualifier elements
as described in Section 4.3.4.4 N-ary/Unary Operators (classes nary-minmax, nary-stats). Note that when applied to
infinite sets of arguments, no maximal argument may exist.
Content MathML
<apply><max/><cn>2</cn><cn>3</cn><cn>5</cn></apply>
Sample Presentation
<mrow>
<mi>max</mi>
<mrow>
<mo>{</mo><mn>2</mn><mo>,</mo><mn>3</mn><mo>,</mo><mn>5</mn><mo>}</mo>
</mrow>
</mrow>Content MathML
<apply><max/>
<bvar><ci>y</ci></bvar>
<condition>
<apply><in/>
<ci>y</ci>
<interval><cn>0</cn><cn>1</cn></interval>
</apply>
</condition>
<apply><power/><ci>y</ci><cn>3</cn></apply>
</apply>Sample Presentation
<mrow>
<mi>max</mi>
<mrow>
<mo>{</mo><mi>y</mi><mo>|</mo>
<mrow>
<msup><mi>y</mi><mn>3</mn></msup>
<mo>∈</mo>
<mfenced open="[" close="]"><mn>0</mn><mn>1</mn></mfenced>
</mrow>
<mo>}</mo>
</mrow>
</mrow>4.4.2.5 Minimum <min/>
| Class | nary-minmax |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| Qualifiers | BvarQ,DomainQ |
| OM Symbols | min |
The min element denotes the minimum function, which returns the smallest of
the arguments to which it is applied. Its arguments may be explicitly specified in the
enclosing apply element, or specified using qualifier
elements as described in Section 4.3.4.4 N-ary/Unary Operators (classes nary-minmax, nary-stats). Note that when applied to infinite sets of arguments, no
minimal argument may exist.
Content MathML
<apply><min/><ci>a</ci><ci>b</ci></apply>
Sample Presentation
<mrow>
<mi>min</mi>
<mrow><mo>{</mo><mi>a</mi><mo>,</mo><mi>b</mi><mo>}</mo></mrow>
</mrow>Content MathML
<apply><min/>
<bvar><ci>x</ci></bvar>
<condition>
<apply><notin/><ci>x</ci><ci type="set">B</ci></apply>
</condition>
<apply><power/><ci>x</ci><cn>2</cn></apply>
</apply>Sample Presentation
<mrow>
<mi>min</mi>
<mrow><mo>{</mo><msup><mi>x</mi><mn>2</mn></msup><mo>|</mo>
<mrow><mi>x</mi><mo>∉</mo><mi>B</mi></mrow>
<mo>}</mo>
</mrow>
</mrow>4.4.2.6 Subtraction <minus/>
| Class | unary-arith, binary-arith |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | unary_minus, minus |
The minus element can be used as a unary arithmetic operator
(e.g. to represent - x), or as a binary arithmetic operator
(e.g. to represent x- y).
If it is used with one argument, minus corresponds to the unary_minus symbol.
Content MathML
<apply><minus/><cn>3</cn></apply>
Sample Presentation
<mrow><mo>−</mo><mn>3</mn></mrow>
If it is used with two arguments, minus corresponds to the
minus symbol
Content MathML
<apply><minus/><ci>x</ci><ci>y</ci></apply>
Sample Presentation
<mrow><mi>x</mi><mo>−</mo><mi>y</mi></mrow>
In both cases, the translation to Strict Content markup is direct, as described in Rewrite: element. It is merely a matter of choosing the symbol that reflects the actual usage.
4.4.2.7 Addition <plus/>
| Class | nary-arith |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| Qualifiers | BvarQ,DomainQ |
| OM Symbols | plus |
The plus element represents the addition operator. Its
arguments are normally specified explicitly in the enclosing
apply element. As an n-ary commutative operator, it can
be used with qualifiers to specify arguments, however,
this is discouraged, and the sum operator should be
used to represent such expressions instead.
Content MathML
<apply><plus/><ci>x</ci><ci>y</ci><ci>z</ci></apply>
Sample Presentation
<mrow><mi>x</mi><mo>+</mo><mi>y</mi><mo>+</mo><mi>z</mi></mrow>
4.4.2.8 Exponentiation <power/>
| Class | binary-arith |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | power |
The power element represents the exponentiation
operator. The first argument is raised to the power of the second
argument.
Content MathML
<apply><power/><ci>x</ci><cn>3</cn></apply>
Sample Presentation
<msup><mi>x</mi><mn>3</mn></msup>
4.4.2.9 Remainder <rem/>
| Class | binary-arith |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | remainder |
The rem element represents the modulus operator, which
returns the remainder that results from dividing the first argument by
the second. That is, when applied to integer arguments a
and b, it returns the unique integer r such that
a = b * q + r, with
|r| less than |b| and a *
r positive.
Content MathML
<apply><rem/><ci> a </ci><ci> b </ci></apply>
Sample Presentation
<mrow><mi>a</mi><mo>mod</mo><mi>b</mi></mrow>
4.4.2.10 Multiplication <times/>
| Class | nary-arith |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| Qualifiers | BvarQ,DomainQ |
| OM Symbols | times |
The times element represents the n-ary multiplication operator. Its
arguments are normally specified explicitly in the enclosing
apply element. As an n-ary commutative operator, it can
be used with qualifiers to specify arguments by rule, however,
this is discouraged, and the product operator should be
used to represent such expressions instead.
Content MathML
<apply><times/><ci>a</ci><ci>b</ci></apply>
Sample Presentation
<mrow><mi>a</mi><mo>⁢</mo><mi>b</mi></mrow>
4.4.2.11 Root <root/>
| Class | unary-arith, binary-arith |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| Qualifiers | degree |
| OM Symbols | root |
The root element is used to extract roots. The kind of root to be taken is
specified by a "degree" element, which should be given as the second child of
the apply element enclosing the root element. Thus, square roots
correspond to the case where degree contains the value 2, cube roots
correspond to 3, and so on. If no degree is present, a default value of 2 is
used.
Content MathML
<apply><root/> <degree><ci type="integer">n</ci></degree> <ci>a</ci> </apply>
Sample Presentation
<mroot><mi>a</mi><mi>n</mi></mroot>
Mapping to Strict Content Markup
In Strict Content markup, the root symbol is always used with two arguments, with the second indicating the degree of the root being extracted.
Content MathML
<apply><root/><ci>x</ci></apply>
Strict Content MathML equivalent
<apply><csymbol cd="arith1">root</csymbol> <ci>x</ci> <cn type="integer">2</cn> </apply>
Content MathML
<apply><root/> <degree><ci type="integer">n</ci></degree> <ci>a</ci> </apply>
Strict Content MathML equivalent
<apply><csymbol cd="arith1">root</csymbol> <ci>a</ci> <cn type="integer">n</cn> </apply>
4.4.2.12 Greatest common divisor <gcd/>
| Class | nary-arith |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| Qualifiers | BvarQ,DomainQ |
| OM Symbols | gcd |
The gcd element represents the n-ary operator which returns
the greatest common divisor of its arguments. Its
arguments may be explicitly specified in the enclosing
apply element, or specified by rule as described in
Section 4.3.4.1 N-ary Operators (classes nary-arith, nary-functional, nary-logical,
nary-linalg, nary-set, nary-constructor).
Content MathML
<apply><gcd/><ci>a</ci><ci>b</ci><ci>c</ci></apply>
Sample Presentation
<mrow> <mi>gcd</mi> <mo>⁡</mo> <mfenced><mi>a</mi><mi>b</mi><mi>c</mi></mfenced> </mrow>
This default rendering is English-language locale specific: other locales may have different default renderings.
When the gcd element is applied to an explicit list of arguments, the
translation to Strict Content markup is direct, using the gcd symbol, as described in Rewrite: element. However, when
qualifiers are used, the equivalent Strict markup is computed via
Rewrite: n-ary domainofapplication.
4.4.2.13 And <and/>
| Class | nary-logical |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| Qualifiers | BvarQ,DomainQ |
| OM Symbols | and |
The and element represents the logical "and" function which is
an n-ary function taking Boolean arguments and returning a Boolean value. It is true if
all arguments are true, and false otherwise. Its arguments may be explicitly specified
in the enclosing apply element, or specified by rule as described in Section 4.3.4.1 N-ary Operators (classes nary-arith, nary-functional, nary-logical,
nary-linalg, nary-set, nary-constructor).
Content MathML
<apply><and/><ci>a</ci><ci>b</ci></apply>
Sample Presentation
<mrow><mi>a</mi><mo>∧</mo><mi>b</mi></mrow>
Content MathML
<apply><and/> <bvar><ci>i</ci></bvar> <lowlimit><cn>0</cn></lowlimit> <uplimit><ci>n</ci></uplimit> <apply><gt/><apply><selector/><ci>a</ci><ci>i</ci></apply><cn>0</cn></apply> </apply>
Strict Content MathML
<apply><csymbol cd="fns2">apply_to_list</csymbol>
<csymbol cd="logic1">and</csymbol>
<apply><csymbol cd="list1">map</csymbol>
<bind><csymbol cd="fns1">lambda</csymbol>
<bvar><ci>i</ci></bvar>
<apply><csymbol cd="relation1">gt</csymbol>
<apply><csymbol cd="linalg1">vector_selector</csymbol>
<ci>i</ci>
<ci>a</ci>
</apply>
<cn>0</cn>
</apply>
</bind>
<apply><csymbol cd="interval1">integer_interval</csymbol>
<cn type="integer">0</cn>
<ci>n</ci>
</apply>
</apply>
</apply>Sample Presentation
<mrow> <munderover> <mo>⋀</mo> <mrow><mi>i</mi><mo>=</mo><mn>0</mn></mrow> <mi>n</mi> </munderover> <mrow> <mo>(</mo> <msub><mi>a</mi><mi>i</mi></msub> <mo>></mo> <mn>0</mn> <mo>)</mo> </mrow> </mrow>
4.4.2.14 Or <or/>
| Class | nary-logical |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| Qualifiers | BvarQ,DomainQ |
| OM Symbols | or |
The or element represents the logical "or" function. It is
true if any of the arguments are true, and false otherwise.
Content MathML
<apply><or/><ci>a</ci><ci>b</ci></apply>
Sample Presentation
<mrow><mi>a</mi><mo>∨</mo><mi>b</mi></mrow>
4.4.2.15 Exclusive Or <xor/>
| Class | nary-logical |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| Qualifiers | BvarQ,DomainQ |
| OM Symbols | xor |
The xor element represents the logical "xor"
function. It is true if there are an odd number of true arguments or
false otherwise.
Content MathML
<apply><xor/><ci>a</ci><ci>b</ci></apply>
Sample Presentation
<mrow><mi>a</mi><mo>xor</mo><mi>b</mi></mrow>
4.4.2.16 Not <not/>
| Class | unary-logical |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | not |
The note element represents the logical not function
which takes one Boolean argument, and returns the opposite Boolean
value.
Content MathML
<apply><not/><ci>a</ci></apply>
Sample Presentation
<mrow><mo>¬</mo><mi>a</mi></mrow>
4.4.2.17 Implies <implies/>
| Class | binary-logical |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | implies |
The implies element represents the logical implication
function which takes two Boolean expressions as arguments. It
evaluates to false if the first argument is true and the second
argument is false, otherwise it evaluates to true.
Content MathML
<apply><implies/><ci>A</ci><ci>B</ci></apply>
Sample Presentation
<mrow><mi>A</mi><mo>⇒</mo><mi>B</mi></mrow>
4.4.2.18 Universal quantifier <forall/>
| Class | quantifier |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| Qualifiers | BvarQ,DomainQ |
| OM Symbols | forall, implies |
The forall element represents the universal ("for all")
quantifier which takes one or more bound variables, and an
argument which specifies the assertion being quantified.
In addition, condition or other qualifiers may be used as
described in Section 4.3.4.8 Quantifiers (class quantifier) to limit the domain
of the bound variables.
Content MathML
<bind><forall/>
<bvar><ci>x</ci></bvar>
<apply><eq/>
<apply><minus/><ci>x</ci><ci>x</ci></apply>
<cn>0</cn>
</apply>
</bind>Sample Presentation
<mrow> <mo>∀</mo> <mi>x</mi> <mo>.</mo> <mfenced> <mrow> <mrow><mi>x</mi><mo>−</mo><mi>x</mi></mrow> <mo>=</mo> <mn>0</mn> </mrow> </mfenced> </mrow>
Mapping to Strict Markup
When the forall element is used with a condition qualifier the
strict equivalent is constructed with the help of logical implication by the rule
Rewrite: quantifier. Thus
<bind><forall/>
<bvar><ci>p</ci></bvar>
<bvar><ci>q</ci></bvar>
<condition>
<apply><and/>
<apply><in/><ci>p</ci><rationals/></apply>
<apply><in/><ci>q</ci><rationals/></apply>
<apply><lt/><ci>p</ci><ci>q</ci></apply>
</apply>
</condition>
<apply><lt/>
<ci>p</ci>
<apply><power/><ci>q</ci><cn>2</cn></apply>
</apply>
</bind>translates to
<bind><csymbol cd="quant1">forall</csymbol>
<bvar><ci>p</ci></bvar>
<bvar><ci>q</ci></bvar>
<apply><csymbol cd="logic1">implies</csymbol>
<apply><csymbol cd="logic1">and</csymbol>
<apply><csymbol cd="set1">in</csymbol>
<ci>p</ci>
<csymbol cd="setname1">Q</csymbol>
</apply>
<apply><csymbol cd="set1">in</csymbol>
<ci>q</ci>
<csymbol cd="setname1">Q</csymbol>
</apply>
<apply><csymbol cd="relation1">lt</csymbol><ci>p</ci><ci>q</ci></apply>
</apply>
<apply><csymbol cd="relation1">lt</csymbol>
<ci>p</ci>
<apply><csymbol cd="arith1">power</csymbol>
<ci>q</ci>
<cn>2</cn>
</apply>
</apply>
</apply>
</bind>Sample Presentation
<mrow> <mo>∀</mo> <mrow> <mrow><mi>p</mi><mo>∈</mo><mi mathvariant="double-struck">Q</mi></mrow> <mo>∧</mo> <mrow><mi>q</mi><mo>∈</mo><mi mathvariant="double-struck">Q</mi></mrow> <mo>∧</mo> <mrow><mo>(</mo><mi>p</mi><mo><</mo><mi>q</mi><mo>)</mo></mrow> </mrow> <mo>.</mo> <mfenced> <mrow><mi>p</mi><mo><</mo><msup><mi>q</mi><mn>2</mn></msup></mrow> </mfenced> </mrow>
<mrow>
<mo>∀</mo>
<mrow><mi>p</mi><mo>,</mo><mi>q</mi></mrow>
<mo>.</mo>
<mfenced>
<mrow>
<mrow>
<mo>(</mo>
<mrow><mi>p</mi><mo>∈</mo><mi mathvariant="double-struck">Q</mi></mrow>
<mo>∧</mo>
<mrow><mi>q</mi><mo>∈</mo><mi mathvariant="double-struck">Q</mi></mrow>
<mo>∧</mo>
<mrow><mo>(</mo><mi>p</mi><mo><</mo><mi>q</mi><mo>)</mo></mrow>
<mo>)</mo>
</mrow>
<mo>⇒</mo>
<mrow>
<mo>(</mo>
<mi>p</mi>
<mo><</mo>
<msup><mi>q</mi><mn>2</mn></msup>
<mo>)</mo>
</mrow>
</mrow>
</mfenced>
</mrow>4.4.2.19 Existential quantifier <exists/>
| Class | quantifier |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| Qualifiers | BvarQ,DomainQ |
| OM Symbols | exists, and |
The exists element represents the existential ("there exists")
quantifier which takes one or more bound variables, and an
argument which specifies the assertion being quantified. In
addition, condition or other qualifiers may be used as
described in Section 4.3.4.8 Quantifiers (class quantifier) to limit the domain
of the bound variables.
Content MathML
<bind><exists/>
<bvar><ci>x</ci></bvar>
<apply><eq/>
<apply><ci>f</ci><ci>x</ci></apply>
<cn>0</cn>
</apply>
</bind>Sample Presentation
<mrow> <mo>∃</mo> <mi>x</mi> <mo>.</mo> <mfenced> <mrow> <mrow><mi>f</mi><mo>⁡</mo><mfenced><mi>x</mi></mfenced></mrow> <mo>=</mo> <mn>0</mn> </mrow> </mfenced> </mrow>
Content MathML
<apply><exists/>
<bvar><ci>x</ci></bvar>
<domainofapplication>
<integers/>
</domainofapplication>
<apply><eq/>
<apply><ci>f</ci><ci>x</ci></apply>
<cn>0</cn>
</apply>
</apply>Strict MathML equivalent:
<bind><csymbol cd="quant1">exists</csymbol>
<bvar><ci>x</ci></bvar>
<apply><csymbol cd="logic1">and</csymbol>
<apply><csymbol cd="set1">in</csymbol>
<ci>x</ci>
<csymbol cd="setname1">Z</csymbol>
</apply>
<apply><csymbol cd="relation1">eq</csymbol>
<apply><ci>f</ci><ci>x</ci></apply>
<cn>0</cn>
</apply>
</apply>
</bind>Sample Presentation
<mrow> <mo>∃</mo> <mi>x</mi> <mo>.</mo> <mfenced separators=""> <mrow><mi>x</mi><mo>∈</mo><mi mathvariant="double-struck">Z</mi></mrow> <mo>∧</mo> <mrow> <mrow><mi>f</mi><mo>⁡</mo><mfenced><mi>x</mi></mfenced></mrow> <mo>=</mo> <mn>0</mn> </mrow> </mfenced> </mrow>
4.4.2.20 Absolute Value <abs/>
| Class | unary-arith |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | abs |
The abs element represents the absolute value
function. The argument should be numerically valued. When the
argument is a complex number, the absolute value is often referred
to as the modulus.
Content MathML
<apply><abs/><ci>x</ci></apply>
Sample Presentation
<mrow><mo>|</mo><mi>x</mi><mo>|</mo></mrow>
4.4.2.21 Complex conjugate <conjugate/>
| Class | unary-arith |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | conjugate |
The conjugate element represents the function defined
over the complex numbers with returns the complex conjugate of
its argument.
Content MathML
<apply><conjugate/>
<apply><plus/>
<ci>x</ci>
<apply><times/><cn>ⅈ</cn><ci>y</ci></apply>
</apply>
</apply>Sample Presentation
<mover> <mrow> <mi>x</mi> <mo>+</mo> <mrow><mn>ⅈ</mn><mo>⁢</mo><mi>y</mi></mrow> </mrow> <mo>¯</mo> </mover>
4.4.2.22 Argument <arg/>
| Class | unary-arith |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | argument |
The arg element represents the unary function which
returns the angular argument of a complex number, namely the
angle which a straight line drawn from the number to zero makes
with the real line (measured anti-clockwise).
Content MathML
<apply><arg/>
<apply><plus/>
<ci> x </ci>
<apply><times/><imaginaryi/><ci>y</ci></apply>
</apply>
</apply>Sample Presentation
<mrow> <mi>arg</mi> <mo>⁡</mo> <mfenced> <mrow> <mi>x</mi> <mo>+</mo> <mrow><mi>i</mi><mo>⁢</mo><mi>y</mi></mrow> </mrow> </mfenced> </mrow>
4.4.2.23 Real part <real/>
| Class | unary-arith |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | real |
The real element represents the unary operator used to
construct an expression representing the "real" part of a
complex number, that is, the x component in x + iy.
Content MathML
<apply><real/>
<apply><plus/>
<ci>x</ci>
<apply><times/><imaginaryi/><ci>y</ci></apply>
</apply>
</apply>Sample Presentation
<mrow> <mo>ℛ</mo> <mo>⁡</mo> <mfenced> <mrow> <mi>x</mi> <mo>+</mo> <mrow><mi>i</mi><mo>⁢</mo><mi>y</mi></mrow> </mrow> </mfenced> </mrow>
4.4.2.24 Imaginary part <imaginary/>
| Class | unary-arith |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | imaginary |
The imaginary element represents the unary operator used to
construct an expression representing the "imaginary" part of a
complex number, that is, the y component in x + iy.
Content MathML
<apply><imaginary/>
<apply><plus/>
<ci>x</ci>
<apply><times/><imaginaryi/><ci>y</ci></apply>
</apply>
</apply>Sample Presentation
<mrow> <mo>ℑ</mo> <mo>⁡</mo> <mfenced> <mrow> <mi>x</mi> <mo>+</mo> <mrow><mi>i</mi><mo>⁢</mo><mi>y</mi></mrow> </mrow> </mfenced> </mrow>
4.4.2.25 Lowest common multiple <lcm/>
| Class | nary-arith |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| Qualifiers | BvarQ,DomainQ |
| OM Symbols | lcm |
The lcm element represents the n-ary operator used to
construct an expression which represents the least common multiple
of its arguments. If no argument is provided, the lcm is 1. If one
argument is provided, the lcm is that argument. The least common
multiple of x and 1 is x.
Content MathML
<apply><lcm/><ci>a</ci><ci>b</ci><ci>c</ci></apply>
Sample Presentation
<mrow> <mi>lcm</mi> <mo>⁡</mo> <mfenced><mi>a</mi><mi>b</mi><mi>c</mi></mfenced> </mrow>
This default rendering is English-language locale specific: other locales may have different default renderings.
4.4.2.26 Floor <floor/>
| Class | unary-arith |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | floor |
The floor element represents the operation that rounds
down (towards negative infinity) to the nearest integer. This
function takes one real number as an argument and returns an
integer.
Content MathML
<apply><floor/><ci>a</ci></apply>
Sample Presentation
<mrow><mo>⌊</mo><mi>a</mi><mo>⌋</mo></mrow>
4.4.2.27 Ceiling <ceiling/>
| Class | unary-arith |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | ceiling |
The ceiling element represents the operation that rounds
up (towards positive infinity) to the nearest integer. This function
takes one real number as an argument and returns an integer.
Content MathML
<apply><ceiling/><ci>a</ci></apply>
Sample Presentation
<mrow><mo>⌈</mo><mi>a</mi><mo>⌉</mo></mrow>
4.4.3 Relations
4.4.3.1 Equals <eq/>
| Class | nary-reln |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| Qualifiers | BvarQ,DomainQ |
| OM Symbols | eq |
The eq elements represents the equality relation. While equality is a binary relation,
el may be used with more than two arguments, denoting a chain
of equalities, as described in Section 4.3.4.3 N-ary Relations (classes nary-reln, nary-set-reln).
Content MathML
<apply><eq/> <cn type="rational">2<sep/>4</cn> <cn type="rational">1<sep/>2</cn> </apply>
Sample Presentation
<mrow> <mrow><mn>2</mn><mo>/</mo><mn>4</mn></mrow> <mo>=</mo> <mrow><mn>1</mn><mo>/</mo><mn>2</mn></mrow> </mrow>
4.4.3.2 Not Equals <neq/>
| Class | binary-reln |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | neq |
The neq element represents the binary inequality
relation, i.e. the relation "not equal to" which returns true unless
the two arguments are equal.
Content MathML
<apply><neq/><cn>3</cn><cn>4</cn></apply>
Sample Presentation
<mrow><mn>3</mn><mo>≠</mo><mn>4</mn></mrow>
4.4.3.3 Greater than <gt/>
| Class | nary-reln |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| Qualifiers | BvarQ,DomainQ |
| OM Symbols | gt |
The gt element represents the "greater than" function
which returns true if the first argument is greater than the second, and
returns false otherwise. While this is a binary relation,
gt may be used with more than two arguments, denoting a chain
of inequalities, as described in Section 4.3.4.3 N-ary Relations (classes nary-reln, nary-set-reln).
Content MathML
<apply><gt/><cn>3</cn><cn>2</cn></apply>
Sample Presentation
<mrow><mn>3</mn><mo>></mo><mn>2</mn></mrow>
4.4.3.4 Less Than <lt/>
| Class | nary-reln |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| Qualifiers | BvarQ,DomainQ |
| OM Symbols | lt |
The lt element represents the "less than" function
which returns true if the first argument is less than the second, and
returns false otherwise. While this is a binary relation,
lt may be used with more than two arguments, denoting a chain
of inequalities, as described in Section 4.3.4.3 N-ary Relations (classes nary-reln, nary-set-reln).
Content MathML
<apply><lt/><cn>2</cn><cn>3</cn><cn>4</cn></apply>
Sample Presentation
<mrow><mn>2</mn><mo><</mo><mn>3</mn><mo><</mo><mn>4</mn></mrow>
4.4.3.5 Greater Than or Equal <geq/>
| Class | nary-reln |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| Qualifiers | BvarQ,DomainQ |
| OM Symbols | geq |
The geq element represents the "greater than or equal to" function
which returns true if the first argument is greater than or equal to
the second, and returns false otherwise. While this is a binary relation,
geq may be used with more than two arguments, denoting a chain
of inequalities, as described in Section 4.3.4.3 N-ary Relations (classes nary-reln, nary-set-reln).
Content MathML
<apply><geq/><cn>4</cn><cn>3</cn><cn>3</cn></apply>
Strict Content MathML
<apply><csymbol cd="fns2">predicate_on_list</csymbol> <csymbol cd="reln1">geq</csymbol> <apply><csymbol cd="list1">list</csymbol> <cn>4</cn><cn>3</cn><cn>3</cn> </apply> </apply>
Sample Presentation
<mrow><mn>4</mn><mo>≥</mo><mn>3</mn><mo>≥</mo><mn>3</mn></mrow>
4.4.3.6 Less Than or Equal <leq/>
| Class | nary-reln |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| Qualifiers | BvarQ,DomainQ |
| OM Symbols | leq |
The leq element represents the "less than or equal to" function
which returns true if the first argument is less than or equal to
the second, and returns false otherwise. While this is a binary relation,
leq may be used with more than two arguments, denoting a chain
of inequalities, as described in Section 4.3.4.3 N-ary Relations (classes nary-reln, nary-set-reln).
Content MathML
<apply><leq/><cn>3</cn><cn>3</cn><cn>4</cn></apply>
Sample Presentation
<mrow><mn>3</mn><mo>≤</mo><mn>3</mn><mo>≤</mo><mn>4</mn></mrow>
4.4.3.7 Equivalent <equivalent/>
| Class | binary-logical |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | equivalent |
The equivalent element represents the relation that
asserts two Boolean expressions are logically equivalent,
that is have the same Boolean value for any inputs.
Content MathML
<apply><equivalent/> <ci>a</ci> <apply><not/><apply><not/><ci>a</ci></apply></apply> </apply>
Sample Presentation
<mrow> <mi>a</mi> <mo>≡</mo> <mrow><mo>¬</mo><mrow><mo>¬</mo><mi>a</mi></mrow></mrow> </mrow>
4.4.3.8 Approximately <approx/>
| Class | binary-reln |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | approx |
The approx element represent the relation that asserts
the approximate equality of its arguments.
Content MathML
<apply><approx/> <pi/> <cn type="rational">22<sep/>7</cn> </apply>
Sample Presentation
<mrow> <mi>π</mi> <mo>≃</mo> <mrow><mn>22</mn><mo>/</mo><mn>7</mn></mrow> </mrow>
4.4.3.9 Factor Of <factorof/>
| Class | binary-reln |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | factorof |
The factorof element is used to indicate the
mathematical relationship that the first argument "is a factor of"
the second. This relationship is true if and only
if b mod a = 0.
Content MathML
<apply><factorof/><ci>a</ci><ci>b</ci></apply>
Sample Presentation
<mrow><mi>a</mi><mo>|</mo><mi>b</mi></mrow>
4.4.4 Calculus and Vector Calculus
4.4.4.1 Integral <int/>
| Class | int |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| Qualifiers | BvarQ,DomainQ |
| OM Symbols | int defint |
The int element is the operator element for a definite or indefinite integral
over a function or a definite over an expression with a bound variable.
Content MathML
<apply><eq/> <apply><int/><sin/></apply> <cos/> </apply>
Sample Presentation
<mrow><mrow><mi>∫</mi><mi>sin</mi></mrow><mo>=</mo><mi>cos</mi></mrow>
Content MathML
<apply><int/> <interval><ci>a</ci><ci>b</ci></interval> <cos/> </apply>
Sample Presentation
<mrow> <msubsup><mi>∫</mi><mi>a</mi><mi>b</mi></msubsup><mi>cos</mi> </mrow>
The int element can also be used with bound variables serving as the
integration variables.
Content MathML
Here, definite integrals are indicated by providing qualifier elements specifying a
domain of integration (here a lowlimit/uplimit pair). This is perhaps
the most "standard" representation of this integral:
<apply><int/> <bvar><ci>x</ci></bvar> <lowlimit><cn>0</cn></lowlimit> <uplimit><cn>1</cn></uplimit> <apply><power/><ci>x</ci><cn>2</cn></apply> </apply>
Sample Presentation
<mrow> <msubsup><mi>∫</mi><mn>0</mn><mn>1</mn></msubsup> <msup><mi>x</mi><mn>2</mn></msup> <mi>d</mi> <mi>x</mi> </mrow>
Mapping to Strict Markup
As an indefinite integral applied to a function, the int element corresponds to
the int symbol from the calculus1 content
dictionary. As a definite integral applied to a function, the int element
corresponds to the defint symbol
from the calculus1 content dictionary.
When no bound variables are present, the translation of an indefinite integral to Strict Content Markup is straight forward. When bound variables are present, the following rule should be used.
Rewrite: int
Translate an indefinite integral, where
is an
arbitrary expression involving the bound variable(s)
<apply><int/> <bvar> </bvar> </apply>
to the expression
<apply>
<apply><csymbol cd="calculus1">int</csymbol>
<bind><csymbol cd="fns1">lambda</csymbol>
<bvar> </bvar>
</bind>
</apply>
</apply>Note that as x is not bound in the original indefinite integral, the integrated function is applied to the variable x making it an explicit free variable in Strict Content Markup expression, even though it is bound in the subterm used as an argument to int.
For instance, the expression
<apply><int/> <bvar><ci>x</ci></bvar> <apply><cos/><ci>x</ci></apply> </apply>
has the Strict Content MathML equivalent
<apply>
<apply><csymbol cd="calculus1">int</csymbol>
<bind><csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<apply><cos/><ci>x</ci></apply>
</bind>
</apply>
<ci>x</ci>
</apply>
For a definite integral without bound variables, the translation is also straightforward.
For instance, the integral of a differential form f over an arbitrary domain C represented as
<apply><int/> <domainofapplication><ci>C</ci></domainofapplication> <ci>f</ci> </apply>
is equivalent to the Strict Content MathML:
<apply><csymbol cd="calculus1">defint</csymbol><ci>C</ci><ci>f</ci></apply>
Note, however, the additional remarks on the translations of other kinds of qualifiers that may be used to specify a domain of integration in the rules for definite integrals following.
When bound variables are present, the situation is more complicated in general, and the following rules are used.
Rewrite: defint
Translate a definite integral, where
is an
arbitrary expression involving the bound variable(s)
<apply><int/> <bvar> </bvar> <domainofapplication> </domainofapplication> </apply>
to the expression
<apply><csymbol cd="calculus1">defint</csymbol> <bind><csymbol cd="fns1">lambda</csymbol> <bvar> </bvar> </bind> </apply>
But the definite integral with an lowlimit/uplimit pair carries the
strong intuition that the range of integration is oriented, and thus swapping lower and
upper limits will change the sign of the result. To accommodate this, use the following special
translation rule:
Rewrite: defint limits
<apply><int/> <bvar> </bvar> <lowlimit> </lowlimit> <uplimit> </uplimit> </apply>
where
is an expression in the variable x
is translated to to the expression:
<apply><csymbol cd="calculus1">defint</csymbol>
<apply><csymbol cd="interval1">oriented_interval</csymbol>
</apply>
<bind><csymbol cd="fns1">lambda</csymbol>
<bvar> </bvar>
</bind>
</apply>The oriented_interval
symbol is also used when translating the interval
qualifier, when it is used to specify the domain of integration.
Integration is assumed to proceed from the left endpoint to the
right endpoint.
The case for multiple integrands is treated analogously.
Note that use of the condition
qualifier also
requires special treatment. In particular, it extends to multivariate domains by
using extra bound variables and a domain corresponding to a cartesian product as in:
<bind><int/>
<bvar><ci>x</ci></bvar>
<bvar><ci>y</ci></bvar>
<condition>
<apply><and/>
<apply><leq/><cn>0</cn><ci>x</ci></apply>
<apply><leq/><ci>x</ci><cn>1</cn></apply>
<apply><leq/><cn>0</cn><ci>y</ci></apply>
<apply><leq/><ci>y</ci><cn>1</cn></apply>
</apply>
</condition>
<apply><times/>
<apply><power/><ci>x</ci><cn>2</cn></apply>
<apply><power/><ci>y</ci><cn>3</cn></apply>
</apply>
</bind>Strict Content MathML equivalent
<apply><csymbol cd="calculus1">defint</csymbol>
<apply><csymbol cd="set1">suchthat</csymbol>
<apply><csymbol cd="set1">cartesianproduct</csymbol>
<csymbol cd="setname1">R</csymbol>
<csymbol cd="setname1">R</csymbol>
</apply>
<apply><csymbol cd="logic1">and</csymbol>
<apply><csymbol cd="arith1">leq</csymbol><cn>0</cn><ci>x</ci></apply>
<apply><csymbol cd="arith1">leq</csymbol><ci>x</ci><cn>1</cn></apply>
<apply><csymbol cd="arith1">leq</csymbol><cn>0</cn><ci>y</ci></apply>
<apply><csymbol cd="arith1">leq</csymbol><ci>y</ci><cn>1</cn></apply>
</apply>
<bind><csymbol cd="fns11">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<bvar><ci>y</ci></bvar>
<apply><csymbol cd="arith1">times</csymbol>
<apply><csymbol cd="arith1">power</csymbol><ci>x</ci><cn>2</cn></apply>
<apply><csymbol cd="arith1">power</csymbol><ci>y</ci><cn>3</cn></apply>
</apply>
</bind>
</apply>
</apply>4.4.4.2 Differentiation <diff/>
| Class | Differential-Operator |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | diff |
The diff element is the differentiation operator element for functions or
expressions of a single variable. It may be applied directly to an actual function
thereby denoting a function which is the derivative of the original function, or it can be
applied to an expression involving a single variable.
Content MathML
<apply><diff/><ci>f</ci></apply>
Sample Presentation
<msup><mi>f</mi><mo>′</mo></msup>
Content MathML
<apply><eq/>
<apply><diff/>
<bvar><ci>x</ci></bvar>
<apply><sin/><ci>x</ci></apply>
</apply>
<apply><cos/><ci>x</ci></apply>
</apply>Sample Presentation
<mrow> <mfrac> <mrow><mi>d</mi><mrow><mi>sin</mi><mo>⁡</mo><mi>x</mi></mrow></mrow> <mrow><mi>d</mi><mi>x</mi></mrow> </mfrac> <mo>=</mo> <mrow><mi>cos</mi><mo>⁡</mo><mi>x</mi></mrow> </mrow>
The bvar element may also contain a degree element, which specifies
the order of the derivative to be taken.
Content MathML
<apply><diff/> <bvar><ci>x</ci><degree><cn>2</cn></degree></bvar> <apply><power/><ci>x</ci><cn>4</cn></apply> </apply>
Sample Presentation
<mfrac> <mrow> <msup><mi>d</mi><mn>2</mn></msup> <msup><mi>x</mi><mn>4</mn></msup> </mrow> <mrow><mi>d</mi><msup><mi>x</mi><mn>2</mn></msup></mrow> </mfrac>
Mapping to Strict Markup
For the translation to strict Markup it is crucial to realize that in the expression case, the variable is actually not bound by the differentiation operator.
Rewrite: diff
Translate an expression
<apply><diff/> <bvar> </bvar> </apply>
where
is an
expression in the variable x
to the expression
<apply>
<apply><csymbol cd="calculus1">diff</csymbol>
<bind><csymbol cd="fns1">lambda</csymbol>
<bvar> </bvar>
</bind>
</apply>
</apply>Note that the differentiated function is applied to the variable x making its status as a free variable explicit in strict markup. Thus the strict equivalent of
<apply><diff/> <bvar><ci>x</ci></bvar> <apply><sin/><ci>x</ci></apply> </apply>
is
<apply>
<apply><csymbol cd="calculus1">diff</csymbol>
<bind><csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<apply><csymbol cd="transc1">sin</csymbol><ci>x</ci></apply>
</bind>
</apply>
<ci>x</ci>
</apply>If the bvar element contains a degree element, use the
nthdiff symbol.
Rewrite: nthdiff
<apply><diff/> <bvar> <degree> </degree></bvar> </apply>
where
is an
is an expression in the variable x
is translated to to the expression:
<apply>
<apply><csymbol cd="calculus1">nthdiff</csymbol>
<bind><csymbol cd="fns1">lambda</csymbol>
<bvar> </bvar>
</bind>
</apply>
</apply>For example
<apply><diff/> <bvar><degree><cn>2</cn></degree><ci>x</ci></bvar> <apply><sin/><ci>x</ci></apply> </apply>
Strict Content MathML equivalent
<apply>
<apply><csymbol cd="calculus1">nthdiff</csymbol>
<cn>2</cn>
<bind><csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<apply><csymbol cd="transc1">sin</csymbol><ci>x</ci></apply>
</bind>
</apply>
<ci>x</ci>
</apply>4.4.4.3 Partial Differentiation <partialdiff/>
| Class | partialdiff |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | partialdiff partialdiffdegree |
The partialdiff element is the partial differentiation operator element for
functions or expressions in several variables.
For the case of partial differentiation of a function, the
containing partialdiff takes two arguments: firstly a list of
indices indicating by position which function arguments are involved in
constructing the partial derivatives, and secondly the actual function
to be partially differentiated. The indices may be repeated.
Content MathML
<apply><partialdiff/> <list><cn>1</cn><cn>1</cn><cn>3</cn></list> <ci type="function">f</ci> </apply>
Sample Presentation
<mrow> <msub> <mi>D</mi> <mrow><mn>1</mn><mo>,</mo><mn>1</mn><mo>,</mo><mn>3</mn></mrow> </msub> <mi>f</mi> </mrow>
Content MathML
<apply><partialdiff/> <list><cn>1</cn><cn>1</cn><cn>3</cn></list> <lambda> <bvar><ci>x</ci></bvar> <bvar><ci>y</ci></bvar> <bvar><ci>z</ci></bvar> <apply><ci>f</ci><ci>x</ci><ci>y</ci><ci>z</ci></apply> </lambda> </apply>
Sample Presentation
<mfrac> <mrow> <msup><mo>∂</mo><mn>3</mn></msup> <mrow> <mi>f</mi><mo>⁡</mo><mfenced><mi>x</mi><mi>y</mi><mi>z</mi></mfenced> </mrow> </mrow> <mrow> <mrow><mo>∂</mo><msup><mi>x</mi><mn>2</mn></msup></mrow> <mrow><mo>∂</mo><mi>z</mi></mrow> </mrow> </mfrac>
In the case of algebraic expressions, the bound variables are given by bvar
elements, which are children of the containing apply element. The bvar
elements may also contain degree element, which specify the order of the partial
derivative to be taken in that variable.
Content MathML
<apply><partialdiff/> <bvar><ci>x</ci></bvar> <bvar><ci>y</ci></bvar> <apply><ci type="function">f</ci><ci>x</ci><ci>y</ci></apply> </apply>
Sample Presentation
<mfrac> <mrow> <msup><mo>∂</mo><mn>2</mn></msup> <mrow> <mi>f</mi> <mo>⁡</mo> <mfenced><mi>x</mi><mi>y</mi></mfenced> </mrow> </mrow> <mrow> <mrow><mo>∂</mo><mi>x</mi></mrow> <mrow><mo>∂</mo><mi>y</mi></mrow> </mrow> </mfrac>
Where a total degree of differentiation must be specified, this is
indicated by use of a degree element at the top level,
i.e. without any associated bvar, as a child of the
containing apply element.
Content MathML
<apply><partialdiff/>
<bvar><ci>x</ci><degree><ci>m</ci></degree></bvar>
<bvar><ci>y</ci><degree><ci>n</ci></degree></bvar>
<degree><ci>k</ci></degree>
<apply><ci type="function">f</ci>
<ci>x</ci>
<ci>y</ci>
</apply>
</apply>Sample Presentation
<mfrac> <mrow> <msup><mo>∂</mo><mi>k</mi></msup> <mrow> <mi>f</mi><mo>⁡</mo><mfenced><mi>x</mi><mi>y</mi></mfenced> </mrow> </mrow> <mrow> <mrow><mo>∂</mo><msup><mi>x</mi><mi>m</mi></msup></mrow> <mrow><mo>∂</mo><msup><mi>y</mi><mi>n</mi></msup></mrow> </mrow> </mfrac>
Mapping to Strict Markup
When applied to a function, the partialdiff element
corresponds to the partialdiff
symbol from the calculus1 content dictionary. No special
rules are necessary as the two arguments of partialdiff
translate directly to the two arguments of
partialdiff.
Rewrite: partialdiffdegree
If partialdiff is used with an expression and
bvar qualifiers it is rewritten to
Strict Content MathML using the
partialdiffdegree symbol.
<apply><partialdiff/> <bvar> <degree> </degree></bvar> <bvar> <degree> </degree></bvar> <degree> </degree> </apply>
is an
arbitrary expression involving the bound variables.
<apply>
<apply><csymbol cd="calculus1">partialdiffdegree</csymbol>
<apply><csymbol cd="list1">list</csymbol>
</apply>
<bind><csymbol cd="fns1">lambda</csymbol>
<bvar> </bvar>
<bvar> </bvar>
</bind>
</apply>
</apply>If any of the bound variables do not use a degree qualifier,
<cn>1</cn> should be used in place of the degree.
If the original expression did not use the total degree qualifier then
the second argument to partialdiffdegree
should be the sum of the degrees, for example
<apply><csymbol cd="arith1">plus</csymbol> </apply>
With this rule, the expression
<apply><partialdiff/>
<bvar><ci>x</ci><degree><ci>n</ci></degree></bvar>
<bvar><ci>y</ci><degree><ci>m</ci></degree></bvar>
<apply><sin/>
<apply><times/><ci>x</ci><ci>y</ci></apply>
</apply>
</apply>is translated into
<apply>
<apply><csymbol cd="calculus1">partialdiffdegree</csymbol>
<apply><csymbol cd="list1">list</csymbol>
<ci>n</ci><ci>m</ci>
</apply>
<apply><csymbol cd="arith1">plus</csymbol>
<ci>n</ci><ci>m</ci>
</apply>
<bind><csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<bvar><ci>y</ci></bvar>
<apply><csymbol cd="transc1">sin</csymbol>
<apply><csymbol cd="arith1">times</csymbol>
<ci>x</ci><ci>y</ci>
</apply>
</apply>
</bind>
<ci>x</ci>
<ci>y</ci>
</apply>
</apply>4.4.4.4 Divergence <divergence/>
| Class | unary-veccalc |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | divergence |
The divergence element is the vector calculus divergence
operator, often called div. It represents the divergence function
which takes one argument which should be a vector of scalar-valued
functions, intended to represent a vector-valued function, and returns
the scalar-valued function giving the divergence of the argument.
Content MathML
<apply><divergence/><ci>a</ci></apply>
Sample Presentation
<mrow><mi>div</mi><mo>⁡</mo><mfenced><mi>a</mi></mfenced></mrow>
Content MathML
<apply><divergence/> <ci type="vector">E</ci> </apply>
Sample Presentation
<mrow><mi>div</mi><mo>⁡</mo><mfenced><mi>E</mi></mfenced></mrow>
<mrow><mo>∇</mo><mo>⋅</mo><mi>E</mi></mrow>
The functions defining the coordinates may be defined implicitly as expressions defined in terms of the coordinate names, in which case the coordinate names must be provided as bound variables.
Content MathML
<apply><divergence/>
<bvar><ci>x</ci></bvar>
<bvar><ci>y</ci></bvar>
<bvar><ci>z</ci></bvar>
<vector>
<apply><plus/><ci>x</ci><ci>y</ci></apply>
<apply><plus/><ci>x</ci><ci>z</ci></apply>
<apply><plus/><ci>z</ci><ci>y</ci></apply>
</vector>
</apply>Sample Presentation
<mrow> <mi>div</mi> <mo>⁡</mo> <mo>(</mo> <mtable> <mtr><mtd> <mi>x</mi> <mo>↦</mo> <mrow><mi>x</mi><mo>+</mo><mi>y</mi></mrow> </mtd></mtr> <mtr><mtd> <mi>y</mi> <mo>↦</mo> <mrow><mi>x</mi><mo>+</mo><mi>z</mi></mrow> </mtd></mtr> <mtr><mtd> <mi>z</mi> <mo>↦</mo> <mrow><mi>z</mi><mo>+</mo><mi>y</mi></mrow> </mtd></mtr> </mtable> <mo>)</mo> </mrow>
4.4.4.5 Gradient <grad/>
| Class | unary-veccalc |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | grad |
The grad element is the vector calculus gradient operator, often called
grad. It is used to represent the grad function, which takes one
argument which should be a scalar-valued function and returns a
vector of functions.
Content MathML
<apply><grad/><ci type="function">f</ci></apply>
Sample Presentation
<mrow><mi>grad</mi><mo>⁡</mo><mfenced><mi>f</mi></mfenced></mrow>
<mrow><mo>∇</mo><mo>⁡</mo><mfenced><mi>f</mi></mfenced></mrow>
The functions defining the coordinates may be defined implicitly as expressions defined in terms of the coordinate names, in which case the coordinate names must be provided as bound variables.
Content MathML
<apply><grad/> <bvar><ci>x</ci></bvar> <bvar><ci>y</ci></bvar> <bvar><ci>z</ci></bvar> <apply><times/><ci>x</ci><ci>y</ci><ci>z</ci></apply> </apply>
Sample Presentation
<mrow> <mi>grad</mi> <mo>⁡</mo> <mrow> <mo>(</mo> <mfenced><mi>x</mi><mi>y</mi><mi>z</mi></mfenced> <mo>↦</mo> <mrow> <mi>x</mi><mo>⁢</mo><mi>y</mi><mo>⁢</mo><mi>z</mi> </mrow> <mo>)</mo> </mrow> </mrow>
4.4.4.6 Curl <curl/>
| Class | unary-veccalc |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | curl |
The curl element is used to represent the curl function
of vector calculus. It takes one argument which should be a vector
of scalar-valued functions, intended to represent a vector-valued
function, and returns a vector of functions.
Content MathML
<apply><curl/><ci>a</ci></apply>
Sample Presentation
<mrow><mi>curl</mi><mo>⁡</mo><mfenced><mi>a</mi></mfenced></mrow>
<mrow><mo>∇</mo><mo>×</mo><mi>a</mi></mrow>
The functions defining the coordinates may be defined implicitly as expressions defined in terms of the coordinate names, in which case the coordinate names must be provided as bound variables.
4.4.4.7 Laplacian <laplacian/>
| Class | unary-veccalc |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | Laplacian |
The laplacian element represents the Laplacian operator of
vector calculus. The Laplacian takes a single argument which is a
vector of scalar-valued functions representing a vector-valued
function, and returns a vector of functions.
Content MathML
<apply><laplacian/><ci type="vector">E</ci></apply>
Sample Presentation
<mrow> <msup><mo>∇</mo><mn>2</mn></msup> <mo>⁡</mo> <mfenced><mi>E</mi></mfenced> </mrow>
The functions defining the coordinates may be defined implicitly as expressions defined in terms of the coordinate names, in which case the coordinate names must be provided as bound variables.
Content MathML
<apply><laplacian/> <bvar><ci>x</ci></bvar> <bvar><ci>y</ci></bvar> <bvar><ci>z</ci></bvar> <apply><ci>f</ci><ci>x</ci><ci>y</ci></apply> </apply>
Sample Presentation
<mrow> <msup><mo>∇</mo><mn>2</mn></msup> <mo>⁡</mo> <mrow> <mo>(</mo> <mfenced><mi>x</mi><mi>y</mi><mi>z</mi></mfenced> <mo>↦</mo> <mrow><mi>f</mi><mo>⁡</mo><mfenced><mi>x</mi><mi>y</mi></mfenced></mrow> <mo>)</mo> </mrow> </mrow>
4.4.5 Theory of Sets
4.4.5.1 Set <set>
| Class | nary-setlist-constructor |
|---|---|
| Attributes | CommonAtt, DefEncAtt, type? |
type Attribute Values
|
"set" | "multiset" | text |
| Content | ContExp* |
| Qualifiers | BvarQ,DomainQ |
| OM Symbols | set, multiset |
The set represents a function which constructs
mathematical sets from its arguments. It is an n-ary function. The
members of the set to be constructed may be given explicitly as
child elements of the constructor, or specified by rule as described
in Section 4.3.1.1 Container Markup for Constructor Symbols. There is no implied ordering to
the elements of a set.
Content MathML
<set> <ci>a</ci><ci>b</ci><ci>c</ci> </set>
Sample Presentation
<mrow>
<mo>{</mo><mi>a</mi><mo>,</mo><mi>b</mi><mo>,</mo><mi>c</mi><mo>}</mo>
</mrow>In general, a set can be constructed by providing a function and a domain of application. The elements of the set correspond to the values obtained by evaluating the function at the points of the domain.
Content MathML
<set>
<bvar><ci>x</ci></bvar>
<condition>
<apply><lt/><ci>x</ci><cn>5</cn></apply>
</condition>
<ci>x</ci>
</set>Sample Presentation
<mrow>
<mo>{</mo>
<mi>x</mi>
<mo>|</mo>
<mrow><mi>x</mi><mo><</mo><mn>5</mn></mrow>
<mo>}</mo>
</mrow>Content MathML
<set>
<bvar><ci type="set">S</ci></bvar>
<condition>
<apply><in/><ci>S</ci><ci type="list">T</ci></apply>
</condition>
<ci>S</ci>
</set>Sample Presentation
<mrow>
<mo>{</mo>
<mi>S</mi>
<mo>|</mo>
<mrow><mi>S</mi><mo>∈</mo><mi>T</mi></mrow>
<mo>}</mo>
</mrow>Content MathML
<set>
<bvar><ci> x </ci></bvar>
<condition>
<apply><and/>
<apply><lt/><ci>x</ci><cn>5</cn></apply>
<apply><in/><ci>x</ci><naturalnumbers/></apply>
</apply>
</condition>
<ci>x</ci>
</set>Sample Presentation
<mrow>
<mo>{</mo>
<mi>x</mi>
<mo>|</mo>
<mrow>
<mrow><mo>(</mo><mi>x</mi><mo><</mo><mn>5</mn><mo>)</mo></mrow>
<mo>∧</mo>
<mrow>
<mi>x</mi><mo>∈</mo><mi mathvariant="double-struck">N</mi>
</mrow>
</mrow>
<mo>}</mo>
</mrow>4.4.5.2 List <list>
| Class | nary-setlist-constructor |
|---|---|
| Attributes | CommonAtt, DefEncAtt, order |
order Attribute Values
|
"numeric" | "lexicographic" |
| Content | ContExp* |
| Qualifiers | BvarQ,DomainQ |
| OM Symbols | interval_cc, list |
The list elements represents the n-ary function which
constructs a list from its arguments. Lists differ from sets in that
there is an explicit order to the elements.
The list entries and order may be given explicitly.
Content MathML
<list> <ci>a</ci><ci>b</ci><ci>c</ci> </list>
Sample Presentation
<mrow> <mo>(</mo><mi>a</mi><mo>,</mo><mi>b</mi><mo>,</mo><mi>c</mi><mo>)</mo> </mrow>
In general a list can be constructed by providing a function and
a domain of application. The elements of the list correspond to the
values obtained by evaluating the function at the points of the
domain. When this method is used, the ordering of the list elements
may not be clear, so the kind of ordering may be specified by the
order attribute. Two orders are supported: lexicographic
and numeric.
Content MathML
<list order="numeric">
<bvar><ci>x</ci></bvar>
<condition>
<apply><lt/><ci>x</ci><cn>5</cn></apply>
</condition>
</list>Sample Presentation
<mrow> <mo>(</mo> <mi>x</mi> <mo>|</mo> <mrow><mi>x</mi><mo><</mo><mn>5</mn></mrow> <mo>)</mo> </mrow>
4.4.5.3 Union <union/>
| Class | nary-set |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| Qualifiers | BvarQ,DomainQ |
| OM Symbols | union |
The union element is used to denote the n-ary union of sets. It takes sets as arguments,
and denotes the set that contains all the elements that occur in any
of them.
Arguments may be explicitly specified.
Content MathML
<apply><union/><ci>A</ci><ci>B</ci></apply>
Sample Presentation
<mrow><mi>A</mi><mo>∪</mo><mi>B</mi></mrow>
Arguments may also be specified using qualifier elements as described in Section 4.3.4.1 N-ary Operators (classes nary-arith, nary-functional, nary-logical, nary-linalg, nary-set, nary-constructor). operator element can be used as a binding operator to construct the union over a collection of sets.
Content MathML
<apply><union/>
<bvar><ci type="set">S</ci></bvar>
<domainofapplication>
<ci type="list">L</ci>
</domainofapplication>
<ci type="set"> S</ci>
</apply>Sample Presentation
<mrow><munder><mo>⋃</mo><mi>L</mi></munder><mi>S</mi></mrow>
4.4.5.4 Intersect <intersect/>
| Class | nary-set |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| Qualifiers | BvarQ,DomainQ |
| OM Symbols | intersect |
The intersect element is used to denote the n-ary
intersection of sets. It takes sets as arguments, and denotes the
set that contains all the elements that occur in all of them. Its arguments may be explicitly specified in the
enclosing apply element, or specified using qualifier
elements as described in Section 4.3.4.1 N-ary Operators (classes nary-arith, nary-functional, nary-logical,
nary-linalg, nary-set, nary-constructor).
Content MathML
<apply><intersect/> <ci type="set"> A </ci> <ci type="set"> B </ci> </apply>
Sample Presentation
<mrow><mi>A</mi><mo>∩</mo><mi>B</mi></mrow>
Content MathML
<apply><intersect/> <bvar><ci type="set">S</ci></bvar> <domainofapplication><ci type="list">L</ci></domainofapplication> <ci type="set"> S </ci> </apply>
Sample Presentation
<mrow><munder><mo>⋂</mo><mi>L</mi></munder><mi>S</mi></mrow>
4.4.5.5 Set inclusion <in/>
| Class | binary-set |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | in |
The in element represents the set inclusion relation.
It has two arguments, an element and a set. It is used to denote
that the element is in the given set.
Content MathML
<apply><in/><ci>a</ci><ci type="set">A</ci></apply>
Sample Presentation
<mrow><mi>a</mi><mo>∈</mo><mi>A</mi></mrow>
When translating to Strict Content Markup, if the type
has value "multiset", then the in symbol from multiset1 should
be used instead.
4.4.5.6 Set exclusion <notin/>
| Class | binary-set |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | notin |
The notin represents the negated set inclusion
relation. It has two arguments, an element and a set. It is
used to denote that the element is not in the given set.
Content MathML
<apply><notin/><ci>a</ci><ci type="set">A</ci></apply>
Sample Presentation
<mrow><mi>a</mi><mo>∉</mo><mi>A</mi></mrow>
When translating to Strict Content Markup, if the type has value "multiset", then
the in symbol from multiset1 should be used instead.
4.4.5.7 Subset <subset/>
| Class | nary-set-reln |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | subset |
The subset element represents the subset relation. It is used to denote that the
first argument is a subset of the second. As described in Section 4.3.4.3 N-ary Relations (classes nary-reln, nary-set-reln), it may also be used as an n-ary operator to express
that each argument is a subset of its predecessor.
Content MathML
<apply><subset/> <ci type="set">A</ci> <ci type="set">B</ci> </apply>
Sample Presentation
<mrow><mi>A</mi><mo>⊆</mo><mi>B</mi></mrow>
4.4.5.8 Proper Subset <prsubset/>
| Class | nary-set-reln |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | prsubset |
The prsubset element represents the proper subset
relation, i.e. that the first argument is a proper subset of the
second. As described in Section 4.3.4.3 N-ary Relations (classes nary-reln, nary-set-reln), it may
also be used as an n-ary operator to express that each argument is a
proper subset of its predecessor.
Content MathML
<apply><prsubset/> <ci type="set">A</ci> <ci type="set">B</ci> </apply>
Sample Presentation
<mrow><mi>A</mi><mo>⊂</mo><mi>B</mi></mrow>
4.4.5.9 Not Subset <notsubset/>
| Class | binary-set |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | notsubset |
The notsubset element represents the negated subset
relation. It is used to denote that the first argument is not a subset of the
second.
Content MathML
<apply><notsubset/> <ci type="set">A</ci> <ci type="set">B</ci> </apply>
Sample Presentation
<mrow><mi>A</mi><mo>⊈</mo><mi>B</mi></mrow>
When translating to Strict Content Markup, if the type has value "multiset", then
the in symbol from multiset1 should be used instead.
4.4.5.10 Not Proper Subset <notprsubset/>
| Class | binary-set |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | notprsubset |
The notprsubset element represents the negated proper
subset relation. It is used to denote that the first argument is not
a proper subset of the second.
Content MathML
<apply><notprsubset/> <ci type="set">A</ci> <ci type="set">B</ci> </apply>
Sample Presentation
<mrow><mi>A</mi><mo>⊄</mo><mi>B</mi></mrow>
When translating to Strict Content Markup, if the type has value "multiset", then
the in symbol from multiset1 should be used instead.
4.4.5.11 Set Difference <setdiff/>
| Class | binary-set |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | setdiff, setdiff |
The setdiff element represents set difference
operator. It takes two sets as arguments, and denotes the set that
contains all the elements that occur in the first set, but not in
the second.
Content MathML
<apply><setdiff/> <ci type="set">A</ci> <ci type="set">B</ci> </apply>
Sample Presentation
<mrow><mi>A</mi><mo>∖</mo><mi>B</mi></mrow>
When translating to Strict Content Markup, if the type has value "multiset", then
the in symbol from multiset1 should be used instead.
4.4.5.12 Cardinality <card/>
| Class | unary-set |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | size, size |
The card element represents the cardinality function,
which takes a set argument and returns its cardinality, i.e. the
number of elements in the set. The cardinality of a set is a
non-negative integer, or an infinite cardinal number.
Content MathML
<apply><eq/> <apply><card/><ci>A</ci></apply> <cn>5</cn> </apply>
Sample Presentation
<mrow> <mrow><mo>|</mo><mi>A</mi><mo>|</mo></mrow> <mo>=</mo> <mn>5</mn> </mrow>
When translating to Strict Content Markup, if the type
has value "multiset", then the size symbol from multiset1 should be used
instead.
4.4.5.13 Cartesian product <cartesianproduct/>
| Class | nary-set |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| Qualifiers | BvarQ,DomainQ |
| OM Symbols | cartesian_product |
The cartesianproduct element is used to represents the
Cartesian product operator. It takes sets as arguments, which may be
explicitly specified in the enclosing apply element, or
specified using qualifier elements as described in Section 4.3.4.1 N-ary Operators (classes nary-arith, nary-functional, nary-logical,
nary-linalg, nary-set, nary-constructor).
Content MathML
<apply><cartesianproduct/><ci>A</ci><ci>B</ci></apply>
Sample Presentation
<mrow><mi>A</mi><mo>×</mo><mi>B</mi></mrow>
4.4.6 Sequences and Series
4.4.6.1 Sum <sum/>
| Class | sum |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| Qualifiers | BvarQ,DomainQ |
| OM Symbols | sum |
The sum element represents the n-ary addition operator.
The terms of the sum are normally specified by rule through the use of
qualifiers. While it can be used with an explicit list of
arguments, this is strongly discouraged, and the plus
operator should be used instead in such situations.
The sum operator may be used either with or without
explicit bound variables. When a bound variable is used, the
sum element is followed by one or more bvar
elements giving the index variables, followed by qualifiers giving
the domain for the index variables. The final child in the enclosing
apply is then an expression in the bound variables, and the
terms of the sum are obtained by evaluating this expression at each
point of the domain of the index variables. Depending on the
structure of the domain, the domain of summation is often given
by using uplimit and lowlimit to specify upper and
lower limits for the sum.
When no bound variables are explicitly given, the final child of
the enclosing apply element must be a function, and the
terms of the sum are obtained by evaluating the function at
each point of the domain specified by qualifiers.
Content MathML
<apply><sum/> <bvar><ci>x</ci></bvar> <lowlimit><ci>a</ci></lowlimit> <uplimit><ci>b</ci></uplimit> <apply><ci>f</ci><ci>x</ci></apply> </apply>
Sample Presentation
<mrow> <munderover> <mo>∑</mo> <mrow><mi>x</mi><mo>=</mo><mi>a</mi></mrow> <mi>b</mi> </munderover> <mrow><mi>f</mi><mo>⁡</mo><mfenced><mi>x</mi></mfenced></mrow> </mrow>
Content MathML
<apply><sum/>
<bvar><ci>x</ci></bvar>
<condition>
<apply><in/><ci>x</ci><ci type="set">B</ci></apply>
</condition>
<apply><ci type="function">f</ci><ci>x</ci></apply>
</apply>Sample Presentation
<mrow> <munder> <mo>∑</mo> <mrow><mi>x</mi><mo>∈</mo><mi>B</mi></mrow> </munder> <mrow><mi>f</mi><mo>⁡</mo><mfenced><mi>x</mi></mfenced></mrow> </mrow>
Content MathML
<apply><sum/>
<domainofapplication>
<ci type="set">B</ci>
</domainofapplication>
<ci type="function">f</ci>
</apply>Sample Presentation
<mrow><munder><mo>∑</mo><mi>B</mi></munder><mi>f</mi></mrow>
Mapping to Strict Content MathML
When no explicit bound variables are used, no special rules are
required to rewrite sums as Strict Content beyond the generic rules
for rewriting expressions using qualifiers. However, when bound
variables are used, it is necessary to introduce a lambda
construction to rewrite the expression in the bound variables as a
function.
Content MathML
<apply><sum/> <bvar><ci>i</ci></bvar> <lowlimit><cn>0</cn></lowlimit> <uplimit><cn>100</cn></uplimit> <apply><power/><ci>x</ci><ci>i</ci></apply> </apply>
Strict Content MathML equivalent
<apply><csymbol cd="arith1">sum</csymbol>
<apply><csymbol cd="interval1">integer_interval</csymbol>
<cn>0</cn>
<cn>100</cn>
</apply>
<bind><csymbol cd="fns1">lambda</csymbol>
<bvar><ci>i</ci></bvar>
<apply><csymbol cd="arith1">power</csymbol><ci>x</ci><ci>i</ci></apply>
</bind>
</apply>4.4.6.2 Product <product/>
| Class | product |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| Qualifiers | BvarQ,DomainQ |
| OM Symbols | product |
The product element represents the n-ary multiplication operator.
The terms of the product are normally specified by rule through the use of
qualifiers. While it can be used with an explicit list of
arguments, this is strongly discouraged, and the times
operator should be used instead in such situations.
The product operator may be used either with or without
explicit bound variables. When a bound variable is used, the
product element is followed by one or more bvar
elements giving the index variables, followed by qualifiers giving
the domain for the index variables. The final child in the enclosing
apply is then an expression in the bound variables, and the
terms of the product are obtained by evaluating this expression at
each point of the domain. Depending on the structure of the domain,
it is commonly given using uplimit and lowlimit
qualifiers.
When no bound variables are explicitly given, the final child of
the enclosing apply element must be a function, and the
terms of the product are obtained by evaluating the function
at each point of the domain specified by qualifiers.
Content MathML
<apply><product/>
<bvar><ci>x</ci></bvar>
<lowlimit><ci>a</ci></lowlimit>
<uplimit><ci>b</ci></uplimit>
<apply><ci type="function">f</ci>
<ci>x</ci>
</apply>
</apply>Sample Presentation
<mrow> <munderover> <mo>∏</mo> <mrow><mi>x</mi><mo>=</mo><mi>a</mi></mrow> <mi>b</mi> </munderover> <mrow><mi>f</mi><mo>⁡</mo><mfenced><mi>x</mi></mfenced></mrow> </mrow>
Content MathML
<apply><product/>
<bvar><ci>x</ci></bvar>
<condition>
<apply><in/>
<ci>x</ci>
<ci type="set">B</ci>
</apply>
</condition>
<apply><ci>f</ci><ci>x</ci></apply>
</apply>Sample Presentation
<mrow> <munder> <mo>∏</mo> <mrow><mi>x</mi><mo>∈</mo><mi>B</mi></mrow> </munder> <mrow><mi>f</mi><mo>⁡</mo><mfenced><mi>x</mi></mfenced></mrow> </mrow>
Mapping to Strict Content MathML
When no explicit bound variables are used, no special rules are
required to rewrite products as Strict Content beyond the generic rules
for rewriting expressions using qualifiers. However, when bound
variables are used, it is necessary to introduce a lambda
construction to rewrite the expression in the bound variables as a
function.
Content MathML
<apply><product/> <bvar><ci>i</ci></bvar> <lowlimit><cn>0</cn></lowlimit> <uplimit><cn>100</cn></uplimit> <apply><power/><ci>x</ci><ci>i</ci></apply> </apply>
Strict Content MathML equivalent
<apply><csymbol cd="arith1">product</csymbol>
<apply><csymbol cd="interval1">integer_interval</csymbol>
<cn>0</cn>
<cn>100</cn>
</apply>
<bind><csymbol cd="fns1">lambda</csymbol>
<bvar><ci>i</ci></bvar>
<apply><csymbol cd="arith1">power</csymbol><ci>x</ci><ci>i</ci></apply>
</bind>
</apply>4.4.6.3 Limits <limit/>
| Class | limit |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| Qualifiers | lowlimit, condition |
| OM Symbols | limit, both_sides, above, below, null |
The limit element represents the operation of taking a limit of a
sequence. The limit point is expressed by specifying a lowlimit and a
bvar, or by specifying a condition on one or more bound variables.
Content MathML
<apply><limit/> <bvar><ci>x</ci></bvar> <lowlimit><cn>0</cn></lowlimit> <apply><sin/><ci>x</ci></apply> </apply>
Sample Presentation
<mrow> <munder> <mi>lim</mi> <mrow><mi>x</mi><mo>→</mo><mn>0</mn></mrow> </munder> <mrow><mi>sin</mi><mo>⁡</mo><mi>x</mi></mrow> </mrow>
Content MathML
<apply><limit/>
<bvar><ci>x</ci></bvar>
<condition>
<apply><tendsto/><ci>x</ci><cn>0</cn></apply>
</condition>
<apply><sin/><ci>x</ci></apply>
</apply>Sample Presentation
<mrow> <munder> <mi>lim</mi> <mrow><mi>x</mi><mo>→</mo><mn>0</mn></mrow> </munder> <mrow><mi>sin</mi><mo>⁡</mo><mi>x</mi></mrow> </mrow>
Content MathML
<apply><limit/>
<bvar><ci>x</ci></bvar>
<condition>
<apply><tendsto type="above"/><ci>x</ci><ci>a</ci></apply>
</condition>
<apply><sin/><ci>x</ci></apply>
</apply>Sample Presentation
<mrow> <munder> <mi>lim</mi> <mrow><mi>x</mi><mo>→</mo><msup><mi>a</mi><mo>+</mo></msup></mrow> </munder> <mrow><mi>sin</mi><mo>⁡</mo><mi>x</mi></mrow> </mrow>
The direction from which a limiting value is approached is given as an argument
limit in Strict Content MathML, which supplies the
direction specifier symbols both_sides, above, and below for this
purpose. The first correspond to the values "all", "above",
and "below" of the type attribute of the tendsto
element below. The null symbol corresponds to the case
where no type attribute is present. We translate
Rewrite: limits condition
<apply><limit/> <bvar> </bvar> <condition> <apply><tendsto/> 0</apply> </condition> </apply>
Strict Content MathML equivalent
<apply><csymbol cd="limit1">limit</csymbol> 0 <csymbol cd="limit1"></csymbol> <bind><csymbol cd="fns1">lambda</csymbol> <bvar> </bvar> </bind> </apply>
where
is an
arbitrary expression involving the bound variable(s), and the choice of
symbol, null depends on the
type attribute of the tendsto element as
described above.
4.4.6.4 Tends To <tendsto/>
| Class | binary-reln |
|---|---|
| Attributes | CommonAtt, DefEncAtt, type? |
type Attribute Values
|
string |
| Content | Empty |
| OM Symbols | limit |
The tendsto element is used to express the relation that
a quantity is tending to a specified value. While this is used
primarily as part of the statement of a mathematical limit, it
exists as a construct on its own to allow one to capture
mathematical statements such as "As x tends to y," and to provide a
building block to construct more general kinds of limits.
The tendsto element takes the attributes type to set the
direction from which the limiting value is approached.
Content MathML
<apply><tendsto type="above"/> <apply><power/><ci>x</ci><cn>2</cn></apply> <apply><power/><ci>a</ci><cn>2</cn></apply> </apply>
Sample Presentation
<mrow> <msup><mi>x</mi><mn>2</mn></msup> <mo>→</mo> <msup><msup><mi>a</mi><mn>2</mn></msup><mo>+</mo></msup> </mrow>
Content MathML
<apply><tendsto/>
<vector><ci>x</ci><ci>y</ci></vector>
<vector>
<apply><ci type="function">f</ci><ci>x</ci><ci>y</ci></apply>
<apply><ci type="function">g</ci><ci>x</ci><ci>y</ci></apply>
</vector>
</apply>Sample Presentation
<mfenced><mtable>
<mtr><mtd><mi>x</mi></mtd></mtr>
<mtr><mtd><mi>y</mi></mtd></mtr>
</mtable></mfenced>
<mo>→</mo>
<mfenced><mtable>
<mtr><mtd>
<mi>f</mi><mo>⁡</mo><mfenced><mi>x</mi><mi>y</mi></mfenced>
</mtd></mtr>
<mtr><mtd>
<mi>g</mi><mo>⁡</mo><mfenced><mi>x</mi><mi>y</mi></mfenced>
</mtd></mtr>
</mtable></mfenced>Mapping to Strict Content MathML
The usage of tendsto to qualify a limit is formally
defined by writing the expression in Strict Content MathML via the
rule Rewrite: limits condition. The meanings of other more
idiomatic uses of tendsto are not formally defined by this
specification. When rewriting these cases to Strict Content MathML,
tendsto should be rewritten to an annotated identifier as
shown below.
4.4.7 Elementary classical functions
4.4.7.1 Common trigonometric functions
| Class | unary-elementary |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | sin |
sin |
cos |
tan |
sec |
csc |
cot |
sinh |
cosh |
tanh |
sech |
csch |
coth |
arcsin |
arccos |
arctan |
arccosh |
arccot |
arccoth |
arccsc |
arccsch |
arcsec |
arcsech |
arcsinh |
arctanh |
These operator elements denote the standard trigonometric and hyperbolic functions and their inverses. Since their standard interpretations are widely known, they are discussed as a group. In the case of inverse functions there are differing definitions in use. For maximum interoperability applications evaluating such expressions should follow the definitions in [Abramowitz1997].
Content MathML
<apply><sin/><ci>x</ci></apply>
Sample Presentation
<mrow><mi>sin</mi><mo>⁡</mo><mi>x</mi></mrow>
Content MathML
<apply><sin/>
<apply><plus/>
<apply><cos/><ci>x</ci></apply>
<apply><power/><ci>x</ci><cn>3</cn></apply>
</apply>
</apply>Sample Presentation
<mrow> <mi>sin</mi> <mo>⁡</mo> <mrow> <mo>(</mo> <mrow><mi>cos</mi><mo>⁡</mo><mi>x</mi></mrow> <mo>+</mo> <msup><mi>x</mi><mn>3</mn></msup> <mo>)</mo> </mrow> </mrow>
4.4.7.2 Exponential <exp/>
| Class | unary-arith |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | exp |
The exp element represents the exponentiation function
associated with the inverse of the ln function. It takes one
argument.
Content MathML
<apply><exp/><ci>x</ci></apply>
Sample Presentation
<msup><mi>e</mi><mi>x</mi></msup>
4.4.7.3 Natural Logarithm <ln/>
| Class | unary-functional |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | ln |
The ln element represents the natural logarithm function.
Content MathML
<apply><ln/><ci>a</ci></apply>
Sample Presentation
<mrow><mi>ln</mi><mo>⁡</mo><mi>a</mi></mrow>
4.4.7.4 Logarithm <log/>
| Class | unary-functional |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| Qualifiers | logbase |
| OM Symbols | log |
The log elements represents the logarithm function
relative to a given base. When present, the logbase
qualifier specifies the base. Otherwise, the base is assumed to be 10.
apply.
Content MathML
<apply><log/> <logbase><cn>3</cn></logbase> <ci>x</ci> </apply>
Sample Presentation
<mrow><msub><mi>log</mi><mn>3</mn></msub><mo>⁡</mo><mi>x</mi></mrow>
Content MathML
<apply><log/><ci>x</ci></apply>
Sample Presentation
<mrow><mi>log</mi><mo>⁡</mo><mi>x</mi></mrow>
Mapping to Strict Content MathML
When mapping log to Strict Content, one uses the
log symbol denoting the function
that returns the log of its second argument with respect to the base
specified by the first argument. When logbase is present, it
determines the base. Otherwise, the default base of 10 must be
explicitly provided in Strict markup. See the following example.
<apply><plus/>
<apply>
<log/>
<logbase><cn>2</cn></logbase>
<ci>x</ci>
</apply>
<apply>
<log/>
<ci>y</ci>
</apply>
</apply>
Strict Content MathML equivalent:
<apply>
<csymbol cd="arith1">plus</csymbol>
<apply>
<csymbol cd="transc1">log</csymbol>
<cn>2</cn>
<ci>x</ci>
</apply>
<apply>
<csymbol cd="transc1">log</csymbol>
<cn>10</cn>
<ci>y</ci>
</apply>
</apply>4.4.8 Statistics
4.4.8.1 Mean <mean/>
| Class | nary-stats |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| Qualifiers | BvarQ,DomainQ |
| OM Symbols | mean, mean |
The mean element represents the function returning arithmetic mean or average of a
data set or random variable.
Content MathML
<apply><mean/> <cn>3</cn><cn>4</cn><cn>3</cn><cn>7</cn><cn>4</cn> </apply>
Sample Presentation
<mrow> <mo>〈</mo> <mn>3</mn><mo>,</mo><mn>4</mn><mo>,</mo><mn>3</mn> <mo>,</mo><mn>7</mn><mo>,</mo><mn>4</mn> <mo>〉</mo> </mrow>
Content MathML
<apply><mean/><ci>X</ci></apply>
Sample Presentation
<mrow><mo>〈</mo><mi>X</mi><mo>〉</mo></mrow>
<mover><mi>X</mi><mo>¯</mo></mover>
Mapping to Strict Markup
When the mean element is applied to an explicit list of arguments, the
translation to Strict Content markup is direct, using the mean symbol from the s_data1 content dictionary, as described in
Rewrite: element. When it is applied to a distribution, then the
mean symbol from the s_dist1 content
dictionary should be used. In the case with qualifiers use Rewrite: n-ary domainofapplication
with the same caveat.
4.4.8.2 Standard Deviation <sdev/>
| Class | nary-stats |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| Qualifiers | BvarQ,DomainQ |
| OM Symbols | sdev, sdev |
The sdev element is used to denote the standard deviation
function for a data set or random variable. Standard deviation is a
statistical measure of dispersion given by the square root of the
variance.
Content MathML
<apply><sdev/> <cn>3</cn><cn>4</cn><cn>2</cn><cn>2</cn> </apply>
Sample Presentation
<mrow> <mo>σ</mo> <mo>⁡</mo> <mfenced><mn>3</mn><mn>4</mn><mn>2</mn><mn>2</mn></mfenced> </mrow>
Content MathML
<apply><sdev/> <ci type="discrete_random_variable">X</ci> </apply>
Sample Presentation
<mrow><mo>σ</mo><mo>⁡</mo><mfenced><mi>X</mi></mfenced></mrow>
Mapping to Strict Markup
When the sdev element is applied to an explicit list of arguments, the
translation to Strict Content markup is direct, using the sdev
symbol from the s_data1 content dictionary, as described in
Rewrite: element. When it is applied to a distribution, then the
sdev symbol from the s_dist1 content
dictionary should be used. In the case with qualifiers use
Rewrite: n-ary domainofapplication with the same caveat.
4.4.8.3 Variance <variance/>
| Class | nary-stats |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| Qualifiers | BvarQ,DomainQ |
| OM Symbols | variance, variance |
The variance element represents the variance of a data set
or random variable. Variance is a statistical measure of dispersion,
averaging the squares of the deviations of possible values from their
mean.
Content MathML
<apply><variance/> <cn>3</cn><cn>4</cn><cn>2</cn><cn>2</cn> </apply>
Sample Presentation
<mrow> <msup> <mo>σ</mo> <mn>2</mn> </msup> <mo>⁡</mo> <mfenced><mn>3</mn><mn>4</mn><mn>2</mn><mn>2</mn></mfenced> </mrow>
Content MathML
<apply><variance/> <ci type="discrete_random_variable"> X</ci> </apply>
Sample Presentation
<mrow> <msup><mo>σ</mo><mn>2</mn></msup> <mo>⁡</mo> <mfenced><mi>X</mi></mfenced> </mrow>
Mapping to Strict Markup
When the variance element is applied to an explicit list of arguments, the
translation to Strict Content markup is direct, using the variance
symbol from the s_data1 content dictionary, as described in
Rewrite: element. When it is applied to a distribution, then the
variance symbol from the s_dist1 content
dictionary should be used. In the case with qualifiers use Rewrite: n-ary domainofapplication
with the same caveat.
4.4.8.4 Median <median/>
| Class | nary-stats |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| Qualifiers | BvarQ, DomainQ |
| OM Symbols | median |
The median element represents an operator returning the
median of its arguments. The median is a number separating the lower
half of the sample values from the upper half.
Content MathML
<apply><median/> <cn>3</cn><cn>4</cn><cn>2</cn><cn>2</cn> </apply>
Sample Presentation
<mrow> <mi>median</mi> <mo>⁡</mo> <mfenced><mn>3</mn><mn>4</mn><mn>2</mn><mn>2</mn></mfenced> </mrow>
Mapping to Strict Markup
When the median element is applied to an explicit list of arguments, the
translation to Strict Content markup is direct, using the median
symbol from the s_data1 content dictionary, as described in
Rewrite: element.
4.4.8.5 Mode <mode/>
| Class | nary-stats |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| Qualifiers | BvarQ, DomainQ |
| OM Symbols | mode |
The mode element is used to denote the mode of its arguments. The mode is
the value which occurs with the greatest frequency.
Content MathML
<apply><mode/> <cn>3</cn><cn>4</cn><cn>2</cn><cn>2</cn> </apply>
Sample Presentation
<mrow> <mi>mode</mi> <mo>⁡</mo> <mfenced><mn>3</mn><mn>4</mn><mn>2</mn><mn>2</mn></mfenced> </mrow>
Mapping to Strict Markup
When the mode element is applied to an explicit list of arguments, the
translation to Strict Content markup is direct, using the mode
symbol from the s_data1 content dictionary, as described in
Rewrite: element.
4.4.8.6 Moment (<moment/>, <momentabout>)
| Class | unary-functional |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| Qualifiers | degree, momentabout |
| OM Symbols | moment, moment |
The moment element is used to denote the ith moment of a set of data set or
random variable. The moment function accepts the degree and
momentabout qualifiers. If present, the degree schema denotes the order of
the moment. Otherwise, the moment is assumed to be the first order moment. When used with
moment, the degree schema is expected to contain a
single child. If present, the momentabout schema denotes the
point about which the moment is taken. Otherwise, the moment is
assumed to be the moment about zero.
Content MathML
<apply><moment/> <degree><cn>3</cn></degree> <momentabout><mean/></momentabout> <cn>6</cn><cn>4</cn><cn>2</cn><cn>2</cn><cn>5</cn> </apply>
Sample Presentation
<msub> <mrow> <mo>〈</mo> <msup> <mfenced><mn>6</mn><mn>4</mn><mn>2</mn><mn>2</mn><mn>5</mn></mfenced> <mn>3</mn> </msup> <mo>〉</mo> </mrow> <mi>mean</mi> </msub>
Content MathML
<apply><moment/> <degree><cn>3</cn></degree> <momentabout><ci>p</ci></momentabout> <ci>X</ci> </apply>
Sample Presentation
<msub> <mrow> <mo>〈</mo><msup><mi>X</mi><mn>3</mn></msup><mo>〉</mo> </mrow> <mi>p</mi> </msub>
Mapping to Strict Markup
When rewriting to Strict Markup, the moment symbol from the s_data1 content
dictionary is used when the moment element is applied
to an explicit list of arguments. When it is applied to a distribution, then the
moment symbol from the s_dist1 content
dictionary should be used. Both operators take
the degree as the first argument, the point as the second, followed by
the data set or random variable respectively.
<apply><moment/> <degree><cn>3</cn></degree> <momentabout><ci>p</ci></momentabout> <ci>X</ci> </apply>
Strict Content MathML equivalent
<apply><csymbol cd="s_dist1">moment</csymbol> <cn>3</cn> <ci>p</ci> <ci>X</ci> </apply>
4.4.9 Linear Algebra
4.4.9.1 Vector <vector>
| Class | nary-constructor |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Qualifiers | BvarQ, DomainQ |
| Content | ContExp* |
| OM Symbol | vector |
A vector is an ordered n-tuple of values representing an element of an n-dimensional vector space.
For purposes of interaction with matrices and matrix multiplication, vectors are regarded as equivalent to a matrix consisting of a single column, and the transpose of a vector as a matrix consisting of a single row.
The components of a vector may be given explicitly as
child elements, or specified by rule as described in Section 4.3.1.1 Container Markup for Constructor Symbols.
Content MathML
<vector> <apply><plus/><ci>x</ci><ci>y</ci></apply> <cn>3</cn> <cn>7</cn> </vector>
Sample Presentation
<mrow> <mo>(</mo> <mtable> <mtr><mtd><mrow><mi>x</mi><mo>+</mo><mi>y</mi></mrow></mtd></mtr> <mtr><mtd><mn>3</mn></mtd></mtr> <mtr><mtd><mn>7</mn></mtd></mtr> </mtable> <mo>)</mo> </mrow>
<mfenced> <mrow><mi>x</mi><mo>+</mo><mi>y</mi></mrow> <mn>3</mn> <mn>7</mn> </mfenced>
4.4.9.2 Matrix <matrix>
| Class | nary-constructor |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Qualifiers | BvarQ, DomainQ |
| Content | ContExp* |
| OM Symbol | matrix |
A matrix is regarded as made up of matrix rows, each of which can be thought of as a special type of vector.
Note that the behavior of the matrix and matrixrow elements is
substantially different from the mtable and mtr presentation
elements.
The matrix element is a constructor
element, so the entries may be given explicitly as child elements,
or specified by rule as described in Section 4.3.1.1 Container Markup for Constructor Symbols. In the latter case, the
entries are specified by providing a function and a 2-dimensional
domain of application. The entries of the matrix correspond to
the values obtained by evaluating the function at the points of
the domain.
Content MathML
<matrix>
<bvar><ci type="integer">i</ci></bvar>
<bvar><ci type="integer">j</ci></bvar>
<condition>
<apply><and/>
<apply><in/>
<ci>i</ci>
<interval><ci>1</ci><ci>5</ci></interval>
</apply>
<apply><in/>
<ci>j</ci>
<interval><ci>5</ci><ci>9</ci></interval>
</apply>
</apply>
</condition>
<apply><power/><ci>i</ci><ci>j</ci></apply>
</matrix>Sample Presentation
<mrow> <mo>[</mo> <msub><mi>m</mi><mrow><mi>i</mi><mo>,</mo><mi>j</mi></mrow></msub> <mo>|</mo> <mrow> <msub><mi>m</mi><mrow><mi>i</mi><mo>,</mo><mi>j</mi></mrow></msub> <mo>=</mo> <msup><mi>i</mi><mi>j</mi></msup> </mrow> <mo>;</mo> <mrow> <mrow> <mi>i</mi> <mo>∈</mo> <mfenced open="[" close="]"><mi>1</mi><mi>5</mi></mfenced> </mrow> <mo>∧</mo> <mrow> <mi>j</mi> <mo>∈</mo> <mfenced open="[" close="]"><mi>5</mi><mi>9</mi></mfenced> </mrow> </mrow> <mo>]</mo> </mrow>
4.4.9.3 Matrix row <matrixrow>
| Class | nary-constructor |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Qualifiers | BvarQ, DomainQ |
| Content | ContExp* |
| OM Symbol | matrixrow |
This element is an n-ary constructor used to represent rows of matrices.
Matrix rows are not directly rendered by themselves outside of the context of a matrix.
4.4.9.4 Determinant <determinant/>
| Class | unary-linalg |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | determinant |
This element is used for the unary function which returns the determinant of its argument, which should be a square matrix.
Content MathML
<apply><determinant/> <ci type="matrix">A</ci> </apply>
Sample Presentation
<mrow><mi>det</mi><mo>⁡</mo><mi>A</mi></mrow>
4.4.9.5 Transpose <transpose/>
| Class | unary-linalg |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | transpose |
This element represents a unary function that signifies the transpose of the given matrix or vector.
Content MathML
<apply><transpose/> <ci type="matrix">A</ci> </apply>
Sample Presentation
<msup><mi>A</mi><mi>T</mi></msup>
4.4.9.6 Selector <selector/>
| Class | nary-linalg |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | vector_selector, matrix_selector |
The selector element is the operator for indexing into vectors, matrices
and lists. It accepts one or more arguments. The first argument identifies the vector,
matrix or list from which the selection is taking place, and the second and subsequent
arguments, if any, indicate the kind of selection taking place.
When selector is used with a single argument, it should be interpreted as
giving the sequence of all elements in the list, vector or matrix given. The ordering
of elements in the sequence for a matrix is understood to be first by column, then by
row; so the resulting list is of matrix rows given entry by entry.
That is, for a matrix (ai,j), where the indices denote row
and column, respectively, the ordering would be a1,1,
a1,2, ... a2,1, a2,2
... etc.
When two arguments are given, and the first is a vector or list, the second argument specifies the index of an entry in the list or vector. If the first argument is a matrix then the second argument specifies the index of a matrix row.
When three arguments are given, the last one is ignored for a list or vector, and in the case of a matrix, the second and third arguments specify the row and column indices of the selected element.
Content MathML
<apply><selector/><ci type="vector">V</ci><cn>1</cn></apply>
Sample Presentation
<msub><mi>V</mi><mn>1</mn></msub>
Content MathML
<apply><eq/>
<apply><selector/>
<matrix>
<matrixrow><cn>1</cn><cn>2</cn></matrixrow>
<matrixrow><cn>3</cn><cn>4</cn></matrixrow>
</matrix>
<cn>1</cn>
</apply>
<matrix>
<matrixrow><cn>1</cn><cn>2</cn></matrixrow>
</matrix>
</apply>Sample Presentation
<mrow>
<msub>
<mrow>
<mo>(</mo>
<mtable>
<mtr><mtd><mn>1</mn></mtd><mtd><mn>2</mn></mtd></mtr>
<mtr><mtd><mn>3</mn></mtd><mtd><mn>4</mn></mtd></mtr>
</mtable>
<mo>)</mo>
</mrow>
<mn>1</mn>
</msub>
<mo>=</mo>
<mrow>
<mo>(</mo>
<mtable><mtr><mtd><mn>1</mn></mtd><mtd><mn>2</mn></mtd></mtr></mtable>
<mo>)</mo>
</mrow>
</mrow>4.4.9.7 Vector product <vectorproduct/>
| Class | binary-linalg |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | vectorproduct |
This element represents the vector product. It takes two three-dimensional vector arguments and represents as value a three-dimensional vector.
Content MathML
<apply><eq/>
<apply><vectorproduct/>
<ci type="vector"> A </ci>
<ci type="vector"> B </ci>
</apply>
<apply><times/>
<ci>a</ci>
<ci>b</ci>
<apply><sin/><ci>θ</ci></apply>
<ci type="vector"> N </ci>
</apply>
</apply>Sample Presentation
<mrow> <mrow><mi>A</mi><mo>×</mo><mi>B</mi></mrow> <mo>=</mo> <mrow> <mi>a</mi> <mo>⁢</mo> <mi>b</mi> <mo>⁢</mo> <mrow><mi>sin</mi><mo>⁡</mo><mi>θ</mi></mrow> <mo>⁢</mo> <mi>N</mi> </mrow> </mrow>
4.4.9.8 Scalar product <scalarproduct/>
| Class | binary-linalg |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | scalarproduct |
This element represents the scalar product function. It takes two vector arguments and returns a scalar value.
Content MathML
<apply><eq/>
<apply><scalarproduct/>
<ci type="vector">A</ci>
<ci type="vector">B</ci>
</apply>
<apply><times/>
<ci>a</ci>
<ci>b</ci>
<apply><cos/><ci>θ</ci></apply>
</apply>
</apply>Sample Presentation
<mrow> <mrow><mi>A</mi><mo>.</mo><mi>B</mi></mrow> <mo>=</mo> <mrow> <mi>a</mi> <mo>⁢</mo> <mi>b</mi> <mo>⁢</mo> <mrow><mi>cos</mi><mo>⁡</mo><mi>θ</mi></mrow> </mrow> </mrow>
4.4.9.9 Outer product <outerproduct/>
| Class | binary-linalg |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | outerproduct |
This element represents the outer product function. It takes two vector arguments and returns as value a matrix.
Content MathML
<apply><outerproduct/> <ci type="vector">A</ci> <ci type="vector">B</ci> </apply>
Sample Presentation
<mrow><mi>A</mi><mo>⊗</mo><mi>B</mi></mrow>
4.4.10 Constant and Symbol Elements
This section explains the use of the Constant and Symbol elements.
4.4.10.1 integers <integers/>
| Class | constant-set |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | Z |
This element represents the set of integers, positive, negative and zero.
Content MathML
<apply><in/> <cn type="integer"> 42 </cn> <integers/> </apply>
Sample Presentation
<mrow><mn>42</mn><mo>∈</mo><mi mathvariant="double-struck">Z</mi></mrow>
4.4.10.2 reals <reals/>
| Class | constant-set |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | R |
This element represents the set of real numbers.
Content MathML
<apply><in/> <cn type="real"> 44.997</cn> <reals/> </apply>
Sample Presentation
<mrow> <mn>44.997</mn><mo>∈</mo><mi mathvariant="double-struck">R</mi> </mrow>
4.4.10.3 Rational Numbers <rationals/>
| Class | constant-set |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | Q |
This element represents the set of rational numbers.
Content MathML
<apply><in/> <cn type="rational"> 22 <sep/>7</cn> <rationals/> </apply>
Sample Presentation
<mrow> <mrow><mn>22</mn><mo>/</mo><mn>7</mn></mrow> <mo>∈</mo> <mi mathvariant="double-struck">Q</mi> </mrow>
4.4.10.4 Natural Numbers <naturalnumbers/>
| Class | constant-set |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | N |
This element represents the set of natural numbers (including zero).
Content MathML
<apply><in/> <cn type="integer">1729</cn> <naturalnumbers/> </apply>
Sample Presentation
<mrow> <mn>1729</mn><mo>∈</mo><mi mathvariant="double-struck">N</mi> </mrow>
4.4.10.5 complexes <complexes/>
| Class | constant-set |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | C |
This element represents the set of complex numbers.
Content MathML
<apply><in/> <cn type="complex-cartesian">17<sep/>29</cn> <complexes/> </apply>
Sample Presentation
<mrow> <mrow><mn>17</mn><mo>+</mo><mn>29</mn><mo>⁢</mo><mi>i</mi></mrow> <mo>∈</mo> <mi mathvariant="double-struck">C</mi> </mrow>
4.4.10.6 primes <primes/>
| Class | constant-set |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | P |
This element represents the set of positive prime numbers.
Content MathML
<apply><in/> <cn type="integer">17</cn> <primes/> </apply>
Sample Presentation
<mrow><mn>17</mn><mo>∈</mo><mi mathvariant="double-struck">P</mi></mrow>
4.4.10.7 Exponential e <exponentiale/>
| Class | constant-arith |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | e |
This element represents the base of the natural logarithm, approximately 2.718.
Content MathML
<apply><eq/> <apply><ln/><exponentiale/></apply> <cn>1</cn> </apply>
Sample Presentation
<mrow> <mrow><mi>ln</mi><mo>⁡</mo><mi>e</mi></mrow> <mo>=</mo> <mn>1</mn> </mrow>
4.4.10.8 Imaginary i <imaginaryi/>
| Class | constant-arith |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | i |
This element represents the mathematical constant which is the square root of -1, commonly written i
Content MathML
<apply><eq/> <apply><power/><imaginaryi/><cn>2</cn></apply> <cn>-1</cn> </apply>
Sample Presentation
<mrow><msup><mi>i</mi><mn>2</mn></msup><mo>=</mo><mn>-1</mn></mrow>
4.4.10.9 Not A Number <notanumber/>
| Class | constant-arith |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | NaN |
This element represents the notion of not-a-number, i.e. the result of an ill-posed floating computation. See [IEEE754].
Content MathML
<apply><eq/> <apply><divide/><cn>0</cn><cn>0</cn></apply> <notanumber/> </apply>
Sample Presentation
<mrow> <mrow><mn>0</mn><mo>/</mo><mn>0</mn></mrow> <mo>=</mo> <mi>NaN</mi> </mrow>
4.4.10.10 True <true/>
| Class | constant-arith |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | true |
This element represents the Boolean value true, i.e. the logical constant for truth.
Content MathML
<apply><eq/>
<apply><or/>
<true/>
<ci type="boolean">P</ci>
</apply>
<true/>
</apply>Sample Presentation
<mrow> <mrow><mi>true</mi><mo>∨</mo><mi>P</mi></mrow> <mo>=</mo> <mi>true</mi> </mrow>
4.4.10.11 False <false/>
| Class | constant-arith |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | false |
This element represents the Boolean value false, i.e. the logical constant for falsehood.
Content MathML
<apply><eq/>
<apply><and/>
<false/>
<ci type="boolean">P</ci>
</apply>
<false/>
</apply>Sample Presentation
<mrow> <mrow><mi>false</mi><mo>∧</mo><mi>P</mi></mrow> <mo>=</mo> <mi>false</mi> </mrow>
4.4.10.12 Empty Set <emptyset/>
| Class | constant-set |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | emptyset, emptyset |
This element is used to represent the empty set, that is the set which contains no members.
Content MathML
<apply><neq/> <integers/> <emptyset/> </apply>
Sample Presentation
<mrow> <mi mathvariant="double-struck">Z</mi><mo>≠</mo><mi>∅</mi> </mrow>
Mapping to Strict Markup
In some situations, it may be clear from context that emptyset
corresponds to the emptyset
However, as there is no method other than annotation for an author to explicitly indicate this,
it is always acceptable to translate to the emptyset symbol from the set1 CD.
4.4.10.13 pi <pi/>
| Class | constant-arith |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | pi |
This element represents pi, approximately 3.142, which is the ratio of the circumference of a circle to its diameter.
Content MathML
<apply><approx/> <pi/> <cn type="rational">22<sep/>7</cn> </apply>
Sample Presentation
<mrow> <mi>π</mi> <mo>≃</mo> <mrow><mn>22</mn><mo>/</mo><mn>7</mn></mrow> </mrow>
4.4.10.14 Euler gamma <eulergamma/>
| Class | constant-arith |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | gamma |
This element denotes the gamma constant, approximately 0.5772.
Content MathML
<apply><approx/> <eulergamma/> <cn>0.5772156649</cn> </apply>
Sample Presentation
<mrow><mi>γ</mi><mo>≃</mo><mn>0.5772156649</mn></mrow>
4.4.10.15 infinity <infinity/>
| Class | constant-arith |
|---|---|
| Attributes | CommonAtt, DefEncAtt |
| Content | Empty |
| OM Symbols | infinity |
This element represents the notion of infinity.
Content MathML
<infinity/>
Sample Presentation
<mi>∞</mi>
4.5 Deprecated Content Elements
4.5.1 Declare <declare>
MathML2 provided the declare element to bind properties like
types to symbols and variables and to define abbreviations for structure sharing. This
element is deprecated in MathML 3. Structure sharing can obtained via the share
element (see Section 4.2.7 Structure Sharing <share> for details).
4.6 The Strict Content MathML Transformation
MathML 3 assigns semantics to content markup by defining a mapping to Strict Content MathML. Strict MathML, in turn, is in one-to-one correspondence with OpenMath, and the subset of OpenMath expressions obtained from content MathML expressions in this fashion all have well-defined semantics via the standard OpenMath Content Dictionary set. Consequently, the mapping of arbitrary content MathML expressions to equivalent Strict Content MathML plays a key role in underpinning the meaning of content MathML.
The mapping of arbitrary content MathML into Strict content MathML is defined algorithmically. The algorithm is described below as a collection of rewrite rules applying to specific non-Strict constructions. The individual rewrite transformations have been described in detail in context above. The goal of this section is to outline the complete algorithm in one place.
The algorithm is a sequence of nine steps. Each step is applied repeatedly to rewrite the input until no further application is possible. Note that in many programming languages, such as XSLT, the natural implementation is as a recursive algorithm, rather than the multi-pass implementation suggested by the description below. The translation to XSL is straightforward and produces the same eventual Strict Content MathML. However, because the overall structure of the multi-pass algorithm is clearer, that is the formulation given here.
To transform an arbitrary content MathML expression into Strict Content MathML, apply each of the following rules in turn to the input expression until all instances of the target constructs have been eliminated:
-
Rewrite non-strict
bindand elminate deprecated elements: Change the outerbindtags in binding expressions toapplyif they have qualifiers or multiple children. This simplifies the algorithm by allowing the subsequent rules to be applied to non-strict binding expressions without case distinction. Note that the later rules will change theapplyelements introduced in this step back tobindelements. Also in this step, deprecatedrelnelements are rewritten toapply, andfnelements are replaced by the child expressions they enclose. -
Apply special case rules for idiomatic uses of qualifiers:
-
Rewrite derivatives with rules Rewrite: diff, Rewrite: nthdiff, and Rewrite: partialdiffdegree to explicate the binding status of the variables involved.
-
Rewrite integrals with the rules Rewrite: int, Rewrite: defint and Rewrite: defint limits to disambiguate the status of bound and free variables and of the orientation of the range of integration if it is given as a
lowlimit/uplimitpair. -
Rewrite limits as described in Rewrite: tendsto and Rewrite: limits condition.
-
Rewrite sums and products as described in Section 4.4.6.1 Sum
<sum/>and Section 4.4.6.2 Product<product/>. -
Rewrite roots as described in Section 4.4.2.11 Root
<root/>. -
Rewrite logarithms as described in Section 4.4.7.4 Logarithm
<log/>. -
Rewrite moments as described in Section 4.4.8.6 Moment (
<moment/>,<momentabout>).
-
-
Rewrite Qualifiers to
domainofapplication: These rules rewrite allapplyconstructions usingbvarand qualifiers to those using only the generaldomainofapplicationqualifier.-
Intervals: Rewrite qualifiers given as
intervalandlowlimit/uplimitto intervals of integers via Rewrite: interval qualifier. -
Multiple
conditions: Rewrite multipleconditionqualifiers to a single one by taking their conjunction. The resulting compoundconditionis then rewritten todomainofapplicationaccording to rule Rewrite: condition. -
Multiple
domainofapplications: Rewrite multipledomainofapplicationqualifiers to a single one by taking the intersection of the specified domains.
-
-
Normalize Container Markup:
-
Rewrite sets and lists by the rule Rewrite: n-ary setlist domainofapplication.
-
Rewrite interval, vectors, matrices, and matrix rows as described in Section 4.4.1.1 Interval
<interval>, Section 4.4.9.1 Vector<vector>, Section 4.4.9.2 Matrix<matrix>and Section 4.4.9.3 Matrix row<matrixrow>. -
Rewrite lambda expressions by the rules Rewrite: lambda and Rewrite: lambda domainofapplication
-
Rewrite piecewise functions as described in Section 4.4.1.9 Piecewise declaration (
<piecewise>,<piece>,<otherwise>).
-
-
Apply Special Case Rules for Operators using
domainofapplicationQualifiers: This step deals with the special cases for the operators introduced in Section 4.4 Content MathML for Specific Operators and Constants. There are different classes of special cases to be taken into account:-
Rewrite
min,max,meanand similar n-ary/unary operators by the rules Rewrite: n-ary unary set, Rewrite: n-ary unary domainofapplication and Rewrite: n-ary unary single. -
Rewrite the quantifiers
forallandexistsused withdomainofapplicationto expressions using implication and conjunction by the rule Rewrite: quantifier. -
Rewrite integrals used with a
domainofapplicationelement (with or without abvar) according to the rules Rewrite: int and Rewrite: defint. -
Rewrite sums and products used with a
domainofapplicationelement (with or without abvar) as described in Section 4.4.6.1 Sum<sum/>and Section 4.4.6.2 Product<product/>.
-
-
Eliminate
domainofapplication: At this stage, anyapplyhas at most onedomainofapplicationchild and special cases have been addressed. Asdomainofapplicationis not Strict Content MathML, it is rewritten-
into an application of a restricted function via the rule Rewrite: restriction if the
applydoes not contain abvarchild. -
into an application of the predicate_on_list symbol via the rules Rewrite: n-ary relations and Rewrite: n-ary relations bvar if used with a relation.
-
into a construction with the apply_to_list symbol via the general rule Rewrite: n-ary domainofapplication for general n-ary operators.
-
into a construction using the suchthat symbol from the set1 content dictionary in an
applywith bound variables via the Rewrite: apply bvar domainofapplication rule.
-
-
Rewrite non-strict token elements:
-
Rewrite numbers represented as
cnelements where thetypeattribute is one of "e-notation", "rational", "complex-cartesian", "complex-polar", "constant" as strictcnvia rules Rewrite: cn sep, Rewrite: cn based_integer and Rewrite: cn constant. -
Rewrite any
ci,csymbolorcncontaining presentation MathML tosemanticselements with rules Rewrite: cn presentation mathml and Rewrite: ci presentation mathml and the analogous rule forcsymbol.
-
-
Rewrite operators: Rewrite any remaining operator defined in Section 4.4 Content MathML for Specific Operators and Constants to a
csymbolreferencing the symbol identified in the syntax table by the rule Rewrite: element. As noted in the descriptions of each operator element, some require special case rules to determine the proper choice of symbol. Some cases of particular note are:-
The order of the arguments for the
selectoroperator must be rewritten, and the symbol depends on the type of the arguments. -
The choice of symbol for the
minusoperator depends on the number of the arguments. -
The choice of symbol for some set operators depends on the values of the
typeof the arguments. -
The choice of symbol for some statistical operators depends on the values of the types of the arguments.
-
-
Rewrite non-strict attributes:
-
Rewrite the
typeattribute: At this point, all elements that accept thetype, other thanciandcsymbol, should have been rewritten into Strict Content Markup equivalents withouttypeattributes, where type information is reflected in the choice of operator symbol. Now rewrite remainingciandcsymbolelements with atypeattribute to a strict expression withsemanticsaccording to rules Rewrite: ci type annotation and Rewrite: csymbol type annotation. -
Rewrite
definitionURLandencodingattributes: If thedefinitionURLandencodingattributes on acsymbolelement can be interpreted as a reference to a content dictionary (see Section 4.2.3.2 Non-Strict uses of<csymbol>for details), then rewrite to reference the content dictionary by thecdattribute instead. -
Rewrite attributes: Rewrite any element with attributes that are not allowed in strict markup to a
semanticsconstruction with the element without these attributes as the first child and the attributes inannotationelements by rule Rewrite: attributes.
-
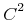
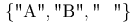
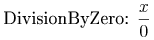
![{\left[{0},{1}\right]}](image/interval1-interval_cc-ex1.gif)
![{\left({0},{1}\right]}](image/interval1-interval_oc-ex1.gif)
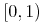
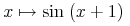
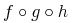
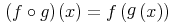
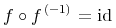
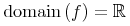
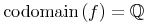
![{{\mathop{{\minormal{image}}}{\left({\minormal{sin}}\right)}}={\left[{\mn{-1}},{1}\right]}}](image/fns1-image-ex1.gif)
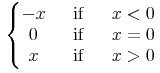
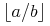
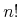
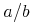
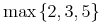
![{{\minormal{max}}{\left.\middle\{y^3\middle|{y\unicode{8712}{\left[{0},{1}\right]}}\middle\}\right.}}](image/minmax1-big_max-ex1.gif)
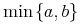

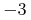
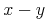
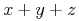
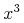
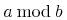
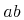
![\sqrt[{n}]{a}](image/arith1-root-ex1.gif)
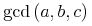
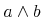
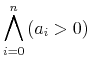
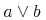
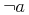
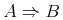
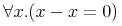
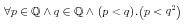
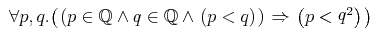
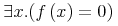
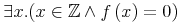
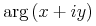
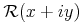
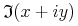
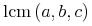
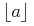
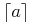
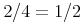
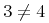
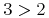
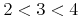
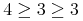
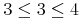
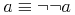
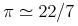
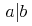
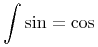
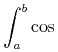
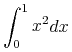
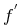
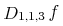
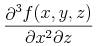
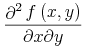
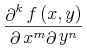
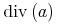
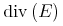
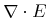
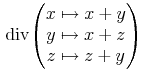
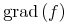
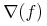
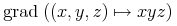
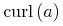
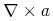
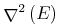
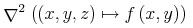
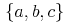
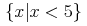
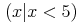
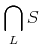
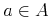
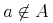
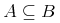
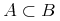
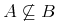
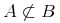
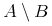
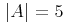
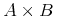
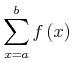
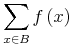
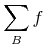
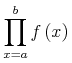
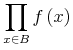
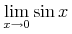
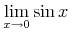
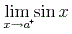
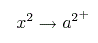
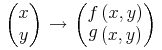
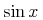
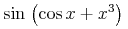
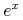
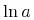
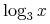
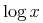
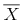
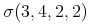
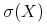


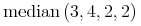
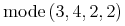
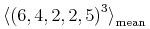
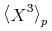
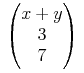
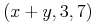
![{\left.[\msub{m}{{i,j}}\middle|{\msub{m}{{i,j}}=\msup{i}{j}};{{i\unicode{8712}{\left[1,5\right]}}\unicode{8743}{j\unicode{8712}{\left[5,9\right]}}}]\right.}](image/linalg6-matrix-ex1.gif)