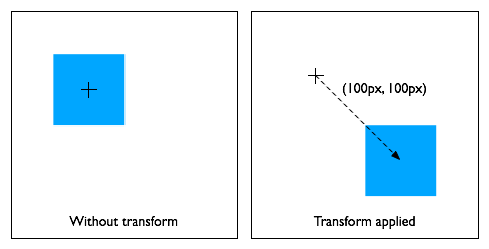Abstract
CSS 2D Transforms allows elements rendered by CSS to be transformed in
two-dimensional space.
Status of this document
This section describes the status of this document at the time of
its publication. Other documents may supersede this document. A list of
current W3C publications and the latest revision of this technical report
can be found in the W3C technical reports
index at http://www.w3.org/TR/.
Publication as a Working Draft does not imply endorsement by the W3C
Membership. This is a draft document and may be updated, replaced or
obsoleted by other documents at any time. It is inappropriate to cite this
document as other than work in progress.
The (archived) public
mailing list www-style@w3.org (see
instructions) is preferred
for discussion of this specification. When sending e-mail, please put the
text “css3-2d-transforms” in the subject, preferably like
this: “[css3-2d-transforms] …summary of
comment…”
This document was produced by the CSS Working Group (part of
the Style Activity).
This document was produced by a group operating under the 5 February
2004 W3C Patent Policy. W3C maintains a public list of any patent disclosures made in
connection with the deliverables of the group; that page also includes
instructions for disclosing a patent. An individual who has actual
knowledge of a patent which the individual believes contains Essential
Claim(s) must disclose the information in accordance with section
6 of the W3C Patent Policy.
The list of changes made to this specification is
available.
Table of contents
1. Introduction
This section is not normative.
The CSS visual
formatting model describes a coordinate system within which each
element is positioned. Positions and sizes in this coordinate space can be
thought of as being expressed in pixels, starting in the upper left corner
of the parent with positive values proceeding to the right and down.
This coordinate space can be modified with the ‘transform’ property. Using
transform, elements can be translated, rotated and scaled in two
dimensional space. The coordinate space behaves as described in the coordinate
system transformations section of the SVG 1.1 specification. This is a
coordinate system with two axes: the X axis increases horizontally to the
right; the Y axis increases vertically downwards.
Specifying a value other than ‘none’ for the ‘transform’ property establishes a
new local coordinate system at the element that it is applied to.
Transformations are cumulative. That is, elements establish their local
coordinate system within the coordinate system of their parent. In this
way, a ‘transform’ property effectively
accumulates all the ‘transform’ properties of its
ancestors. The accumulation of these transforms defines a current
transformation matrix (CTM) for the element.
The transform property does not affect the flow of the content
surrounding the transformed element. However, the value of the overflow
area takes into account transformed elements. This behavior is similar to
what happens when elements are translated via relative positioning.
Therefore, if the value of the ‘overflow’ property is ‘scroll’
or ‘auto’, scrollbars will appear as needed
to see content that is transformed outside the visible area.
Any value other than ‘none’ for
the transform results in the creation of both a stacking context and a
containing block. The object acts as a containing block for fixed
positioned descendants.
Need to go into more detail here about why fixed
positioned objects should do this, i.e., that it's much harder to
implement otherwise.
There are two roles for transformations in layout: (1)
transformations that adjust the position of the affected content without
changing the normal layout of that content (much like relative
positioning) and (2) transformation of the content prior to layout that
affects the layout of that content. See
http://lists.w3.org/Archives/Public/www-style/2007Oct/0209
for examples of both cases. The "transform" property (as defined in this
document) is equally useful for both roles. This document is focused on
satisfying the first role. There is, however, an architectural question
that arises because there needs to be a way to distinguish which role an
author of a stylesheet wants. The key question is which is the default
behavior/role for the "transform" property and how is the other
behavior/role indicated by a stylesheet author. If you have an opinion on
this topic, please send feedback.
What do fixed backgrounds do in transforms? They should
probably ignore the transform completely, since - even transformed - the
object should be acting as "porthole" through which the fixed background
can be viewed in its original form.
This property should also be applicable to SVG elements.
We also need to specify that SVG transforms *do* combine
with this transform, e.g., if a <foreignObject> is inside
transformed SVG and then defines a transform of its own. This means we may
potentially have to examine the current SVG transform and combine with it
to set the correct transform.
A two-dimensional transformation is applied to an element through the
‘transform’ property. This property
contains a list of transform functions.
The final transformation value for an element is obtained by performing a
matrix concatenation of each entry in the list. The set of transform
functions is similar to those allowed by SVG.
| Name:
| transform
|
| Value:
| none | <transform-function> [ <transform-function> ]*
|
| Initial:
| none
|
| Applies to:
| block-level and inline-level elements
|
| Inherited:
| no
|
| Percentages:
| refer to the size of the element's box
|
| Media:
| visual
|
| Computed value:
| Same as specified value.
|
The ‘transform-origin’
property establishes the origin of transformation for an element. This
property is applied by first translating the element by the negated value
of the property, then applying the element's transform, then translating
by the property value. This effectively moves the desired transformation
origin of the element to (0,0) in the local coordinate system, then
applies the element's transform, then moves the element back to its
original position.
If only one value is specified, the second value is assumed to be
‘center’. If at least one value is
not a keyword, then the first value represents the horizontal position and
the second represents the vertical position. Negative <percentage>
and <length> values are allowed.
| Name:
| transform-origin
|
| Value:
| [ [ <percentage> | <length> | left | center | right ] [
<percentage> | <length> | top | center | bottom ]? ] | [ [
left | center | right ] || [ top | center | bottom ] ]
|
| Initial:
| 50% 50%
|
| Applies to:
| block-level and inline-level elements
|
| Inherited:
| no
|
| Percentages:
| refer to the size of the element's box
|
| Media:
| visual
|
| Computed value:
| For <length> the absolute value, otherwise a percentage
|
The value of the transform
property is a list of <transform-functions> applied in the order
provided. The individual transform functions are separated by whitespace.
The set of allowed transform functions is given below. In this list the
type <translation-value> is defined as a <length> or
<percentage> value, and the <angle> type is defined by CSS Values and Units.
- matrix(<number>, <number>,
<number>, <number>, <number>, <number>)
- specifies a 2D transformation in the form of a transformation
matrix of six values. matrix(a,b,c,d,e,f) is equivalent to applying the
transformation matrix [a b c d e f].
- translate(<translation-value>[,
<translation-value>])
- specifies a 2D
translation by the vector [tx, ty], where tx is the first
translation-value parameter and ty is the optional second
translation-value parameter. If <ty> is not provided, ty
has zero as a value.
- translateX(<translation-value>)
- specifies a translation
by the given amount in the X direction.
- translateY(<translation-value>)
- specifies a translation
by the given amount in the Y direction.
- scale(<number>[, <number>])
- specifies a 2D scale
operation by the [sx,sy] scaling vector described by the 2 parameters. If
the second parameter is not provided, it is takes a value equal to the
first.
- scaleX(<number>)
- specifies a scale operation using the [sx,1] scaling vector, where sx
is given as the parameter.
- scaleY(<number>)
- specifies a scale operation using the [1,sy] scaling vector, where sy
is given as the parameter.
- rotate(<angle>)
- specifies a 2D
rotation by the angle specified in the parameter about the origin of
the element, as defined by the transform-origin property.
- skewX(<angle>)
- specifies a skew
transformation along the X axis by the given angle.
- skewY(<angle>)
- specifies a skew
transformation along the Y axis by the given angle.
- skew(<angle> [, <angle>])
- specifies a skew
transformation along the X and Y axes. The first angle parameter
specifies the skew on the X axis. The second angle parameter specifies
the skew on the Y axis. If the second parameter is not given then a value
of 0 is used for the Y angle (ie. no skew on the Y axis).
The <translation-value> values are defined as [<percentage>
| <length>]. All other value types are described as CSS types.
If a list of transforms is provided, then the net effect is as if each
transform had been specified separately in the order provided. For
example,
<div style="transform:translate(-10px,-20px) scale(2) rotate(45deg) translate(5px,10px)"/>
is functionally equivalent to:
<div style="transform:translate(-10px,-20px)">
<div style="transform:scale(2)">
<div style="transform:rotate(45deg)">
<div style="transform:translate(5px,10px)">
</div>
</div>
</div>
</div>
div {
transform: translate(100px, 100px);
}
Move the element by 100 pixels in both the X and Y directions.
div {
height: 100px; width: 100px;
transform: translate(80px, 80px) scale(1.5, 1.5) rotate(45deg);
}
Move the element by 80 pixels in both the X and Y directions, then scale
the element by 150%, then rotate it 45 degrees clockwise about the Z axis.
Note that the scale and rotate operate about the center of the element,
since the element has the default transform-origin of 50% 50%.
6. Transitions and animations
between transform values
When animating or transitioning the value of a transform property the
rules described below are applied. The ‘from’ transform is the transform at the start
of the transition or current keyframe. The ‘end’ transform is the transform at the end of
the transition or current keyframe.
- If the ‘
from’ and
‘to’ transforms are both single
functions of the same type:
- For translate, translateX, translateY, scale, scaleX, scaleY,
rotate, skew, skewX and skewY functions:
- the individual components of the function are interpolated
numerically.
- For matrix:
- the matrix is decomposed using the
method described by unmatrix into separate translation, scale,
rotation and skew matrices, then each decomposed matrix is
interpolated numerically, and finally combined in order to produce a
resulting 3x2 matrix.
- If both the ‘
from’ and
‘to’ transforms are "none":
- There is no interpolation necessary
- If one of the ‘
from’ or
‘to’ transforms is "none":
- The ‘
none’ is replaced by
an equivalent identity function list for the corresponding transform
function list.
For example, if the ‘from’
transform is "scale(2)" and the ‘to’ transform is "none" then the value
"scale(1)" will be used as the ‘to’ value, and animation will proceed
using the rule above. Similarly, if the ‘from’ transform is "none" and the
‘to’ transform is "scale(2)
rotate(50deg)" then the animation will execute as if the ‘from’ value is "scale(1) rotate(0)".
The identity functions are translate(0), translateX(0),
translateY(0), scale(1), scaleX(1), scaleY(1), rotate(0), rotateX(0),
rotateY(0), skewX(0), skewY(0), skew(0, 0) and matrix(1, 0, 0, 1, 0,
0).
- If both the ‘
from’ and
‘to’ transforms have the same
number of transform functions and corresponding functions in each
transform list are of the same type:
- Each transform function is animated with its corresponding
destination function in isolation using the rules described above. The
individual values are then applied as a list to produce resulting
transform value.
- Otherwise:
- The transform function lists are each converted into the equivalent
matrix value and animation proceeds using the rule for a single
function above.
In some cases, an animation might cause a transformation matrix to be
singular or non-invertible. For example, an animation in which scale moves
from 1 to -1. At the time when the matrix is in such a state, the
transformed element is not rendered.
7. Matrix
decomposition for animation
When interpolating between 2 matrices, each is decomposed into the
corresponding translation, rotation, scale, skew, and perspective values.
Not all matrices can be accurately described by these values. Those that
can't are decomposed into the most accurate representation possible, using
the technique below. This technique is taken from The "unmatrix" method in
"Graphics Gems II, edited by Jim Arvo". The pseudocode below works on a
4x4 homogeneous matrix. A 3x2 2D matrix is therefore first converted to
4x4 homogeneous form.
Input: matrix ; a 4x4 matrix
Output: translation ; a 3 component vector
rotation ; Euler angles, represented as a 3 component vector
scale ; a 3 component vector
skew ; skew factors XY,XZ,YZ represented as a 3 component vector
perspective ; a 4 component vector
Returns false if the matrix cannot be decomposed, true if it can
Supporting functions (point is a 3 component vector, matrix is a 4x4 matrix):
float determinant(matrix) returns the 4x4 determinant of the matrix
matrix inverse(matrix) returns the inverse of the passed matrix
matrix transpose(matrix) returns the transpose of the passed matrix
point multVecMatrix(point, matrix) multiplies the passed point by the passed matrix
and returns the transformed point
float length(point) returns the length of the passed vector
point normalize(point) normalizes the length of the passed point to 1
float dot(point, point) returns the dot product of the passed points
float cos(float) returns the cosine of the passed angle in radians
float asin(float) returns the arcsine in radians of the passed value
float atan2(float y, float x) returns the principal value of the arc tangent of
y/x, using the signs of both arguments to determine
the quadrant of the return value
Decomposition also makes use of the following function:
point combine(point a, point b, float ascl, float bscl)
result[0] = (ascl * a[0]) + (bscl * b[0])
result[1] = (ascl * a[1]) + (bscl * b[1])
result[2] = (ascl * a[2]) + (bscl * b[2])
return result
// Normalize the matrix.
if (matrix[3][3] == 0)
return false
for (i = 0; i < 4; i++)
for (j = 0; j < 4; j++)
matrix[i][j] /= matrix[3][3]
// perspectiveMatrix is used to solve for perspective, but it also provides
// an easy way to test for singularity of the upper 3x3 component.
perspectiveMatrix = matrix
for (i = 0; i < 3; i++)
perspectiveMatrix[i][3] = 0
perspectiveMatrix[3][3] = 1
if (determinant(perspectiveMatrix) == 0)
return false
// First, isolate perspective.
if (matrix[0][3] != 0 || matrix[1][3] != 0 || matrix[2][3] != 0)
// rightHandSide is the right hand side of the equation.
rightHandSide[0] = matrix[0][3];
rightHandSide[1] = matrix[1][3];
rightHandSide[2] = matrix[2][3];
rightHandSide[3] = matrix[3][3];
// Solve the equation by inverting perspectiveMatrix and multiplying
// rightHandSide by the inverse.
inversePerspectiveMatrix = inverse(perspectiveMatrix)
transposedInversePerspectiveMatrix = transposeMatrix4(inversePerspectiveMatrix)
perspective = multVecMatrix(rightHandSide, transposedInversePerspectiveMatrix)
// Clear the perspective partition
matrix[0][3] = matrix[1][3] = matrix[2][3] = 0
matrix[3][3] = 1
else
// No perspective.
perspective[0] = perspective[1] = perspective[2] = 0
perspective[3] = 1
// Next take care of translation
translate[0] = matrix[3][0]
matrix[3][0] = 0
translate[1] = matrix[3][1]
matrix[3][1] = 0
translate[2] = matrix[3][2]
matrix[3][2] = 0
// Now get scale and shear. 'row' is a 3 element array of 3 component vectors
for (i = 0; i < 3; i++)
row[i][0] = matrix[i][0]
row[i][1] = matrix[i][1]
row[i][2] = matrix[i][2]
// Compute X scale factor and normalize first row.
scale[0] = length(row[0])
row[0] = normalize(row[0])
// Compute XY shear factor and make 2nd row orthogonal to 1st.
skew[0] = dot(row[0], row[1])
row[1] = combine(row[1], row[0], 1.0, -skew[0])
// Now, compute Y scale and normalize 2nd row.
scale[1] = length(row[1])
row[1] = normalize(row[1])
skew[0] /= scale[1];
// Compute XZ and YZ shears, orthogonalize 3rd row
skew[1] = dot(row[0], row[2])
row[2] = combine(row[2], row[0], 1.0, -skew[1])
skew[2] = dot(row[1], row[2])
row[2] = combine(row[2], row[1], 1.0, -skew[2])
// Next, get Z scale and normalize 3rd row.
scale[2] = length(row[2])
row[2] = normalize(row[2])
skew[1] /= scale[2]
skew[2] /= scale[2]
// At this point, the matrix (in rows) is orthonormal.
// Check for a coordinate system flip. If the determinant
// is -1, then negate the matrix and the scaling factors.
pdum3 = cross(row[1], row[2])
if (dot(row[0], pdum3) < 0)
for (i = 0; i < 3; i++) {
scale[0] *= -1;
row[i][0] *= -1
row[i][1] *= -1
row[i][2] *= -1
// Now, get the rotations ou
rotate[1] = asin(-row[0][2]);
if (cos(rotate[1]) != 0)
rotate[0] = atan2(row[1][2], row[2][2]);
rotate[2] = atan2(row[0][1], row[0][0]);
else
rotate[0] = atan2(-row[2][0], row[1][1]);
rotate[2] = 0;
return true;
Each component of each returned value is linearly interpolated with the
corresponding component of the other matrix. The resulting components are
then recomposed into a final matrix as though combining the following
transform functions:
matrix3d(1,0,0,0, 0,1,0,0, 0,0,1,0, perspective[0], perspective[1], perspective[2], perspective[3])
translate3d(translation[0], translation[1], translation[2])
rotateX(rotation[0]) rotateY(rotation[1]) rotateZ(rotation[2])
matrix3d(1,0,0,0, 0,1,0,0, 0,skew[2],1,0, 0,0,0,1)
matrix3d(1,0,0,0, 0,1,0,0, skew[1],0,1,0, 0,0,0,1)
matrix3d(1,0,0,0, skew[0],1,0,0, 0,0,1,0, 0,0,0,1)
scale3d(scale[0], scale[1], scale[2])
8. DOM Interfaces
This section describes the interfaces and functionality added to the
DOM to support runtime access to the functionality described above.
8.1. CSSMatrix
- Interface CSSMatrix
-
The CSSMatrix interface represents a 4x4 homogeneous
matrix.
- IDL Definition
-
interface CSSMatrix {
attribute float a;
attribute float b;
attribute float c;
attribute float d;
attribute float e;
attribute float f;
void setMatrixValue(in DOMString string) raises(DOMException);
CSSMatrix multiply(in CSSMatrix secondMatrix);
CSSMatrix multiplyLeft(in CSSMatrix secondMatrix);
CSSMatrix inverse() raises(DOMException);
CSSMatrix translate(in float x, in float y);
CSSMatrix scale(in float scaleX, in float scaleY);
CSSMatrix skew(in float angleX, in float angleY);
CSSMatrix rotate(in float angle);
};
- Attributes
-
-
a-f of type float
- Each of these attributes represents one of the values in the 3x2
matrix.
- Methods
-
-
setMatrixValue
-
The
setMatrixValue method replaces
the existing matrix with one computed from parsing the passed string
as though it had been assigned to the transform property in a CSS
style rule.
Parameters
-
string of type
DOMString
- The string to parse.
No Return Value
Exceptions
-
DOMException SYNTAX_ERR
- Thrown when the provided string can not be parsed into a
CSSMatrix.
-
multiply
-
The
multiply method returns a new
CSSMatrix which is the result of this matrix multiplied by the
passed matrix, with the passed matrix to the right. This matrix is
not modified.
Parameters
-
secondMatrix of type
CSSMatrix
- The matrix to multiply.
Return Value
-
CSSMatrix
- The result matrix.
No Exceptions
-
multiplyLeft
-
The
multiplyLeft method returns a new
CSSMatrix which is the result of this matrix multiplied by the
passed matrix, with the passed matrix to the left. This matrix is
not modified.
Parameters
-
secondMatrix of type
CSSMatrix
- The matrix to multiply.
Return Value
-
CSSMatrix
- The result matrix.
No Exceptions
-
inverse
-
The
inverse method returns a new
matrix which is the inverse of this matrix. This matrix is not
modified.
No Parameters
Return Value
-
CSSMatrix
- The inverted matrix.
Exceptions
-
DOMException NOT_SUPPORTED_ERR
- Thrown when the CSSMatrix can not be inverted.
-
translate
-
The
translate method returns a new
matrix which is this matrix post multiplied by a translation matrix
containing the passed values. This matrix is not modified.
Parameters
-
x of type
float
- The X component of the translation value.
-
y of type
float
- The Y component of the translation value.
Return Value
-
CSSMatrix
- The result matrix.
No Exceptions
-
scale
-
The
scale method returns a new matrix
which is this matrix post multiplied by a scale matrix containing
the passed values. If the y component is undefined, the x component
value is used in its place. This matrix is not modified.
Parameters
-
scaleX of type
float
- The X component of the scale value.
-
scaleY of type
float
- The (optional) Y component of the scale value.
Return Value
-
CSSMatrix
- The result matrix.
No Exceptions
-
rotate
-
The
rotate method returns a new
matrix which is this matrix post multiplied by a rotation matrix.
The rotation value is in degrees. This matrix is not modified.
Parameters
-
angle of type
float
- The angle of rotation.
Return Value
-
CSSMatrix
- The result matrix.
No Exceptions
-
skew
-
The
skew method returns a new matrix
which is this matrix post multiplied by a skew matrix. The rotation
value is in degrees. This matrix is not modified.
Parameters
-
angleX of type
float
- The angle of skew along the X axis.
-
angleY of type
float
- The angle of skew along the Y axis.
Return Value
-
CSSMatrix
- The result matrix.
No Exceptions
In addition to the interface listed above, the
getComputedStyle method of the Window object has
been updated. The transform property
of the style object returned by getComputedStyle contains a
DOMString of the form "matrix(a, b, c, d, e, f)" representing the 3x2
matrix that is the result of applying the individual functions listed in
the transform property.
9. References
Normative references
-
Other references
-
Property index
| Property
| Values
| Initial
| Applies to
| Inh.
| Percentages
| Media
|
| transform
| none | <transform-function> [ <transform-function> ]*
| none
| block-level and inline-level elements
| no
| refer to the size of the element's box
| visual
|
| transform-origin
| [ [ <percentage> | <length> | left | center | right ] [
<percentage> | <length> | top | center | bottom ]? ] | [ [
left | center | right ] || [ top | center | bottom ] ]
| 50% 50%
| block-level and inline-level elements
| no
| refer to the size of the element's box
| visual
|
Index
- transform, 2.
- transform-origin, 3.