Combining Presentation and Content Markup

Issue update_mixing	`wiki (member only)`
Update Combining Presentation and Content Markup
The current chapter describes MathML2, it will need to be updated in later drafts.
Resolution	None recorded

5.1 Why Two Different Kinds of Markup?

Chapters 3 and 4 describe two kinds of markup for encoding mathematical material in documents.

Presentation markup captures notational structure. It encodes the notational structure of an expression in a sufficiently abstract way to facilitate rendering to various media. Thus, the same presentation markup can be rendered with relative ease on screen in either wide and narrow windows, in ASCII or graphics, in print, or it can be enunciated in a sensible way when spoken. It does this by providing information such as structured grouping of expression parts, classification of symbols, etc.

Presentation markup does not directly concern itself with the mathematical structure or meaning of an expression. In many situations, notational structure and mathematical structure are closely related, so a sophisticated processing application may be able to heuristically infer mathematical meaning from notational structure, provided sufficient context is known. However, in practice, the inference of mathematical meaning from mathematical notation must often be left to the reader.

Employing presentation tags alone may limit the ability to re-use a MathML object in another context, especially evaluation by external applications.

Content markup captures mathematical structure. It encodes mathematical structure in a sufficiently regular way in order to facilitate the assignment of mathematical meaning to an expression by application programs. Though the details of mapping from mathematical expression structure to mathematical meaning can be extremely complex, in practice, there is wide agreement about the conventional meaning of many basic mathematical constructions. Consequently, much of the meaning of a content expression is easily accessible to a processing application, independently of where or how it is displayed to the reader. In many cases, content markup could be cut from a Web browser and pasted into a mathematical software tool with confidence that sensible values will be computed.

Since content markup is not directly concerned with how an expression is displayed, a renderer must infer how an expression should be presented to a reader. While a sufficiently sophisticated renderer and style sheet mechanism could in principle allow a user to read mathematical documents using personalized notational preferences, in practice, rendering content expressions with notational nuances may still require intervention of some sort.

Employing content tags alone may limit the ability of the author to precisely control how an expression is rendered.

Both content and presentation tags are necessary in order to provide the full expressive capability one would expect in a mathematical markup language. Often the same mathematical notation is used to represent several completely different concepts. For example, the notation xⁱ may be intended (in polynomial algebra) as the i-th power of the variable x, or as the i-th component of a vector x (in tensor calculus). In other cases, the same mathematical concept may be displayed in one of various notations. For instance, the factorial of a number might be expressed with an exclamation mark, a Gamma function, or a Pochhammer symbol.

Thus the same notation may represent several mathematical ideas, and, conversely, the same mathematical idea often has several notations. In order to provide authors with the ability to precisely control notation while at the same time encoding meanings in a machine-readable way, both content and presentation markup are needed.

In general, if it is important to control exactly how an expression is rendered, presentation markup will generally be more satisfactory. If it is important that the meaning of an expression can be interpreted dependably and automatically, then content markup will generally be more satisfactory.

5.2 Mixed Markup

MathML offers authors elements for both content and presentation markup. Whether to use one or the other, or a combination of both, depends on what aspects of rendering and interpretation an author wishes to control, and what kinds of re-use he or she wishes to facilitate.

5.2.1 Reasons to Mix Markup

In many common situations, an author or authoring tool may choose to generate either presentation or content markup exclusively. For example, a program for translating legacy documents would most likely generate pure presentation markup. Similarly, an educational software package might very well generate only content markup for evaluation in a computer algebra system. However, in many other situations, there are advantages to mixing both presentation and content markup within a single expression.

If an author is primarily presentation-oriented, interspersing some content markup will often produce more accessible, more re-usable results. For example, an author writing about linear algebra might write:

<mrow>
  <apply>
    <power/>
    <ci>x</ci>
    <cn>2</cn>
  </apply>
  <mo>+</mo>
  <msup>
    <mi>v</mi>
    <mn>2</mn>
  </msup>
</mrow>

where v is a vector and the superscript denotes a vector component, and x is a real variable. On account of the linear algebra context, a visually impaired reader may have directed his or her voice synthesis software to render superscripts as vector components. By explicitly encoding the power, the content markup yields a much better voice rendering than would likely happen by default.

If an author is primarily content-oriented, there are two reasons to intersperse presentation markup. First, using presentation markup provides a way of modifying or refining how a content expression is rendered. For example, one might write:

<apply>
  <in/>
  <ci><mi mathvariant="bold">v</mi></ci>
  <ci>S</ci>
</apply>

In this case, the use of embedded presentation markup allows the author to specify that v should be rendered in boldface. In the same way, it is sometimes the case that a completely different notation is desired for a content expression. For example, here we express a fact about factorials, n = n!/(n-1)!, using the ascending factorial notation:

<apply>
  <equivalent/>
  <ci>n</ci>
  <apply>
     <divide/>
     <semantics>
        <apply>
           <factorial/>
           <ci>n</ci>
        </apply>
        <annotation-xml encoding="MathML-Presentation">
           <msup>
              <mn>1</mn>
              <mover accent="true">
                 <mi>n</mi>
                 <mo>&OverBar;</mo>
              </mover>
           </msup>
        </annotation-xml>
     </semantics>
     <semantics>
        <apply>
           <factorial/>
           <apply><minus/><ci>n</ci><cn>1</cn></apply>
        </apply>
        <annotation-xml encoding="MathML-Presentation">
           <msup>
              <mn>1</mn>
              <mover accent="true">
                 <mrow><mi>n</mi><mo>-</mo><mn>1</mn></mrow>
                 <mo>&OverBar;</mo>
              </mover>
           </msup>
        </annotation-xml>
     </semantics>
   </apply>
</apply>

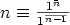
This content expression would render using the given notation as: $n \equiv \frac{1^{\bar{n}}}{1^{\frac{}{n-1}}}$

A second reason to use presentation within content markup is that there is a continually growing list of areas of discourse that do not have pre-defined content elements for encoding their objects and operators. As a consequence, any system of content markup inevitably requires an extension mechanism that combines notation with semantics in some way. MathML content markup specifies several ways of attaching an external semantic definitions to content objects. It is necessary, however, to use MathML presentation markup to specify how such user-defined semantic extensions should be rendered.

For example, the "rank" operator from linear algebra is not included as a pre-defined MathML content element. Thus, to express the statement rank(u^Tv)=1 we use a semantics element to bind a semantic definition to the symbol rank.

<apply>
  <eq/>
  <apply>
    <semantics>
      <mi>rank</mi>
      <annotation-xml encoding="OpenMath">
        <OMS name="rank" cd="linalg4" xmlns="http://www.openmath.org/OpenMath"/>
      </annotation-xml>
    </semantics>
    <apply> 
      <times/> 
      <apply> <transpose/> <ci>u</ci> </apply> 
      <ci>v</ci> 
    </apply>
  </apply>
  <cn>1</cn>
</apply>

Here, the semantics of rank have been given using a symbol from an OpenMath [OpenMath2000] content dictionary (CD).

5.2.2 Combinations that are prohibited

The main consideration when presentation markup and content markup are mixed together in a single expression is that the result should still make sense. When both kinds of markup are contained in a presentation expression, this means it should be possible to render the resulting mixed expressions simply and sensibly. Conversely, when mixed markup appears in a content expression, it should be possible to simply and sensibly assign a semantic interpretation to the expression as a whole. These requirements place a few natural constraints on how presentation and content markup can be mixed in a single expression, in order to avoid ambiguous or otherwise problematic expressions.

Two examples illustrate the kinds of problems that must be avoided in mixed markup. Consider:

<mrow>
  <bvar> x </bvar> <mo> + </mo> <bvar> y </bvar>
</mrow>

In this example, the content element bvar has been indiscriminately embedded in a presentation expression. Since bvar requires an enclosing context for its meaning, this expression is unclear.

Similarly, consider:

<apply>
  <ci> x </ci> <mo> + </mo> <ci> y </ci>
</apply>

Here, the mo element is problematic. Should a renderer infer that the usual arithmetic operator is intended, and act as if the prefix content element plus had been used? Or should this be literally interpreted as the operator x applied to two arguments, <mo>+</mo> and <mi>y</mi> ? Even if we were to decide that <mo>+</mo> was the operator, then what should its meaning be? These questions do not have particularly compelling answers, so this kind of mixing of content and presentation markup is also prohibited.

5.2.3 Presentation Markup Contained in Content Markup

The use of presentation markup within content markup is limited to situations that do not effect the ability of content markup to unambiguously encode mathematical meaning. Specifically, presentation markup may only appear in content markup in three ways:

within ci and cn token elements
within the csymbol element
within the semantics element

Any other presentation markup occurring within a content markup is a MathML error. More detailed discussion of these three cases follows:

Presentation markup within token elements.: The token elements ci and cn are permitted to contain any sequence of MathML characters (defined in Chapter 6 Characters, Entities and Fonts), presentation elements, and sep empty elements. Contiguous blocks of MathML characters in ci and cn elements are rendered as if they were wrapped in mi and mn elements respectively. If a token element contains both MathML characters and presentation elements, contiguous blocks of MathML characters (if any) are treated as if wrapped in mi or mn elements as appropriate, and the resulting collection of presentation elements are rendered as if wrapped in an mrow element.
Presentation markup within the csymbol element.: The csymbol element may contain either MathML characters interspersed with presentation markup, or content elements of the container type. It is a MathML error for a csymbol element to contain both presentation and content elements. When the csymbol element contains both raw data and presentation markup, the same rendering rules that apply to content elements of the token type should be used.
Presentation markup within the semantics element.: One of the main purposes of the semantics element is to provide a mechanism for incorporating arbitrary MathML expressions into content markup in a semantically meaningful way. In particular, any valid presentation expression can be embedded in a content expression by placing it as the first child of a semantics element. The meaning of this wrapped expression should be indicated by one or more annotation elements also contained in the semantics element.

5.2.4 Content Markup Contained in Presentation Markup

The guiding principle for embedding content markup within presentation expressions is that the resulting expression should still have an unambiguous rendering. In general, this means that embedded content expressions must be semantically meaningful, since rendering of content markup depends on its meaning.

Certain content elements derive part of their semantic meaning from the surrounding context, such as whether a bvar element is qualifying an integral, logical quantifier or lambda expression. Another example would be whether a degree element occurs in a root or partialdiff element. Thus, in a presentation context, elements such as these do not have a clearly defined meaning, and hence there is no obvious choice for a rendering. Consequently, they are not allowed.

Using the terminology of Section 4.1.2 The Scope of Content Markup, we see that operator, relation, container, constant and symbol elements make sense on their own, while elements of the qualifier and condition type do not. (Note that interval may be used either as a general container, or as a qualifier.)

Outside these categories, certain elements deserve specific comment: the elements declare, sep, annotation and annotation-xml can only appear in very specific contexts and consequently are not permitted as direct sub-expressions of any presentation element. Finally, the element semantics carries with it sufficient information to be permitted in presentation.

The complete list of content elements that cannot appear as a child in a presentation element is: annotation, annotation-xml, sep, declare, bvar, condition, degree, logbase, lowlimit, uplimit.

Note that within presentation markup, content expressions may only appear in locations where it is valid for any MathML expression to appear. In particular, content expressions may not appear within presentation token elements. In this regard mixing presentation and content are asymmetrical.

Note that embedding content markup in presentation will often require applications to render operators outside of an apply context. E.g., it may be necessary to render abs, plus, root or sin outside of an application. Content/presentation mixing does not introduce any new requirements, however, since unapplied operators are already permitted in content expressions, for example:

<apply><compose/><sin/><apply><inverse/><root/></apply></apply>

5.3 Parallel Markup

Some applications are able to make use of both presentation and content information. For these applications it is desirable to provide both forms of markup for the same mathematical expression. This is called parallel markup.

Parallel markup is achieved with the semantics element. Parallel markup for an expression can be used on its own, or can be incorporated as part of a larger content or presentation tree.

5.3.1 Top-level Parallel Markup

In many cases what is desired is to provide presentation markup and content markup for a mathematical expression as a whole. To achieve this, a single semantics element is used pairing two markup trees, with the first branch being the MathML presentation markup, and the second branch being the MathML content markup.

The following example encodes the boolean arithmetic expression (a+b)(c+d) in this way.

<semantics>
  <mrow>
    <mrow><mo>(</mo><mi>a</mi> <mo>+</mo> <mi>b</mi><mo>)</mo></mrow>
    <mo>&InvisibleTimes;</mo>
    <mrow><mo>(</mo><mi>c</mi> <mo>+</mo> <mi>d</mi><mo>)</mo></mrow>
  </mrow>
  <annotation-xml encoding="MathML-Content">
    <apply><and/>
      <apply><xor/><ci>a</ci> <ci>b</ci></apply>
      <apply><xor/><ci>c</ci> <ci>d</ci></apply>
    </apply>
  </annotation-xml>
</semantics>

This example is non-trivial in the sense that the content markup could not be easily derived from the presentation markup alone.

5.3.2 Fine-grained Parallel Markup

Top-level pairing of independent presentation and content markup is sufficient for many, but not all, situations. Applications that allow treatment of sub-expressions of mathematical objects require the ability to associate presentation, content or information with the parts of an object with mathematical markup. Top-level pairing with a semantics element is insufficient in this type of situation; identification of a sub-expression in one branch of a semantics element gives no indication of the corresponding parts in other branches.

The ability to identify corresponding sub-expressions is required in applications such as mathematical expression editors. In this situation, selecting a sub-expression on a visual display can identify a particular portion of a presentation markup tree. The application then needs to determine the corresponding annotations of the sub-expressions; in particular, the application requires the sub-expressions of the annotation-xml tree in MathML content notation.

It is, in principle, possible to provide annotations for each presentation node by incorporating semantics elements recursively.

<semantics>
  <mrow>
    <semantics>
      <mrow><mo>(</mo><mi>a</mi> <mo>+</mo> <mi>b</mi><mo>)</mo></mrow>
      <annotation-xml encoding="MathML-Content">
        <apply><plus/><ci>a</ci> <ci>b</ci></apply>
      </annotation-xml>
    </semantics>
    <mo>&InvisibleTimes;</mo>
    <semantics>
      <mrow><mo>(</mo><mi>c</mi> <mo>+</mo> <mi>d</mi><mo>)</mo></mrow>
      <annotation-xml encoding="MathML-Content">
        <apply><plus/><ci>c</ci> <ci>d</ci></apply>
      </annotation-xml>
    </semantics>
  </mrow>

  <annotation-xml encoding="MathML-Content">
    <apply><times/>
      <apply><plus/><ci>a</ci> <ci>b</ci></apply>
      <apply><plus/><ci>c</ci> <ci>d</ci></apply>
    </apply>
  </annotation-xml>
</semantics>

To be complete this example would be much more verbose, wrapping each of the individual leaves mi, mo and mn in a further seven semantics elements.

This approach is very general and works for all kinds of annotations (including non-MathML annotations and multiple annotations). It leads, however, to O(n log n) increase in size of the document. This is therefore not a suitable approach for fine-grained parallel markup of large objects.

5.3.3 Parallel Markup via Cross-References: `id` and `xref`

To better accommodate applications that must deal with sub-expressions of large objects, MathML uses cross-references between the branches of a semantics element to identify corresponding sub-structures.

Cross-referencing is achieved using id and xref attributes within the branches of a containing semantics element. These attributes may optionally be placed on MathML elements of any type.

The following example shows this cross-referencing for the boolean arithmetic expression (a+b)(c+d).

<semantics>
  <mrow id="E">
    <mrow id="E.1">
      <mo id="E.1.1">(</mo>
      <mi id="E.1.2">a</mi>
      <mo id="E.1.3">+</mo>
      <mi id="E.1.4">b</mi>
      <mo id="E.1.5">)</mo>
    </mrow>
    <mo id="E.2">&InvisibleTimes;</mo>
    <mrow id="E.3">
      <mo id="E.3.1">(</mo>
      <mi id="E.3.2">c</mi>
      <mo id="E.3.3">+</mo>
      <mi id="E.3.4">d</mi>
      <mo id="E.3.5">)</mo>
    </mrow>
  </mrow>

  <annotation-xml encoding="MathML-Content">
    <apply xref="E">
      <and xref="E.2"/>
      <apply xref="E.1">
        <xor xref="E.1.3"/><ci xref="E.1.2">a</ci><ci xref="E.1.4">b</ci>
      </apply>
      <apply xref="E.3">
        <xor xref="E.3.3"/><ci xref="E.3.2">c</ci><ci xref="E.3.4">d</ci>
      </apply>
    </apply>
  </annotation-xml>
</semantics>

An id attribute and a corresponding xref appearing within the same semantics element create a correspondence between sub-expressions.

In creating these correspondences by cross-reference, all of the id attributes referenced by any xref must be in the same branch of an enclosing semantics element. This constraint guarantees that these correspondences do not create unintentional cycles. (Note that this restriction does not exclude the use of id attributes within the other branches of the enclosing semantics element. It does, however, exclude references to these other id attributes originating in the same semantics element.)

There is no restriction on which branch of the semantics element may contain the destination id attributes. It is up to the application to determine which branch to use.

In general, there will not be a one-to-one correspondence between nodes in parallel branches. For example, a presentation tree may contain elements, such as parentheses, that have no correspondents in the content tree. It is therefore often useful to put the id attributes on the branch with the finest-grained node structure. Then all of the other branches will have xref attributes to some subset of the id attributes.

In absence of other criteria, the first branch of the semantics element is a sensible choice to contain the id attributes. Applications that add or remove annotations will then not have to re-assign attributes to the semantics trees.

In general, the use of id and xref attributes allows a full correspondence between sub-expressions to be given in text that is at most a constant factor larger than the original. The direction of the references should not be taken to imply that sub-expression selection is intended to be permitted only on one child of the semantics element. It is equally feasible to select a subtree in any branch and to recover the corresponding subtrees of the other branches.

5.3.4 Annotation Cross-References using XLink: `id` and `href`

It is possible to give cross-references between a MathML expression and a non-MathML XML annotation using the XLink protocol [XLink]. As an example, the boolean expression of the previous section can be annotated with OpenMath, and cross-linked as follows:

<semantics>
  <mrow id="E">
    <mrow id="E.1">
      <mo id="E.1.1">(</mo>
      <mi id="E.1.2">a</mi>
      <mo id="E.1.3">+</mo>
      <mi id="E.1.4">b</mi>
      <mo id="E.1.5">)</mo>
    </mrow>
    <mo id="E.2">&InvisibleTimes;</mo>
    <mrow id="E.3">
      <mo id="E.3.1">(</mo>
      <mi id="E.3.2">c</mi>
      <mo id="E.3.3">+</mo>
      <mi id="E.3.4">d</mi>
      <mo id="E.3.5">)</mo>
    </mrow>
  </mrow>

  <annotation-xml encoding="MathML-Content">
    <apply xref="E">
      <and xref="E.2"/>
      <apply xref="E.1">
        <xor xref="E.1.3"/><ci xref="E.1.2">a</ci><ci xref="E.1.4">b</ci>
      </apply>
      <apply xref="E.3">
        <xor xref="E.3.3"/><ci xref="E.3.2">c</ci><ci xref="E.3.4">d</ci>
      </apply>
    </apply>
  </annotation-xml>

  <annotation-xml encoding="OpenMath" 
                  xmlns:om="http://www.openmath.org/OpenMath"
                  xmlns:xlink="http://www.w3.org/1999/xlink">

    <om:OMA xlink:href="#xpointer(id('E'))" xlink:type="simple">
      <om:OMS name="and" cd="logic1" 
              xlink:href="#xpointer(id('E.2'))" xlink:type="simple"/>

      <om:OMA xlink:href="#xpointer(id('E.1'))" xlink:type="simple">
        <om:OMS name="xor" cd="logic1" 
                xlink:href="#xpointer(id('E.1.3'))" xlink:type="simple"/>
        <om:OMV name="a" 
                xlink:href="#xpointer(id('E.1.2'))" xlink:type="simple"/>
        <om:OMV name="b" 
                xlink:href="#xpointer(id('E.1.4'))" xlink:type="simple"/>
      </om:OMA>

      <om:OMA xlink:href="#xpointer(id('E.3'))" xlink:type="simple">
        <om:OMS name="xor" cd="logic1" 
                xlink:href="#xpointer(id('E.3.3'))" xlink:type="simple"/>
        <om:OMV name="c" 
                xlink:href="#xpointer(id('E.3.2'))" xlink:type="simple"/>
        <om:OMV name="d" 
                xlink:href="#xpointer(id('E.3.4'))" xlink:type="simple"/>
      </om:OMA>
    </om:OMA>
  </annotation-xml>
</semantics>

Here OMA, OMS and OMV are elements defined in the OpenMath standard for representing application, symbol and variable, respectively. The references from the OpenMath annotation are given by the xlink:href attributes which in this case use XPointer [XPointer] to refer to ids within the current document.

Note that the application might or might not have a mechanism for extending DTDs. It will be the case, therefore that some applications will give well-formed, but not "valid", XML within annotation-xml elements. Consequently, some MathML applications using annotation-xml will not be validated. More flexibility is offered by the use of XML Schemas.

5.4 Tools, Style Sheets and Macros for Combined Markup

The interaction of presentation and content markup can be greatly enhanced through the use of various tools. While the set of tools and standards for working with XML applications is rapidly evolving at the present, we can already outline some specific techniques.

In general, the interaction of content and presentation is handled via transformation rules on MathML trees. These transformation rules are sometimes called "macros". In principle, these rules can be expressed using any one of a number of mechanisms, including DSSSL, Java programs operating on a DOM, etc. We anticipate, however, that the principal mechanism for these transformations in most applications shall be XSLT.

In this section we discuss transformation rules for two specific purposes: for notational style sheets, and to simplify parallel markup.

5.4.1 Notational Style Sheets

Authors who make use of content markup may be required to deploy their documents in locales with notational conventions different than the default content rendering. It is therefore expected that transformation tools will be used to determine notations for content elements in different settings. Certain elements, e.g. lambda, mean and transpose, have widely varying common notations and will often require notational selection. Some examples of notational variations are given below.

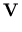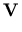$\mathbf{V}$ versus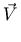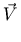 $\vec{V}$
tan x versus tg x
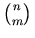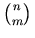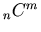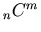${n \choose m}$ versus ${}_nC^m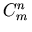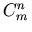$ versus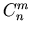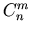 versus
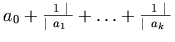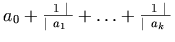$a_0 + \frac{ ~1 ~ |}{| ~a_1 ~} + \ldots + \frac{~1 ~ |}{| ~ a_k~}$ versus $[a_0, a_1, \ldots, a_k]$

Other elements, for example plus and sin, are less likely to require these features.

Selection of notational style is sometimes necessary for correct understanding of documents by locale. For instance, the binomial coefficient 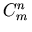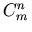C^n_m in French notation is equivalent to 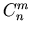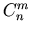C^m_n in Russian notation.

A natural way for a MathML application to bind a particular notation to the set of content tags is with an XSLT style sheet [XSLT]. The examples of this section shall assume this is the mechanism to express style choices. (Other choices are equally possible, for example an application program may provide menus offering a number of rendering choices for all content tags.)

When writing XSLT style sheets for mathematical notation, some transformation rules can be purely local, while others will require multi-node context to determine the correct output notation. The following example gives a local transformation rule that could be included in a notational style sheet displaying open intervals as ]a,b[ rather than as (a,b).

<xsl:template match="m:interval">
  <m:mrow>
    <xsl:choose>
      <xsl:when test="@closure='closed'">
        <m:mfenced open="[" close="]" separators=",">
          <xsl:apply-templates/>
        </m:mfenced>
      </xsl:when>
      <xsl:when test="@closure='open'">
        <m:mfenced open="]" close="[" separators=",">
          <xsl:apply-templates/>
        </m:mfenced>
      </xsl:when>
      <xsl:when test="@closure='open-closed'">
        <m:mfenced open="]" close="]" separators=",">
          <xsl:apply-templates/>
        </m:mfenced>
      </xsl:when>
      <xsl:when test="@closure='closed-open'">
        <m:mfenced open="[" close="[" separators=",">
          <xsl:apply-templates/>
        </m:mfenced>
      </xsl:when>
      <xsl:otherwise>
        <m:mfenced open="[" close="]" separators=",">
          <xsl:apply-templates/>
        </m:mfenced>
      </xsl:otherwise>
    </xsl:choose>
  </m:mrow>
</xsl:template>

Here m is established as the MathML namespace.

An example of a rule requiring context information would be:

<xsl:template match="m:apply[m:factorial]">
  <m:mrow>
    <xsl:choose>
      <xsl:when test="not(*[2]=m:ci) and not(*[2]=m:cn)">
        <m:mrow>
          <m:mo>(</m:mo>
          <xsl:apply-templates select="*[2]" />
          <m:mo>)</m:mo>
        </m:mrow>
      </xsl:when>
      <xsl:otherwise>
        <xsl:apply-templates select="*[2]" />
      </xsl:otherwise>
    </xsl:choose>
    <m:mo>!</m:mo>
  </m:mrow>
</xsl:template>

Other examples of context-dependent transformations would be, e.g. for the apply of a plus to render a-b+c, rather than a+ -b+c, or for the apply of a power to render sin²x, rather than sin x².

Notational variation will occur both for built-in content elements as well as extensions. Notational style for extensions can be handled as described above, with rules matching the names of any extension tags, and with the content handling (in a content-faithful style sheet) proceeding as described in Section 5.4.3 Style Sheets for Extensions.

5.4.2 Content-Faithful Transformations

There may be a temptation to view notational style sheets as a transformation from content markup to equivalent presentation markup. This viewpoint is explicitly discouraged, since information will be lost and content-oriented applications will not function properly.

We define a "content-faithful" transformation to be a transformation that retains the original content in parallel markup (Section 5.3 Parallel Markup).

Tools that support MathML should be "content-faithful", and not gratuitously convert content elements to presentation elements in their processing. Notational style sheets should be content-faithful whenever they may be used in interactive applications.

It is possible to write content-faithful style sheets in a number of ways. Top-level parallel markup can be achieved by incorporating the following rules in an XSLT style sheet:

<xsl:template match="m:math">
   <m:semantics>
      <xsl:apply-templates/>

      <m:annotation-xml m:encoding="MathML-Content">
         <xsl:copy-of select="."/>
      </m:annotation-xml>
   </m:semantics>
</xsl:template>

The notation would be generated by additional rules for producing presentation from content, such as those in Section 5.4.1 Notational Style Sheets. Fine-grained parallel markup can be achieved with additional rules treating id attributes. A detailed example is given in [RodWatt2000].

5.4.3 Style Sheets for Extensions

The presentation tags of MathML form a closed vocabulary of notational structures, but are quite rich and can be used to express a rendering of most mathematical notations. Complex notations can be composed from the basic elements provided for presentation markup. In this sense, the presentation ability of MathML is open-ended. It is often useful, however, to give a name to new notational schemas if they are going to be used often. For example, we can shorten and clarify the ascending factorial example of Section 5.2.1 Reasons to Mix Markup, with a rule which replaces

<mx:a-factorial>X</mx:a-factorial>

with

<semantics>
   <apply> <factorial/> <ci>X</ci> </apply>
   <annotation-xml encoding="MathML-Presentation">
      <msup>
         <mn>1</mn>
         <mover accent="true">
            <mi>X</mi>
            <mo>&OverBar;</mo>
         </mover>
      </msup>
   </annotation-xml>
</semantics>

Then the example would be more clearly written as:

<apply>
  <equivalent/>
  <ci>n</ci>
  <apply>
     <divide/>
     <mx:a-factorial><ci>n</ci></mx:a-factorial>
     <mx:a-factorial>
        <apply><minus/><ci>n</ci><cn>1</cn></apply>
     </mx:a-factorial>
   </apply>
</apply>

Likewise, the content tags form a fixed vocabulary of concepts covering the types of mathematics seen in most common applications. It is not reasonable to expect users to compose existing MathML content tags to construct new content concepts. (This approach is fraught with technical difficulties even for professional mathematicians.) Instead, it is anticipated that applications whose mathematical content concepts extend beyond what is offered by MathML will use annotations and attributes within semantics and csymbol elements, and that these annotations will use content description languages outside of MathML.

Often the naming of a notation and the identification of a new semantic concept are related. This allows a single transformation rule to capture both a presentation and a content markup for an expression. This is one of the areas of MathML that benefits most strongly from the use of macro processing.

<mx:rank/>

and

<mx:tr>X</mx:tr>

and respectively transform them to

<semantics>
   <ci><mo>rank</mo></ci>
   <annotation-xml encoding="OpenMath">
      <OMS name="rank" cd="linalg4" xmlns="http://www.openmath.org/OpenMath"/>
   </annotation-xml>
</semantics>

and

<apply>
 <transpose/>
 <ci>X</ci>
</apply>

The lengthy sample encoding of rank(u^Tv)=1, from Section 5.2.1 Reasons to Mix Markup could then be condensed to

<apply>
  <eq/>
  <apply>
    <mx:rank/>
    <apply> <times/> <mx:tr>u</mx:tr> <ci>v</ci> </apply>
   </apply>
  <cn>1</cn>
</apply>

From this example we see how the combination of presentation and content markup could become much simpler and effective to generate as standard style sheet libraries become available.

5 Combining Presentation and Content Markup