| Issue cds_normative | wiki (member only) |
|---|---|
| Are CDs normative in MathML3 | |
|
The CDs now contain a lot of information that is not in any normative part of MathML any more (after the rewriting of Chapter 3). This means that we may have to make the CDs in this chapter normative |
|
| Resolution | None recorded |
C.1 About Content Dictionaries
The primary role of MathML content elements is to provide a mechanism for recording
that a particular notational structure has a particular mathematical meaning. To this
end, every content element must have a mathematical definition associated with it in
some form. These definitions are provided in the form of content
dictionaries, XML files of a certain structure (see . The purpose of this appendix is to provide a default
set of content dictionaries for the K-14 fragment of mathematics. Authors may adopt
these and come up with additional ones, fixing additional content elements that are
encoded via the csymbol element.
Content Dictionaries (CDs) are central to the MathML philosophy of transmitting mathematical information. It is the Content Dictionaries which actually hold the meanings of the objects being transmitted.
For example if application A is talking to application B, and sends, say, an equation involving multiplication of matrices, then A and B must agree on what a matrix is, and on what matrix multiplication is, and even on what constitutes an equation. All this information is held within some Content Dictionaries which both applications agree upon.
Intuitively, a Content Dictionary holds the meanings of (various) mathematical "words", that are represented by symbols in Content MathML
With a set of symbol definitions (perhaps from several Content Dictionaries), A and B can now talk in a common "language".
The concept of a content dictionary has initially been introduced by the OpenMath1 format [OpenMath2000], and has been stabilized and generalized to abstract content dictionaries in the OpenMath2 standard [OpenMath2004], keeping a variant of OpenMath1 CDs as a reference encoding. MathML 3 introduces a content dictionary format that is designed to meet the requirements of the MathML language, while meeting the requirements of OpenMath abstract CDs. We will introduce the format in the next section and then include the MathML3 content dictionaries for the K-14 fragments as part of the MathML3 recommendataion. These CDs are called the MathML3 Recommendation Content Dictionaries
When working with the content elements, it can be useful to keep in mind the following.
-
The role of the content elements is analogous to data entry in a mathematical system. The information that is provided is there to facilitate the successful parsing of an expression as the intended mathematical object by a receiving application.
-
MathML content elements do not by themselves "perform" any mathematical evaluations or operations. They do not "evaluate" in a browser and any "action" that is ultimately taken on those objects is determined entirely by the receiving mathematical application. For example, editing programs and applications geared to computation for the lower grades would typically leave 3 + 4 as is, whereas computational systems targeting a more advanced audience might evaluate this as 7. Similarly, some computational systems might evaluate sin(0) to 0, whereas others would leave it unevaluated. Yet other computational systems might be unable to deal with pure symbolic expressions like sin(x) and may even regard them as data entry errors. None of this has any bearing on the correctness of the original MathML representation. Where evaluation is mentioned at all in the descriptions below, it is merely to help clarify the meaning of the underlying operation.
-
Apart from the instances where there is an explicit interaction with presentation tagging, there is no required rendering (visual or aural) – only a suggested default. As such, the presentations that are included in this section are merely to help communicate to the reader the intended mathematical meaning by association with the same expression written in a more traditional notation.
C.2 The MathML3 Content Dictionary Format
We will now detail the MathML3 Content Dictionary format, on an abstract level and discuss the special case of the MathML Recommendation CDs. Note that the latter are not the only possible ones, any individual or group can set up and publish CDs for the purposes of communication.
| Editorial note: MiKo | |
| the material here is copied frm OM-style abstract content dictionaries. | |
C.2.1 Content Dictionaries
An abstract Content Dictionary consists of the following mandatory pieces of information:
-
A name which is an XML1.1 name [xml11].
-
A description of the Content Dictionary.
-
A revision date, the date of the last change to the Content Dictionary. Dates should be stored in the ISO-compliant format YYYY-MM-DD, e.g. 1966-02-03. For the MathML specification CDs the revision date is the date of the publication of the respective MathML recommendation.
-
A review date, a date until which the content dictionary is guaranteed to remain unchanged.
Issue mcd_dates wiki (member only) ISSUE-4 (member only) Revision date for MathML3 Spec content dictionaries There is not really a sensible review date for MathML3 spec CDs. We have no idea, when the spec will be revised. Unless we want to make them less normative than the MathML3 spec, and set up a revision process, then we will have to make this optional (and remove the requirement in OpenMath3)
Resolution None recorded -
A version number which consists of a major and minor part. For the MathML specification CDs, this is the version number of the respective MathML recommendation.
-
A status, which is one of
-
official: i.e. approved by W3C as part of the MathML specification -
experimental: under development and thus liable to change; -
private: used by a private group of users; -
obsolete: an obsolete Content Dictionary kept only for archival purposes.
Issue official_mcd wiki (member only) ISSUE-5 (member only) Approving bodies for CDs? OpenMath2 standard only allows
officialstatus for CDs approved by the OM Society. This seems overly proprietary. The MathML CDs should also be official. Change in OpenMath 3?Resolution None recorded -
-
A CD base which, when combined with the CD name, forms a unique identifier for the Content Dictionary. It may or may not refer to an actual location from which it can be retrieved.
-
A series of one or more symbol definitions as described below.
C.2.2 Symbol Definitions
A symbol definition consists of the following pieces of information:
-
A mandatory name which is an XML1.1 name [xml11].
-
A mandatory description of the symbol, which can be as formal or informal as the author likes.
-
An optional role as described in Section C.2.3 Symbol Roles.
-
A mandatory default rendering specification (see Section C.2.4 Default Rendering Specifications for details.
-
Zero or more attribute specifications for the case, where the MathML token takes attributes.
-
Zero or more signature declarations for type information
-
Zero or more commented mathematical properties which are mathematical properties of the symbol expressed in a human-readable way.
-
Zero or more properties which are mathematical properties of the symbol. A property can be expressed in natural language and as a MathML expression tree in the same property. The former is directly aimed at human readers, and the latter could be used for validation or evaluation in mathematical software systems.
property may be given an optional kind attribute. An author of a Content Dictionary may use this to indicate whether, for example, the property provides an algorithm for evaluation of the concept it is associated with. At present no fixed scheme is mandated for how this information should be encoded or used by an application.
-
Zero or more mathematical examples which are intended to demonstrate the use of the symbol within a content MathML expression tree.
C.2.3 Symbol Roles
We say that a symbol is used to construct an MathML expression tree
if it is the first child of an apply, bind or error
element. The role of a symbol is a restriction on how it may be used to
construct a compound expression tree and, in the case of the key in an attribution
object, a clarification of how that attribution should be interpreted. The possible
roles are:
-
binder The symbol may appear as the first child of a
bindelement. -
application The symbol may appear as the first child of an
applyelement. -
constant The symbol cannot be used to construct a compound expression tree.
-
error The symbol may appear as the first child of a
errorelement.
| Issue mathml_roles | wiki (member only) |
|---|---|
| More Roles for MathML? | |
|
Those are the roles in OpenMath. Do we need more in MathML? We could have one
for constructor (so that we know that it is a container element in legacy
markup)... That could later be mapped to application. But maybe this would be
better done by the |
|
| Resolution | None recorded |
A symbol cannot have more than one role and cannot be used to construct a compound expression tree object in a way which requires a different role (using the definition of construct given earlier in this section). This means that one cannot use a symbol which binds some variables to construct, say, an application object. However it does not prevent the use of that symbol as an argument in an application object (where by argument we mean a child with index greater than 1).
If no role is indicated then the symbol can be used anywhere. Note that this is not the same as saying that the symbol's role is constant.
C.2.4 Default Rendering Specifications
| Issue mcd_rendering | wiki (member only) ISSUE-6 (member only) |
|---|---|
| A MathML format for rendering? | |
|
How do we want to specify rendings. There are a couple of options:
in the latter cases: what do we do for role:application? There are solutions from ORCCA or OMDoc |
|
| Resolution | None recorded |
3.3 Content Dictionary: Basic Content Elements
The basic content Elements
C.1
MMLdefinition: interval
- Description
-
This is the MathML constructor element for building an interval on the real line. While an interval can be expressed by combining relations appropriately, they occur here explicitly because of the frequency of their use.
- Discussion
-
The
intervalelement is used to represent simple mathematical intervals of the real number line. It takes an attributeclosure, which can take on any of the values "open", "closed", "open-closed", or "closed-open", with a default value of "closed".A single
intervalelement occuring as the second child of anapplyelement and preceded by one of the pre-defined n-ary operators is interpreted as a shorthand notation for adomainofapplication. All other uses of anintervalelement as a child of an apply should be interpreted as ordinary function arguments unless otherwise dictated by the function definition.More general domains should be constructed using a
domainofapplicationelement or one of the other shortcut notations described in Section 4.2.7 Qualifiers.The
intervalelement expects two child elements that evaluate to real numbers. or one or morebvarelements and a child element that is aconditiondefining theinterval.The
intervalelement denotes an interval on the real line with the values represented by its children as end points. Theclosureattribute is used to qualify the type of interval being represented. For example,<interval closure="open-closed"><ci>a</ci><ci>b</ci></interval>
represents the open-closed interval often written (a,b].
- Classification
- constructor
- MMLattribute
-
Name Value Default type closed | open | open-closed | closed-open closed - Signature
-
[type=interval-type](algebraic,algebraic) -> interval(interval-type)
- Example
<interval closure="open"> <ci>x</ci> <cn>1</cn> </interval>
- Example
<interval closure="open-closed"> <cn>0</cn> <cn>1</cn> </interval>
- Example
<interval> <bvar><ci>x</ci></bvar> <condition> <apply><lt/><cn>0</cn><ci>x</ci></apply> </condition> </interval>- Example
<apply><int/> <interval><cn>0</cn><cn>1</cn></interval> <ci type="function">f</ci> </apply>
C.2
MMLdefinition: inverse
- Description
-
This MathML element is applied to a function in order to construct a new function that is to be interpreted as the inverse function of the original function. For a particular function F, inverse(F) composed with F behaves like the identity map on the domain of F and F composed with inverse(F) should be an identity function on a suitably restricted subset of the Range of F. The MathML definitionURL attribute should be used to resolve notational ambiguities, or to restrict the inverse to a particular domain or to make it one-sided.
- Discussion
-
The
inverseelement is applied to a function in order to construct a generic expression nfor the functional inverse of that function. As with other MathML functions,inversemay either be applied to arguments, or it may appear alone, in which case it represents an abstract inversion operator acting on other functions.A typical use of the
inverseelement is in an HTML document discussing a number of alternative definitions for a particular function so that there is a need to write and define f(-1)(x). To associate a particular definition with f(-1), use thedefinitionURLandencodingattributes.Given functions, it is natural to have functional inverses. This is handled by the
inverseelement.Functional inverses can be problematic from a mathematical point of view in that they implicitly involve the definition of an inverse for an arbitrary function F. Even at the K-through-12 level the concept of an inverse F -1 of many common functions F is not used in a uniform way. For example, the definitions used for the inverse trigonometric functions may differ slightly depending on the choice of domain and/or branch cuts.
MathML adopts the view: if F is a function from a domain D to D', then the inverse G of F is a function over D' such that G(F(x)) = x for x in D. This definition does not assert that such an inverse exists for all or indeed any x in D, or that it is single-valued anywhere. Also, depending on the functions involved, additional properties such as F(G(y)) = y for y in D' may hold.
The
inverseelement is applied to a function whenever an inverse is required. For example, application of the inverse sine function to x, i.e. sin-1 (x), is encoded as:<apply> <apply> <inverse/> <sin/> </apply> <ci> x </ci> </apply>While
arcsinis one of the predefined MathML functions, an explicit reference to sin-1(x) might occur in a document discussing possible definitions ofarcsin. - Classification
- operator
- Signature
-
(function) -> function
[definitionURL=URI](function) -> function(definition)
- Property
-
ForAll( y, such y in domain( f^(-1) ), f( f^(-1)(y) ) = y
<apply><forall/> <bvar><ci>y</ci></bvar> <bvar><ci type="function">f</ci></bvar> <condition> <apply><in/> <ci>y</ci> <apply><csymbol definitionURL="domain"><mtext>Domain</mtext></csymbol> <apply><inverse/><ci type="function">f</ci></apply> </apply> </apply> </condition> <apply><eq/> <apply><ci type="function">f</ci> <apply><apply><inverse/><ci type="function">f</ci></apply> <ci>y</ci> </apply> </apply> <ci>y</ci> </apply> </apply> - Example
<apply><inverse/> <sin/> </apply>
- Example
<apply><inverse definitionURL="www.example.com/MathML/Content/arcsin"/> <sin/> </apply>
- Example
<apply> <apply><inverse/> <ci type="matrix"> a </ci> </apply> <ci> A </ci> </apply>
C.3
MMLdefinition: lambda
- Description
-
This is the operation of lambda calculus that constructs a function from an expression and a variable. Lambda is an n-ary function, where all but an optional domain of application and the last argument are bound variables and the last argument is an expression possibly involving those variables. The lambda function can be viewed as the inverse of function application.
For example, Lambda( x, F ) is written as \lambda x [F] in the lambda calculus literature. The expression F may contain x but the full lambda expression is regarded to be free of x. A computational application receiving a MathML lambda expression should not evaluate x or test for x. Such an application may apply the lambda expression as a function to arguments in which case any result that is computed is computed through parameter substitutions into F.
Note that a lambda expression on an arbitrary function applied to a the bound variable is equivalent to that arbitrary function. A domain of application can be used to restrict the defined function to a specific domain.
- Discussion
-
The
lambdaelement is used to construct a user-defined function from an expression, bound variables, and qualifiers. In a lambda construct with n (possibly 0) bound variables, the first n children arebvarelements that identify the variables that are used as placeholders in the last child for actual parameter values. The bound variables can be restricted by an optionaldomainofapplicationqualifier or one of its shorthand notations. The meaning of thelambdaconstruct is an n-ary function that returns the expression in the last child where the bound variables are replaced with the respective arguments.The
lambdaelement is used to construct a user-defined function from an expression. The last child is an expression defining the function in terms of the bound variables declared by thebvarand anydomainofapplication(see Section 4.2.7 Qualifiers) elements coming before it. The last element is typically anapplyelement, but can also be any container element. The following constructs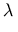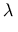 (x, sin x)
(x, sin x)
<lambda> <bvar><ci>x</ci></bvar> <apply><sin/><ci>x</ci></apply> </lambda>
The following constructs the constant function
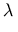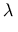 (x, 3)
(x, 3)
<lambda><bvar><ci> x </ci></bvar><cn>3</cn></lambda>
The lambda calculus allows a user to construct a function from a variable and an expression. For example, the lambda construct underlies the common mathematical idiom illustrated here:
Let f be the function taking x to x2 + 2
There are various notations for this concept in mathematical literature, such as
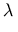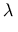 (x,
F(x)) = F or
(x,
F(x)) = F or 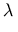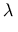 (x, [F]) =F,
where x is a free variable in F.
(x, [F]) =F,
where x is a free variable in F.
This concept is implemented in MathML with the
lambdaelement. A lambda construct with n (possibly 0) internal variables is encoded by alambdaelement, where the first n children arebvarelements containing the identifiers of the internal variables. This is followed by an optionaldomainofapplicationqualifier (see Section 4.2.7 Qualifiers) and an expression defining the function. The defining expression is typically anapply, but can also be any expression.The following constructs
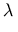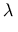 (x, sin(x+1)):
(x, sin(x+1)):
<lambda> <bvar><ci> x </ci></bvar> <apply> <sin/> <apply> <plus/> <ci> x </ci> <cn> 1 </cn> </apply> </apply> </lambda>To use
declareandlambdato construct the function f for which f( x) = x2 + x + 3 use:<declare type="function"> <ci> f </ci> <lambda> <bvar><ci> x </ci></bvar> <apply> <plus/> <apply> <power/> <ci> x </ci> <cn> 2 </cn> </apply> <ci> x </ci> <cn> 3 </cn> </apply> </lambda> </declare>The following markup declares and constructs the function J such that J(x, y) is the integral from x to y of t4 with respect to t.
<declare type="function"> <ci> J </ci> <lambda> <bvar><ci> x </ci></bvar> <bvar><ci> y </ci></bvar> <apply> <int/> <bvar><ci> t </ci></bvar> <lowlimit><ci> x </ci></lowlimit> <uplimit><ci> y </ci></uplimit> <apply> <power/> <ci>t</ci> <cn>4</cn> </apply> </apply> </lambda> </declare>The function J can then in turn be applied to an argument pair.
- Classification
- constructor
- Signature
-
(bvar*,anything) -> function
(domainofapp,function) -> function
(bvar+,domainofapp,anything) -> function
- Property
-
ForAll( F, lambda(x,F(x)) = F )
<apply><forall/> <bvar><ci>F</ci></bvar> <apply><eq/> <lambda> <bvar><ci>x</ci></bvar> <apply><ci>F</ci><ci>x</ci></apply> </lambda> <ci>F</ci> </apply> </apply> - Example
-
a simple lambda construct.
<lambda> <bvar><ci> x </ci></bvar> <apply><sin/> <apply> <plus/> <ci> x </ci> <cn> 1 </cn> </apply> </apply> </lambda> - Example
-
The next example constructs a one-argument function in which the argument b specifies the upper bound of a specific definite integral.
<lambda> <bvar><ci> b </ci></bvar> <apply> <int/> <bvar><ci> x </ci></bvar> <lowlimit><ci> a </ci></lowlimit> <uplimit><ci> b </ci></uplimit> <apply> <fn><ci> f </ci></fn> <ci> x </ci> </apply> </apply> </lambda> - Example
-
The
domainofapplicationchild restricts the possible values of the arguments of the constructed function. For instance, the following twolambdaconstructs are representations of a function on the integers.<lambda> <bvar><ci> x </ci></bvar> <domainofapplication><integers/></domainofapplication> <apply><sin/><ci> x </ci></apply> </lambda>
- Example
-
If a
lambdaconstruct does not contain bound variables, then the arity of the constructed function is unchanged, and thelambdaconstruct is redundant, unless it also contains adomainofapplicationconstruct that restricts existing functional arguments, as in this example, which is a variant representation for the function above. In particular, if the last child of alambdaconstruct is not a function, say a number, then thelambdaconstruct will not be a function, but the same number. Of course, in this case adomainofapplicationdoes not make sense<lambda> <domainofapplication><integers/></domainofapplication> <sin/> </lambda>
C.4
MMLdefinition: compose
- Description
-
This is the MathML constructor for composing functions. In order for a composition to be meaningful, the range of the first function should be the domain of the second function, etc. . However, since no evaluation takes place in MathML, such a construct can safely be used to make statements such as that f composed with g is undefined.
The result is a new function whose domain is the domain of the first function and whose range is the range of the last function and whose definition is equivalent to applying each function to the previous outcome in turn as in:
(f @ g )( x ) == f( g(x) ).
This function is often denoted by a small circle infix operator.
- Discussion
-
The
composeelement represents the function composition operator. Note that MathML makes no assumption about the domain and codomain of the constituent functions in a composition; the domain of the resulting composition may be empty.The
composeelement is an n-ary operator. As an n-ary operator, therefore it may take qualifiers. - Classification
- function
- Signature
-
(function*) -> function
- Property
-
ForAll( x, (f@g)(x) = f(g(x) )
<apply><forall/> <bvar><ci>x</ci></bvar><bvar><ci>f</ci></bvar><bvar><ci>g</ci></bvar> <apply><eq/> <apply><apply><compose/><ci>f</ci><ci>g</ci></apply> <ci>x</ci> </apply> <apply><ci>f</ci><apply><ci>g</ci><ci>x</ci></apply></apply> </apply> </apply> - Example
-
The use of fn is deprecated. Use type="function" instead.
<apply><compose/> <ci type="function"> f </ci> <ci type="function"> g </ci> <sin/> </apply> - Example
<apply> <compose/> <ci type="function"> f </ci> <ci type="function"> g </ci> <ci type="function"> h </ci> </apply>
- Example
<apply> <apply><compose/> <fn><ci> f </ci></fn> <fn><ci> g </ci></fn> </apply> <ci> x </ci> </apply>- Example
<apply> <fn><ci> f </ci></fn> <apply> <fn><ci> g </ci></fn> <ci> x </ci> </apply> </apply>
C.5
MMLdefinition: ident
- Description
-
The ident element represents the identity function. MathML makes no assumption about the function space in which the identity function resides. Proper interpretation of the domain (and hence codomain) of the identity function depends on the context in which it is used.
- Classification
- constructor
- Signature
-
function
- Property
-
ForAll( x, ident(x) = x )
<apply><forall/> <bvar><ci>x</ci></bvar> <apply><eq/> <apply><ident/><ci>x</ci></apply> <ci>x</ci> </apply> </apply> - Example
<apply> <eq/> <apply><compose/> <fn><ci> f </ci></fn> <apply><inverse/> <fn><ci> f </ci></fn> </apply> </apply> <ident/> </apply>- Example
<apply><eq/> <apply><compose/> <ci type="function"> f </ci> <apply><inverse/><ci type="function"> f </ci></apply> </apply> <ident/> </apply>
C.6
MMLdefinition: domain
- Description
-
The domain element denotes the domain of a given function, which is the set of values over which it is defined.
- Discussion
-
The
domainelement denotes the domain of a given function, which is the set of values over which it is defined. - Classification
- function
- Signature
-
(function) -> set
- Example
-
If f is a function from the reals to the rationals, then:
<apply> <eq/> <apply><domain/> <fn><ci> f </ci></fn> </apply> <reals/> </apply>
C.7
MMLdefinition: codomain
- Description
-
The codomain (range) element denotes the codomain of a given function, which is a set containing all values taken by the function. The codomain may contain additional points which are not realized by applying the the function to elements of the domain.
- Discussion
-
The
codomainelement denotes the codomain of a given function, which is a set containing all values taken by the function. It is not necessarily the case that every point in the codomain is generated by the function applied to some point of the domain. (For example I may know that a function is integer-valued, so its codomain is the integers, without knowing (or stating) which subset of the integers is mapped to by the function.)Codomain is sometimes also called Range.
- Classification
- function
- Signature
-
(function) -> set
- Property
-
ForAll( y, Exists(x,y =f(x)), member(y,codomain(f)) )
- Example
-
If f is a function from the reals to the rationals, then:
<apply> <eq/> <apply><codomain/> <fn><ci> f </ci></fn> </apply> <rationals/> </apply>
C.8
MMLdefinition: image
- Description
-
The image element denotes the image of a given function, which is the set of values taken by the function. Every point in the image is generated by the function applied to some point of the domain.
- Discussion
-
The
imageelement denotes the image of a given function, which is the set of values taken by the function. Every point in the image is generated by the function applied to some point of the domain. - Classification
- function
- Signature
-
(function) -> set
- Property
-
ForAll( x, x in image(f), ThereExists(y,f(y)=x) )
- Example
-
The real
sinfunction is a function from the reals to the reals, taking values between -1 and 1.<apply><eq/> <apply><image/><sin/></apply> <interval><cn>-1</cn><cn> 1</cn></interval> </apply>
- Example
<apply><forall/> <bvar><ci>x</ci></bvar> <condition> <apply><in/> <ci>x</ci> <apply><image/><ci>f</ci></apply> </apply> </condition> <apply><in/> <ci>x</ci> <apply><codomain/><ci>f</ci></apply> </apply> </apply>
C.9
MMLdefinition: piecewise
- Description
-
The piecewise, piece, and otherwise elements are used to support 'piecewise' declarations of the form H(x) = 0 if x less than 0, H(x) = 1 otherwise. The piece and otherwise elements describe evaluation rules. If no rule applies or if more than one rule applies but they give different answers then the expression is undefined.
- Discussion
-
The
piecewise,piece, andotherwiseelements are used to support "piecewise" declarations of the form " H(x) = 0 if x less than 0, H(x) = 1 otherwise".The declaration is constructed using the
piecewiseelement. This contains zero or morepieceelements, and optionally oneotherwiseelement. Eachpieceelement contains exactly two children. The first child defines the value taken by thepiecewiseexpression when the condition specified in the associated second child of thepieceis true. The degenerate case of nopieceelements and nootherwiseelement is treated as undefined for all values of the domain.otherwiseallows the specification of a value to be taken by thepiecewisefunction when none of the conditions (second child elements of thepieceelements) is true, i.e. a default value.It should be noted that no "order of execution" is implied by the ordering of the
piecechild elements withinpiecewise. It is the responsibility of the author to ensure that the subsets of the function domain defined by the second children of thepieceelements are disjoint, or that, where they overlap, the values of the corresponding first children of thepieceelements coincide. If this is not the case, the meaning of the expression is undefined.The
piecewiseelements are constructors.The
piecewise,piece,otherwiseelements are used to support "piecewise" declarations of the form " H(x) = 0 if x less than 0, H(x) = x otherwise".<piecewise> <piece> <cn>0</cn> <apply><lt/><ci>x</ci><cn>0</cn></apply> </piece> <otherwise><ci>x</ci></otherwise> </piecewise> - Classification
- constructor
- Signature
-
(piece*, otherwise?) -> algebraic
(piece*, otherwise?) -> anything
- Property
-
ForAll( x, x in domain(f), the evaluation rules collectively produce at most one value in codomain(f) )
- Example
<piecewise> <piece><cn> 0</cn><apply><lt/><ci> x</ci> <cn> 0</cn></apply></piece> <otherwise><ci>x</ci></otherwise> </piecewise>
- Example
-
The value of the abs function evaluated at x can be written as:
<piecewise> <piece> <apply><minus/><ci>x</ci></apply> <apply><lt/><ci> x</ci><cn> 0</cn></apply> </piece> <piece> <cn>0</cn> <apply><eq/><ci>x</ci><cn>0</cn></apply> </piece> <piece> <ci>x</ci> <apply><gt/><ci>x</ci><cn>0</cn></apply> </piece> </piecewise>
C.10
MMLdefinition: piece
- Description
-
The piece element is used to construct the conditionally defined values as part of a piecewise object.
- Classification
- constructor
- Signature
-
(algebraic, boolean) -> piece
(anything, boolean) -> piece
- Example
<piecewise> <piece><cn>0</cn><apply><lt/><ci> x</ci> <cn> 0</cn></apply></piece> <otherwise><ci>x</ci></otherwise> </piecewise>
C.11
MMLdefinition: otherwise
- Description
-
The otherwise element is used to describe the value of a piecewise construct when none of the conditions of the associated pieces are satisfied.
- Classification
- constructor
- Signature
-
(algebraic) -> otherwise
(anything) -> otherwise
- Example
<piecewise> <piece><cn> 0</cn><apply><lt/><ci> x</ci> <cn> 0</cn></apply></piece> <otherwise><ci>x</ci></otherwise> </piecewise>
3.4 Content Dictionary: Arithmetic Algebra and Logic
C.1
MMLdefinition: quotient
- Description
-
quotient is the binary function used to represent the operation of integer division. quotient(a,b) denotes q such that a = b*q+r, with |r| less than |b| and a*r non-negative.
- Discussion
-
The
quotientelement is the operator used for division modulo a particular base. When thequotientoperator is applied to integer arguments a and b, the result is the "quotient of a divided by b". That is,quotientreturns the unique integer q such that a = q b + r. (In common usage, q is called the quotient and r is the remainder.) - Classification
- function
- MMLattribute
-
Name Value Default type MathMLType integer - Signature
-
(integer, integer) -> integer
- Property
-
ForAll( [a,b], b != 0, a = b*quotient(a,b) + rem(a,b) )
<apply><forall/> <bvar><ci>a</ci></bvar> <bvar><ci>b</ci></bvar> <condition><apply><neq/><ci>b</ci><cn>0</cn></apply></condition> <apply><eq/> <ci>a</ci> <apply><plus/> <apply><times/> <ci>b</ci> <apply><quotient/><ci>a</ci><ci>b</ci></apply> </apply> <apply><rem/><ci>a</ci><ci>b</ci></apply> </apply> </apply> </apply> - Example
-
Various mathematical applications will use this data in different ways. Editing applications might choose an image such as shown below, while a computationally based application would evaluate it to 2 whena=13 and b=5.
<apply><quotient/> <ci> a </ci> <ci> b </ci> </apply>
- Example
<apply> <quotient/> <cn>5</cn> <cn>4</cn> </apply>
C.2
MMLdefinition: factorial
- Description
-
This is the unary operator used to construct factorials. Factorials are defined by n! = n*(n-1)* ... * 1
- Classification
- function
- MMLattribute
-
Name Value Default type MathMLType integer - Signature
-
(algebraic) -> algebraic
(integer) -> integer
- Property
-
ForAll( n, n \gt 0, n! = n*(n-1)! )
<apply><forall/> <bvar><ci>n</ci></bvar> <condition><apply><gt/><ci>n</ci><cn>0</cn></apply></condition> <apply><eq/> <apply><factorial/><ci>n</ci></apply> <apply><times/> <ci>n</ci> <apply><factorial/> <apply><minus/><ci>n</ci><cn>1</cn></apply> </apply> </apply> </apply> </apply> - Property
-
0! = 1
<apply><eq/> <apply><factorial/><cn>0</cn></apply> <cn>1</cn> </apply> - Example
-
If this were evaluated at n = 5 it would evaluate to 120.
<apply><factorial/> <ci>n</ci> </apply>
C.3
MMLdefinition: divide
- Description
-
This is the binary MathML operator that is used indicate the mathematical operation a "divided by" b.
- Classification
- function
- MMLattribute
-
Name Value Default type MathMLType real - Signature
-
(algebraic, algebraic) -> algebraic
(complex, complex) -> complex
(real, real) -> real
(rational, rational) -> rational
(integer, integer) -> rational
- Property
-
Division by Zero error
<apply><forall/> <bvar><ci>a</ci></bvar> <apply><eq/> <apply><divide/><ci> a </ci><cn> 0 </cn></apply> <notanumber/> </apply> </apply> - Property
-
ForAll( a, a!= 0, a/a = 1 )
<apply><forall/> <bvar><ci>a</ci></bvar> <condition><apply><neq/><ci>a</ci><cn>0</cn></apply></condition> <apply><eq/> <apply><divide/><ci>a</ci><ci>a</ci></apply> <cn>1</cn> </apply> </apply> - Example
-
As a MathML expression, this does not evaluate. However, on receiving such an expression, some applications may attempt to evaluate and simplify the value. For example, when a=5 and b=2 some mathematical applications may evaluate this to 2.5 while others will treat is as a rational number.
<apply><divide/> <ci> a </ci> <ci> b </ci> </apply>
C.4
MMLdefinition: max
- Description
-
This is the n-ary operator used to represent the maximum of a set of elements. The elements may be listed explicitly or they may be described by a
domainofapplication, for example, the maximum over all x in the set A. Thedomainofapplicationis often abbreviated by placing a condition directly on a bound variable.The
maxoperator is a n-ary operators may use the domain of application qualifiers as described in Section 4.4.10 Lifted Associative Commutative Operators. For example, theminandmaxfunctions accept abvarschema in cases where the maximum or minimum is being taken over a set of values specified by aconditionschema together with an expression to be evaluated on that set. In MathML1.0, thebvarelement was optional when using acondition; if aconditionelement containing a single variable was given by itself following aminormaxoperator, the variable was implicitly assumed to be bound, and the expression to be maximized or minimized (if absent) was assumed to be the single bound variable. This usage is deprecated in MathML 2.0 in favor of explicitly stating the bound variable(s) and the expression to be maximized or minimized in all cases.The
minandmaxelements may also be applied to a list of values in which case no qualifier schemata are used. - Classification
- function
- MMLattribute
-
Name Value Default type MathMLType real - Signature
-
(algebraic*) -> algebraic
(domainofapp,function) -> algebraic
(bvar+,domainofapp,algebraic) -> algebraic
- Property
-
ForAll( x in S, max(y in S,y) \geq x )
- Example
-
Maximum of a finite listing of elements
<apply><max/><cn>2</cn><cn>3</cn><cn>5</cn></apply> - Example
-
Max(y^3, y in (0,1))
<apply> <max/> <bvar><ci>y</ci></bvar> <condition> <apply><in/><ci>y</ci><interval><cn>0</cn><cn>1</cn> </interval></apply> </condition> <apply><power/><ci> y</ci><cn>3</cn></apply> </apply> - Example
-
When the objects are to be compared explicitly they are listed as arguments to the function as in:
<apply> <max/> <ci> a </ci> <ci> b </ci> </apply>
- Example
-
In MathML1.0, the bound variable and expression to be evaluated (x) could be omitted in the example below: this usage is deprecated in MathML2.0 in favor of explicitly stating the bound variable and expression in all cases:
<apply> <max/> <bvar><ci>x</ci></bvar> <condition> <apply><and/> <apply><in/><ci>x</ci><ci type="set">B</ci></apply> <apply><notin/><ci>x</ci><ci type="set">C</ci></apply> </apply> </condition> <ci>x</ci> </apply>
C.5
MMLdefinition: min
- Description
-
This is the n-ary operator used to represent the minimum of a set of elements. The elements may be listed explicitly or they may be described by a
condition, e.g., the minimum over all x in the set A.The elements must all be comparable if the result is to be well defined.
The
minoperator is a are n-ary operators may use the domain of application qualifiers as described in Section 4.4.10 Lifted Associative Commutative Operators. For example, theminandmaxfunctions accept abvarschema in cases where the maximum or minimum is being taken over a set of values specified by aconditionschema together with an expression to be evaluated on that set. In MathML1.0, thebvarelement was optional when using acondition; if aconditionelement containing a single variable was given by itself following aminormaxoperator, the variable was implicitly assumed to be bound, and the expression to be maximized or minimized (if absent) was assumed to be the single bound variable. This usage is deprecated in MathML 2.0 in favor of explicitly stating the bound variable(s) and the expression to be maximized or minimized in all cases.The
minandmaxelements may also be applied to a list of values in which case no qualifier schemata are used. - Discussion
-
The element
minis used to compare the values of its arguments. It returns the minimum of these values respectively. - Classification
- function
- MMLattribute
-
Name Value Default type MathMLType real - Signature
-
(algebraic*) -> algebraic
(domainofapp,function) -> algebraic
(bvar+,domainofapp,anything) -> algebraic
- Example
-
Minimum of a finite listing of elements
<apply><min/><cn>2</cn><cn>3</cn><cn>5</cn></apply> - Example
-
min(y^2, y in (0,1))
<apply> <min/> <bvar><ci>y</ci></bvar> <condition> <apply><in/><ci>y</ci><interval><cn>0</cn><cn>1</cn></interval></apply> </condition> <apply><power/><ci> y</ci><cn>2</cn></apply> </apply> - Example
-
The elements to be compared may also be described using bound variables with a
conditionelement and an expression to be minimized, as in:Note that the bound variable must be stated even if it might be implicit in conventional notation.
<apply> <min/> <bvar><ci>x</ci></bvar> <condition> <apply><notin/><ci> x </ci><ci type="set"> B </ci></apply> </condition> <apply> <power/> <ci> x </ci> <cn> 2 </cn> </apply> </apply>
C.6
MMLdefinition: minus
- Description
-
This is the subtraction operator for an additive group.
If one argument is provided this operator constructs the additive inverse of that group element. If two arguments, say a and b, are provided it constructs the mathematical expression a - b.
- Discussion
-
The
minuselement is the subtraction operator.The
minuselement can be used as a unary arithmetic operator (e.g. to represent - x), or as a binary arithmetic operator (e.g. to represent x- y). - Classification
- function
- MMLattribute
-
Name Value Default type MathMLType real - Signature
-
(real) -> real
(algebraic) -> algebraic
(real,real) -> real
(algebraic,algebraic) -> algebraic
[type=MathMLtype](MathMLtype) -> MathMLtype
[type=MathMLtype](MathMLtype,MathMLtype) -> MathMLtype
(set,set) -> set
(multiset,multiset) -> multiset
- Property
-
ForAll( x, x-x=0 )
<apply><forall/> <bvar><ci> x </ci></bvar> <apply><eq/> <apply><minus/><ci> x </ci><ci> x </ci></apply> <cn>0</cn> </apply> </apply> - Example
-
If this were evaluated at x=5 and y=2 it would yield 3.
<apply> <minus/> <ci> x </ci> <ci> y </ci> </apply>
- Example
<apply><minus/> <cn>3</cn> </apply>
C.7
MMLdefinition: plus
- Description
-
This is the n-ary addition operator of an algebraic structure. Ordinarily, the operands are provided explicitly. As an n-ary operation the operands can also be generated by allowing a function or expression vary over a domain of application though the sum element is normally used for that purpose. If no operands are provided, the expression represents the additive identity. If one operand, a, is provided the expression evaluates to "a". If two or more operands are provided, the expression represents the (semi) group element corresponding to a left associative binary pairing of the operands. The meaning of mixed operand types not covered by the signatures shown here are left up to the target system.
To use different type coercion rules different from those indicated by the signatures, use the definitionURL attribute to identify a new definition.
- Discussion
-
The
pluselement is the addition operator.As an n-ary operator, the operands may in principle also be provided using a domain of application as described in Section 4.4.10 Lifted Associative Commutative Operators. However, such expressions can already be represented explicitly using sum so the
plusdoes not normally take qualifiers. - Classification
- function
- MMLattribute
-
Name Value Default type MathMLType real - Signature
-
[type=MathMLtype](anything*) -> MathMLtype
(set*) -> set
(multiset*) -> multiset
(algebraic*) -> algebraic
(real*) -> real
(complex*) -> complex
(integer*) -> integer
(domainofapp,function) -> algebraic
(bvar+,domainofapp,algebraic) -> algebraic
- Property
-
an sum of no terms is 0
<apply><eq/> <apply><plus/></apply> <cn>0</cn> </apply> - Property
-
a sum of one term is equal to itself
<apply><forall/> <bvar><ci>a</ci></bvar> <apply><eq/> <apply><plus/><ci>a</ci></apply> <cn>a</cn> </apply> </apply> - Property
-
Commutativity
<apply><forall/> <bvar><ci>a</ci></bvar> <bvar><ci>b</ci></bvar> <condition> <apply><and/> <apply><in/><ci>a</ci><reals/></apply> <apply><in/><ci>b</ci><reals/></apply> </apply> </condition> <apply><eq/> <apply><plus/><ci>a</ci><ci>b</ci></apply> <apply><plus/><ci>b</ci><ci>a</ci></apply> </apply> </apply> - Example
<apply><plus/> <cn>3</cn> </apply>
- Example
<apply><plus/> <cn>3</cn> <cn>5</cn> </apply>
- Example
-
If this were evaluated at x = 5, y = 2 and z = 1 it would yield 8.
<apply> <plus/> <ci> x </ci> <ci> y </ci> <ci> z </ci> </apply>
C.8
MMLdefinition: power
- Description
-
This is the binary powering operator that is used to construct expressions such as a "to the power of" b. In particular, it is the operation for which a "to the power of" 2 is equivalent to a * a.
- Discussion
-
The
powerelement is a generic exponentiation operator. That is, when applied to arguments a and b, it returns the value of "a to the power of b". - Classification
- function
- MMLattribute
-
Name Value Default type MathMLType real - Signature
-
(algebraic, algebraic) -> algebraic
(complex, complex) -> complex
(real, real) -> complex
(rational, integer) -> rational
(integer, integer) -> rational
[type=MathMLtype](anything,anything) -> MathMLtype
- Property
-
ForAll( a, a!=0, a^0=1 )
<apply><forall/> <bvar><ci>a</ci></bvar> <condition><apply><neq/><ci>a</ci><cn>0</cn></apply></condition> <apply><eq/> <apply><power/><ci>a</ci><cn>0</cn></apply> <cn>1</cn> </apply> </apply> - Property
-
ForAll( a, a^1=a )
<apply><forall/> <bvar><ci>a</ci></bvar> <apply><eq/> <apply><power/><ci>a</ci><cn>1</cn></apply> <ci>a</ci> </apply> </apply> - Property
-
ForAll( a, 1^a=1 )
<apply><forall/> <bvar><ci>a</ci></bvar> <apply><eq/> <apply><power/><cn>1</cn><ci>a</ci></apply> <cn>1</cn> </apply> </apply> - Example
<apply><power/><cn>2</cn><ci>x</ci></apply>
- Example
<apply><power/><ci> x </ci><cn> 3 </cn></apply>
- Example
-
If this were evaluated at x= 5 it would yield 125.
<apply> <power/> <ci> x </ci> <cn> 3 </cn> </apply>
C.9
MMLdefinition: rem
- Description
-
This is the binary operator used to represent the integer remainder a mod b. For arguments a and b, such that a = b*q + r with |r| < |b| it represents the value r.
- Discussion
-
The
remelement is the operator that returns the "remainder" of a division modulo a particular base. When theremoperator is applied to integer arguments a and b, the result is the "remainder of a divided by b". That is,remreturns the unique integer, r such that a = q b+ r, where r < q. (In common usage, q is called the quotient and r is the remainder.) - Classification
- function
- MMLattribute
-
Name Value Default type MathMLType integer - Signature
-
(integer, integer) -> integer
[type=MathMLtype](MathMLtype,MathMLtype) -> MathMLtype
- Property
-
rem(a, 0) is undefined
- Property
-
ForAll( [a,b], b!=0, a = b*quotient(a,b) + rem(a,b))
<apply><forall/> <bvar><ci>a</ci></bvar> <bvar><ci>b</ci></bvar> <condition><apply><neq/><ci>b</ci><cn>0</cn></apply></condition> <apply><eq/> <ci>a</ci> <apply><plus/> <apply><times/> <ci>b</ci> <apply><quotient/><ci>a</ci><ci>b</ci></apply> </apply> <apply><rem/> <ci>a</ci> <ci>b</ci> </apply> </apply> </apply> </apply> - Example
-
If this were evaluated at a = 15 and b = 8 it would yield 7.
<apply><rem/><ci> a </ci><ci> b </ci></apply>
C.10
MMLdefinition: times
- Description
-
This is the n-ary multiplication operator of a ring. Ordinarily, the operands are provided explicitly. As an n-ary operation the operands can also be generated by allowing a function or expression vary over a domain of application though the product element is normally used for that purpose. If no arguments are supplied then this represents the multiplicative identity. If one argument is supplied, this represents an expression that would evaluate to that single argument.
- Discussion
-
The
timeselement is the n-ary multiplication operator.The operands are usually listed explicitly. As an n-ary operator, the operands may in principle also be provided using a domain of application as described in Section 4.4.10 Lifted Associative Commutative Operators. However, such expressions can already be represented explicitly by using product so thetimesdoes not normally take qualifiers. - Classification
- function
- MMLattribute
-
Name Value Default type MathMLType real - Signature
-
(algebraic*) -> algebraic
(complex*) -> complex
(real*) -> real
(rational*) -> rational
(integer*) -> integer
(domainofapp,function) -> algebraic
(bvar+,domainofapp,anything) -> algebraic
- Property
-
ForAll( [a,b], condition(in({a,b}, Commutative)), a*b=b*a )
- Property
-
ForAll( [a,b,c], Associative, a*(b*c)=(a*b)*c ), associativity
- Property
-
multiplicative identity
<apply><forall/> <bvar><ci>a</ci></bvar> <apply><eq/> <apply><times/><cn>1</cn><ci>a</ci></apply> <ci>a</ci> </apply> </apply> - Property
-
a*0=0
- Property
-
Commutative property
<apply><forall/> <bvar><ci>a</ci></bvar> <bvar><ci>b</ci></bvar> <condition> <apply><and/> <apply><in/><ci>a</ci><reals/></apply> <apply><in/><ci>b</ci><reals/></apply> </apply> </condition> <apply><eq/> <apply><times/><ci>a</ci><ci>b</ci></apply> <apply><times/><ci>b</ci><ci>a</ci></apply> </apply> </apply> - Property
-
a*0=0
<apply><forall/> <bvar><ci>a</ci></bvar> <apply><eq/> <apply><times/><cn>0</cn><ci>a</ci></apply> <cn>0</cn> </apply> </apply> - Example
-
If this were evaluated at a = 5.5 and b = 3 it would yield 16.5.
<apply><times/><ci>a</ci><ci>b</ci></apply>
C.11
MMLdefinition: root
- Description
-
This is the binary operator used to construct the nth root of an expression. The first argument "a" is the expression and the second object "n" denotes the root, as in ( a ) ^ (1/n)
- Discussion
-
The
rootelement is used to construct roots. The kind of root to be taken is specified by a "degree" child, which should be given as the second child of theapplyelement enclosing therootelement. Thus, square roots correspond to the case wheredegreecontains the value 2, cube roots correspond to 3, and so on.Note that MathML3 supports a
degreeelement in the legacy container representation (see Section 4.4.8 degree for details). If nodegreeis present, a default value of 2 is used. - Classification
- function
- MMLattribute
-
Name Value Default type real | complex | principal_branch | MathMLType real - Signature
-
(algebraic) -> root(degree(2),algebraic)
(anything) -> root(degree(2),anything)
(degree,anything) -> root
- Property
-
ForAll( bvars(a,n), root(degree(n),a) = a^(1/n) )
- Example
-
The nth root of a is is given by
<apply><root/> <degree><ci> n </ci></degree> <ci> a </ci> </apply>
C.12
MMLdefinition: gcd
- Description
-
This is the n-ary operator used to construct an expression which represents the greatest common divisor of its arguments. If no argument is provided, the gcd is 0. If one argument is provided, the gcd is that argument.
- Classification
- function
- MMLattribute
-
Name Value Default type MathMLType integer - Signature
-
[type=MathMLtype](MathMLtype*) ->MathMLtype
(integer*) -> integer
(domainofapp,function) -> algebraic
(bvar+,domainofapp,algebraic) -> algebraic
- Property
<apply><forall/> <forall/> <bvar><ci>x</ci></bvar> <apply><eq/> <apply><gcd/> <ci>x</ci> <cn>1</cn> </apply> <cn>1</cn> </apply> </apply>- Example
<apply><gcd/> <cn>12</cn> <cn>17</cn> </apply>
- Example
<apply><gcd/> <cn>3</cn> <cn>5</cn> <cn>7</cn> </apply>
- Example
-
If this were evaluated at a = 15, b = 21, c = 48, it would yield 3
<apply> <gcd/> <ci> a </ci> <ci> b </ci> <ci> c </ci> </apply>
C.13
MMLdefinition: and
- Description
-
This is the n-ary logical "and" operator. It is used to construct the logical expression which were it to be evaluated would have a value of "true" when all of its operands have a truth value of "true", and "false" otherwise.
- Discussion
-
The
andelement is the Boolean "and" operator.As an n-ary operator, its operands may also be generated as described inSection 4.4.10 Lifted Associative Commutative Operators Therefore it may take qualifiers.
- Classification
- function
- MMLattribute
-
Name Value Default type MathMLType boolean - Signature
-
(boolean*) -> boolean
- Property
-
ForAll( p, (true and p = p) )
- Property
-
ForAll( [p,q], (p and q = q and p) )
- Property
-
x and not(x) = false
- Example
-
If this were evaluated and both a and b had truth values of "true", then the result would be "true".
<apply><and/> <ci>a</ci> <ci>b</ci> </apply>
C.14
MMLdefinition: or
- Description
-
The is the n-ary logical "or" operator. The constructed expression has a truth value of true if at least one of its arguments is true.
- Discussion
-
The
orelement is the Boolean "or" operator.As an n-ary operator, its operands may also be generated as described inSection 4.4.10 Lifted Associative Commutative Operators Therefore it may take qualifiers.
- Classification
- function
- MMLattribute
-
Name Value Default type MathMLType boolean - Signature
-
(boolean*) -> boolean
[type="boolean"](symbolic*) -> boolean
- Example
<apply> <or/> <ci> a </ci> <ci> b </ci> </apply>
C.15
MMLdefinition: xor
- Description
-
The is the n-ary logical "xor" operator. The constructed expression has a truth value of true if an odd number of its arguments are true.
- Discussion
-
As an n-ary operator, its operands may also be generated as described inSection 4.4.10 Lifted Associative Commutative Operators Therefore it may take qualifiers.
- Classification
- function
- MMLattribute
-
Name Value Default type MathMLType boolean - Signature
-
(boolean*) -> boolean
[type="boolean"](symbolic*) -> symbolic
- Property
-
x xor x = false
- Property
-
x xor not(x) = true
- Example
<apply> <xor/> <ci> a </ci> <ci> b </ci> </apply>
C.16
MMLdefinition: not
- Description
-
This is the unary logical "not" operator. It negates the truth value of its single argument. e.g., not P is true when P is false and false when P is true.
- Discussion
-
The
notoperator is the Boolean"not" operator. - Classification
- function
- MMLattribute
-
Name Value Default type MathMLType boolean - Signature
-
(boolean) -> boolean
[type="boolean"](algebraic) -> boolean
- Example
<apply> <not/> <ci> a </ci> </apply>
C.17
MMLdefinition: implies
- Description
-
This is the binary "implies" operator. It is used to construct the logical expression "A implies B".
- Discussion
-
The
implieselement is the Boolean relational operator "implies". - Classification
- function
- MMLattribute
-
Name Value Default type MathMLType boolean - Signature
-
(boolean,boolean) -> boolean
- Property
-
false implies x
- Example
-
Mathematical applications designed for the evaluation of such expressions would evaluate this to "true" when a = "false" and b = "true".
<apply> <implies/> <ci> A </ci> <ci> B </ci> </apply>
C.18
MMLdefinition: forall
- Description
-
The forall operator is the logical "For all" quantifier. The bound variables, if any, appear first and are tagged using the bvar element. Next comes an optional condition on the bound variables. The last argument is the boolean expression that is asserted to be true for all values of the bound variables that meet the specified conditions (if any).
- Discussion
-
The
forallelement represents the universal quantifier of logic. It is usually used in conjunction with one or more bound variables, an optionalconditionelement, and an assertion. It may also be used with a domain of application and function as described in Section 4.2.7 Qualifiers in which case the assertion corresponds to applying the function to an element of the specified domain., which should take the form of anapplyelement.The universal quantifier
forallis used in conjunction with one or morebvarschemata to represent simple logical assertions. There are two main main ways of using the logical quantifier operators. The first usage is for representing a simple, quantified assertion. For example, the statement "there exists x < 9" would be represented as:<bind> <exists/> <bvar><ci> x </ci></bvar> <apply><lt/><ci>x</ci><cn>9</cn></apply> </bind>
The second usage is for representing implications. Hypotheses are given by a
conditionelement following the bound variables. For example the statement "for all x < 9, x < 10" would be represented as:<bind> <forall/> <bvar><ci>x</ci></bvar> <condition><apply><lt/><ci>x</ci><cn>9</cn></apply></condition> <apply><lt/><ci>x</ci><cn>10</cn></apply> </bind>
Note that in both these usages one or more
bvarqualifiers are mandatory. - Classification
- function
- MMLattribute
-
Name Value Default type MathMLType boolean - Signature
-
(domainofapp,function) -> boolean
(bvar+,domainofapp?,boolean) -> boolean
- Example
-
The example encodes a simple identity.
<apply> <forall/> <bvar><ci> x </ci></bvar> <apply><eq/> <apply> <minus/><ci> x </ci><ci> x </ci> </apply> <cn>0</cn> </apply> </apply>
- Example
-
The example is more involved, and makes use of an optional
conditionelement.<apply> <forall/> <bvar><ci> p </ci></bvar> <bvar><ci> q </ci></bvar> <condition> <apply><and/> <apply><in/><ci> p </ci><rationals/></apply> <apply><in/><ci> q </ci><rationals/></apply> <apply><lt/><ci> p </ci><ci> q </ci></apply> </apply> </condition> <apply><lt/> <ci> p </ci> <apply> <power/> <ci> q </ci> <cn> 2 </cn> </apply> </apply> </apply>
- Example
-
The example uses both the
forallandexistsquantifiers.<apply> <forall/> <bvar><ci> n </ci></bvar> <condition> <apply><and/> <apply><gt/><ci> n </ci><cn> 0 </cn></apply> <apply><in/><ci> n </ci><integers/></apply> </apply> </condition> <apply> <exists/> <bvar><ci> x </ci></bvar> <bvar><ci> y </ci></bvar> <bvar><ci> z </ci></bvar> <condition> <apply><and/> <apply><in/><ci> x </ci><integers/></apply> <apply><in/><ci> y </ci><integers/></apply> <apply><in/><ci> z </ci><integers/></apply> </apply> </condition> <apply> <eq/> <apply> <plus/> <apply><power/><ci> x </ci><ci> n </ci></apply> <apply><power/><ci> y </ci><ci> n </ci></apply> </apply> <apply><power/><ci> z </ci><ci> n </ci></apply> </apply> </apply> </apply>
- Example
<apply> <forall/> <bvar><ci> x </ci></bvar> <condition><apply><lt/><ci> x </ci><cn> 0 </cn></apply></condition> <ci> x </ci> </apply>
C.19
MMLdefinition: exists
- Description
-
This is the MathML operator that is used to assert existence, as in "There exists an x such that x is real and x is positive."
- The first argument indicates the bound variable,
- The second optional argument places conditions on that bound variable.
- The last argument is the expression that is asserted to be true.
- Discussion
-
The
existselement represents the existential quantifier of logic. Typically, it is used in conjunction with one or more bound variables, an optionalconditionelement, and an assertion, which may take the form of either anapplyorrelnelement.Theexistselement may also be used with a general domain of application and function as described in Section 4.2.7 Qualifiers. For such uses the assertion is obtained by applying the function to an element of the specified domain.The universal quantifier
forallis used in conjunction with one or morebvarschemata to represent simple logical assertions. There are two main main ways of using the logical quantifier operators. The first usage is for representing a simple, quantified assertion. For example, the statement "there exists x < 9" would be represented as:<bind> <exists/> <bvar><ci> x </ci></bvar> <apply><lt/><ci>x</ci><cn>9</cn></apply> </bind>
The second usage is for representing implications. Hypotheses are given by a
conditionelement following the bound variables. For example the statement "for all x < 9, x < 10" would be represented as:<bind> <forall/> <bvar><ci>x</ci></bvar> <condition><apply><lt/><ci>x</ci><cn>9</cn></apply></condition> <apply><lt/><ci>x</ci><cn>10</cn></apply> </bind>
Note that in both these usages one or more
bvarqualifiers are mandatory. - Classification
- function
- MMLattribute
-
Name Value Default type MathMLType boolean - Signature
-
(bvar+,boolean) -> boolean
(bvar+,domainofapp,anything) -> boolean
- Example
-
The following example encodes the sense of the expression "there exists an x such that f(x) = 0".
<apply><exists/> <bvar><ci>x</ci></bvar> <apply><eq/> <apply><ci>f</ci> <ci>x</ci> </apply> <cn>0</cn> </apply> </apply>
- Example
<apply> <exists/> <bvar><ci> x </ci></bvar> <domainofapplication> <ci type="set">C</ci> </domainofapplication> <apply> <eq/> <apply> <power/><ci>x</ci><cn>2</cn> </apply> <cn>4</cn> </apply> </apply>
C.20
MMLdefinition: abs
- Description
-
A unary operator which represents the absolute value of its argument. In the complex case this is often referred to as the modulus.
- Discussion
-
The
abselement represents the absolute value of a real quantity or the modulus of a complex quantity. - Classification
- function
- MMLattribute
-
Name Value Default type MathMLType real - Signature
-
(algebraic) -> algebraic
(real) -> real
(complex) -> real
- Property
-
for all x and y, abs(x) + abs(y) >= abs(x+y)
- Example
-
The following example encodes the absolute value of x.
<apply><abs/><ci>x</ci></apply>
C.21
MMLdefinition: conjugate
- Description
-
The unary "conjugate" arithmetic operator is used to represent the complex conjugate of its argument.
- Discussion
-
The
conjugateelement represents the complex conjugate of a complex quantity. - Classification
- function
- Signature
-
(algebraic) -> algebraic
(complex) -> complex
- Example
-
The following example encodes the conjugate of x + iy.
<apply><conjugate/> <apply><plus/> <ci> x </ci> <apply><times/> <cn> ⅈ </cn> <ci> y </ci> </apply> </apply> </apply>
C.22
MMLdefinition: arg
- Description
-
The unary "arg" operator is used to construct an expression which represents the "argument" of a complex number.
- Discussion
-
The
argoperator gives the "argument" of a complex number, which is the angle (in radians) it makes with the positive real axis. Real negative numbers have argument equal to +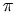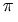 .
.
- Classification
- function
- MMLattribute
-
Name Value Default type MathMLType real - Signature
-
(complex) -> real
- Example
-
The following example encodes the argument operation onx + iy.
<apply><arg/> <apply><plus/> <ci> x </ci> <apply><times/><imaginaryi/><ci>y</ci></apply> </apply> </apply>
C.23
MMLdefinition: real
- Description
-
A unary operator used to construct an expression representing the "real" part of a complex number.
- Discussion
-
The
realoperator (introduced in MathML 2.0) gives the real part of a complex number, that is the x component in x + i y - Classification
- function
- MMLattribute
-
Name Value Default type MathMLType real - Signature
-
(complex) -> real
- Property
-
ForAll( [x,y], x in R, Y in R, real(x+i*y)=x) )
<apply><forall/> <bvar><ci>x</ci></bvar> <bvar><ci>y</ci></bvar> <condition> <apply><and/> <apply><in/><ci>x</ci><reals/></apply> <apply><in/><ci>y</ci><reals/></apply> </apply> </condition> <apply><eq/> <apply><real/> <apply><plus/> <ci> x </ci> <apply><times/><imaginaryi/><ci>y</ci></apply> </apply> </apply> <ci> x </ci> </apply> </apply> - Example
-
The following example encodes the real operation onx + iy.A MathML-aware evaluation system would return the x component, suitably encoded.
<apply><real/> <apply><plus/> <ci> x </ci> <apply><times/><imaginaryi/><ci>y</ci></apply> </apply> </apply>
C.24
MMLdefinition: imaginary
- Description
-
The unary function used to construct an expression which represents the imaginary part of a complex number.
- Discussion
-
The
imaginaryoperator (introduced in MathML 2.0) gives the imaginary part of a complex number, that is, the y component in x + i y. - Classification
- function
- MMLattribute
-
Name Value Default type MathMLType real - Signature
-
(complex) -> real
- Property
-
ForAll( [x,y], Imaginary(x + i*y) = y )
<apply><forall/> <bvar><ci type="real"> x </ci></bvar> <bvar><ci type="real"> y </ci></bvar> <apply><eq/> <apply><imaginary/> <apply><plus/> <ci type="real"> x </ci> <apply><times/><imaginaryi/><ci>y</ci></apply> </apply> </apply> <ci type="real"> y </ci> </apply> </apply> - Example
-
The following example encodes the imaginary operation on x + iy.A MathML-aware evaluation system would return the y component, suitably encoded.
<apply><imaginary/> <apply><plus/> <ci> x </ci> <apply><times/><imaginaryi/><ci>y</ci></apply> </apply> </apply>
C.25
MMLdefinition: lcm
- Description
-
This n-ary operator is used to construct an expression which represents the least common multiple of its arguments. If no argument is provided, the lcm is 1. If one argument is provided, the lcm is that argument. The least common multiple of x and 1 is x.
- Discussion
-
The
lcmelement (introduced in MathML 2.0) is used to denote the lowest common multiple of its arguments.As an n-ary operator, its operands may also be generated as described in Section 4.4.10 Lifted Associative Commutative Operators Therefore it may take qualifiers.
- Classification
- function
- MMLattribute
-
Name Value Default type MathMLType integer - Signature
-
[type=MathMLtype](MathMLtype*) -> MathMLtype
(integer*) -> integer
(algebraic*) -> algebraic
(domainofapp,function) -> algebraic
(bvar+,domainofapp,anything) -> algebraic
- Property
-
ForAll( x, lcm(x,1)=x )
<apply><forall/> <bvar><ci>x</ci></bvar> <apply><eq/> <apply><lcm/><ci>x</ci><cn>1</cn></apply> <ci>x</ci> </apply> </apply> - Example
<apply><lcm/> <cn>12</cn> <cn>17</cn> </apply>
- Example
<apply><lcm/> <cn>3</cn> <cn>5</cn> <cn>7</cn> </apply>
- Example
-
If this were evaluated at a = 2, b = 4, c = 6 it would yield 12.
<apply> <lcm/> <ci> a </ci> <ci> b </ci> <ci> c </ci> </apply>
C.26
MMLdefinition: floor
- Description
-
The floor element is used to denote the round-down (towards -infinity) operator.
- Discussion
-
The
floorelement (introduced in MathML 2.0) is used to denote the round-down (towards -infinity) operator. - Classification
- function
- MMLattribute
-
Name Value Default type MathMLType integer - Signature
-
(real) -> integer
[type=MathMLtype](algebraic) -> algebraic
- Property
-
ForAll( x, floor(x) <= x )
<apply><forall/> <bvar><ci>x</ci></bvar> <apply><leq/> <apply><floor/> <ci>x</ci> </apply> <ci>x</ci> </apply> </apply> - Example
-
If this were evaluated at a = 15.015, it would yield 15.
<apply> <floor/> <ci> a </ci> </apply>
- Example
<apply> <forall/> <bvar><ci> a </ci></bvar> <apply><and/> <apply><leq/> <apply><floor/> <ci>a</ci> </apply> <ci>a</ci> </apply> <apply><lt/> <ci>a</ci> <apply><plus/> <apply><floor/> <ci>a</ci> </apply> <cn>1</cn> </apply> </apply> </apply> </apply>
C.27
MMLdefinition: ceiling
- Description
-
The ceiling element is used to denote the round-up (towards +infinity) operator.
- Discussion
-
The
ceilingelement (introduced in MathML 2.0) is used to denote the round-up (towards +infinity) operator. - Classification
- function
- MMLattribute
-
Name Value Default type MathMLType integer - Signature
-
(real) -> integer
[type=MathMLtype](algebraic) -> algebraic
- Property
-
ForAll( x, ceiling(x) >= x )
<apply><forall/> <bvar><ci>x</ci></bvar> <apply><geq/> <apply><ceiling/> <ci>x</ci> </apply> <ci>x</ci> </apply> </apply> - Example
-
If this were evaluated at a = 15.015, it would yield 16.
<apply> <ceiling/> <ci> a </ci> </apply>
- Example
<apply> <forall/> <bvar><ci> a </ci></bvar> <apply><and/> <apply><lt/> <apply><minus/> <apply><ceiling/> <ci>a</ci> </apply> <cn>1</cn> </apply> <ci>a</ci> </apply> <apply><leq/> <ci>a</ci> <apply><ceiling/> <ci>a</ci> </apply> </apply> </apply> </apply>
3.5 Content Dictionary: Relations
C.1
MMLdefinition: eq
- Description
-
This n-ary function is used to indicate that two or more quantities are equal. There must be at least two arguments.
- Discussion
-
The
eqelement is the relational operator "equals".As an n-ary operator, its operands may also be generated as described in Section 4.4.10 Lifted Associative Commutative Operators Therefore it may take qualifiers.
- Classification
- nary relation
- Signature
-
(real,real+) -> boolean
(boolean, boolean+) -> boolean
(set,set+) -> set
(multiset,multiset+) -> multiset
(domainofapp,function) -> boolean
(bvar+,domainofapp,anything) -> boolean
- Property
-
Symmetric
- Property
-
Transitive
- Property
-
Reflexive
- Example
<apply><eq/> <cn type="rational">2<sep/>4</cn><cn type="rational">1<sep/>2</cn> </apply>
- Example
<apply><eq/><ci type="set">A</ci><ci type="set">B</ci></apply>
- Example
<apply><eq/><ci type="multiset">A</ci><ci type="multiset">B</ci></apply>
- Example
-
If this were tested at a = 5.5 and b = 6 it would yield the truth value false.
<apply><eq/><ci> a </ci><ci> b </ci></apply>
C.2
MMLdefinition: neq
- Description
-
This binary relation represents the relation "not equal to" which returns true unless the two arguments are equal.
- Discussion
-
The
neqelement is the "not equal to" relational operator.The
neqelement is a binary relation. - Classification
- function
- Signature
-
(real,real) -> boolean
(boolean,boolean) -> boolean
(set,set) -> set
(multiset,multiset) -> multiset
- Property
-
Symmetric
- Example
<apply><neq/><cn>3</cn><cn>4</cn></apply>
- Example
-
If this were tested at a = 5.5 and b = 6 it would yield the truth value true.
<apply> <neq/> <ci> a </ci> <ci> b </ci> </apply>
C.3
MMLdefinition: gt
- Description
-
This n-ary function represents the relation "greater than" which returns true if each argument in turn is greater than the one following it. There must be at least two arguments.
- Discussion
-
The
gtelement is the "greater than" relational operator.The
gtelement is an n-ary relation. As an n-ary operator, its operands may also be generated as described in Section 4.4.10 Lifted Associative Commutative Operators Therefore it may take qualifiers. - Classification
- function
- Signature
-
(real,real+) -> boolean
(domainofapp,function) -> boolean
(bvar+,domainofapp,algebraic) -> boolean
- Property
-
Transitive
- Example
<apply><gt/><cn>3</cn><cn>2</cn></apply>
- Example
-
If this were tested at a = 5.5 and b = 6 it would yield the truth value false.
<apply><gt/><ci>a</ci><ci>b</ci></apply>
C.4
MMLdefinition: lt(role: application)
- Description
-
This n-ary function represents the relation "less than" which returns true if each argument in turn is less than the one following it. There must be at least two arguments.
- Discussion
-
The
ltelement is the "less than" relational operator.The
ltelement is an n-ary relation. As an n-ary operator, its operands may also be generated as described in Section 4.4.10 Lifted Associative Commutative Operators Therefore it may take qualifiers. - Classification
- function
- Signature
-
(real,real+) -> boolean
( domainofapp , function ) -> boolean
( bvar+ , domainofapp , algebraic) -> boolean
- Property
-
Transitive
- Example
<apply><lt/><cn>2</cn><cn>3</cn><cn>4</cn></apply>
- Example
-
If this were tested at a = 5.5 and b = 6 it would yield the truth value "true".
<apply> <lt/> <ci> a </ci> <ci> b </ci> </apply>
C.5
MMLdefinition: geq
- Description
-
This element represents the n-ary greater than or equal to function. which returns true if each argument in turn is greater than or equal to the one following it. . There must be at least two arguments.
- Discussion
-
The
geqelement is the relational operator "greater than or equal".The
geqelement is an n-ary relation. As an n-ary operator, its operands may also be generated as described in Section 4.4.10 Lifted Associative Commutative Operators Therefore it may take qualifiers. - Classification
- function
- Signature
-
(real,real+) -> boolean
( domainofapp , function ) -> boolean
( bvar+ , domainofapp , algebraic ) -> boolean
- Property
-
Transitive
- Property
-
Reflexive
- Example
<apply><geq/><cn>4</cn><cn>3</cn><cn>3</cn></apply>
- Example
-
If this were tested for a = 5.5 and b = 5.5 it would yield the truth value true.
<apply> <geq/> <ci> a </ci> <ci> b </ci> </apply>
C.6
MMLdefinition: leq
- Description
-
This n-ary function represents the relation "less than or equal to" which returns true if each argument in turn is less or equal to the one following it. There must be at least two arguments.
- Discussion
-
The
leqelement is the relational operator "less than or equal".The
leqelement is an n-ary relation. As an n-ary operator, its operands may also be generated as described in Section 4.4.10 Lifted Associative Commutative Operators Therefore it may take qualifiers. - Classification
- function
- Signature
-
(real,real+) -> boolean
( domainofapp , function ) -> boolean
( bvar+ , domainofapp , arithmetic ) -> boolean
- Property
-
Transitive
- Property
-
Reflexive
- Example
<apply><leq/><cn>3</cn><cn>3</cn><cn>4</cn></apply>
- Example
-
If a = 5.4 and b = 5.5 this will yield the truth value true.
<apply> <leq/> <ci> a </ci> <ci> b </ci> </apply>
C.7
MMLdefinition: equivalent
- Description
-
This element represents the n-ary logical equivalence function in which two boolean expressions are said to be equivalent if their truth values are equal for all choices of values of the boolean variables appearing in them.
- Discussion
-
The
equivalentelement is the "equivalence" relational operator.Its operands may be generated by allowing a function or expression to vary over a domain of application. Therefore it may take qualifiers.
- Classification
- nary relation
- Signature
-
(boolean,boolean+) -> boolean
(domainofapp,function) -> boolean
(bvar+,domainofapp,boolean) -> boolean
- Property
-
Symmetric
- Property
-
Transitive
- Property
-
Reflexive
- Example
-
This yields the truth value true for all values of a.
<apply> <equivalent/> <ci> a </ci> <apply> <not/> <apply> <not/> <ci> a </ci> </apply> </apply> </apply>
C.8
MMLdefinition: approx
- Description
-
This element is used to indicate that two or more quantities are approximately equal. If a more precise definition of approximately equal is required the definintionURL should be used to identify a suitable definition.
- Discussion
-
The
approxelement is the relational operator "approximately equal". This is a generic relational operator and no specific arithmetic precision is implied - Classification
- binary relation
- MMLattribute
-
Name Value Default type MathMLType real - Signature
-
(real,real+) -> boolean
(domainofapp,function) -> boolean
(bvar+,domainofapp,boolean) -> boolean
- Property
-
Symmetric
- Property
-
Transitive
- Property
-
Reflexive
- Example
<apply><approx/><pi/><cn type="rational">22<sep/>7</cn></apply>
C.9
MMLdefinition: factorof
- Description
-
This is the binary MathML operator that is used indicate the mathematical relationship a "is a factor of" b. This relationship is true just if b mod a = 0
- Discussion
-
The
factorofelement is the relational operator element on two integers a and b specifying whether one is an integer factor of the other.The
factorofelement is an binary relational operator - Classification
- function
- MMLattribute
-
Name Value Default type MathMLType integer - Signature
-
(integer, integer) -> boolean
- Property
-
ForAll( [a,b], a and b integers, a divides b if there is an integer c such that a*c = b )
- Example
<apply><factorof/> <ci> a </ci> <ci> b </ci> </apply>
3.6 Content Dictionary: Calculus and Vector Calculus
C.1
MMLdefinition: int
- Description
-
The indefinite integral of a function.
- Discussion
-
The
intelement is the operator element for an integral. - Classification
- function
- Signature
-
(function) -> function
- Example
-
The integral over the sine function is cosine function.
<apply><eq/><apply><int/><sin/></apply><cos/></apply>
C.2
MMLdefinition: int
- Description
-
The definite integral of a function over a domain of application.
- Discussion
-
The
defintelement is the operator element for function over a domain of integration. - Classification
- function
- Signature
-
(set,function) -> function
- Example
-
This example specifies an interval of the real line as the domain of integration with an
intervalelement. In this form the integrand is provided as a function and no mention is made of a bound variable..<apply><defint/> <interval><ci>a</ci><ci>b</ci></interval> <cos/> </apply> - Example
<apply><defint/><ci type="set">D</ci><ci type="function">f</ci></apply>
C.3
MMLdefinition: int
- Description
-
The definite (without
conditionor indefinite (with) integral of an algebraic expression with respect to a bound variable. - Discussion
-
The
Intelement is the operator element for an integral, bound variables serve as the integration variables and definite integrals are indicated by providing a domain of integration. - Classification
- function
- Signature
-
(bvar,algebraic) -> algebraic
(bvar+,domainofapp,algebraic) -> algebraic
- Example
-
This example specifies an interval of the real line as the domain of integration with an
intervalelement. In this form the integrand is provided as a function and no mention is made of a bound variable..<apply><Int/> <interval><ci>a</ci><ci>b</ci></interval> <cos/> </bind> - Example
-
This example specifies the integrand using an expression involving a bound variable and an interval
<bind><Int/> <bvar><ci>x</ci></bvar> <domainofapplication><apply><interval/><ci>a</ci><ci>b</ci></apply></domainofapplication> <apply><cos/><ci>x</ci></apply> </bind> - Example
<bind><Int/> <bvar><ci> x </ci></bvar> <condition><apply><in/><ci>x</ci><ci type="set">D</ci></apply></condition> <apply><ci type="function">f</ci><ci>x</ci></apply> </bind>
C.4
MMLdefinition: diff
- Description
-
The
diffelement is the differentiation operator element for functions of a single variable. - Discussion
-
diffis applied directly to an actual function such as sine or cosine, thereby denoting a function which is the derivative of the original function, as in<apply><diff/><ci type="function>f</ci></apply>
If
diffis given a number n as a second argument, then it is interpreted as a n-fold differentiation operator.<apply><ndiff/><cn>2</cn><ci type="function>f</ci></apply>
- Classification
- function
- Signature
-
function -> function
- Example
-
diff(sin) = cos
<apply><eq/><apply><diff/><sin/></apply><cos/></apply> - Example
-
diff (2,sin) = sin
<apply><eq/><apply><ndiff/><cn>2</cn><sin/></apply><sin/></apply>
C.5
MMLdefinition: Diff
- Description
-
Diffis the algebraic differentiation operator. - Discussion
-
Issue algebraic_diff wiki (member only) ISSUE-10 (member only) Algebraic differentiation operator In the
diffoperator, we used abvarschema to specify the bound variables. But in the new canonical MathML, we only allowbvarinbind(which carries the expectation of alpha-equivalence). Thus we cannot make algebraicdiffa binding operator, and have to pass the differentiation variable as a regular argument (i.e. nobvarFor seeing how things work out in the concert of things, I have added an
Diffsymbol to the content dictionarycalculus_veccalcfor algebraic differentiation. Have a look, how it works.Resolution None recorded Diffis the binding operator for operator takes two (or three) arguments: an expression involving a single variable such as sin(x), or cos(x) or a polynomial in x and the variable modulo which the derivative is being taken. For instance:<bind><Diff/> <bvar><ci>x</ci></bvar> <apply><ci>f</ci><ci>x</ci></apply><ci>x</ci> </bind>
If
Diffis given a number n as a third argument, then it is interpreted as a n-fold algebraic differentiation operator.Issue algebraic_ndiff wiki (member only) ISSUE-10 (member only) nfold algebraic differentiation I have some trouble representing the iterated differentiation operator. I actually think that the degree should be something that is a parameter to the binding operator, so the following would be the most natural representation.
<bind> <apply><Diff/><cn>3</cn></apply> <bvar><ci>x</ci></bvar> <apply><ci>f</ci><ci>x</ci></apply> </apply>
But this messes up the
cdroleclassification in OpenMath. Rather than a binder, theDiffoperator is now of role application, but Diff(3) is of role binder. I do not see any way around introducing more complex roles (or relegating the role checking to the type systym e.g. STS.). I am pretty sure that this problem will also appear somewhere else. Maybe we can re-interpret the rolebindingas "has to be at the head of an application of abindobject. This might actually work, let's keep our fingers crossed that we will not come into even more complex representational situations.Resolution None recorded - Classification
- binding constructor
- Signature
-
(var,algebraic) -> algebraic
- Property
-
ForAll( [x,n], n!=0, diff( x^n , x ) = n*x^(n-1) )
- Example
-
diff( sin(x) , x ) = cos
<apply><eq/> <bind><Diff/> <bvar><ci>x</ci></bvar> <apply><sin/><ci>x</ci></apply> </bind> <apply><cos/><ci>x</ci></apply> </apply> - Example
-
Diff(x^2,x)
<apply><Diff/> <apply><power/><ci>x</ci><cn>2</cn></apply> <ci>x</ci> </apply> - Example
-
Diff(f(x),x)
The derivative with respect to x of an expression in x such as f (x) can be written as:
<apply><Diff/> <apply><ci type="function">f</ci><ci>x</ci></apply> <ci>x</ci> </apply> - Example
-
anDiff( sin(x) , x, 2) = sin(x)
<apply><eq/> <apply><Diff/> <apply><sin/><ci>x</ci></apply> <ci>x</ci> <cn>2</cn> </apply> <apply><sin/><ci>x</ci></apply> </apply>
C.6
MMLdefinition: partialdiff
- Description
-
This symbol is used to express partial differentiation. It occurs in two forms: one form corresponding to the differentiation of algebraic expressions (often displayed using the Leibnitz notation), and the other to express partial derivatives of actual functions (often expressed as $D_{1,2} f $ )
For the first form, the arguments are the bound variables followed by the algebraic expression. The result is an algebraic expression. Repetitions of the bound variables are indicated using the degree element. The total degree is indicated by use of a degree element at the top level.
For the second form, there are two arguments: a list of indices indicating by position which coordinates are involved in constructing the partial derivatives, and the actual function. The coordinates may be repeated.
- Discussion
-
The
partialdiffelement is the partial differentiation operator element for functions or algebraic expressions in several variables.In the case of algebraic expressions, the bound variables are given by
bvarelements, which are children of the containingapplyelement. Thebvarelements may also containdegreeelement, which specify the order of the partial derivative to be taken in that variable.For the expression case the actual variable is designated by a
bvarelement that is a child of the containingapplyelement. Thebvarelements may also contain adegreeelement, which specifies the order of the derivative to be taken.Where a total degree of differentiation must be specified, this is indicated by use of a
degreeelement at the top level, i.e. without any associatedbvar, as a child of the containingapplyelement.For the case of partial differentiation of a function, the containing
applytakes two child elements: firstly a list of indices indicating by position which coordinates are involved in constructing the partial derivatives, and secondly the actual function to be partially differentiated. The coordinates may be repeated.The
partialdiffoperator accepts zero or morebvarschemata, and an optionaldegreequalifier schema. Thebvarschema specify, in order, the variables with respect to which the derivative is being taken. Eachbvarelement may contain adegreeschema which is used to specify the order of the derivative being taken with respect to that variable. The optionaldegreeschema qualifier associated with thepartialdiffelement itself (that is, appearing as a child of the enclosingapplyelement rather than of one of thebvarqualifiers) is used to represent the total degree of the differentiation. Eachdegreeschema used withpartialdiffis expected to contain a single child schema. For example,<bind><partialdiff/> <bvar> <degree><cn>2</cn></degree> <ci>x</ci> </bvar> <bvar><ci>y</ci></bvar> <bvar><ci>x</ci></bvar> <degree><cn>4</cn></degree> <ci type="function">f</ci> </apply>denotes the mixed partial derivative ( d4 / d2x dy dx ) f.
- Classification
- function
- MMLattribute
-
Name Value Default type function | algebraic algebraic - Signature
-
(bvar+,degree?,algebraic) -> algebraic
(vector,function) -> function
- Property
-
ForAll( [x,y], partialdiff( x * y , x ) = partialdiff(x,x)*y + partialdiff(y,x)*x )
- Property
-
ForAll( [x,a,b], partialdiff( a + b , x ) = partialdiff(a,x) + partialdiff(b,x) )
- Example
-
d^k/(dx^m dy^n) f(x,y)
<apply><partialdiff/> <bvar><ci> x </ci><degree><ci>m</ci></degree></bvar> <bvar><ci> y </ci><degree><ci>n</ci></degree></bvar> <degree><ci>k</ci></degree> <apply><ci type="function">f</ci><ci>x</ci><ci>y</ci></apply> </apply> - Example
-
d^2/(dx dy) f(x,y)
<apply><partialdiff/> <bvar><ci>x</ci></bvar> <bvar><ci>y</ci></bvar> <apply><ci type="function">f</ci><ci>x</ci><ci>y</ci></apply> </apply> - Example
-
D_{1,1,3}(f)
<apply><partialdiff/> <list><cn>1</cn><cn>1</cn><cn>3</cn></list> <ci type="function">f</ci> </apply>
C.7
MMLdefinition: divergence
- Description
-
This symbol is used to represent the divergence function.
Given, one argument which is a vector of scalar valued functions defined on the coordinates x_1, x_2, ... x_n. It returns a scalar value function. That function satisfies the defining relation:
divergence(F) = \partial(F_(x_1))/\partial(x_1) + ... + \partial(F_(x_n))/\partial(x_n)
The functions defining the coordinates may be defined implicitly as expressions defined in terms of the coordinate names, in which case the coordinate names must be provided as bound variables.
- Discussion
-
The
divergenceelement is the vector calculus divergence operator, often called div. - Classification
- unary function
- Signature
-
(vector(function)) -> function
(bvar+,vector(algebraic)) -> algebraic
- Example
<apply> <divergence/> <ci> a </ci> </apply>
- Example
<apply><divergence/><ci type="vector"> E</ci></apply>
- Example
<declare><ci>F</ci><vector><ci>f1</ci><ci>f2</ci><ci>f3</ci></vector></declare> <apply><divergence/><ci>F</ci></apply>
- Example
<apply><divergence/> <bvar><ci>x</ci></bvar><bvar><ci>y</ci></bvar><bvar><ci>z</ci></bvar> <vector> <apply><plus/><ci>x</ci><ci>y</ci></apply> <apply><plus/><ci>x</ci><ci>z</ci></apply> <apply><plus/><ci>z</ci><ci>y</ci></apply> </vector> </apply>- Example
-
If a is a vector field defined inside a closed surface S enclosing a volume V, then the divergence of a is given by
<apply> <eq/> <apply><divergence/><ci type="vectorfield">a</ci></apply> <apply> <limit/> <bvar><ci> V </ci></bvar> <condition> <apply> <tendsto/> <ci> V </ci> <cn> 0 </cn> </apply> </condition> <apply> <divide/> <apply> <int encoding="text" definitionURL="SurfaceIntegrals.htm"/> <bvar><ci> S</ci></bvar> <ci> a </ci> </apply> <ci> V </ci> </apply> </apply> </apply>
C.8
MMLdefinition: grad
- Description
-
The gradient element is the vector calculus gradient operator, often called grad. It represents the operation that constructs a vector of partial derivatives vector( df/dx_1 , df/dx_2, ... df/dx_n )
- Discussion
-
The
gradelement is the vector calculus gradient operator, often called grad. - Classification
- unary function
- Signature
-
(function) -> vector(function)
(bvar+,algebraic) -> vector(algebraic)
- Example
-
Where for example f is a scalar function of three real variables.
<apply><grad/><ci type="function"> f</ci></apply>
- Example
<apply><grad/> <bvar><ci>x</ci></bvar><bvar><ci>y</ci></bvar><bvar><ci>z</ci></bvar> <apply><times/><ci>x</ci><ci>y</ci><ci>z</ci></apply> </apply>
C.9
MMLdefinition: curl
- Description
-
This symbol is used to represent the curl operator. It requires both a coordinates and a vector of expressions defined over those coordinates. It returns a vector valued expression.
In its functional form the coordinates are implicit in the definition of the function so it needs only one argument which is a vector valued function and returns a vector of functions.
Given F = F(x,y,z) = ( f1(x,y,z) , f2(x,y,z), f3(x,y,z) ) and coordinate names (x,y,z) the following relationship must hold:
curl(F) = i X \partial(F)/\partial(x) + j X \partial(F)/\partial(y) + j X \partial(F)/\partial(Z) where i,j,k are the unit vectors corresponding to the x,y,z axes respectivly and the multiplication X is cross multiplication.
- Discussion
-
The
curlelement is the vector calculus curl operator. - Classification
- unary function
- Signature
-
(bvar,bvar,bvar,algebraic) -> vector(algebraic)
(vector(function) ) -> vector(function)
- Property
-
curl(F) = i X \partial(F)/\partial(x) + j X \partial(F)/\partial(y) + j X \partial(F)/\partial(Z)
- Example
-
Where for example a is a vector field.
<apply><curl/><ci>a</ci></apply>
- Example
<apply><curl/><ci type="vector">f</ci></apply>
C.10
MMLdefinition: laplacian
- Description
-
This is the element used to indicate an application of the laplacian operator. It may be applied directly to expressions, in which case the coordinate names are provided in order by use of bvar. It may also be applied directly to a function F in which case, the definition below is for F = F(x_1, x_2, ... x_n) where x_1, x_2, ... x_n are the coordinate names.
laplacian(F) = \partial^2(F)/\partial(x_1)^2 + ... + \partial^2(F)/\partial(x_n)^2
- Discussion
-
The
laplacianelement is the vector calculus laplacian operator. - Classification
- unary function
- Signature
-
(bvar+,algebraic) -> algebraic
(scalar_valued_function) -> scalar_valued_function
- Example
<apply><laplacian/><ci type="vector"> E</ci></apply>
- Example
<declare><ci>F</ci><vector><ci>f1</ci><ci>f2</ci><ci>f3</ci></vector></declare> <apply><laplacian/><ci>F</ci></apply>
- Example
<apply><laplacian/> <bvar><ci>x</ci></bvar><bvar><ci>y</ci></bvar><bvar><ci>z</ci></bvar> <apply><ci>f</ci> <ci>x</ci><ci>y</ci> </apply> </apply>- Example
-
Where for examplef is a scalar function of three real variables.
<apply> <eq/> <apply><laplacian/> <ci> f </ci> </apply> <apply> <divergence/> <apply><grad/> <ci> f </ci> </apply> </apply> </apply>
3.7 Content Dictionary: Theory of Sets
C.1
MMLdefinition: set
- Description
-
The set element is the container element that constructs a set of elements. They may be explicitly listed, or defined by expressions or functions evaluated over a domain of application. The domain of application may be given explicitly, or provided by means of one of the shortcut notations.
- Discussion
-
Editorial note: MiKo Take the listandsetparts of the discussion apart and make theMMLdefinitions selfcontained, maybe move some of the discussion into the CD descriptionThe
setelement is the container element that constructs a set of elements. The elements of a set can be defined either by explicitly listing the elements, or by evaluating a function over a domain of application as described in Section 4.2.7 Qualifiers.The
typeattribute indicates type of the set. Predefined values: "normal", "multiset". "multiset" indicates that repetitions are allowed. The default value is "normal".Issue type_on_set wiki (member only) Keep typeattribute onset?It seems very awkward to keep this, it would probably be better to have an
multisetcontent dictionary as OpenMath does.Resolution None recorded The child elements of a possibly empty
listelement are the actual components of an ordered list. For example, an ordered list of the three symbols a, b, and c is encoded as<list><ci>a</ci><ci>b</ci><ci>c</ci></list>
Sets and lists can also be constructed by evaluating a function over a domain of application, each evaluation corresponding to a term of the set or list. In the most general form a domain is explicitly specified by a
domainofapplicationelement together with optionalbvarelements. Qualifications involving adomainofapplicationelement can be abbreviated in several ways as described in Section 4.2.7 Qualifiers. For example, abvarand aconditionelement can be used to define lists where membership depends on satisfying certain conditions.An
orderattribute can be used to specify what ordering is to be used. When the nature of the child elements permits, the ordering defaults to a numeric or lexicographic ordering.Sets are structured much the same as lists except that there is no implied ordering and the
typeof set may be "normal" or "multiset" with "multiset" indicating that repetitions are allowed.For both sets and lists, the child elements must be valid MathML content elements. The type of the child elements is not restricted. For example, one might construct a list of equations, or of inequalities.
The child elements of a possibly empty
listelement are the actual components of an ordered list. For example, an ordered list of the three symbols a, b, and c is encoded as<list><ci>a</ci><ci>b</ci><ci>c</ci></list>
Sets and lists can also be constructed by evaluating a function over a domain of application, each evaluation corresponding to a term of the set or list. In the most general form a domain is explicitly specified by a
domainofapplicationelement together with optionalbvarelements. Qualifications involving adomainofapplicationelement can be abbreviated in several ways as described in Section 4.2.7 Qualifiers. For example, abvarand aconditionelement can be used to define lists where membership depends on satisfying certain conditions.An
orderattribute can be used to specify what ordering is to be used. When the nature of the child elements permits, the ordering defaults to a numeric or lexicographic ordering.Sets are structured much the same as lists except that there is no implied ordering and the
typeof set may be "normal" or "multiset" with "multiset" indicating that repetitions are allowed.For both sets and lists, the child elements must be valid MathML content elements. The type of the child elements is not restricted. For example, one might construct a list of equations, or of inequalities.
- Classification
- constructor
- MMLattribute
-
Name Value Default order lexicographic | numeric none - Signature
-
(anything*) -> list
[order=ordering](anything*) -> list
(domainofapp,function) -> list
(bvar+,domainofapp,anything) -> list
[order=ordering](domainofapp,function) -> list(ordering)
[order=ordering](bvar*,domainofapp,anything) -> list(ordering)
- Example
<list><ci>a</ci><ci>b</ci><ci>c</ci></list>
- Example
<list order="numeric"> <bvar><ci>x</ci></bvar> <condition> <apply><lt/><ci>x</ci><cn>5</cn></apply> </condition> </list>
C.2
MMLdefinition: list
- Description
-
The list element is the container element that constructs a list of elements. They may be explicitly listed, or defined by expressions or functions evaluated over a domain of application. The domain of application may be given explicitly, or provided by means of one of the shortcut notations.
- Classification
- constructor
- MMLattribute
-
Name Value Default order lexicographic | numeric none - Signature
-
(anything*) -> list
[order=ordering](anything*) -> list
(domainofapp,function) -> list
(bvar+,domainofapp,anything) -> list
[order=ordering](domainofapp,function) -> list(ordering)
[order=ordering](bvar*,domainofapp,anything) -> list(ordering)
- Example
<list> <ci> a </ci> <ci> b </ci> <ci> c </ci> </list>
- Example
<list order="numeric"> <bvar><ci> x </ci></bvar> <condition> <apply><lt/> <ci> x </ci> <cn> 5 </cn> </apply> </condition> </list>
C.3
MMLdefinition: union
- Description
-
This is the set-theoretic operation of union of sets. This n-ary operator generalizes to operations on multisets by tracking the frequency of occurrence of each element in the union. As an n-ary operation the operands can be generated by allowing a function or expression to range over the elements of a domain of application. Thus it accepts qualifiers.
- Discussion
-
The
unionelement is the operator for a set-theoretic union or join of two (or more) sets. The operands are usually listed explicitly.As an n-ary operator, its operands may also be generated as described in Section 4.4.10 Lifted Associative Commutative Operators Therefore it may take qualifiers.
- Classification
- nary set function
- Signature
-
(set*) -> set
(multiset*) -> multiset
(domainofapp, set_valued_function) -> set
(bvar+,domainofapp,set_valued_expression) -> set
(domainofapp, multiset_valued_function) -> multiset
(bvar+,domainofapp,multiset_valued_expression) -> multiset
- Example
<apply><union/> <ci> A </ci> <ci> B </ci> </apply>
- Example
<apply> <union/> <bvar><ci type="set"> S </ci></bvar> <domainofapplication><ci type="list">L</ci></domainofapplication> <ci type="set"> S </ci> </apply>
C.4
MMLdefinition: intersect
- Description
-
This n-ary operator indicates the intersection of two sets. If the two sets are multisets, the result is a multiset. in which each element is present with a repetition determined by the smallest number of occurrences in any of the sets (multisets) that occur as arguments.
- Discussion
-
The
intersectelement is the operator for the set-theoretic intersection or meet of two (or more) sets. The operands are usually listed explicitly.As an n-ary operator, its operands may also be generated as described in Section 4.4.10 Lifted Associative Commutative Operators Therefore it may take qualifiers.
- Classification
- nary function
- Signature
-
(set*) -> set
(multiset*) -> multiset
(domainofapp, set_valued_function) -> set
(bvar+,domainofapp,set_valued_expression) -> set
(domainofapp, multiset_valued_function) -> multiset
(bvar+,domainofapp,multiset_valued_expression) -> multiset
- Example
<apply><intersect/> <ci type="set"> A </ci> <ci type="set"> B </ci> </apply>
- Example
<apply> <intersect/> <bvar><ci type="set"> S </ci></bvar> <domainofapplication><ci type="list">L</ci></domainofapplication> <ci type="set"> S </ci> </apply>
C.5
MMLdefinition: in
- Description
-
The in element is the relational operator used for a set-theoretic inclusion ('is in' or 'is a member of').
- Discussion
-
The
inelement is the relational operator used for a set-theoretic inclusion ("is in" or "is a member of").The
inelement is a binary set relation. - Classification
- function
- Signature
-
(anything,set) -> boolean
(anything,multiset) -> boolean
- Example
<apply><in/> <ci> a </ci> <ci type="set"> A </ci> </apply>
C.6
MMLdefinition: notin
- Description
-
The notin element is the relational operator element used to construct set-theoretic exclusion ('is not in' or 'is not a member of').
- Discussion
-
The
notinelement is the relational operator element used for set-theoretic exclusion ("is not in" or "is not a member of").The
notinelement is a binary set relation. - Classification
- function
- Signature
-
(anything,set) -> boolean
(anything,multiset) -> boolean
- Example
<apply><notin/> <ci> a </ci> <ci type="set"> A </ci> </apply>
C.7
MMLdefinition: subset
- Description
-
The subset element is the n-ary relational operator element for a set-theoretic containment ('is a subset of').
- Discussion
-
The
subsetelement is the relational operator element for a set-theoretic containment ("is a subset of").The
subsetelement is an n-ary set relation. As an n-ary operator, its operands may also be generated as described in Section 4.4.10 Lifted Associative Commutative Operators Therefore it may take qualifiers. - Classification
- function
- Signature
-
(set*) -> boolean
(multiset*) -> boolean
(domainofapp,function) -> boolean
(bvar+,domainofapp,algebraic) -> boolean
- Example
<apply><subset/> <ci type="set"> A </ci> <ci type="set"> B </ci> </apply>
- Example
<apply> <subset/> <subset/> <bvar><ci type="set">S</ci></bvar> <condition> <apply><in/> <ci>S</ci> <ci type="list">T</ci> </apply> </condition> <ci>S</ci> </apply>
C.8
MMLdefinition: prsubset
- Description
-
The
prsubsetelement is the n-ary relational operator element for set-theoretic proper containment ('is a proper subset of'). - Discussion
-
The
prsubsetelement is the relational operator element for set-theoretic proper containment ("is a proper subset of").The
prsubsetelement is an n-ary set relation. As an n-ary operator, its operands may also be generated as described in Section 4.4.10 Lifted Associative Commutative Operators Therefore it may take qualifiers. - Classification
- function
- Signature
-
(set*) -> boolean
(multiset*) -> boolean
(domainofapp,function) -> boolean
(bvar+,domainofapp,boolean) -> boolean
- Example
<apply><prsubset/> <ci type="set"> A </ci> <ci type="set"> B </ci> </apply>
- Example
<apply> <prsubset/> <bvar><ci type="integer">i</ci></bvar> <lowlimit><cn>0</cn></lowlimit> <uplimit><cn>10</cn></uplimit> <apply><selector/> <ci type="vector_of_sets">S</ci> <ci>i</ci> </apply> </apply>
C.9
MMLdefinition: notsubset
- Description
-
The notsubset element is the relational operator element for the set-theoretic relation 'is not a subset of'.
- Discussion
-
The
notsubsetelement is the relational operator element for the set-theoretic relation "is not a subset of".The
notsubsetelement is a binary set relation. - Classification
- function
- Signature
-
(set, set) -> boolean
(multiset,multiset) -> boolean
- Example
<apply><notsubset/> <ci type="set"> A </ci> <ci type="set"> B </ci> </apply>
C.10
MMLdefinition: notprsubset
- Description
-
The notprsubset element is the element for constructing the set-theoretic relation 'is not a proper subset of'.
- Discussion
-
The
notprsubsetelement is the operator element for the set-theoretic relation "is not a proper subset of".The
notprsubsetelement is a binary set relation. - Classification
- function
- Signature
-
(set,set) -> boolean
(multiset,multiset) -> boolean
- Example
<apply><notprsubset/> <ci type="set"> A </ci> <ci type="set"> B </ci> </apply>
C.11
MMLdefinition: setdiff
- Description
-
The setdiff element is the operator element for a set-theoretic difference of two sets.
- Discussion
-
The
setdiffelement is the operator element for a set-theoretic difference of two sets. - Classification
- binary set function
- Signature
-
(set,set) -> set
(multiset,multiset) -> multiset
- Example
<apply><setdiff/> <ci type="set"> A </ci> <ci type="set"> B </ci> </apply>
C.12
MMLdefinition: card
- Description
-
The card element is the operator element for deriving the size or cardinality of a set. The size of a multset is simply the total number of elements in the multiset.
- Discussion
-
The
cardelement is the operator element for the size or cardinality of a set. - Classification
- unary function
- Signature
-
(set) -> scalar
(multiset) -> scalar
- Example
-
where A is a set with 5 elements.
<apply><eq/> <apply><card/><ci> A </ci></apply> <ci> 5 </ci> </apply>
C.13
MMLdefinition: cartesianproduct
- Description
-
The cartesianproduct element is the operator for a set-theoretic cartesian product of two (or more) sets. The cartesian product of multisets produces a multiset since n-tuples may be repeated if elements in the base sets are repeated.
- Discussion
-
The
cartesianproductelement is the operator element for the Cartesian product of two or more sets. If A and B are two sets, then the Cartesian product of A and B is the set of all pairs (a,b) with a in A and b in B.As an n-ary operator, its operands may also be generated as described in Section 4.4.10 Lifted Associative Commutative Operators Therefore it may take qualifiers.
- Classification
- nary function
- Signature
-
(set*) -> set
(multiset*) -> multiset
- Example
<apply><cartesianproduct/> <ci> A </ci> <ci> B </ci> </apply>
- Example
<apply><cartesianproduct/> <reals/> <reals/> <reals/> </apply>
3.8 Content Dictionary: Sequences and Series
C.1
MMLdefinition: sum
- Description
-
The sum element denotes the summation operator. It may be qualified by providing a domainofapplication. This may be provided using one of the shorthand notations for domainofapplication such as an uplimit,lowlimit pair or a condition or an interval. The index for the summation is specified by a bvar element.
- Discussion
-
The
sumelement denotes the summation operator. The most general form of a sum specifies the terms of the sum by using adomainofapplicationelement to specify a domain. If no bound variables are specified then terms of the sum correspond to those produced by evaluating the function that is provided at the points of the domain, while if bound variables are present they are the index of summation and they take on the values of points in the domain. In this case the terms of the sum correspond to the values of the expression that is provided, evaluated at those points. Depending on the structure of the domain, the domain of summation can be abbreviated by usinguplimitandlowlimitto specify upper and lower limits for the sum.The
sumfunction accept thebvar,lowlimit,uplimit,interval,conditionanddomainofapplicationschemata. If bothlowlimitanduplimitschemata are present, they denote the limits of the sum or product. The limits may alternatively be specified using theinterval,conditionordomainofapplicationschema. Thebvarschema signifies the internal variable in the sum or product. A typical example might be:<apply> <sum/> <bvar><ci>i</ci></bvar> <lowlimit><cn>0</cn></lowlimit> <uplimit><cn>100</cn></uplimit> <apply> <power/> <ci>x</ci> <ci>i</ci> </apply> </apply>When used with
sumorproduct, each qualifier schema is expected to contain a single child schema; otherwise an error is generated. - Classification
- function
- Signature
-
(function ) -> function
(bvar,algebraic ) -> algebraic
(domainofapp,function) -> function
(bvar+,domainofapp,algebraic) -> algebraic
- Example
<apply><sum/> <bvar> <ci> x </ci></bvar> <lowlimit><ci> a </ci></lowlimit> <uplimit><ci> b </ci></uplimit> <apply><ci> f </ci><ci> x </ci></apply> </apply>
- Example
<apply><sum/> <bvar><ci> x </ci></bvar> <condition><apply> <in/><ci> x </ci><ci type="set">B</ci></apply></condition> <apply><ci type="function"> f </ci><ci> x </ci></apply> </apply>
- Example
<apply> <sum/> <domainofapplication> <ci type="set"> B </ci> </domainofapplication> <ci type="function"> f </ci> </apply>
C.2
MMLdefinition: product
- Description
-
The product element denotes the product operator. It may be qualified by providing a domainofapplication. This may be provided using one of the shorthand notations for domainofapplication such as an uplimit,lowlimit pair or a condition or an interval. The index for the product is specified by a bvar element.
- Discussion
-
The
productelement denotes the product operator. The most general form of a product specifies the terms of the product by using adomainofapplicationelement to specify the domain. If no bound variables are specified then terms of the product correspond to those produced by evaluating the function that is provided at the points of the domain, while if bound variables are present they are the index of product and they take on the values of points in the domain. In this case the terms of the product correspond to the values of the expression that is provided, evaluated at those points. Depending on the structure of the domain, the domain of product can be abbreviated by usinguplimitandlowlimitto specify upper and lower limits for the product.The
sumfunction accepts thebvar,lowlimit,uplimit,interval,conditionanddomainofapplicationschemata. If bothlowlimitanduplimitschemata are present, they denote the limits of the sum or product. The limits may alternatively be specified using theinterval,conditionordomainofapplicationschema. Thebvarschema signifies the internal variable in the sum or product. - Classification
- function
- Signature
-
(function) -> function
(bvar,algebraic) -> algebraic
(domainofapp,function) -> function
(bvar+,domainofapp,algebraic) -> algebraic
- Example
<apply><product/> <bvar><ci> x </ci></bvar> <lowlimit> <ci> a </ci></lowlimit> <uplimit><ci> b </ci></uplimit> <apply><ci type="function"> f </ci><ci> x </ci></apply> </apply>
- Example
<apply><product/> <bvar><ci> x </ci></bvar> <condition><apply> <in/><ci> x </ci><ci type="set">B</ci></apply></condition> <apply><ci> f </ci><ci> x </ci></apply> </apply>
C.3
MMLdefinition: limit
- Description
-
The limit element represents the operation of taking a limit of a sequence. The limit point is expressed by specifying a lowlimit and a bvar, or by specifying a condition on one or more bound variables.
- Discussion
-
The
limitelement represents the operation of taking a limit of a sequence. The limit point is expressed by specifying alowlimitand abvar, or by specifying aconditionon one or more bound variables.The
limitfunction accepts zero or morebvarschemata, and optionalconditionandlowlimitschemata. Aconditionmay be used to place constraints on thebvar. Thebvarschema denotes the variable with respect to which the limit is being taken. Thelowlimitschema denotes the limit point. When used withlimit, thebvarandlowlimitschemata are expected to contain a single child schema; otherwise an error is generated. - Classification
- function
- Signature
-
(bvar+, lowlimit, uplimit, algebraic) -> real
(bvar+, condition , algebraic) -> real
- Example
<apply> <limit/> <bvar><ci> x </ci></bvar> <lowlimit><cn> 0 </cn></lowlimit> <apply><sin/><ci> x </ci></apply> </apply>
- Example
<apply><limit/> <bvar><ci>x</ci></bvar> <condition> <apply><tendsto/><ci>x</ci><cn>0</cn></apply> </condition> <apply><sin/><ci>x</ci></apply> </apply>- Example
<apply> <limit/> <bvar><ci> x </ci></bvar> <condition> <apply> <tendsto type="above"/> <ci> x </ci> <ci> a </ci> </apply> </condition> <apply><sin/> <ci> x </ci> </apply> </apply>
C.4
MMLdefinition: tendsto
- Description
-
The tendsto element is used to express the relation that a quantity is tending to a specified value.
- Discussion
-
The
tendstoelement is used to express the relation that a quantity is tending to a specified value. While this is used primarily as part of the statement of a mathematical limit, it exists as a construct on its own to allow one to capture mathematical statements such as "As x tends to y," and to provide a building block to construct more general kinds of limits that are not explicitly covered by the recommendation.The
tendstoelement takes the attributestypeto set the direction from which the limiting value is approached. It occurs as a container so that it can more easily be used in the construction of a limit expression. Predefined values: "above", "below", "two-sided". The default value is "two-sided".Issue type_on_tendsto wiki (member only) keep typeattribute ontendsto?It seems very awkward to keep this, it would probably be better to have an
tendsto_xxxsymbol where xxx is thetypevalue. (this would be closer to what OpenMath does now).Resolution None recorded - Classification
- function
- MMLattribute
-
Name Value Default type above | below | all | MathMLType all - Signature
-
(algebraic,algebraic) -> tendsto
[ type=direction ](algebraic,algebraic) -> tendsto(direction)
- Example
<apply><tendsto type="above"/> <apply><power/><ci> x </ci><cn> 2 </cn></apply> <apply><power/><ci> a </ci><cn> 2 </cn></apply> </apply>
- Example
-
To express (x, y)
 (f(x, y),
g(x,y)), one might use vectors, as in:
(f(x, y),
g(x,y)), one might use vectors, as in:
<apply><tendsto/> <vector><ci> x </ci><ci> y </ci></vector> <vector> <apply><ci type="function">f</ci><ci> x </ci><ci> y </ci></apply> <apply><ci type="function">g</ci><ci> x </ci><ci> y </ci></apply> </vector> </apply>
3.9 Content Dictionary: Elementary Classical Functions
The names of the common trigonometric functions supported by MathML are listed below. Since their standard interpretations are widely known, they are discussed as a group.
sin |
cos |
tan |
sec |
csc |
cot |
sinh |
cosh |
tanh |
sech |
csch |
coth |
arcsin |
arccos |
arctan |
arccosh |
arccot |
arccoth |
arccsc |
arccsch |
arcsec |
arcsech |
arcsinh |
arctanh |
- Discussion
-
These operator elements denote the standard trigonometric functions.
C.1
MMLdefinition: exp
- Description
-
This element represents the exponentiation function as described in Abramowitz and Stegun, section 4.2. It takes one argument.
- Discussion
-
The
expelement represents the exponential function associated with the inverse of thelnfunction. In particular, exp(1) is approximately 2.718281828. - Classification
- unary function
- Signature
-
(real) -> real
(complex) -> complex
- Property
<apply><eq/> <apply><exp/><cn>0</cn></apply> <cn>1</cn> </apply>
- Property
-
for all k if k is an integer then e^(z+2*pi*k*i)=e^z
- Example
<apply><exp/><ci> x </ci></apply>
C.2
MMLdefinition: ln
- Description
-
This element represents the ln function (natural logarithm) as described in Abramowitz and Stegun, section 4.1. It takes one argument.
- Discussion
-
The
lnelement represents the natural logarithm function. - Classification
- unary function
- Signature
-
(real) -> real
(complex) -> complex
- Property
-
-pi lt Im ln x leq pi
- Example
-
If a = e, (where e is the base of the natural logarithms) this will yield the value 1.
<apply><ln/><ci> a </ci></apply>
C.3
MMLdefinition: log
- Description
-
This element represents the log function. It is defined in Abramowitz and Stegun, Handbook of Mathematical Functions, section 4.1 If its first argument is a logbase element, it specifies the base and the second argument is the argument to which the function is applied using that base. If no logbase element is present, the base is assumed to be 10.
- Discussion
-
The
logelement is the operator that returns a logarithm to a given base. The base may be specified using alogbaseelement, which should be the first element followinglog, i.e. the second child of the containingapplyelement. If thelogbaseelement is not present, a default base of 10 is assumed.The
logfunction accepts only thelogbaseschema. If present, thelogbaseschema denotes the base with respect to which the logarithm is being taken. Otherwise, the log is assumed to be base 10. When used withlog, thelogbaseschema is expected to contain a single child schema; otherwise an error is generated. - Classification
- function
- Signature
-
(logbase,real) -> real
(logbase,complex) -> complex
(real) -> real
(complex) -> complex
- Property
-
a^b = c implies log_a c = b
- Example
-
This markup represents "the base 3 logarithm of x". For natural logarithms base e, the
lnelement should be used instead.<apply><log/> <logbase><cn> 3 </cn></logbase> <ci> x </ci> </apply>
- Example
<apply><log/><ci>x</ci></apply>
C.4
MMLdefinition: sin
- Description
-
This element represents the sin function as described in Abramowitz and Stegun, section 4.3. It takes one argument.
- Classification
- function
- Signature
-
(real) -> real
(complex) -> complex
- Property
-
sin(0) = 0
- Property
-
sin(integer*Pi) = 0
- Property
-
sin(x) = (exp(ix)-exp(-ix))/2i
- Example
<apply><sin/><ci> x </ci></apply>
- Example
<apply> <sin/> <apply> <plus/> <apply><cos/> <ci> x </ci> </apply> <apply> <power/> <ci> x </ci> <cn> 3 </cn> </apply> </apply> </apply>
C.5
MMLdefinition: cos
- Description
-
This element represents the cos function as described in Abramowitz and Stegun, section 4.3. It takes one argument. It takes one argument.
- Classification
- function
- Signature
-
(real) -> real
(complex) -> complex
- Property
-
cos(0) = 1
- Property
-
cos(integer*Pi+Pi/2) = 0
- Property
-
cos(x) = (exp(ix)+exp(-ix))/2
- Example
<apply><cos/><ci>x</ci></apply>
C.6
MMLdefinition: tan
- Description
-
This element represents the tan function as described in Abramowitz and Stegun, section 4.3. It takes one argument.
- Classification
- function
- Signature
-
(real) -> real
(complex) -> complex
- Property
-
tan(integer*Pi) = 0
- Property
-
tan(x) = sin(x)/cos(x)
- Example
<apply><tan/><ci>x</ci></apply>
C.7
MMLdefinition: sec
- Description
-
This element represents the sec function as described in Abramowitz and Stegun, section 4.3. It takes one argument.
- Classification
- function
- Signature
-
(real) -> real
(complex) -> complex
- Property
-
sec(x) = 1/cos(x)
- Example
<apply><sec/><ci>x</ci></apply>
C.8
MMLdefinition: csc
- Description
-
This element represents the csc function as described in Abramowitz and Stegun, section 4.3. It takes one argument.
- Classification
- function
- Signature
-
(real) -> real
(complex) -> complex
- Property
-
csc(x) = 1/sin(x)
- Example
<apply><csc/><ci>x</ci></apply>
C.9
MMLdefinition: cot
- Description
-
This element represents the cot function as described in Abramowitz and Stegun, section 4.3. It takes one argument. It takes one argument.
- Classification
- function
- Signature
-
(real) -> real
(complex) -> complex
- Property
-
cot(integer*Pi+Pi/2) = 0
- Property
-
cot(x) = cos(x)/sin(x)
- Property
-
cot A = 1/tan A
- Example
<apply><cot/><ci>x</ci></apply>
C.10
MMLdefinition: sinh
- Description
-
This element represents the sinh function as described in Abramowitz and Stegun, section 4.5. It takes one argument.
- Classification
- function
- Signature
-
(real) -> real
(complex) -> complex
- Property
-
sinh A = 1/2 * (e^A - e^(-A))
- Example
<apply><sinh/><ci>x</ci></apply>
C.11
MMLdefinition: cosh
- Description
-
This symbol represents the cosh function as described in Abramowitz and Stegun, section 4.5. It takes one argument. It takes one argument.
- Classification
- function
- Signature
-
(real) -> real
(complex) -> complex
- Property
-
cosh A = 1/2 * (e^A + e^(-A))
- Example
<apply><cosh/><ci>x</ci></apply>
C.12
MMLdefinition: tanh
- Description
-
This element represents the tanh function as described in Abramowitz and Stegun, section 4.5. It takes one argument.
- Classification
- function
- Signature
-
(real) -> real
(complex) -> complex
- Property
-
tanh A = sinh A / cosh A
- Example
<apply><tanh/><ci>x</ci></apply>
C.13
MMLdefinition: sech
- Description
-
This element represents the sech function as described in Abramowitz and Stegun, section 4.5. It takes one argument.
- Classification
- function
- Signature
-
(real) -> real
(complex) -> complex
- Property
-
sech A = 1/cosh A
- Example
<apply><sech/><ci>x</ci></apply>
C.14
MMLdefinition: csch
- Description
-
This element represents the csch function as described in Abramowitz and Stegun, section 4.5. It takes one argument.
- Classification
- function
- Signature
-
(real) -> real
(complex) -> complex
- Property
-
csch A = 1/sinh A
- Example
<apply><csch/><ci>x</ci></apply>
C.15
MMLdefinition: coth
- Description
-
This element represents the coth function as described in Abramowitz and Stegun, section 4.5. It takes one argument.
- Classification
- function
- Signature
-
(real) -> real
(complex) -> complex
- Property
-
coth A = 1/tanh A
- Example
<apply><coth/><ci>x</ci></apply>
C.16
MMLdefinition: arcsin
- Description
-
This element represents the arcsin function which is the inverse of the sin function as described in Abramowitz and Stegun, section 4.4. It takes one argument.
- Classification
- function
- Signature
-
(real) -> real
(complex) -> complex
- Property
-
arcsin(z) = -i ln (sqrt(1-z^2)+iz)
- Example
<apply><arcsin/><ci>x</ci></apply>
C.17
MMLdefinition: arccos
- Description
-
This element represents the arccos function which is the inverse of the cos function as described in Abramowitz and Stegun, section 4.4. It takes one argument.
- Classification
- function
- Signature
-
(real) -> real
(complex) -> complex
- Property
-
arccos(z) = -i ln(z+i \sqrt(1-z^2))
- Example
<apply><arccos/><ci>x</ci></apply>
C.18
MMLdefinition: arctan
- Description
-
This element represents the arctan function which is the inverse of the tan function as described in Abramowitz and Stegun, section 4.4. It takes one argument.
- Classification
- function
- Signature
-
(real) -> real
(complex) -> complex
- Property
-
arctan(z) = (ln(1+iz)-ln(1-iz))/2i
- Example
<apply><arctan/><ci>x</ci></apply>
C.19
MMLdefinition: arccosh
- Description
-
This symbol represents the arccosh function as described in Abramowitz and Stegun, section 4.6. It takes one argument.
- Classification
- function
- Signature
-
(real) -> real
(complex) -> complex
- Property
-
arccosh(z) = 2*ln(\sqrt((z+1)/2) + \sqrt((z-1)/2))
- Example
<apply><arccosh/><ci>x</ci></apply>
C.20
MMLdefinition: arccot
- Description
-
This element represents the arccot function as described in Abramowitz and Stegun, section 4.4. It takes one argument.
- Classification
- function
- Signature
-
(real) -> real
(complex) -> complex
- Property
-
arccot(-z) = - arccot(z)
- Example
<apply><arccot/><ci>x</ci></apply>
C.21
MMLdefinition: arccoth
- Description
-
This element represents the arccoth function as described in Abramowitz and Stegun, section 4.6. It takes one argument.
- Classification
- function
- Signature
-
(real) -> real
(complex) -> complex
- Property
-
arccoth(z) = (ln(-1-z)-ln(1-z))/2
- Example
<apply><arccoth/><ci>x</ci></apply>
C.22
MMLdefinition: arccsc
- Description
-
This element represents the arccsc function as described in Abramowitz and Stegun, section 4.4. It takes one argument.
- Classification
- function
- Signature
-
(real) -> real
(complex) -> complex
- Property
-
arccsc(z) = -i ln(i/z + \sqrt(1 - 1/z^2))
- Example
<apply><arccsc/><ci>x</ci></apply>
C.23
MMLdefinition: arccsch
- Description
-
This element represents the arccsch function as described in Abramowitz and Stegun, section 4.6. It takes one argument.
- Classification
- function
- Signature
-
(real) -> real
(complex) -> complex
- Property
-
arccsch(z) = ln(1/z + \sqrt(1+(1/z)^2))
- Example
<apply><arccsch/><ci>x</ci></apply>
C.24
MMLdefinition: arcsec
- Description
-
This element represents the arcsec function as described in Abramowitz and Stegun, section 4.4. It takes one argument.
- Classification
- function
- Signature
-
(real) -> real
(complex) -> complex
- Property
-
arcsec(z) = -i ln(1/z + i \sqrt(1-1/z^2))
- Example
<apply><arcsec/><ci>x</ci></apply>
C.25
MMLdefinition: arcsech
- Description
-
This element represents the arcsech function as described in Abramowitz and Stegun, section 4.6. It takes one argument.
- Classification
- function
- Signature
-
(real) -> real
(complex) -> complex
- Property
-
arcsech(z) = 2 ln(\sqrt((1+z)/(2z)) + \sqrt((1-z)/(2z)))
- Example
<apply><arcsech/><ci>x</ci></apply>
C.26
MMLdefinition: arcsinh
- Description
-
This element represents the arcsinh function as described in Abramowitz and Stegun, section 4.6. It takes one argument.
- Classification
- function
- Signature
-
(real) -> real
(complex) -> complex
- Property
-
arcsinh z = ln(z + \sqrt(1+z^2))
- Example
<apply><arcsinh/><ci>x</ci></apply>
C.27
MMLdefinition: arctanh
- Description
-
This element represents the arctanh function as described in Abramowitz and Stegun, section 4.6. It takes one argument.
- Classification
- function
- Signature
-
(real) -> real
(complex) -> complex
- Property
-
arctanh(z) = - i * arctan(i * z)
- Example
<apply><arctanh/><ci>x</ci></apply>
3.10 Content Dictionary: Statistics
C.1
MMLdefinition: mean
- Description
-
The mean value of a set of data, or of a random variable. See CRC Standard Mathematical Tables and Formulae, editor: Dan Zwillinger, CRC Press Inc., 1996, section 7.7.1
- Discussion
-
meanis the operator element representing a mean or average. - Classification
- nary function
- Signature
-
(random_variable) -> scalar
(scalar+) -> scalar
- Example
<apply><mean/><ci type="discrete_random_variable"> X </ci></apply>
- Example
<apply><mean/><cn>3</cn><cn>4</cn><cn>3</cn><cn>7</cn><cn>4</cn></apply>
- Example
<apply><mean/><ci> X </ci></apply>
C.2
MMLdefinition: sdev
- Description
-
This element represents a function denoting the sample standard deviation of its arguments. The arguments are either all data, or a discrete random variable, or a continuous random variable.
For numeric data at least two values are required and this is the square root of (the sum of the squares of the deviations from the mean of the arguments, divided by the number of arguments less one). For a "discrete_random_variable", this is the square root of the second moment about the mean. This further generalizes to identifiers of type continuous_random_variable.
See CRC Standard Mathematical Tables and Formulae, editor: Dan Zwillinger, CRC Press Inc., 1996, (7.7.11) section 7.7.1.
- Discussion
-
sdevis the operator element representing the statistical standard deviation operator. - Classification
- nary function
- Signature
-
(scalar,scalar+) -> scalar
(discrete_random_variable) -> scalar
(continuous_random_variable) -> scalar
- Example
<apply><sdev/><cn>3</cn><cn>4</cn><cn>2</cn><cn>2</cn></apply>
- Example
-
sdevis an n-ary operator.<apply><sdev/><ci type="discrete_random_variable"> X </ci></apply>
C.3
MMLdefinition: variance
- Description
-
This symbol represents a function denoting the variance of its arguments, that is, the square of the standard deviation. The arguments are either all data in which case there are two or more of them, or an identifier of type discrete_random_variable, or continuous_random_variable. See CRC Standard Mathematical Tables and Formulae, editor: Dan Zwillinger, CRC Press Inc., 1996, [7.1.2] and [7.7].
- Discussion
-
varianceis the operator element representing the statistical variance operator. - Classification
- nary function
- Signature
-
(scalar,scalar+) -> scalar
(descrete_random_variable) -> scalar
(continuous_random_variable) -> scalar
- Example
<apply><variance/><cn>3</cn><cn>4</cn><cn>2</cn><cn>2</cn></apply>
- Example
-
varianceis an n-ary operator.<apply><variance/><ci type="discrete_random_variable"> X </ci></apply>
C.4
MMLdefinition: median
- Description
-
This symbol represents an n-ary function denoting the median of its arguments. That is, if the data were placed in ascending order then it denotes the middle one (in the case of an odd amount of data) or the average of the middle two (in the case of an even amount of data). See CRC Standard Mathematical Tables and Formulae, editor: Dan Zwillinger, CRC Press Inc., 1996, section 7.7.1
- Discussion
-
medianis the operator element representing the statistical median operator. - Classification
- nary function
- Signature
-
(scalar+) -> scalar
- Example
<apply><median/><cn>3</cn><cn>4</cn><cn>2</cn><cn>2</cn></apply>
- Example
-
medianis an n-ary operator.<apply> <median/> <ci> X </ci> </apply>
C.5
MMLdefinition: mode
- Description
-
This represents the mode of n data values. The mode is the data value that occurs with the greatest frequency. See CRC Standard Mathematical Tables and Formulae, editor: Dan Zwillinger, CRC Press Inc., 1996, section 7.7.1
- Discussion
-
modeis the operator element representing the statistical mode operator. - Classification
- nary function
- Signature
-
(scalar+) -> scalar
- Example
<apply><mode/><cn>3</cn><cn>4</cn><cn>2</cn><cn>2</cn></apply>
- Example
-
modeis an n-ary operator.<apply> <mode/> <ci> X </ci> </apply>
C.6
MMLdefinition: moment
- Description
-
This symbol is used to denote the i'th moment of a set of data, or a random variable. Unless otherwise specified, the moment is about the origin. For example, the i'th moment of X about the origin is given by moment( i , 0 , x ).
The first argument indicates which moment about that point is being specified. For the i'th moment the first argument should be i. The second argument specifies the point about which the moment is computed. It is either an actual point ( e.g. 0 ), or a function which can be used on the data to compute that point. To indicate a central moment, specify the element "mean". The third argument is either a discrete or continuous random variable, or the start of a sequence of data. If there is a sequence of data then the i'th moment is (1/n) (x_1^i + x_2^i + ... + x_n^i).
See CRC Standard Mathematical Tables and Formulae, editor: Dan Zwillinger, CRC Press Inc., 1996, section 7.7.1
- Discussion
-
The
momentelement represents the statistical moment operator. Use the qualifierdegreefor the n in " n-th moment". Use the qualifiermomentaboutfor the p in "moment about p".The
momentfunction accepts thedegreeandmomentaboutschema. If present, thedegreeschema denotes the order of the moment. Otherwise, the moment is assumed to be the first order moment. When used withmoment, thedegreeschema is expected to contain a single child schema; otherwise an error is generated. If present, themomentaboutschema denotes the point about which the moment is taken. Otherwise, the moment is assumed to be the moment about zero. - Classification
- function
- Signature
-
(degree,momentabout?,scalar+) -> scalar
(degree,momentabout?,discrete_random_variable) -> scalar
(degree,momentabout?,continuous_random_variable) -> scalar
- Example
-
The third moment about the point p of a discrete random variable
momentis an operator taking qualifiers (see Section 4.2.7 Qualifiers). The third moment of the distribution X about the point p is written:<apply> <moment/> <degree><cn>3</cn></degree> <momentabout><ci>p</ci></momentabout> <ci>X</ci> </apply> - Example
-
The 3rd central moment of a set of data.
<apply><moment/> <degree><cn>3</cn></degree> <momentabout><mean/></momentabout> <cn>6</cn><cn>4</cn><cn>2</cn><cn>2</cn><cn>5</cn> </apply> - Example
-
The 3rd central moment of a discrete random variable.
<apply><moment/> <degree><cn>3</cn></degree> <momentabout><mean/></momentabout> <ci type="discrete_random_variable"> X </ci> </apply> - Example
-
The 3rd moment about the origin of a set of data.
<apply><moment/> <degree><cn>3</cn></degree> <momentabout><cn>0</cn></momentabout> <cn>6</cn><cn>4</cn><cn>2</cn><cn>2</cn> </apply>
C.7
MMLdefinition: momentabout
- Description
-
This qualifier element is used to identify the point about which a moment is to be computed. It may be an explicit point, or it may identify a method by which the point is to be computed from the given data. For example the moment may be computed about the mean by specifying the element used for the mean.
- Discussion
-
The
momentaboutelement is a qualifier element used with themomentelement to represent statistical moments. Use the qualifiermomentaboutfor the p in "moment about p". - Classification
- constructor
- Signature
-
(function) -> method
(scalar) -> point
- Example
-
The third moment of the distribution X about the point p of a discrete random variable is written:
<apply> <moment/> <degree> <cn> 3 </cn> </degree> <momentabout> <ci> p </ci> </momentabout> <ci> X </ci> </apply> - Example
-
The 3rd central moment of a set of data.
<apply><moment/> <degree><cn> 3 </cn></degree> <momentabout><mean/></momentabout> <cn>6</cn><cn>4</cn><cn>2</cn><cn>2</cn><cn>5</cn> </apply>
3.11 Content Dictionary: Linear Algebra
C.1
MMLdefinition: vector
- Description
-
A vector is an ordered n-tuple of values representing an element of an n-dimensional vector space. The "values" are all from the same ring, typically real or complex. Where orientation is important, such as for pre or post multiplication by a matrix a vector is treated as if it were a column vector and its transpose is treated a row vector. The type attribute can be used to explicitly specify that a vector is a "row" vector. See CRC Standard Mathematical Tables and Formulae, editor: Dan Zwillinger, CRC Press Inc., 1996, [2.4]
- Discussion
-
vectoris the container element for a vector. The child elements form the components of the vector.For purposes of interaction with matrices and matrix multiplication, vectors are regarded as equivalent to a matrix consisting of a single column, and the transpose of a vector behaves the same as a matrix consisting of a single row. Note that vectors may be rendered either as a single column or row.
In general a vector can be constructed by providing a function and a 1-dimensional domain of application. The entries of the vector correspond to the values obtained by evaluating the function at the points of the domain. The qualifications defined by a
domainofapplicationelement can also be abbreviated in several ways including aconditionplaced on a bound variable and an expression involving that variable.The
vectorelement constructs vectors from an n-dimensional vector space so that its n child elements typically represent real or complex valued scalars as in the three-element vector<vector> <apply><plus/><ci>x</ci><ci>y</ci></apply> <cn>3</cn> <cn>7</cn> </vector>
A vector can also be constructed by evaluating a function over a specific domain of application, each evaluation corresponding to an entry in the vector. In its most general form a domain is explicitly specified by a
domainofapplicationelement and a function. Optionally thedomainofapplicationcan be augmented by abvarelement and an algebraic expression expressed in terms of it. Qualifications defined by adomainofapplicationelement can be abbreviated in several ways as described in Section 4.2.7 Qualifiers. - Classification
- constructor
- MMLattribute
-
Name Value Default type row | column | MathMLType column - Signature
-
(real*) -> vector(type=real)
[type=vectortype]((anything)*) -> vector(type=vectortype)
(domainofapp,function) -> vector
(bvar+,domainofapp,anything) -> vector
- Property
-
vector=column_vector
- Property
-
matrix * vector = vector
- Property
-
matrix * column_vector = column_ vector
- Property
-
row_vector*matrix = row_vector
- Property
-
transpose(vector) = row_vector
- Property
-
transpose(column_vector) = row_vector
- Property
-
transpose(row_vector) = column_vector
- Property
-
distributive over scalars
- Property
-
associativity.
- Property
-
Matrix * column vector
- Property
-
row vector * Matrix
- Example
-
vectoris a constructor element.<vector><cn>1</cn><cn>2</cn><cn>3</cn><ci>x</ci></vector>
- Example
<vector type="row"><cn>1</cn><cn>2</cn><cn>3</cn><ci>x</ci></vector>
- Example
<vector> <bvar><ci type="integer">i</ci></bvar> <lowlimit><ci>1</ci></lowlimit> <uplimit><ci>10</ci></uplimit> <apply><power/> <ci>x</ci> <ci>i</ci> </apply> </vector>
C.2
MMLdefinition: matrix
- Description
-
This is the constructor for a matrix. It requires matrixrow's as arguments. It is used to represent matrices. See CRC Standard Mathematical Tables and Formulae, editor: Dan Zwillinger, CRC Press Inc., 1996, [2.5.1].
- Discussion
-
The
matrixelement is the container element for matrix rows, which are represented bymatrixrow. Thematrixrows contain the elements of a matrix.In general a matrix can be constructed by providing a function and a 2-dimensional domain of application. The entries of the matrix correspond to the values obtained by evaluating the function at the points of the domain. The qualifications defined by a
domainofapplicationelement can also be abbreviated in several ways including aconditionelement placing constraints directly on bound variables and an expression in those variables.The
matrixelement is used to represent mathematical matrices. It has zero or more child elements, all of which arematrixrowelements. These in turn expect zero or more child elements that evaluate to algebraic expressions or numbers. These sub-elements are often real numbers, or symbols as in<matrix> <matrixrow> <cn> 1 </cn> <cn> 2 </cn> </matrixrow> <matrixrow> <cn> 3 </cn> <cn> 4 </cn> </matrixrow> </matrix>
The
matrixrowelements must always be contained inside of a matrix, and all rows in a given matrix must have the same number of elements.Note that the behavior of the
matrixandmatrixrowelements is substantially different from themtableandmtrpresentation elements.A matrix can also be constructed by evaluating a bivariate function over a specific domain of application, each evaluation corresponding to an entry in the matrix. In its most general form a domain of application is explicitly specified by a
domainofapplicationelement and a function which when evaluated at points of the domain produces entries in the matrix. Optionally thedomainofapplicationcan be augmented bybvarelements and an algebraic expression expressed in terms of them. - Classification
- constructor
- MMLattribute
-
Name Value Default type real | complex | integer | symbolic | integer | MathMLType real - Signature
-
(matrixrow*) -> matrix
[type=matrixtype](matrixrow*) -> matrix(type=matrixtype)
(domainofapp,function) -> matrix
(bvar,bvar,domainofapp,anything) -> matrix
- Property
-
scalar multiplication
- Property
-
scalar multiplication
Matrix*column vector
- Property
-
scalar multiplication
Addition - Property
-
scalar multiplication
Matrix*Matrix - Example
-
matrixis a constructor element.<matrix> <matrixrow><cn>0</cn> <cn> 1 </cn> <cn> 0 </cn></matrixrow> <matrixrow><cn>0</cn> <cn> 0 </cn> <cn> 1 </cn></matrixrow> <matrixrow><cn>1</cn> <cn> 0 </cn> <cn> 0 </cn></matrixrow> </matrix>
- Example
<matrix> <bvar><ci type="integer">i</ci></bvar> <bvar><ci type="integer">j</ci></bvar> <condition> <apply><and/> <apply><in/> <ci>i</ci> <interval><ci>1</ci><ci>5</ci></interval> </apply> <apply><in/> <ci>j</ci> <interval><ci>5</ci><ci>9</ci></interval> </apply> </apply> </condition> <apply><power/> <ci>i</ci> <ci>j</ci> </apply> </vector>
C.3
MMLdefinition: matrixrow
- Description
-
This symbol is an n-ary constructor used to represent rows of matrices. Its arguments should be members of a ring.
- Discussion
-
The
matrixrowelement is the container element for the rows of a matrix. - Classification
- constructor
- Signature
-
(ringelement+) -> matrixrow
- Example
<matrixrow><cn>1</cn><cn>2</cn></matrixrow>
C.4
MMLdefinition: determinant
- Description
-
The "determinant" of a matrix. This is a unary function. See CRC Standard Mathematical Tables and Formulae, editor: Dan Zwillinger, CRC Press Inc., 1996, [2.5.4].
- Discussion
-
The
determinantelement is the operator for constructing the determinant of a matrix. - Classification
- function
- Signature
-
(matrix)-> scalar
- Example
-
determinantis a unary operator.<apply><determinant/> <ci type="matrix"> A </ci> </apply>
C.5
MMLdefinition: transpose
- Description
-
The transpose of a matrix or vector. See CRC Standard Mathematical Tables and Formulae, editor: Dan Zwillinger, CRC Press Inc., 1996, [2.4] and [2.5.1].
- Discussion
-
The
transposeelement is the operator for constructing the transpose of a matrix. - Classification
- function
- Signature
-
(vector)->vector(type=row)
(matrix)->matrix
(vector[type=row])->vector
- Property
-
transpose(transpose(A))= A
- Property
-
transpose(transpose(V))= V
- Example
-
transposeis a unary operator.<apply><transpose/><ci type="matrix">A</ci></apply>
- Example
<apply><transpose/><ci type="vector">V</ci></apply>
C.6
MMLdefinition: selector
- Description
-
The operator used to extract sub-objects from vectors, matrices matrix rows and lists. Elements are accessed by providing one index element for each dimension. For matrices, sub-matrices are selected by providing one fewer index items. For a matrix A and a column vector V : select(i, j, A) is the i,j th element of A. select(i, A) is the matrixrow formed from the i'th row of A. select(i, V) is the i'th element of V. select(V) is the sequence of all elements of V. select(A) is the sequence of all elements of A, extracted row by row. select(i, L) is the i'th element of a list. select(L) is the sequence of elements of a list.
- Discussion
-
The
selectorelement is the operator for indexing into vectors matrices and lists. It accepts one or more arguments. The first argument identifies the vector, matrix or list from which the selection is taking place, and the second and subsequent arguments, if any, indicate the kind of selection taking place.When
selectoris used with a single argument, it should be interpreted as giving the sequence of all elements in the list, vector or matrix given. The ordering of elements in the sequence for a matrix is understood to be first by column, then by row. That is, for a matrix ( ai,j), where the indices denote row and column, the ordering would be a 1,1, a 1,2, ... a 2,1, a2,2 ... etc.When three arguments are given, the last one is ignored for a list or vector, and in the case of a matrix, the second and third arguments specify the row and column of the selected element.
When two arguments are given, and the first is a vector or list, the second argument specifies an element in the list or vector. When a matrix and only one index i is specified as in
- Example
<apply> <selector/> <matrix> <matrixrow><cn>1</cn><cn>2</cn></matrixrow> <matrixrow><cn>3</cn><cn>4</cn></matrixrow> </matrix> <cn>1</cn> </apply>
it refers to the i-th matrixrow. Thus, the preceding example selects the following row:
- Example
<matrixrow> <cn> 1 </cn> <cn> 2 </cn> </matrixrow>
selectoris classified as an n-ary linear algebra operator even though it can take only one, two, or three arguments. - Classification
- function
- Signature
-
(matrix,scalar,scalar)->scalar
(matrix,scalar)->matrixrow
(matrix)->scalar*
((vector|list|matrixrow),scalar )->scalar
(vector|list|matrixrow)->scalar*
- Property
-
For all vectors V, V = vector(selector(V))
- Property
-
For all matrix rows Mrow, Mrow = matrixrow(selector(Mrow))
- Example
<apply><selector/><ci type="matrix">M</ci><cn>3</cn><cn>2</cn></apply>
C.7
MMLdefinition: vectorproduct
- Description
-
The vector or cross product of two nonzero three-dimensional vectors v1 and v2 is defined by
v1 x v2 = n norm(v1) * norm(v2) sin(theta) where n is the unit normal vector perpendicular to both, adhering to the right hand rule. CRC Standard Mathematical Tables and Formulae, editor: Dan Zwillinger, CRC Press Inc., 1996, [2.4]
- Discussion
-
The
vectorproductis the operator element for deriving the vector product of two vectors.The
vectorproductelement is a binary vector operator. - Classification
- function
- Signature
-
(vector,vector)->vector
- Property
-
if v1 and v2 are parallel then their vector product is 0
- Example
<apply><vectorproduct/><ci>u</ci><ci>v</ci></apply>
- Example
-
where A and B are vectors, N is a unit vector orthogonal to A and B, a, b are the magnitudes of A, B and
 is the angle between A and B.
is the angle between A and B.
<apply> <eq/> <apply><vectorproduct/> <ci type="vector"> A </ci> <ci type="vector"> B </ci> </apply> <apply><times/> <ci> a </ci> <ci> b </ci> <apply><sin/> <ci> θ </ci> </apply> <ci type="vector"> N </ci> </apply> </apply>
C.8
MMLdefinition: scalarproduct
- Description
-
This symbol represents the scalar product function. It takes two vector arguments and returns a scalar value. The scalar product of two vectors a, b is defined as |a| * |b| * cos(\theta), where \theta is the angle between the two vectors and |.| is a euclidean size function. Note that the scalar product is often referred to as the dot product.
- Discussion
-
The
scalarproductis the operator element for deriving the scalar product of two vectors.The
scalarproductelement is a binary vector operator. - Classification
- function
- Signature
-
(vector,vector) -> scalar
- Property
-
if the scalar product of two vectors is 0 then they are orthogonal.
- Example
<apply><scalarproduct/><ci>u</ci><ci>v</ci></apply>
- Example
-
where A and B are vectors, a, b are the magnitudes of A, B and
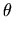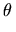 is the angle between A and B.
is the angle between A and B.
<apply> <eq/> <apply><scalarproduct/> <ci type="vector"> A </ci> <ci type="vector">B </ci> </apply> <apply><times/> <ci> a </ci> <ci> b </ci> <apply><cos/> <ci> θ </ci> </apply> </apply> </apply>
C.9
MMLdefinition: outerproduct
- Description
-
This symbol represents the outer product function. It takes two vector arguments and returns a matrix. It is defined as follows: if we write the {i,j}'th element of the matrix to be returned as m_{i,j}, then: m_{i,j}=a_i * b_j where a_i,b_j are the i'th and j'th elements of a, b respectively.
- Discussion
-
The
outerproductis the operator element for deriving the outer product of two vectors.The
outerproductelement is a binary vector operator. - Classification
- function
- Signature
-
(vector,vector) -> matrix
- Example
<apply><outerproduct/><ci>u</ci><ci>v</ci></apply>
- Example
-
where A and B are vectors.
<apply> <outerproduct/> <ci type="vector">A</ci> <ci type="vector">B</ci> </apply>
3.12 Content Dictionary: Constants and Symbol Elements
C.1
MMLdefinition: integers
- Description
-
integers represents the set of all integers.
- Classification
- constant
- Signature
-
set
- Property
-
n is an integer implies n+1 is an integer.
<apply><implies/> <apply><in/><ci>n</ci><integers/></apply> <apply><in/><apply><plus/><ci>n</ci><cn>1</cn></apply><integers/></apply> </apply> - Property
-
0 is an integer
<apply><in/><cn>0</cn><integers/></apply> - Property
-
n is an integer implies -n is an integer
<apply><implies/> <apply><in/><ci>n</ci><integers/></apply> <apply><in/><apply><minus/><ci>n</ci></apply><integers/></apply> </apply> - Example
<apply><in/> <cn type="integer"> 42 </cn> <integers/> </apply>
C.2
MMLdefinition: reals
- Description
-
reals represents the set of all real numbers.
- Discussion
-
realsrepresents the set of all real numbers. - Classification
- symbol
- Signature
-
set
- Property
-
(S \subset R and exists y in R : forall x in S x \le y) implies exists z in R such that ( ( forall x in S x \le z) and ( (forall x in S x \le w) implies z le w))
- Property
-
for all a,b | a,b rational with a<b implies there exists rational a,c s.t. a<c and c<b
- Example
<apply><in/> <cn type="real"> 44.997 </cn> <reals/> </apply>
C.3
MMLdefinition: rationals
- Description
-
rationals represents the set of all rational numbers.
- Discussion
-
rationalsrepresents the set of all rational numbers. - Classification
- constant
- Signature
-
set
- Property
-
for all z where z is a rational, there exists integers p and q with p/q = z
<apply><forall/> <bvar><ci>z</ci></bvar> <condition><apply><in/><ci>z</ci><rationals/></apply></condition> <apply><exists/> <bvar><ci>p</ci></bvar> <bvar><ci>q</ci></bvar> <apply><and/> <apply><in/><ci>p</ci><integers/></apply> <apply><in/><ci>q</ci><integers/></apply> <apply><eq/> <apply><divide/><ci>p</ci><ci>q</ci></apply><integers/></apply> <ci>z</ci> </apply> </apply> </apply> - Property
-
ForAll( [a,b], a and b are rational, a < b implies there exists c such that a < c and c < b )
- Example
<apply><in/> <cn type="rational"> 22 <sep/>7</cn> <rationals/> </apply>
C.4
MMLdefinition: naturalnumbers
- Description
-
naturalnumbers represents the set of all natural numbers, i.e.. non-negative integers.
- Discussion
-
naturalnumbersrepresents the set of all natural numbers, i.e. non-negative integers. - Classification
- constant
- Signature
-
set
- Property
-
For all n | n is a natural number implies n+1 is a natural number.
<apply><forall/> <bvar><ci>n</ci></bvar> <apply><implies/> <apply><in/><ci>n</ci><naturalnumbers/></apply> <apply><in/> <apply><plus/><ci>n</ci><cn>1</cn></apply> <naturalnumbers/> </apply> </apply> </apply> - Property
-
0 is a natural number.
<apply><in/><cn>0</cn><naturalnumbers/></apply> - Property
-
for all n | n in the natural numbers is equivalent to saying n=0 or n-1 is a natural number
- Example
<apply><in/> <cn type="integer">1729</cn> <naturalnumbers/> </apply>
C.5
MMLdefinition: complexes
- Description
-
complexes represents the set of all complex numbers, i.e., numbers which may have a real and an imaginary part.
- Discussion
-
complexesrepresents the set of all complex numbers, i.e. numbers which may have a real and an imaginary part. - Classification
- constant
- Signature
-
set
- Property
-
for all z | if z is complex then there exist reals x,y s.t. z = x + i * y
- Example
<apply><in/> <cn type="complex">17<sep/>29</cn> <complexes/> </apply>
C.6
MMLdefinition: primes
- Description
-
primes represents the set of all natural prime numbers, i.e., integers greater than 1 which have no positive integer factor other than themselves and 1.
- Discussion
-
primesrepresents the set of all natural prime numbers, i.e. integers greater than 1 which have no positive integer factor other than themselves and 1. - Classification
- constant
- Signature
-
set
- Property
-
ForAll( [d,p], p is prime, Implies( d | p , d=1 or d=p ) )
<apply><forall/> <bvar><ci>d</ci></bvar> <bvar><ci>p</ci></bvar> <condition> <apply><and/> <apply><in/><ci>p</ci><primes/></apply> <apply><in/><ci>d</ci><naturalnumbers/></apply> </apply> </condition> <apply><implies/> <apply><factorof/><ci>d</ci><ci>p</ci></apply> <apply><or/> <apply><eq/><ci>d</ci><cn>1</cn></apply> <apply><eq/><ci>d</ci><ci>p</ci></apply> </apply> </apply> </apply> - Example
<apply> <in/> <cn type="integer">17</cn> <primes/> </apply>
C.7
MMLdefinition: exponentiale
- Description
-
exponentiale represents the mathematical constant which is the exponential base of the natural logarithms, commonly written e . It is approximately 2.718281828..
- Discussion
-
exponentialerepresents the mathematical constant which is the exponential base of the natural logarithms, commonly written e. It is approximately 2.718281828.. - Classification
- constant
- Signature
-
real constant
- Property
-
ln(e) = 1
<apply><eq/> <apply><ln/><exponentiale/></apply> <cn>1</cn> </apply> - Property
-
e is approximately 2.718281828
<apply><approx/> <exponentiale/> <cn>2.718281828 </cn> </apply> - Property
-
e = the sum as j ranges from 0 to infinity of 1/(j!)
- Example
<apply> <eq/> <apply><ln/><exponentiale/></apply> <cn>1</cn> </apply>
C.8
MMLdefinition: imaginaryi
- Description
-
imaginaryi represents the mathematical constant which is the square root of -1, commonly written i
- Discussion
-
imaginaryirepresents the mathematical constant which is the square root of -1, commonly written i. - Classification
- constant
- Signature
-
complex
- Property
-
sqrt(-1) = i
<apply><eq/> <imaginaryi/> <apply><root/><degree><cn>2</cn></degree><cn>-1</cn></apply> </apply> - Example
<apply> <eq/> <apply><power/> <imaginaryi/> <cn>2</cn> </apply> <cn>-1</cn> </apply>
C.9
MMLdefinition: notanumber
- Description
-
notanumber represents the result of an ill-defined floating point operation, sometimes also called NaN.
- Discussion
-
notanumberrepresents the result of an ill-defined floating point operation, sometimes also called NaN. - Classification
- constant
- Signature
-
undefined
- Example
<apply><eq/> <apply><divide/><cn>0</cn><cn>0</cn></apply> <notanumber/> </apply>
C.10
MMLdefinition: true
- Description
-
true represents the logical constant for truth.
- Discussion
-
truerepresents the logical constant for truth. - Classification
- constant
- Signature
-
boolean
- Property
-
not true = false
<apply><eq/> <apply><not/><true/></apply> <false/> </apply> - Property
-
For all boolean p, p or true is true
<declare type="boolean"><ci>p</ci></declare> <apply><forall/> <bvar><ci>p</ci></bvar> <apply><eq/> <apply><or/><ci>p</ci><true/></apply> <true/> </apply> </apply> - Example
<apply> <eq/> <apply><or/> <true/> <ci type = "boolean">P</ci> </apply> <true/> </apply>
C.11
MMLdefinition: false
- Description
-
false represents the logical constant for falsehood.
- Discussion
-
falserepresents the logical constant for falsehood. - Classification
- constant
- Signature
-
boolean
- Property
-
not true = false
<apply><eq/> <apply><not/><true/></apply> <false/> </apply> - Property
-
p and false = false
<declare type="boolean"><ci>p</ci></declare> <apply><forall/> <bvar><ci>p</ci></bvar> <apply><and/><ci>p</ci><false/></apply> <false/> </apply> - Example
<apply><eq/> <apply><and/> <false/> <ci type = "boolean">P</ci> </apply> <false/> </apply>
C.12
MMLdefinition: emptyset
- Description
-
emptyset represents the empty set.
- Discussion
-
emptysetrepresents the empty set. - Classification
- constant
- Signature
-
set
- Property
-
for all sets S, intersect(S,emptyset) = emptyset
<apply><forall/><bvar><ci type="set">S</ci></bvar> <apply><eq/> <apply><intersect/><emptyset/><ci>S</ci></apply> <emptyset/> </apply> </apply> - Example
<apply><neq/> <integers/> <emptyset/> </apply>
C.13
MMLdefinition: pi
- Description
-
pi represents the mathematical constant which is the ratio of a circle's circumference to its diameter, approximately 3.141592653.
- Discussion
-
pirepresents the mathematical constant which is the ratio of a circle's circumference to its diameter, approximately 3.141592653. - Classification
- constant
- Signature
-
real
- Property
<apply><approx/> <cn>pi</cn> <cn> 3.141592654 </cn> </apply>
- Property
-
pi = 4 * the sum as j ranges from 0 to infinity of ((1/(4j+1))-(1/(4j+3)))
- Example
<apply><approx/> <pi/> <cn type = "rational">22<sep/>7</cn> </apply>
C.14
MMLdefinition: eulergamma
- Description
-
A symbol to convey the notion of the gamma constant as defined in Abramowitz and Stegun, Handbook of Mathematical Functions, section 6.1.3. It is the limit of 1 + 1/2 + 1/3 + ... + 1/m - ln m as m tends to infinity, this is approximately 0.5772 15664.
- Discussion
-
eulergammarepresents Euler's constant, approximately 0.5772156649 - Classification
- constant
- Signature
-
real
- Property
-
gamma is approx. 0.5772156649
<apply><approx/> <eulergamma/> <cn> .5772156649 </cn> </apply> - Property
-
gamma = limit_(m -> infinity)(sum_(j ranges from 1 to m)(1/j) - ln m)
- Example
<eulergamma/>
- Example
<apply><approx/> <eulergamma/> <cn>0.5772156649</cn> </apply>
C.15
MMLdefinition: infinity
- Description
-
Infinity. Interpretation depends on the context. The default value is the positive infinity used to extend the real number line. The "type" attribute can be use to indicate that this is a "complex" infinity.
- Discussion
-
infinityrepresents the concept of infinity. Proper interpretation depends on context. - Classification
- constant
- Signature
-
constant
- Property
-
infinity/infinity is not defined.
<apply><eq/> <apply><divide/><infinity/><infinity/></apply> <notanumber/> </apply> - Property
-
for all reals x, x \lt infinity
<apply><forall/> <bvar><ci>n</ci></bvar> <condition><apply><in/><ci>n</ci><reals/></apply></condition> <apply><lt/><ci>n</ci><infinity/></apply> </apply> - Example
<infinity/>
- Example
<apply><eq/> <apply><limit/> <bvar><ci>x</ci></bvar> <condition><apply><tendsto/><ci>x</ci><infinity/></apply></condition> <apply><divide/><cn>1</cn><ci>x</ci></apply> </apply> <cn>0</cn> </apply>
3.13 Content Dictionary: General MathML Errors
C.1
MMLdefinition: unhandled_symbol
- Description
-
This symbol represents the error which is raised when an application reads a symbol which is present in the mentioned content dictionary, but which it has not implemented.
When receiving such a symbol, the application should act as if it had received the MathML error object constructed from
unhandled_symboland the unhandled symbol as in the example below. - Classification
- Error Specifier
- Example
-
The application does not implement the Complex numbers:
<error> <csymbol cd="error" name="unhandled_symbol"/> <csymbol cd="setname1" name="C"/> </error>
C.2
MMLdefinition: unexpected_symbol
- Description
-
This symbol represents the error which is raised when an application reads a symbol which is not present in the mentioned content dictionary.
When receiving such a symbol, the application should act as if it had received the MathML error object constructed from unexpected_symbol and the unexpected symbol as in the example below.
- Classification
- Error Specifier
- Example
-
The application received a mistyped symbol
<error> <csymbol cd="error" name="unexpected_symbol"/> <csymbol cd="arith1" name="plurse"/> </error>
C.3
MMLdefinition: unsupported_CD
- Description
-
This symbol represents the error which is raised when an application reads a symbol where the mentioned content dictionary is not present.
When receiving such a symbol, the application should act as if it had received the MathML error object constructed from
unsupported_CDand the symbol from the unsupported Content Dictionary as in the example below. - Classification
- Error Specifier
- Example
-
The application does not know about the CD
specfun<error> <csymbol cd="error" name="unsupported_CD"/> <csymbol cd="specfun" name="BesselJ"/> </error>