Abstract
This is a specification of a model-theoretic semantics for RDF and RDFS, and
some basic results on entailment. This version does not cover reification or
special meanings associated with the use of RDF containers. This document was
written with the intention of providing a precise
semantic theory for RDF and RDFS, and to sharpen the notions of consequence
and inference. It reflects the current understanding of the RDF Core working
group at the time of writing. In some particulars this differs from the account
given in Resource Description
Framework (RDF) Model and Syntax Specification, and these exceptions are
noted.
This version of the specification has some substantial changes from earlier
versions, as well as correcting several errors. It is likely to be further revised
in later versions.
Status of this Document
This section describes the status of this document at the
time of its publication. Other documents may supersede this
document. The latest status of this document series is maintained
at the W3C.
This work is part of the W3C Semantic
Web Activity. It has been produced by the RDF Core Working Group which is
chartered to address a list of issues raised since
RDF 1.0 was issued. This document reflects the Working Group's recent deliberation
of some of these issues, but the Working Group has not yet decided whether or
how to integrate this document with the RDF 1.0 specification ultimately.
This document is a W3C Working Draft for review by W3C
members and other interested parties. It is a draft document and
may be updated, replaced, or obsoleted by other documents at any
time. It is inappropriate to use W3C Working Drafts as reference
material or to cite them as other than "work in progress". A list
of current public W3C Working Drafts can be found as part of the W3C Technical Reports and
Publications.
Please address feedback on this document to www-rdf-comments@w3.org, a
mailing list with public
archive). The editors and the Working Group plan to address
feedback in future revisons of this document.
Table of Contents
0. Introduction
0.1 Model-theoretic semantics
0.2 Graph Syntax
0.3 Definitions
1. Interpretations
1.1 Technical notes
1.2 Urirefs, resources and literals
1.3 Interpretations
1.4 Denotations of ground graphs
1.5 Unlabeled nodes as existential assertions
1.6 Comparison with formal logic
2. Simple Entailment
2.1 Skolemization
3. RDF interpretations
4. RDF-entailment and RDF closures
5. RDFS interpretations
6. RDFS-entailment and RDFS closures
6.1 A note on rdfs:Literal
Appendix A. Summary of model theory
Appendix B. Proofs of lemmas
Appendix C. Open Issues
Appendix D. Acknowledgements
References
Change Log
A model-theoretic semantics
for a language assumes that the language refers to a 'world', and describes
the minimal conditions that a world must satisfy in order to assign an appropriate
meaning for every expression in the language. A particular world is called an
interpretation, so that model theory might be better called 'interpretation
theory'. The idea is to provide an abstract, mathematical account of the properties
that any such interpretation must have, making as few assumptions as possible
about its actual nature or intrinsic structure. Model theory tries to be metaphysically
and ontologically neutral. It is typically couched in the language of set theory
simply because that is the normal language of mathematics - for example, this
semantics assumes that names denote things in a set IR called the 'universe'
- but the use of set-theoretic language here is not supposed to imply that the
things in the universe are set-theoretic in nature.
The chief utility of such a semantic theory is not to suggest any particular
processing model, or to provide any deep analysis of the nature of the things
being described by the language (in our case, the nature of resources), but
rather to provide a technical tool to analyze the semantic properties of proposed
operations on the language; in particular, to provide a way to determine when
they preserve meaning.
This document describes a model theory for RDF(S) which treats the language
as simple assertional language, in which each triple makes a distinct assertion
and the meaning of any triple is not changed by adding other triples. This imposes
a fairly strict monotonic discipline on the language, so that it cannot express
closed world assumptions, local default preferences, and several other commonly-used
non-monotonic constructs. There are several aspects of meaning in RDF which
are ignored by this semantics. It treats URIs as simple names, ignoring aspects
of meaning encoded in particular URI forms [RFC 2396].
It does not provide any analysis of time-varying data or of changes to URI denotations.
It gives only a rudimentary treatment of literals, ignoring datatyping. It ignores
RDF containers and reification. Some of these may
be covered by future extensions of the model theory.
Any semantic theory must be attached to a syntax. Of the several syntactic
forms for RDF, we have chosen the RDF graph as introduced in [RDFMS]
as the primary syntax, largely for its simplicity. We understand linear RDF
notations such as N-Triples and rdf/xml
[RDF/XML] as lexical notations for specifying RDF graphs.
(There are well-formed graphs that cannot be described by these notations, however.)
Two RDF documents, in whatever lexical form, are syntactically equivalent if
and only if they map to the same RDF graph. The model theory assigns interpretations
directly to the graph; we will refer to this as the 'graph syntax' to avoid
ambiguity, since the bare term 'syntax' is often assumed to refer to a lexicalization.
An RDF graph can be defined in terms of labeled nodes and arcs, but we will
use an equivalent but more convenient definition, in which a graph is defined
to be a set of triples. This makes it easier to state many of the technical
results.
To describe RDF graphs it is first necessary to define the things
that can act as nodes and arcs of the graph. There are three kinds of node in
any RDF graph: urirefs, literal nodes, and blank nodes. A uriref is defined
to be a URI reference in the sense of [RFC 2396].We
do not distinguish between urirefs and uriref nodes because urirefs are considered
to be nodes in themselves. A literal node is a particular occurrence
of a literal; and blank (or unlabeled) nodes are considered to be drawn from
some set of 'anonymous' entities which have no 'label' and are unique to the
graph. Finally, every arc in an RDF graph is labelled with a uriref. The same
uriref may label several arcs and also be a node in the graph. An RDF graph
can then be defined as a set of triples of the form <S, P, O>, where P
is a uriref, S is either a uriref or a blank node, and O is either a uriref,
a blank node, or a literal. Note that a given uriref may occur in more than
one graph, but blank nodes and literal nodes are unique to each graph. This
reflects the fact that urirefs are considered to have a 'global' meaning
but blank nodes and literals do not: blank nodes because they are local to the
graph, and literals because each occurrence of a literal is considered to be
unique. (This may be altered in future; at present
it is the most conservative assumption for the model theory to make, since some
datatyping schemes may assign different interpretations to several occurrences
of the same literal.)
It is convenient to adopt a familiar abuse of terminology and identify
a single triple with the graph consisting of the singleton set containing that
triple.
The convention that relates such a set of triples to a picture
of an RDF graph can then be stated as follows. Draw one oval for each blank
node and uriref, and one rectangle for each literal node, which occur in either
the S or O position in any triple in the set, and write each uriref or literal
as the label of its shape. (Notice that several occurrences of a literal produce
several rectangles with the same label, but several occurrences of a uriref
only produce one oval.) Then for each triple <S,P,O>, draw an arrowed
line from the shape produced from S to the shape produced from O, and label
it with P.
To indicate blank nodes in the triples of a graph we will use the nodeID convention
used in the N-triples syntax described
in [RDFTestCases]. However, we will often use letters
or short letter sequences to stand in place of urirefs, in the interests of
brevity. Note that while these node identifiers
(formerly called bNodes) identify blank nodes in the surface syntax, these expressions
are not considered to be the label of the graph node they identify.
In particular, two N-triples
documents which differ only by re-naming their node identifiers will be
understood to describe identical RDF graphs. Node
identifiers of blank nodes play a role in an ntripleDoc
analogous to that played by bound variables in a logical expression. They are
local to the document and serve only to indicate a 'connection' between other
expressions.
Other RDF serializations may use other means of indicating the graph structure;
for our purposes, the important syntactic property of RDF graphs is that each
distinct item in an RDF graph is treated as a distinct referring entity in the
graph syntax.
Several definitions will be important in what follows.
A subgraph of an RDF graph
is simply a subset of the triples in the graph. Notice that each triple
in a graph is considered to be a subgraph.
The result of taking the set-union
of two or more RDF graphs (i.e. sets of triples) is another graph, which we
will call the merge of the graphs. Each of the original graphs is
a subgraph of the merged graph. Notice that when forming a merged graph, two
occurrences of a given uriref as nodes in two different graphs become a single
node in the union graph (since by definition they are the same uriref), but
blank nodes and literal nodes are not 'merged' in this way; and arcs are of
course never merged.In particular, this means that every blank node in a merged
graph can be identified as coming from one particular graph in the original
set of graphs.
Notice that one does not, in general, obtain the merge of a set
of graphs by concatenating their corresponding N-triples documents and
constructing the graph described by the merged document, since if some of the
documents use the same node identifiers, the merged document will describe a
graph in which some of the blank nodes have been 'accidentally' merged. To merge
Ntriples documents it is necessary to check if the same nodeID is used in two
or more documents, and to replace it with a distinct nodeID in each of them,
before merging the documents.
An RDF graph will be said to be ground
if it has no blank nodes. If it has no literals then
it will be said to be plain. A plain ground graph contains only triples
of urirefs.
We will refer to a set of urirefs
as a vocabulary. The vocabulary of a graph is the set of urirefs that
it contains.
(We do not include literals in the vocabulary because they are
treated differently in the model theory. Urirefs are treated as names whose
value is specified by an interpretation, while the value of a literal is determined
by something external to the interpretation, such as a datatyping scheme.)
An instance of an RDF graph
is, intuitively, a similar graph in which some blank nodes may have been replaced
by urirefs. However, it is technically convenient to allow blank nodes to
be 'replaced' by other blank nodes, so we need to state this rather more precisely.
Say that one triple is an instance of another if it can be obtained by substituting
zero or more urirefs or blank nodes for blank nodes in the original; and that
a graph is an instance of another just when every triple in the first graph
is an instance of a triple in the second graph, and every
triple in the second graph has an instance in the first graph. Note that
any graph is an instance of itself.
This allows blank nodes in the second graph to be replaced by
urirefs in the instance (notice that this might cause some nodes to be identified
that were previously distinct) but it also allows them to be replaced by other
blank nodes. In particular, this means that the two graphs:
aaa bbb _:xxx .
aaa bbb _:yyy .
and
aaa bbb _:zzz .
with, respectively, three nodes and two arcs, and two nodes and
one arc, are instances of each other. Similarly,
_:xxx bbb _:xxx .
is an instance of
_:xxx bbb _:yyy .
A proper instance
of a graph is an instance in which at least one blank node has been replaced
by a uriref.
An instance with respect
to a vocabulary V is an instance in which all the urirefs in the instance
which were substituted for blank nodes in the original are drawn from V.
Throughout this document, the fact that two sets are given different names
should not be taken to imply that they are disjoint. We will explicitly state
any disjointness or containment conditions as they arise. In the same spirit,
the fact that one set is stated to be a subset of another should not be interpreted
as saying that these sets cannot be identical, unless this is stated explicitly.
We assume that there is no restriction on the domains and ranges of properties;
in particular, a property may be applied to itself. When classes are introduced
in RDFS, we will assume that they can contain themselves. This might seem to
violate one of the axioms of standard (Zermelo-Fraenkel) set theory, the axiom
of foundation, which forbids infinitely descending chains of membership. However,
the semantic model given here distinguishes properties and classes as objects
from their extensions - the sets of object-value pairs which satisfy
the property, or things that are 'in' the class - thereby allowing the extension
of a property or class to contain the property or class itself without violating
the axiom of foundation. In particular, this use of a class extension mapping
allows classes to contain themselves. For example, it is quite OK for (the extension
of) a 'universal' class to contain the class itself as a member, a convention
that is often adopted at the top of a classification hierarchy. (If an extension
contained itself then the axiom would be violated, but that case never arises.)
The technique is described more fully in [Hayes&Menzel], which gives a semantics for an infinitary
extension of full first-order logic.
Notice that the question of whether or not a class contains itself as a member
is quite different from the question of whether or not it is a subclass of itself.
RDF uses two kinds of referring expression, urirefs and literals. We make very
simple and basic assumptions about these. Urirefs are treated as logical constants,
i.e. as names which denote resources; no assumptions are made about the nature
of resources. In this version of the model theory, literals are treated as simple
names which are mapped to values, and no particular assumptions are made about
the role of datatype specifications. This is not intended to be a definitive
treatment of literals, and will probably be replaced by a more thorough treatment
in later versions of the model theory.
An interpretation assigns meanings to symbols in a particular vocabulary of
urirefs. Some interpretations may assign special meanings to the symbols in
a particular namespace, which we will call a reserved vocabulary.We will
use two reserved vocabularies in this document, defined using the Qname syntax
with the prefixes rdf: and rdfs: as follows:
Prefix rdf: namespace URI: http://www.w3.org/1999/02/22-rdf-syntax-ns#
Prefix rdfs: namespace URI: http://www.w3.org/2000/01/rdf-schema#
Interpretations which share the special meaning of a particular reserved vocabulary
will be named for that vocabulary, so that we will speak of 'rdf-interpretations'
and 'rdfs-interpretations', etc.. An interpretation with no reserved vocabulary
will be called a simple interpretation, or simply an interpretation.
We do not take any position here on the way that node labels may be composed
from other expressions, e.g. from relative URIs or Qnames; the model theory
simply assumes that such lexical issues have been resolved in some way that
is globally coherent, so that a single uriref can be taken to have the same
meaning wherever it occurs.
Similarly, the model theory given here has no special provision for tracking
temporal changes; it assumes, implicitly, that urirefs have the same meaning
whenever they occur.
This version of the model theory tries to be as noncommittal
as possible about the meaning of literals. The theory makes no assumptions about
the exact nature of literals (other than that they can be distinguished from
urirefs) or of what kinds of entity they denote. In particular, it is agnostic
on the question of whether or not literal values are considered to be resources.
Here, we simply assume a global set LV of values denoted by
literals, and a fixed mapping XL from literal nodes
to LV, and require that all interpretations conform to XL on literal nodes.
This leaves open the question of the exact nature of literals, their language-sensitivity
and so on, while acknowledging their special status as expressions with a 'fixed'
interpretation. At the time of writing, various alternative
techniques for handling literal meanings and relating them to datyping schemes
are under discussion, which would use different methods for specifying the XL
mapping. The particular scheme chosen will be described in a later version of
this document.
The following definition of an interpretation is couched in mathematical
language, but what it amounts to intuitively is that an interpretation provides
just enough information about a possible way the world might be - a 'possible
world' - in order to fix the truth-value (true or false) of any ground RDF triple.
It does this by specifying for each uriref, what it is supposed to be a name
of; and also, if it should be used to indicate a property, what values that
property has for each thing in the universe. Together with our assumed fixed
interpretation of literals, this is just enough to fix the truth-value of any
ground triple, and hence any ground RDF graph.(We will
show how to determine the truthvalues of all graphs in the following section.)
Notice that if we left any of this information out, it would be possible for
some well-formed triple to be left without a determinate value; and also that
any other information - such as the exact nature of the things in the
universe - would, regardless of its intrinsic interest, be irrelevant to the
actual truth-values of any triple in the world being specified.
Asserting an RDF graph amounts to claiming that it is true, which
is another way of saying that the world it describes is, in fact, so arranged
as to be an interpretation which makes it true. In other words, asserting a
piece of RDF amounts to asserting a constraint on the possible
ways the world might be. Notice that there is no presumption here that any RDF
graph contains enough information to specify a single unique interpretation.
It is very difficult, and usually impossible, to assert enough in any language
to completely constrain the interpretations to a single possible world, so there
is no such thing as 'the' unique RDF interpretation. In general, increasing
the size of a graph decreases the set of interpretations that an assertion of
the graph allows to be true. The use of 'public' URIs in an RDF graph is often
taken to imply that an assertion of the graph implicitly assents to the truth
of other RDF graphs that define the meaning of that URI. To apply the model
theory to this kind of situation, one should think of the restriction on the
world represented by an assertion of the merge of the
asserted graph together with whatever RDF graphs are assumed to define the public
vocabulary, in order to fully convey the intended meaning of the 'public' assertion.
This only applies to uses of RDF that are intended to be the assertion
of propositional content. A fully adequate account of what it means to make
an assertion in a Web context is a research problem that is beyond the scope
of this document.
All interpretations will be relative to a set of urirefs, called the vocabulary
of the interpretation, so that one has to speak, strictly, of an interpretation
of an RDF vocabulary, rather than of RDF itself.
A simple interpretation I of a vocabulary V is defined by:
1. A non-empty set IR of resources, called the domain or
universe of I.
2. A mapping IEXT from IR into the powerset of IRx(IR union LV) (i.e. the set
of sets of pairs <x,y> with x in IR and y in IR or LV)
3. A mapping IS from V into IR
IEXT(x) is a set of pairs which identify the arguments for which the property
is true, i.e. a binary relational extension, called the
extension of
x. This trick of distinguishing a relation as an object from its relational
extension allows a property to occur in its own extension, as
noted earlier.
Note that no particular relationship is assumed between IR
and LV.
It is convenient to define IP to be the subset of IR with
a nonempty extension; intuitively, IP is the set of properties.
In the next sections we give the exact rules for how an interpretation
of a vocabulary determines the truth-values of any RDF graph, by a recursive
definition of the "denotation" - the semantic "value" -
of any RDF expression in terms of those of its immediate subexpressions. RDF
has two kinds of denotation: node labels denote things, and sets of triples
denote truthvalues.
The denotation of a ground RDF graph in I is given recursively by the following
rules, which extend the interpretation mapping I from labels to ground graphs.
These rules (and extensions of them given later) work by defining the denotation
of any piece of RDF syntax E in terms of the denotations of the immediate syntactic
constitutents of E, hence allowing the denotation of any piece of RDF to be
determined by a kind of syntactic recursion.
| if E is a literal node then I(E) = XL(E) |
| if E is a uriref then I(E) = IS(E) |
| if E is an asserted triple <s, p, o> then I(E) = true if <I(s),I(o)>
is in IEXT(I(p)), otherwise I(E)= false. |
| if E is a ground RDF graph then I(E) = false if I(E') = false
for some asserted triple E' in E, otherwise I(E) =true. |
The use of the phrase "asserted triple" in the third condition is a deliberate
weasel-worded artifact, intended to allow an RDF graph or document to contain
triples which are being used for some non-assertional purpose. Strictly speaking
this phrase is meaningless, since strict conformity to the RDF 1.0 specification
[RDFMS] assumes that all triples in a document are asserted;
but making the distinction allows RDF parsers and inference engines to conform
to the RDF syntax and to respect the RDF model theory without necessarily being
fully committed to it. However, RDF as presently defined provides no syntactic
means to distinguish asserted from nonasserted triples, the distinction can
be safely ignored in the remainder of the document, which assumes that all triples
in a graph are asserted.To apply the subsequent results to RDF containing unasserted
triples, it would be necessary to restrict the definitions to the sets of asserted
triples in the graphs, which in turn would require some means to distinguish
asserted from unasserted triples.
As an illustrative example, the following is a small interpretation
for the artificial vocabulary {a, b, c}, where the letters should
be understood to stand for urirefs.We use letters for brevity, and use integers
to indicate the 'things' in the universe. This is not meant to imply that RDF
interpretations should be interpreted as being about arithmetic, but more to
emphasize that the exact nature of the things in the universe is irrelevant.
IR= {1, 2}; IP = {1}
IEXT: 1->{<1,2>,<2,1>}
IS: a->1, b->1, c->2
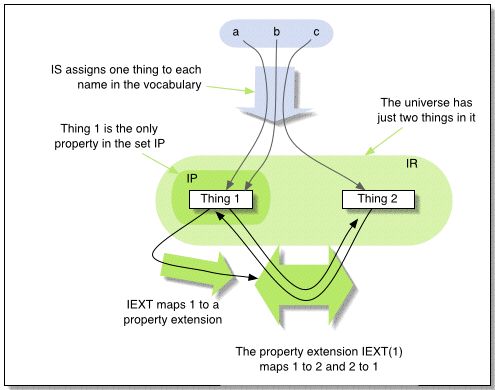
Figure 1: An example of an interpretation. Note, this is not
a picture of an RDF graph.
This interpretation makes these triples true:
a b c
c a a
c b a
(for example, I(<a b c>) = true if <I(a),I(c)>
is in IEXT(I(b)), i.e. if <1,2> is in IEXT(1), which is {<1,2>,<2,1>}
and so does contain <1,2> and so I(<a b c>) is true)
and these triples false:
a c b
a b b
c a c
(for example, I(<a c b>) = true if <I(a),I(b)>,
i.e.<1,2>, is in IEXT(I(c)); but I(c)=2 and
IEXT is not defined on 2, so the condition fails and I(<a c b>)
= false.)
The truth-value of any triple containing a literal would
depend on whether or not the literal denotes the items in the property extension,
which in turn would depend on the global XL mapping. In
practice this would be decided by some kind of datatyping scheme, which is beyond
the scope of the current version of the model theory.
To emphasize: this is only one possible interpretation of this vocabulary;
there are (infinitely) many others. For example, if we modified this interpretation
by attaching the property extension to 2 instead of 1, none
of the above six triples would be true.
Blank nodes are treated as simply indicating the existence
of a thing without saying anything about how that thing is or might be named.
(Note that this is not the same as assuming that the blank node indicates an
'unknown' uriref. This decision can be defended on both philosophical and pragmatic
grounds.See http://www.w3.org/2000/03/rdf-tracking/#rdfms-identity-anon-resources
for a summary and pointers to the extended discussions. The discussion of skolemization
in section 2.1 is also relevant.)
We now show how an interpretation can specify the truth-value of a graph containing
blank nodes. This will require some definitions, as the theory so far provides
no meaning for unlabeled nodes. Suppose I is an interpretation and A is a mapping
from some set of unlabeled nodes to the universe IR
of I, and define I+A to be an extended interpretation which is like I except
that it uses A to give the interpretation of unlabeled nodes. Define anon(E)
to be the set of unlabeled nodes in E. Then we can extend the above rules to
include the two new cases that are introduced when unlabeled nodes occur in
the graph:
| If E is an unlabeled node then [I+A](E) = A(E) |
| If E is an RDF graph then I(E) = true if [I+A'](E) = true for some
mapping A' from anon(E) to IR, otherwise I(E)= false. |
Notice that we have not changed the definition of an interpretation;
it still consists of the same values IR, IEXT and IS. We have simply extended
the rules for defining denotations under an interpretation, so that the same
interpretation that provides a truth-value for ground graphs also assigns truth-values
to graphs with unlabeled nodes, even though it provides no denotation for the
unlabeled nodes themselves. Notice also that the unlabeled nodes themselves
are perfectly well-defined entities with a robust notion of identity; they differ
from other nodes only in not being assigned a denotation by an interpretation,
reflecting the intuition that they have no 'global' meaning (i.e. outside the
graph in which they occur).
This effectively treats all unlabeled nodes as having the same meaning as existentially
quantified variables in the RDF graph in which they occur. Notice however that
that since two unlabeled nodes cannot have the same label, there is no need
to specify the scope of the quantifier within a graph, and no need to use any
explicit quantifier syntax.( If we were to apply the semantics directly to N-triples
syntax, we would need to indicate the quantifier scope, since in this lexicalization
syntax the same node identifier may occur several times corresponding to a single
blank node in the graph. The above rule amounts to the convention that would
place the quantifiers just outside, or at the outer edge of, the N-triple document
corresponding to the graph.)
For example, with this convention, the graph defined by the following triples
is false in the interpretation shown in figure 1:
_:x a b
c b _:x
since if A' maps the unlabeled node to 1 then the first triple is false in
[I+A'], and if it maps it to 2 then the second triple is false.(Note that each
of these triples, when taken as a single graph, is true in I, but their conjunction
is not; and that if a different node ID were used in the two triples, indicating
that the RDF graph had two blank nodes instead of one, then A' could map one
node to 2 and the other to 1, and the resulting graph would be true under the
interpretation I.)
Notice that if the vocabulary of an RDF graph E contains urirefs that are
not in the vocabulary of an interpretation I - that is, if I simply does not
give a semantic value to some name that is used in E - then the RDF truth-conditions
will always yield the value 'false' for some triple in E.
With this semantics, it is simple to translate a
plain
RDF graph into a logical expression with essentially the same meaning, as several
authors have noted previously [Marchiori&Saarela],
[Fikes&McGuinness].
Each node labeled with a uriref translates to a logical constant which is its
label and each unlabeled node to a distinct variable. An arc labeled with p
from a node n1 to a node n2 maps to an atomic assertion that the relation p
holds true between the expressions s and o gotten by translating n1 and n2 respectively
(written as (p s o) in KIF syntax); and finally, an RDF
graph translates to the existential closure of the conjunction of the translations
of all the arcs in the graph.This requires us to introduce bound variables to
correspond to the blank nodes of the graph, similarly to the use of node identifiers
in the N-Triples syntax.
For example, the graph defined in the above example translates to the logical
expression (written in the extended KIF syntax defined in [Hayes&Menzel])
(exists (?y)(and (a ?y b)(b c ?y)))
This translation maps the model theory exactly. Notice however that the resulting
expression may contain the same symbol in both relation and object positions
(e.g. 'b' in this example), which is considered syntactically illegal
in many versions of logic.To map to a more conventional logical syntax one can
use a 'dummy' ternary relation symbol to assert that a binary relation holds
between two arguments. For example,[Fikes&McGuinness]
translate the RDF triple
s p o
into the KIF expression
(PropertyValue p s o)
The above example would then map to
(exists (?y)(and (PropertyValue a ?y b)(PropertyValue b c ?y)))
Under this translation, to obtain the appropriate KIF interpretation one has
to interpret (PropertyValue a b c) to mean ((IEXT a) b c).
A translation of an RDF graph containing literals would also need
to somehow ensure that literals are interpreted appropriately in the logical
semantics. This may require some external semantic constraint to be imposed
on the normal logical meaning.
Following conventional terminology,
we say that I satisfies E if I(E)=true, and that a set S of expressions
(simply) entails E if every interpretation which satisfies every member
of S also satisfies E.If
the singleton set {E} entails E' then we will simply say that E entails E'.
In later sections these notions will be adapted to classes of interpretations
with particular reserved vocabularies, but throughout this section entailment
should be interpreted as simple RDF entailment.
Entailment is the key idea which connects model-theoretic semantics
to real-world applications. As noted earlier, making an assertion amounts to
claiming that the world is an interpretation which assigns the value true to
the assertion. If A entails B, then any interpretation that makes A true also
makes B true, so that an assertion of A already contains the same "meaning"
as an assertion of B; we could say that the meaning of B is somehow contained
in, or subsumed by, that of A. If A and B entail each other, then they both
"mean" the same thing, in the sense that asserting either of them
makes the same claim about the world. The interest of this observation arises
most vividly when A and B are different expressions, since then the relation
of entailment is exactly the appropriate semantic licence to justify an application
inferring or generating one of them from the other. Through the notions of satisfaction,
entailment and validity, formal semantics gives a rigorous definition to a notion
of "meaning" that can be related directly to computable methods of
determining whether or not meaning is preserved by some transformation on a
representation of knowledge.
Any process or technique which constructs a graph E from
some other graphs S is said to be (simply) valid if S entails E, otherwise
invalid. Note that being an invalid process does not mean that
the conclusion is false, and being valid does not guarantee truth. However,
validity represents the best guarantee that any assertional language can offer:
if given true inputs, it will never draw a false conclusion from them.
In this section we give a few basic results about simple entailment and valid
inference. Simple entailment can be recognized by relatively simple syntactic
comparisons. The two basic forms of simply valid proof step in RDF are, in logical
terms, the inference from (P and Q) to P, and the inference from (foo baz) to
(exists (?x) (foo ?x)) .
Several
of the lemmas are restricted to plain graphs, ie those
without literals. This no-literals restriction arises from a technicality.
Since we make no assumptions about the
XL mapping, we cannot guarantee that different
literals have different meanings. Since all interpretations must conform to
the same global mapping on literals, it is possible that a
ground triple containing a literal might entail
a different ground triple, which would make the 'only if'cases of several of
these lemmas false. If this case can be ruled out - for example, if XL were
known to be one-to-one - then the results would apply to all graphs.
Note, these results apply only to simple entailment, not to the more subtle
notions of entailment introduced in later sections. Proofs, all of which are
straightforward, are given in appendix B.
Subgraph Lemma. A graph entails
all its subgraphs .
Instance Lemma.A graph is
entailed by all its instances.
If an instance of a graph E' is a subgraph of another graph E then
it follows from the subgraph and instance lemmas that E entails E'. As we show
below, this is in fact a necessary as well as sufficient condition for entailment,
so it is useful to give a name to the syntactic condition that captures non-entailment.
Say that a graph E' is separable from a graph E if
no instance of E' is a subgraph of E. In particular, a ground graph is separable
from E just when it is not a subgraph of E, and a ground triple is separable
just in case it isn't in the graph. Graphs which are not separable from E are
entailed by E; but for all others, there is a way to arrange the world so that
they are false and E true.
For ground graphs, the subgraph lemma can be strengthened
to provide simple necessary and sufficient conditions for entailment.
Conjunction Lemma.If E is ground,
then I satisfies E if and only if it satisfies every
triple in E.
I.e. a ground graph is equivalent in meaning to the logical conjunction of
its component triples.
The following is an immediate consequence.
Plain Subgraph Lemma. If
E and E' are ground and E' is plain, then E entails
E' if and only if E' is a subgraph of E.
If I satisfies E, then I may contain arbitrarily much more information than
is necessary to specify the truth of E; an interpretation - a world - can be
larger than strictly needed to establish the truthvalues of a particular set
of triples. It is therefore useful to define a notion of the minimal part of
an interpretation which is just enough to make a given graph true.
Say that I' is a subinterpretation of I when vocab(I') is a subset
of vocab(I), IR'is a subset of IR, I'(x)=I(x) wherever I'(x) is defined, and
IEXT'(x) is a subset of IEXT(x) wherever IEXT'(x) is defined. Intuitively, I'
defines a 'part' of the world defined by I. If I' is a subinterpretation of
I and I' satisfies E, then I must also satisfy E.
Now define I to be a minimal
interpretation of E if I satisfies E, but no other subinterpretation of I satisfies
E. It is clear that if I satisfies E, then a minimal satisfying interpretation
exists with a vocabulary precisely the vocabulary of E. The minimal interpretations
can be characterized by the following lemma.
Minimality lemma. If I is a minimal satisfying
interpretation of E, then I fails to satisfy every plain triple which has no
instance in E.
The next lemma is proven by a simple version of the technique used to prove
Herbrand's theorem in first-order logic, hence the name:
Herbrand Lemma.
Any RDF graph has a satisfying interpretation.
This means that there is no such thing as an inconsistency or a contradiction
in RDF, which is not surprising since the language does not contain negation.
The previous lemmas have the following conclusion, which can be
used to show necessary conditions for entailment.
Strong Herbrand Lemma.
Any RDF graph E has a satisfying interpretation that does not satisfy any graph
which is separable from E.
In particular, the interpretation assigns the value 'false' to all ground triples
that are not in E. This emphasizes the extent to which ground RDF triples are
independent of each other; contrast this situation with a logic in which implications
can be expressed. We will show later that the strong Herbrand lemma fails in
almost any extension to 'basic' RDF.
The relationship between merging and entailment is simple, and obvious from
the definitions:
Merging lemma. The merge
of a set S of RDF graphs is entailed by S, and entails every member of S.
This means that a set of graphs can be treated as equivalent to a single graph
as far as the model theory is concerned.
Notice that unlabeled nodes are not identified with other nodes in a merge,
and indeed this reflects a basic principle of RDF graph inference: in contrast
to urirefs, which have a global identity which carries across all graphs, blank
nodes should not be identified with other nodes or re-labeled with urirefs,
in order to ensure that the resulting graph is entailed by what one starts with.
To state this condition precisely, we need to first exclude
a counterexample. It is possible for a graph to contain two triples one of which
is an instance of the other, for example:
aaa bbb _:x .
aaa bbb ccc .
Such an internally redundant graph is equivalent to one of its
own instances, since replacing the blank node by ccc would result
in a single-triple graph which is a subgraph of the original. To rule out such
cases of internal redundancy, we will say that an RDF graph
is lean if none of its triples is a proper instance of any other.
Then the above principle is made precise in the following two lemmas:
Anonymity lemma 1.
Suppose E is a lean graph and E' is a proper instance of E. Then E does
not entail E'.
Anonymity lemma 2.
Suppose that E is a lean graph and that E' is like E except that two distinct
unlabeled nodes in E have been identified in E'. Then E does not entail E'.
This means that there is no valid RDF inference process which can produce an
RDF graph in which a single unlabeled node occurs in triples originating from
several different graphs. (Of course, such a graph can be constructed, but it
will not be entailed by the original documents. It must reflect the addition
of new information about the identity of two unlabeled nodes.)
Putting several of these results together, the main result for simple RDF inference
is:
Interpolation Lemma.
S entails a plain graph E if and only if a subgraph of the merge of S is an
instance of E.
The interpolation lemma completely characterizes simple RDF entailment in syntactic
terms. To tell whether a set of RDF graphs entails another, find a subgraph
of their merge and replace urirefs by unlabeled nodes to get the second. Of
course, there is no need to actually construct the merge. If working backwards
from the consequent E (the graph that may be entailed by the others), the most
efficient technique would be to treat unlabeled nodes as variables in a process
of subgraph-matching, allowing them to bind to 'matching' uriref labels in the
antecedent graph(s) in S, i.e. those which may entail the consequent graph.
The interpolation lemma shows that this process is valid, and is also complete
if the subgraph-matching algorithm is. The existence of complete subgraph-checking
algorithms also shows that RDF is decidable, i.e. there is a terminating algorithm
which will determine for any finite set S and any graph E, whether or not S
entails E.
Notice however that such a variable-binding process would only
be appropriate when applied to the conclusion of a
proposed entailment. This corresponds to using the document as a
goal or a query, in contrast to asserting it, i.e. claiming it to
be true. If an RDF document is asserted, then it would be invalid
to bind new values to any of its unlabeled nodes, since (by the
anonymity lemmas) the resulting graph would not be entailed by the
assertion.
It might be thought that the operation of changing a bound
variable would be an example of an inference which was valid but
not covered by the interpolation lemma, e.g. the inference of
_:x foo baz
from
_:y foo baz
Recall however that by our conventions, these two
expressions describe identical RDF graphs.
Skolemization is a syntactic transformation routinely used in automatic inference
systems in which existential variables are replaced by 'new' functions applied
to universal variables. While not itself strictly a valid operation, skolemization
adds no new content to an expression, in the sense that a skolemized expression
has the same entailments as the original expression provided they do not contain
the new skolem functions.
In RDF, skolemization simplifies to the special case where an existential variable
is replaced by a 'new' constant name, i.e. a uriref which is guaranteed to not
occur anywhere else.To be precise, a skolemization
of E (with respect to V) is a ground instance of E with respect to a vocabulary
V which is disjoint from the vocabulary of E.
The following lemma shows that skolemization has the same properties in RDF
as it has in conventional logics.
Skolemization Lemma. Suppose
sk(E) is a skolemization of E with respect to V. Then sk(E) entails E; and if
sk(E) entails F and the vocabulary of F is disjoint from V, then E entails F
.
Intuitively, this lemma shows that asserting a skolemization expresses
a similar content to asserting the original graph, in many respects. In effect,
it simply gives 'arbitrary' names to the anonymous entities whose existence
was asserted by the use of blank nodes. However, care is needed, since these
'arbitrary' names have the same status as any other urirefs once published.
Also, skolemization would not be an appropriate operation when applied to anything
other than the antecendent of an entailment. A skolemization of a query would
represent a completely different query.
We now consider interpretations which impose some extra semantic constraints
on the following (rather small) reserved vocabulary, which we will call rdfV:
| RDF reserved vocabulary |
rdf:type rdf:Property |
(As noted earlier, this version of the model theory assigns no special meaning
to the part of the RDF vocabulary concerned with reification, or the RDF container
vocabulary.)
An rdf-interpretation of a vocabulary V is
an interpretation I on (V union rdfV) which satisfies the following extra conditions:
IP contains I(rdf:type) |
if x is in IP then IEXT(I(rdf:type))
contains <x, I(rdf:Property)> |
This forces every rdf interpretation to contain a thing which can be interpreted
as the 'type' of properties. (The second condition could be regarded as defining
IP to be the set of resources in the universe of the interpretation which have
the value I(rdf:Property) of the property I(rdf:type).
This way of construing subsets of the universe will be central in interpretations
of RDFS.)
For example, the following rdf-interpretation extends the simple interpretation
in figure 1:
IR = {1, 2, T }; IP = {1, T}
IEXT: 1->{<1,2>,<2,1>}, T->{<1,P>,<T,P>}
IS: a->1, b->1, c->2, rdf:type->T, rdf:Property->P
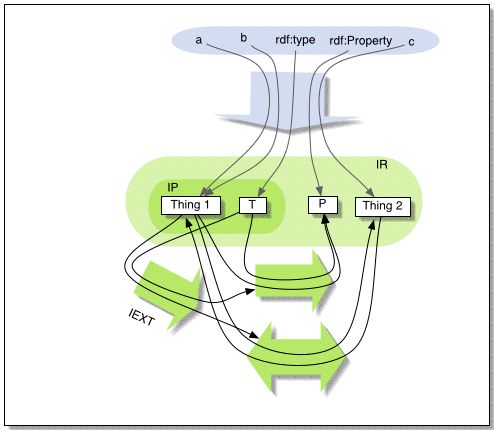
Figure 2: An example of an rdf-interpretation.
This is not the smallest rdf-interpretation which extends the earlier example,
since we could have made I(rdf:Property) be 2 and IEXT(T) be {<1,2>,<T,2>},
and managed without having P in the universe. In general, a given entity in
an interpretation may play several 'roles' at the same time, as long as this
can be done without violating any of the required semantic conditions.
It is important to note that every rdf-interpretation is also a
simple interpretation.
We will say that S rdf-entails E when every rdf-interpretation which
satisfies every member of S also satisfies E. This follows
the wording of the definition of simple entailment
in section 2, but refers only to rdf-interpretations instead of all simple interpretations.
This is an example of vocabulary
entailment , i.e. entailment relative to a set of interpretations which
satisfy extra semantic conditions on a reserved vocabulary.
Vocabulary entailment is more powerful than simple entailment, in the sense
that a given set of premises entails more consequences. In general, as the reserved
vocabulary is increased and extra semantic conditions imposed, the class of
satisfying interpretations is restricted, and hence the corresponding notion
of entailment becomes more powerful. For example, if S simply entails E then
it also rdf-entails E, since every rdf-interpretation is also a simple interpretation;
but S may rdf-entail E even though it does not simply entail it. Intuitively,
a conclusion may follow from some of the extra assumptions incorporated in the
semantic conditions imposed on the reserved vocabulary.
Another way of expressing this is that any restriction on interpretations decreases
the number of possible ways that an interpretation might be a counterexample
to E's following from S.
Simple entailment is therefore the weakest form of RDF entailment, which holds
for any reserved vocabulary; it could be characterized as entailment which depends
only on the basic triples syntax of RDF graphs, without making any further assumptions
about the meaning of any urirefs. Simple entailment is the vocabulary entailment
of the empty vocabulary.
It is easy to see that the lemmas in section 2 do not hold for rdf-entailment.
For example, the triple
rdf:type rdf:type rdf:Property .
is true in every rdf-interpretation, and hence rdf-entailed by the empty set,
which immediately contradicts the interpolation lemma for rdf-entailment.
Rather than develop a separate theory of the syntactic conditions for recognising
entailment for each reserved vocabulary, we will use a general technique for
reducing these broader notions of entailment to simple entailment, by defining
the closure of an RDF graph relative to a set of semantic conditions.
The basic idea is to rewrite the semantic conditions as a set of syntactic inference
rules, and define the closure to be the result of applying those rules to exhaustion.
The resulting graphs will contain RDF triples which explicitly state all the
special meanings embodied in the extra semantic conditions, in effect axiomatizing
them in RDF itself.
Therdf-closure of an RDF graph
E is the graph gotten by adding triples to E according to the following (very
simple) rules:
1. Add the following triple (which is true in any rdf-interpretation):
rdf:type rdf:type rdf:Property
2. Apply the following rule recursively to generate all legal RDF triples (i.e.
until none of the rules apply or the graph is unchanged.) Here xxx
and yyy stand for any uriref, bNode or literal expression,
aaa for any uriref.
|
if E contains |
then add |
| rdf1 |
xxx aaa yyy . |
aaa rdf:type rdf:Property . |
(This rule will generate the triple mentioned in 1 in two steps from any RDF
triple; nevertheless, we mention the triple explicitly since it is required
to be in the closure of even an empty set of graphs.)
The following lemma is the basic result on rdf-entailment, and illustrates
a general pattern of how to characterize vocabulary entailment syntactically.
RDF closure lemma.
Any satisfying rdf-interpretation of E satisfies the rdf-closure of E; and any
minimal simple satisfying interpretation of the rdf-closure of E is a satisfying
rdf-interpretation of E.
The relationship between simple entailment and rdf-entailment then
follows:
RDF
entailment lemma. S rdf-entails a E if and only if the rdf-closure
of the merge of S simply entails E.
Note, we do not mean to suggest that actually generating the full closure would
be the best process to use in order to determine namespace-entailment. In more
complex cases it may be more efficient to use a process of backchaining on the
closure rules, for example.
RDF Schema [RDFSchema] extends RDF to include a larger
reserved vocabulary rdfsV with more complex semantic constraints:
| RDFS reserved vocabulary |
rdf:type rdf:Property rdfs:domain rdfs:range rdfs:Resource rdfs:Literal
rdfs:Class rdfs:subClassOf rdfs:subPropertyOf |
(rdfs:seeAlso, rdfs:isDefinedBy, rdfs:comment
and rdfs:label are omitted, as the model theory places no constraints
on their meanings. The account given here of rdfs:domain
and rdfs:range reflect our current
understanding of multiple domain and range restrictions under which such
assertions are understood conjunctively, and they allow
cyclic assertions of
rdfs:subClassOf and
rdfs:subPropertyOf.)
Although not strictly necessary, it is convenient to state the RDFS semantics
in terms of a new semantic construct, a 'class', i.e. a resource which represents
a set of things in the universe which have the same value of the rdf:type
property. We will define a mapping ICEXT (for the Class Extension in I) from
classes to their extensions, in terms of the relational extension of rdf:type,
as follows:
ICEXT(x) = {y | <y,x> is in IEXT(I(rdf:type)) }
An rdfs-interpretation of V is a simple
interpretation of (V union rdfsV) which satisfies the following semantic conditions.
The first two of these are simply definitions of IC and ICEXT, which could be
used to eliminate these concepts from the rest of the conditions; as noted earlier,
the conditions on IR and IP could also be regarded as definitions.
|
x is in ICEXT(y) iff <x,y> is in IEXT(I(rdf:type))
IC = ICEXT(I(rdfs:Class))
|
|
ICEXT(I(rdfs:Resource)) = IR
IP is a subset of ICEXT(I(rdf:Property))
|
|
IC contains:
I(rdfs:Resource), I(rdf:Property), I(rdfs:Class),
I(rdfs:Literal)
|
|
IP contains:
I(rdf:type), I(rdfs:domain),
I(rdfs:range), I(rdfs:subPropertyOf), I(rdfs:subClassOf)
|
|
IEXT(I(rdfs:domain)) contains
<I(rdfs:domain), I(rdf:Property)>,
<I(rdfs:range), I(rdf:Property)>, <I(rdf:type),
I(rdfs:Resource)>
|
|
IEXT(I(rdfs:range)) contains
<I(rdfs:domain), I(rdfs:Class)>,
<I(rdfs:range), I(rdfs:Class)>,
<I(rdf:type), I(rdfs:Class)>
|
|
If <x,y> is in IEXT(I(rdfs:range)) and <u,v>
is in IEXT(x) then v is in ICEXT(y)
|
|
If <x,y> is in IEXT(I(rdfs:domain)) and <u,v>
is in IEXT(x) then u is in ICEXT(y)
|
|
If <x,y> is in IEXT(I(rdfs:subClassOf)) then ICEXT(x)
is a subset of ICEXT(y)
|
|
If <x,y> is in IEXT(I(rdfs:subPropertyOf)) then
IEXT(x) is a subset of IEXT(y)
|
The IEXT condition on rdf:Property in an rdf-interpretation
is equivalent to the ICEXT condition on rdf:Property above; so
these clearly imply all the conditions on an rdf-interpretation. It follows
that any rdfs-interpretation is also an rdf-interpretation of the same vocabulary.
We will not attempt to give a pictorial diagram of an rdfs-interpretation.
As before, we say that S rdfs-entails E when every rdfs-interpretation which
satisfies all of S also satisfies E. We will approach rdfs-entailment similarly
to rdf-entailment, by defining rdfs-closures. These require more complex
rules to reflect the consequences of the semantic constraints on the rdfs reserved
vocabulary. For example, the fact that the subset relationship is transitive
means that two subClassOf assertions may entail a third, different, triple.
The rdfs-closure of an RDF
graph E is the graph gotten by adding triples to E according to the following
rules:
1. Add the following triples, which are true in any rdfs-interpretation. These
assign classes, domains and ranges to the properties in the rdfs vocabulary.
(There are several other triples which are true in every rdfs-interpretation,
but they will be generated from these by other rules.)
rdfs:Resource rdf:type rdfs:Class
rdfs:Literal rdf:type rdfs:Class
rdfs:Class rdf:type rdfs:Class
rdf:Property rdf:type rdfs:Class
rdf:type rdf:type rdf:Property
rdf:type rdfs:domain rdfs:Resource
rdf:type rdfs:range rdfs:Class
rdfs:domain rdf:type rdf:Property
rdfs:domain rdfs:domain rdf:Property
rdfs:domain rdfs:range rdfs:Class
rdfs:range rdf:type rdf:Property
rdfs:range rdfs:domain rdf:Property
rdfs:range rdfs:range rdfs:Class
rdfs:subPropertyOf rdf:type rdf:Property
rdfs:subPropertyOf rdfs:domain rdf:Property
rdfs:subPropertyOf rdfs:range rdf:Property
rdfs:subClassOf rdf:type rdf:Property
rdfs:subClassOf rdfs:domain rdfs:Class
rdfs:subClassOf rdfs:range rdfs:Class
2. Apply the following rules recursively to generate all legal RDF triples
(i.e. until none of the rules apply or the graph is unchanged.) Here, xxx,
yyy and zzz stand for any uriref, bNode or
literal, aaa for any uriref, and uuu for any
uriref or bNode (but not a literal).
| |
If E contains: |
then add: |
| rdf1 |
xxx aaa yyy
|
aaa rdf:type rdf:Property |
| rdfs2 |
xxx aaa yyy
aaa rdfs:domain zzz
|
xxx rdf:type zzz |
| rdfs3 |
xxx aaa uuu
aaa rdfs:range zzz
|
uuu rdf:type zzz |
| rdfs4a |
xxx aaa yyy |
xxx rdf:type rdfs:Resource |
| rdfs4b |
xxx aaa uuu |
uuu rdf:type rdfs:Resource |
| rdfs5 |
aaa rdfs:subPropertyOf bbb
bbb rdfs:subPropertyOf ccc
|
aaa rdfs:subPropertyOf ccc |
| rdfs6 |
xxx aaa yyy
aaa rdfs:subPropertyOf bbb
|
xxx bbb yyy |
| rdfs7 |
xxx rdf:type rdfs:Class
|
xxx rdfs:subClassOf rdfs:Resource
|
| rdfs8 |
xxx rdfs:subClassOf yyy
yyy rdfs:subClassOf zzz
|
xxx rdfs:subClassOf zzz |
| rdfs9 |
xxx rdfs:subClassOf yyy
aaa rdf:type xxx
|
aaa rdf:type yyy |
Unlike the simpler rdf closure rules, the outputs of some of these rules may
trigger others. For example, these rules will generate the complete transitive
closures of all subclass and subproperty heirarchies, together with all of the
resulting type information about everything which can be inferred to be a member
of any of the classes, and will propagate all assertions in the graph up the
subproperty heirarchy, re-asserting them for all super-properties.They will
generate all assertions of the form
xxx rdf:type rdfs:Resource
for every xxx in V, and of the form
xxx rdfs:subClassOf rdfs:Resource
for every class name; and several more 'universal' facts, such as
rdf:Property rdf:type rdfs:Class
rdf:Property rdfs:subClassOf rdfs:Resource
However, it is easy to see that the rules will indeed terminate on any finite
RDF graph, since there are only finitely many triples that can be formed from
a given finite vocabulary.
A similar pair of results apply here as in the case of rdf-entailment, though
the first takes longer to prove. The restriction to minimal interpretations
is needed to
RDFS Closure Lemma. Any
satisfying rdfs-interpretation of E satisfies the rdfs-closure of E; and any
minimal simple satisfying interpretation of the rdfs-closure of E is a satisfying
rdfs-interpretation of E.
RDFS Entailment Lemma. S rdfs-entails
a graph E if and only if the rdfs-closure of the merge of S simply entails E.
The semantic conditions on rdfs-interpretations described
in section 5 do not include the condition that ICEXT(I(rdfs:Literal))
must be a subset of LV. While this would seem to be required
for conformance with [RDFMS], there is no way to impose
this condition by any RDF assertion or syntactic closure rule. This arises
from the fact that there are severe restrictions on what can be said about literals
in RDF, since RDF does not allow properties to be asserted of literals.The closure
rules for rdfs-entailment have explicit exceptions which reflect this syntactic
restriction. Similarly, while properties may be asserted of the the class
rdfs:Literal, none of these can be validly transferred to literals themselves.
The reader should be careful not to confuse literals with their denotations.
For example, a triple of the form
xxx rdf:type rdfs:Literal
is legal if xxx is a uriref (or blank node identifier), but should not be interpreted
as asserting that xxx is a literal. What it says is that the uriref xxx denotes
an element of LV, ie has the same meaning as some literal in any interpretation.
There is however no way in current RDF to specify exactly what literal such
a uriref might be equal to. Notice that there are no closure rules to generate
such triples.
|
RDF/RDFS model theory summary
|
|
0. Domains and mappings of interpretation I
|
|
vocab(I): set of urirefs ; LV: (global) set of literal values ; IR: set
of resources (universe); IP: subset of IR (properties) ; IC: subset of
IR (classes).
|
|
XL: literals -> LV
IS: vocab(I) -> IR
IEXT: IP -> subsets of (IR x (IR union LV))
ICEXT: IC -> subsets of IR
|
|
1. Basic equations
|
|
E is:
|
I(E) is:
|
|
a literal node
|
XL(E)
|
|
a (node labeled with a) uriref
|
IS(E)
|
|
an asserted triple <s p o>
|
true if <I(s), I(o)> is in IEXT(I(p)), otherwise false
|
|
any other triple
|
not defined
|
|
a ground RDF graph
|
false if I(E') =false for any asserted triple E' in E, otherwise true
|
|
an unlabeled node (blank node)
|
not defined ; but [I+A](E) = A(E)
|
|
an RDF graph
|
true if [I+A'](E) = true for some A': anon(E) -> IR, otherwise false.
|
|
2. Class extensions
|
|
E is:
|
I(E) is in IC; ICEXT(I(E)) includes:
|
|
rdfs:Resource
|
IR (The universe of the interpretation)
|
|
rdf:Property
|
IP (Properties; subset of IR, domain of IEXT)
|
|
rdfs:Class
|
IC (Classes; subset of IR, domain of ICEXT)
|
|
rdfs:Literal
|
a subset of LV (Literal values)
|
|
3. Property extensions
|
|
E is:
|
I(E) is in IP; <x,y> is in IEXT(I(E)) iff:
|
|
rdf:type
|
x is in ICEXT(y)
|
|
E is:
|
I(E) is in IP; if <x,y> is in IEXT(I(E)) then:
|
|
rdfs:domain
|
if <u,v> is in IEXT(x) then u is in ICEXT(y)
|
|
rdfs:range
|
if <u,v> is in IEXT(x) then v is in ICEXT(y)
|
|
rdfs:subClassOf
|
ICEXT(x) is a subset of ICEXT(y)
|
|
rdfs:subPropertyOf
|
IEXT(x) is a subset of IEXT(y)
|
| 4. Domain and Range |
IEXT(I(rdfs:domain)) contains: |
<I(rdfs:domain), I(rdf:Property)>
<I(rdfs:range), I(rdf:Property)>
<I(rdf:type), I(rdfs:Resource)>
|
IEXT(I(rdfs:range)) contains: |
<I(rdfs:domain), I(rdfs:Class)>
<I(rdfs:range), I(rdfs:Class)>
<I(rdf:type), I(rdfs:Class)>
|
Subgraph Lemma.
A graph entails all its subgraphs.
Proof. Obvious, from definitions of subgraph and
entailment.
If the graph is true in I then for some A, all its triples are true in [I+A],
so every subset of triples is true in I. QED
Instance Lemma. A graph
is entailed by all its instances.
Proof. Suppose I satisfies E' and E' is an instance
of E. Then for some mapping A on the blank nodes of E', [I+A] satisfies every
triple in E'. For each blank node b in E, define B(b)=[I+A](c), where c is the
blank node or uriref that is substituted for b in E', or c=b if nothing was
substituted for it. Then [I+B](E)=[I+A](E')=true, so I satisfies E. But I was
arbitrary; so E' entails E. QED.
Conjunction Lemma.If
E is ground,
then I satisfies E if and only if it satisfies every
triple in E.
Proof. Obvious, from definition of denotation for ground
graphs. QED
Plain Subgraph Lemma.
If E and E' are ground and E' is plain, then E entails E' if and only if E'
is a subgraph of E.
Proof. 'If' follows directly from subgraph lemma; 'only if' follows from previous
lemma and definition of entailment. (The reason for the
restriction to plain graphs was noted in the text.
) QED
Herbrand Lemma. Any RDF
graph has a satisfying interpretation.
Proof. We will construct the interpretation from the graph, by providing 'just
enough' entities and extensions to make the graph true. Since the exact nature
of the things in the universe is irrelevant, it is convenient to use the nodes
of the graph themselves as their own denotations. (That was
Herbrand's
idea.) We need to be slightly careful about literals, however: we are not free
to use literals to denote themselves, since all interpretations must conform
to the global XL mapping on literals. The following construction
takes care to avoid any 'accidental' identities between the interpretations
of different expressions; this is not strictly necessary for this proof, but
illustrates the .
The universe of I is defined as follows. First, let U1 be the set of denotations
of literals which occur in the graph: U1={XL(x): x occurs in G}. Now, define
U2 to be the set of urirefs that occur in the graph, i.e. the vocabulary V of
the graph. Finally, let U3 be the set of blank nodes in the graph; and define
the universe IR to be the disjoint union of U1, U2 and U3. This may seem a rather
odd kind of set, but it is well-defined.
Now define IS to be the identity mapping on the vocabulary of the graph; and
IEXT as follows: <x,y> is in IEXT(z) just when there is a triple in the
graph of the form <x z y> or else of the form <x z L> where L is
a literal and XL(L)=y. Define the mapping A to be the identity mapping on blank
nodes of the graph.
Clearly I satisfies all ground triples in the graph, and [I+A] satisfies the
entire graph; so I satisfies the graph. QED
An interpretation constructed in this way, so that the IS mapping is the identity
mapping, is called a Herbrand interpretation. Herbrand interpretations
are minimal, and every minimal interpretation has a corresponding Herbrand interpretation
which assigns the same truthvalues to every triple, and hence to every graph.
Minimality lemma. If I is a minimal
satisfying interpretation of E, then I fails to satisfy every plain
triple which has no instance in E.
Proof. We will argue by reductio. Suppose I satisfies
some such triple <S P O>, i.e.. IEXT(I(P)) contains <I(S),I(O)>,
and consider the subinterpretation I' which is like I except that IEXT(I'(P))
does not contain that pair. Since <S P O> has no instances in E, [I'+A](x)=[I+A](x)
for any mapping A from blank nodes and any triple x in E, and I satisfies E,
so I' satisfies E; so I is not minimal. QED
The reason for the restriction to plain graphs was noted
in the text.
Notice that every thing in the universe of a minimal interpretation
of E must be the denotation of at least one node in E, and that every pair in
any property extension must have at least one corresponding triple in E that
it makes true; for if not, one could delete some of the interpretation and still
satisfy E. We will make use of this property in later proofs.
Strong Herbrand Lemma.
Any RDF graph E has a satisfying interpretation which does not satisfy any graph
which is separable from E.
Proof. For plain separable graphs this follows from the Herbrand
and minimality lemmas and the observation that a Herbrand interpretation is
minimal. However, the construction in the proof of the Herbrand Lemma in fact
establishes this result for arbitrary separable graphs. Consider the Herbrand
interpretation I constructed in the proof of the Herbrand lemma, and let <S
P O> be a triple which has no instances in E. Then either S is a uriref or
literal and there are no triples of the form <S P O'> in E, or O is a
uriref or literal and there are no triples of the form <S' P O> in E.
Consider the first case (the other case is similar); then by the construction
in the earlier proof, IEXT(I(P)) contains no pairs of the form <I(S), x>;
so there is no mapping A from blank nodes to IR that could make the triple true
in [I+A]; so the triple is false in I. Similarly for the other case. QED
Merging lemma. The
merge of a set S of RDF graphs is entailed by S, and
entails every member of S.
Proof. Obvious, from definitions of entailment and
merge. All members of S are true iff all triples in the merge of S are true.
QED.
Anonymity lemma 1.
Suppose E is a lean graph and E' is a proper instance of E. Then E does
not entail E'.
Proof. Since E' is a proper instance and E is
lean,
E' contains a triple which has no instances in E; otherwise the triple in E
which it is a proper instance of would have had a proper instance in E. By the
strong Herbrand lemma, there exists an interpretation which satisfies E but
not E'. So E does not entail E'. QED
Anonymity lemma 2.
Suppose that E is a lean graph and that E' is like E except that two distinct
unlabeled nodes in E have been identified in E'. Then E does not entail E'.
Proof. First we assume that the blank nodes occur in two distinct triples in
E. Suppose that E contains the triples
S1 P1 _:x1
S2 P2 _:x2
where E' contains the triples
S1 P1 _:x
S2 P2 _:x
(The arguments for the cases where the blank nodes occur in other positions
in the triples are similar.) Since E is lean, it contains no other triples of
the form <S1 P1 O'> or <S2 P2 O'>. Let I be a Herbrand interpretation
of E; then I(S1) is distinct from I(S2) and IEXT(I(P1)) ={<I(S1), _:x1>}and
IEXT(I(P2))={<I(S2), _:x2>}. Let A be any mapping from the blank nodes
of E' to IR, then in order for both triples to be true in [I+A], [I+A](_:x)
would have to equal both _:x1 and _:x2; but these are distinct; so I does not
satisfy E'.
The only remaining case is where E contains a single triple with two blank
nodes which are identified in E':
_:x1 P _:x2
where E' contains
_:x P _:x
The argument here is similar; the Herbrand interpretation I now has IEXT(I(P))
= {<_:x1,_:x2>} and there is no mapping from the second triple that could
satisfy this, so again I satisfies E but not E'. QED.
Note that the 'minimal' nature of the Herbrand construction provides an interpretation
that is sufficient to make a graph true, but only just sufficient. This
is a basic technique for showing that one graph does not entail another and
for establishing a precise correspondence between syntactic relationships and
entailment.
Interpolation Lemma.
S entails E if and only if a subgraph of the merge of S is an instance of E.
Proof. 'if' is a direct consequence of the merging and
instance lemmas.
To prove 'only if' we will show the converse. This is just a re-statement of
the strong Herbrand lemma. Assume that no subgraph of the merge of S is an instance
of E, i.e. that all subgraphs of the merge of S fail to be instances of E; i.e.,
that E is separable from the merge of S. Then by the strong Herbrand lemma the
merge of S does not entail E. So, by the merging lemma, S does not entail E.
QED.
Skolemization Lemma.
Suppose sk(E) is a skolemization of E with respect to V. Then sk(E) entails
E; and if sk(E) entails F and the vocabulary of F is disjoint from V, then E
entails F .
Proof. sk(E) entails E by the interpolation lemma.
Now, suppose that sk(E) entails F where F shares no vocabulary with V; and
suppose I is some interpretation satisfying E. Then for some mapping A from
the blank nodes of E, [I+A] satisfies E. Define an interpretation I' of the
vocabulary of sk(E) by: IR'=IR, IEXT'=IEXT, I'(x)=I(x) for x in the vocabulary
of E, and I'(x)=[I+A](y) for x in V, where y is the blank node in E that is
replaced by x in sk(E).Clearly I' satisfies sk(E), so I' satisfies F. But I'(F)=[I+A](F)
since the vocabulary of F is disjoint from that of V; so I satisfies F. So E
entails F. QED.
RDF closure lemma.
Any satisfying rdf-interpretation of E satisfies the rdf-closure of E; and any
minimal simple satisfying interpretation of the rdf-closure of E is a satisfying
rdf-interpretation of E.
Proof. This follows from a comparison of the rdf
closure rules with the semantic conditions on an
rdf-interpretation. Although the argument is very simple in this case, we
give it here in full to illustrate the general technique.
The first part follows from the fact that the closure rules are
all rdf-valid. To show this, suppose I is an rdf-interpretation; then for any
aaa in the vocabulary of I, if a triple of the form xxx aaa yyy is true in I,
then IEXT(I(aaa)) is nonempty then I(aaa) is in IP, so IEXT(I(rdf:type)) contains
<I(aaa),I(rdf:Property)>, so the triple <aaa rdf:type rdf:Property>
is true in I. Since I is an rdf-interpretation, its vocabulary contains rdf:type
and IP contains I(rdf:type), so in particular the triple
rdf:type rdf:type rdf:Property
is true in I. That establishes that the closure rules are rdf-valid.
To prove the other part of the lemma we must show that the closure
rules are together sufficient to force any minimal interpretation to be an rdf-interpretation
of E. The simplest way to argue this is to show the converse, viz. that any
minimal simple interpretation of the rdf-closure that violates one of the semantic
conditions for an rdf-interpretation of E would thereby fail to satisfy the
closure. Suppose therefore that I is a minimal simple interpretation of the
rdf-closure of E.
If I violates the first constraint then IP does not contain I(rdf:type);
in that case, the added triple in the first closure rule is false in I. So assume
that I violates the second constraint. Then there is some x in IP for which
IEXT(I(rdf:type)) does not contain <x,I(rdf:Property)>. Since I is minimal,
there is some node aaa in E with I(aaa)=x; and since I(aaa) is in IP, there
is a pair <y,z> in IEXT(I(aaa)) and a triple
bbb aaa ccc
in E with I(bbb)=y and I(ccc)=z. Then the closure of E contains
the triple
aaa rdf:type rdf:Property
which is false in I. So I fails to satisfy the rdf-closure.
QED.
Notice the need for the minimality assumption, which 'forces'
the semantic violation to be made explicit in the syntax of the graph itself.
The second part of the lemma could be false for an arbitrary simple interpretation
of the closure, which might fail to meet the required semantic conditions on
some part of the universe that was not referred to in the graph itself. In general,
one cannot infer, from the lack of an assertion in a graph, that what that assertion
would say if it were in the graph must be false in a satisfying interpretation
of the graph. Minimal interpretations, however, embody a 'closed
world assumption' which would sanction such an inference. To prove an entailment
we need to prove something about all interpretations; but to prove the converse,
it is enough to show that a single interpretation exists with the right
properties, and this is where the special properties of minimal interpretations
are useful.
RDF
entailment lemma. S rdf-entails E if and only if the rdf-closure of
the merge of S simply entails E.
Proof. Follows from the merging lemma, the RDF closure lemma
and the definition of entailment. By the merging lemma, we can identify S with
the merge of S, i.e. we can treat a set of graphs as a single graph MS.
So suppose that MS rdf-entails E, and let I be a simple interpretation of the
rdf-closure c(MS) of of MS. Then there is a minimal simple subinterpretation
I' of I which satisfies c(MS); so, by the previous lemma, I' is a satisfying
rdfs-interpretation of E. Therefore I satisfies E (since I' is a subinterpretation
of I).
Conversely, suppose that c(MS) simply entails E, and let I be an rdf-interpretation
of MS; then by the previous lemma, I satisfies c(MS), so I satisfies E (since
every rdf-interpretation is a simple interpretation). QED.
RDFS Closure Lemma. Any satisfying
rdfs-interpretation of E satisfies the rdfs-closure of E; and any minimal simple
satisfying interpretation of the rdf-closure of E is a satisfying rdfs-interpretation
of E.
Proof.(Sketch) As in the proof of the
RDF closure lemma, this follows from a point-by-point comparison of the rdfs
closure rules with the semantic conditions on an
rdfs-interpretation. A full proof would be long but tedious.We will illustrate
the form of the argument by considering some typical cases in detail.
The first part follows from the fact that the rdfs closure rules
are all rdfs-valid, which can be checked case by case. For example, consider
the closure rule rdfs5, and suppose I is an rdfs-interpretation which satisfies
<aaa rdfs:subPropertyOf bbb > and <bbb rdfs:subPropertyOf
ccc>. Then by the semantic conditions on an rdfs-interpretation, IEXT(I(aaa))
is subset of IEXT(I(bbb)) and IEXT(I(bbb)) is a subset of IEXT(I(ccc)); so IEXT(I(aaa))
is a subset of IEXT(I(ccc)); so I satisfies <aaa rdfs:subPropertyOf
ccc >. The other cases are similarly straighforward.
To demonstrate the other part of the lemma we must show that
the closure rules are together sufficient to restrict any minimal interpretation
to be an rdfs-interpretation. The simplest way to argue this is to show the
converse, by demonstrating that any minimal simple interpretation of the rdfs-closure
c(E) of E that violates one of the semantic conditions for an rdfs-interpretation
of E would thereby make some triple in c(E) false. Again, this can be checked
by a detailed examination of the cases that arise. Suppose that I is a minimal
simple interpretation of E.
If I violates any of the conditions involving the rdfs-vocabulary
then it is easy to check that one of the 'added' triples would be false, eg
if IEXT(I(rdfs:domain) does not contain <I(rdfs:domain),I(rdf:Property)>
then the triple
rdfs:domain rdfs:domain rdf:Property
is false in I.
If I violates the condition on IEXT(I(rdfs:range)),
then there exist x, y, u and v in IR with <x,y> in IEXT(I(rdfs:range))
,<u,v> in IEXT(x) but v not in ICEXT(y). Since I is a minimal interpretation
and satisfies c(E), the closure must contain two triples
aaa rdfs:range bbb
ccc aaa ddd
where I(aaa)=x, I(bbb)=y, I(ccc)=u and I(ddd)=v; but I makes the
triple
ddd rdf:type bbb
false, since I(ddd) is not in ICEXT(I(bbb)); but by the closure
rule rdfs3, this triple is in c(E); so I fails to satisfy c(E). The IEXT(I(rdfs:domain))
case is similar.
Finally, suppose that I violates the condition on rdfs:subClassOf.
Then for some x and y in IR, <x,y> is in IEXT(I(rdfs:subClassOf))
but there is some z in ICEXT(x) but not in ICEXT(y). Again, since I is minimal,
these entities must occur in triples in c(E) of the form respectively
aaa rdfs:subClassOf bbb
ccc rdf:type aaa
where I(aaa)=x, I(bbb)=y and I(ccc)=z, and where the triple
ccc rdf:type bbb
is false in I; so I does not satisfy c(E) by a similar argument,
using the closure rule rdfs9. Again, the case for a violation of the the condition
on rdfs:subPropertyOf is similar. QED.
RDFS Entailment Lemma. S rdfs-entails
E iff the rdfs-closure of the merge of S simply entails E.
Proof. Exactly similar to proof of RDF entailment lemma. QED.
1. The appropriate treatment of the RDF container vocabulary
has not yet been fully determined. See http://www.w3.org/2000/03/rdf-tracking/#rdf-containers-otherapproaches.
2. The appropriate treatment of RDF reification is currently
under discussion.
3. The appropriate treatment of literals in RDF is currently
under discussion. If this is resolved so as to take detailed account of XML
datatypes (see http://www.w3.org/2000/03/rdf-tracking/#rdfms-xml-schema-datatypes)
then this may require considerable extensions to the model theory. See also
http://www.w3.org/2000/03/rdf-tracking/#rdfms-literal-is-xml-structure.
4. The description of RDF graphs in section may need to be
modified in detail. See http://www.w3.org/2000/03/rdf-tracking/#rdfms-literalsubjects
and http://www.w3.org/2000/03/rdf-tracking/#rdfms-contexts;
in addition, if a simple treatment of literal datatyping is adopted then it may
be more appropriate to identify literals as unique nodes, similarly to urirefs.
This document has benefited from inputs from many members of the RDF
Core Working Group. Dan Connolly clarified the relationship between RDF
and RDFS and suggested the 'set of triples' definition of RDF graph. The idea
of graph syntax is from Ora Lassila. Sergey Melnick suggested using a translation
into logic. Jeremy Carroll noticed the need for the lean
graph condition. Jos deRoo, Graham Klyne, Jeremy Carroll and Patrick Stickler
found errors in earlier drafts and suggested many stylistic improvements.
The use of an explicit extension mapping to allow self-application without
violating the axiom of foundation was suggested by Chris Menzel. Peter Patel-Schneider
found several major errors in an earlier draft, and suggested several important
technical improvements.
- [RDF/XML]
- Dave Beckett (editor),
XML Syntax Specification (Revised), 18 December 2001 (W3C Working Draft).
- [RDFMS]
- Ora Lassila, Ralph R. Swick (editors), Resource Description Framework (RDF)
Model and Syntax Specification, 22 February 1999.
- [RDFSchema]
- Dan Brickley, R.V. Guha (editors), Resource Description
Framework (RDF) Schema Specification 1.0, 27 March 2000 (W3C Candidate
Recommendation).
- [RDFTestCases]
- Art Barstow, Dave Beckett (editors), RDF Test Cases
, 15 November 2001 (W3C Working Draft).
- [RFC 2396]
- T. Berners-Lee, Fielding and Masinter, RFC 2396 - Uniform Resource Identifiers
(URI): Generic Syntax, August 1998.
- [KIF]
- Michael R. Genesereth, Knowledge Interchange Format,
1998 (draft American National Standard).
- [Hayes&Menzel]
- Patrick Hayes, Christopher Menzel,
A Semantics for the Knowledge Interchange Format , 6 August 2001 (Proceedings
of 2001 Workshop on the IEEE Standard Upper
Ontology)
- [DAML]
- Frank van Harmelen, Peter F. Patel-Schneider, Ian Horrocks (editors), Reference Description of the
DAML+OIL (March 2001) ontology markup language
- [Marchiori&Saarela]
- Massimo Marchioi, Janne Saarela,
Query + Metadata + Logic = Metalog, 1998
- [Fikes&McGuinness]
- Richard Fikes, Deborah L. McGuinness,
An Axiomatic Semantics for RDF, RDF Schema, and DAML+OIL, KSL Technical
Report KSL-01-01, 2001
Overall presentation re-organized; many changes to wording, extra explanatory
sentences added, typos and errors corrected.
Definition of RDF graph corrected.
Faulty statements of several lemmas corrected, proofs of lemmas added.
'rdf entailment' changed to 'simple entailment'. Reserved vocabularies introduced,
concept of vocabulary entailment introduced,
rdf-entailment more clearly distinguished from rdfs-entailment.
Treatment of literals and rdfs:Literal changed slightly (XL applied to literal
nodes rather than literals; RDF graph syntax not required to merge literal nodes;
interpretations not required to contain all literal values.)
Missing domain/range rdfs closure rules added.
References to rdfs:ConstraintResource and rdfs:ConstraintProperty removed.(Subsequent
to
resolution of issue rdfms-constraint-properties-resource. )

