This section is informative.
This section defines the SMIL 2.0 Layout Modules, which are composed of a BasicLayout module and three modules with additional functionality that build on top of the BasicLayout module: the AudioLayout, MultiWindowLayout, and HierarchicalLayout modules. The modules contain elements and attributes allowing for positioning of media elements on the visual rendering surface, and control of audio volume. Since these elements and attributes are defined in modules, designers of other markup languages can choose whether or not to include this functionality in their languages. Therefore, language designers incorporating other SMIL modules do not need to include the layout modules if sufficient layout functionality is already present.
This section is informative.
The functionality in this module is essentially identical with the layout functionality in [SMIL10].
Like SMIL 1.0, SMIL 2.0 BasicLayout modules includes a layout model for organizing media elements into regions on the visual rendering surface. The layout element is used in the document head to declare a set of regions on which media elements are rendered. Media elements declare which region they are to be rendered into with the region attribute.
Each region has a set of CSS2 compatible properties such as top, left, height, width, and backgroundColor. These properties can be declared using a syntax defined by the type attribute of the layout element. In this way, media layout can be described using the SMIL 1.0 basic layout syntax or CSS2 syntax.
For example, to describe a region with the id "r" at location 15,20 that is 100 pixels wide by 50 pixels tall using the SMIL basic layout model:
<layout> <region id="r" top="15px" left="20px" width="100px" height="50px"/> </layout>
To create the same region using CSS2 syntax:
<layout type="text/css">
[region="r"] { top: 15px; left: 20px; width: 100px; height:50px; }
</layout>
To display a media element in the region declared above, specify the region's id as the region attribute of the media element:
<ref region="r" src="http://..." />
Additionally, implementations may choose to allow using the CSS syntax to set the media layout directly. This can be done by using the selector syntax to set layout properties on the media elements. For example, to display all video and image elements in a rectangle at the same size and position as the examples above:
<layout type="text/css">
video, img { top:15px; left:20px; width:100px; height=50px; }
</layout>
Note that multiple layout models could be specified within a control structure such as the SMIL switch element, each with a different type. The first layout with a type supported by the implementation will be the one used.
This section defines the elements and attributes that make up the functionality in the SMIL BasicLayout module.
The layout element determines how the elements in the document's body are positioned on an abstract rendering surface (either visual or acoustic).
The layout element must appear before any of the declared layout is used in the document. If present, the layout element must appear in the head section of the document. If a document contains no layout element, the positioning of the body elements is implementation-dependent.
It is recommended that profiles including the SMIL 2.0 BasicLayout also support the SMIL 2.0 BasicContentControl module. A document can then support multiple alternative layouts by enclosing several layout elements within the SMIL switch element. This could also be used to describe the document's layout using different layout languages. Support for the system test attributes in the SMIL BasicContentControl module also enables greater author flexibility as well as user accessibility.
Default layout values can be assigned to all renderable elements by selecting the empty layout element <layout></layout>. If the document does not include a layout element, then the positioning of media elements is implementation dependent.
Element attributes
If the type attribute of the layout element has the value "text/smil-basic-layout", it may contain the following elements:
Languages incorporating the BasicLayout module need to define what additional elements are allowed as children. If the type attribute of the layout element has another value, the element contains character data.
The region element controls the position, size and scaling of media object elements.
In the following example fragment, the position of a text element is set to a 5 pixel distance from the top border of the rendering window:
<smil> <head> <layout> <root-layout width="320" height="480" /> <region id="a" top="5" /> </layout> </head> <body> <text region="a" src="text.html" dur="10s" /> </body> </smil>
The position of a region, as specified by its top, bottom, left, and right attributes, is always relative to the parent geometry, which is defined by the parent element. For the SMIL BasicLayout module, all region elements must have as their immediate parent a layout element, and the region position is defined relative to the root window declared in the sibling root-layout element.
When region sizes, as specified by width and height attributes are declared relative with the "%" notation, the size of a region is relative to the size of the parent geometry. Sizes declared as absolute pixel values maintain those absolute values.
Conflicts between the region size and position attributes width, height, bottom, left, right, and top are resolved according to the rules for absolutely positioned, replaced elements in [CSS2]. The default values of region position and size attributes is specified as auto. This attribute value has the same meaning here that it does in [CSS2].
Element attributes
The region element can have the following visual attributes:
The default value of fit is hidden.
Note that the fit attribute applies to visual media once it has an intrinsic two-dimensional size, such as images and video. It does not apply to visual media that is rendered and adapted to varying circumstances, such as the visual display of HTML, until its two-dimensional spatial dimensions have been determined, such as after an HTML page has been laid out to specific size.
The root-layout element determines the value of the layout properties of the root element, which in turn determines the size of the window in which the SMIL presentation is rendered.
If more than one root-layout element is parsed within a single layout element, this is an error, and the document should not be displayed. This does not include root-layout elements skipped by the player (e.g. because the enclosing layout element was skipped due to an unrecognized type or a test attribute evaluated to false).
The semantics of the root-layout element are as in SMIL 1.0: the attributes of the root-layout element determine the size of the top level presentation window, and the declared sibling regions are arranged within this top level window. If either the height or width of the root-layout element is not specified, the value of the attribute is implementation dependent.
The root-layout element can have the following attributes:
Element content
The root-layout element is an empty element.
This element supports the SMIL 1.0 syntax where the root-layout element is an empty sibling of the top level region elements.
The language integrating this module must specify which elements have a region attribute and any inheritance of the attribute.
SMIL 2.0 BasicLayout module is consistent with the visual rendering model defined in CSS2, it reuses the formatting properties defined by the CSS2 specification, and newly introduces the fit attribute [CSS2]. The reader is expected to be familiar with the concepts and terms defined in CSS2.
A profile integrating the SMIL 2.0 Basic Layout module must define default values for all layout-related attributes of elements. These should be consistent with the initial values of the corresponding properties in CSS2, if any. In particular the values of the display and position properties should be defined.
A profile integrating the SMIL 2.0 Basic Layout module must define the content models for the layout element if any elements beyond those specified here are to be allowed as children.
A profile integrating the SMIL 2.0 Basic Layout module must provide a means of declaring an XML identifier on region elements. This value is used as the argument value to the region attribute. In addition, the integrating profile must specify which elements have a region attribute and any inheritance of the attribute.
See the full DTD for the SMIL Layout modules.
This section is informative.
This section defines the functionality in the SMIL 2.0 AudioLayout module. This level contains an attribute providing audio rendering surface volume control.
This section is normative.
The functionality in this module builds on top of the functionality in the BasicLayout module, which is a required prerequisite for inclusion of the AudioLayout module.
This section is normative.
SMIL 2.0 AudioLayout module supports control of aural media volumes via a new property on the region element, soundLevel. Multimedia assigned to a region with an explicit soundLevel attribute will have its audio rendered at the given relative sound intensity.
This section defines the elements and attributes that make up the SMIL 2.0 AudioLayout module.
The region element defined in
the BasicLayout module is extended
with the addition of
the soundLevel attribute.
The region element can have the following aural attributes:
This section is informative.
This section defines the functionality in the SMIL 2.0 MultiWindowLayout module. This level contains elements and attributes providing for creation and control of multiple top level windows on the rendering device.
This section is normative.
The functionality in this module builds on top of the functionality in the BasicLayout module, which is a required prerequisite for inclusion of the MultiWindowLayout module.
This section is normative.
In [[SMIL 1.0]], and the SMIL 2.0 BasicLayout module, each presentation is rendered into a single root window of a specific size/shape. The root window contains all of the regions used to manage the rendering of specific media objects.
This specification supports the concept of multiple top-level windows. Since there is no longer a single root window, we use the term top level instead. The assignment of the regions to individual top level windows allows independent placement and resizing of each top-level window, if supported by the including profile and implementation. The initial placement of the top level windows on the display device and any available means of relocating the top level windows is implementation dependent.
A top level window is declared with the element in a manner similar to the SMIL 1.0 root-layout window, except that multiple instances of the element may occur within a single layout element:
<layout> <viewport id="WinV" title="Video" width="320" height="240"/> <region id="pictures" title="pictures" height="100%" fit="meet"/> </viewport> <viewport id="WinC" title="Captions" width="320" height="60"> <region id="captions" title="caption text" top="90%" fit="meet"/> </viewport> </layout>
In this example, two top-level windows are defined ("WinV" and "WinC"), and two regions are defined with one region ("pictures") assigned to WinV and the other ("captions") to WinC. The definitions of the top-level windows and the contained regions use a hierarchical syntax, unlike the older root-layout element.
The top-level windows function as rendering containers only, that is, they do not carry temporal significance. In other words, each window does not define a separate timeline or any other time-container properties. There is still a single master timeline for the SMIL presentation, no matter how many top-level windows have been created. This is important to allow synchronization between media displayed in separate top-level windows.
The display of top level windows can be controlled automatically by the player, or manually by the user of the application. If a window is closed (by the user) while any of the elements displayed in that window are active, there is no effect on the timeline (if any) of those elements. However, a player may choose not to decode content as a performance improvement. The means provided to a user to close top level windows is implementation dependent.
For SMIL 1.0 compatibility, the root-layout element will continue to support SMIL 1.0 layout semantics. The new element will support the extension semantics and the improved, nested syntax.
Note also that any one region may belong to at most one top-level (or root-level) window. Regions not declared as children of a element belong to the root-layout window. If no root-layout element has been declared, the region is assigned to an additional window according to the semantics in the BasicLayout module.
This section defines the elements and attributes that make up the SMIL 2.0 MultiWindowLayout module.
The element determines the size of the a window in which the SMIL presentation is rendered, as well as serving as a top level window in which to place child region elements.
Multiple elements may appear within a single layout element, each declaring an independent top-level window.
Each instance of a element determines the size of a separate top-level presentation window, and the descendant regions are arranged within this top-level window and relative to the coordinate system of this window.
This module also provides control over when windows open and close in a presentation. Note that the precise mapping of windows on to the host environment is implementation dependent. It is expected that implementations will "pop up" independent desktop windows if they can, but other means of supporting multiple viewports, such as by using frames, are allowed. When automatically opening and closing windows, applications should try to comply with the WAI User Agent Guidelines [UAAG] and allow the user to choose whether to be warned that windows are being opened and closed, and given a method for disabling automatic opening and closing of windows.
Element attributes
The element can have the following attributes:
The element may contain any number of region elements, or be empty.
Allowing multiple elements within a single layout element supports multiple top level windows.
The layout element defined in the SMIL BasicLayout module is extended with the addition that the element is added to the content model of the layout element if the type attribute of the layout element has the value "text/smil-basic-layout". In this case it can contain the following elements:
See the full DTD for the SMIL Layout modules.
This section is informative.
This section defines the functionality in the SMIL 2.0 HierarchicalLayout module. This module contains elements and attributes for advanced positioning of media elements on the visual rendering surface and builds upon the SMIL 2.0 BasicLayout module.
The SMIL 2.0 HierarchicalLayout module extends the basic layout model for organizing media elements into regions on the visual rendering surface providing much greater author control and flexibility. These extensions are important for certain classes of multimedia presentations in which author control of object placement is critical.
This module:
- extends the definition of the region element to allow for the specification of hierarchical regions;
- introduces a new layout element, regPoint, for controlling relative placement with an associated region (the registration element facility);
- allows an object placed in a region to override the setting of a region's fit and backgroundColor attributes;
- includes additional attributes, regPoint and regAlign, that specify how a media object's presentation can be aligned relative to the set of defined registration points (the registration alignment facility); and
- provides additional attributes, top, bottom, left, and right, that specify exact positioning of objects within a region (the so-called sub-region positioning facility).
This section is normative.
The functionality in this module builds on top of the functionality in the BasicLayout module, which is a required prerequisite for inclusion of the HierarchicalLayout module.
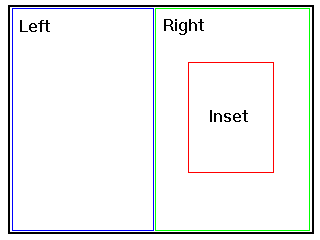
A new feature in this module is support for hierarchical layout. This allows for the declaration of regions nested inside other regions, much like regions are laid out inside the top level window declared by the element. For example, the following declares a top level window of 640 by 480 pixels, regions "left" and "right" which covers the left and right sides of the window respectively, and a hierarchical region "inset" that is centered within "right".
<layout>
<viewport width="640px" height="480px" />
<region id="left" top="0%" left="0%"
width="50%" height="100%" />
<region id="right" top="0%" left="50%"
width="50%" height="100%">
<region id="inset" top="25%" left="25%"
width="50%" height="50%" />
</region>
</viewport>
</layout>
The resulting layout looks like this:

By default, each hierarchical region shares the z-index (depth) value of its parent. Hierarchical regions may also introduce their own local z-index value. In this case, all hierarchical regions with a common direct parent define local z-indexes within the z-index value of their parent. For example, if a parent region has a z-index value of "4" and two hierarchical children of that parent define z-indexes of "1" and "2", respectively, then each of these are treated as further sub-divisions of the parent's z-index of "4".
If two hierarchical regions with the same z-index attribute value overlap, the existing rules for z-index processing (from the BasicLayout module) are applied. Specifically, the rule concerning time priority is maintained, meaning that in the case of a z-index conflict, the media visible in the overlap will be determined by the region that is rendering the media that has most recently begun in time. If the conflicting media began at the same time, then the rule using the textual order of the media elements in the SMIL document is applied.
For example:
<layout>
<root-layout width="640px" height="480px" />
<region id="whole" top="0px" left="0px" width="640px"
height="480px" z-index="5"/>
<region id="right" top="0px" left="320px" width="320px"
height="480px" z-index="4">
<region id="inset" top="140px" left="80" width="160px"
height="200px" z-index="6"/>
<region id="inset2" top="140px" left="80" width="160px"
height="200px" z-index="6"/>
<region id="inset3" top="140px" left="80" width="160px"
height="200px" z-index="7"/>
</region>
</layout>
...
<par>
<img id="A" region="whole" src="imageA.jpg" dur="10s"/>
<img id="B" region="inset" src="imageB.jpg" dur="10s"/>
</par>
<par>
<img id="D" region="inset2" src="imageD.jpg" begin="1s" dur="10s"/>
<img id="C" region="inset" src="imageC.jpg" begin="0s" dur="10s"/>
</par>
<par>
<img id="E" region="inset2" src="imageE.jpg" dur="10s"/>
<img id="F" region="inset3" src="imageF.jpg" dur="10s"/>
</par>
Where hierarchical layout provides a facility for defining a set of regions with a common parent, it does not provide any facility for determining where in any particular region a given media object will be placed. The SMIL 2.0 HierarchicalLayout module solves this problem by defining a set of attributes which, when placed on an object using the region attribute, allow that media item to be explicitly positioned within a region. These attributes are collectively referred to as sub-region positioning attributes. The sub-region positioning argument values follow the conventions of CSS2 the absolute positioning property values.
For example, suppose a region "d" is defined:
<layout> ... <region id="d" ... /> ... </layout>
The following code describes the placement of an object at a particular offset within a region, using the SMIL 2.0 HierarchicalLayout syntax:
<ref id="a" ... region="d" top="5%" left="3" />
Each placement attribute defines a new, temporary boundary of the region for the referenced media object. In this case, the top-left point of the media object is displayed 5% from the top and 3 pixels from the left in region "d".
All other placement operations, such as the fit attribute, operate on the region as if it had its relevant edges moved to the position specified by the placement attributes. For example, the following document fragment describes a region and a media object reference that make use of sub-region positioning:
<layout>
...
<region id="d" ... fit ="fill" />
...
</layout>
<body> ...
<ref src="..." ... region="d" fit="hidden"
top="5%" left="3" bottom="10%" right="15%" />
...
</body>
In this example, the effective boundaries of the region for the placement of this object are defined by adjusting the top, bottom, left and right edges of the region by the values shown, and then filling the resulting sub-region with the specified image as directed by the fit attribute. If the size of the media object being displayed is smaller than that of the resulting sub-region, the display will be similar to:
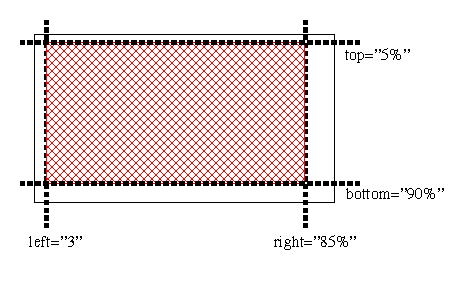
The use of sub-region placement is intended as a light-weight alternative to defining many single-use regions. Often, the dimensions used for the sub-region will match the dimensions of the media object being placed, but in all cases the values of the fit attribute will govern rendering of the object in the sub-region.
Rules for handling clipping of objects within regions based on the sub-region attributes are provided below.
The SMIL 2.0 HierarchicalLayout module includes the ability to use the fit and backgroundColor attributes on objects displayed in a region in order to override the declared behavior of the region.
A registration element is an element defined within this module that is used to define a point within a region and a default object alignment algorithm about that point. The element can be used in a media object element, where it is associated with a region and an optional override alignment algorithm. The placement values within registration elements can be either percentages or pixels.
The use of registration points allows for consistent relative placement across regions. As such, registration points are defined outside of any single region.
For example, the following code describes two registration points (with id values "midPoint" and "topMargin"), one of which is defined as a relative location and one at a fixed pixel location, using the SMIL 2.0 HierarchicalLayout syntax:
<layout> <regPoint id="midPoint" top="50%" left="50%" regAlign="center" /> <regPoint id="topMargin" top="10" left="15" regAlign="topLeft" /> <region id="a" ... /> <region id="b" ... /> </layout>
In this example, the registration point with the id value "midPoint" has a default alignment algorithm that centers the media object about the defined point, while the registration point with the id value "topMargin" has a default alignment algorithm that places the top-left point of the media object at the registration point.
Various media elements could be displayed in the regions using the alignment points as follows:
<ref region="a" src="rtsp://..." dur="2s" regPoint="midPoint" />
<ref region="b" src="http://..." dur="2s"
regPoint="midPoint" regAlign="bottomRight"/>
<ref region="a" src="http://..." dur="2s" regPoint="topMargin" />
<ref region="b" src="http://..." dur="2s"
regPoint="topMargin" regAlign="center"/>
In the first example, a media object is centered in the middle of region a. In the second example, a media object has its bottom right corner centered in the middle of region b. Similarly, in the third example, a media object has its top left corner placed at a point 10,15 within region a, and in the fourth example, an object is centered around the point 10,15 in region b.
Registration points can be used to coordinate the placement of a set of media objects that do not share the same sizes. (For example, a set of images can be aligned to the center of a region.) They can also be used to coordinate the display of images about a particular point in a region, as in:
<layout>
<regPoint id="middle" top="50%" left="50%" regAlign="center" />
<region id="a" ... />
</layout>
...
<seq>
<ref region="a" src="rtsp://..." dur="2s" regPoint="middle"
regAlign="bottomRight"/>
<ref region="a" src="http://..." dur="2s" regPoint="middle"
regAlign="bottomLeft"/>
<ref region="a" src="http://..." dur="2s" regPoint="middle"
regAlign="topLeft"/>
<ref region="a" src="http://..." dur="2s" regPoint="middle"
regAlign="topRight"/>
</seq>
In this example, four objects are aligned over time to the middle of region. If any media element extends outside the bounds of a region, it will be clipped to the region.
Note that registration points are global within the context of a layout, and are not tied to a particular region, but can be reused across regions. As such, pixel-based offsets should be used with care.
For authoring convenience, SMIL HierarchicalLayout module provides several pre-defined region registration points including topLeft, topMid, topRight, midLeft, center, midRight, bottomLeft, bottomMid, and bottomRight.
For example, media objects can be centered in any region like this:
<ref ..." regPoint="center" regAlign="center" />
The default value of regAlign for a region is topLeft. If the regAlign attribute is used without a regPoint attribute, the alignment operation is relative to the upper left point of the region containing this object, that is, the behavior is the same as if the regPoint were to be specified as topLeft.
Rules for handling clipping of objects within regions based on the regPoint and regAlign attributes are defined below.
This section defines the elements and attributes that make up the SMIL 2.0 HierarchicalLayout module.
This element is defined as in the BasicLayout module with extensions presented here.
In order to support the registration point functionality described above, one new element is added to the content model of the layout element.
SMIL HierarchicalLayout module does not provide any new attributes to the layout element.
Element content
If the type attribute of the layout element has the value "text/smil-basic-layout", it can contain the following elements:
All element content except regPoint are defined above in the BasicLayout and MultiWindowLayout modules. The regPoint element is described below.
The region element controls the position, size and scaling of media object elements. This module extends the definition of the region element to include the definition of hierarchical regions.
The position of a region, as specified by its top and left attributes, is always relative to the parent geometry, which is defined by the parent element. For the SMIL 2.0 HierarchicalLayout module, all hierarchical region elements must have as their immediate parent a region or element. The position of the hierarchical region is defined relative to that parent element.
When region sizes, as specified by width and height attributes are declared relative with the "%" notation, the size of the hierarchical region is relative to the size of the parent region. Sizes declared as absolute pixel values are absolute values even when used with a child region.
Note that a (hierarchical) region may be defined in such a way as to extend beyond the limits of its parent. In this case the child region must be clipped to the parent boundaries.
If a z-index attribute is defined on the hierarchical region, it is evaluated as a local index within that of the parent.
In the HierarchicalLayout module, the region element has no additional attributes beyond that provided in the other included layout modules. However, the semantics of the z-index attribute are extended to support hierarchical regions.
Element content
SMIL HierarchicalLayout module extends the region element content model to optionally include other region elements.
The regPoint element determines the (x, y) coordinates of a point relative to a region upper-left corner for use in aligning elements in the document's body on regions within a visual rendering surface. A regPoint may be defined using absolute (pixel) or relative (percentage) based values. The regPoint functionality is not defined and may not be used for media without intrinsic size.
For the purposes of regPoint functionality, media and regions are defined to be rectangular, with perpendicular sides, with the sides ordered clockwise top, right, bottom, and left. The top side is the edge closest to the point or edge of the display device considered "up".
The regPoint element may only appear as an immediate child of a layout element.
If the registration point or alignment functionality is used on a media object, the interaction between the regPoint value, the regAlign value, and the fit attribute value of the region in which the media object is displayed is as follows:
For example, a wide-screen video can be made to play in "letterbox" mode in a region, whose width-to-height ratio is smaller, by using regPoint ="center" and regAlign ="center" and setting the region's fit value to "meet". The result is the video will touch the left and right edges of the region and will be centered vertically with the gaps above and below filled in with the region's background color.
Element content
None.
While the SMIL 2.0 BasicLayout module provides only the region attribute on elements to place them on the rendering surface, the HierarchicalLayout module includes attributes to refine the position of media content within a region, and to refine the visual presentation of the media within the region.
This module provides fine control over the background color surrounding media elements by allowing the media element to override the background color of a region in which the media is being shown.
One set of attributes (the sub-region positioning attributes) allows a "sub-region" to be defined that is wholly contained within the enclosing layout region for that object; the other set of attributes can be used to define a registration point to be used with that object and an optional layout algorithm that will override the default algorithm associated with the registration point.
If the fit attribute and registration alignment attributes are both relevant to the placement of a particular object, the interaction is the same as described in the regPoint definition. If sub-region positioning attributes are used on an object with applicable fit or alignment attributes, the fit or alignment attributes apply to the sub-region. The fit setting on the referenced region does not apply to a sub-region.
For both sub-region positioning and registration point use, the value of the z-index attribute on the associated region is used. If media objects overlap, existing rules for resolving z-index conflicts are applied.
Note that placement within the region may be defined in such a way as to extend the media object beyond the limits of the region. In this case the media object must be clipped to the region boundaries.
The media specific background color attribute will be ignored if it is used on an element without a region attribute that specifies the identifier of region element in the layout section.
Conflicts between the region size attributes bottom, left, right, and top are resolved according to the rules for absolutely positioned, replaced elements in [CSS2].
The sub-region positioning attributes will be ignored if they are used on an element without a region attribute that specifies the identifier of region element in the layout section.
The regPoint attribute is used in conjunction with the regPoint element. If a regPoint attribute is missing or refers to a non-existent regPoint element the value of the regAlign attributes are applied to the top-left point of the region containing the media object.
The fit attribute is used on an element in conjunction with the region attribute to control the display of the element on the rendering surface. A value of the fit attribute given on the element will override the value of fit declared in the referenced region element.
See the full DTD for the SMIL Layout modules.
<!-- ======================================================================= -->
<!-- SMIL 2.0 Layout Modules =============================================== -->
<!-- file: SMIL-layout.mod
This is SMIL 2.0.
Copyright 2000 W3C (MIT, INRIA, Keio), All Rights Reserved.
Authors: Jacco van Ossenbruggen, Aaron Cohen
Revision: $Id: SMIL-layout.mod,v 1.17 2000/08/23 12:38:15 jvanoss Exp $
This DTD module is identified by the PUBLIC and SYSTEM identifiers:
PUBLIC "-//W3C//ELEMENTS SMIL 2.0 Layout//EN"
SYSTEM "SMIL-layout.mod"
==================================================================== -->
<!-- ================== BasicLayout ======================================== -->
<!-- ================== BasicLayout Profiling Entities ===================== -->
<!ENTITY % layout.attrib "">
<!ENTITY % region.attrib "">
<!ENTITY % rootlayout.attrib "">
<!ENTITY % layout.content "EMPTY">
<!ENTITY % region.content "EMPTY">
<!ENTITY % rootlayout.content "EMPTY">
<!-- ================== BasicLayout Entities =============================== -->
<!ENTITY % viewport-attrs "
height CDATA 'auto'
width CDATA 'auto'
close (never|whenNotActive) 'never'
open (always|whenActive) 'always'
%BackgroundColor.attrib;
%BackgroundColor-deprecated.attrib;
">
<!ENTITY % region-attrs "
bottom CDATA 'auto'
left CDATA 'auto'
right CDATA 'auto'
top CDATA 'auto'
z-index CDATA #IMPLIED
showBackground (always|whenActive) 'always'
%Fit.attrib;
">
<!-- ================== BasicLayout Elements =============================== -->
<!--
Layout contains the region and root-layout elements defined by
smil-basic-layout or other elements defined an external layout
mechanism.
-->
<!ENTITY % layout.qname "layout">
<!ELEMENT %layout.qname; %layout.content;>
<!ATTLIST %layout.qname; %layout.attrib;
%Core.attrib;
%I18n.attrib;
type CDATA 'text/smil-basic-layout'
>
<!-- ================== Region Element ======================================-->
<!ENTITY % region.qname "region">
<!ELEMENT %region.qname; %region.content;>
<!ATTLIST %region.qname; %region.attrib;
%Core.attrib;
%I18n.attrib;
%viewport-attrs;
%region-attrs;
>
<!-- ================== Root-layout Element =================================-->
<!ENTITY % root-layout.qname "root-layout">
<!ELEMENT %root-layout.qname; %rootlayout.content; >
<!ATTLIST %root-layout.qname; %rootlayout.attrib;
%Core.attrib;
%I18n.attrib;
%viewport-attrs;
>
<!-- ================== AudioLayout ======================================== -->
<!ENTITY % AudioLayout.module "IGNORE">
<![%AudioLayout.module;[
<!-- ================== AudioLayout Entities ============================= -->
<!ENTITY % audio-attrs "
soundLevel CDATA '100%'
">
<!-- ================ AudioLayout Elements =============================== -->
<!-- ================ Add soundLevel to region element =================== -->
<!ATTLIST %region.qname; %audio-attrs;>
]]> <!-- end AudioLayout.module -->
<!-- ================ MultiWindowLayout ==================================== -->
<!ENTITY % MultiWindowLayout.module "IGNORE">
<![%MultiWindowLayout.module;[
<!-- ============== MultiWindowLayout Profiling Entities ================= -->
<!ENTITY % viewport.attrib "">
<!ENTITY % viewport.content "EMPTY">
<!-- ============== MultiWindowLayout Elements =========================== -->
<!--================= viewport element =================================== -->
<!ENTITY % viewport.qname "viewport">
<!ELEMENT %viewport.qname; %viewport.content;>
<!ATTLIST %viewport.qname; %viewport.attrib;
%Core.attrib;
%I18n.attrib;
%viewport-attrs;
>
]]> <!-- end MultiWindowLayout.module -->
<!-- ====================== HierarchicalLayout ============================= -->
<!ENTITY % HierarchicalLayout.module "IGNORE">
<![%HierarchicalLayout.module;[
<!-- ========== HierarchicalLayout Profiling Entities ==================== -->
<!ENTITY % regPoint.attrib "">
<!ENTITY % regPoint.content "EMPTY">
<!-- ============ HierarchicalLayout Elements ============================ -->
<!ENTITY % regPoint.qname "regPoint">
<!ELEMENT %regPoint.qname; %regPoint.content;>
<!ATTLIST %regPoint.qname; %regPoint.attrib;
%Core.attrib;
%I18n.attrib;
%Sub-region.attrib;
%RegistrationPoint.attrib;
>
]]> <!-- end HierarchicalLayout.module -->
<!-- end of SMIL-layout.mod -->