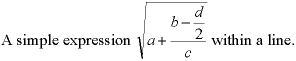
Paul Topping pault@mathtype.com
Design Science, Inc. www.mathtype.com
May
14, 1998
MathML is an XML application for representing mathematical expressions: their presentation, their semantics, or both. The implementation of the functionality it offers will rely on whatever mechanisms are available for interfacing XML applications to HTML and the browsers that accept it. The requirements that MathML makes of these mechanisms, and of browsers generally, are not unique but would be useful in many high-quality publishing contexts.
The purpose of this document is to describe the demands that MathML makes on browsers, XML, style mechanisms (XSL, CSS, etc.), and rendering. These areas where MathML requires support overlap and, therefore, we shall refer to them collectively as the "browser environment".
This paper was derived from a paper that the present author submitted to the "XML in HTML" Coordination Meeting ,held February 11-12, 1998, and from the notes for a presentation given by Robert Sutor at the "Shaping the Future of HTML" Workshop, held May 4-5, 1998.
MathML is an XML application for representing mathematical expressions; their presentation, their semantics, or both. The MathML specification is a product of the W3C's Math Working Group; it was issued as a W3C Recommendation on the 7th April 1998. MathML consists of approximately 100 elements and their attributes. The elements may be divided into two major categories: presentation elements and content elements. Presentation elements may be used to express the two-dimensional layout of mathematical expressions. Content elements are used to express the semantics of mathematical expressions up to the level of calculus. Content elements have default presentations, but may be combined with presentation elements to customize the layout of expressions. (Some MathML examples.)
The design of MathML and its supporting software aims for the following practical goals:
MathML objects have some general characteristics that might affect the design of supporting components in the browser environment:
For these reasons, efficiency in access, and ease of editing, the MathML language for each object should be able to be part of a single HTML page, rather than linked in from separate documents. However, linking must still be allowed.
High-quality graphical rendering of MathML objects is probably the most important need of MathML in that, if that doesn't work well, few will use MathML. Here are the requirements for rendering:
As graphical rendering is obviously the most important method of a MathML object and the chief task of a browser, it is worth looking more closely at how such a method could be implemented. Although it should be possible for a rendering method to draw directly to the screen or printer, rendering by generating a platform-independent intermediate form that can be processed by the browser is preferable. That intermediate form could be CSS, XSL, PGML, VML, Java 2-d graphics, or some other 2-d rendering system. Ideally, a MathML plug-in would perform the following:
The first problem that anyone encounters when trying to embed mathematics within an HTML text line is that the current markup does not allow precise positioning with respect to the baseline in any easy way. Consider the following properly formatted line (faked by putting the text and the math in a single GIF):
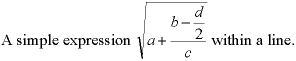
Note that the bottom edge of the variable "a" is aligned perfectly with the baseline of the surrounding text. The expression is not simply centered vertically. Indeed, the calculation of the correct vertical shift is one of the main challenges in properly rendering mathematics. Compare the above example with the following version using the align="baseline" attribute:
A simple expression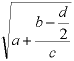 
within a line.
Or this one using the align="middle" attribute:
A simple expression 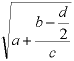within a line.
While it may be possible to use style sheets, and perhaps the SPAN element with TOP and POSITION attributes, to adjust embedded objects vertically, this is not practical for documents containing hundreds of math expressions within sentences. The expressions would have to be re-adjusted whenever the font size or any other formatting attribute changed.
While "baseline, baseline, baseline" has been the constant wail of the Math Working Group (and anyone else that has tried to put math on a web page), it has too often been assumed that this requirement is unique to math. Baseline positioning becomes an issue for virtually any object that contains letters which is also small enough for the author to consider putting within a line of text. An obvious example is a fancy, embellished capital letter starting a document ("drop caps" are just one type of "initial capital"; there are many others). Any text-using notation also requires baseline positioning for readability or for effect.
It is important that the formatting of a mathematical expression be compatible with the font and point size of the surrounding text. As this may be set by the viewer, not the author, it is not even possible to know how much screen real estate will be required for a MathML object at authoring time. Therefore, there needs to be negotiation between the browser and the object while formatting the page.
Line-breaking of mathematical expressions complicates this negotiation. Expressions are often naturally wider than the browser page and, therefore, may need to be rendered on multiple lines. Unlike normal text, line-breaking of equations cannot be performed by the browser as it requires mathematical knowledge to be done properly. MathML is designed to maintain structural information useful for deciding good line-breaks so it can help in this process.
When a browser needs to allocate page space to a MathML object, it must ask the object for its extent, passing it information on the font context, the available page width, and an indication of whether the expression is to be in-line or displayed in its own paragraph. The object must return the size of the area required for its rendering and a baseline offset value.
Although current browsers do not perform page-breaking but display a long document as a continuously scrollable stream, this may change in future browsers. If so, page-breaking of equations must be taken into account, much like line-breaking.
Obviously, a computer language like MathML does nothing by itself --- it requires software that can interpret it. Although any software may be designed to interpret MathML, here we are concerned with so-called "user agents", or browsers, that serve as a general-purpose presenters of data. In the current context, a browser applies two kinds of processing to the content it handles: direct rendering to the user (screen display, printing, conversion to speech) and various kinds of mediation between the content and other software (e.g. copying to the clipboard, doing something when the user clicks on some part of the rendering etc.). Such processing must be done using software components that can be invoked by the browser.
Intrinsic to the XML concept is that of extension. It is obvious that we cannot keep expanding the kinds of data that browsers are required to handle directly. XML is a general mechanism for extending the domain of content (MathML is a good example of that). In order to fully achieve the goals of XML, we need to have general mechanisms for connecting software to the content. This can be thought of as the XML/HTML interface, but perhaps it is better described as the XML/browser interface because not only does it deal with how XML can be incorporated into HTML at the language level, it also must deal with how the browser (i.e. the HTML processor) interfaces with software components that process XML.
A MathML object might be processed many different ways:
This implies that a MathML object respond to a set of methods, each responsible for processing the MathML in a certain way. The set of methods to which a particular object can respond may be defined by both the document and the browser environment. Such methods may be implemented in the browser itself, by scripts in the content, or by external software components that the browser can invoke. There may be multiple implementations of these methods and it may be necessary to allow the user to specify which is to be used, or the preference may be stated in the content itself.
Methods may be invoked by the browser directly (e.g. rendering), by scripts initiated by button clicks, etc., or by the user directly (e.g. clicking or double-clicking on the object with the mouse, selecting it and invoking a method from a menu). Typically, the browser software will know of some of the methods available for a given object, but it must be prepared to build a list of these methods at document-processing time based on information collected from the content and from available external software components.
Access to MathML elements and attributes by software should be via the XML Object Model within the W3C's Document Object Model (DOM), rather than by parsing MathML source directly. This should be the case for both MathML object methods and scripts that manipulate MathML objects. MathML methods should also gain access to their surrounding document context via DOM as well. This will require that methods be passed some kind of context object that they can use to obtain the ambient document properties at their current location.
It is important to have an array of facilities available for implementing MathML methods, including:
It should be possible for each method of an object to be written in a different programming language and have its definition come from different sources (i.e. script in the document, external software component).