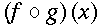 .
.
| Up: Table of Contents | REC-MathML-19980407; revised 19990707 |
This section provides detailed descriptions of the MathML content tags. They are grouped in categories which broadly reflect the area of mathematics from which they come, and also the grouping in the MathML DTD. There is no linguistic difference in MathML between operators and functions. Their separation here and in the DTD is for reasons of clarity.
When working with the content elements, keep in mind the following.
The role of the content elements is analogous to data entry in a mathematical system. The information that is provided is there to facilitate the successful parsing of an expression as the intended mathematical object by a receiving application.
MathML content elements do not by themselves "perform" any mathematical evaluations or operations. They do not "evaluate" in a browser and any "action" that is ultimately taken on those objects is determined entirely by the receiving mathematical application. For example, editing programs and applications geared to computation for the lower grades would typically leave 3 + 4 as is, while computational systems targeting a more advanced audience might evaluate this to as 7. Similarly, some computational systems might evaluate sin(0) to 0 while others would leave it unevaluated. Yet other computational systems might be unable to deal with pure symbolic expressions sin(x) and may even regard it as a data entry error. None of this has any bearing on the correctness of the original MathML representation. Where evaluation is mentioned at all in the descriptions below, it is merely to help clarify the meaning of the underlying operation.
Apart from the instances where there is an explicit interaction with presentation tagging, there is no required rendering (visual or aural) -- only a suggested default. As such, the presentations that are included in this section are merely to help communicate to the reader the intended mathematical meaning by association with the same expression written in a more traditional notation.
The available content elements are:
The cn element uses the attribute type to represent other types of numbers such as integer, rational, real, complex etc. and base to specify the numerical base.
In addition to simple PCDATA, cn accepts as content PCDATA separated by the <sep/> element. This determines the different parts needed to construct a rational or complex-cartesian number.
Alternative input notations for numbers are possible, but must be explicitly defined by using the definitionURL attribute to refer to a written specification of how a <sep/> separated sequence of real numbers is to be interpreted.
All attributes are CDATA:
<cn type="real"> 12345.7 </cn>
<cn type="integer"> 12345 </cn>
<cn type="integer" base="16"> AB3 </cn>
<cn type="rational"> 12342 <sep/> 2342342 </cn>
<cn type="complex-cartesian"> 12.3 <sep/> 5 </cn>
<cn type="complex-polar"> 2 <sep/> 3.1415 </cn>
<cn type="constant"> π </cn>
By default, contiguous blocks of PCDATA contained in cn elements should render as if it were wrapped in an mn presentation elements. Similarly, presentation markup contained in a cn element should render as it normally would. A mixture of PCDATA and presentation markup should render as if it were contained wrapped in an mrow element, with contiguous blocks of PCDATA wrapped in mn elements.
However, not all mathematical systems that encounter content based tagging do visual or aural rendering. The receiving applications are free to make use of a number in the manner it normally handles numerical data. Some systems might simplify the rational number 12342/2342342 to 6171/1171171 while pure floating point based systems might approximate this as .5269085385e-2. All numbers might be re-expressed in base 10. The role of MathML is simply to record enough information about the mathematical object and its structure so that it may be properly parsed.
The following renderings of the above MathML expressions are included both to help clarify the meaning of the corresponding MathML encoding and as suggestions for authors of rendering applications. In each case, no mathematical evaluation is intended or implied.
12345.7
12345
AB316
12342 / 2342342
12.3 + 5 i
Polar( 2 , 3.1415 )
π
The ci element is used to specify a symbolic name. Such names are used to identify types of mathematical objects. By default they are assumed to represent complex scalars. The ci element may contain arbitrary presentation markup in its content (see chapter 3) so that its presentation as a symbol can be very elaborate.
The ci element uses the type attribute to specify the type of object that it represents. Valid types include integer, rational, real, float, complex, complex-polar, complex-cartesian, constant, and more generally, any of the names of the MathML container elements (e.g. vector) or their type values. The definitionURL attribute can be used to extend the definition of ci to include other types. For example, a more advanced use might require a "complex-vector".
1. <ci> x </ci>
2. <ci type="vector"> V </ci>
3. <ci>
<msub>
<mi>x</mi>
<mi>a</mi>
</msub>
</ci>
1. x
2. V
3. xi
The apply element allows a function or operator to be applied to its arguments. Nearly all expression construction in MathML content markup is carried out by applying operators or functions to arguments. The first child of apply is the operator, to be applied, with the other child elements as arguments.
The apply element is conceptually necessary in order to distinguish between a function or operator, and an instance of its use. The expression constructed by applying a function to 0 or more arguments is always an element from the range of the function.
Proper usage depends on the operator that is being applied. For example, the plus operator may have zero or more arguments. while the minus operator requires 1 or 2 arguments to be properly formed.
If the object being applied as a function is not already one of the elements known to be a function (such as fn, sin or plus) then it is treated as if it were the contents of an fn element.
Some operators such as diff and int make use of "named" arguments. These special arguments are elements which appear as children of the apply element and identify "parameters" such as the variable of differentiation or the domain of integration.
1. <apply><factorial/>
<cn>3</cn>
</apply>
2. <apply><plus/>
<cn>3</cn>
<cn>4</cn>
</apply>
3. <apply><sin/>
<ci>x</ci>
</apply>
A mathematical system which has been passed an apply element is free to do with it whatever it normally does with such mathematical data. It may be that no rendering is involved (e.g. a syntax validator), or that the "function application" is evaluated and that only the result is rendered (e.g. sin(0) -> 0).
When an unevaluated "function application" is rendered there are a wide variety of appropriate renderings. The choice often depends on the function or operator being applied. Applications of basic operations such as plus are generally presented using an infix notation while applications of sin would use a more traditional functional notation such as sin (x). Consult the default rendering for the operator being applied.
Applications of user-defined functions (see fn) which are not evaluated by the receiving or rendering application would typically render using a traditional functional notation unless an alternative presentation is specified using the semantics tag.
The first child of reln is the relational operator, to be applied, with the other child elements as arguments.
See the Usage Guide for further details.
<reln><eq/> <ci> a </ci> <ci> b </ci> </reln> <reln><lt/> <ci> a </ci> <ci> b </ci> </reln>
a = b
a < b
It is the primary mechanism used to extend the collection of "known" mathematical functions. The definitionURL attribute allows for a specific written definition to be referenced by URL. (New functions may also be introduced by using a declaration in conjunction with a lambda expression.)
1. <fn><ci> L </ci> </fn>
2. <fn definitionURL="http://www.openmath.org/CDs/MyDC/MyDefinition">
<ci>
<msub>
<mi>J</mi>
<mn>0</mn>
</msub>
</ci>
</fn>
3. <fn>
<apply> <plus/>
<ci> f </ci>
<ci> g </ci>
</apply>
</fn>
1. L
2. J0
3. f + g
The interval element is used to represent simple mathematical intervals of the real number line. It takes an attribute closure which can take on any of the values open, closed, open-closed, or closed-open, with a default value of closed.
More general domains are constructed by using the condition and bvar elements to bind free variables to constraints.
The interval element expects either two child elements which evaluate to real numbers or one child element which is a condition defining the interval. interval accepts a closure attribute which specifies if the interval is open, closed, or half open.
1. <interval>
<ci> a </ci>
<ci> b </ci>
</interval>
2. <interval closure="open-closed">
<ci> a </ci>
<ci> b </ci>
</interval>
[a,b]
(a,b]
The inverse element is applied to a function in order to construct a generic expression for the functional inverse of that function. (See also the discussion of inverse in section 4.1.3.7). As with other MathML functions, inverse may either be applied to arguments, or it may appear alone, in which case it represents an abstract inversion operator acting on other functions.
A typical use of the inverse element is in an HTML document discussing a number of alternative definitions for a particular function so that there is a need to write and define f (-1)(x).
To associate a particular definition with f (-1), use the definitionURL attribute.
1. <apply><inverse/>
<ci> f </ci>
</apply>
2. <apply><inverse definitionURL="MyDefinition"/>
<ci> f </ci>
</apply>
3. <apply>
<apply><inverse/>
<ci type="matrix"> a </ci>
</apply>
<ci> A </ci>
</apply>
<cn type="complex"> 3 <sep/> 4 </cn>
It is used to define general sets and lists in situations where the elements cannot be explicitly enumerated. Condition contains either a single reln or apply element; the apply element is used to construct compound conditions." For example, it is used below to describe the set of all x such that x < 5. See the discussion on sets in section section 4.4.6.
See the Usage Guide for further details.
1. <condition>
<reln><in/><ci> x </ci><ci type="set"> R </ci></reln>
</condition>
2. <condition>
<apply> <and/>
<reln><gt/><ci> x </ci><cn> 0 </cn></reln>
<reln><lt/><ci> x </ci><cn> 1 </cn></reln>
</apply>
</condition>
3. <apply>
<max/>
<bvar><ci> x </ci></bvar>
<condition>
<apply> <and/>
<reln><gt/><ci> x </ci><cn> 0 </cn></reln>
<reln><lt/><ci> x </ci><cn> 1 </cn></reln>
</apply>
</condition>
<apply>
<minus/>
<ci> x </ci>
<apply>
<sin/>
<ci> x </ci>
</apply>
</apply>
</apply>
1. x in R
2. x > 0 and x < 1
3. maxx { x - sin x | 0 < x < 1}
The various attributes of the declare element assign properties to the object being declared or determine where the declaration is in effect.
By default, the scope of a declaration is "local" to the surrounding container element. Setting the value of the scope attribute to "global" extends the scope of the declaration to the enclosing math element. As discussed in Section 4.3.2.8, MathML contains no provision for making document-wide declarations at present, though it is anticipated this capability will be added in future revisions of MathML, when supporting technologies become available. declare takes 1 or 2 children. The first, mandatory, child is a ci containing the identifier being declared.
The second, optional, child is a constructor initialising the variable<declare type="vector"> <ci> V </ci> </declare>
<declare type="vector">
<ci> V </ci>
<vector>
<cn> 1 </cn><cn> 2 </cn><cn> 3 </cn>
</vector>
</declare>
The constructor type and the type of the element declared must agree. For example, if the type attribute of the declaration is fn, the second child (constructor) must be an element equivalent to an fn element (This would include actual fn elements, lambda elements and any of the defined function in the basic set of content tags.) If no type is specified in the declaration then the type attribute of the declared name is set to the type of the constructor (second child) of the declaration. The type attribute of the declaration can be especially useful in the special case of the second element being a symantic tag,
All attributes are CDATA:
<declare type="fn" nargs="2" scope="local">
<ci> f </ci>
<apply><plus/>
<ci> F </ci><ci> G </ci>
</apply>
</declare>
declares f to be a two-variable function with the
property that
f(x,y) = (F + G)(x,y).
The declaration
<declare type="fn">
<ci> J </ci>
<lambda>
<bvar><ci> x </ci></bvar>
<apply><ln/>
<ci> x </ci>
</apply>
</lambda>
</declare>
associates the name J with a one-variable function defined so
that J(x) = ln x (Note that because of the type attribute of
the declare element, the second argument must be something of
type fn, namely a known function like sin, an fn
construct, or a lambda construct.)
The type attribute on the declaration is only necessary if if the type cannot be inferred from the type of the second argument.
Even when a declaration is in effect it is still possible to override attributes values selectively as in <ci type="integer"> V </ci> . This capability is needed in order to write statements of the form "Let S be a member of S".
Since the declare construct is not directly rendered, most declarations are likely to be invisible to a reader. However, declarations can produce quite different effects in an application which evaluates or manipulates MathML content. While the declaration
<declare>
<ci> v </ci>
<vector>
<cn> 1 </cn>
<cn> 2 </cn>
<cn> 3 </cn>
</vector>
</declare>
is active the symbol v acquires all the properties of the
vector, and even its dimension and components have meaningful values.
This may affect how v is rendered by some applications, as well
as how it is treated mathematically.
See the Usage Guide for further details.
<lambda>
<bvar><ci> x </ci></bvar>
<apply><sin/>
<apply><plus/>
<ci> x </ci>
<cn> 1 </cn>
</apply>
</apply>
</lambda>
The following examples constructs a one argument function in which the argument b specifies the upper bound of a specific definite integral.
<lambda>
<bvar><ci> b </ci></bvar>
<apply>
<int/>
<bvar>
<ci> x </ci>
</bvar>
<lowlimit>
<ci> a </ci>
</lowlimit>
<uplimit>
<ci> b </ci>
</uplimit>
<apply><fn><ci> f </ci></fn>
<ci> x </ci>
</apply>
</apply>
</lambda>
Such constructs are often used
conjunction with declare to construct new
functions.
Lambda(x,f(x))
To override the default semantics for the <compose/> element, or to associate a more specific definition for function composition, use the definitionURL attribute.
See the Usage Guide for further details.
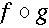 .
.
The following markup represents<apply><compose/> <fn><ci> f </ci></fn> <fn><ci> g </ci></fn> </apply>
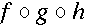 .
.
<apply><compose/> <ci type="fn"> f </ci> <ci type="fn"> g </ci> <ci type="fn"> h </ci> </apply>
The following examples both represent 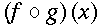 .
.
<apply>
<apply><compose/>
<fn><ci> f </ci></fn>
<fn><ci> g </ci></fn>
</apply>
<ci> x </ci>
</apply>
<apply><fn><ci> f </ci></fn>
<apply>
<fn><ci> g </ci></fn>
<ci> x </ci>
</apply>
</apply>
The indent element represents the identity function. MathML makes no assumption about the function space in which the identity function resides. That is, proper interpretation of the domain (and hence range) of the identity function depends on the context in which it is used.
To override the default semantics for the <ident/> element, or to associate a more specific definition, use the definitionURL attribute.
See the Usage Guide for further details.
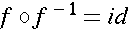 .
.
<reln><eq/>
<apply><compose/>
<fn><ci> f </ci></fn>
<apply><inverse/>
<fn><ci> f </ci></fn>
</apply>
</apply>
<ident/>
</reln>
id
The quotient element is the operator used for division modulo a particular base. When the quotient operator is applied to integer arguments a and b, the result is the "quotient of a divided by b". That is, quotient returns the unique integer, q such that a = q b + r. (In common usage, q is called the quotient and r is the remainder.)
The quotient element takes the attribute definitionURL if it is desired to override the default semantics.
The quotient element is a binary arithmetic operator.
See the Usage Guide for further details.
Various mathematical applications will use this data in different ways. Editing applications might choose an image such as shown below, while a computationally based application would evaluate it to 2 when a = 13 and b = 5.<apply><quotient/> <ci> a </ci> <ci> b </ci> </apply>
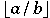
The exp element represents the exponential function associated with the inverse of the ln function. In particular, exp(1) is approximately 2.718281828.
exp takes the attribute definitionURL which may be used to override the default semantics.
The exp element is a unary arithmetic operator.
See the Usage Guide for further details.
<apply><exp/> <ci> x </ci> </apply>
ex
The factorial element is used to construct factorials.
The factorial element takes the attribute definitionURL which may be used to override the default semantics.
The factorial element is a unary arithmetic operator.
See the Usage Guide for further details.
If this were evaluated at n = 5 it would evaluate to 120.<apply><factorial/> <ci> n </ci> </apply>
n!
The divide element takes the attribute definitionURL which may be used to override the default semantics.
The divide element is a binary arithmetic operator. See the Usage Guide for further details.
As a MathML expresssion, this does not evaluate. However, on receiving such an expression, some applications may attempt to evaluate and simplify the value. For example, when a=5 and b=2 some mathematical applications may evaluate this to 2.5 while others will treat is as a rational number.<apply> <divide/> <ci> a </ci> <ci> b </ci> </apply>
a/b
The elements max and min are used to compare the values of their arguments. They return the maximum and minimum of these values respectively.
The max and min elements take the attribute definitionURL which can be used to override the default semantics.
The max and min elements are n-ary arithmetic operators. See the Usage Guide for further details.
The elements to be compared may also be described using bound variables with a condition element and an expression to be maximised, as in:<apply><max/> <ci> a </ci> <ci> b </ci> </apply>
<apply><min/>
<bvar><ci>x</ci></bvar>
<condition>
<reln><notin/><ci> x </ci><ci type="set"> B </ci></reln>
</condition>
<apply>
<power/>
<ci> x </ci>
<cn> 2 </cn>
</apply>
</apply>
Note that the bound variable may be implicit:
<apply><max/>
<condition>
<apply><and/>
<reln><in/><ci>x</ci><ci type="set">B</ci></reln>
<reln><notin/><ci>x</ci><ci type="set">C</ci></reln>
</apply>
</condition>
</apply>
1. max {a, b}
2. minx { x2 | x notin B }
3. max { x in B and x notin C}
The minus element is the subtraction operator.
The minus element takes the attribute definitionURL which can be used to override the default semantics.
The minus element can be used as a unary arithemtic operator (e.g. to represent -x) or as a binary arithmetic operator (e.g. to represent x-y). See the Usage Guide for further details.
If this were evaluated at x= 5 and y = 2 it would yield 3.<apply> <minus/> <ci> x </ci> <ci> y </ci> </apply>
x - y
The plus element takes the attribute definitionURL which can be used to override the default semantics.
The plus element is an n-ary arithemtic operator. See the Usage Guide for further details.
If this were evaluated at x = 5, y = 2 and z = 1 it would yield 8.<apply><plus/> <ci> x </ci> <ci> y </ci> <ci> z </ci> </apply>
x + y + z
The power element takes the attribute definitionURL which can be used to override the default semantics.
The power element is an binary arithmetic operator. See the Usage Guide for further details.
If this were evaluated at x= 5 it would yield 125.<apply><power/> <ci> x </ci> <cn> 3 </cn> </apply>
x3
The rem element is the operator which returns the "remainder" of a division modulo a particular base. When the rem operator is applied to integer arguments a and b, the result is the "remainder of a divided by b". That is, rem returns the unique integer, r such that a = q b + r, where r < q. (In common usage, q is called the quotient and r is the remainder.)
The rem element takes the attribute definitionURL which can be used to override the default semantics.
The rem element is a binary arithmetic operator. See the Usage Guide for further details.
<apply><rem/> <ci> a </ci> <ci> b </ci> </apply>If this were evaluated at a = 15 and b = 8 it would yield 7.
a mod b
The times element is the multiplication operator.
times takes the attribute definitionURL which can be used to override the default semantics.
If this were evaluated at a = 5.5 and b = 3 it would yield 16.5.<apply> <times/> <ci> a </ci> <ci> b </ci> </apply>
a b
The root element is used to construct roots. The kind of root to be taken is specified by a degree element, which should be given as the first child of the apply element enclosing the root element. Thus, square roots correspond to the case where degree contains the value 2, cube roots correspond to 3, and so on. If no degree is present, a default value of 2 is used.
The root element takes the attribute definitionURL which can be used to override the default semantics.
The root element is an operator taking qualifiers. See the Usage Guide for further details.
The nth root of a is is given by
<apply> <root/> <degree><ci> n </ci></degree> <ci> a </ci> </apply>
The gcd element is used to denote the greatest common divisor of its arguments.
The gcd takes the attribute definitionURL which can be used to override the default semantics.
The gcd element is an n-ary operator. See the Usage Guide for further details.
If this were evaluated at a = 15, b = 21, c = 48 it would yield 3.<apply> <gcd/> <ci> a </ci> <ci> b </ci> <ci> c </ci> </apply>
GCD(a, b, c)
The and element is the boolean "and" operator.
The and element takes the attribute definitionURL which can be used to override the default semantics.
The and element is an n-ary logical operator. See the Usage Guide for further details.
If this were evaluated and both a and b had truth values of "true", then the value would be "true".<apply><and/> <ci> a </ci> <ci> b </ci> </apply>
a and b
The or element is the boolean "or" operator.
The or element takes the attribute definitionURL which can be used to override the default semantics.
The or element is an n-ary logical operator. See the Usage Guide for further details.
<apply><or/> <ci> a </ci> <ci> b </ci> </apply>
a or b
The xor element is the boolean "exclusive or" operator.
xor takes the attribute definitionURL which can be used to override the default semantics.
The xor element is an n-ary logical operator. See the Usage Guide for further details.
<apply><xor/> <ci> a </ci> <ci> b </ci> </apply>
a XOR b
The not operator is the boolean "not" operator.
The not element takes the attribute definitionURL which can be used to override the default semantics.
The not element is an unary logical operator. See the Usage Guide for further details.
<apply><not/> <ci> a </ci> </apply>
NOT a
The implies element is the boolean "implies" relational operator.
The implies element takes the attribute definitionURL which can be used to override the default semantics.
The implies element is a binary logical operator. See the Usage Guide for further details.
Mathematical applications designed for the evaluation of such expressions would evaluate this to "true" when a = "false" and b = "true".<reln><implies/> <ci> A </ci> <ci> B </ci> </reln>
The forall element represents the universal quantifier of logic. It must used in conjunction with one or more bound variables, an optional condition element, and an assertion, which may either take the form of an apply or reln element.
The forall element takes the attribute definitionURL which can be used to override the default semantics.
The forall element is an quantifier. See the Usage Guide for further details.
The first example encodes the sense of the expression "for all x, x - x = 0".
<apply>
<forall/>
<bvar><ci> x </ci></bvar>
<reln><eq/>
<apply>
<minus/><ci> x </ci><ci> x </ci>
</apply>
<cn>0</cn>
</reln>
</apply>
A more involved example, making use of an optional condition element encodes the sense of the expression "for all p, q in Q such that p < q, p < q2".
<apply>
<forall/>
<bvar><ci> p </ci></bvar>
<bvar><ci> q </ci></bvar>
<condition>
<apply><and/>
<reln><in/><ci> p </ci><ci type="set"> Q </ci></reln>
<reln><in/><ci> q </ci><ci type="set"> Q </ci></reln>
<reln><lt/><ci> p </ci><ci> q </ci></reln>
</apply>
</condition>
<reln><lt/>
<ci> p </ci>
<apply>
<power/>
<ci> q </ci>
<cn> 2 </cn>
</apply>
</reln>
</apply>
A final example, utilizing both the forall and exists quantifiers, encodes the sense of the expression "for all n > 0, n in Z, there exist x, y, z in Z such that xn + yn = zn".
<apply>
<forall/>
<bvar><ci> n </ci></bvar>
<condition>
<apply><and/>
<reln><in/><ci> n </ci><ci type="set"> Z </ci></reln>
<reln><gt/><ci> n </ci><cn> 0 </cn></reln>
</apply>
</condition>
<apply>
<exists/>
<bvar><ci> x </ci></bvar>
<bvar><ci> y </ci></bvar>
<bvar><ci> z </ci></bvar>
<condition>
<apply><and/>
<reln><in/><ci> x </ci><ci type="set"> Z </ci></reln>
<reln><in/><ci> y </ci><ci type="set"> Z </ci></reln>
<reln><in/><ci> z </ci><ci type="set"> Z </ci></reln>
</apply>
</condition>
<reln>
<eq/>
<apply><plus/>
<apply><power/><ci> x </ci><ci> n </ci></apply>
<apply><power/><ci> y </ci><ci> n </ci></apply>
</apply>
<apply><power/><ci> z </ci><ci> n </ci></apply>
</reln>
</apply>
</apply>
1. for all
2.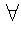
The exists element represents the existential quantifier of logic. It must used in conjuction with one or more bound variables, an optional condition element, and an assertion, which may either take the form of an apply or reln element.
The exists element takes the attribute definitionURL which can be used to override the default semantics.
The exists element is an quantifier. See the Usage Guide for further details.
The following example encodes the sense of the expression "there exists an x such that f(x) = 0".
<apply>
<exists/>
<bvar><ci> x </ci></bvar>
<reln><eq/>
<apply>
<fn><ci> f </ci></fn>
<ci> x </ci>
</apply>
<cn>0</cn>
</reln>
</apply>
1. there exists
2.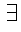
The abs element represents the absolute value of a real quantity or the modulus of a complex quantity.
The abs element takes the attribute definitionURL which can be used to override the default semantics.
The abs element is a unary arithmetic operator. See the Usage Guide for further details.
The following example encodes the absolute value of x.
<apply> <abs/> <ci> x </ci> </apply>
|x|
The conjugate element represents the complex conjugate of a complex quantity.
The conjugate element takes the attribute definitionURL which can be used to override the default semantics.
The conjugate element is a unary arithmetic operator. See the Usage Guide for further details.
The following example encodes the conjugate of x + i y.
<apply><conjugate/>
<apply><plus/>
<ci> x </ci>
<apply><times/>
<cn> ⅈ </cn>
<ci> y </ci>
</apply>
</apply>
</apply>
The eq element is the "equals" relational operator.
The eq element takes the attribute definitionURL which can be used to override the default semantics.
The equals element is an n-ary relation. See the Usage Guide for further details.
If this were tested at a = 5.5 and b = 6 it would yield the truth value "FALSE".<reln><eq/> <ci> a </ci> <ci> b </ci> </reln>
a = b
The neq element is the "not equal to" relational operator.
neq takes the attribute definitionURL which can be used to override the default semantics.
The neq element is an binary relation. See the Usage Guide for further details.
If this were tested at a = 5.5 and b = 6 it would yield the truth value "TRUE".<reln><neq/> <ci> a </ci> <ci> b </ci> </reln>
The gt element takes the attribute definitionURL which can be used to override the default semantics.
The gt element is an n-ary relation. See the Usage Guide for further details.
If this were tested at a = 5.5 and b = 6 it would yield the truth value "FALSE".<reln><gt/> <ci> a </ci> <ci> b </ci> </reln>
A > B
The lt element is the "less than" relational operator.
The lt element takes the attribute definitionURL which can be used to override the default semantics.
The lt element is an n-ary relation. See the Usage Guide for further details.
If this were tested at a = 5.5 and b = 6 it would yield the truth value "TRUE".<reln><lt/> <ci> a </ci> <ci> b </ci> </reln>
A < B
The geq element is the "greater than or equal" relational operator.
The geq element takes the attribute definitionURL which can be used to override the default semantics.
The geq element is an n-ary relation. See the Usage Guide for further details.
If this were tested for a = 5.5 and b = 5.5 it would yield the truth value "TRUE".<reln><geq/> <ci> a </ci> <ci> b </ci> </reln>
The leq element is the "less than or equal" relational operator.
The leq element takes the attribute definitionURL which can be used to override the default semantics.
The leq element is an n-ary relation. See the Usage Guide for further details.
If a = 5.4 and b = 5.5 this will yield the truth value "TRUE".<reln><leq/> <ci> a </ci> <ci> b </ci> </reln>
The ln element is the natural logarithm operator.
The ln element takes the attribute definitionURL which can be used to override the default semantics.
The ln element is an unary calculus operator. See the Usage Guide for further details.
If a = e this will yield the value 1.<apply><ln/> <ci> a </ci> </apply>
ln a
The log element takes the attribute definitionURL which can be used to override the default semantics.
The log element can be used as either an operator taking qualifiers or a unary calculus operator. See the Usage Guide for further details.
<apply> <log/>
<logbase>
<cn> 3 </cn>
</logbase>
<ci> x </ci>
</apply>
This markup represents "the base 3 log of x". For natural logarithms base
e, the ln element should be used instead.
log3 x
The int element is the operator element for an integral. The lower limit, upper limit and bound variable are given by (optional) child elements, lowlimit, uplimit and bvar in the enclosing apply element. The integrand is also specified as a child element of the enclosing apply element.
The domain of integration may alternatively be specified by using an interval element, or by a condition element. In such cases, if a bound variable of integration is intended, it must be specified explicitly. (The condition may involve more than one symbol.)
The int element takes the attribute definitionURL which can be used to override the default semantics.
The int element an operator taking qualifiers. See the Usage Guide for further details.
This example specifies a lowlimit, uplimit, and bvar.
<apply>
<int/>
<bvar>
<ci> x </ci>
</bvar>
<lowlimit>
<cn> 0 </cn>
</lowlimit>
<uplimit>
<ci> a </ci>
</uplimit>
<apply>
<fn><ci> f </ci></fn>
<ci> x </ci>
</apply>
</apply>
This example specifies the domain of integration with an interval element.
<apply><int/>
<bvar>
<ci> x </ci>
</bvar>
<interval>
<ci> a </ci>
<ci> b </ci>
</interval>
<apply><cos/>
<ci> x </ci>
</apply>
</apply>
The final example specifies the domain of integration with an condition element.
<apply><int/>
<bvar>
<ci> x </ci>
</bvar>
<condition>
<reln><in/>
<ci> x </ci>
<ci type="set"> D </ci>
</reln>
</condition>
<apply><fn><ci> f </ci></fn>
<ci> x </ci>
</apply>
</apply>
The diff element is the differentiation operator element for functions of a single real variable. The bound variable is given by a bvar element which is a child of the containing apply element. The bvar elements may also contain a degree element, which specifies the order of the derivative to be taken.
The diff element takes the attribute definitionURL which can be used to override the default semantics.
The diff element is an operator taking qualifiers. See the Usage Guide for further details.
<apply><diff/>
<bvar>
<ci> x </ci>
</bvar>
<apply><fn><ci> f </ci></fn>
<ci> x </ci>
</apply>
</apply>
The partialdiff element is the partial differentiation operator element for functions of several real variables. The bound variables are given by bvar elements, which are children of the containing apply element. The bvar elements may also contain a degree element, which specifies the order of the partial derivative to be taken in that variable.
The partialdiff element takes the attribute definitionURL which can be used to override the default semantics.
The partialdiff element is an operator taking qualifiers. See the Usage Guide for further details.
<apply><partialdiff/>
<bvar>
<ci> x </ci>
<degree>
<cn> 2 </cn>
</degree>
</bvar>
<bvar>
<ci> y </ci>
</bvar>
<apply><fn><ci> f </ci></fn>
<ci> x </ci>
<ci> y </ci>
</apply>
</apply>
The lowlimit element is the container element used to indicate the "lower limit" of an operator using qualifiers. For example, in an integral, it can be used to specify the lower limit of integration. Similarly, it is also used to specify the lower limit of an index for sums and products.
The meaning of the lowlimit element depends on the context it is being used in. For further details about how qualifiers are used in conjunction with operators taking qualifiers, consult the Usage Guide.
<apply><int/>
<bvar>
<ci> x </ci>
</bvar>
<lowlimit>
<ci> a </ci>
</lowlimit>
<uplimit>
<ci> b </ci>
</uplimit>
<apply><fn><ci> f </ci></fn>
<ci> x </ci>
</apply>
</apply>
The default rendering of the lowlimit element and its contents depends on the context. In the preceding example, it should be rendered as a subscript to the integral sign:
Consult the descriptions of individual operators which make use of the lowlimit construct for default renderings.
The uplimit element is the container element used to indicate the "upper limit" of an operator using qualifiers. For example, in an integral, it can be used to specify the upper limit of integration. Similarly, it is also used to specify the upper limit of an index for sums and products.
The meaning of the uplimit element depends on the context it is being used in. For further details about how qualifiers are used in conjunction with operators taking qualifiers, consult the Usage Guide.
<apply><int/>
<bvar>
<ci> x </ci>
</bvar>
<lowlimit>
<ci> a </ci>
</lowlimit>
<uplimit>
<ci> b </ci>
</uplimit>
<apply><fn><ci> f </ci></fn>
<ci> x </ci>
</apply>
</apply>
The default rendering of the uplimit element and its contents depends on the context. In the preceding example, it should be rendered as a superscript to the integral sign:
Consult the descriptions of individual operators which make use of the uplimit construct for default renderings.
The meaning of the bvar element depends on the context it is being used in. For further details about how qualifiers are used in conjunction with operators taking qualifiers, consult the Usage Guide.
<apply><diff/>
<bvar>
<ci> x </ci>
<degree>
<cn> 2 </cn>
</degree>
</bvar>
<apply><power/>
<ci> x </ci>
<cn> 2 </cn>
</apply>
</apply>
<apply><int/>
<bvar><ci> x </ci></bvar>
<condition>
<reln><in/><ci> x </ci><ci> D </ci></reln>
</condition>
<apply><fn><ci> f </ci></fn>
<ci> x </ci>
</apply>
</apply>
The default rendering of the bvar element and its contents depends on the context. In the preceding examples, it should be rendered as the x in the d x of the integral, and as the x in the denominator of the derivative symbol:
Note that in the case of the derivative, the default rendering of the degree child of the bvar element is as an exponent.
Consult the descriptions of individual operators which make use of the uplimit construct for default renderings.
The degree element is the container element for the "degree" or "order" of an operation. There are a number basic mathematical constructs which come in families, such as derivatives and moments. Rather than introduce special elements for each of these families, MathML uses a single general construct, the degree element for this concept of "order".
The meaning of the degree element depends on the context it is being used in. For further details about how qualifiers are used in conjunction with operators taking qualifiers, consult the Usage Guide.
<apply><partialdiff/>
<bvar>
<ci> x </ci>
<degree>
<ci> n </ci>
</degree>
</bvar>
<bvar>
<ci> y </ci>
<degree>
<ci> m </ci>
</degree>
</bvar>
<apply><sin/>
<apply> <times/>
<ci> x </ci>
<ci> y </ci>
</apply>
</apply>
</apply>
The default rendering of the degree element and its contents depends on the context. In the preceding example, the degree elements would be rendered as the exponents in the differentiation symbols:
Consult the descriptions of individual operators which make use of the uplimit construct for default renderings.
The set element is the container element which constructs a set of elements. The elements of a set can be defined either by explicitly listing the elements, or by using the bvar and condition elements.
The set element is a constructor container. See the Usage Guide for further details.
<set> <ci> b </ci> <ci> a </ci> <ci> c </ci> </set>
<set>
<bvar><ci> x </ci></bvar>
<condition>
<reln><lt/>
<ci> x </ci>
<cn> 5 </cn>
</reln>
</condition>
</set>
1. {a,b,c}
2. {x | x < 5 }
The list element is the container element which constructs a list of elements. Elements can be defined either by explicitly listing the elements, or by using the bvar and condition elements.
Lists differ from sets in that there is an explicit order to the elements. Two orders are supported: lexicographic and numeric. The kind of ordering which should be used is specified by the order attribute.
The list element is a constructor container. See the Usage Guide for further details.
<list> <ci> b </ci> <ci> a </ci> <ci> c </ci> </list>
<list order="numeric">
<bvar><ci> x </ci></bvar>
<condition>
<reln>
<ci> x </ci>
<cn> 5 </cn>
</reln>
</condition>
</list>
1. [a, b, c]
2. [x | x < 5 ]
The union element is the operator for a set-theoretic union or join of two (or more) sets.
The union attribute takes the attribute definitionURL which can be used to override the default semantics.
The union element is an n-ary set operator. See the Usage Guide for further details.
<apply><union/> <ci> A </ci> <ci> B </ci> </apply>
The intersect element takes the attribute definitionURL which can be used to override the default semantics.
The intersect element is an n-ary set operator. See the Usage Guide for further details.
<apply><intersect/> <ci type="set"> A </ci> <ci type="set"> B </ci> </apply>
The in element is the relational operator used for a set-theoretic inclusion ("is in" or "is a member of").
The in element takes the attribute definitionURL which can be used to override the default semantics.
The in element is a binary set relation. See the Usage Guide for further details.
<reln> <in/> <ci> a </ci> <ci type="set"> A </ci> </reln>
The notin element takes the attribute definitionURL which can be used to override the default semantics.
The notin element is a binary set relation. See the Usage Guide for further details.
<reln><notin/> <ci> a </ci> <ci> A </ci> </reln>
The subset element is the realtional operator element for a set-theoretic containment ("is a subset of").
The subset element takes the attribute definitionURL which can be used to override the default semantics.
The subset element is an n-ary set relation. See the Usage Guide for further details.
<reln><subset/> <ci> A </ci> <ci> B </ci> </reln>
The prsubset element is the relational operator element for set-theoretic proper containment ("is a proper subset of").
The prsubset element takes the attribute definitionURL which can be used to override the default semantics.
The subset element is an n-ary set relation. See the Usage Guide for further details.
<reln><prsubset/> <ci> A </ci> <ci> B </ci> </reln>
The notsubset is the relational operator element for the set-theoretic relation "is not a subset of".
The notsubset element takes the attribute definitionURL which can be used to override the default semantics.
The notsubset element is a binary set relation. See the Usage Guide for further details.
<reln><notsubset/> <ci> A </ci> <ci> B </ci> </reln>
The notprsubset is the operator element for the set-theoretic relation "is not a proper subset of".
The notprsubset takes the attribute definitionURL which can be used to override the default semantics.
The notprsubset element is a binary set relation. See the Usage Guide for further details.
<reln><notprsubset/> <ci> A </ci> <ci> B </ci> </reln>
The setdiff is the operator element for a set-theoretic difference of two sets.
The setdiff element takes the attribute definitionURL which can be used to override the default semantics. setdiff is a binary operator.
The setdiff element is a binary set operator. See the Usage Guide for further details.
<apply><setdiff/> <ci> A </ci> <ci> B </ci> </apply>
The sum element denotes the summation operator. Upper and lower limits for the sum, and more generally a domains for the bound variables are specified using uplimit, lowlimit or a condition on the bound variables. The index for the summation is specified by a bvar element.
The sum element takes the attribute definitionURL which can be used to override the default semantics.
The sum element is an operator taking qualifiers. See the Usage Guide for further details.
<apply><sum/>
<bvar>
<ci> x </ci>
</bvar>
<lowlimit>
<ci> a </ci>
</lowlimit>
<uplimit>
<ci> b </ci>
</uplimit>
<apply><fn><ci> f </ci></fn>
<ci> x </ci>
</apply>
</apply>
<apply><sum/>
<bvar>
<ci> x </ci>
</bvar>
<condition>
<reln> <in/>
<ci> x </ci>
<ci type="set"> B </ci>
</reln>
</condition>
<apply><fn><ci> f </ci></fn>
<ci> x </ci>
</apply>
</apply>
The product element denotes the product operator. Upper and lower limits for the product, and more generally a domains for the bound variables are specified using uplimit, lowlimit or a condition on the bound variables. The index for the product is specified by a bvar element.
The product element takes the attribute definitionURL which can be used to override the default semantics.
The product element is an operator taking qualifiers. See the Usage Guide for further details.
<apply><product/>
<bvar>
<ci> x </ci>
</bvar>
<lowlimit>
<ci> a </ci>
</lowlimit>
<uplimit>
<ci> b </ci>
</uplimit>
<apply><fn><ci> f </ci></fn>
<ci> x </ci>
</apply>
</apply>
<apply><product/>
<bvar>
<ci> x </ci>
</bvar>
<condition>
<reln> <in/>
<ci> x </ci>
<ci type="set"> B </ci>
</reln>
</condition>
<apply><fn><ci> f </ci></fn>
<ci> x </ci>
</apply>
</apply>
Usage Guide
The limit element is operation of taking a limit of a sequence. The limit point is expressed by specifying a lowlimit and a bvar or by specifying a condition on one or more bound variables.
The limit element takes the attribute definitionURL which can be used to override the default semantics.
The limit element is an operator taking qualifiers. See the Usage Guide for further details.
<apply><limit/>
<bvar>
<ci> x </ci>
</bvar>
<lowlimit>
<cn> 0 </cn>
</lowlimit>
<apply><sin/>
<ci> x </ci>
</apply>
</apply>
<apply><limit/>
<bvar>
<ci> x </ci>
</bvar>
<condition>
<reln>
<tendsto type="above"/>
<ci> x </ci>
<ci> a </ci>
</reln>
</condition>
<apply><sin/>
<ci> x </ci>
</apply>
</apply>
The tendsto element is used to express the relation that a quantity is tending to a specified value.
The tendsto element takes the attributes type to set the direction from which the the limiting value is approached and definitionURL which can be used to override the default semantics.
The tendsto element is a binary relational operator. See the Usage Guide for further details.
<reln>
<tendsto type="above"/>
<apply><power/>
<ci> x </ci>
<cn> 2 </cn>
</apply>
<apply><power/>
<ci> a </ci>
<cn> 2 </cn>
</apply>
</reln>
To express (x, y) -> (f(x, y), g(x, y)), one might use vectors, as in:
<reln>
<tendsto/>
<vector>
<ci> x </ci>
<ci> y </ci>
</vector>
<vector>
<apply><fn><ci> f </ci></fn>
<ci> x </ci>
<ci> y </ci>
</apply>
<apply><fn><ci> g </ci></fn>
<ci> x </ci>
<ci> y </ci>
</apply>
</vector>
</reln>
x2 -> a2
(x, y) -> (f(x, y), g(x, y))
The names of the common trigonometric functions supported by MathML are listed below. Since their standard intepretations are widely known, they are discussed as a group.
| <sin/> | <cos/> | <tan/> |
| <sec/> | <csc/> | <cot/> |
| <sinh/> | <cosh/> | <tanh/> |
| <sech/> | <csch/> | <coth/> |
| <arcsin/> | <arccos/> | <arctan/> |
These operator elements denote the standard trigonometrical functions.
These elements all take the attribute definitionURL which can be used to override the default semantics.
They are all unary trigonometric operators. See the Usage Guide for further details.
<apply><sin/> <ci> x </ci> </apply>
<apply><sin/>
<apply><plus/>
<apply><cos/>
<ci> x </ci>
</apply>
<apply><power/>
<ci> x </ci>
<cn> 3 </cn>
</apply>
</apply>
</apply>
sin x
sin(cos x + x3)
mean takes the attribute definitionURL which can be used to override the default semantics.
Usage Guide<apply><mean/> <ci> X </ci> </apply>
sdev takes the attribute definitionURL which can be used to override the default semantics.
Usage Guide<apply><sdev/> <ci> X </ci> </apply>
variance takes the attribute definitionURL which can be used to override the default semantics.
Usage Guide<apply><variance/> <ci> X </ci> </apply>
median takes the attribute definitionURL which can be used to override the default semantics.
Usage Guide<apply><median/> <ci> X </ci> </apply>
median(X)
mode takes the attribute definitionURL which can be used to override the default semantics.
Usage Guide<apply> <mode/> <ci> X </ci> </apply>
mode(X)
moment takes the attribute definitionURL which can be used to override the default semantics.
<apply><moment/>
<degree>
<cn> 3 </cn>
</degree>
<ci> X </ci>
</apply>
Usage Guide
For purposes of interaction with matrices and matrix multiplication vectors are regarded as equivalent to a matrix consisting of a single column and the transpose of a vector behaves the same as a matrix consisting of a single row.
Usage Guide<vector> <cn> 1 </cn> <cn> 2 </cn> <cn> 3 </cn> <ci> x </ci> </vector>
<matrix>
<matrixrow>
<cn> 0 </cn> <cn> 1 </cn> <cn> 0 </cn>
</matrixrow>
<matrixrow>
<cn> 0 </cn> <cn> 0 </cn> <cn> 1 </cn>
</matrixrow>
<matrixrow>
<cn> 1 </cn> <cn> 0 </cn> <cn> 0 </cn>
</matrixrow>
</matrix>
Usage Guide
Usage Guide<matrixrow> <cn> 1 </cn> <cn> 2 </cn> </matrixrow> <matrixrow> <cn> 3 </cn> <ci> x </ci> </matrixrow>
determinant takes the attribute definitionURL which can be used to override the default semantics.
Usage Guide<apply><determinant/> <ci type="matrix"> A </ci> </apply>
det A
transpose takes the attribute definitionURL which can be used to override the default semantics.
Usage Guide<apply><transpose/> <ci type="matrix"> A </ci> </apply>
At
The selector element is the operator for indexing into vectors matrices and lists. It accepts one or more arguments. The first argument identifies the vector, matrix or list from which the selection is taking place, and the second and subsequent arguments, if any, indicate the kind of selection taking place.
When selector is used with a single argument, it should be interpreted as giving the sequence of all elements in the list, vector or matrix given. The ordering of elements in the sequence for a matrix is understood to be first by column, then by row. That is, for a matrix (ai,j), where the indicies denote row and column, the ordering would be a1,1, a1,2, ... a2,1, a2,2 ... etc
When three arguments are given, the last one is ignored for a list or vector, and in the case of a matrix, the second and third arguments specify the row and column of the selected element.
When two arguments are given, and the first is a vector or list, the second argument specifies an element in the list or vector. When a matrix and only one index i is specified as in
<apply><selector/>
<matrix>
<matrixrow>
<cn> 1 </cn> <cn> 2 </cn>
</matrixrow>
<matrixrow>
<cn> 3 </cn> <cn> 4 </cn>
</matrixrow>
</matrix>
<cn> 1 </cn>
</apply>
it refers to ith matrixrow. Thus, the preceding
example selects the following row:
<matrixrow> <cn> 1 </cn> <cn> 2 </cn> </matrixrow>
selector takes the attribute definitionURL which can be used to override the default semantics.
selector is classified as an n-ary linear algebra operator even though it can take only one, two, or three arguments.
<apply><selector/> <ci type="matrix"> A </ci> <cn> 3 </cn> <cn> 2 </cn> </apply>
annotation takes the attribute encoding to define the encoding being used.
<semantics>
<apply><plus/>
<apply><sin/>
<ci> x </ci>
</apply>
<cn> 5 </cn>
</apply>
<annotation encoding="TeX">
\sin x + 5
</annotation>
</semantics>
The representations which are XML based are enclosed in an annotation-xml element while those representations which are to be parsed as PCDATA are enclosed in an annotation element.
semantics takes the attribute definitionURL which can be used to reference an external source for some or all of the semantic information.
An important purpose of the semantics construct is to associate specific semantics with a particular presentation, or additional presentation information with a content construct. The default rendering of a semantics element is the default rendering of its first child. When a MathML-presentation annotation is provided, a MathML renderer may optionally use this information to render the MathML construct. This would typically be the case when the first child is a MathML content construct and the annotation is provided to give a preferred rendering differing from the default for the content elements.
<semantics>
<apply><plus/>
<apply><sin/>
<ci> x </ci>
</apply>
<cn> 5 </cn>
</apply>
<annotation encoding="Maple">
sin(x) + 5
</annotation>
<annotation-xml encoding="MathML-Presentation">
...
...
</annotation-xml>
<annotation encoding="Mathematica">
Sin[x] + 5
</annotation>
<annotation encoding="TeX">
\sin x + 5
</annotation>
<annotation-xml encoding="OpenMath">
<OMA>..</OMA>
</annotation-xml>
</semantics>
annotation-xml is a semantic mapping element.
<semantics>
<apply><plus/>
<apply><sin/>
<ci> x </ci>
</apply>
<cn> 5 </cn>
</apply>
<annotation-xml encoding="OpenMath">
<OMA><OMS name="plus"/>
<OMA><OMS name="sin"/>
<OMV name="x"/>
</OMA>
5
</OMA>
</annotation-xml>
</semantics>
See also semantics in
the Usage Guide.