W3C MathML TestSuite: Version 3: Test-case complex1

Alternatives:
(mml file) (full) (simple) (plain) (form) (slideshow)
File:
TortureTests/Complexity/complex1
CVS-ID:
Author:
Design Science, Inc. (D. Doyle, E. Cannon, E. Tabacman, R.Miner)
Description:
short complexity test
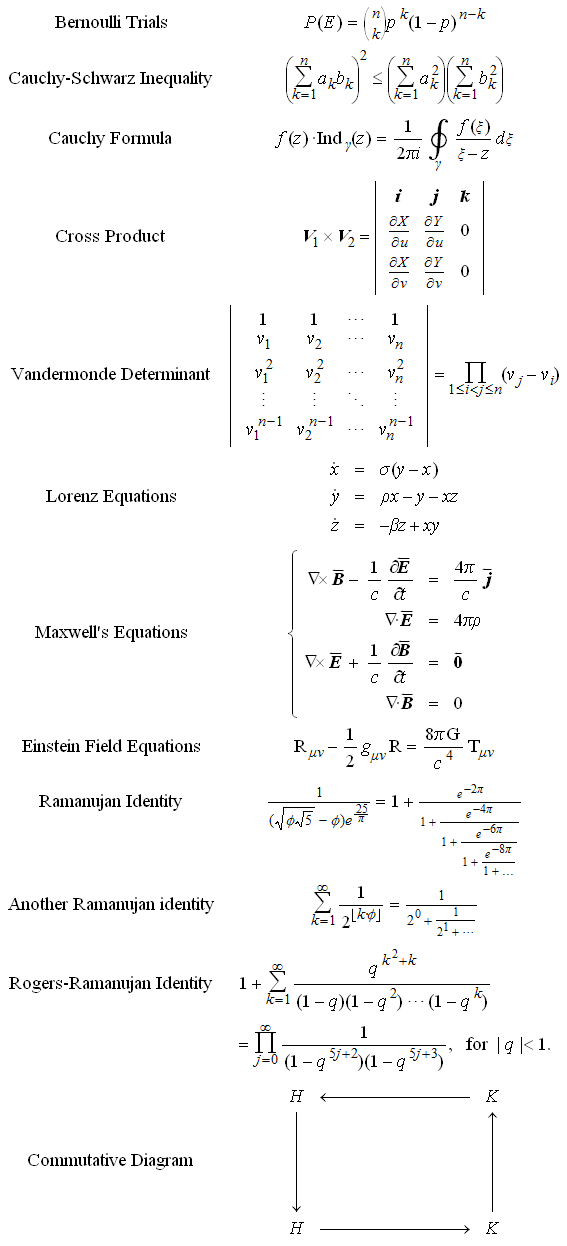
Sample Rendering:
Your browser's rendering:
\begin{matrix} Bernoulli Trials & P (E) Probability of event E: Get exactly k heads in n coin flips. = (\binom{n}{k}) Number of ways to get exactly k heads in n coin flips {p Probability of getting heads in one flip}_{}^{k Number of heads} {(1 - p) Probability of getting tails in one flip}_{}^{n - k Number of tails} \\ Cauchy-Schwarz Inequality & {(\sum_{k = 1}^{n} a_{k}^{} b_{k}^{})}_{}^{2} \leq (\sum_{k = 1}^{n} a_{k}^{2}) (\sum_{k = 1}^{n} b_{k}^{2}) \\ Cauchy Formula & f (z) \cdot {Ind}_{γ}^{} (z) = \frac{1}{2 π i} \oint_{γ}^{} \frac{f (ξ)}{ξ - z} d ξ \\ Cross Product & V_{1}^{} \times V_{2}^{} = | \begin{matrix} i & j & k \\ \frac{\partial X}{\partial u} & \frac{\partial Y}{\partial u} & 0 \\ \frac{\partial X}{\partial v} & \frac{\partial Y}{\partial v} & 0 \end{matrix} | \\ Vandermonde Determinant & | \begin{matrix} 1 & 1 & \dots & 1 \\ v_{1}^{} & v_{2}^{} & \dots & v_{n}^{} \\ v_{1}^{2} & v_{2}^{2} & \dots & v_{n}^{2} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ v_{1}^{n - 1} & v_{2}^{n - 1} & \dots & v_{n}^{n - 1} \end{matrix} | = \prod_{1 \leq i < j \leq n}^{} (v_{j}^{} - v_{i}^{}) \\ Lorenz Equations & \begin{array}{rcl} x_{}^{˙} & = & σ (y - x) \\ y_{}^{˙} & = & ρ x - y - x z \\ z_{}^{˙} & = & - β z + x y \end{array} \\ Maxwell's Equations & {\begin{array}{rcl} \nabla ​ \times B_{}^{↼} - \frac{1}{c} \frac{\partial ​ E_{}^{↼}}{\partial ​ t} & = & \frac{4 π}{c} j_{}^{↼} \\ \nabla ​ \cdot E_{}^{↼} & = & 4 π ρ \\ \nabla ​ \times E_{}^{↼} + \frac{1}{c} \frac{\partial ​ B_{}^{↼}}{\partial ​ t} & = & 0_{}^{↼} \\ \nabla ​ \cdot B_{}^{↼} & = & 0 \end{array} \\ Einstein Field Equations & R_{μ ν}^{} - \frac{1}{2} g_{μ ν}^{} R = \frac{8 π G}{c_{}^{4}} T_{μ ν}^{} \\ Ramanujan Identity & \frac{1}{(\sqrt{φ \sqrt{5}} - φ) e_{}^{\frac{25}{π}}} = 1 + \frac{e_{}^{- 2 π}}{1 + \frac{e_{}^{- 4 π}}{1 + \frac{e_{}^{- 6 π}}{1 + \frac{e_{}^{- 8 π}}{1 + \dots}}}} \\ Another Ramanujan identity & \sum_{k = 1}^{\infty} \frac{1}{2_{}^{⌊ k \cdot ​ φ ⌋}} = \frac{1}{2_{}^{0} + \frac{1}{2_{}^{1} + \dots \frac{1}{2_{}^{1} + \frac{1}{2_{}^{2} + \dots \frac{1}{2_{}^{3} + \frac{1}{2_{}^{5} + \dots}}}}}} \\ Rogers-Ramanujan Identity & 1 + \sum_{k = 1}^{\infty} \frac{q_{}^{k_{}^{2} + k}}{(1 - q) (1 - q_{}^{2}) \dots (1 - q_{}^{k})} \frac{q_{}^{2}}{(1 - q)} + \frac{q_{}^{6}}{(1 - q) (1 - q_{}^{2})} + \dots = \prod_{j = 0}^{\infty} \frac{1}{(1 - q_{}^{5 j + 2}) (1 - q_{}^{5 j + 3})} \frac{1}{(1 - q_{}^{2}) (1 - q_{}^{3})} \times \frac{1}{(1 - q_{}^{7}) (1 - q_{}^{8})} \times \dots, f o r | q | < 1 . \\ Commutative Diagram & \begin{matrix} H & \leftarrow & K \\ ↓ & ↑ \\ H & \to & K \end{matrix} \end{matrix}
Source Code:
<math xmlns:dsi="http://www.dessci.com/mathml" xmlns="http://www.w3.org/1998/Math/MathML"> 
  <mtable> 
    <mtr> 
      <mtd> 
        <mtext>Bernoulli Trials</mtext> 
      </mtd> 
      <mtd> 
        <mrow> 
          <maction actiontype="statusline"> 
            <mrow> 
              <mi>P</mi> 
              <mo stretchy="false">(</mo> 
              <mi>E</mi> 
              <mo stretchy="false">)</mo> 
            </mrow> 
            <mtext>Probability of event E: Get exactly k heads in n coin flips. 
            </mtext> 
          </maction> 
          <mo>=</mo> 
          <maction actiontype="statusline"> 
            <mrow> 
              <mo>(</mo> 
              <mfrac linethickness="0"> 
                <mi>n</mi> 
                <mi>k</mi> 
              </mfrac> 
              <mo>)</mo> 
            </mrow> 
            <mtext>Number of ways to get exactly k heads in n coin flips 
            </mtext> 
          </maction> 
          <msubsup> 
            <maction actiontype="statusline"> 
              <mi>p</mi> 
              <mtext>Probability of getting heads in one flip 
              </mtext> 
            </maction> 
            <mrow/> 
            <maction actiontype="statusline"> 
              <mi>k</mi> 
              <mtext>Number of heads</mtext> 
            </maction> 
          </msubsup> 
          <msubsup> 
            <maction actiontype="statusline"> 
              <mrow> 
                <mo stretchy="false">(</mo> 
                <mn>1</mn> 
                <mo>-</mo> 
                <mi>p</mi> 
                <mo stretchy="false">)</mo> 
              </mrow> 
              <mtext>Probability of getting tails in one flip 
              </mtext> 
            </maction> 
            <mrow/> 
            <maction actiontype="statusline"> 
              <mrow> 
                <mi>n</mi> 
                <mo>-</mo> 
                <mi>k</mi> 
              </mrow> 
              <mtext>Number of tails</mtext> 
            </maction> 
          </msubsup> 
        </mrow> 
      </mtd> 
    </mtr> 
    <mtr> 
      <mtd> 
        <mtext>Cauchy-Schwarz Inequality</mtext> 
      </mtd> 
      <mtd> 
        <mstyle displaystyle="true"> 
          <mrow> 
            <msubsup> 
              <mrow> 
                <mo>(</mo> 
                <munderover> 
                  <mo>&#x2211;</mo> 
                  <mrow> 
                    <mi>k</mi> 
                    <mo>=</mo> 
                    <mn>1</mn> 
                  </mrow> 
                  <mi>n</mi> 
                </munderover> 
                <msubsup> 
                  <mi>a</mi> 
                  <mi>k</mi> 
                  <mrow/> 
                </msubsup> 
                <msubsup> 
                  <mi>b</mi> 
                  <mi>k</mi> 
                  <mrow/> 
                </msubsup> 
                <mo>)</mo> 
              </mrow> 
              <mrow/> 
              <mn>2</mn> 
            </msubsup> 
            <mo>&#x2264;</mo> 
            <mrow> 
              <mo>(</mo> 
              <munderover> 
                <mo>&#x2211;</mo> 
                <mrow> 
                  <mi>k</mi> 
                  <mo>=</mo> 
                  <mn>1</mn> 
                </mrow> 
                <mi>n</mi> 
              </munderover> 
              <msubsup> 
                <mi>a</mi> 
                <mi>k</mi> 
                <mn>2</mn> 
              </msubsup> 
              <mo>)</mo> 
            </mrow> 
            <mrow> 
              <mo>(</mo> 
              <munderover> 
                <mo>&#x2211;</mo> 
                <mrow> 
                  <mi>k</mi> 
                  <mo>=</mo> 
                  <mn>1</mn> 
                </mrow> 
                <mi>n</mi> 
              </munderover> 
              <msubsup> 
                <mi>b</mi> 
                <mi>k</mi> 
                <mn>2</mn> 
              </msubsup> 
              <mo>)</mo> 
            </mrow> 
          </mrow> 
        </mstyle> 
      </mtd> 
    </mtr> 
    <mtr> 
      <mtd> 
        <mtext>Cauchy Formula</mtext> 
      </mtd> 
      <mtd> 
        <mstyle displaystyle="true"> 
          <mrow> 
            <mi>f</mi> 
            <mo stretchy="false">(</mo> 
            <mi>z</mi> 
            <mo stretchy="false">)</mo> 
            <mtext>&#x2009;</mtext> 
            <mo>&#x00B7;</mo> 
            <msubsup> 
              <mi>Ind</mi> 
              <mi>&#x03B3;</mi> 
              <mrow/> 
            </msubsup> 
            <mo stretchy="false">(</mo> 
            <mi>z</mi> 
            <mo stretchy="false">)</mo> 
            <mo>=</mo> 
            <mfrac> 
              <mn>1</mn> 
              <mrow> 
                <mn>2</mn> 
                <mi>&#x03C0;</mi> 
                <mi>i</mi> 
              </mrow> 
            </mfrac> 
            <munderover> 
              <mo>&#x222E;</mo> 
              <mi>&#x03B3;</mi> 
              <mrow/> 
            </munderover> 
            <mfrac> 
              <mrow> 
                <mi>f</mi> 
                <mo stretchy="false">(</mo> 
                <mstyle scriptlevel="1"> 
                  <mi>&#x03BE;</mi> 
                </mstyle> 
                <mo stretchy="false">)</mo> 
              </mrow> 
              <mrow> 
                <mstyle scriptlevel="1"> 
                  <mi>&#x03BE;</mi> 
                </mstyle> 
                <mo>-</mo> 
                <mi>z</mi> 
              </mrow> 
            </mfrac> 
            <mtext>&#x2009;</mtext> 
            <mi>d</mi> 
            <mstyle scriptlevel="1"> 
              <mi>&#x03BE;</mi> 
            </mstyle> 
          </mrow> 
        </mstyle> 
      </mtd> 
    </mtr> 
    <mtr> 
      <mtd> 
        <mtext>Cross Product</mtext> 
      </mtd> 
      <mtd> 
        <mrow> 
          <msubsup> 
            <mstyle fontweight="bold"> 
              <mi>V</mi> 
            </mstyle> 
            <mn>1</mn> 
            <mrow/> 
          </msubsup> 
          <mo>&#x00D7;</mo> 
          <msubsup> 
            <mstyle fontweight="bold"> 
              <mi>V</mi> 
            </mstyle> 
            <mn>2</mn> 
            <mrow/> 
          </msubsup> 
          <mo>=</mo> 
          <mrow> 
            <mo>|</mo> 
            <mtable equalrows="false"> 
              <mtr> 
                <mtd> 
                  <mstyle fontweight="bold"> 
                    <mi>i</mi> 
                  </mstyle> 
                </mtd> 
                <mtd> 
                  <mstyle fontweight="bold"> 
                    <mi>j</mi> 
                  </mstyle> 
                </mtd> 
                <mtd> 
                  <mstyle fontweight="bold"> 
                    <mi>k</mi> 
                  </mstyle> 
                </mtd> 
              </mtr> 
              <mtr> 
                <mtd> 
                  <mfrac> 
                    <mrow> 
                      <mo>&#x2202;</mo> 
                      <mi>X</mi> 
                    </mrow> 
                    <mrow> 
                      <mo>&#x2202;</mo> 
                      <mi>u</mi> 
                    </mrow> 
                  </mfrac> 
                </mtd> 
                <mtd> 
                  <mfrac> 
                    <mrow> 
                      <mo>&#x2202;</mo> 
                      <mi>Y</mi> 
                    </mrow> 
                    <mrow> 
                      <mo>&#x2202;</mo> 
                      <mi>u</mi> 
                    </mrow> 
                  </mfrac> 
                </mtd> 
                <mtd> 
                  <mn>0</mn> 
                </mtd> 
              </mtr> 
              <mtr> 
                <mtd> 
                  <mfrac> 
                    <mrow> 
                      <mo>&#x2202;</mo> 
                      <mi>X</mi> 
                    </mrow> 
                    <mrow> 
                      <mo>&#x2202;</mo> 
                      <mi>v</mi> 
                    </mrow> 
                  </mfrac> 
                </mtd> 
                <mtd> 
                  <mfrac> 
                    <mrow> 
                      <mo>&#x2202;</mo> 
                      <mi>Y</mi> 
                    </mrow> 
                    <mrow> 
                      <mo>&#x2202;</mo> 
                      <mi>v</mi> 
                    </mrow> 
                  </mfrac> 
                </mtd> 
                <mtd> 
                  <mn>0</mn> 
                </mtd> 
              </mtr> 
            </mtable> 
            <mo>|</mo> 
          </mrow> 
        </mrow> 
      </mtd> 
    </mtr> 
    <mtr> 
      <mtd> 
        <mtext>Vandermonde Determinant</mtext> 
      </mtd> 
      <mtd> 
        <mstyle displaystyle="true"> 
          <mrow> 
            <mrow> 
              <mo>|</mo> 
              <mtable equalrows="false"> 
                <mtr> 
                  <mtd> 
                    <mn>1</mn> 
                  </mtd> 
                  <mtd> 
                    <mn>1</mn> 
                  </mtd> 
                  <mtd> 
                    <mo>&#x22EF;</mo> 
                  </mtd> 
                  <mtd> 
                    <mn>1</mn> 
                  </mtd> 
                </mtr> 
                <mtr> 
                  <mtd> 
                    <msubsup> 
                      <mi>v</mi> 
                      <mn>1</mn> 
                      <mrow/> 
                    </msubsup> 
                  </mtd> 
                  <mtd> 
                    <msubsup> 
                      <mi>v</mi> 
                      <mn>2</mn> 
                      <mrow/> 
                    </msubsup> 
                  </mtd> 
                  <mtd> 
                    <mo>&#x22EF;</mo> 
                  </mtd> 
                  <mtd> 
                    <msubsup> 
                      <mi>v</mi> 
                      <mi>n</mi> 
                      <mrow/> 
                    </msubsup> 
                  </mtd> 
                </mtr> 
                <mtr> 
                  <mtd> 
                    <msubsup> 
                      <mi>v</mi> 
                      <mn>1</mn> 
                      <mn>2</mn> 
                    </msubsup> 
                  </mtd> 
                  <mtd> 
                    <msubsup> 
                      <mi>v</mi> 
                      <mn>2</mn> 
                      <mn>2</mn> 
                    </msubsup> 
                  </mtd> 
                  <mtd> 
                    <mo>&#x22EF;</mo> 
                  </mtd> 
                  <mtd> 
                    <msubsup> 
                      <mi>v</mi> 
                      <mi>n</mi> 
                      <mn>2</mn> 
                    </msubsup> 
                  </mtd> 
                </mtr> 
                <mtr> 
                  <mtd> 
                    <mo>&#x22EE;</mo> 
                  </mtd> 
                  <mtd> 
                    <mo>&#x22EE;</mo> 
                  </mtd> 
                  <mtd> 
                    <mo>&#x22F1;</mo> 
                  </mtd> 
                  <mtd> 
                    <mo>&#x22EE;</mo> 
                  </mtd> 
                </mtr> 
                <mtr> 
                  <mtd> 
                    <msubsup> 
                      <mi>v</mi> 
                      <mn>1</mn> 
                      <mrow> 
                        <mi>n</mi> 
                        <mo>-</mo> 
                        <mn>1</mn> 
                      </mrow> 
                    </msubsup> 
                  </mtd> 
                  <mtd> 
                    <msubsup> 
                      <mi>v</mi> 
                      <mn>2</mn> 
                      <mrow> 
                        <mi>n</mi> 
                        <mo>-</mo> 
                        <mn>1</mn> 
                      </mrow> 
                    </msubsup> 
                  </mtd> 
                  <mtd> 
                    <mo>&#x22EF;</mo> 
                  </mtd> 
                  <mtd> 
                    <msubsup> 
                      <mi>v</mi> 
                      <mi>n</mi> 
                      <mrow> 
                        <mi>n</mi> 
                        <mo>-</mo> 
                        <mn>1</mn> 
                      </mrow> 
                    </msubsup> 
                  </mtd> 
                </mtr> 
              </mtable> 
              <mo>|</mo> 
            </mrow> 
            <mo>=</mo> 
            <munderover> 
              <mo>&#x220F;</mo> 
              <mrow> 
                <mn>1</mn> 
                <mo>&#x2264;</mo> 
                <mi>i</mi> 
                <mo>&lt;</mo> 
                <mi>j</mi> 
                <mo>&#x2264;</mo> 
                <mi>n</mi> 
              </mrow> 
              <mrow/> 
            </munderover> 
            <mo stretchy="false">(</mo> 
            <msubsup> 
              <mi>v</mi> 
              <mi>j</mi> 
              <mrow/> 
            </msubsup> 
            <mo>-</mo> 
            <msubsup> 
              <mi>v</mi> 
              <mi>i</mi> 
              <mrow/> 
            </msubsup> 
            <mo stretchy="false">)</mo> 
          </mrow> 
        </mstyle> 
      </mtd> 
    </mtr> 
    <mtr> 
      <mtd> 
        <mtext>Lorenz Equations</mtext> 
      </mtd> 
      <mtd> 
        <mtable columnalign="right center left" equalcolumns="false"> 
          <mtr> 
            <mtd> 
              <munderover accent="true"> 
                <mi>x</mi> 
                <mrow/> 
                <mo>&#x02D9;</mo> 
              </munderover> 
            </mtd> 
            <mtd> 
              <mo>=</mo> 
            </mtd> 
            <mtd> 
              <mrow> 
                <mi>&#x03C3;</mi> 
                <mo stretchy="false">(</mo> 
                <mi>y</mi> 
                <mo>-</mo> 
                <mi>x</mi> 
                <mo stretchy="false">)</mo> 
              </mrow> 
            </mtd> 
          </mtr> 
          <mtr> 
            <mtd> 
              <munderover accent="true"> 
                <mi>y</mi> 
                <mrow/> 
                <mo>&#x02D9;</mo> 
              </munderover> 
            </mtd> 
            <mtd> 
              <mo>=</mo> 
            </mtd> 
            <mtd> 
              <mrow> 
                <mi>&#x03C1;</mi> 
                <mi>x</mi> 
                <mo>-</mo> 
                <mi>y</mi> 
                <mo>-</mo> 
                <mi>x</mi> 
                <mi>z</mi> 
              </mrow> 
            </mtd> 
          </mtr> 
          <mtr> 
            <mtd> 
              <munderover accent="true"> 
                <mi>z</mi> 
                <mrow/> 
                <mo>&#x02D9;</mo> 
              </munderover> 
            </mtd> 
            <mtd> 
              <mo>=</mo> 
            </mtd> 
            <mtd> 
              <mrow> 
                <mo>-</mo> 
                <mi>&#x03B2;</mi> 
                <mi>z</mi> 
                <mo>+</mo> 
                <mi>x</mi> 
                <mi>y</mi> 
              </mrow> 
            </mtd> 
          </mtr> 
        </mtable> 
      </mtd> 
    </mtr> 
    <mtr> 
      <mtd> 
        <mtext>Maxwell's Equations</mtext> 
      </mtd> 
      <mtd> 
        <mstyle displaystyle="true"> 
          <mrow> 
            <mo>{</mo> 
            <mtable columnalign="right center left" equalrows="false" equalcolumns="false"> 
              <mtr> 
                <mtd> 
                  <mrow> 
                    <mo>&#x2207;</mo> 
                    <mtext>&#x200B;</mtext> 
                    <mo>&#x00D7;</mo> 
                    <munderover accent="true"> 
                      <mstyle fontweight="bold"> 
                        <mi>B</mi> 
                      </mstyle> 
                      <mrow/> 
                      <mo stretchy="true">&#x21BC;</mo> 
                    </munderover> 
                    <mo>-</mo> 
                    <mtext>&#x2009;</mtext> 
                    <mfrac> 
                      <mn>1</mn> 
                      <mi>c</mi> 
                    </mfrac> 
                    <mtext>&#x2009;</mtext> 
                    <mfrac> 
                      <mrow> 
                        <mo>&#x2202;</mo> 
                        <mtext>&#x200B;</mtext> 
                        <munderover accent="true"> 
                          <mstyle fontweight="bold"> 
                            <mi>E</mi> 
                          </mstyle> 
                          <mrow/> 
                          <mo stretchy="true">&#x21BC;</mo> 
                        </munderover> 
                      </mrow> 
                      <mrow> 
                        <mo>&#x2202;</mo> 
                        <mtext>&#x200B;</mtext> 
                        <mi>t</mi> 
                      </mrow> 
                    </mfrac> 
                  </mrow> 
                </mtd> 
                <mtd> 
                  <mo>=</mo> 
                </mtd> 
                <mtd> 
                  <mrow> 
                    <mfrac> 
                      <mrow> 
                        <mn>4</mn> 
                        <mi>&#x03C0;</mi> 
                      </mrow> 
                      <mi>c</mi> 
                    </mfrac> 
                    <mtext>&#x2009;</mtext> 
                    <munderover accent="true"> 
                      <mstyle fontweight="bold"> 
                        <mi>j</mi> 
                      </mstyle> 
                      <mrow/> 
                      <mo stretchy="true">&#x21BC;</mo> 
                    </munderover> 
                  </mrow> 
                </mtd> 
              </mtr> 
              <mtr> 
                <mtd> 
                  <mrow> 
                    <mo>&#x2207;</mo> 
                    <mtext>&#x200B;</mtext> 
                    <mo>&#x00B7;</mo> 
                    <munderover accent="true"> 
                      <mstyle fontweight="bold"> 
                        <mi>E</mi> 
                      </mstyle> 
                      <mrow/> 
                      <mo stretchy="true">&#x21BC;</mo> 
                    </munderover> 
                  </mrow> 
                </mtd> 
                <mtd> 
                  <mo>=</mo> 
                </mtd> 
                <mtd> 
                  <mrow> 
                    <mn>4</mn> 
                    <mi>&#x03C0;</mi> 
                    <mi>&#x03C1;</mi> 
                  </mrow> 
                </mtd> 
              </mtr> 
              <mtr> 
                <mtd> 
                  <mrow> 
                    <mo>&#x2207;</mo> 
                    <mtext>&#x200B;</mtext> 
                    <mo>&#x00D7;</mo> 
                    <munderover accent="true"> 
                      <mstyle fontweight="bold"> 
                        <mi>E</mi> 
                      </mstyle> 
                      <mrow/> 
                      <mo stretchy="true">&#x21BC;</mo> 
                    </munderover> 
                    <mtext>&#x2009;</mtext> 
                    <mo>+</mo> 
                    <mtext>&#x2009;</mtext> 
                    <mfrac> 
                      <mn>1</mn> 
                      <mi>c</mi> 
                    </mfrac> 
                    <mtext>&#x2009;</mtext> 
                    <mfrac> 
                      <mrow> 
                        <mo>&#x2202;</mo> 
                        <mtext>&#x200B;</mtext> 
                        <munderover accent="true"> 
                          <mstyle fontweight="bold"> 
                            <mi>B</mi> 
                          </mstyle> 
                          <mrow/> 
                          <mo stretchy="true">&#x21BC;</mo> 
                        </munderover> 
                      </mrow> 
                      <mrow> 
                        <mo>&#x2202;</mo> 
                        <mtext>&#x200B;</mtext> 
                        <mi>t</mi> 
                      </mrow> 
                    </mfrac> 
                  </mrow> 
                </mtd> 
                <mtd> 
                  <mo>=</mo> 
                </mtd> 
                <mtd> 
                  <munderover accent="true"> 
                    <mstyle fontweight="bold"> 
                      <mn>0</mn> 
                    </mstyle> 
                    <mrow/> 
                    <mo stretchy="true">&#x21BC;</mo> 
                  </munderover> 
                </mtd> 
              </mtr> 
              <mtr> 
                <mtd> 
                  <mrow> 
                    <mo>&#x2207;</mo> 
                    <mtext>&#x200B;</mtext> 
                    <mo>&#x00B7;</mo> 
                    <munderover accent="true"> 
                      <mstyle fontweight="bold"> 
                        <mi>B</mi> 
                      </mstyle> 
                      <mrow/> 
                      <mo stretchy="true">&#x21BC;</mo> 
                    </munderover> 
                  </mrow> 
                </mtd> 
                <mtd> 
                  <mo>=</mo> 
                </mtd> 
                <mtd> 
                  <mn>0</mn> 
                </mtd> 
              </mtr> 
            </mtable> 
          </mrow> 
        </mstyle> 
      </mtd> 
    </mtr> 
    <mtr> 
      <mtd> 
        <mtext>Einstein Field Equations</mtext> 
      </mtd> 
      <mtd> 
        <mstyle displaystyle="true"> 
          <mrow> 
            <msubsup> 
              <mstyle fontstyle="normal"> 
                <mi>R</mi> 
              </mstyle> 
              <mstyle scriptlevel="1"> 
                <mrow> 
                  <mi>&#x03BC;</mi> 
                  <mi>&#x03BD;</mi> 
                </mrow> 
              </mstyle> 
              <mrow/> 
            </msubsup> 
            <mo>-</mo> 
            <mfrac> 
              <mn>1</mn> 
              <mn>2</mn> 
            </mfrac> 
            <mtext>&#x2009;</mtext> 
            <msubsup> 
              <mi>g</mi> 
              <mstyle scriptlevel="1"> 
                <mrow> 
                  <mi>&#x03BC;</mi> 
                  <mi>&#x03BD;</mi> 
                </mrow> 
              </mstyle> 
              <mrow/> 
            </msubsup> 
            <mtext>&#x2009;</mtext> 
            <mstyle fontstyle="normal"> 
              <mi>R</mi> 
            </mstyle> 
            <mo>=</mo> 
            <mfrac> 
              <mrow> 
                <mn>8</mn> 
                <mi>&#x03C0;</mi> 
                <mstyle fontstyle="normal"> 
                  <mi>G</mi> 
                </mstyle> 
              </mrow> 
              <msubsup> 
                <mi>c</mi> 
                <mrow/> 
                <mn>4</mn> 
              </msubsup> 
            </mfrac> 
            <mtext>&#x2009;</mtext> 
            <msubsup> 
              <mstyle fontstyle="normal"> 
                <mi>T</mi> 
              </mstyle> 
              <mstyle scriptlevel="1"> 
                <mrow> 
                  <mi>&#x03BC;</mi> 
                  <mi>&#x03BD;</mi> 
                </mrow> 
              </mstyle> 
              <mrow/> 
            </msubsup> 
          </mrow> 
        </mstyle> 
      </mtd> 
    </mtr> 
    <mtr> 
      <mtd> 
        <mtext>Ramanujan Identity</mtext> 
      </mtd> 
      <mtd> 
        <mrow> 
          <mfrac> 
            <mn>1</mn> 
            <mrow> 
              <mo stretchy="false">(</mo> 
              <msqrt> 
                <mrow> 
                  <mi>&#x03C6;</mi> 
                  <msqrt> 
                    <mn>5</mn> 
                  </msqrt> 
                </mrow> 
              </msqrt> 
              <mo>-</mo> 
              <mi>&#x03C6;</mi> 
              <mo stretchy="false">)</mo> 
              <msubsup> 
                <mi>e</mi> 
                <mrow/> 
                <mfrac> 
                  <mn>25</mn> 
                  <mi>&#x03C0;</mi> 
                </mfrac> 
              </msubsup> 
            </mrow> 
          </mfrac> 
          <mo>=</mo> 
          <mn>1</mn> 
          <mo>+</mo> 
          <mstyle scriptlevel="1"> 
            <mfrac> 
              <msubsup> 
                <mi>e</mi> 
                <mrow/> 
                <mstyle scriptlevel="2"> 
                  <mrow> 
                    <mo>-</mo> 
                    <mn>2</mn> 
                    <mi>&#x03C0;</mi> 
                  </mrow> 
                </mstyle> 
              </msubsup> 
              <mrow> 
                <mn>1</mn> 
                <mo>+</mo> 
                <mfrac> 
                  <msubsup> 
                    <mi>e</mi> 
                    <mrow/> 
                    <mstyle scriptlevel="2"> 
                      <mrow> 
                        <mo>-</mo> 
                        <mn>4</mn> 
                        <mi>&#x03C0;</mi> 
                      </mrow> 
                    </mstyle> 
                  </msubsup> 
                  <mrow> 
                    <mn>1</mn> 
                    <mo>+</mo> 
                    <mfrac> 
                      <msubsup> 
                        <mi>e</mi> 
                        <mrow/> 
                        <mstyle scriptlevel="2"> 
                          <mrow> 
                            <mo>-</mo> 
                            <mn>6</mn> 
                            <mi>&#x03C0;</mi> 
                          </mrow> 
                        </mstyle> 
                      </msubsup> 
                      <mrow> 
                        <mn>1</mn> 
                        <mo>+</mo> 
                        <mfrac> 
                          <msubsup> 
                            <mi>e</mi> 
                            <mrow/> 
                            <mstyle scriptlevel="2"> 
                              <mrow> 
                                <mo>-</mo> 
                                <mn>8</mn> 
                                <mi>&#x03C0;</mi> 
                              </mrow> 
                            </mstyle> 
                          </msubsup> 
                          <mrow> 
                            <mn>1</mn> 
                            <mo>+</mo> 
                            <mo>&#x2026;</mo> 
                          </mrow> 
                        </mfrac> 
                      </mrow> 
                    </mfrac> 
                  </mrow> 
                </mfrac> 
              </mrow> 
            </mfrac> 
          </mstyle> 
        </mrow> 
      </mtd> 
    </mtr> 
    <mtr> 
      <mtd> 
        <mtext>Another Ramanujan identity</mtext> 
      </mtd> 
      <mtd> 
        <mstyle displaystyle="true"> 
          <mrow> 
            <munderover> 
              <mo>&#x2211;</mo> 
              <mrow> 
                <mi>k</mi> 
                <mo>=</mo> 
                <mn>1</mn> 
              </mrow> 
              <mi>&#x221E;</mi> 
            </munderover> 
            <mfrac> 
              <mn>1</mn> 
              <msubsup> 
                <mn>2</mn> 
                <mrow/> 
                <mrow> 
                  <mo stretchy="false">&#x230A;</mo> 
                  <mi>k</mi> 
                  <mo>&#x00B7;</mo> 
                  <mtext>&#x200B;</mtext> 
                  <mi>&#x03C6;</mi> 
                  <mo stretchy="false">&#x230B;</mo> 
                </mrow> 
              </msubsup> 
            </mfrac> 
            <mo>=</mo> 
            <mstyle scriptlevel="1"> 
              <mfrac> 
                <mn>1</mn> 
                <mrow> 
                  <msubsup> 
                    <mn>2</mn> 
                    <mrow/> 
                    <mstyle scriptlevel="2"> 
                      <mn>0</mn> 
                    </mstyle> 
                  </msubsup> 
                  <mo>+</mo> 
                  <mfrac> 
                    <mn>1</mn> 
                    <mrow> 
                      <msubsup> 
                        <mn>2</mn> 
                        <mrow/> 
                        <mstyle scriptlevel="2"> 
                          <mn>1</mn> 
                        </mstyle> 
                      </msubsup> 
                      <mo>+</mo> 
                      <maction actiontype="toggle"> 
                        <mo>&#x22EF;</mo> 
                        <mfrac> 
                          <mn>1</mn> 
                          <mrow> 
                            <msubsup> 
                              <mn>2</mn> 
                              <mrow/> 
                              <mstyle scriptlevel="2"> 
                                <mn>1</mn> 
                              </mstyle> 
                            </msubsup> 
                            <mo>+</mo> 
                            <mfrac> 
                              <mn>1</mn> 
                              <mrow> 
                                <msubsup> 
                                  <mn>2</mn> 
                                  <mrow/> 
                                  <mstyle scriptlevel="2"> 
                                    <mn>2</mn> 
                                  </mstyle> 
                                </msubsup> 
                                <mo>+</mo> 
                                <maction actiontype="toggle"> 
                                  <mo>&#x22EF;</mo> 
                                  <mfrac> 
                                    <mn>1</mn> 
                                    <mrow> 
                                      <msubsup> 
                                        <mn>2</mn> 
                                        <mrow/> 
                                        <mstyle scriptlevel="2"> 
                                          <mn>3</mn> 
                                        </mstyle> 
                                      </msubsup> 
                                      <mo>+</mo> 
                                      <mfrac> 
                                        <mn>1</mn> 
                                        <mrow> 
                                          <msubsup> 
                                            <mn>2</mn> 
                                            <mrow/> 
                                            <mstyle scriptlevel="2"> 
                                              <mn>5</mn> 
                                            </mstyle> 
                                          </msubsup> 
                                          <mo>+</mo> 
                                          <mo>&#x2026;</mo> 
                                        </mrow> 
                                      </mfrac> 
                                    </mrow> 
                                  </mfrac> 
                                </maction> 
                              </mrow> 
                            </mfrac> 
                          </mrow> 
                        </mfrac> 
                      </maction> 
                    </mrow> 
                  </mfrac> 
                </mrow> 
              </mfrac> 
            </mstyle> 
          </mrow> 
        </mstyle> 
      </mtd> 
    </mtr> 
    <mtr> 
      <mtd> 
        <mtext>Rogers-Ramanujan Identity</mtext> 
      </mtd> 
      <mtd> 
        <mstyle displaystyle="true"> 
          <mrow> 
            <mn>1</mn> 
            <mo>+</mo> 
            <maction actiontype="highlight" dsi:background="#0000ff"> 
              <maction actiontype="toggle"> 
                <mrow> 
                  <munderover> 
                    <mo>&#x2211;</mo> 
                    <mrow> 
                      <mi>k</mi> 
                      <mo>=</mo> 
                      <mn>1</mn> 
                    </mrow> 
                    <mi>&#x221E;</mi> 
                  </munderover> 
                  <mfrac> 
                    <msubsup> 
                      <mi>q</mi> 
                      <mrow/> 
                      <mrow> 
                        <msubsup> 
                          <mi>k</mi> 
                          <mrow/> 
                          <mn>2</mn> 
                        </msubsup> 
                        <mo>+</mo> 
                        <mi>k</mi> 
                      </mrow> 
                    </msubsup> 
                    <mrow> 
                      <mo stretchy="false">(</mo> 
                      <mn>1</mn> 
                      <mo>-</mo> 
                      <mi>q</mi> 
                      <mo stretchy="false">)</mo> 
                      <mo stretchy="false">(</mo> 
                      <mn>1</mn> 
                      <mo>-</mo> 
                      <msubsup> 
                        <mi>q</mi> 
                        <mrow/> 
                        <mn>2</mn> 
                      </msubsup> 
                      <mo stretchy="false">)</mo> 
                      <mo>&#x22EF;</mo> 
                      <mo stretchy="false">(</mo> 
                      <mn>1</mn> 
                      <mo>-</mo> 
                      <msubsup> 
                        <mi>q</mi> 
                        <mrow/> 
                        <mi>k</mi> 
                      </msubsup> 
                      <mo stretchy="false">)</mo> 
                    </mrow> 
                  </mfrac> 
                </mrow> 
                <mrow> 
                  <mfrac> 
                    <msubsup> 
                      <mi>q</mi> 
                      <mrow/> 
                      <mn>2</mn> 
                    </msubsup> 
                    <mrow> 
                      <mo stretchy="false">(</mo> 
                      <mn>1</mn> 
                      <mo>-</mo> 
                      <mi>q</mi> 
                      <mo stretchy="false">)</mo> 
                    </mrow> 
                  </mfrac> 
                  <mo>+</mo> 
                  <mfrac> 
                    <msubsup> 
                      <mi>q</mi> 
                      <mrow/> 
                      <mn>6</mn> 
                    </msubsup> 
                    <mrow> 
                      <mo stretchy="false">(</mo> 
                      <mn>1</mn> 
                      <mo>-</mo> 
                      <mi>q</mi> 
                      <mo stretchy="false">)</mo> 
                      <mo stretchy="false">(</mo> 
                      <mn>1</mn> 
                      <mo>-</mo> 
                      <msubsup> 
                        <mi>q</mi> 
                        <mrow/> 
                        <mn>2</mn> 
                      </msubsup> 
                      <mo stretchy="false">)</mo> 
                    </mrow> 
                  </mfrac> 
                  <mo>+</mo> 
                  <mo>&#x22EF;</mo> 
                </mrow> 
              </maction> 
            </maction> 
            <mo>=</mo> 
            <maction actiontype="highlight" dsi:background="#0000ff"> 
              <maction actiontype="toggle"> 
                <mrow> 
                  <munderover> 
                    <mo>&#x220F;</mo> 
                    <mrow> 
                      <mi>j</mi> 
                      <mo>=</mo> 
                      <mn>0</mn> 
                    </mrow> 
                    <mi>&#x221E;</mi> 
                  </munderover> 
                  <mfrac> 
                    <mn>1</mn> 
                    <mrow> 
                      <mo stretchy="false">(</mo> 
                      <mn>1</mn> 
                      <mo>-</mo> 
                      <msubsup> 
                        <mi>q</mi> 
                        <mrow/> 
                        <mrow> 
                          <mn>5</mn> 
                          <mi>j</mi> 
                          <mo>+</mo> 
                          <mn>2</mn> 
                        </mrow> 
                      </msubsup> 
                      <mo stretchy="false">)</mo> 
                      <mo stretchy="false">(</mo> 
                      <mn>1</mn> 
                      <mo>-</mo> 
                      <msubsup> 
                        <mi>q</mi> 
                        <mrow/> 
                        <mrow> 
                          <mn>5</mn> 
                          <mi>j</mi> 
                          <mo>+</mo> 
                          <mn>3</mn> 
                        </mrow> 
                      </msubsup> 
                      <mo stretchy="false">)</mo> 
                    </mrow> 
                  </mfrac> 
                </mrow> 
                <mrow> 
                  <mfrac> 
                    <mn>1</mn> 
                    <mrow> 
                      <mo stretchy="false">(</mo> 
                      <mn>1</mn> 
                      <mo>-</mo> 
                      <msubsup> 
                        <mi>q</mi> 
                        <mrow/> 
                        <mn>2</mn> 
                      </msubsup> 
                      <mo stretchy="false">)</mo> 
                      <mo stretchy="false">(</mo> 
                      <mn>1</mn> 
                      <mo>-</mo> 
                      <msubsup> 
                        <mi>q</mi> 
                        <mrow/> 
                        <mn>3</mn> 
                      </msubsup> 
                      <mo stretchy="false">)</mo> 
                    </mrow> 
                  </mfrac> 
                  <mo>&#x00D7;</mo> 
                  <mfrac> 
                    <mn>1</mn> 
                    <mrow> 
                      <mo stretchy="false">(</mo> 
                      <mn>1</mn> 
                      <mo>-</mo> 
                      <msubsup> 
                        <mi>q</mi> 
                        <mrow/> 
                        <mn>7</mn> 
                      </msubsup> 
                      <mo stretchy="false">)</mo> 
                      <mo stretchy="false">(</mo> 
                      <mn>1</mn> 
                      <mo>-</mo> 
                      <msubsup> 
                        <mi>q</mi> 
                        <mrow/> 
                        <mn>8</mn> 
                      </msubsup> 
                      <mo stretchy="false">)</mo> 
                    </mrow> 
                  </mfrac> 
                  <mo>&#x00D7;</mo> 
                  <mo>&#x22EF;</mo> 
                </mrow> 
              </maction> 
            </maction> 
            <mo>,</mo> 
            <mtext>&#x205F;&#x0200A;</mtext> 
            <mtext>&#x205F;&#x0200A;</mtext> 
            <mstyle fontstyle="normal"> 
              <mrow> 
                <mi>f</mi> 
                <mi>o</mi> 
                <mi>r</mi> 
              </mrow> 
            </mstyle> 
            <mtext>&#x205F;</mtext> 
            <mo stretchy="false">|</mo> 
            <mi>q</mi> 
            <mo stretchy="false">|</mo> 
            <mo>&lt;</mo> 
            <mn>1</mn> 
            <mi>.</mi> 
          </mrow> 
        </mstyle> 
      </mtd> 
    </mtr> 
    <mtr> 
      <mtd> 
        <mtext>Commutative Diagram</mtext> 
      </mtd> 
      <mtd> 
        <mtable equalcolumns="false" equalrows="false"> 
          <mtr> 
            <mtd> 
              <mi>H</mi> 
            </mtd> 
            <mtd> 
              <mo>&#x2190;</mo> 
            </mtd> 
            <mtd> 
              <mi>K</mi> 
            </mtd> 
          </mtr> 
          <mtr> 
            <mtd> 
              <mo>&#x2193;</mo> 
            </mtd> 
            <mtd> 
              <mspace height="100px" width="150px"/> 
            </mtd> 
            <mtd> 
              <mo>&#x2191;</mo> 
            </mtd> 
          </mtr> 
          <mtr> 
            <mtd> 
              <mi>H</mi> 
            </mtd> 
            <mtd> 
              <mo>&#x2192;</mo> 
            </mtd> 
            <mtd> 
              <mi>K</mi> 
            </mtd> 
          </mtr> 
        </mtable> 
      </mtd> 
    </mtr> 
  </mtable> 
</math>