1 Introduction
A distinguishing feature of mathematics is the use of a complex and highly evolved system of two-dimensional symbolic notations. The MathML [MathML2] format is the World Wide Web Consortitum's (W3C) answer to the problem of the problem of communicating these notations on the web.
However, MathML does not cover all mathematical practice; due to the inherent complexity of the material, mathematicicans also make use of various forms of diagrams to visualize their ideas and the objects in question. For diagrams, the W3C provides the Scalable Vector Graphics (SVG) format [SVG1.1].
In isolation, both MathML and SVG are very successful, they cover the respective practice, and are supported in numerous browsers, printer drivers, and authoring tools. The W3C has put out a joint DTD and Schema [XHTML-MathML-SVG] for a modular integration of MathML and SVG into XHTML.
Unfortuntaely, this is not enough to cover mathematical practice. Since the diagrams are about mathematical objects, they can contain mathematical formulae, and since diagrams are sometimes used to communicate mathemtatical objects they can occur inside mathematical formulae. This practice, requires a mixing of MathML and SVG, which is not explicitly supported by the existing recommendations. Moreover, this extended use of MathML and SVG is only marginally covered by existing implementations.
Currently, the only document markup system that can combine mathematics with diagrams is the TeX/LaTeX suite of programs. In this note we will develop guidelines for the extended use of mixing MathML and SVG, and discuss current tool support based practical cases where graphics and mathematical notation are mixed. These will serve as the basis for the discussion in the next section. We can distinguish three cases:
mathematical formulae integrated into some sort of diagram or drawing (section 2 Mathematical Formulae in Diagrams),
some kind of drawing or diagram inside mathematical formulae, e.g. instead of a sub-formula, or as a presentational device (see section 3 Diagrams as Sub-Formulae).
non-hierarchic mixing of formulae and graphics (see section 4 Non-Hierarchical Mixing of Formulae and Graphics).
As we will see, the first two can be solved by interpretations of the current recommentations, while the third one is problematic. We will close with some general remarks about mixing namespaces in XML.
2 Mathematical Formulae in Diagrams
2.1 Use Cases
We start out with the case, where Mathematical formulae are integrated into some kind of drawing or diagram. This is a very common case in the STEM (Science, Technology, Engineering, and Mathematics Literature.
Let us consider the two examples below. The left diagram is a commutative diagrams, such diagrams are used in mathematics to visualize and argue about complex configurations of sets and mappings. The right diagram is a tree-representation of an analytical tableau.
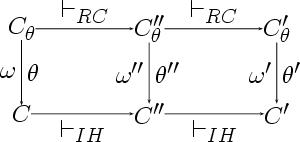
In both cases, mathematical formalae are confined to boxes, without overlap to the graphical structures in the diagram.
2.2 Guidelines
The XHTML + MathML + SVG Profile [XHTML-MathML-SVG] allows to
embed MathML into SVG inside the foreignobject
element. Consider the following example (adapted for MathML content from the SVG 1.1
recommendation [SVG1.1]).
<?xml version="1.0" standalone="yes"?>
<svg width="4in" height="3in" version="1.1" xmlns = 'http://www.w3.org/2000/svg'>
<desc>This example uses the 'switch' element to provide a
fallback graphical representation of an paragraph, if
MathML is not supported.</desc>
<!-- The 'switch' element will process the first child element
whose testing attributes evaluate to true.-->
<switch>
<!-- Process the embedded MathML if the requiredExtensions attribute
evaluates to true (i.e., the user agent supports MathML embedded within SVG). -->
<foreignObject width="100" height="50"
requiredExtensions="xmlns="http://www.w3.org/1998/Math/MathML">
<!-- MathML content goes here -->
<math xmlns="http://www.w3.org/1998/Math/MathML>
<mfrac>
<mn> 1 </mn>
<mrow>
<msup><mi> x </mi><mn> 3 </mn></msup>
<mo> + </mo>
<mfrac><mi> x </mi><mn> 3 </mn></mfrac>
</mrow>
</mfrac>
</math>
</foreignObject>
<!-- Else, process the following alternate SVG. -->
<text font-size="10" font-family="italic">
<tspan x="10" y="10">1/(x^3+(x/3))</tspan>
</text>
</switch>
</svg>Note that the width and height attributes on the
foreignObject are required, which may pose a problem for embedded
MathML objects, which scale by different mechanisms than diagrams (glyphs
re-sizing does not always conserve aspect ratio),
3 Diagrams as Sub-Formulae
In this section discuss the case of diagrams or images inside of mathematical formulae. We will looke at some use cases and the give guidelines to accomodate diagrams and images in MathML representations.
3.1 Use Cases
Let us look at some example of images or diagrams inside mathematical
formulae. Since MathML supplies the mglyph element, the
question we have to ask ourselves in all of these cases, whether the
diagram is not really a specialized glyph
Even though the use of diagrams or images inside of mathematical formulae is relatively rare in published mathematics (an exception seems to be slide presentations or other educational material), such cases do exist, e.g. in Graham, Knuth, Patashnik: Concrete Mathematics, where the authors use the first formula below to talk about the probabilities of certain events involing dice and the second one for theories about the number of ways to pay a certain amount using a variety of coins.
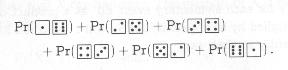

In these example, it is somewhat plausible to think that the dice (after all
the dice are present Unicode as characters 2680 (1) to 2685 (6). But the coins are
not, they could however be integrated into MathML using the mglyph
element; The MathML specification has
this
example about braid group notation.
Later in the book Graham, Knuth, Patashnik talk about tiling rectangles with dominoes, and use the following formulae

Here the assumption that the complex configurations of dominos are glyphs becomes more implausible, after all, there are infinitely many of the. Consider this formula, to see that the math done with these kinds of diagrams is not restricted to trivial formulae
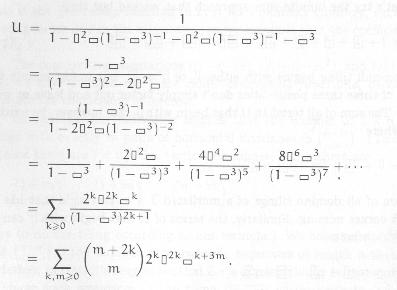
Finally, they use the following formula to reason about graphs.
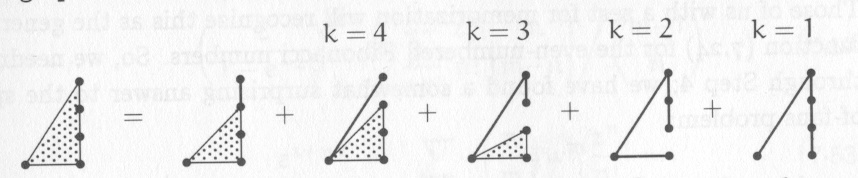
3.2 Guidelines
The MathML2 specification provides the semantics element for
"The semantics element is designed to group
together various sources of information related to a particular
mathematical object. For example, it is often used to provide both
a content representation of the object and a
presentation."
Clearly, the graphical representation of a mathematical object is a
"presentation" of the element, so we can use the
semantics element as in the following example:
<semantics>
<csymbol definitionURL="elementary-stats.html#dice-4up"/>
<annotation-xml encoding="SVG1.1">
<svg xmlns="http://www.w3.org/2000/svg" height="137px">
<rect stroke="black" fill="none" rx="5px" width="40px" height="40px"/>
<circle stroke="black" fill="black" cy="30px" cx="30px" r="5px"/>
<circle stroke="black" fill="black" cy="30px" cx="10px" r="5px"/>
<circle stroke="black" fill="black" cy="20px" cx="20px" r="5px"/>
<circle stroke="black" fill="black" cy="10px" cx="30px" r="5px"/>
<circle stroke="black" fill="black" cy="10px" cx="10px" r="5px"/>
</svg>
</annotation-xml>
<annotation encoding="image/jpeg"> copy dice4.jpg here </annotation>
<annotation encoding="image/gif" other="dice.gif"/>
</semantics>Issue (linking-external-content):
Do we want to use syntax like this for
external links? We cannot use definitionURL since it would
conflict with the use in the types case. Somewhere in the spec we say that
semantics is for associating "inline" information, so the use
here could be inappropriate. But it would sure the convenient, since we
otherwise have to invent a way to do references here. One way would be to use
something like
<semantics> <csymbol definitionURL="elementary-stats.html#dice-4up"/> <annotation-xml encoding="application/xhtml+xml"><img src="dice.gif"/></annotation-xml> </semantics>
but that would be a relatively roundabout way.
Resolution:
None recorded.
The first child of the semantics element is the MathML
object whith which the additional information is associated, it can be
a presentation- or content MathML representation. This child is
mandatory in a semantics element, it can be seen as a fallback
representation in MathML, if the MathML application processing the
semantics element cannot process any of the annotation and
annotation-xml children. In our case, we have chosen to represent the
dice as a csymbol element, another choice would have been to give
an alternate text represented in a mtext element.
4 Non-Hierarchical Mixing of Formulae and Graphics
4.1 Use Cases
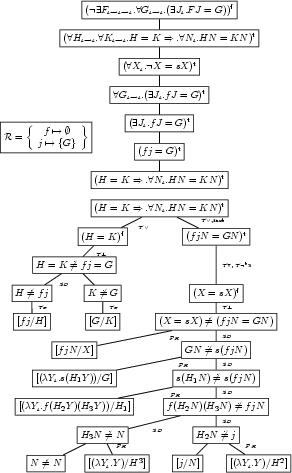
Sometimes Mathematicians want to highlight some properties of formulae by graphical means. Let us look at two examples of diagrammatic embellishments mathematical formulae
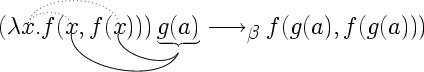

In the first diagram, a -term has been been graphically enhanced to make highlight the dependencies of bound variables (by dotted arcs) and the substitution of actual parameters for formal ones (by the solid arcs). In the second example, a formula in Discourse Representation Theory (DRT; the boxes are actually complex formulae here) is internally annotated by an arrow to show a dependency.
4.2 (Lack of) Guidelines and Implementations
In both cases (though more pronounced in the second one), the compound
graphics cannot be separated into parts that are "only math"
or "only diagram", with disjoint bounding boxes. In fact,
document formatting engines like the pstricks package that
was used to produce these images make use of the fact that both the math,
as well as the diagram parts get converted into the same target format
(PostScript in this case) and can be overlayed.
| Editorial note: MiKo | |
| Again, a MathML to SVG converter can handle this (potentially). Need to talk somewhere about why this is not desirable. What about AMAYA, Mozilla? We need a worked-out example for this. | |
5 Conclusions
We have discussed some use-cases for an integration of the images and and MathML specifications. Simple mathematical diagrams can already be represented in current SVG+MathML applications, but for many relevant classes of mathematical diagrams, the state of the art is not sufficient for mathematical practice. Currently, the only document markup system that can combine mathematics with diagrams is the TeX/LaTeX suite of programs. To make MathML (and the W3C languages) a viable alternative for main-stream technical publications, we need to develop the mixture of MathML and SVG further, alleviating the problems discussed in this note.
Note that these are only an instance of the more general problem of mixing namespaces in general. The hierarchical mixing cases discussed in sections 2 Mathematical Formulae in Diagrams and 3 Diagrams as Sub-Formulae are relatively simple, since the embeddings respect bounding boxes. Presentation agents only need to negotiate box sizes, alignment, and flow of control. Moreover, nesting depths for namespaces with depth greater than one (e.g. SVG in MathML in SVG) seem very rare. But already the very natural mixed case discussed in 4 Non-Hierarchical Mixing of Formulae and Graphics, break this hierarchical black-box model. In particular, prsentation agents would have to negotiate inner coordinates, etc.
| Editorial note: MiKo | |
| Talk about general Problems of mixing Namespaces in XML | |