6 December 2000
This is an updated version of an earlier draft of the conceptual graph standard that was developed by the NCITS.T2 Committee on Information Interchange and Interpretation. Comments and suggestions should be sent to the conceptual graph mailing list, cg@cs.uah.edu, or to the editor, John F. Sowa.
7 Conceptual Graph Interchange Form (CGIF)
Annex A (Informative) Presentation Formats
Annex B (Normative) Metalevel Conventions
Annex C (Informative) Bibliography
The earlier draft of the CG standard was developed by the NCITS.T2 Committee on Information Interchange and Interpretation. During that development, the following members of NCITS.T2 commented on and/or contributed to this CG Standard:
In addition to the NCITS.T2 committee members, the following users and implementers of conceptual graph systems commented on early drafts of this CG Standard, tested its implementability in whole or in part, and/or suggested revisions or extensions to the specifications:
This CG Standard specifies the syntax and semantics of conceptual graphs (CGs) and their representation as machine-readable character strings in the conceptual graph interchange form (CGIF). CGs have been developed as a conceptual schema language, as specified by ISO/IEC 14481 on Conceptual Schema Modeling Facilities (CSMF). CGIF has been designed for interchange between CSMF systems or between other IT systems that require a structured representation for logic. This Standard also provides guidance for implementers of IT systems that use conceptual graphs as an internal representation or as an external representation for interchange with other IT systems. The external representations are readable by humans and may also be used in communications between humans or between humans and machines.
An IT system is in conformance with this CG Standard if it can accept information expressed in the conceptual graph interchange form (CGIF) defined in Chapter 7, translate that information to some internal representation, and then translate its internal representation to CGIF in a form that is equivalent to the original input according to the criteria defined in Chapter 9. The level of conformance of the IT system shall be specified by a conformance pair, which consists of two identifiers called the style and the expressiveness:
Chapter 9 specifies the identifiers that shall be used to represent the style and expressiveness of a conformance pair.
The following normative documents contain provisions, which, through reference in this text, constitute provisions of this CG Standard. For dated references, subsequent amendments to, or revisions of, any of these publications do not apply. However, parties to agreements based on this CG Standard are encouraged to investigate the possibility of applying the most recent editions of the normative documents indicated below. Members of ISO and IEC maintain registers of currently valid International Standards. ANSI maintains a register of currently valid American National Standards.
ISO/IEC 10646-1:1993, Information Technology (IT) - Universal Multiple-Octet Coded Character Set (UCS).
ISO/IEC 14481:1998, Information Technology (IT) - Conceptual Schema Modeling Facilities (CSMF).
ANSI X3.42:1990, Information Technology (IT) - Representation of numerical values in character strings for information interchange.
For the purpose of this CG Standard, the terms and definitions given in ISO/IEC 10646-1, ISO/IEC 14481, ANSI X3.42, and the following list apply. Some terms may be shortened to acronyms or abbreviations, which are listed in parentheses after the term. The term "abstract syntax", for example, may be abbreviated "AS", and "conceptual relation" may be abbreviated "relation".
A conceptual graph (CG) is a representation for logic specified by the abstract syntax (AS) defined in Chapter 6 of this CG Standard. Informally, a CG is a structure of concepts and conceptual relations where every arc links a concept node and a conceptual relation node. Formally, the abstract syntax specifies the CG structures and constraints without commitments to any concrete notation or implementation. Chapter 6 presents the abstract specifications of conceptual graphs in ten normative sections; each section concludes with an informative note that illustrates and explains the abstract details. CGs may be implemented in any machine-readable representation or any humanly readable style that preserves the information specified by the abstract syntax.
For communication between machines, Chapter 7 specifies a concrete syntax called the conceptual graph interchange form (CGIF), which has a simplified syntax and a restricted character set designed for compact storage and efficient parsing. Chapter 8 specifies syntactic extensions, which can be translated to the basic CGIF form that maps to the abstract syntax. For communication with human users, two concrete notations have become traditional: a graphic notation called the display form (DF) and a more compact notation called the linear form (LF). Although the CGIF notation and the extensions are specified in the normative Chapters 7 and 8, the DF and LF notations are described only by recommended guidelines in the nonnormative Appendix A. Chapter 9 defines the semantics of conceptual graphs by a normative translation to predicate calculus.
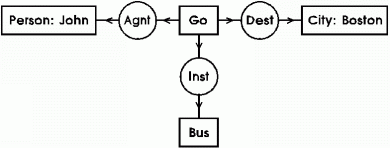
To illustrate the abstract syntax and concrete notations presented in this CG Standard, Figure 1 shows the display form of a conceptual graph that represents the propositional content of the English sentence John is going to Boston by bus.
Figure 1. CG Display Form for "John is going to Boston by bus."

In DF, concepts are represented by rectangles: [Go], [Person: John], [City: Boston], and [Bus]. Conceptual relations are represented by circles or ovals: (Agnt) relates [Go] to the agent John, (Dest) relates [Go] to the destination Boston, and (Inst) relates [Go] to the instrument bus. For n-adic relations, the arcs are numbered from 1 to n; for dyadic relations, the number 1 may be replaced by an arrowhead pointing toward the relation, and the number 2 may be replaced by an arrowhead pointing away from the relation.
As a mnemonic aid, an arrow pointing toward the circle may be read "has a(n)"; an arrow pointing away may be read "which is a(n)"; and any abbreviations may be expanded to the full forms. With this convention, Figure 1 could be read as three English sentences:
This English reading is a convenience that has no normative status. The numbering or direction of the arcs takes precedence over any such mnemonics.
The linear form for CGs is intended as a more compact notation than DF, but with good human readability. It is exactly equivalent in expressive power to the abstract syntax and the display form. Following is the LF for Figure 1:
[Go]- (Agnt)->[Person: John] (Dest)->[City: Boston] (Inst)->[Bus].In this form, the concepts are represented by square brackets instead of boxes, and the conceptual relations are represented by parentheses instead of circles. A hyphen at the end of a line indicates that the relations attached to the concept are continued on subsequent lines.
Both DF and LF are designed for communication with humans or between humans and machines. For communication between machines, the conceptual graph interchange form (CGIF) has a simpler syntax and a more restricted character set. Following is the CGIF for Figure 1:
[Go *x] (Agnt ?x [Person: John]) (Dest ?x [City: Boston]) (Inst ?x [Bus])CGIF is intended for transfer between IT systems that use CGs as their internal representation. For communication with systems that use other internal representations, CGIF can be translated to the Knowledge Interchange Format (KIF):
(exists ((?x Go) (?y Person) (?z City) (?w Bus))
(and (Name ?y John) (Name ?z Boston)
(Agnt ?x ?y) (Dest ?x ?z) (Inst ?x ?w)))
Although DF, LF, CGIF, and KIF look very different, their semantics is
defined by the same logical foundations. Any semantic information expressed in
any one of them can be translated to the others without loss or distortion.
Formatting and stylistic information, however, may be lost in translations
between DF, LF, CGIF, and KIF.
A conceptual graph g is a bipartite graph that has two kinds of nodes called concepts and conceptual relations.
Comment.
To illustrate this definition, consider the conceptual graph in Figure 1 for the sentence John is going to Boston by bus. The term bipartite means that every arc of a CG links a conceptual relation to a concept; there are no arcs that link concepts to concepts or relations to relations. Two of the six arcs in the CG belong to (Agnt), two belong to (Dest), and the remaining two belong to (Inst).
A conceptual graph g with n conceptual relations can be constructed from n star graphs, one for each conceptual relation in g. Since Figure 1 has three conceptual relations, it could be constructed from the following three star graphs, which are represented in the linear form (LF):
[Person: John]<-(Agnt)<-[Go] [Go]->(Dest)->[City: Boston] [Go]->(Inst)->[bus].These three star graphs constitute a disconnected CG, which does not indicate whether the three copies of [Go] refer to the same instance or different instances of going. If they refer to the same instance, the three identical concepts of type [Go] could be overlaid or joined to form the connected CG in Figure 1.
Every concept has a concept type t and a referent r.
Comment.
This abstract definition does not say how the type and referent are represented. In computer storage, they may be represented by a pair of pointers, one pointing to a specification of the concept type and the other pointing to a specification of the referent. In the concrete notations, the type field is on the left, and the referent field is on the right. In the concept [Bus], "Bus" is the type, and the referent field contains a blank, which represents an existential quantifier; the actual referent is a physical entity of type Bus that exists somewhere in the world. In the concept [Person: John], "Person" specifies the type, and the name "John" designates some person who is the referent.
Every conceptual relation r has a relation type t and a nonnegative integer n called its valence.
Certain conceptual relations, called actors, may have side effects that are not represented in the abstract syntax; formally, however, actors are treated like other conceptual relations.
Comment.
In Figure 1, Agnt, Dest, and Inst are dyadic relation types. Examples of monadic relation types include Psbl for possibility and Past for the past tense. A 0-adic conceptual relation is logically equivalent to the proposition stated by its defining conceptual graph. Figure 2 shows the between relation (Betw) as an example of a triadic relation (valence 3), whose first two arcs are linked to two things that are on either side of a third. That graph may be read A person is between a rock and a hard place.
Figure 2. A conceptual relation of valence 3
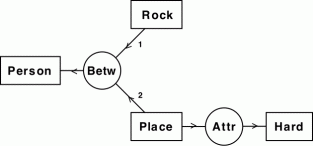
The signature of a relation represents a constraint on the types of concepts that may be linked to its arcs. For Agnt, the signature is (Act,Animate), which indicates that the type of the concept linked to its first arc must be Act or some subtype, such as Go, and the type of the concept linked to its second arc must be Animate or some subtype, such as Person. For Betw, the signature is (Entity,Entity,Entity), which shows that all three concepts must be of type Entity, which is the most general type that imposes no constraints whatever.
For a conceptual relation with n arcs, the first n-1 arcs have arrows that point toward the circle, and the n-th or last arc points away. In LF, Figure 2 may be represented in the following form:
[Person]<-(Betw)-
<-1-[Rock]
<-2-[Place]->(Attr)->[Hard].
The hyphen after the relation indicates that its other arcs are continued
on subsequent lines. The two arcs that point toward the relation are numbered 1
and 2. The arc that points away is the last or third arc; the number 3 may be
omitted, since it is implied by the outward pointing arrow. For monadic
relations, both the number 1 and the arrow pointing toward the circle are
optional. For dyadic relations, the arcs are either numbered 1 and 2, or the
first arc points toward the circle and the second arc points away.
For any nonnegative integer n, an n-adic lambda expression e is a conceptual graph, called the body of e, in which n concepts have been designated as formal parameters of e.
Comment.
This abstract definition does not specify how the formal parameters are designated. The traditional notation, which is used in LF and DF, is to mark a parameter with the Greek letter lambda λ. If n is greater than 1, the parameters may be marked λ1, λ2, ..., λn. As an example, the conceptual graph for the sentence John is going to Boston could be converted to the following dyadic lambda expression by replacing the name John with the symbol λ1 and the name Boston with λ2:
[Person: λ1]<-(Agnt)<-[Go]->(Dest)->[City: λ2].Since this is a dyadic lambda expression, its signature is a pair of types <Person,City>, which come from the type fields of the formal parameters. This lambda expression may be used to define a conceptual relation that relates a person to a city.
To simplify the parsing, the CGIF notation avoids the character λ and represents lambda expressions in a form that shows the signature explicitly:
(lambda (Person*x, City*y) [Go *z] (Agnt ?z ?x) (Dest ?z ?y))For every n-adic lambda expression, the keyword lambda is following by a list of n pairs that specify the formal parameters. Each pair consists of a type, such as Person, and a defining label, such as *x. The list of n types is the signature of the lambda expression.
A type hierarchy is a partially ordered set T whose elements are called type labels. Each type label in T is specified as primitive or defined.
Comment.
The type hierarchy starts with some set of primitive type labels, which includes at least Entity and Absurdity. The definitional mechanisms introduce new type labels, whose place in the hierarchy is determined by their definitions. As an example, the following equation defines the type label MaineFarmer by a lambda expression for a farmer located (Loc) in Maine:
MaineFarmer = [Farmer: λ]->(Loc)->[State: Maine].The character "λ" indicates that the concept [Farmer] is the formal parameter, and the sequence (Farmer) is the signature of the lambda expression. The type label of the formal parameter is always a supertype of the newly defined type: Farmer ≥ MaineFarmer. As an alternate notation, type labels can be defined with the keyword type and a variable:
type MaineFarmer(*x) is [Farmer: ?x]->(Loc)->[State: Maine].Either the type label MaineFarmer or its defining lambda expression could be placed in the type field of a concept. The following two conceptual graphs are equivalent ways of saying Every Maine farmer is laconic:
[MaineFarmer: ∀]->(Attr)->[Laconic].The second graph may be read Every farmer who is located in the state of Maine is laconic. Either graph could be converted to the other by interchanging the type label and its defining lambda expression.[ [Farmer: λ]->(Loc)->[State: Maine]: ∀]->(Attr)->[Laconic].
A relation hierarchy is a partially ordered set R whose elements are called relation labels. Each relation label is specified as primitive or defined, but not both.
Comment.
As an example, the relation type GoingTo could be defined by a CG that makes GoingTo a synonym for a dyadic lambda expression:
[Relation: GoingTo]->(Def)->[LambdaExpression:
[Person: λ1]<-(Agnt)<-[Go]->(Dest)->[City: λ2] ].
This definition says that the relation GoingTo is defined by a lambda
expression that relates a person (marked by λ1), who is the agent
(Agnt) of the concept [Go], to a city (marked by λ2), which is the
destination (Dest) of [Go]. With this relation, the graph for the sentence
John is going to Boston could be represented by the following CG: [Person: John]->(GoingTo)->[City: Boston].This graph can be expanded to a more detailed graph by replacing the relation type label GoingTo with its definition:
[Person: John]->([Person: λ1]<-(Agnt)<-[Go]-
->(Dest)->[City: λ2])->[City: Boston].
The next step is to remove the lambda expression from inside the circle or
parentheses, to join the first parameter [Person: λ1] with the
concept attached to the first arc, and to join the second parameter [City:
λ2] with the concept attached to the second arc: [Person: John]<-(Agnt)<-[Go]->(Dest)->[City: Boston].This graph says that the person John is the agent of going and that the city Boston is the destination of going. Each step of this derivation could be reversed to derive the original graph from the expanded graph.
The referent of a concept is specified by a quantifier, a designator, and a descriptor.
Comment.
The quantifier, designator, and descriptor determine the connections between the CG formalism and the entities it refers to. Those connections are implementation dependent because they go beyond the notation to people, things, actions, and events that are outside the computer system. An existential quantifier declares that at least one instance of the type exists; a defined quantifier may specify other quantities or amounts. A designator specifies the referent by showing its form (literal) or by pointing to it (locator); an undefined designator says nothing about the referent. The three kinds of locators differ in the way the referent is determined: an individual marker, specifies a unique concept in the catalog of individuals of a knowledge base; an indexical is a symbol that determines the referent by an implementation-defined search that is not defined by this CG Standard; and a name is a symbol that determines the referent by some conventions that are independent of the current knowledge base. A descriptor is a CG that describes some aspect of the referent. Following are some examples:
[Proposition: [Cat]<-(Agnt)<-[Chase]->(Thme)->[Mouse]].This graph may be read There exists a proposition, which states that a cat is chasing a mouse. A concept with a completely blank referent, such as [Cat], has an implicit existential quantifier and a blank conceptual graph as descriptor. Since a blank graph does not say anything about the referent, the concept [Cat] by itself simply means There exists a cat.
[Situation: %English"A plumber is carrying a pipe."]
In each of the above concepts, there is an implicit existential; the concept [String: "abcdefg"], for example, may be read There exists a string, whose form is represented by the literal "abcdefg". Two or more designators in the same concept represent different ways of indicating the same referent, as in the concept [Cat: Yojo #5549], which says that the cat named Yojo is cataloged as individual #5549.
The defined quantifiers include the universal quantifier, which is represented by the character "∀" or the string "@every", and collections such as {1, 2, 3} or {Tom, Dick, Harry}. The translation rules specified in Section 8.2 translate the universal quantifier to an existential quantifier and a pair of negations. They translate collections to multiple concepts, each containing an existential referent.
To illustrate descriptors and literals in the referent field, Figure 3 shows a concept [Situation] with a nested conceptual graph that may be read A plumber is carrying a pipe. In the nested graph, the agent relation (Agnt) indicates that the plumber is the one who is doing the action, and the theme relation (Thme) indicates that the pipe is the theme of the action. That nested CG is a descriptor that describes the situation.
Figure 3. A conceptual graph with a descriptor and two
literal referents
![]()
The situation node in Figure 3 is linked via the image relation (Imag) to a concept of type Picture, whose referent field contains an encoded literal of the image. In CGIF, the character "%" marks an encoded literal, which is followed by an identifier that specifies the format and a string that represents the encoding of an image. The situation node is also linked via an Imag relation to a concept of type Sound, whose referent field might contain an encoded literal that represents the sound. In Figure 3, the nonnormative display form uses letters to give a pronounceable approximation to the sound; a multimedia system might reproduce the sound when the user clicks on the concept node. Such features, however, are outside the scope of this CG Standard.
A context C is a concept whose designator is a nonblank conceptual graph g.
Comment.
A context is a concept with a nested conceptual graph that describes the referent. In Figure 3, the concept of type Situation is an example of a context; the nested graph describes the situation as one in which a plumber is carrying a pipe. Figure 4 shows a CG with two contexts; it expresses the sentence Tom believes that Mary wants to marry a sailor.
Figure 4. A conceptual graph containing a nest of two
contexts
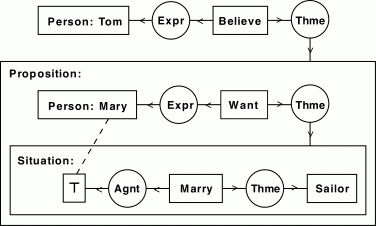
In Figure 4, Tom is the experiencer (Expr) of the concept [Believe], which is linked by the theme relation (Thme) to a proposition that Tom believes. The proposition box contains another conceptual graph, which says that Mary is the experiencer of [Want], which has as theme a situation that Mary hopes will come to pass. That situation is described by another nested graph, which says that Mary (represented by the concept [⊤]) marries a sailor. The dotted line, called a coreference link, shows that the concept [⊤] in the situation box refers to the same individual as the concept [Person: Mary] in the proposition box. Following is the linear form of Figure 4:
[Person: Tom]<-(Expr)<-[Believe]->(Thme)-
[Proposition: [Person: Mary *x]<-(Expr)<-[Want]->(Thme)-
[Situation: [?x]<-(Agnt)<-[Marry]->(Thme)->[Sailor] ]].
Both the display form and the linear form follow the same rules for the
scope of quantifiers. The part of the graph outside the nested contexts contains
three concepts: [Person: Tom], [Believe], and the proposition that Tom believes.
That part of the graph asserts information that is assumed to be true of the
real world. Inside the proposition box are three more concepts: [Person: Mary],
[Want], and the situation that Mary wants. Since those three are only asserted
within the context of Tom's belief, the graph does not imply that they must
exist in the real world. Since Mary is a named individual, one might give her
the benefit of the doubt and assume that she also exists; but her desire and the
situation she supposedly desires exist in the context of Tom's belief. If his
belief is false, the referents of those concepts might not exist in the real
world. Inside the context of the desired situation are the concepts [Marry] and
[Sailor], whose referents exist within the scope of Mary's desire, which itself
exists only within the scope of Tom's belief.
A coreference set C in a conceptual graph g is a set of one or more concepts selected from g or from graphs nested in contexts of g.
Comment.
In the display form, the members of a coreference set C may be shown by connecting them with dotted lines, called coreference links. In Figure 4, the dotted line connecting [Person: Mary] to [⊤] is an example of a coreference link. The concept [⊤] is within the scope of [Person: Mary], which is the dominant node. Since the two concepts represent the same individual, any information in the dominant node may be copied to the other node. The type label Person or the referent Mary, for example, could be copied from the dominant node to the concept [⊤].
In CGIF, which is defined in Chapter 7, the members of a coreference set are marked by coreference labels. One of the dominant nodes is marked with a defining label, prefixed with an asterisk; all the other nodes, are marked with bound labels, prefixed with a question mark.
A knowledge base is a context of type KnowledgeBase whose designator is a conceptual graph consisting of four concepts:
The contents of the knowledge base must satisfy the following constraints:
The type labels KnowledgeBase, TypeHierarchy, RelationHierarchy, CatalogOfIndividuals, and Assertion are metalevel labels that need not be specified in T. However, if a knowledge base contains information about a knowledge base, including knowledge bases that may be nested inside itself, then its type hierarchy must specify the metalevel labels.
Comment.
The outermost context of a knowledge base B corresponds to what Peirce called the sheet of assertion. Its designator is a CG that asserts the information that is assumed to be true in B. The type hierarchy and the relational hierarchy define the labels that appear in the concepts and conceptual relations of any conceptual graphs in any of the contexts nested in B. The catalog of individuals contains global information about the referents identified by individual markers in any concepts in B. As an example, the following catalog specifies individual markers for four entities: a cat, a dog, a village, and a state.
[CatalogOfIndividuals:
[Cat: #5539]-
(Name)->[Word: "Yojo"]
(Attr)->[Black]
(Loc)->[Village: #3711]->(Name)->[Word: "Croton-on-Hudson"] ]
[Dog: #7603]-
(Name)->[Word: "Macula"]
(Attr)->[Spotted]
(Loc)->[State: #2072]->(Name)->[Word: "New Hampshire"] ]]
Four concepts in the nested CG have individual markers: #5539 marks a cat
named Yojo; #3714 marks a village named Croton-on-Hudson; #7603 marks a dog
named Macula; and #2092 marks a state named New Hampshire. The other concepts
and relations specify additional information about the four cataloged
individuals. The outermost context of the same knowledge base may make further
assertions about them, but the problem of finding the individuals themselves is
outside the scope of the formalism.
Individuals that are not cataloged might be implied by existential quantifiers in some concepts of a knowledge base. As an example, O might assert that for every human being x, there exists exactly one father y of x and exactly one mother z of x. Any finite knowledge base, however, must eventually stop with some persons whose parents cannot be identified, even though their existence is implied.
The structures that can be represented in CGs are more general and more highly organized than the information in most commercial databases and knowledge bases. Most such systems can be represented as special cases of a CG knowledge base:
The conceptual graph interchange form (CGIF) is a representation for conceptual graphs intended for transmitting CGs across networks and between IT systems that use different internal representations. All features defined by the abstract syntax of Chapter 6 and the extensions of Chapter 8 are representable in CGIF. The CGIF syntax ensures that all necessary syntactic and semantic information about a symbol is available before the symbol is used; therefore, all translations can be performed during a single pass through the input stream. The CGIF syntax is specifed in terms of the Extended BNF (EBNF) rules and metalevel conventions, which are defined in Annex B.
The lexical categories of CGIF are defined as sequences of characters as specified in ISO/IEC 10646-1. Characters outside the 7-bit subset of ISO/IEC 10646-1 occur only in strings that represent identifiers, names, literals, and comments. By using escape sequences in such strings, it is possible to encode and transmit CGIF in the 7-bit subset of ISO/IEC 10646-1. Numerical values are represented by the conventions of ANSI X3.42. The following lexical categories may be used in EBNF rules in this chapter or in the translation rules in chapters 8 and 9:
The CGIF lexical categories can be recognized by a finite-state tokenizer or preprocessor. No characters of white space (blanks or other nonprinting characters) are permitted inside any lexical item other than delimited strings (names, comments, or quoted strings). Zero or more characters of white space may be inserted or deleted between any lexical categories without causing an ambiguity or changing the syntactic structure of CGIF. The only white space that should not be deleted is inside delimited strings.
Comment ::= DelimitedStr(";")
DelimitedStr(D) ::= D (AnyCharacterExcept(D) | D D)* D
Exponent ::= ("e" | "E") ("+" | "-")? UnsignedInt
Floating ::= ("+" | "-") ("." UnsignedInt Exponent?
| UnsignedInt ("." UnsignedInt? Exponent?
| Exponent ) )
Identifier ::= (Letter | "_") (Letter | Digit | "_")*
Identifiers beginning with "_" followed by one or more digits are generated by the Gensym rule defined in Section 8.2. Such identifiers should be avoided unless they have been generated by a call to the Gensym rule.
Integer ::= ("+" | "-") UnsignedInt
Name ::= DelimitedStr("'")
Number ::= Floating | Integer
QuotedStr ::= DelimitedStr('"')
UnsignedInt ::= Digit+
Every syntactic category of CGIF is first described in English and then defined formally by an EBNF rule, as defined in Annex B. Each EBNF rule is followed by an English statement of possible constraints and implications. Context-sensitive constraints, which are determined by the abstract syntax defined in Chapter 6 or by the extended syntax defined in Chapter 8, are stated with a reference to the governing section in Chapter 6 or 8. In all questions of interpretation, the EBNF rules take precedence over the English descriptions and statements. The following syntactic categories may be used in EBNF rules and translation rules:
The CGIF syntactic categories are defined by a context-free grammar that can be processed by a recursive-descent parser. Zero or more characters of white space (blanks or other nonprinting characters) are permitted between any two successive constituents of any grammar rule that defines a syntactic category.
Actor ::= "<" Type(N) Arc* "|" Arc* Comment? ">"The arcs that precede the vertical bar are called input arcs, and the arcs that follow the vertical bar are called output arcs. The valence N of the actor type must be equal to the sum of the number of input arcs and the number of output arcs.
Arc ::= Concept | BoundLabel
BoundLabel ::= "?" Identifier
CG ::= (Concept | Relation | Actor | SpecialContext | Comment)*The alternatives may occur in any order provided that any bound coreference label must occur later in the CGIF stream and must be within the scope of the defining label that has an identical identifier. The definition permits an empty CG, which contains nothing. An empty CG, which says nothing, is always true.
Concept ::= "[" Type(1)? {CorefLinks?, Referent?} Comment? "]"
If the type is omitted, the default type is Entity. This rule permits
the coreference labels to come before or after the referent. If the referent
is a CG that contains bound labels that match a defining label on the current
concept, the defining label must precede the referent.
In Figure 4, for example, the concept [Person: Mary] could be written in CGIF as [Person:'Mary'*x]; the coreferent concept [⊤] could be written [?x], and its implict type would be Entity.
Conjuncts(N) ::= TypeTerm(N) ("&" TypeTerm(N))*
The conjunction list must have the same valence N as every type term.
CorefLinks ::= DefLabel | BoundLabel*If a dominant concept node, as specified in Section 6.9, has any coreference label, it must be either a defining label or a single bound label that has the same identifier as the defining label of some co-nested concept.
DefLabel ::= "*" IdentifierThe concept in which a defining label appears is called the defining concept for that label; a defining concept may contain at most one defining label and no bound coreference labels. Any defining concept must be a dominant concept as defined in Section 6.9.
Every bound label must be resolvable to a unique defining coreference label within the same context or some containing context. When conceptual graphs are imported from one context into another, however, three kinds of conflicts may arise:
In cases (1) and (2), any possible conflict can be detected by scanning no further than the right bracket "]" that encloses the context into which the graph is being imported. Therefore, in those two cases, the newly imported defining coreference label and all its bound labels must be replaced with an identifier that is guaranteed to be distinct. In case (3), there is no conflict that could affect the semantics of the conceptual graphs or any correctly designed CG tool; but since a human reader might be confused by the similar labels, a CG tool may replace the identifier of one of the defining coreference labels and all its bound labels.
Descriptor ::= Structure | CGA context-free rule, such as this, cannot express the condition that a CG is only called a descriptor when it is nested inside some concept.
Designator ::= Literal | Locator | Quantifier
Disjuncts(N) ::= Conjuncts(N) ("|" Conjuncts(N))*
The disjunction list must have the same valence N as every conjunction
list.
FormalParameter ::= Type(1) [DefLabel]The defining label is required if the body of the lambda expression contains any matching bound labels.
Indexical ::= "#" Identifier?The identifier specifies some implementation-dependent method that may be used to replace the indexical with a bound label.
IndividualMarker ::= "#" UnsignedIntThe integer specifies an index to some entry in a catalog of individuals.
LambdaExpression(N) ::= "(" "lambda" Signature(N) CG ")"
A lambda expression with N formal parameters is called an N-adic labda
expression. The simplest example, represented "(lambda ())", is a 0-adic
lambda expression with a blank CG.
Literal ::= Number | QuotedStr
Locator ::= Name | IndividualMarker | Indexical
Negation ::= "~[" CG "]"A negation is an abbreviation for a concept of type Proposition with an attached relation of type Neg. It has a simpler syntax, which does not permit coreference labels or attached conceptual relations. If such options are required, the negation can be expressed by the unabbreviated form with an explicit Neg relation.
Quantifier ::= "@" (UnsignedInt | Identifier ("{" Arc* "}")?)
The symbol @some is called the existential quantifier,
and the symbol @every is called the universal quantifier. If
the quantifier is omitted, the default is @some.
Referent ::= ":" {Designator?, Descriptor?}
Relation ::= "(" Type(N) Arc* Comment? ")"
The valence N of the relation type must be equal to the number of arcs.
Signature ::= "(" (FormalParameter ("," FormalParameter)*)? ")"
SpecialConLabel ::= "if" | "then" | "either" | "or" | "sc"The five special context labels and the two identifiers "else" and "lambda" are reserved words that may not be used as type labels.
SpecialContext ::= Negation | "[" SpecialConLabel ":"? CG "]"
Structure ::= ("%" Identifier)? "{" Arc* "}"
Type(N) ::= TypeLabel(N) | TypeExpression(N)A concept type must have valence N=1. A relation type must have valence N equal to the number of arcs of any relation or actor of that type. The type label or the type expression must have the same valence as the type.
TypeExpression(N) ::= LambdaExpression(N) | "(" Disjuncts(N) ")"
The type expression must have the same valence N as the lambda
expression or the disjunction list.
TypeLabel(N) ::= IdentifierThe type label must have an associated valence N.
TypeTerm(N) ::= "~"? Type(N)The type term must have the same valence N as the type.
Comment.
As an example, the DF representation in Figure 1 was translated to LF, CGIF, and KIF in Section 5.1. Following is a translation of Figure 2 from DF to CGIF:
(Betw [Rock] [Place *x1] [Person]) (Attr ?x1 [Hard])For more compact storage and transmission, all white space not contained in comments or enclosed in quotes may be eliminated:
(Betw[Rock][Place*x1][Person])(Attr?x1[Hard])This translation takes the option of nesting all concept nodes inside the conceptual relation nodes. A logically equivalent translation, which uses more coreference labels, moves the concepts outside the relations:
[Rock *x1] [Place *x2] [Person *x3] (Betw ?x1 ?x2 ?x3) [Hard ?x4] (Attr ?x2 ?x4)The concept and relation nodes may be listed in any order provided that every bound label follows the defining node for that label.
Following is a translation of Figure 3 from DF to CGIF:
[Situation *x1 (Agnt [Plumber] [Carry *x2]) (Thme ?x2 [Pipe])] (Imag ?x1 [Sound: %WAV"..."; The literal string encodes the audio. ]) (Imag ?x1 [Picture: %JPEG"..."; The literal string encodes the image. ])This example shows how literals of any kind may be represented in the referent field of a concept. The identifiers "WAV" and "JPEG" specify the method of encoding. In DF, the sound might be represented by a transcription such as "Clink Clankety Scrape" or it could be converted to audio when someone clicks a mouse on the concept node. To avoid storing multiple copies of large literals, such as sound or video, a single copy might be stored outside the CG system with only a locator in the referent field.
Following is a translation of Figure 4 from DF to CGIF:
[Person: Tom *x1] [Believe *x2] (Expr ?x2 ?x1)
(Thme ?x2 [Proposition
[Person: Mary *x3] [Want *x4]
(Thme ?x4 [Situation
(Agnt [Marry *x5] ?x3) (Thme ?x5 [Sailor]) ]) ])
Note that the concept [⊤] in Figure 4, which may be represented
[?x3] in LF or CGIF, may also be omitted completely in CGIF since the
coreference label ?x3 inside the conceptual relation of type Agnt is sufficient
to show the connection. As these examples illustrate, CGIF is not as readable as
DF, but it contains the equivalent semantic information. To reconstruct an exact
image of the original DF, the comment fields in the concept and relation nodes
may contain additional layout information to specify the style and placement of
the nodes.
Whenever a feature of the abstract syntax (AS) specified in Chapter 6 has the same name as some CGIF category of Section 7.2, the AS feature is represented by a string defined by that CGIF category. The mapping of AS features to CGIF categories is not one to one because of the following exceptions:
Each subsection from 7.3.1 to 7.3.10 specifies the CGIF strings that represent the AS features defined in the section from 6.1 to 6.10 respectively.
A conceptual relation that is represented by an Actor string may have side effects that are not represented in the abstract syntax or the translation to predicate calculus defined in Chapter 8.
TypeHierarchy ::= "[" "TypeHierarchy"
(TypeDefinition | TypeLabelOrdering)* "]"
A type definition is a star graph containing a conceptual relation of type Def that relates a type label to a lambda expression:
TypeDefinition ::= "(" "Def"
"[" "TypeLabel" "\"" ConTypeLabel "\"" "]"
"[" "LambdaExpression" "\"" LambdaExpression "\"" "]" ")"
A type label ordering is a star graph containing a conceptual relation of type EQ, GT, or LT that relates two type labels:
TypeLabelOrdering ::= "(" ("EQ" | "GT" | "LT")
"[" "TypeLabel" "\"" ConTypeLabel "\"" "]"
"[" "TypeLabel" "\"" ConTypeLabel "\"" "]" ")"
For two type labels s and t, the type label ordering has a conceptual
relation of type EQ iff s=t, of type GT iff s>t, and of type LT iff s<t.
The type definitions and type label orderings that define a type hierarchy must obey the following constraints:
(GT [TypeLabel "Entity"] [TypeLabel "Absurdity"]).
For more concise storage and transmission, multiple star graphs for the type label ordering may be abbreviated by using a collection as defined in Section 8.2. As an example, the following star graph asserts that the type label "Entity" is related to each type label in the collection by the relation GT:
(GT [TypeLabel "Entity"]
[TypeLabel @Col{"Physical", "Abstract", "Independent",
"Relative", "Mediating", "Continuant", "Occurrent"}])]
The translation rules in Section 8.2 would expand this star graph to
seven separate star graphs -- one for each type label in the collection.
RelationHierarchy ::= "[" "RelationHierarchy"
(RelationDefinition | ValenceSpec | RelationLabelOrdering)* "]"
A relation definition is a star graph containing a conceptual relation of type Def that relates a relation label to a lambda expression:
RelationDefinition ::= "(" "Def"
"[" "RelationLabel" "\"" RelTypeLabel "\"" "]"
"[" "LambdaExpression" "\"" LambdaExpression "\"" "]" ")"
A valence specification is a star graph containing a conceptual relation of type Has that relates a relation label to its valence:
ValenceSpec ::= "(" "Has"
"[" "RelationLabel" "\"" RelTypeLabel "\"" "]"
"[" "Valence" Integer "]" ")"
A relation label ordering is a star graph containing a conceptual relation of type EQ, GT, or LT that relates two type labels:
RelationLabelOrdering ::= "(" ("EQ" | "GT" | "LT")
"[" "RelationLabel" "\"" RelTypeLabel "\"" "]"
"[" "RelationLabel" "\"" RelTypeLabel "\"" "]" ")"
For two relation labels r and s, the relation label ordering has
a conceptual relation of type EQ iff r=s, of type GT iff r>s, and of type
LT iff r<s.
The most general relation type of valence n would be defined by a lambda expression (lambda(Entity,...,Entity)), in which the signature is a list of n concepts of type Entity. A relation of that type would always be true when linked to n concepts of any type.
The relation definitions, valence specifications, and relation label orderings that define a relation hierarchy must obey the following constraints:
For more concise storage and transmission, multiple star graphs for relation label orderings and valence specifications may be abbreviated by using collections. As an example, the following star graph asserts that each of the four type labels in the collection has the valence 2:
(Has [TypeLabel @Col{"EQ", "GT", "LT", "Has"}] [Valence 2])
The translation rules in Section 8.2 would expand this star graph to
four separate star graphs -- one for each type label in the collection.
KB ::= "[" "KnowledgeBase" ":"
{ "[" "TypeHierarchy" ":" CG.T "]",
"[" "RelationHierarchy" ":" CG.R "]",
"[" "CatalogOfIndividuals" ":" CG.C "]",
"[" "Assertion" ":" CG.O "]" } "]"
When the pattern part of this rule matches a CGIF string that represents
a knowledge base, the CGs used as designators of the four nested concepts are
assigned to the variables T, R, C, and O. Those CGs must obey the following
constraints:
Although CGIF requires that every bound coreference label be preceded by a matching defining coreference label, there is no such restriction on the type labels and the relation labels. Therefore, the definitions of type and relation labels may be recursive or mutually recursive. Any implementation of CGIF must be prepared to allocate internal storage space for type and relation labels before their definitions and partial ordering have been specified.
Comment.
The CGs T and R specify the possible type and relation labels that may appear in any concept in the knowledge base together with their definitions and the partial orderings of the type and relation hierarchies. The CG C catalogs all the entities that represent individuals that may be explicitly referenced in the knowledge base; it may also assert some background knowledge about those individuals. All other assertions that are known or assumed to be true in the current knowledge base are stated by the CG O.
Since a knowledge base is also a concept, it may be linked to conceptual relations in a conceptual graph that makes a statement about the knowledge base, the CGs nested inside it, and the entities those CGs may refer to. Such a graph could be nested in the outermost context of another knowledge base, which would then be a metaknowledge base about the nested knowledge base. Knowledge bases may be nested to any depth; a metaknowledge base may contain assertions about knowledge bases nested inside itself, but no knowledge base may contain references to a knowledge base in which it is nested.
The abstract definitions in Chapter 6 define the core structures of conceptual graphs, which are sufficient to represent all of first-order and higher-order logic. To represent logic more concisely, however, the extended syntax supports special contexts and defined quantifiers, which can all be translated to the core structures. The translation rules defined in Section B.2 provide a mechanism for mapping the extended syntax to CGIF, whose mapping to the abstract syntax is defined in Section 7.3.
All Boolean operators can be represented in terms of conjunction and negation. The conjunction of two CGs is represented by including them in the same context. The negation of any CG is represented by including it in a negation. For convenience and readability, some combinations of conjunction and negation are defined as special contexts, whose syntax is defined by EBNF rules and whose semantics is defined by translation rules that convert them to the basic CGIF notation.
The first two special context labels are "If" and "Then", which are used to represent material implication. The syntactic category IfThen is defined as a context with the label "If" whose designator is any CG and a context with the label "Then":
IfThen ::= "[" "If" CG "[" "Then" CG "]" "]"Any CGIF string of this form can be translated to a basic CGIF string by the TrIfThen translation rule:
TrIfThen ::= "[" "If" CG.x "[" "Then" CG.y "]" "]"
=> "~[" x "~[" y "]" "]"
The first line of this rule matches any IfThen string; during the match,
it assigns the string that represents the first CG to the variable x and the
string that represents the second CG to y. Then the second line generates a
string that encloses the two Concept strings x and y in nested negations.
As an example, the following CGIF string represents the sentence If Sam has a car, then Sam drives the car:
[If (Has [Person 'Sam'] [Car]
[Then [Drive *x] (Agnt ?x [Person 'Sam']) (Thme ?x [Car #]) ]]
The TrIfThen rule translates this string to the following: ~[ (Has [Person 'Sam'] [Car]
~[ [Drive *x] (Agnt ?x [Person 'Sam]) (Thme ?x [Car #]) ]]
This string is corresponds to the sentence It is false that Sam has a
car, and Sam does not drive the car.
The Either and Or contexts represent disjunction. The syntactic category EitherOr is defined as a context that has the special label "Either" that contains a conceptual graph and zero or more contexts with the special label "Or":
EitherOr ::= "[" "Either" CG
("[" "Or" CG "]")* "]"
Any CGIF string of this form can be translated to the basic CGIF form by
the TrEither translation rule and the TrOrs rule: TrEither ::= "[" "Either" CG.x
("[" "Or" CG "]")*.y "]"
=> "~[" x TrOrs(y) "]"
The first line of this rule matches a context with the label "Either" and
assigns the first CG, which may be blank, to the variable x. The second
line matches zero or more contexts with the label "Or" and assigns all of them
to the variable y. Then the third line generates a negative context containing x
and the result of translating y by the TrOrs rule. TrOrs ::= ("[" "Or" CG.x "]")?.y String.z RightEnd
=> (y="" ? "" | "~[" x "]" TrOrs(z))
The first line of this rule matches an optional context with the special
label "Or"; during the match, it assigns the nested CG to x, the possibly
nonexistent context to y, and the remainder of the input string to z. Then the
second line has a conditional that tests to see whether y is empty; if so, it
returns the empty string; otherwise, it returns a negation of x followed by the
result of applying the TrOrs rule to the string z.
As an example, the following CGIF string has two nested Or contexts to represent the sentence Either Sam has a car, or Sam rides a bus:
[Either [Or (Has [Person Sam] [Car]) ] [Or [Ride *x] (Agnt ?x [Person Sam]) (Inst ?x [Bus]) ]]The TrEither and TrOrs rule translate this string to the following:
~[ ~[ (Has [Person Sam] [Car]) ] ~[ [Ride *x] (Agnt ?x [Person Sam]) (Inst ?x [Bus]) ]]Since the Either context contains the Or contexts within its scope, it is the place to put a concept that has coreference links to all the options. As an example, consider the following sentence Either a cat is on a mat, or it is eating, or it is chasing a mouse. The concept [Cat] must be placed in a context outside all three disjunctions:
[Either [Cat *x] [Or (On ?x [Mat]) ] [Or (Agnt [Eat] ?x) ] [Or [Chase *y] (Agnt ?y ?x) (Thme ?y [Mouse]) ]]This graph is logically equivalent to the graph that represents the sentence Every cat is on a mat, is eating, or is chasing a mouse or to the graph for the sentence If there exists a cat, then it is on a mat, it is eating, or it is chasing a mouse. In all these sentences, the cat is a hypothetical or generic cat. If the speaker has a particular cat in mind, then the concept [Cat: *x] would have to be moved outside the context of Either:
[Cat *x] [Either [Or (On ?x [Mat]) ] [Or (Agnt [Eat] ?x) ] [Or [Chase *y] (Agnt ?y ?x) (Thme ?y [Mouse]) ]]This graph corresponds to the sentence There exists a certain cat, which is on a mat, is eating, or is chasing a mouse.
As an example, consider the following CGIF representation the sentence Every cat is on a mat:
(On [Cat @every] [Mat])The occurrence of the symbol "@every" in the referent field of the concept [Cat @every] triggers a translation rule that generates the following basic CGIF representation:
~[ [Cat: *_5219] ~[ (On ?_5219 [Mat]) ]]The translation rule generates a new coreference label whenever it is invoked. In this case, it generated the defining label *_5219 with the corresponding bound label ?_5219. The nest of two negations in the translated CGIF corresponds to an implication. Therefore, it can be read If there exists a cat, then it is on a mat.
Following are some other constructions that can be introduced by translation rules:
[ [Farmer: λ]->(Loc)->[State: Maine]: {*}∀].
The type field contains a lambda expression for farmer located (Loc) in
the state of Maine, and the referent field contains the generic set symbol {*}
and a universal quantifier ∀. Altogether, this concept may be read the set
of all farmers located in the state of Maine.
The macros allow the full power of logic to be used for defining generalized quantifiers. The character "¬" in the referent field represents the universal negative quantifier, which is read as the English word no. The qualifier @>18 may be read as more than 18. In combination, they can represent the sentence No trailer truck has more than 18 wheels:
[TrailerTruck: ¬]->(Part)->[Wheel: {*}@>18].
The first step of the macro expansion produces a graph for the sentence
It is false that a trailer truck has more than 18 wheels: ¬[ [TrailerTruck]->(Part)->[Wheel: {*}@>18] ].
This graph, in combination with Figure 4.8, can be used to say that every
trailer truck has at least 18 and no more than 18 wheels. The qualifier @=18 can
be defined by the conjunction of both these forms to say that every trailer
truck has exactly 18 wheels.
(∀x:Woman)(∃y:Man)married(x,y).The first formula may be read For every woman x, there exists a man y, where x married y or more simply Every woman married some man. That formula does not guarantee that each woman found a unique man, but it leaves the possibility open. The second formula, however, could be read Some man married every woman. If there is more than one woman, the man would be a bigamist.(∃y:Man)(∀x:Woman)married(x,y).
In EGs and CGs, the scope is normally shown by context enclosures, which correspond to the parentheses in predicate calculus. To reduce the number of contexts, another way of showing scope is to assume precedence levels for the various kinds of quantifiers. By convention, the universal quantifier ∀ has higher precedence than the existential quantifiers in the same context. With that convention, the two sentences may be represented by the following conceptual graphs:
(Past)->[Situation: [Woman: ∀]<-(Agnt)<-[Marry]->(Thme)->[Man] ].The first graph may be read Every woman married some man, but the second is more contorted: There exists a man that every woman married. The PAST relation attached to the contexts shows the past tense explicitly.[Man: *x] (Past)->[Situation: [Woman: ∀]<-(Agnt)<-[Marry]->(Thme)->[?x] ].
In English, scope is often shown by special words and stylistic conventions. The word certain, in the sentence Every woman married a certain man, suggests that the existential quantifier for a certain man has higher precedence than the universal quantifier for every woman. Therefore, the CG symbol @certain may be defined as an existential quantifier with a higher precedence than ∀:
(Past)->[ [Woman: ∀]<-(Agnt)<-[Marry]->(Thme)->[Man: @certain] ].In this graph, the quantifier @certain has highest precedence, ∀ has middle precedence, and the existential in [Marry] has lowest precedence. That means that for each woman, there is a separate instance of marrying, but the same man is the bridegroom in each instance. Following are the three precedence levels for CG quantifiers:
When new quantifiers are defined, they are assigned to one or another of these levels. The symbol @1, for example, represents the quantifier ∃!, which means there exists exactly one. It has the same low precedence as the implicit existential. For complex mixtures of quantifiers, the scope can be delimited by transparent contexts (marked by context brackets [ ] with no type label).
When a conceptual graph is represented in CGIF, the grammar rules permit several different options, all of which are logically equivalent. As an example, consider the following CGIF representation for Figure 1, which was discussed in Chapter 5:
[Go *x] (Agnt ?x [Person: John]) (Dest ?x [City: Boston]) (Inst ?x [Bus])As another option, the grammar permits all concept nodes to be moved to the front with all arcs represented by bound variables:
[Go *x] [Person: John *y] [City: Boston *z] [Bus *w] (Agnt ?x ?y) (Dest ?x ?z) (Inst ?x ?z)This representation takes somewhat more space and requires more coreference labels. However, it has a more direct mapping to predicate calculus:
(∃x:Go)(∃y:Person)(∃z:City)(∃w:Bus)
(Name(y,'John') ∧ Name(z,'Boston') ∧
Agnt(x,y) ∧ Dest(x,z) ∧ Inst(x,w))
In CGIF, the names John and Boston are represented in the referent fields
of concepts. In predicate calculus, the Name predicate is added to indicate that
they are names. In KIF, however, the absence of a question mark indicates that
they are constants, and the Name predicate may be omitted. Following is the
corresponding statement in KIF: (exists ((?x Go) (?w Bus))
(and (Person John) (City Boston)
(Agnt ?x John) (Dest ?x Boston) (Inst ?x ?w)))
For a given abstract CG, all the variations of CGIF permitted by the
grammar are logically equivalent, and they map to statements in predicate
calculus or KIF that are logically equivalent. For output, an IT system may
generate any variation of CGIF permitted by the grammar; for input, it must be
able to recognize all of them.
The translation from CGIF to predicate calculus is defined by the function φ. If u is any CG, then φ(u) is the corresponding predicate calculus formula. As examples, following are five English sentences and their represetations in CGIF, predicate calculus, and KIF:
(On [Cat: @every] [Mat])
(∀x:Cat)(∃y:Mat)On(x,y)
(forall (?x cat) (exists (?y mat) (on ?x ?y)))
~[(On [Dog: @every] [Mat])]
~(∀x:Dog)(∃y:Mat)on(x,y)
(not (forall (?x dog) (exists (?y mat) (on ?x ?y))))
[Dog *x] ~[(On ?x [Mat])]
(∃x:Dog)~(∃y:Mat)On(x,y)
(exists (?x dog) (not (exists (?y mat) (on ?x ?y))))
[Either [Or (On [Cat: Yojo] [Mat])] [Or (Agnt [Run] [Dog: Macula])] ]
((∃x:Cat)(∃y:Mat)(Name(x,'Yojo') ∧ On(x,y)) ∨ ((∃z:Dog)(∃w:Run)(Name(z,'Macula') ∧ Agnt(w,z)))
(or (exists (?y mat) (and (cat Yojo) (on Yojo ?y)))
(exists (?w run) (and (dog Macula) (agnt ?w Macula))))
[If (On [Cat *x] [Mat]) [Then (Attr ?x [Happy])] ]
(∀x:Cat)(∀y:Mat)(On(x,y) &implies; (∃z:Happy)Attr(x,z))
(forall ((?x cat) (?y mat))
(=> (on ?x ?y)
(exists (?z happy) (attr ?x ?z))))
All operations on conceptual graphs are based on combinations of six canonical formation rules, each of which performs one basic graph operation. Logically, each rule has one of three possible effects: it makes a CG more specialized, it makes a CG more generalized, or it changes the shape of a CG while leaving it logically equivalent to the original. All the rules come in pairs: for each specialization rule, there is a corresponding generalization rule; and for each equivalence rule, there is another equivalence rule that transforms a CG to its original shape. These rules are fundamentally graphical: they are easier to show than to describe.
The first two rules, which are illustrated in Figure 5, are copy and simplify. At the top is a CG for the sentence "The cat Yojo is chasing a mouse." The down arrow represents the copy rule. One application of the rule copies the Agnt relation, and a second application copies the subgraph ->(Thme)->[Mouse]. Both copies are redundant, since they add no new information. The up arrow represents two applications of the simplify rule, which performs the inverse operation of erasing redundant copies. The copy and simplify rules are called equivalence rules because any two CGs that can be transformed from one to the other by any combination of copy and simplify rules are logically equivalent. The two formulas in predicate calculus that are derived from the CGs in Figure 5 are also logically equivalent. The top CG maps to the following formula:
which is true or false under exactly the same circumstances as the formula that corresponds to the bottom CG:
By the inference rules of predicate calculus, either of these two formulas can be derived from the other.
Figure 5. Copy and simplify rules
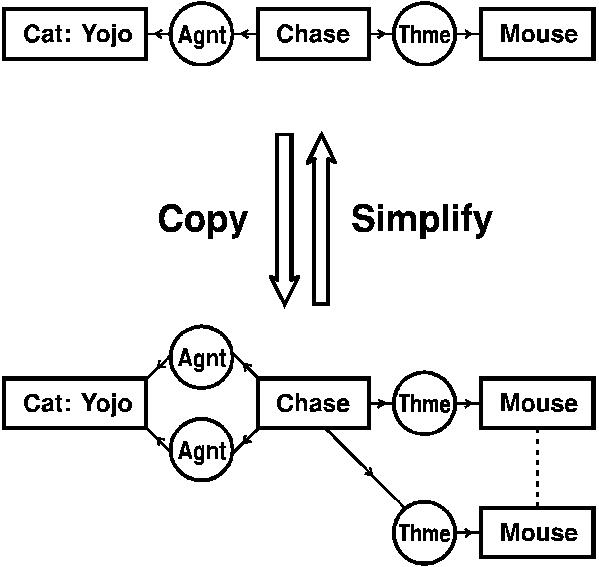
Figure 6 illustrates the restrict and unrestrict rules. At the top is a CG for the sentence "A cat is chasing an animal." By two applications of the restrict rule, it is transformed to the CG for "The cat Yojo is chasing a mouse." The first step is a restriction by referent of the concept [Cat], which represents some indefinite cat, to the more specific concept [Cat: Yojo], which represents an individual cat named Yojo. The second step is a restriction by type of the concept [Animal] to a concept of the subtype [Mouse]. Two applications of the unrestrict rule perform the inverse transformation of the bottom graph to the top graph. The restrict rule is called a specialization rule, and the unrestrict rule is a generalization rule. The more specialized graph implies the more general one: if the cat Yojo is chasing a mouse, it follows that a cat is chasing an animal. The same implication holds for the corresponding formulas in predicate calculus. The more general formula
is implied by the more specialized formula:
Figure 6. Restrict and unrestrict rules
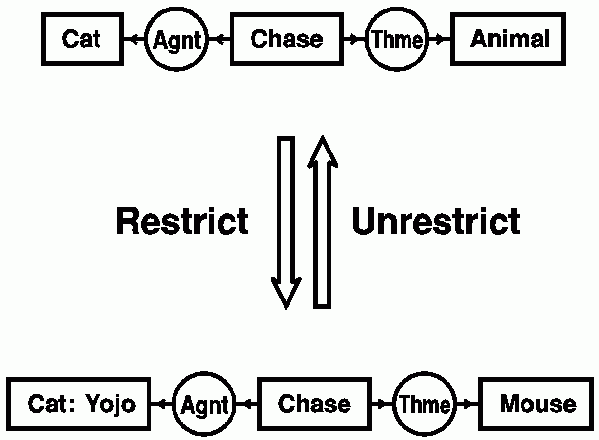
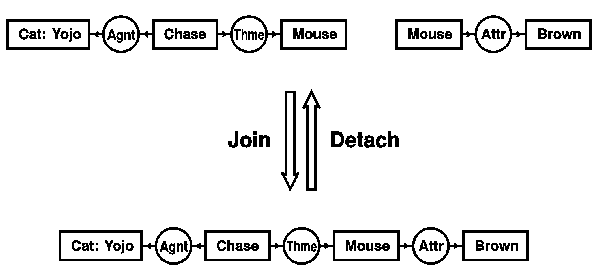
Figure 7 illustrates the join and detach rules. At the top are two CGs for the sentences "Yojo is chasing a mouse" and "A mouse is brown." The join rule overlays the two identical copies of the concept [Mouse] to form a single CG for the sentence "Yojo is chasing a brown mouse." The detach rule performs the inverse operation. The result of join is a more specialized graph that implies the one derived by detach. The same implication holds for the corresponding formulas in predicate calculus. The conjunction of the formulas for the top two CGs
is implied by the formula for the bottom CG:
Figure 7. Join and detach rules
Although the canonical formation rules are easy to visualize, the formal specifications require more detail. They are most succinct for the simple graphs, which are CGs with no contexts, no negations, and no quantifiers other than existentials. The following specifications, stated in terms of the abstract syntax, can be applied to a simple graph u to derive another simple graph w.
Although the six canonical formation rules have been explicitly stated in terms of conceptual graphs, equivalent operations can be performed on any notation for logic.
For nested contexts, the formation rules depend on the number of negations. A positive context (sign +) is nested in an even number of negations (possibly zero). A negative context (sign -) is nested in an odd number of negations.
Let u be a conceptual graph in which some concept is a context whose designator is a nested conceptual graph v. The following canonical formation rules convert u to another CG w by operating on the nested graph v, while leaving everything else in u unchanged.
~[ ~[v]] => [SC: v].A double negation or a scoping context around a conceptual graph may be drawn or erased at any time. If v is a conceptual graph, the following three forms are logically equivalent:
~[ ~[v]], [SC: v], v.
In summary, negation reverses the effect of generalization and specialization, but it has no effect on the equivalence rules.
The canonical formation rules are the foundation for all logical operations on CGs. For each rule, there is a corresponding inference rule for predicate calculus. If some rule transforms a CG u to a CG v where u implies v, then the corresponding formula φ(u) in predicate calculus implies the formula φ(v). The graph rules, however, are usually simpler than the corresponding rules in predicate calculus.
By handling the syntactic details of conceptual graphs, the generalization and specialization rules enable the rules of inference to be stated in a general form that is independent of the graph notation.
The corresponding rules of lambda contraction are the inverses of the rules of lambda expansion: if any conceptual graph g could have been derived by lambda expansion from a CG u, then g may be contracted to form u. These rules are the graph equivalents of Church's rules for lambda calculus. Like Church's version, they can be used as equivalence rules in proofs.
The abstract syntax (AS) is independent of any notation. It allows a concept to be identified with a block of computer storage or with multimedia presentations that use colors, three dimensions, specialized shapes, sound, and motion. The display form (DF) is intended as a readable two-dimensional representation that can be drawn on paper or computer screens. The linear form (LF) is convenient for keyboard entry of CGs or for printing CGs in a more compact form than DF. Neither DF nor LF is a normative notation, and implementations of CG tools that conform to this CG Standard may extend or modify DF or LF to adapt them to specialized applications.
Unlike the abstract form, the concrete notations must deal with the limitations of some physical medium: material such as paper, plastic, or glass; images displayed on a two-dimensional surface or in a three-dimensional space; or structures of bits and pointers in computer storage. The physical medium may introduce features that are not part of the formal definition:
These constraints introduce extraneous features that may be important for human factors or computer efficiency, but they are irrelevant to the abstract syntax, the semantics, and the formal operations.
The display form (DF) is a concrete representation for CGs that can be printed or displayed on two-dimensional surfaces. It is designed to enhance readability while representing the abstract syntax as closely as possible. Any information about the display form that is not explicitly derived from AS or CGIF is called layout information. Conformance to this CG Standard does not require the preservation of layout information across translations to and from CGIF or to and from other conceptual schema languages such as KIF. Following are the basic principles for mapping the abstract form to the display form:
Figure 8. Five possible orientations of the type and
referent fields
Since DF is not normative, a CG tool that conforms to this CG Standard may modify or extend DF for particular applications or I/O devices. An application to poultry farming, for example, might display a concept of type Chicken in the shape of a chicken.
The following EBNF rules define a recommended context-free syntax of the linear form (LF). The starting symbol is CG, which represents a linear representation of a conceptual graph. The referent field, which is common to both the linear form and the display form, is defined in Section 7.2. To minimize dependencies on implementation-dependent encodings, these rules contain no character constants. The symbol BeginConcept, for example, which is normally represented by the left bracket "[", could be redefined as some other symbol if necessary. The recommended print forms are listed in Section 4.5.
CG ::= ConceptBranch | Relation (ConceptLink | ConceptList)
ConceptBranch ::= Concept (RelationLink | RelationList)?
RelationBranch ::= Relation (ConceptLink | ConceptList)?
ConceptLink ::= Arc ConceptBranch
RelationLink ::= Arc RelationBranch
ConceptList ::= BeginLinks ConceptLink (LinkSep ConceptLink)* EndLinks
RelationList ::= BeginLinks RelationLink (LinkSep RelationLink)* EndLinks
Concept ::= BeginConcept Type (FieldSep Referent)? EndConcept
Relation ::= BeginRelation Type EndRelation
Arc ::= Integer? (LeftArc | RightArc)
Type ::= TypeLabel | LambdaExpression
Annex B represents the metalevel conventions for EBNF rules and translation rules. None of the notation in this annex appears in CGIF, and none of it is required to be implemented in any CG tools. Annex B is normative only because the metalevel conventions it defines are used to define CGIF in the normative chapters 7, 8, and 9 of this CG Standard.
The syntax of CGIF and LF is specified by metalevel rules written in Extended Backus-Naur Form (EBNF). Each EBNF rule is a context-free grammar rule that has a single category symbol on the left, a defining marker "::=" in the middle, and a defining expression on the right. The following EBNF rule is a metametalevel rule that specifies the syntax of every EBNF rule, including itself:
EBNFRule ::= CategorySymbol DefiningMarker DefiningExpressionEach EBNF rule defines the category symbol on the left as the name of a class of strings specified by the defining expression on the right. Each defining expression is a regular expression constructed from the following metalevel categories:
DefiningExpression ::= Term
((WhiteSpace | WhiteSpace? "|" WhiteSpace?) Term)*
The concatenator indicates sequence: each term must match a string of
the corresponding type in the order in which they occur. The alternator, which
may include optional white space on either side, indicates options: either the
term on its right or the term on its left, but not both, must match a string
of the corresponding type. If a defining expression contains both
concatenators and alternators, the concatenators have higher precedence
(tighter binding) than the alternators.
DefiningMarker ::= WhiteSpace? "::=" WhiteSpace?In an EBNF rule, it indicates that the category on its left is defined by the expression on its right.
Set ::= "{" DefiningExpression ("," DefiningExpression)* "}"
Each defining expression in the set must match exactly one string, but
the strings they match may occur in any order.
Term ::= (CategorySymbol | Literal | Set | "(" DefiningExpression ")" )
("*" | "+" | "?")?
The iterator indicates zero or more occurrences of the preceding string,
the repeater indicates one or more occurrences, and the option indicates zero
or one occurrence. No category symbol that appears in an EBNF rule or a translation rule in this CG Standard may contain embedded white space. In an English sentence, however, a category symbol whose identifier contains an embedded uppercase letter may be written with white space inserted before that letter, and uppercase letters may be translated to lowercase. For example, the category symbol written "WhiteSpace" in an EBNF rule may be written "white space" in an English sentence.
The EBNF rules described in Section B.1 specify the syntax of a language, but not its semantics. To specify semantics, the syntactic categories of a source language may be translated to some target language, such as predicate calculus, whose semantics is independently defined. This section defines translation rules, which augment the EBNF rules with variable assignments, tests, and translation sequences. Each translation rule is a sequence consisting of a rule name, a defining marker "::=", a defining expression, a translation marker "=>", and target.
TranslationRule ::= RuleName "::=" DefiningExpression "=>" TargetA translation rule may be called by passing a source string to a program called a parser, which matches the defining expression to the source string. If the match is successful, the value of the target is returned as the value of the rule call. If the match is unsuccessful or some rule call in the target fails, the rule call is said to fail. The parts of a translation rule are constructed from the metalevel categories of Section B.1 and the following additional categories:
Conditional ::= "(" TranSequence Test "?" TranSequence ":" TranSequence ")"
The value of the first translation sequence is tested for equality "="
or nonequality "!=". If the test is true, the value of the conditional is the
value of the second translation sequence; otherwise, it is the value of the
third translation sequence.
DefiningExpression ::= TranTerm
((WhiteSpace | WhiteSpace? "|" WhiteSpace?) TranTerm)*
Any defining expression of an EBNF rule as specified in Section B.1 is
valid in a translation rule. The only difference is that the translation terms
may have an optional variable assignment and an optional test.
GenerationTerm ::= Literal | Variable | RuleCall | ConditionalThe value of the generation term is the value of the literal, variable, rule call, or conditional.
RuleCall ::= RuleName "(" TranSequence ")"
When a rule is called, the value of the translation sequence is parsed
by the defining expression of the rule. Then the value of the target sequence
of the rule is returned as the value of the rule call. A failure of a rule
call during parsing causes the current option to fail. If all parsing options
fail or the target sequence of the rule fails, then the rule call fails.
Test ::= ("=" | "!=") (GenerationTerm | "(" TranSequence ")")
If the preceding string matches the value that follows, the equal test
is true and the nonequal test is false. Otherwise, the nonequal test is true
and the equal test is false.
TranTerm ::= (CategorySymbol | Literal | "(" DefiningExpression ")" )
("*" | "+" | "?")? VarAssignment? Test?
If a test occurs at the end of any term, a copy of the string matched by
the term is tested. If the test is true, the parser continues; otherwise, it
backtracks to another option in the defining expression.
TranSequence ::= GenerationTerm (WhiteSpace GenerationTerm)*The value of the translation sequence is the concatenation of the values of all the generation terms in the order in which they occur.
VarAssignment ::= "." VariableThe string of the source language matched by the immediately preceding term is assigned as the value of the variable. Any value previously assigned to the variable must be saved in case a subsequent mismatch in the parsing of the source string causes the parser to backtrack and try another option. A variable that has never been assigned a value has the empty string "" as its default value.
Comment.
As an example, the following translation rule named Paragraph matches any text string and replaces all blank lines by the HTML paragraph tag "<p>".
Paragraph ::= LeftEnd String.Front
("\n" WhiteSpace? "\n" String.Back)? RightEnd
=> Front (""=Back ? "" : "\n<p>" Paragraph(Back))
When this rule is called to parse any string, the category named LeftEnd
matches the start of the source string. Then the category named String matches
any string of zero or more characters, which it assigns to the variable named
Front. In this case, the parser can scan ahead to look for the first occurrence
of a line feed "\n" followed by optional white space, another line feed, and any
string up to the right end, which it assigns to the variable Back. If the parser
fails to find a sequence of two line feeds separated by white space, it assigns
the entire source string to Front and leaves Back with the default value "".
After the parser finishes matching the defining expression to the source string, the target sequence is evaluated to generate the value of the rule call. In this case, it generates the value of Front concatenated to the value of the conditional. If Back is the empty string, the conditional returns the empty string. Otherwise, it returns the value "\n<p>" concatenated to the result of calling Paragraph to continue processing Back.
This CG Standard is based on the CG syntax and semantics as published in an article by John Sowa [15] and further elaborated in two books [16,18]. CGs have been the topic of three special issues of journals [1,17,23] and the proceedings of a series of international conferences and workshops [2,3,4,6,7,9,10,12,19,20,21]. Conceptual graphs have been recommended as a conceptual schema language [11], and they have been implemented in tools for software specification and modeling [5]. They have also been used as the primary knowledge representation language for natural language generation [8], metaphor [22], and information extraction [13,14].
 Last Modified:
Last Modified: