Redefining Web-of-Trust: reputation, recommendations, responsibility and trust among peers

Urals State University
Institute of Physics and Applied Mathematics

Abstract

This paper proposes a web-of-trust construction approach starting with axiomatic propositions. Different from the classic web-of-trust (i.e. trust relationships graph closure), the proposed method relies on actual peer experience as the final judgment while public trust statements (further called ``recommendations'') just introduce responsible cooperation, allowing participants to make assumptions on reputation of previously unknown entities.
The method was initially targeted to address the problem of spam (UBE) in environments with reliable authentication (which today's SMTP protocol is not, but supposedly will be).

Rationale

First, we have to understand the dimensionality of the problem. In the first approach we may expect the number of variables to be equal to the number of participants, . Every variable represents a public reputation of some participant regarding some fixed topic. Numerous reputation services use this approach, such as e-mail blacklists and whitelists or extensively studied eBay[9] reputation system. There are reputation models which involve explicit or implicit recommendations to calculate public reputation values, such as EigenTrust algorithm[16] and a family of algorithms based on Markov chains (e.g. PageRank[1]).

Still, there is no evidence that all participants share the same opinions or the same law. So, generally, reputation have to be recognized to be an opinion. This raises dimensionality of a perfect map of reputation to . Straightforward aggregation is meaningless here: 1 billion of Chinese people think that something is good, but my relatives think it is bad. Opinion is meaningful in the context of the owner!

The task of data storage could hardly be solved with a central database or Distributed HashTable[20]. Considering context issues, it seems natural to let every participant host own opinion and experience, own ``map of trust''. At the same time we know that most participants can not support a map of size (in other words, to trace every other participant). Many researchers considered an idea of Web-of-Trust, a graph formed by participant's expressed pairwise directed trust relationships [4,6,12,13,15,18,19,21,26]. In this web a trust between distant entities is derived as a function of chains (paths) connecting those entities. M. Richardson et al [14] provide a good formal description of the approach.

Still, web-of-trust models did not give me a confidence that they can not be subverted or manipulated by attacks of the scale already experienced by the Internet (i.e. several millions of hosts controlled by malicious software; attacks of 1,000 magnitude seem to be commercialized already). A list of possible dangers also has such entries as a system bias introduced by a leading software vendor due to globally self-reinforced default settings, or a trust inflation when a participant has expressed his trust to so much parties, that their averaged opinion will become a ``body temperature, average by hospital''.

The purpose of this paper is to introduce a stable balanced reputation propagation scheme on arbitrary topologies. Section 2 introduces definitions and the basic event counting scheme, section 2.3 addresses the cornerstone process of deriving reputation of previously unknown entities from recommendations made by known ones. Section 3 studies the case of exchanging and using aggregated opinions (reputation maps). Possible applications to electronic messaging are discussed in Section 4.

Measuring reputation; definitions

General considerations

Mui [12] describes reputation typology including the following aspects: context, personalization, individual or group, direct or indirect (the latter includes prior-derived, group-derived and propagated). This paper discusses personalized () reputation regarding some fixed context. Individual and group, direct and indirect flavours of reputation are defined via the basic uniform notion of responsibility for elementary events. A reputation context is represented as a set of all relevant (past) events $\mathbb{U}$ plus compliance requirements. Generally, we must consider $\mathbb{U}(t)$ but for the sake of simplicity I will focus on a static model. Propagation of reputation is performed by a social network of recommendations derived from the same notion of responsibility.

An unresponsible recommendation and imposed responsibility (both sound like definitions of a self-assured power) are of no interest to us. There are no disctinction between groups and individuals; I use the same word ``entities'' to describe them (see Sec. 2.4).

Reputation is ...

A reputation is an expectation about an agent's behavior based on information about or observations of its past behavior. [3]

So, a reputation is based on a responsibility, i.e. an association between events (behavior elements) and entities (agents). A reputation can not exist in anonymized environments. Speaking in terms of the formal model being explained a definition of a reputation is:
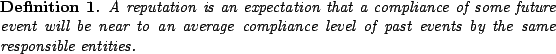
$\begin{definition} A reputation is an expectation that a compliance of some futu... ...mpliance level of past events by the same responsible entities. \end{definition}$

Requirements for compliance are fixed. The simplest example is ``the mail (event) is a spam (non-compliant)''. So, an elementary (simple) event $\varepsilon$ initiated by entity , $\varepsilon \in \mathrm{E}_{e}$ , may be valued by another entity as $\rho_{v}(\varepsilon) \in [0,1]$

Our compliance expectation on a future event is based on compliance of past events by the same responsible entities, $\rho(\varepsilon) = \rho(\bigcup E_{e_i})$ . A reputation of an entity is a compliance expectation on events initiated by that entity: $\rho(e) = \rho(\varepsilon)$ . Considering the initiator only (i.e. one fully responsible entity) and assuming events to be of equal value (not distinctively priced) we have

$\begin{displaymath} \rho_{v}(e) = \rho_{v}(\mathrm{E}_{e}) = \frac {\sum_{\vare... ...hrm{E}_{e}} \rho_{v}(\varepsilon) } {\vert\mathrm{E_e}\vert} \end{displaymath}$

(1)

where $\vert\mathrm{E_e}\vert$ is the number of elements (events), $\mathrm{E_e}$ is generally a set of events which affect reputation of (it is equal to the set of events initiated by here). We will distinct as a set of known events and $\mathbb{E}_e$ as a set of all such events whether known or unknown to us. (This is the last time I mention $\mathbb{E}$ in this paper.)

Recommendation: responsibility for other's events

$\begin{definition} A recommendation is an expressed opinion of an entity that so... ...is compliant, which opinion the recommender is responsible for. \end{definition}$
Full responsibility for an event mean that the event will be included into the entity's relevant event set, thus affecting the reputation of the entity. A reputation of a recommending entity will be affected by any event that affects a reputation of recommended one.

It is useful, if recommendation could be of different certainty ("cautious", fuzzy, ), so a weight of a recommended event will be lesser than weights of events initiated by the entity itself (or, another way, the recommended event belongs to the event set of the recommender in a fuzzy way having membership degree $\mu_E=c$ ). To migrate to fuzzy sets a compliance-of-a-set function (Eq. 1) have to be generalized; it will be equal to a weighted mean (centroid):

$\begin{displaymath} \rho(\mathrm{E}) = \frac {\sum_{\varepsilon \in \mathrm{E}}... ...vert\mathrm{E}\vert = \sum_{\varepsilon \in E} c_{\varepsilon} \end{displaymath}$

(2)

**Figure 1:** Recommendation relationship; recommends with certainty
$\includegraphics[angle=0, scale=0.4]{eps/two.eps}$

**Figure 2:** The case of dependent recommender; depends on in recommending ; black and white ``raisins'' are known events
$\includegraphics[angle=0, scale=0.25]{eps/crispdep.eps}$

Discounted inclusion $\subset _c$

is an operator further used to express recommendation and, therefore, fuzzy inclusion of a recommended event set into the recommender's set of responsibility. $\mathrm{E}_e \subset_c \mathrm{E}_r$ if entity

recommends entity

with certainty

, so $\forall \epsilon \in \mathrm{E}_e: \mu_{\mathrm{E}_r}(\epsilon) \ge c \cdot \mu_{\mathrm{E}_e}(\epsilon)$ . This relation is further depicted as shown on Figure 1. An operation of set discounting $c\mathrm{E}$ is defined as follows: $\mu_{c\mathrm{E}}(\epsilon) = c\mu_{\mathrm{E}}(\epsilon)$ . So, $\mathrm{E}_e \subset_c \mathrm{E}_r \Leftrightarrow c\mathrm{E}_e \subset \mathrm{E}_r$ where the subsethood on the right side is the original fuzzy containment by Zadeh: $A \subset B$ is true if $\mu_A(\epsilon) \le \mu_B(\epsilon)$ for every $\epsilon$ . (Discounted inclusion is not supposed to be a good general fuzzy subsethood measure[2], but it fits our purposes well.)

Note: this way we define a closure model using multiplication as a concatenation function and maximum as an aggregation function. This combination has a feature of strong global invariance[14].

More on transitivity of trust:

it became a common point that trust is not generally transitive. Namely, we trust Alice, Alice trusts Bob; this does not directly lead us to trusting Bob. As it will become clear later in this paper, transitivity of responsibility (and recommendation) does not mean transitivity of trust. In this example our trust to Alice and distrust to Bob may reside in the plane of our own experience, while trust to Bob by Alice is a recommendation or an opinion of Alice, so it is the different ``plane''. Combining these planes we will probably obtain a whole different result than trusting to Bob because Alice does.

So, what the entity is responsible for?

A set of all events that affect a reputation of an entity

was denoted as

. It contains events initiated by

(membership degree

) as well as events initiated by recommended entities including those recommended by recommended ones, transitively (membership degree is equal to certainty

for transitive cases). Recursive formulae:

$\begin{displaymath} E_e = O_e \cup \underline{R}_e = O_e \cup \bigcup c_{er_i}E_{r_i} \end{displaymath}$

(3)

where
$c_{er_i}$ is a certainty of recommendation of by ;
- a set of events, initiated by ;
$\underline{R}_e$ - appropriately discounted events by entities recommended by .

So, according to Definitions 1 and 2, we expect events initiated by some known entity to have compliance level of $\rho(E_e)$ as of Eq. 3.

What about recommended entities?

Due to Definition 2 a recommender entity is responsible for events initiated by recommended ones. So, according to Definition 1, a reputation of a recommended entity depends on reputations of recommenders (i.e. events by recommended entities belong to wider sets than own event set of the initiator). Thus, for recommended entities we have:

$\begin{displaymath} E_e = O_e \cup \underline{R}_e \cup \overline{R}_e = O_e ... ...er_i}E_{r_i} \cup \bigcup c_{m_je}E_{m_j} \footnotemark \end{displaymath}$

(4)

where are recommender entities. As a result, ``an echo'' of an event traverses edges in either direction, because everything that affects a reputation of a recommender, also affects reputations of recommended entities and vice-versa.

Groups and individuals

Group may be understood as an entity recommending its member entities and, probably, initiating no own events. This way, a membership in a community mean a recommendation by the community; at the same time the reputation of the community is formed by behavior of its members. In other words, there is a feedback: communities are interested in including good members and correcting (or excluding) bad ones. So, addressing the problem, the exact knowledge of participants is not necessary: having to guess a reputation of a distant entity we may rely on our established opinion on reputations of bigger aggregates (communities) letting that communities trace situation inside them (i.e. to provide us with information on relative reputability of members).

Note: the notion of ``an entity'' is very generic, allowing a granularity shift: 1st level entities may be messages, not authors, while authors are considered as recommender entities. A shift in the opposite direction is also possible, e.g. taking e-mail domains as first level entities.

Locality

The purpose of the model is to extrapolate own experience to previously unknown areas, not to let an authority to persuade us in something in the presence of evidence to the contrary:

$\begin{proposition} More specific experience is considered to be more precise and more relevant \end{proposition}$

Particularly, in crisp cases we take into consideration the nearest recommenders only. Experience on a recommender-of-a-known-recommender (``superrecommender'') is considered to be more general and less precise. The proposition may be also spelled as ``we do not need recommendations for known entities''.

Fuzzification of Prop. 1 is achieved in the following way: if known entities and recommend and recommends with some certainties (e.g. $c_{re}$ , see Figure 3.a), then we consider $\rho(r)$ as more specific and refined. Still, we can not rely on $\rho(r)$ only as we do in the crisp way ( $\rho(e) = \rho(r)$ ). We put

$\begin{displaymath} \rho(e) = \rho( c_{re} E_{r} \cup (c_{se} - c_{sr}c_{re}) E_{s} ) \end{displaymath}$

(5)

i.e. we decrease the superrecommender's significance by the transitively inherited part. If the superrecommender recommends just because of transitive relation ( $c_{se} = c_{sr}c_{re}$ ) then it will not be counted. The method fits the crisp case in corner points.

Note: in more general case of multiple sub-recommenders (see Fig. 3.b) we decrease significance of a superrecommender by the value of $c_{te} = \max(c_{sr_i}c_{r_ie})$ , i.e. by the certainty of transitively obtained responsibility.

**Figure 3:** A dependent recommender; fuzzy case
a) $\includegraphics[angle=0, scale=0.22]{eps/fsuper.eps}$ b) $\includegraphics[angle=0, scale=0.24]{eps/diamond.eps}$

**Figure 4:** Case of interdependent cautious recommenders
$\includegraphics[angle=0, scale=0.25]{eps/inter.eps}$

The case of interdependent recommenders

assumes that recommenders do recommend each other with some certainties (figure 4). It may be resolved as a variant of the previous case by introduction of a synthetic entity which incorporates the responsibility common to both recommenders.

Formally, $E_{r_1} \subset_{c_{r_2r_1}} E_{r_2}$ and $E_{r_2} \subset_{c_{r_1r_2}} E_{r_1}$ , both and recommend with certainties $c_{r_1e}$ and $c_{r_2e}$ ; we introduce entity $r_{\cap}$ , having $c_{r_{\cap}r_1} = c_{r_2r_1}$ and $c_{r_{\cap}r_2} = c_{r_1r_2}$ . So, $E_{r_{\cap}} = c_{r_2r_1}E_{r_1} \cup c_{r_1r_2}E_{r_2}$ , and we may say that $c_{r_1r_{\cap}}=c_{r_2r_{\cap}}=1.0$ or that $E_{\cap}$ is a Zadeh subset (or -discounted) of both $E_{r_1}$ and $E_{r_2}$ . Intuitively and according to Proposition 1 we consider $\rho(E_{\cap})$ as well refined and relevant estimate for $\rho(E_e)$ as $\rho(E_{r_i})$ , and appropriately reduce significance of supersets:

$\begin{displaymath} \rho(E_e) = \rho \big( c_{\cap e}E_{\cap} \cup (c_{r_1e}-c_{\cap e}) E_{r1} \cup (c_{r_2e}-c_{\cap e}) E_{r2} \big) \end{displaymath}$

(6)

where $c_{\cap e} = max\big(c_{r_2r_1}c_{r_1e}, c_{r_1r_2}c_{r_2e}\big)$

The universal recommender

is a construct resolving cases of no certain recommenders or no recommenders at all. Entity $\mathbf{u}$ is supposed to be recommending any other entity with certainty

. $\rho(\mathbb{U})$ may be derived from experience or be preset in cases when, for example, we deny events initiated by unknown and unrecommended entities and, therefore, have no knowledge of their compliance. Generally, the number of events by $\mathbf{u}$ or $\vert\mathbb{U}\vert$ is supposed to be very large (or infinite) so the scheme of exact event counting (introduced by Equation 1 and Proposition 1) which uses $\vert E\vert$ as an averaging weight will recognize an entity with no certain recommender as not recommended at all.

This situation leads us to the hypothesis that sometimes size doesn't matter, see the next section.

The metaphora of a colored map: coarsening

In the previous section I have addressed the case of an event compliance expectation, which is based on an exact knowledge of previous events and recommendation relationships between initiating entities. The next case to be addressed is an expectation of an event compliance when no exact data on previous events exist, just aggregated opinions on initiating entities. This approach may be required in a broad range of situations, such as: non-disclosure of private information, advisers of limited trustworthiness or non-comparability of different experiences. The ``size doesn't matter'' approach may be also interpreted in the following way: we have enough of experience on known entities to have stable opinion on their compliance (reputation), so a particular number of interactions (events) with this or that entity is not relevant.
$\begin{proposition}[Size doesn't matter] Opinions from the same source are of th... ...l or irrelevant, only average values $\rho(E_i)$ are counted. \end{proposition}$

The metaphora

for this approach is a colored map having a fractal quality, i.e. diversity does not depend on scale. Guessing the average ``color'' of some previously unknown area we rely on the narrowest known super-areas (Prop. 1). To extend the metaphora to fuzzy cases we may suppose that the map is made of color glass pieces of different transparency that may be stacked (i.e. multiple non-comparable supersets).
$\begin{definition} Reputation map is a set of opinions on reputations of entitie... ...ded by the same source: $\{\rho_v(e_1), \ldots, \rho_v(e_n)\}$. \end{definition}$
(One possible way to form a map of arbitrary scale from own experience of interactions $\{E_{e_1}, \ldots, E_{e_n}\}$ is to remove ``redundant'' entities at the same time trying to minimize the precision loss, which is calculated as a difference between actual reputation values of removed entities and values extrapolated from the resulting map. I.e. the hypothetical method is focused on removing ``white horses on snow covered field'' first.)

The remaining question is how to extrapolate a reputation map to entities not mentioned there.

Using maps

Suppose, we have some reputation map and we have been contacted by a previously unknown entity. We have to make a decision whether it is reputable or not. So, we will look for recommenders, then recommenders of recommenders, recursively, until we will find an entity which is present in the map or cumulative recommendation certainty will go under minimal acceptable threshold or we will get tired.

Arithmetics used in map calculations directly follows from Equations 1, 2 and Proposition 2: averaging in the way of $\frac {\sum c_{r_ie} \rho(E_{r_i}) \vert E_{r_i}\vert} {\sum c_{r_ie} \vert E_{r_i}\vert}$ transforms into $\frac{\sum c_{r_ie} \rho(r_i)}{\sum c_{r_ie}}$ , i.e. an average of $\rho(r_i)$ weighted by $c_{r_ie}$ .

Note: Instead of $\rho(E_{r_i})$ we will be using $\rho(r_i)$ . The former was equal to the latter in Section 2, while in this section we obtain $\rho(r_i)$ without details of $E_{r_i}$ .

Thus, the case of independent recommenders leads us to the following estimation: $\rho(e) = \frac {\sum c_{r_ie}\rho(r_i)} {\sum c_{r_ie}}$ .

The case of a dependent recommender produces:

$\begin{displaymath} \rho(e) = \frac {c_{r_2e}\rho(r_2) + (c_{r_1e}-c_{r_1r_2}c_{r_2e})\rho(r_1)} {c_{r_2e} + (c_{r_1e}-c_{r_1r_2}c_{r_2e})} \end{displaymath}$

(7)

Interdependent recommenders still require some work. Adding the same construct as in Sec. 2.5, we may get a solution by coarsening Eq. 6, but we have to obtain estimate of $\rho(r_{\cap})$ . By formation, it is straightforward to expect $\rho(r_{\cap}) = \frac { \rho(r_1)c_{r_2r_1} + \rho(r_2)c_{r_1r_2} } { c_{r_2r_1} + c_{r_1r_2} }$ , because of Eq. 2 plus neglection of set sizes and intersections. This estimate may also be explained by taking $r_{\cap}$ as an entity recommending and with appropriate certainties and applying Prop. 2.

So, finally,

$\begin{displaymath} \rho(e) = \frac { c_{r_\cap e} \rho(r_{\cap}) + (c_{r_1e}-... ...r_\cap e}) \rho(r_2) } { c_{r_1e} + c_{r_2e} - c_{r_\cap e} } \end{displaymath}$

(8)

where $c_{\cap e} = max\big(c_{r_2r_1}c_{r_1e}, c_{r_1r_2}c_{r_2e}\big)$ , as before.

Considering the universal recommender, the situation is different from Section 2.5: absence of certain recommenders is not equal to absence of recommenders at all. Due to Proposition 2 and Equation 7, significance of $\rho(\mathbf{u})$ is reduced by the maximum certainty of recommendation by known entities (so is equal to $1.0-\max\{c_{r_ie}\}$ ). Or, in other words, the more certain recommendation exists, the less an entity belongs to the ``general public''.

Opinion propagation and reflexion

In Section 3 we were operating with opinions gained from some source. What have we do getting different opinions from different sources?

One construction that may help us in ranking opinion sources is a reputation of an opinion source or derivative reputation: a reputation map provided by some entity may be interpreted as a set of ``second-order'' recommendations: $c'_{ve_i}=\rho_v(e_i)$ . Thus, a reputation of an opinion source is defined as:

$\begin{displaymath} \rho'_w(v) = \frac {\sum c'_{ve_i}\rho_w(e_i)} {\sum c'_{ve_i}} = \frac {\sum \rho_v(e_i) \rho_w(e_i) } { \sum \rho_v(e_i)} \end{displaymath}$

(9)

This way an entity may make own opinion public (i.e. to provide ``soft'' recommendations) with no risk for own ability to communicate. $\rho'$ corresponds to a separation of ``a reputation as an actor'' and ``a reputation as a recommender'' declared in other trust models.

Definitions of $\rho'', \rho''', \ldots, \rho^{(x)}, \rho^{(x+1)}$ follow from $c^{(x+1)}_{ve_i}=\rho^{(x)}_v(e_i)$ .

Possible applications to electronic messaging

The upcoming IETF MARID specification is targeted to introduce a checkable association between e-mails and some stable identities (say DNS domains) thus resolving a problem of forged e-mail sender addresses. In the terms of this paper it is ``a responsibility''. This makes reputation calculations possible (the problem of message ranking by a human recipient is trivially resolvable, e.g. by an additional IMAP flag).

The issue of recommendation relationships is more sophisticated. The most natural source of such recommendations (or subset/superset relations) is some directory and naming system: it would be in good conformance with DNS-based identities. Unfortunately, the current DNS does not have enough of expressive power, being mostly degraded into flat name-to-ip hashtable. As [7] starts with, ``The DNS was designed as a replacement for the older `host table' system''. Thus, a significant effort is needed to introduce recommendation relationships (i.e. web of trust).

Still, recommendations aside, a variety of existing reputation service concepts, such as blacklists, whitelists, accreditation services may be expressed as opinion sources in the terms of the explained model.

Acknowledgments

Discussions on the smtp-verify sublist of IRTF ASRG provided the basic requirements for this work. I especially thank Alan DeKok, Yakov Shafranovich, Mark Baugher and John Levine for discussions on web-of-trust applicability as a solution to the problem of spam. I also thank Ed Gerck for focusing on the basics.

Bibliography

1 L. Page, S. Brin, et al: The PageRank Citation Ranking: Bringing Order to the Web, 1998, http://www-db.stanford.edu/~backrub/pageranksub.ps

2 Francisco Botana: Deriving fuzzy subsethood measures from violations of the implication between elements, LNAI 1415 (1998) 234-243

3 A. Abdul-Rahman, S. Hailes: Supporting trust in virtual communities, in Proceedings 3rd Ann. Hawaii Int'l Conf. System Sciences, 2000, vol 6, p. 6007

4 Bin Yu, M.P. Singh: A social mechanism of reputation management in electronic communities, in Proc. of CIA-2000

5 P. Resnick, R. Zeckhauser, E. Friedman, K. Kuwabara: Reputation systems, Communications of the ACM, Volume 43, Issue 12, 2000

6 Bin Yu, M.P. Singh: A social mechanism of reputation management in electronic communities. in Proc. of CIA'2000, 154-165

7 J. Klensin, RFC 3467 ``Role of the Domain Name System (DNS)'', 2001

8 K. Aberer, Z. Despotovic: Managing trust in a P2P information system, in proc. of CIKM'01

9 P. Resnick, R. Zeckhauser: Trust among strangers in internet transactions: empirical analysis of eBay's reputation system, Technical report, University of Michigan, 2001

10 R. Cox, A. Muthitacharoen, R.T. Morris: Serving DNS using a peer-2-peer lookup service, in IPTPS, Mar. 2002

11 L. Mui, M. Mohtashemi, A. Halberstadt: A computational model of trust and reputation, HICSS'02

12 L. Mui, PhD thesis: Computational models of trust and reputation: agents, evolutionary games and social networks, MIT, 2002, http://medg.lcs.mit.edu/ftp/lmui/

13 Bin Yu, M.P. Singh: Detecting deception in reputation management, in Proceedings of AAMAS'03

14 M. Richardson, R. Agrawal, P. Domingos: Trust management for the Semantic Web, in Proc. of ISWC'2003

15 Jennifer Golbeck, Bijan Parsia, James Hendler: Trust networks on the Semantic Web, in Proc. of CIA'2003.

16 S.D. Kamvar, M.T. Schlosser, H. Garcia-Molina: The EigenTrust algorithm for reputation management in P2P networks, in Proceedings of the WWW'2003

17 ``Lightweight MTA Authentication Protocol (LMAP) Discussion and Comparison'', John Levine, Alan DeKok. Internet Draft, 2004

18 Jennifer Golbeck, James Hendler: Reputation network analysis for email filtering, for the 1st Conf. on Email and Anti-Spam, 2004

19 Jennifer Golbeck, James Hendler: Inferring reputation on the semantic web, for EKAW'04.

20 Michal Feldman, Antonio Garcia-Martinez, John Chuang: Reputation management in peer-to-peer distributed hash tables, http://www.sims.berkeley.edu/$$mfeldman/research/

21 R. Guha, R. Kumar, P. Raghavan, A. Tomkins: Propagation of trust and distrust, in Proc. of WWW'2004

22 A. Fernandes, E. Kotsovinos, S. Ostring, B. Dragovic: Pinocchio: incentives for honest participation in distributed trust management, in Proceedings of iTrust'2004

23 Philipp Obreiter: A case for evidence-aware distributed reputation systems, in Proceedings of iTrust'2004

24 Paolo Massa, Bobby Bhattacharjee: Using trust in recommender systems: an experimental analysis, in Proceedings of iTrust'2004

25 Radu Jurca, Boi Faltings: Truthful reputation information in electronic markets without independent verification, icwww.epfl.ch/publications/documents/IC_TECH_REPORT_200408.pdf

26 Web-o-Trust effort by Russell Nelson, http://www.web-o-trust.org/

About this document ...

Redefining Web-of-Trust: reputation, recommendations, responsibility and trust among peers

This document was generated using the LaTeX2HTML translator Version 2002-2 (1.70)

The command line arguments were:
latex2html -split 1 -transparent -white -antialias -antialias_text accounting2.tex

The translation was initiated by on 2004-07-18

2004-07-18