Appendix F: Implementation Requirements

Contents

• F.1 Introduction
• F.2 Error processing
• F.3 Version control
• F.4 Clamping values which are restricted to a particular range
• F.5 'path' element implementation notes
• F.6 Elliptical arc implementation notes
  • F.6.1 Elliptical arc syntax
  • F.6.2 Out-of-range parameters
  • F.6.3 Parameterization alternatives
  • F.6.4 Conversion from center to endpoint parameterization
  • F.6.5 Conversion from endpoint to center parameterization
  • F.6.6 Correction of out-of-range radii
• F.7 Text selection implementation notes
• F.8 Printing implementation notes

This appendix is normative.

F.1 Introduction

The following are notes about implementation requirements corresponding to various features in the SVG language.

F.2 Error processing

There are various scenarios where an SVG document fragment is technically in error:

• When the content does not conform to the XML 1.0 specification [XML10], such as the use of incorrect XML syntax
• When an element or attribute is encountered in the document which is not part of the SVG DTD and which is not properly identified as being part of another namespace (see "Namespaces in XML" [XML-NS])
• When an element has an attribute or property value which is not permissible according to this specification
• Other situations that are described as being in error in this specification

A document can go in and out of error over time. For example, document changes from the SVG DOM or from animation can cause a document to become in error and a further change can cause the document to become correct again.

The following error processing shall occur when a document is in error:

• The document shall be rendered up to, but not including, the first element which has an error. (Exception: if a 'path' element is the first element which has an error and the only errors are in the path data specification, then render the 'path' up to the point of the path data error. See 'path' element implementation notes.) This approach will provide a visual clue to the user/developer about where the error might be in the document.
• If the document has animations, the animations shall stop at the point at which an error is encountered and the visual presentation of the document shall reflect the animated status of the document at the point the error was encountered.
• A highly perceptive indication of error shall occur. For visual rendering situations, an example of an indication of error would be to render a translucent colored pattern such as a checkerboard on top of the area where the SVG content is rendered.
• If the user agent has access to an error reporting capability such as status bar, it is recommended that the user agent provide whatever additional detail it can to enable the developer/user to quickly find the source of the error. For example, the user agent might provide an error message along with a line number and character number at which the error was encountered.

Because of situations where a block of scripting changes might cause a given SVG document fragment to go into and out of error, error processing shall occur only at times when document presentation (e.g., rendering to the display device) is updated. In particular, error processing shall be disabled whenever redraw has been suspended via DOM calls to suspendRedraw().

F.3 Version control

The SVG user agent must verify the reference to the PUBLIC identifier in the <!DOCTYPE> statement or the namespace reference in the xmlns attribute on the 'svg' element to ensure that the given document (or document fragment) identifies a version of the SVG language which the SVG user agent supports. If the version information is missing or the version information indicates a version of the SVG language which the SVG user agent does not support, then the SVG user agent is not required to render that document or fragment. In particular, it is not required that an SVG user agent attempt to render future versions of the SVG language. If the user environment provides such an option, the user agent should alert or otherwise notify the user that the version of the file is not supported and suggest an alternate processing option (e.g., installing an updated version of the user agent) if such an option exists.

An SVG user agent which supports the SVG Recommendation should alert or otherwise notify the user whenever it encounters an SVG document (or document fragment) whose <!DOCTYPE> statement or corresponding xmlns attribute corresponds to a working draft version of the SVG specification. All content based on working drafts of this specification should be updated to the SVG Recommendation.

F.4 Clamping values which are restricted to a particular range

Some numeric attribute and property values have restricted ranges, such as color component values. When out of range values are provided, but user agent shall defer any error checking until after presentation time, as composited actions might produce intermediate values which are out of range but final values which are within range.

Color values are not in error if they are out of range, even if final computations produce an out of range color value at presentation time. It is recommended that user agents clamp color values to the nearest color value (possibly determined by simple clipping) which the system can process as late as possible (e.g., presentation time), although it is acceptable for user agents to clamp color values as early as parse time. Thus, implementation dependencies might preclude consistent behavior across different systems when out of range color values are used.

Opacity values out of range are not in error and should be clamped to the range 0 to 1 at the time which opacity values have to be processed (e.g., at presentation time or when it is necessary to perform intermediate filter effect calculations).

F.5 'path' element implementation notes

A conforming SVG user agent must implement path rendering as follows:

• Error handling:
  • The general rule for error handling in path data is that the SVG user agent shall render a 'path' element up to (but not including) the path command containing the first error in the path data specification. This will provide a visual clue to the user/developer about where the error might be in the path data specification. This rule will greatly discourage generation of invalid SVG path data.
  • If a path data command contains an incorrect set of parameters, then the given path data command is rendered up to and including the last correctly defined path segment, even if that path segment is a sub-component of a compound path data command, such as a "lineto" with several pairs of coordinates. For example, for the path data string "M 10,10 L 20,20,30", there is an odd number of parameters for the "L" command, which requires an even number of parameters. The user agent is required to draw the line from (10,10) to (20,20) and then perform error reporting since "L 20 20" is the last correctly defined segment of the pat data specification.
  • Wherever possible, all SVG user agents shall report all errors to the user.
• Markers, directionality and zero-length path segments:
  • If markers are specified, then a marker is drawn on every applicable vertex, even if the given vertex is the end point of a zero-length path segment and even if "moveto" commands follow each other.
  • Certain line-capping and line-joining situations and markers require that a path segment have directionality at its start and end points. Zero-length path segments have no directionality. In these cases, the following algorithm is used to establish directionality: to determine the directionality of the start point of a zero-length path segment, go backwards in the path data specification within the current subpath until you find a segment which has directionality at its end point (e.g., a path segment with non-zero length) and use its ending direction; otherwise, temporarily consider the start point to lack directionality. Similarly, to determine the directionality of the end point of a zero-length path segment, go forwards in the path data specification within the current subpath until you find a segment which has directionality at its start point (e.g., a path segment with non-zero length) and use its starting direction; otherwise, temporarily consider the end point to lack directionality. If the start point has directionality but the end point doesn't, then the end point uses the start point's directionality. If the end point has directionality but the start point doesn't, then the start point uses the end point's directionality. Otherwise, set the directionality for the path segment's start and end points to align with the positive X-axis in user space.
  • If 'stroke-linecap' is set to butt and the given path segment has zero length, do not draw the linecap for that segment; however, do draw the linecap for zero-length path segments when 'stroke-linecap' is set to either round or square. (This allows round and square dots to be drawn on the canvas.)
• The S/s commands indicate that the first control point of the given cubic bezier segment is calculated by reflecting the previous path segments second control point relative to the current point. The exact math is as follows. If the current point is (curx, cury) and the second control point of the previous path segment is (oldx2, oldy2), then the reflected point (i.e., (newx1, newy1), the first control point of the current path segment) is:

   
  (newx1, newy1) = (curx - (oldx2 - curx), cury - (oldy2 - cury))
                 = (2*curx - oldx2, 2*cury - oldy2)
  

• A non-positive radius value is an error.
• Unrecognized contents within a path data stream (i.e., contents that are not part of the path data grammar) is an error.

F.6 Elliptical arc implementation notes

F.6.1 Elliptical arc syntax

An elliptical arc is a particular path command.  As such, it is described by the following parameters in order:

(x₁, y₁) are the absolute coordinates of the current point on the path, obtained from the last two parameters of the previous path command.

r_X and r_Y are the radii of the ellipse (also known as its semi-major and semi-minor axes).

is the angle from the x-axis of the current coordinate system to the x-axis of the ellipse.

f_A is the large arc flag, and is 0 if an arc spanning less than or equal to 180 degrees is chosen, or 1 if an arc spanning greater than 180 degrees is chosen.

f_S is the sweep flag, and is 0 if the line joining center to arc sweeps through decreasing angles, or 1 if it sweeps through increasing angles.

(x₂, y₂) are the absolute coordinates of the final point of the arc.

This parameterization of elliptical arcs will be referred to as endpoint parameterization.  One of the advantages of endpoint parameterization is that it permits a consistent path syntax in which all path commands end in the coordinates of the new "current point".  The following notes give rules and formulae to help implementers deal with endpoint parameterization.

F.6.2 Out-of-range parameters

Arbitrary numerical values are permitted for all elliptical arc parameters, but where these values are invalid or out of range, an implementation must make sense of them as follows:

If the endpoints (x₁, y₁) and (x₂, y₂) are identical, then this is equivalent to omitting the elliptical arc segment entirely.

If r_X = 0 or r_Y = 0 then this arc is treated as a straight line segment (a "lineto") joining the endpoints.

If r_X or r_Y have negative signs, these are dropped (the absolute value is used instead).

If r_X , r_Y and are such that there is no solution (basically, the ellipse is not big enough to reach from (x₁, y₁) to (x₂, y₂)) then the ellipse is scaled up uniformly until there is exactly one solution (until the ellipse is just big enough).

is taken mod 360 degrees.

Any nonzero value for either of the flags f_Aor f_S is taken to mean the value 1.

This forgiving yet consistent treatment of out-of-range values ensures that

The inevitable approximations arising from computer arithmetic cannot cause a valid set of values written by one SVG implementation to be treated as invalid when read by another SVG implementation.  This would otherwise be a problem for common boundary cases such as a semicircular arc.

Continuous animations that cause parameters to pass through invalid values are not a problem.  The motion remains continuous.

F.6.3 Parameterization alternatives

An arbitrary point (x, y) on the elliptical arc can be described by the 2-dimensional matrix equation

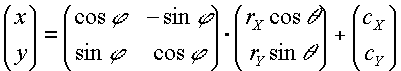(F.6.3.1)

(c_X, c_Y) are the coordinates of the center of the ellipse.

r_X and r_Y are the radii of the ellipse (also known as its semi-major and semi-minor axes).

is the angle from the x-axis of the current coordinate system to the x-axis of the ellipse.

ranges from:

      which is the start angle of the elliptical arc prior to the stretch and rotate operations.

      which is the end angle of the elliptical arc prior to the stretch and rotate operations.

      which is the difference between these two angles.

If one thinks of an ellipse as a circle that has been stretched and then rotated, then

,

and

are the start angle, end angle and sweep angle, respectively of the arc prior to the stretch and rotate operations.  This leads to an alternate parameterization which is common among graphics APIs, which will be referred to as center parameterization.  In the next sections, formulas are given for mapping in both directions between center parameterization and endpoint parameterization.

F.6.4 Conversion from center to endpoint parameterization

Given:

                           

the task is to find:
 
                       

Here are the formulas:

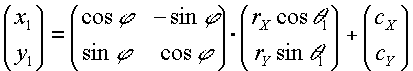	(F.6.4.1)
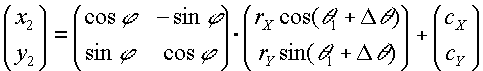	(F.6.4.2)
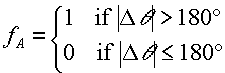	(F.6.4.3)
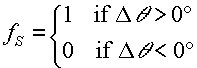	(F.6.4.4)

F.6.5 Conversion from endpoint to center parameterization

Given:

                        

the task is to find:
 
                          

The equations simplify after a translation which places the origin at the midpoint of the line joining (x₁, y₁) to (x₂, y₂), followed by a rotation to line up the coordinate axes with the axes of the ellipse.  All transformed coordinates will be written with primes.  They are computed as intermediate values on the way toward finding the required center parameterization variables.  This procedure consists of the following steps:

Step 1: Compute (x₁', y₁') according to the formula

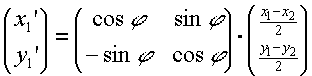(F.6.5.1)

Step 2: Compute (c_X ', c_Y ') according to the formula

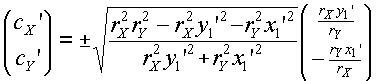	(F.6.5.2)
where the + sign is chosen if          and the - sign is chosen if

Step 3: Compute (c_X, c_Y) from (c_X ', c_Y ')

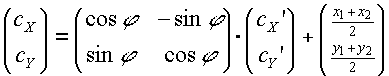(F.6.5.3)

Step 4: Compute

and

In general, the angle between two vectors (u_X, u_Y) and (v_X, v_Y) can be computed as

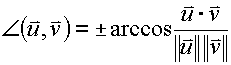	(F.6.5.4)
where the ± sign appearing here is the sign of uX vY - uY vX

This angle function can be used to express

and

as follows:

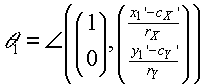	(F.6.5.5)
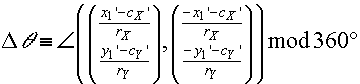	(F.6.5.6)

where

is fixed in the range -360° <

< 360° such that:

if

0, then

< 0,

else if

1, then

> 0.

F.6.6 Correction of out-of-range radii

This section formalizes the adjustments to out-of-range r_X and r_Y mentioned in F.6.2. Algorithmically these adjustments consist of the following steps:

Step 1: Ensure radii are non-zero

If r_X = 0 or r_Y = 0, then treat this as a straight line from (x₁, y₁) to (x₂, y₂) and stop.  Otherwise,

Step 2: Ensure radii are positive

Take the absolute value of r_X and r_Y:

(F.6.6.1)

Step 3: Ensure radii are large enough

Using the primed coordinate values of equation (F.6.5.1), compute

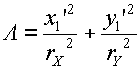(F.6.6.2)

If the result of the above equation is less than or equal to 1, then no further change need be made to r_X and r_Y.  If the result of the above equation is greater than 1, then make the replacements

(F.6.6.3)

Step 4: Proceed with computations

Proceed with the remaining elliptical arc computations, such as those in section F.6.5.  Note: As a consequence of the radii corrections in this section, equation (F.6.5.2) for the center of the ellipse always has at least one solution (i.e. the radicand is never negative).  In the case that the radii are scaled up using equation (F.6.6.3), the radicand of (F.6.5.2) is zero and there is exactly one solution for the center of the ellipse.

F.7 Text selection implementation notes

The following implementation notes describe the algorithm for deciding which characters are selected during a text selection operation.

The text selection operation determines the start selection character(s) and start selection subregion and the end selection character(s) and end selection subregion. To determine the start selection character(s), the SVG user agent determines which rendered glyph received the initial select event (e.g., the initial mouse down event) and which character(s) corresponds to the given glyph (note that for ligatures, a single glyph represents multiple characters). For all of the glyphs used to render the given character(s), determine start selection subregion depending on whether the selection/pointer event occurred in the top/left, top/right, bottom/left or bottom/right subregion of the character cell area that encompasses all of the glyphs used to render the given character(s).

The end character(s) and the relevant end character(s) subregion are determined using a similar method, except use the pointer location at the end of the select operation (e.g., when the user releases the given mouse button).

For systems which support pointer devices such as a mouse, the user agent is required to provide a mechanism for selecting text even when the given text has associated event handlers or links, which might block text selection due to event processing precedence rules (see Pointer events). One implementation option for platforms which support a pointer device such as a mouse, the user agent may provide for a small additional region around character cells which initiate text selection operations but do not initiate event handlers or links.

For horizontal text (i.e., when the baseline of the glyph is parallel to the primary text advance direction):

• If the start selection subregion is either the top/left or bottom/left, then the selection starts between the start character(s) and the previous character in visual rendering order for the 'text' element. (If this is the first character in visual rendering order for the 'text' element, then the selection starts with this first character in visual rendering order. Note that the bi-directional algorithm might result in the selection being between two characters that are not contiguous in lexical order.)
• If the start selection subregion is either the top/right or bottom/right, then the selection starts between the start character(s) and the next character in visual rendering order for the 'text' element. (If this is the last character in visual rendering order for the 'text' element, then the selection starts with this last character in visual rendering order. Note that the bi-directional algorithm might result in the selection being between two characters that are not contiguous in lexical order.)

For vertical text (i.e., when the baseline of the glyph is perpendicular to the primary text advance direction):

• If the start selection subregion is either the top/left or top/right, then the selection starts between the start character(s) and the previous character in visual rendering order for the 'text' element. (If this is the first character in visual rendering order for the 'text' element, then the selection starts with this first character in visual rendering order. Note that the bi-directional algorithm might result in the selection being between two characters that are not contiguous in lexical order.)
• If the start selection subregion is either the bottom/left or bottom/right, then the selection starts between the start character(s) and the next character in visual rendering order for the 'text' element. (If this is the last character in visual rendering order for the 'text' element, then the selection starts with this last character in visual rendering order. Note that the bi-directional algorithm might result in the selection being between two characters that are not contiguous in lexical order.)

When the user agent is implementing selection of bi-directional text in lexical order and the selection starts (or ends) between characters which are not contiguous in lexical order, then there might be multiple potential combinations of characters that can be considered part of the selection. The algorithms to choose among the combinations of potential selection options shall choose the selection option which most closely matches the text string's visual rendering order.

F.8 Printing implementation notes

For user agents which support both zooming on display devices and printing, it is recommended that the default printing option produce printed output that reflects the display device's current view of the current SVG document fragment (assuming there is no media-specific styling), taking into account any zooming and panning done by the user, the current state of animation, and any document changes due to DOM and scripting . Thus, if the user zooms into a particular area of a map on the display device and then requests a hardcopy, the hardcopy should show the same view of the map as appears on the display device. If a user pauses an animation and prints, the hardcopy should show the same graphics as the currently paused picture on the display device. If scripting has added or removed elements from the document, then the hardcopy should reflect the same changes that would be reflected on the display.

When an SVG document is rendered on a static-only device such as a printer which do not support SVG's animation and scripting and facilities, then the user agent shall ignore any animation and scripting elements in the document and render the remaining graphics elements according to the rules in this specification.