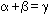
Dave Raggett <dsr@w3.org>,
Davy Batsalle <batsalle@email.enst.fr>
27th November 1997
The Web lacks an effective means for embedding mathematical expressions in Web pages. Hitherto, authors have been forced to use bitmapped images which are slow to load, complex to produce, and look bad when printed.
EzMath provides an easy to learn notation for embedding mathematical expressions in Web pages. The notation is inspired by how expressions are spoken aloud, together with a few abbreviations for conciseness.
EzMath covers a widely used subset of mathematics and can be used to create MathML content tags conforming to the W3C mathematical markup language. EzMath focusses on the meaning of mathematical notation rather than just how it looks on paper (or screen).
EzMath is available as freeware from http://www.w3.org/People/Raggett/EzMath/
This section describes some earlier work on using computers to typeset mathematical expressions. In each case we use the same example:
EzMath:
limit as x tends to a of function f(x)
One of the first well known computer packages for typesetting mathematical formulae is eqn[1], developed by Bell Labs for use with the Unix typesetting system troff[2]. Eqn uses a regular grammar that is surprisingly readable and helped to inspire the approach taken by EzMath. A comparison of EzMath and Eqn is given in section 3.4.
Eqn:
lim from {x -> a} f(x)
Eqn was eclipsed by Donald Knuth's TEX[3]. This offered much greater control over typesetting details and has become the most popular method for electronic typesetting of mathematics. TEX is a lot more cryptic, making heavy use of macros. Leslie Lampson's LaTEX[4] is a common macro package for TEX. The American Mathematical Society has developed its own macro package and guidelines for using TEX called AMS-TEX[5].
TEX:
\lim_{x \rightarrow a} f(x)
The SGML community came up with their own solutions, notably the ISO 12083 standard[6] which grew out of earlier work on the AAP DTD[7].
AAP Math:
<lim><op><rf>lim</rf></op><ll>x → a</ll><opd>f(x)</opd></lim>
ISO 12083:
<subform><roman>lim</roman></subform><bottom>x → a</bottom> f(x)
At the time of writing there is no direct way to include mathematical expressions in Web pages. As a result people resort to rendering expressions using other tools, such as Word or LaTEX and converting them into bitmapped images in the GIF format.
This has a number of serious drawbacks: It makes pages slow to download. It means you have to manage a number of GIF files as well as the HTML page they belong to. The pages look terrible when printed out (the high resolution of printed pages exacerbates the limitations of the bitmapped images). The font size for expressions is fixed and doesn't match the end-user's font preferences. There is no effective answer for people who can't see the images. The expressions can't be moved to a mathematical manipulation package.
Conventional mathematical notations rely on a shared understanding by the mathematicians who write and read these notations. The notations are generally incomplete and ambiguous. The same symbols tend to be reused for different functions, especially in different fields of mathematics.
In calculus f' stands for the first derivative of f but can mean any other entity different from f in other fields.
Is i an integer variable, the index of a matrix or the square root of -1? What about j ?
What is the function of 2 in SU2, log2 x x2 x2 or as indices on a tensor?
I grateful acknowledge the use here of examples taken from [14].
Both TEX and ISO 12083 focus on the visual presentation of mathematics rather than its meaning. For instance, in TEX you would represent the second derivative of f with respect to x as:
{{d^2f} \over {dx^2}}
This is fine for people reading the visual rendering of the TEX markup, but causes difficulties for people with visual disabilities using a speech synthesiser, or for software that wants to manipulate the mathematical expressions. The problems stem from having to guess the intended meaning.
This is critical to the Web, which aims to make information accessible to all. A satisfactory solution for representing mathematical expressions for the Web must be able to be effectively rendered to a wide variety of media, including bitmapped displays, fixed character grid displays, Braille, paper and speech synthesisers.
The Web encourages the development of active documents. It should be possible to paste expressions into tools for mathematical manipulation, such as Mathematica[9] and Maple[10]. Web pages may also offer an ability to graph expressions or otherwise manipulate them in place.
EzMath is the outcome of work at MIT and HP Labs aimed at providing an easy to learn notation using plain text that would make sense by itself as well being straightforward to render to the screen or to a speech synthesiser. It is inspired by the way you would speak an expression if you were asked to read it over the phone.
The scope of EzMath is broadly speaking designed to meet the needs for most of the formulas used from kindergarten to the end of high school in the US. Further work is planned to extend the coverage to meet the needs of 1st and 2nd year undergraduates. For a discussion of the relationship between EzMath and the W3C MathML notation, see section 3.3
When speaking it can be tricky to be unambigous about the way an expression is grouped. To make the grouping explicit, EzMath allows you to use { and }.
For example:
x times {y plus z}
is interpreted as x times y plus z. You can also use common symbols such as * for times and + for plus. EzMath supports infix, prefix and postfix operators using the conventional relative precedences for these operators. A table summarising operator precedences is given section 4.3.
Greek letters are reserved words, for instance:
alpha + beta = gamma
yields:
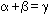
EzMath supports variants for how to say things like powers. The following are all equivalent:
x to the power of 3
x cubed
x^3
as are:
x to the power of 2
x squared
x^2
Identifiers consist of a single letter optionally followed by one or more digits. The "times" operator is often implicit, as below for bx, which is interpreted as b times x. For instance, the following are equivalent:
a times x squared plus b times x plus c equals 0
ax^2+bx+c=0
which yields:
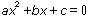
The implicit times operator is useful for expressions such as:
(x+1)(x-1) = x(x-1) + (x-1) = x^2 - 1
In x(x-1) and f(x-1), which is multiplication and which is function application? EzMath requires you to make this explicit using the "function" keyword, as in:
function f(x) = ax+b
which simply yields:
If you are going to use a function identifier several times it is convenient to declare it as a function in advance:
declare f as function; y = f(a) + f(b)
The keyword "wrt" is used as an abbreviation for "with respect to" for integrals and derivatives, as in:
integral from 0 to pi of sin ax wrt x
which yields:
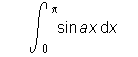
The keyword "wrt" avoids the ambiguities that "d" would introduce. Would the "d" the identifier 'd' or does it introduce the variable of integration? Here are some examples for derivatives:
derivative of f wrt x
2nd derivative of f wrt x
partial derivative of f wrt x
total derivative of f wrt x
Ezmath supports 1st, 2nd, 3rd, 4th, 5th etc. and "n th". For the latter a space is needed between the letter 'n' and the "th" since "nth" would be misinterpreted as the sequence of identifiers 'n', 't' and 'h'. Limits are represented as follows:
limit as x tends to infinity of function f(x)
which yield:
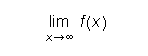
Intervals are represented as:
open interval from a to b
closed interval from a to b
open closed interval from a to b
closed open interval from a to b
EzMath supports vectors, matrices and determinants, for instance:
vector V
vector (3, 2, 7)
unit vector j
matrix M
matrix (1, 2; 2, 1)
inverse of matrix M
transpose of matrix M
determinant (1, 2; 2, 1)
where comma is used to separate items on the same row and semicolon to separate items on separate rows. Identifiers for vectors and matrices are rendered in a bold upright font. For example, typing:
matrix M = matrix (1,2;2,1)
yields:
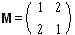
and
determinant (a sub 11, a sub 12; a sub 21, a sub 22)
= a sub 11 a sub 22 - a sub 21 a sub 12
yields:
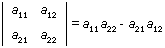
The following illustrates set operations in EzMath:
set S
set of x such that y
a union b
x is in S
x is a member of S
x is not in S
x is not a member of S
Support for Vector Calculus is still at a tentative stage:
div vector E = 4 pi rho
curl vector B = 0
Currently div and curl are rendered as "div" and "curl" respectively. To show these functions with the nabla symbol you need to write:
nabla dot vector E = 4 pi rho
nabla cross vector B = 0
EzMath includes some presentation features, e.g.
bold x renders x in bold font
cursive S renders S in a cursive font
italic I renders I in an italic font
upright F renders F in an upright font
bigger X renders X bigger than normal
smaller X renders X smaller than normal
x bar places a bar above the x
x hat places a 'hat' above the x
x sub c subscript
x sup alpha superscript
You can define things for later use, effecting how something is rendered and what it means:
declare U, V, W as vector; U cross V
thereafter in the current scope any occurrence of the identifiers U, V or W are interpreted as vectors. This information is retained when converting to MathML, see section 3.3.
Somewhat more speculative is the form:
for any F let F bar denote inverse F
which defines a mapping from a presentation form to its semantics. This is used when translating to MathML, see section 3.3
A free plugin for EzMath is available from HP Labs[11]. At the time this paper was written (November '97), we had developed a Netscape plugin for use on Windows 95/NT. We hope to port this to the Macintosh and to provide an ATL based ActiveX control for Windows by the time of the WWW'7 conference.
The Netscape plugin for use with Navigator 3.0 or 4.0 is invoked using the EMBED element, e.g.
<EMBED type="text/ezmath" width="100%" height="70"
math="x = {-b plus or minus square root of {b^2 - 4ac}}/2a">
The width and height parameters are required. It would much easier if these could be supplied by the plugin itself, based upon the rendered size of the expression, but unfortunately Netscape Navigator doesn't allow this.
If you are using Netscape 4.0 or above, you can use the OBJECT element, as in:
<OBJECT type="text/ezmath" width="100%" height="70">
<PARAM name=math
value"x = {-b plus or minus square root of {b^2 - 4ac}}/2a">
x = {-b plus or minus square root of {b^2 - 4ac}}/2a
</OBJECT>
This representation is compatible with HTML 4.0[12] and will also work with Internet Explorer using the ActiveX control for EzMath. Once again width and height are both required. We are told that for IE 4.0, it should be practical to use the simpler form:
<OBJECT type="text/ezmath">
x = {-b plus or minus square root of {b^2 - 4ac}}/2a
</OBJECT>
but were unable to get sufficient information from Microsoft by the time of writing to test this.
If you want to include an expression as part of a text line, you may find align=absmiddle helps. It is unfortunate that neither Netscape nor Microsoft yet support a robust means to vertically align a plugin/control so that the math baseline is aligned with the baseline of the surrounding text.
When you click with the right or left mouse buttons on expressions rendered with the EzMath control, a dialog box appears. This offers the following features:
A standalone editor for EzMath is also available for Windows 95/NT. The majority of the EzMath code is written in ANSI C and is platform independent. A platform dependent part is used to interface to the platform and plugin specific code.
The platform independent part consists of the following:
The W3C working group for Mathematics has developed an XML based representation for mathematical expressions[13]. MathML is not suited for hand entry and has been designed for program to program interchange of mathematical expressions. It is not concise, but it is straight forward to manipulate and to render.
The MathML tag set has two parts: one part designed for capturing the visual presentation of mathematical notations and the other which is designed to describe the meanings of a small but widely used subset of mathematics (Kindergarten though end of high school). This part is generally referred to as the MathML content tag set.
The EzMath plugin and standalone editor can be used as a convenient way to create MathML content tags. The following example contrasts the EzMath and corresponding MathML:
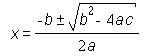
EzMath: x = {-b plus or minus square root of {b squared - 4ac}}/2a
MathML:
<e>
<eq/>
<ci>x</ci>
<apply>
<over/>
<apply>
<fn>
<mo>±</mo>
</fn>
<apply>
<minus/>
<ci>b</ci>
</apply>
<apply>
<root/>
<apply>
<minus/>
<apply>
<power/>
<ci>b</ci>
<cn>2</cn>
</apply>
<apply>
<times/>
<apply>
<times/>
<cn>4</cn>
<ci>a</ci>
</apply>
<ci>c</ci>
</apply>
</apply>
<cn>2</cn>
</apply>
</apply>
<apply>
<times/>
<cn>2</cn>
<ci>a</ci>
</apply>
</apply>
</e>
MathML content tags use a prefix notation where the operator appears first followed by its operands. The APPLY element is used as a container for the operator and its operands. The E element is used in place of APPLY for relational operators such as equals, which is represented as <EQ/>. Entities are used for special symbols such as ± which denotes the symbol for "plus or minus".
Because of the similarities between EzMath and eqn, it is interesting to make a closer comparison. Eqn was developed for use as part of the troff typesetting tool provided with Unix.
Eqn is more fussy than EzMath about the use of white space. For instance Greek letters aren't recognized unless delimited by space, thus f( theta ) is ok, but not f(theta).
When you want to use both subscripts and superscripts, e.g.
to express 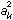 EzMath treats the following as equivalent:
EzMath treats the following as equivalent:
a sub k sup 2
a sup 2 sub k
Eqn is sensitive to the order in which sub and sup occur. If the sup comes before the sup the subscript is applied to the superscript and not to the base! This approach was rejected for EzMath based upon early feedback from would be users.
Eqn is much more limited than EzMath when it comes to being explicit about the meaning. For instance, eqn doesn't provide special syntax for derivatives:
Ezmath: derivative of y wrt x Eqn: dy / dx
As previously noted this makes it harder to provide effective renderings to speech or to export the meaning to mathematical manipulation packages.
To define matrices in eqn, you define columns of items using the above keyword to separate items. Each column is preceded by lcol, ccol or rcol, which indicate whether the items in the column should be left, center or right aligned within the column:
matrix {
lcol 1 above 3
rcol 2 above 4
}
EzMath takes a different approach, using comma to separate items in the same row, and semicolon to separate rows:
matrix (1, 2; 3, 4)
EzMath is basically an English language transliteration of the MathML content tags. This makes it easier to understand, easier to write, and in most cases considerably more concise than MathML.
In the following grammar non-terminals are in upper case. Square brackets are used to group things. The ? * + and & characters are used as follows:
STATEMENT
::= EXPRESSION [LIST-DELIM EXPRESSION]* ["TEXT"]? [.]
EXPRESSION
::= BRACKETED-EXPRESSION
::= FUNCTION
::= PREFIX-OP [of]? EXPRESSION
::= EXPRESSION INFIX-OP EXPRESSION
::= EXPRESSION ORDINAL-OP EXPRESSION
::= EXPRESSION POSTFIX-OP
::= NUMBER
::= IDENTIFIER
BRACKETED-EXPRESSION
::= LEFT-BRACKET EXPRESSION?
[LIST-DELIM EXPRESSION]* RIGHT-BRACKET
LEFT-BRACKET
::= {
::= (
RIGHT-BRACKET
::= }
::= )
LIST-DELIM
::= ,
::= ;
FUNCTION
::= CORE-FUNC [of]? EXPRESSION
::= FUNCTION
::= INTEGRAL
::= SET
::= MATRIX
::= VECTOR
::= COMPLEX
::= DERIVATIVE
::= LIMIT
::= SUM
::= PRODUCT
::= DETERMINANT
::= EITHER
::= INTERVAL
::= EQUATION
::= LOG
::= ROOT
::= DECLARE
::= FOR
CORE-FUNC
::= abs
::= mod
::= sin
::= cos
::= tan
::= sec
::= cotan
::= sinh
::= cosh
::= tanh
::= sech
::= csch
::= coth
::= arcsin
::= arccos
::= arctan
::= exp
::= ln
::= grad
::= div
::= curl
FUNCTION
::= function FN-NAME OF?
::= function FN-NAME ( EXPRESSION )
FN-NAME
::= EXPRESSION
OF
::= of EXPRESSION
INTEGRAL
::= integral [FROM? TO? OF? ]& WRT?
::= integral over DOMAIN OF? WRT?
DOMAIN
::= EXPRESSION
FROM
::= from EXPRESSION
TO
::= to EXPRESSION
WRT
::= wrt EXPRESSION
LIMIT
::= limit AS-TENDS-TO? OF?
AS-TENDS-TO
::= as EXPRESSION tends to EXPRESSION
DERIVATIVE
::= derivative OF? WRT?
MATRIX
::= matrix BRACKETED-EXPRESSION
::= matrix IDENTIFIER
VECTOR
::= vector BRACKETED-EXPRESSION
::= vector IDENTIFIER
COMPLEX
::= complex (real , imaginary)
::= complex IDENTIFIER
INTERVAL
::= [open? closed?]& interval [FROM? TO?]&
SUM
::= sum [FROM? TO? OF?]&
PRODUCT
::= product [FROM? TO? OF?]&
DETERMINANT
::= determinant BRACKETED-EXPRESSION
::= determinant IDENTIFIER
EITHER
::= either EXPRESSION WHEN? [or EXPRESSION WHEN?]*
WHEN
::= when EXPRESSION
EQUATION
::= equation EXPRESSION [:] EXPRESSION
LOG
::= log of? EXPRESSION base EXPRESSION?
ROOT
::= square root of? EXPRESSION
::= EXPRESSION ORDINAL-OP root of? EXPRESSION
DECLARE
::= declare IDENTIFIER [, IDENTIFIER] as TYPE
FOR
::= for any IDENTIFIER [, IDENTIFIER]
let EXPRESSION denote EXPRESSION
The following describes the rules used by the EzMath tokenizer:
#define IsWhite(c) (c == ' ' || c == '\t' || c == '\n' || c== '\r')
#define IsLetter(c) (('a' <= c && c <= 'z') || ('A' <= c && c <= 'Z'))
#define IsDigit(c) ('0' <= c && c <= '9')
#define IsAlphaNumeric(c) (IsLetter(c) || IsDigit(c))
#define IsVisible(c) (32 < c && c < 127)
#define IsSymbol(c) (!IsLetter(c) && !IsDigit(c) && IsVisible(c))
Symbol tokens consist of one or more characters matching the IsSymbol set. These are generally used for operators or punctuation.
Name tokens start with a letter matching IsLetter followed by characters matching IsLetter or IsDigit. EzMath's tokeniser recognizes terms defined in the dictionary consisting of several name or symbol tokens separated by white space, e.g.
x to the power of y
is tokenized as the 3 tokens:
"x", "to the power of" and "y"
while "sin ax" is tokenized as "sin", "a" and "x". Greek letters are denoted by reserved words e.g."alpha" for lower case alpha and "Alpha" for upper case alpha. In the case that several dictionary terms match the current lexical position, the longest known term is used. The dictionary classifies each term into the categories: number, identifier, operator or function. Each term may be associated with methods for parsing and formatting.
| Description | Symbol/name | Precedence | Grouping | Aliases | Comments |
|---|---|---|---|---|---|
| prefix | partial | 800 | right | derivatives | |
| prefix | total | 800 | right | derivatives | |
| prefix | unit vector | 800 | right | see "vector" | |
| prefix | transpose | 800 | right | matrix or vector | |
| prefix | inverse | 800 | right | matrix or function | |
| prefix | open | 800 | right | intervals | |
| prefix | closed | 800 | right | intervals | |
| prefix | double | 800 | right | integrals | |
| prefix | triple | 800 | right | integrals | |
| prefix | surface | 800 | right | integrals | |
| prefix | volume | 800 | right | integrals | |
| prefix | contour | 800 | right | integrals | |
| infix | superscript | 800 | right | sup | not for powers |
| infix | subscript | 800 | right | sub and _ | |
| infix | modulo | 800 | right | mod | |
| postfix | factorial | 780 | left | ! | e.g. 6! |
| postfix | per cent | 775 | left | % | |
| postfix | degrees | 770 | left | angles | |
| postfix | minutes | 770 | left | angles | |
| postfix | seconds | 770 | left | angles | |
| prefix | variance | 770 | right | var | statistics |
| prefix | median | 770 | right | statistics | |
| prefix | mode | 770 | right | statistics | |
| prefix | mean | 770 | right | statistics | |
| prefix | standard deviation | 770 | right | sdev | statistics |
| prefix | moment | 770 | right | statistics | |
| postfix | prime | 770 | left | accent | |
| postfix | double prime | 770 | left | accent | |
| postfix | tilde | 770 | left | accent | |
| postfix | hat | 770 | left | accent | |
| postfix | bar | 770 | left | accent | |
| postfix | dot | 770 | left | accent | |
| postfix | double dot | 770 | left | ddot | accent |
| postfix | arrow | 770 | left | accent | |
| prefix | bold | 770 | right | font style | |
| prefix | upright | 770 | right | font style | |
| prefix | italic | 770 | right | italic | font style |
| prefix | cursive | 770 | right | font style | |
| prefix | smaller | 770 | right | font style | |
| prefix | bigger | 770 | right | font style | |
| postfix | st | 770 | left | ordinal | |
| postfix | nd | 770 | left | ordinal | |
| postfix | rd | 770 | left | ordinal | |
| postfix | th | 770 | left | ordinal | |
| infix | to the power of | 760 | right | ^ | power |
| postfix | squared | 760 | left | ^2 | power |
| postfix | cubed | 760 | left | ^3 | power |
| prefix | plus | 600 | right | + | |
| prefix | minus | 600 | right | - | |
| prefix | not | 600 | right | - | |
| prefix | gradient | 600 | right | grad | |
| infix | fraction | 580 | right | renders as x/y | |
| infix | divide | 580 | right | special divide sign | |
| infix | circle times | 520 | right | ||
| infix | circle plus | 520 | right | ||
| infix | circle minus | 520 | right | ||
| infix | dot | 500 | right | ||
| infix | cross | 500 | right | ||
| infix | composed with | 500 | right | function composition | |
| infix | times | 480 | right | * | |
| infix | over | 450 | right | ||
| infix | / | 450 | right | ||
| infix | plus | 400 | right | + | |
| infix | minus | 400 | right | - | |
| infix | plus or minus | 400 | right | ||
| infix | intersection | 380 | right | intersect | sets |
| infix | union | 360 | right | sets | |
| infix | is superset of | 360 | right | sets | |
| infix | is superset or equals | 360 | right | sets | |
| infix | is not a superset of | 360 | right | sets | |
| infix | is subset of | 360 | right | sets | |
| infix | is subset or equals | 360 | right | sets | |
| infix | is not a subset of | 360 | right | sets | |
| infix | is in | 360 | right | is a member of | set membership |
| infix | is not in | 360 | right | is not a member of | set membership |
| infix | maps to | 340 | right | ||
| infix | equals | 300 | left | = | comparison |
| infix | equivalent | 300 | left | equiv | comparison |
| infix | congruent | 300 | left | comparison | |
| infix | less than | 300 | left | < | comparison |
| infix | greater than | 300 | left | > | comparison |
| infix | not equals | 300 | left | != | comparison |
| infix | less than or equals | 300 | left | <= | comparison |
| infix | greater than or equals | 300 | left | >= | comparison |
| when | tends to | base | denote |
| from | to | wrt | of |
| if | and | or | |
| . | : | , | ; |
| Greek upper case letters | |||
|---|---|---|---|
| Alpha | Beta | Chi | Delta |
| Epsilon | Phi | Gamma | Eta |
| Iota | Kappa | Lambda | Mu |
| Nu | Omicron | Pi | Theta |
| Rho | Sigma | Tau | Upsilon |
| Omega | Xi | Psi | Zeta |
| Greek lower case letters | |||
|---|---|---|---|
| alpha | beta | chi | celta |
| epsilon | phi | gamma | eta |
| iota | kappa | lambda | mu |
| nu | omicron | pi | theta |
| rho | sigma | tau | upsilon |
| omega | xi | psi | zeta |
| Miscellaneous named symbols | |||
|---|---|---|---|
| for all | there exists | therefore | proportional |
| angle | perpendicular | infinity | nabla |
| omega pi | curly phi | curly Upsilon | curly theta |
| double arrow | left arrow | right arrow | up arrow |
| down arrow | horizontal bar | vertical bar | bullet |
| clubs | diamonds | hearts | spades |
| ellipsis | aleph | imaginary | real |
| weierstrass | empty set | bra | ket |
| lfloor | rfloor | lceil | rceil |
[1][2] "UNIX Text Processing", Dale Dougherty and Tim O'Reilly, Hayden Books Indianapolis, 1987. ISBN 0-672-46291-5
[3] "TEX for the Impatient", Paul W. Abrahams, Addison Wesley Reading Mass., 1990. ISBN 0-201-51375-7
[4] "LATEX : A Documentation Preparation System, 2nd edition", Leslie Lamport, Addison Wesley Reading Mass., 1994. ISBN 0-201-52983-1
[5] "AMS TEX Resources", American Mathematical Society 1997, http://www.ams.org/TeX/home.html
[6] "ISO 12083 DTD", ISO 12083:1993, Information and Documentation -- Electronic Manuscript Preparation and Markup, Geneva, 1993.
[7] "AAP Math DTD", ANSI/NISO Z39.59-1988, Standard for Electronic Manuscript Preparation and MarkUp, Bethesda, 1988.
[8] "Practical SGML", Eric van Herwijnen, Kluwer Academic Publishers Norwell Mass., 1994. ISBN 0-7923-9434-8
[9] "Mathematica", Wolfram Research, Urbana Champagne Illinois, http://www.wolfram.com/mathematica/
[10] "Maple", Waterloo Maple, Ontario. http://www.maplesoft.on.ca/
[11] "HP Labs", Hewlett Packard Laboratories, Bristol England, http://www.hpl.hp.co.uk/
[12] "HTML 4.0", W3C Recommendation for HTML 4.0, December 1997, http://www.w3.org/TR. For an easy to read user guide see, "Raggett on HTML 4", Dave Raggett, Jenny Lam, Ian Alexander & Michael Kmiec, "Addison Wesley Longman Reading Mass., 1997. ISBN 0-201-17805-2
[13] "MathML", W3C Recommendation for the Mathematical Markup Language, January 1998, http://www.w3.org/TR
[14] "Standard dtd's and scientific publishing", N.A.F.M. Poppelier, E. van Herwijnen, C.A. Rowley, EPSIG News 5 (1992) #3, September 1992, p. 10-19.
EzMath is available as a free plugin from Hewlett Packard Laboratories, Filton Road, Stoke Gifford Bristol BS12 6QZ, United Kingdom. Tel: +44 (0) 117 979 9910, Fax: +44 (0) 117 922 8516.