This article was originally entitled "The Fractal nature of the web". Since then, i have been assured that while many people seem to use fractal to refer to a Zipf (1/f) distribution, it should really only be used in spaces of finite dimension, like the two-dimensional planes of MandelBrot sets. The correct term for the Web, then, is scale-free.
This isn't an observation so much as a requirement.
I have discussed elsewhere how we must avoid the two opposite social deaths of a global monoculture and a set of isolated cults, and how the fractal patterns found in nature seem to present themselves as a good compromise. It seems that the compromise between stability and diversity is served by there the same amount of structure at all scales. I have no mathematical theory to demonstrate that this is an optimization of some metric for the resilience of society and its effectiveness as an organism, nor have I even that metric. (Mail me if you do!)
However, it seems from experience that groups are stable when they have a set of peers, when they have a substructure. Neither the set of peers nor the substructure must involve huge numbers, as groups cannot "scale", that is, work effectively with a very large number of liaisons with peers, or when composed as a set of a very large number of parts. If this is the case then by induction there must be a continuum of group sizes from the vary largest to the very smallest.
This seems to be a general rule which can guide our design, and against which we can measure actual patterns of use.
It is in fact another aspect of the tension between many languages and one global language. Locally defined languages are easy to create, needing local consensus about meaning: only a limited number of people have to share a mental pattern of relationships which define the meaning. However, global languages are so much more effective at communication, reaching the parts that local languages cannot. This tension is exemplified in the standards process, when ideas have to be exposed to successively larger and larger groups, with friction and hard work at each stage.
Other interesting things to model passing though a fractal system include DNA traits in intermarrying populations Someone suggested (who?) that the invention of the bicycle made a great difference to average health in the Welsh valleys because it allowed greater intermarrying and so increased the effective gene pool size Clearly, global travel could end up reducing the diversity. viruses propagating through schools and traveling business people; and problems propagating to someone who has a solution are more good exercises (State your assumptions!).
Whether we like it or not, early measurements of web traffic by the DEC WRL firewall showed DEC employees browsing sites with a Zipf (1/n) distribution of popularity. (Anyone got any other measurements? [Neilsen 1997]). Recent analyses suggest the Web becoming smaller for its size seem to use.
How can we use knowledge of the Web's fractal nature? By planning network bandwidth between long-range and short-range communication, planning for cache usage, etc. The physical network can be expected to have a variety of scale geographically, like the road system. However, the structure of the Web is interestingly different because of the lack of two-dimensional constraint. The challenge is to use this flexibility in building an effective society on top of the Web.
What do we mean by "effective"? We mean we would like to combine scientist's creative ability and knowledge to find a cure for AIDS. We would like to preserve world peace by allowing xenophobia to disperse in a web of understanding, while at the same time preserving the diversity of culture which gives the human race its richness. These are of course the same classic problems of the management of a large organization, of combining individual creativity with corporate vision.
If the web of society has an imbalance, we pay for it. We pay for insufficient global understanding with war. We pay for insufficient family communication with broken families and unsupported individuals. At any level of scale, missing social structure at that scale will prevent problems at that scale being addressed, and also prevent resources at that scale being used. It would therefore be great to have a way of measuring for a given web the degree to which it has a balanced fractal pattern, and if not where its weaknesses are.
Those looking for the "small world" effect chose metrics such as the maximum or mean value of the shortest path between any two points. This gives us a metric for effectiveness at the global scale, but not of the chewiness.
Clustering algorithms can produce globs of various sizes, and a measure of the chewiness of a web may be that the cluster sizes have a Zipf distribution. For example, using Jon Kleinberg's algorithm (which for a link matrix A associates concepts with the eigenvectors of A*A), the strength of the cluster is the value of the eigenvalue, and (while this does not directly indicate size) an interesting test would be on the relative absolute values (squares?) of successive eigenvalues.
Looking it at from the point of view of an individual (a graph node), an interesting question is the proportion of the traffic which is to local or more distant nodes. In Marchiori's model [Marchiori] traffic flows between two nodes in inverse proportion to the resistance of the shortest path. The total "efficiency" is deemed to be the total flow between all pairs of nodes. Can we measure a "chewiness" which measures the approximation of the system to a fractal distribution of long and short range communication? If the Marchiori model were modified to use parallel conductance (more like a real signal flow system) then would this be simpler?
Suppose for example we look at the amount of connection we have with nodes whose distance, or groups whose size, is of each order of magnitude and look for smoothness up to the global level.
2000/03
Well, here I was thinking that while it is intuitively clear that society has to be fractal, I didn't know a mathematical justification for it, when Jon Kleinberg comes up with what for me is his second cool web result.
This is a paper takes the case of a two-dimensional grid. It imagines each cell having a certain distribution of links of various lengths. It demonstrates that in order to achieve the connectivity a la 6 degrees of separation which scales with the log of the size of the system, then the distribution of link density as a function of distance must be precisely an inverse-square law. That is, each cell must have the same number of links (on average) to cells 1-10 squares away as to cells 10-100 away, etc. Anything more local or more global leads to less of a small-world phenomenon: this is the only scalable solution.
True, this applies to a geographical grid, and a square rather uniform one at that. However, He does generalize it to more dimensions. Furthermore, you can see logically how the system works. To get a postcard to an arbitrary person in Massachusetts through a network of friends, you must have enough local friends to be able to find someone who will know someone in Massachusetts. The person they find in Massachusetts must be able to pass it to people successively closer and closer to the target. this only works if there is connectivity on each scale. True, no one has derived the metric of the number of hops a message takes as being an essential metric for systems, but on the other hand there is a clear analogy with the number of hops between a problem and a solution in a large organization .
Other work:
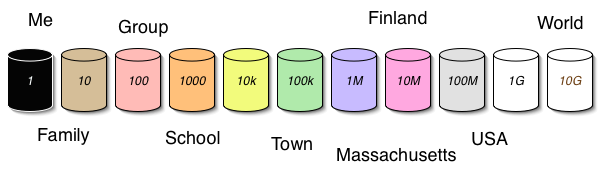
There will I am sure be a lot of ways in which the fractal requirement is used in web design. You can also use it in that task of figuring out how you fit in to society at large (and at small). Do your personal interactions spread across the scales? Here is a self-help chart to help think about this. You fill in the groups in your life.
| Scale | 1 | 10 | 1000 | 10k | 100k | 1M | 10M | 100M | 1G |
|---|---|---|---|---|---|---|---|---|---|
| Group | You |
family,
group |
... | ... | town? | city? | country? | USA | World population |
| Time spent | ? | ? | ? | ? | ? | ? | ? | ? | ? |
| Money spent | ? | ? | ? | ? | ? | ? | ? | ? | ? |
| etc | ? | ? | ? | ? | ? | ? | ? | ? | ? |
Another way to do this is find 11 jars, and label one with each scale in powers of 10. (You don't have to paint them but it helps).

Put marbles in each can for each time period you spend on matters at a given scale, such as an international meeting, or a school sportsfield, or with your family, or alone in a treehouse. How well balanced do the jars become?
As a social person, do you spend enough time with groups of each size? If not, are there people one click from you who do, and through whom you are indirectly present in those groups? One of the concerns is that the last column - the global column - tends in my observation to get the smallest amount money at least, as in the US federal and state and town taxes are spread around the other areas but the level of international aid is very much lower. The cool thing is that I think people are born with DNA which gives them a healthy interest at all these levels. People who stick at one scale all their lives feel very uncomfortable. Maybe our preferences have evolved to form naturally a fractal society.
One of the interesting things about assuming a fractal
distribution is you can think about the number of ontologies an
the time it takes to make them, and the total cost of using
ontologies. So let us for example naivel assume that
ontologies are evenly spread across orders of magnitude; committe
size goes as log(community), time as comitee^2,
cost is shared across community.
| Scale | Eg | Committe size | Cost per ontology (weeks) | Cost for me |
| 0 | Me | 1 | 1 | 1.000000 |
| 10 | My team | 4 | 16 | 1.600000 |
| 100 | Group | 7 | 49 | 0.490000 |
| 1000 | 10 | 100 | 0.100000 | |
| 10k | Enterprise | 13 | 169 | 0.016900 |
| 100k | Business area | 16 | 256 | 0.002560 |
| 1M | 19 | 361 | 0.000361 | |
| 10M | 22 | 484 | 0.000048 | |
| 100M | National, State | 25 | 625 | 0.000006 |
| 1G | EU, US | 28 | 784 | 0.000001 |
| 10G | Planet | 31 | 961 | 0.000000 |
... when we are all in one big domain of discourse but people are all making their own local ontologies? (2007/3/3)
Rather than 'domain of discourse' , or set of things considered, I think of 'community', set of agents communicating using certain terms. When one thinks in terms of domain of discourse, one tends to conclude that everyone who talk at all about a car (say) has cars in their domain of discourse and so everyone must share the model which includes the single class Car.
It isn't like that though. An agent plays a role in many different overlapping communities. When I tag a photo as being of my car, or I agree to use my car in a car pool, or when I register the car with the Registry of Motor Vehicles, I probably use different ontologies. There is some finite effort it would take to integrate the ontologies, to establish some OWL (or rules, etc) to link them.
Why do I think the structure should be will be fractal? Clearly there will be many more small communities, local ontologies, than global ones. Why a 1/f distribution? Well, it seems to occur in many systems including the web, and may be optimal for some problems. That we should design for a fractal distribution of ontologies is a hunch. But it does solve the issue you raise. Some aspects of the web have been shown to be fractal already.
Here are some properties of the interconnections:Yes, if web-based means an overlapping set of many ontologies in a fractal distribution. In his fractal tangle, there wil be several recurring patterns at different scales. One pattern is a local integration within (say) an enterprise, which starts point-point (problems scale as n^2) and then shifts with EIA to a hub-and-spoke as you say, where the effort scales as N. Then the hub is converted to use RDF, and that means the hub then plugs into a external bus, as it connects to shared ontologies.
So the idea is that in any one message, some of the terms will be from a global ontology, some from subdomains. The amount of data which can be reused by another agent will depend on how many communities they have in common, how many ontologies they share.
In other words, one global ontology is not a solution to the problem, and a local subdomain is not a solution either. But if each agent has uses a mix of a few ontologies of different scale, that is forms a global solution to the problem.
The conjecture is that there is some model which reasonably well described these systems, and that given that model one can show that the scale-free distribution of communities is optimal.
There are many other questions. Of course existing systems on the earth may be very much influenced by the geographical reality of a two-dimensional surface. Historical groups have been nested geographically. So though there may be aspects in which community size is scale-free, that maybe a completely different optimisation problem from the one we have when on the Internet anyone can connect to anyone. If you could devise an algorithm for connecting people into groups, and so that they each participated in communities of different sizes in a scale-free way, then how much more effective (at solving problems, etc) can you make a web-based society which ignores geographical borders? To what extent does humanity as currently connected by the web in fact deviate from geographical nesting anyway?
Jacob Nielsen "Zipf Curves and Website Popularity", (Sidebar to column Increasing returns for websites)
RÉKA ALBERT et al: Diameter of the World-Wide Web, Nature 401, 130 (1999) Brief communications
Berners-Lee, T, "Weaving the Web", HarperSanFrancisco 1999, pp199-204
Dill, S, et al., "Self-similarity in the web" ACM Transactions on Internet Technology (TOIT) Volume 2 ,B Issue 3 B (August 2002). Thanks Jim Hendler for the pointer. Findings seem to justify the ideas above.
DECWRL results, presented at an early WWW conference.
Marchiori M & Latora V, "Harmony in the small world". Private communication 1999. Later published in Physica A, vol. 285 (pages 539--546), 2000.
Jon Kleinberg, The small-world phenomenon: An algorithmic perspective. Cornell Computer Science Technical Report 99-1776, October 1999. (ps, In)
Daniel A. Menascé et al., Fractal Characterization of Web Workloads,
Things which turned up later, not necessarily referencing this.
T. Berners-Lee and L.Kagal, The Fractal Nature of the Semantic Web AI Magazine, 2007.
Tim Berners-Lee, "Its just like a bag of chips", in Gov 2.0 Expo 2010. Now a Design Issues Article.
Joab Jackson, Berners-Lee deconstructs a bag of chips IT World, May 27, 2010
Paul Barford and Sally Floyd, Self-similarity and long range dependence in networks" web site.
Clay Shirky,Power Laws, Weblogs, and Inequality
Kottke, Weblogs and power laws, February 09, 2003 at 06:39 pm. Distribution of links to the top blogs follows a power law.
Richard McManus, Fractal Web applied to Blogging, January 15, 2004. "As you have seen, the Tim Berners-Lee interview [with Christopher Lydon] has inspired me to think and write about how I can improve my 'fractibility' (if there is such a word)!)"
Thomas Heatherwick, "Humanize: A Maker's Guide o Designing Our Cities", Simon & Schuster, 2023, "It should unfold like a fractal, revealing more of itself the closer you get to it" - p350