A couple of times people have refereed my to the Conceptual Graphs work. Mary Keeler came deliberately from a CG conference bearing the message of how the Semantic Web was really just Conceptual Graphs - or vice versa. However, the articles I looked over at that point didn't give me a good sense of what CGs were about - apart from a fervent desire to implement some ideas of Charles S. Peirce. I think the tendency of the CG examples to relate to natural language rather than hard logic made it more difficult for someone of my own leanings toward rigid logical processing for the Sweb to understand what the CG folks were driving at. Anyway, on 2001/1/5, I found a pointer John Sowa's "the CG Standard", and read through it. It now seems clear that CGs stand -- as their spec says - very much on a level with KIF. They are a logic, which has a tradition of being visualized in circles-and-arrows diagrams extended to new depths, but a logic all the same, which includes, as the Semantic Web should, higher order logic. And so -- here are a few comments about the comparison.
To put it in a nutshell, Conceptual Graphs (CGs) are a logic language used for describing closed worlds of logic. They have traditionally had a strong emphasis on two-dimensional graphical representations, but there are conventional serializations, one "Linear Form" much comparable with N3, and one CG Interchange Format (CGIF) which is more official. With various pros and cons, they are basically as expressive as KIF -- and so in way only have to be webized to a basis for the Semantic Web.
Here I go over a few differences and similarities between CGs and Semantic Web work based on RDF.
I will ignore completely "nonsemantic information" ([1], sec2 ) in this short comparison.
Let's take the principles of webizing a language and look at how that applies to CGIF or LF, to imagine a semantic web based on CGIF.
The first thing we clearly have to so is modify the CG syntaxes so that each concept and each relation can be a first class object, by having a URI. The syntax modification is just to allow the characters in a URI to be included, so that an arbitrary concept can be referenced, or an arbitrary relation used. A typical way to map URI space to CG identifiers would be to make URI of a CGIF identifier a concatenation of the URI of the CGIF document, and a hash sign and the local CG identifier -- making the local exsting identifier a fregament identifier in URI terms.
Having mentally webized the language, then the question is how such a semantic web language maps onto say languages. This is simplified by the fact that the CG spec [1] gives a mapping to KIF.
CG and RDF share concept of type. CGs have the restriction that that the worlds of concepts and types, and that of relationships and relationship types, are disjoint. Therefore, you cannot use a CG to express something about a relation using a relation. If one wanted a true bidirectional mapping, then CGs would have (it seems at first reading) to more or less reify -- to describe at a meta level - an arbitrary RDF graph. However, this would not in my opinion be useful. The designers of CGs intended this disjunction, and so the natural mapping is directly from CG concept types to RDF Classes, and from CG relations to Properties, and from CG Relation Types to RDF Classes which are subclasses of rdf:Property.
The semantic web logic language has to be universal in that it must allow expression of any other language; but it certainly does not force every language to be universal itself.
The CG concept of a knowledge base (KB) contains a few centralized ideas. These are not in fact architectural problem with CGs - they are just engineering decisions which were made without the web scaling requirement. Removing does no damage the CG idea at all.
The main difference which stands out at first reading is that RDF properties are always dyadic, while CG relations are monadic.
The RDF base model, and the N3 method of extending it to a logical framework, seem to be supported as a base structure, although the lack of N-ary forms shows up as a mismatch, but the existence of arcs explicitly in the CG model of an N-adic relation suggests a natural mapping back into dyadic RDF when n>2. This just leaves a little tension as the two forms coexist.
The CG world is a bipartite graph - one composed of two relations and concepts, which are disjoint. The RDF world, while it does consist of links which can be thought of as going from thing, via a property, to a thing, does not make properties and things disjoint. Everything is a Thing.
Some similarities of the CG work and the semantic web to date are striking. Both are inspired largely by circles and arrows diagrams, and in LF and N3 this even shows though in some syntactic forms. People have through the ages been writing circles and arrows on whatever material they had to hand [Enquire, cavewriting] and in N3 I tried to take this very simply into unicode with
w3c:Michael >- org:member -> w3c:team .
There was a certain feeling of recognition on seeing John Sowa's
[Go]- (Agnt)->[Person: John] (Dest)->[City: Boston] (Inst)->[Bus].
which in N3 would be
@prefix : <#>. [a :Go] >- :agent -> [a :Person; = <#John>]; >- :dest -> [ a :City; = <#Boston>]; >- :inst -> [ a :Bus].
remarkable down to the final period. Both syntaxes also have backward arrows a <- (p) <- b in CG's LF, and a<-p-<b in N3. (See also: the same in RDF)
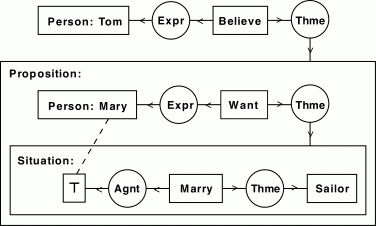
The concept of "context" occurs very equivalently in CGs and N3, where in both cases a formula is built using quotation. In N3, the braces were introduced to encapsulate a set of information and talk about it as a set. Using an example from [1], loosely "Tom believes that Mary wants to marry a sailor":
[Person: Tom]<-(Expr)<-[Believe]->(Thme)-
[Proposition: [Person: Mary *x]<-(Expr)<-[Want]->(Thme)-
[Situation: [?x]<-(Agnt)<-[Marry]->(Thme)->[Sailor] ]].
In N3 this would be, mapping dyadic relations to RDF properties,
<#Tom> a :Person; :believes [a :Proposition; = {
<#Mary> a :Person; :wants [ a :Situation; = {
<#Mary> :marriedTo [ a :Sailor ]
]}
]}.
(In the above, the "=" is an statement of equivalence which makes up for the inability otherwise of N3 syntax to allow an anonymous context to be subject and object of a statement.) In RDF, my own style is to assume that often the type of a thing, when it can be deduced from the predicate's range or domain, should not be stated explicitly. For example, the object of any believes may be a proposition, and the object of any wants may be a situation. So an N3 expression of the above in practice might be more like:
<#Tom> :believes {
<#Mary> :wants {
<#Mary> :marriedTo [ a :Sailor ]
}
}.
Leaving aside the question of whether this is a good model for the English sentence, and a lot of philosophy and linguistics (which I generally avoid by not trying to express natural language). The CG world often uses diagrams, such as this one from [1] to describe the above formula:

In N3, the circle-and-arrow diagram I would draw would include an arrow from the rectangle for the situation to the [circle] for the marriage to indicate that there is a universal quantification there.
There are other mappings which once could made, none of which give quite such a neat result. One mapping of CGs to RDF would map the CG arcs to RDF properties, which for the above would be:
[ a :Belief;
:expr <#Tom>;
:thme: [ a Proposition; = {
[ a :Want;
:expr <#Mary>;
:thme [ a :Situation; = {
[ a :Marriage; :agent <#Mary>; :thme: [a :Sailor]]
}
]
}]
].
In English this would be, "There is a belief, experienced by Tom, that "there is a want, felt by Mary, that there should be a situation: ``Mary is married to a Sailor'' ".
I have not gone into the comparison in great detail in this area. Both N3 and CFIF have existential and universal quantification, though the universal quantification is declared an area of the spec under development called "defined quantifiers". Both have, like RDF, implicit existential quantification from anonymous nodes.
A question I did not resolve in CGIF if how one can determine the scope of a quantifier introduced using the "?x" and "*x" terminology. There was a clarification in [1] that (I think) universal quantifiers have a higher scope than existentials of the same scope -- the same convention as in N3. In N3 in the model one has to link the quantified variable directly to its scope context using a log:forAll or log:forSome statement.
N3 has no Lambda as such. Once can write out a double implication define the meaning of a new term (Property or small set of related properties) by giving a double implication with the equivalent formula, using universally quantified variables for the formal parameters.
The issues faced in the two designs do a appear to have a high overlap. The semantic web has to work also in an open context, defining the meaning, if any, of a nested expression when referred to out of context.
Conceptual Graphs are easily integrated with the Semantic Web as it is, the mapping being apparently very straightforward. The export of a CG in CGIF or LF into N3 looks to be a suitable exercise for the reader ;-). An interesting and more challenging exercise would be to build a CG machine -- and a modified CG syntax -- which can import a graph containing URIs which reference external concepts. The problem that relation types in CGs are not concepts is not huge, as there are many systems - especially ontological systems -which have a similar restrictions and with whom interchange would be possible.
There is an interesting subset of CGs, called "simple graph" which are all one context, with no negations or "defined quantifiers", but which can contain universal quantifiers, and these map directly into the RDF M&S 1.0, or N3 without braces.
The RDF base model, and the N3 method of extending it to a logical framework, seem to be supported as a base structure, although the lack of N-ary forms shows up as a mismatch.
All in all, there is a huge overlap, making the two technologies very comparable and hopefully easily interworkable.
| CG | RDF/N3 | Comment |
| concept | resource/node | |
| relation | Property | In RDF, Properties are only dyadic; inCG, relations are n-adic |
| type | Class | In RDF, "type" is the Property stating membership of resource in a Class. |
| arc | Property - for N>3 | Arcs in CG are used to model nadics in terms of dyadics, a la RDF. An arc is considered a pair, rather than a triple. It has a small integer associated with it (cf XLink role, or rdf:1, rdf:2 etc) |
| context | context (N3 only) | Remarkable coincidence of terms |
| coreference | daml:equivalent/ = | Rather complex CG architecture for a simple function? In CG, a coreference set (a form of equivalence class) has a single defining ("dominant") concept. This makes the equivalence not completely symmetrical. Perhaps it is simply useful in practice to use a dominant concept as a name for the coreference set. |
| actor | - | Philosophical difference: in SWeb, real world is linked directly to things and properties, rather thn have another layer of represnetation. In CGs, links to "reality" are represented as separate from the main CG. |
| abstract syntax | model | |
| identifiers | URI | CGIF identifiers are NOT case sensistive. URIs and XML IDs are. (This was a result of difficulty in specifying case insenistivity in a international way.) |
| knowledge base | A consistent self-contained set of types, | |
| Linear Form | N3 | Syntaxes introiduced for human readability, both driven by the need to serialize circles and arrows diagrams showing though in the syntax (>- agent -> bus .) and coincidentally similar uses of [] and . as delimiters |
| signature | range, domain | As RDF's properties are only diadic, the signature is range and domain. More importantly philosophically, a lambda expression has a sole definitive signature, whereas about Properties there may exist defintive and third party statements about their range and domain. |
[1] John F. Sowa, ed. "Conceptual Graph Standard", ["standard" state of which I am not certain. Some parts are labelled under deveopment].
[2] John F. Sowa, Conceptual Graphs, web page
Related DesignIssues: