Conventions:
*** Discussion Parts will be color-coded in blue. ***
*** Comments/Issues will be color-coded in green. ***
Abstract Model for RIF
The main motivation for defining an abstract model for RIF is extensibility. The idea behind extensibility based on a common abstract model is motivated by the following proposed definition of the notion of a dialect:
- a dialect MUST restricts/define which parts of the abstract model you are allowed to use in its instance rulesets and how.
- a dialect MUST assign a semantics to this restricted part (model-theoretic, proof-theoretic, operational in that order of preference)
- a dialect MAY assign "roundtrippable" own syntaxes (for instance, BLD defines a represenation syntax as well as an XML syntax) and even define the semantics in terms of one of those special syntaxes (for instance BLD's semantics is defined in terms of its representation syntax).
- BLD should define a minimal dialect and other dialects MUST agree with the semantics of BLD on the part of the abstract model they share with BLD.
Several formal restrictions on a dialect are not straightforward to be expressed in an XML Schema. For instance, a dialect defined in terms of an XML syntax, which is a restriction of BLD may not be easy trivial to be defined in terms of an XML Schema (e.g. non-recursive Datalog), whereas we expect such restrictions to be expressible in terms of restricted usage of the abstract model. Similar considerations apply when we want to speak about dialect intersections, unions, etc. which are easy to define in terms of intersections and unions of dialect-specific restrictions on abstract model.
In order to enable this, the present page shall illustrate a simplified basic model of RIF in OWL and RDF(S) that shall allow such generic definitions of dialects.
The abstract model proposed is derived from the RIFRAF, several proposed abstract syntaxes asn06, asn07, a-EBNF, basic UML diagrams and an initial version of an OWL ontology for RIF proposed earlier. This proposal is motivated by the fact that the working group has not yet achieved consensus which of those previous proposals should serve as the basis for a RIF abstract model, which could serve as a basis for dialect extensions or restrictions of BLD.
We take the following starting points:
- We introduce a simple RDFS/OWL ontology to describe metadata concepts and attributes for describing rulesets in a certain dialect.
We define a dialect in terms of constraints over instance RDF graphs which represent such rule sets. This has the nice side-effect that we thereby define an RDF syntax for RIF dialects as a by-product.
- We define mappings back and forth between the RDF graphs complying to the defined dialect restrictions and RIF BLD/XML documents.
- We define a sample new dialect (stratified Datalog) to illustrate the approach.
We focus here on BLD to illustrate the general ideas of the proposed model but plan to extend the abstract model towards other dialects such as [PRD] later on.
Abstract RDFS ontology for RIF
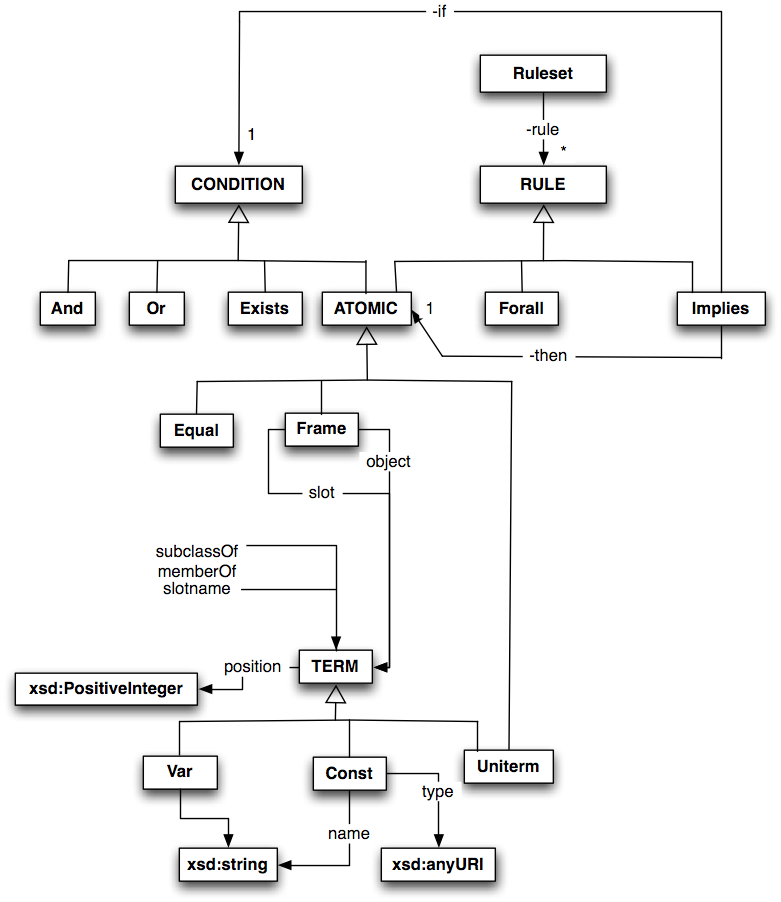
In order to get to an RDFS/OWL ontology for the abstract model of RIF, we start off from the Abstract UML diagrams for RIF BLD Conditions

and RIF BLD Rulesets

I take Christian's Ruleset model as a starting point, as resolved at F2F7.
A simple translation of these models into OWL/RDFS lets us end up with the following simple model:
@prefix : <http://www.w3.org/2007/rifAbstractModel#> @prefix rdf: <http://www.w3.org/1999/02/22-rdf-syntax-ns#> @prefix rdfs: <http://www.w3.org/2000/01/rdf-schema#> @prefix owl: <http://www.w3.org/2002/07/owl#> @prefix <http://www.w3.org/2001/XMLSchema#> # Classes and properties of the original abstract condition model: :CONDITION a rdfs:Class. :And rdfs:subclassOf :CONDITION. :Or rdfs:subclassOf :CONDITION. :Exists rdfs:subclassOf :CONDITION. :ATOMIC rdfs:subclassOf :CONDITION. :Equal rdfs:subclassOf :ATOMIC. :Uniterm rdfs:subclassOf :ATOMIC. :TERM a rdfs:Class. :Uniterm rdfs:subclassOf :TERM. :Var rdfs:subclassOf :TERM. :Const rdfs:subclassOf :TERM. :formula a owl:ObjectProperty. :formula rdfs:domain [ owl:unionOf ( :And :Or :Exists :Forall) ]. :formula rdfs:range :CONDITION. :arg a owl:ObjectProperty. :arg rdfs:domain :Uniterm. :arg rdfs:range :TERM. :declare a owl:ObjectProperty. :declare rdfs:domain [ owl:unionOf ( :Exists :Forall ) ]. :declare rdfs:range :Var. # Shall Vars in a declare also possibly be ordered? :side a owl:ObjectProperty. :side rdfs:domain :Equal. :side rdfs:range :TERM. :op a owl:ObjectProperty. :op rdfs:domain :Uniterm. :op rdfs:range :Const. # Classes and properties of the original abstract ruleset model: :Ruleset a rdfs:Class. :RULE a rdfs:Class. :Forall rdfs:subClasOf :RULE. :Implies rdfs:subclassOf :RULE. :ATOMIC rdfs:subclassOf :RULE. :rule a owl:ObjectProperty. :rule rdfs:domain :Ruleset. :rule rdfs:range :RULE. :if a owl:ObjectProperty. :if rdfs:domain :Implies. :if rdfs:range :CONDITION. :then a owl:ObjectProperty. :then rdfs:domain :Implies. :if rdfs:range :ATOMIC.
In order to represent actual rule metadata we miss properties to denote constant names, variable names and datatypes, which are present in the current EBNF syntax, but not in the UML models. We there fore extend the vocabulary defined so far as follows:
:name a owl:DataTypeProperty. :name rdfs:domain [ owl:unionOf ( :Var :Const ) ]. :name rdfs:range xsd:String. :type a owl:DataTypeProperty. :type rdfs:domain :Const. :type rdfs:range xsd:anyURI.
Not sure whether anyURI is appropriate here, but I took it in absence of a simple type for IRIs
In principle this vocabulary should allow us to losslessly represent each RIF BLD Ruleset as a an RDF Graph (ie. a set of RDF triples). However, we observe that this model is
- overspecific in terms of later generalizations, extensions beyond the basic model, particularly slotted syntax and dialects extending BLD.
- incomplete in disambiguating certain features of the UML diagram, such as for instance ordering of arguments in TERMs and cardinalities of certain properties.
- incomplete in terms of specifying the constraints which apply for RDF Graphs specifying valid BLD Conditions and Ruleset.:op
- unnecessarily complex usign OWL specific constructs, although OWL itself is not appropriate as such to express constraints over closed rulesets.
Didn't yet think about disambiguation of Built-ins or e.g. Lists in the abstract model.
In order to address 1. and 2. we suggest the following modification to the model:
Introduce generic superclasses in favor of owl:unionOf constructs.
Allow arguments of Uniterms being :named.
- Introduce generic position property to denote order of certain attributes (e.g. arguments, formulas).
Thus, we remove the following statements in the above model:
:formula rdfs:domain [ owl:unionOf ( :And :Or :Exists :Forall) ].
:declare rdfs:domain [ owl:unionOf ( :Exists :Forall ) ].
:name rdfs:domain [ owl:unionOf ( :Var :Const ) ].
:type rdfs:domain :Const.
in favor of the following:
:QUANTIFIEDFORMULA rdfs:subclassOf :FORMULA. :CONDITION rdfs:subclassOf :FORMULA. :formula rdfs:domain :FORMULA. :formula rdfs:range :FORMULA. :Forall rdfs:subclassOf :QUANTIFIEDFORMULA. :Exists rdfs:subclassOf :QUANTIFIEDFORMULA. :declare rdfs:domain :QUANTIFIEDFORMULA. :TYPEDENTITY a rdf:Class. :NAMEDENTITY a rdf:Class. :ORDEREDENTITY a rdf:Class. :Var rdfs:subclassOf :NAMEDENTITY. :Const rdfs:subclassOf :NAMEDENTITY. :Const rdfs:subclassOf :TYPEDENTITY. :name rdfs:domain :NAMEDENTITY. :type rdfs:domain :TYPEDENTITY. :position a owl:DataTypeProperty. :position rdfs:domain :ORDEREDENTITY. :position rdfs:range xsd:positiveInteger. # Arguments can be ordered and/or have a slotname (slotted arguments): # ie. we don't make a difference in the abstract model between "slot" and "argument" :TERM rdfs:subclassOf :ORDEREDENTITY. :slotname rdfs:domain :TERM. :slotname rdfs:range :TERM. # We treat here Frames as special :Uniterms :Frame rdfs:subclassOf :ATOMIC. :object rdfs:domain :Frame. :object rdfs:range :TERM. :slot rdfs:domain :Frame. :slot rdfs:range :TERM. :subclassOf rdfs:domain :TERM. :subclassOf rdfs:range :TERM. :memberOf rdf:domain :TERM. :memberOf rdf:range :TERM. ## Should ordered rulesets be foreseen here? # Formulae can be ordered within a ruleset/conjunction/disjunction, etc.: # :FORMULA rdfs:subclassOf :ORDEREDENTITY. ## Should ordered-relevance of Variables in a :declare be foreseen here? # :Var rdfs:subclassOf :ORDEREDENTITY.
I am not entirely happy with the :ORDEREDPROPERTY class. Alternatively, we could (maybe better remove :ORDEREDENTITY and replace it by :ORDEREDPROPERTY, then we could make :arg rdfs:subProperyOf of :ORDEREDPROPERTY. :rule rdfs:subProperyOf of :ORDEREDPROPERTY. etc. and adapt the constraints below such that each value of an :ORDEREDPROPERTY needs to have exactly one :position associated and positions need to be consecutive, etc. |
Note we generalized the :formula property to a more general use than originally, e.g. now it would be allowed that an :And formula has an :Forall formula assigned as conjunct which is beyond BLD, or that an ATOMIC formula has :formula properties defined, which meaning is not really clear from the abstract model.
- Nonetheless, this is in spirit of the notion of a generic abstract model, where dialect specific restrictions are specified separately.
We will later on forbid the improper use of the :formula property by adding respective, dialect specific constraints.
- In order to carry naming and argument order information for slots and unordered arguments explicit, we introduce the
:position and :slotname attributes for :TERMs. Note that allowing arbitrary terms as slotnames is beyond BLD, but allowed in extensions of F-Logic, thus we picked this in order to enable extensibility of the model later on.
In order to address 3. and 4., we will get rif of OWL specific constructs and thus end up in a pure RDFS model. However we still need to formulate the formal constraints on RDF graphs which represent valid RIF BLD rulesets. In absence of a proper constraint language for RDF or OWL (see e.g. [1]), we will explore 3 different ways to express dialect specific constraints in terms of either
- sets of SPARQL ASK queries,
RIF conditions on the RDF graph (assuming an embedding of the abstract instance Graph of a ruleset in RIF following the SWC document), or
- OWL axioms read as constraints, following the semantics of [1].
Constraints on the abstract model
Constraints specifying valid BLD Datasets:
- No allquantified formulae are allowed as :CONDITIONs in BLD:
- As SPARQL boolean query:
ASK { ?f a :CONDITION . ?f a :Forall .}should return 'no'.Note that this is not optimal: :CONDITION membership triples needn't be explicitly given in the RDF graph, assuming that in the RDF serialization we keep the convention not to mention the capitalized "keywords". Thus, we'd need to take inferred RDF triples as well into account, ie. I would need to refer to SPARQL with more than simple RDF underneath. There are engines allowing to add RDFS entailment rules, similar to the ones mentioned by Jos, but this is not (yet) standardized. Alternatively, we could define constraints and conditions on RIF/RDF graphs in RIF itself, but we' need a dialect with negation as failure for that, see the queries below where we use SPARQL's !Bound heavily to emulate NAF, or where inequality '!=' is used in the CWA sense of inequality.
- As a RIF condition:
Forall ?f ( notok :- ( And ( ?f[ rdf:type -> :CONDITION ] ?f[ rdf:type -> :Forall ] ) ) )
We use the following notation for expressing constraints on the abstract model as RIF conditions: We will use naf to denote negation as failure: Although not present in BLD we need naf to represent some conditions. We will use the local constant notok to denote that a constraint has been violated.
- In an OWL Axiom, read as constraint:
:CONDITION ∩ :Forall ⊆ ⊥
- As SPARQL boolean query:
- Each Equality has exactly two sides specified:
- As SPARQL boolean queries:
# Test whether there are less than two sides: ASK { ?e a :Equal . OPTIONAL { ?e :side ?left ; :side ?right . FILTER (?left != ?right) } FILTER (!Bound(?left) ) } # Test whether there are more than two sides: ASK { ?e :side ?s1, ?s2, ?s3 . FILTER (?s1 != ?s2 && ?s2 != ?s3 && ?s2 != s3) } }should both return 'no'. - As a RIF condition:
Forall ?e ?left ?right ( hasAtLeastTwoSides(?e) :- And( ?e[:side->?left, side->?right] naf(?left = ?right) ) ) Forall ?e ?s1 ?s2 ?s3 ( hasMoreThanTwoSides(?e) :- And( ?e[:side->?s1, side->?s2, side->?s3] naf(?s1 = ?s2) naf(?s1 = ?s3) naf(?s2 = ?s3) ) ) Forall ?e ( notok :- And (?e[rdf:type -> :Equal] Or ( naf(hasTwoSides(?e) hasMoreThanTwoSides(?e) ) ) )
- In an OWL Axiom, read as constraint:
:Equal ⊆ =2 :side
- As SPARQL boolean queries:
Each :Uniterm has exactly one :op which is a :Const.
- As SPARQL boolean queries:
# Test whether there is a :Uniterm without :op ASK { ?u a :Uniterm. OPTIONAL { ?u :op ?o . } FILTER (!Bound(?o) ) } # The :op property is functional: ASK { [ :op ?o1, ?o2] . FILTER (?o1 != ?o2) } } # Test whether there is a non-{{{:Const}}} {{{:op}}}: ASK { ?u :op ?o. OPTIONAL { ?o1 a :Const . FILTER(?o = ?o1) . } FILTER (!Bound(?o1) ) }should all return 'no'. - As a RIF condition:
Note: The hasNonConstOp rule has to be evaluated under at most RDF embedding, if RDFS semantics is adopted the last rule is redundant by the range inference! Could be maybe avoided, if domain and range are not at all specified for explicit (non-abstract, ie. non-all-uppercase) classes in the RDFS ontology.
Forall ?u ?o ( hasOp(?u) :- ?u[:op->?o] ) Forall ?u ?o1 ?o2 hasAtLeastTwoOps(?u) :- And( ?u[:op->?o1, :op->?o2] naf(?o1 = ?o2) ) ) Forall ?u ?c hasNonConstOp(?u) :- And( ?u[:op->?c] naf(?c[rdf:type Const] ) Forall ?u notok :- Or( hasNonConstOp(?u) hasAtLeastTwoOps(?u) And( ?u[rdf:type->:Uniterm] naf(hasOp(?u)) ) )
- In an OWL Axiom, read as constraint:
:Uniterm ⊆ =1 :op ∩ &forall :op . :Const
- As SPARQL boolean queries:
The :name property is functional:
- As SPARQL boolean queries:
ASK { [ :name ?n1,?n2 ]. FILTER( ?n1 != ?n2 ) }should return 'no'. - As a RIF condition:
Forall ?x ?n1 ?n2 notok :- And( ?x[:name->?n1,:name->?n2] naf(?n1 = ?n2) )
- In an OWL Axiom, read as constraint:
&Tau ⊆ ≤1 :name
- As SPARQL boolean queries:
The :type property is functional:
- As SPARQL boolean queries:
ASK { [ :type ?t1,?t2 ]. FILTER( ?t1 != ?t2 ) }should return 'no'. - As a RIF condition:
Forall ?x ?t1 ?t2 notok :- And( ?x[:type->?t1,:type->?t2] naf(?t1 = ?t2) )
- In an OWL Axiom, read as constraint:
&Tau ⊆ ≤1 :type
- As SPARQL boolean queries:
Each :arg of a :Uniterm has a :position and all positions are differently numbered from 1 upwards.
- As SPARQL boolean queries:
# Test whether there is an :arg without position. ASK { ?u :arg ?a. OPTIONAL { ?a :position ?p . } FILTER (!Bound(?p) ) } # Test whether there are two :args with the same position. ASK { ?u :arg ?a1,?a2. ?a1 :position ?p . ?a2 :position ?p .FILTER( ?a1 != ?a2 ) } # Test whether there is an :arg with the two different positions. ASK { ?u :arg [ :position ?p1,?p2 ]. FILTER( ?p1 != ?p2 ) } # Test whether, given that there are args, one has position 1: ASK { ?u :arg ?a. OPTIONAL { ?u :arg ?a1. ?a1 :position 1 . } FILTER ( !Bound(?a1) ) } # Test whether, given that there are args, each position is a positive integer: ASK { ?u :arg [ :position ?p ] FILTER (!xsd:positiveInteger(?p) ) } # Test whether, given that there are args, all positions are consecutive: ASK { ?u :arg ?a. ?a :position ?p1,?p2 FILTER (?p1 - ?p2 > 1) OPTIONAL {?u :arg ?a :position ?p3 FILTER( ?p3 = ?p1 - 1 ) } FILTER( !Bound(?p3) ) }should all return 'no'. - As a RIF condition:
Forall ?a ?p hasPosition(?a) :- ?a[:position->?p] Forall ?a1 ?a1 ?p ?u hasTwoSamePosArgs(?u) :- And( ?u[:arg->?a1,:arg->?a2] naf(?a1 = ?a2) ?a1[:position->?p] ?a2[:position-?p] ) Forall ?a ?p1 ?p2 ?u hasTwoPosArg(?u) :- And( ?u[:arg->?a[:position->?p1,:position->?p2]] naf(?p1 = ?p2) ) Forall ?u ?a hasPositionOne(?u) :- ?u[:arg->?a[:position->1]] # Test whether, given that there are args, each position is a positive integer: # Can only be expressed if we have built-ins or typed literals! We assume the former # for the moment, denoting built-in calls by '&' : Forall ?u ?a ?p hasNonPosIntegerPositionArg(?u) :- And( ?u[:arg->?a[:position->?p] naf(&xsd:positiveInteger(?p))) Forall ?u ?a ?a1 ?a2 ?a3 ?p1 ?p2 ?p3 hasNonConsecutiveArgs(?u) :- And( ?u[:arg->?a[:position->?p1,:position->?p2] &op:numeric-greater-than(&op:numeric-subtract( ?p1 ?p2 ) 1 ) ?p3 = &op:numeric-subtract( ?p1 1 ) naf hasArgWithPos(?u,?p3) Forall ?u ?a ?p hasArgWithPos(?u,?p) :- ?u[:arg->?a[:position->?p Forall ?u ?a notok :- And(?u[:arg->?a] Or( naf(hasPosition(?a)) hasTwoSamePosArgs(?u) hasTwoPosArg(?u) naf(hasPositionOne(?u)) hasNonPosIntegerPositionArg(?u) hasNonConsecutiveArgs(?u) ) ) - In an OWL Axiom, read as constraint:
- ** Can only be partially represented in the Form of OWL constraints ***
- As SPARQL boolean queries:
- Check that predicate and function names should be disjoint.
- As SPARQL boolean queries:
# Test whether there is a Uniterm in predicate position (:formula) and a Uniterm in a term position (:arg) with the same operator name. ASK { [ :formula [ :op [ :name ?n ] ] ] . [ :arg [ :op [:name ?n] ] ] . } # Test whether there are two Uniterms with the same operator names, but different arities # (just check whether a position occurs in one which doesn't occur in the other). ASK { ?u :op [:name ?n]; :arg [ :position ?p. ] ?u1 :op [:name ?n] FILTER( ?u != ?u1) OPTIONAL { ?u1 :arg [ :position ?p1. ] FILTER( ?p = ?p1 ) } FILTER( !Bound(?p1) ) }should both return 'no'.For these two constraints, do we actually only need to check same :Const :names or also same operator :types? In the latter case, we'd need to extend the checking queries slightly.
- As a RIF condition:
Forall ?f ?g ?h ?o1 ?n ?a ?o2 notok :- And( ?f[:formula->?g[:op->?o1[:name->?n]]] ?h[:arg->?a[:op->o2[:name->?n]]] ) Forall ?u ?u1 ?o ?o1 ?p notok :- And( ?u[:op->?o[:name->?n]] ?u1[:op->?o1[:name->?n]] hasArgWithPos(?u,?p)) naf(hasArgWithPos(?u1,?p)) ) - In an OWL Axiom, read as constraint:
- ** can't be represented in the Form of OWL constraints ***
- As SPARQL boolean queries:
The :formula attribute is functional for :QUANTIFIEDFORMULAs
- As SPARQL boolean queries:
ASK { [a :QUANTIFIEDFORMULA; :formula ?f1,?f2 ]. FILTER( ?f1 != ?f2 ) }should both return 'no'.Note that this needs RDFS inference before the SPARQL query is evaluated, since membership in :QUANTIFIEDFORMULA is inferred
- As a RIF condition:
Forall ?q ?f1 ?f2 notok :- And( ?q[rdf:type->:QUANTIFIEDFORMULA,:formula->?f1,:formula->?f2] naf(?f1 = ?f2) )
- In an OWL Axiom, read as constraint:
&:QUANTIFIEDFORMULA ⊆ ≤1 :formula
- As SPARQL boolean queries:
All variables occurring on :RULEs need to be quantified. If we want to formalize that, that would need to add some recursive metadata definitions of a new properties :occurringInRule and :scopes in the abstract model ontology:
:occursIn a rdfs:Property. :occursIn rdfs:domain :Var. # ?v :occurrsInRule ?r needs to be defined in the sense that it reflects ' ?v occurs in a subTERM in ?r ' ". :scopes a rdfs:Property. # The first Var is the declared Variable in a :QUANTIFIEDFORMULA :scopes rdfs:domain :Var. # The second Var is the Variable in scope of the declared Var in a subterm of a subformula. :scopes rdfs:range :Var. # ?v :occursIn ?r needs to be defined to reflect this scoping relation.
plus a constraint:Except explicitly adding those triples to the metadata, this could be done implicitly only with a rule/constraint language which allows recursive definitions of rules on top of RDF. Interestingly, RIF itself could serve for this purpose, or I could also write it down as SPARQL CONSTRUCT, following [2], if SPARQL would allow for fixppoint semantics of CONSTRUCTS (which would make SPARQL itself kind of a rule language).
- As SPARQL boolean queries:
ASK { ?v :occursIn ?r . OPTIONAL{ ?v1 :scopes ?v } FILTER !Bound(?v1).}should return 'no'. - As a RIF condition:
Forall ?v ?v[:occursIn->?v] :- ?v[rdf:type->:Var] Forall ?v ?t ?t1 ?v[:occursIn->?t] :- And( Or( ?t[:arg->?t1] ?t[:side->?t1] ?t[:formula->?t1) ?v occursIn ?t1 ) Forall ?v ?t ?t1 ?v[:occursIn->?t :- And( Or( ?t[:arg->?t1] ?t[:side->?t1] ?t[:formula->?t1) ?v occursIn ?t1 ) Forall ?q ?v ?v1 ?f ?v[:scopes->?v1] :- And( ?q[rdf:type :QUANTIFIEDFORMULA,:declares->?v[:name->?n],:formula->?f] ?v1[:name->?n,:occursIn->?f] Forall ?v ?v1 spoped(?v1) :- ?v[:scopes->?v1] Forall ?v ?v1 ?r notok :- And( ?v[:occursIn ?r[rdf:type->:RULE]], naf(scoped(?v)) )Actually, when writing this down, this raised another question: Why do we call the arguments of equals 'side' and not 'arg' like arguments in other predicates? Isn't :Equal just a special binary predicate?
- In an OWL Axiom, read as constraint:
- ** can't be represented in the Form of OWL constraints ***
- As SPARQL boolean queries:
--TBD:-- More constraints still missing:
- Several minimality cardinality constraints from the diagram are still missing
It is not allowed to declare variables with the same name twice, ie. Forall ?x ?x, or should that be ok?
- Most constraints on the usage of the frames and slotted syntax are still missing.
Interesting questions: * What happens if a dialect adds additional metadata? Shall transformations to BLD ignore it or report an error or what? How can non-existence of additional medadata be checked?
Modified Abstract Model Diagram
*** under progress ***
From XML to RDF
The translation from the XML syntax to RDF is given by the tables as follows. We use the following notation here: <i>newBlank</i> is a new unique blank node identifier to be generated by the translation, and by <i>blankFor<strong>X</strong></i> we denote the respective new blanknode identifier obtained from translating <i><strong>X</strong></i>.
(To be very correct, maybe we should in the end add that the translation should add statements #!html _:blank<sub>i</sub> owl:differentFrom _:blank<sub>j</sub>. for all newly generated blankNodes?) |
| Presentation Syntax | XML Syntax | RDF Triples |
|---|---|---|
And (
conjunct1
. . .
conjunctn
) | <And> <formula>conjunct1</formula> . . . <formula>conjunctn</formula> </And> |
@prefix : <http://www.w3.org/2007/rifAbstractModel#> _:newBlank a :And. _:newBlank :formula _:blankForconjunct1. . . . _:newBlank :formula _:blankForconjunctn. |
Or ( disjunct1 . . . disjunctn ) | <Or> <formula>disjunct1</formula> . . . <formula>disjunctn</formula> </Or> |
_:newBlank a :Or. _:newBlank :formula _:blankFordisjunct1. . . . _:newBlank :formula _:blankFordisjunctn. |
Exists
variable1
. . .
variablen (
body
) | <Exists> <declare>variable1</declare> . . . <declare>variablen</declare> <formula>body</formula> </Exists> |
_:newBlank a :Exists. _:newBlank :declare _:blankForvariable1. . . . _:newBlank :declare _:blankForvariablen. _:newBlank :formula _:blankForbody. |
predfunc (
argument1
. . .
argumentn
) | <Uniterm> <op>predfunc</op> <arg>argument1</arg> . . . <arg> argumentn</arg> </Uniterm> |
_:newBlank a :Uniterm. _:newBlank :op _:blankForop. _:newBlank :arg _:blankForargument1. _:blankForargument1 :position 1. . . . _:newBlank :arg _:blankForargumentn. _:blankForargumentn :position n. |
left = right | <Equal> <side>left</side> <side>right</side> </Equal> |
_:newBlank a :Equal. _:newBlank :side _:blankForleft. _:newBlank :side _:blankForright. |
name^^space |
<Const type="space">name</Const> |
_:newBlank a :Const. _:newBlank :name "name". _:newBlank :type "space". |
?name | <Var>name</Var> |
_:newBlank a :Var. _:newBlank :name "name". |
predfunc (
key1 -> filler1
. . .
keyn -> fillern
) | <Uniterm> <op>predfunc</op> <slot>key1 filler1</slot> . . . <slot>keyn fillern</slot> </Uniterm> |
_:newBlank a :Uniterm. _:newBlank :op _:blankForop. _:newBlank :arg _:blankForfiller1. _:blankForfiller1 :slotname _:blankForkey1. _:blankForfiller1 :position 1. . . . _:newBlank :arg _:blankForfillern. _:blankForfillern :slotname _:blankForkeyn. _:blankForfiller1 :position n. |
inst [
key1 -> filler1
. . .
keyn -> fillern
] | <Frame> <object>inst</object> <slot>key1 filler1</slot> . . . <slot>keyn fillern</slot> </Frame> |
_:newBlank a :Frame. _:newBlank :object _:blankForinst. _:newBlank :slot _:blankForfiller1. _:blankForfiller1 :slotname _:blankForkey1. . . . _:newBlank :arg _:blankForfillern. _:blankForfillern :slotname _:blankForkeyn. |
inst # class [
key1 -> filler1
. . .
keyn -> fillern
] | <Frame>
<object>
<Member>
<lower>inst</lower>
<upper>class</upper>
</Member>
</object>
<slot>key1 filler1</slot>
. . .
<slot>keyn fillern</slot>
</Frame> |
_:newBlank a :Frame. _:newBlank :object _:blankForinst. _:blankForinst :memberOf _:blankForclass. _:newBlank :slot _:blankForfiller1. _:blankForfiller1 :slotname _:blankForkey1. . . . _:newBlank :arg _:blankForfillern. _:blankForfillern :slotname _:blankForkeyn. |
sub ## super [
key1 -> filler1
. . .
keyn -> fillern
] | <Frame>
<object>
<Subclass>
<lower>sub</lower>
<upper>super</upper>
</Subclass>
</object>
<slot>key1 filler1</slot>
. . .
<slot>keyn fillern</slot>
</Frame> |
_:newBlank a :Frame. _:newBlank :object _:blankForsub. _:blankForsub :subclassOf _:blankForsuper. _:newBlank :slot _:blankForfiller1. _:blankForfiller1 :slotname _:blankForkey1. . . . _:newBlank :arg _:blankForfillern. _:blankForfillern :slotname _:blankForkeyn. |
inst # class | <Member> <lower>inst</lower> <upper>class</upper> </Member> |
_:blankForinst :memberOf _:blankForclass. |
sub ## super | <Subclass> <lower>sub</lower> <upper>super</upper> </Subclass> |
_:blankForsub :subclassOf _:blankForsuper. |
Ruleset (
clause1
. . .
clausen
) | <Ruleset> <rule>clause1</rule> . . . <rule>clausen</rule> </Ruleset> |
_:newBlank a :Ruleset. _:newBlank :rule _:blankForclause1. . . . _:newBlank :rule _:blankForclausen. #If we'd consider rules odered, we' additionally need to add: |
Forall
variable1
. . .
variablen (
body
) | <Forall> <declare>variable1</declare> . . . <declare>variablen</declare> <formula>body</formula> </Forall> |
_:newBlank a :Forall. _:newBlank :declare _:blankForvariable1. . . . _:newBlank :declare _:blankForvariablen. _:newBlank :formula _:blankForbody. |
head :- body | <Implies> <if>body</if> <then>head</then> </Implies> |
_:newBlank :a :Implies. _:newBlank :if _:blankForbody. _:newBlank :then _:blankForhead. |
From RDF to XML
There is no normative way to get from RDF to arbitrary XML. Probably a feasible way could be SPARQL > XSLT. Need to test the feasibility of that. The key point here is to extract a ruleset from an RDF graph.
Dialect example: RIF HiLog
Lift the restriction to constants in :op, and to unique arity? allow :TERMs in :op and :object positions, etc.
Dialect example: Datalog
Add a restriction, ie. forbid function symbols, slotted terms.
Dialect example: Datalog with stratified NAF
References
1. Boris Motik, Ian Horrocks, and Ulrike Sattler. Bridging the Gap Between OWL and Relational Databases. In Proc. of the 16th International World Wide Web Conference (WWW 2007), pages 807-816, Banff, AB, Canada, May 8-12 2007. ACM Press.
2. Axel Polleres, François Scharffe, and Roman Schindlauer. SPARQL++ for mapping between RDF vocabularies. In OTM 2007, Part I : Proceedings of the 6th International Conference on Ontologies, DataBases, and Applications of Semantics (ODBASE 2007), volume 4803 of Lecture Notes in Computer Science, pages 878-896, Vilamoura, Algarve, Portugal, November 2007. Springer.