Representing Probabilistic Knowledge
in the Semantic Web
The aim of this position paper is (1) to propose a vocabulary for representing probabilistic knowledge in RDF, and (2) to present a framework for probability calculation using RDF and Bayesian network.
Why Probability in RDF?
In the real world, especially in the scientific fields like Life Science, it is often the case that relationship between resources holds probabilistically, or we are not completely certain of some facts but only with uncertainty. Such relationships can be best described with probabilistic expression. However, there has been not a standard vocabulary for representing probabilistic relationships in RDF so far .
The aim of this position paper is (1) to propose a vocabulary for representing probabilistic knowledge in RDF, and (2) to present a framework for probability calculation using RDF and Bayesian network.
Metastatic Cancer Case (1)
Here is an example of probabilistic relationship borrowed from Pearl[1988], originally by Cooper.
Metastatic cancer is a possible cause of a brain tumor and is also an explanation for increased serum calcium. In turn, either of these could explain a patient falling into a coma. Sever headache is also possibly associated with a brain tumor.
The (conditional) probabilities are given as following:
(These tables read horizontally, for example, P(BrainTumor=TRUE | MetastaticCancer = TRUE) = 0.20.)
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
We introduced five propositions to describe this case:
| Proposition | TRUE if and only if |
|---|---|
| MetastaticCancer | The patient has a metastatic cancer. |
| SerumCalcium | The serum calcium of the patient shows an increase. |
| BrainTumor | The patient has a brain tumor. |
| Coma | The patient has fallen into a coma. |
| HeadAche | The patient has severe headaches. |
Now we are asked to get the posterior probability of each proposition, given an observation. For example, to get the probability for a patient to have a metastatic cancer who suffers from severe headaches, but not in coma.
Describing Probabilistic Knowledge
To describe such probabilistic relations in RDF, I'd like to propose the following vocabulary.
To Describe Propositions
Proposition here refers to a predicate with zero or more arguments (and modifiers). It is different from statement in that we cannot say if the content is true or not, so it is virtual or infinite in a sense.
A proposition is expressed by a blank node of type prob:Clause. A node of type prob:Clause usually takes a property prob:Predicate with a blank node of type rdf:Property as its value, which corresponds to the predicate of the proposition and zero or more properties that correspond to the arguments and modifiers.
The following is an example of the description in N3.
[ a prob:Clause;
prob:predicate ex:p;
role:foo ex:r1;
...
role:bar ex:r2
].To Describe Negations
To describe that a proposition X is a negation of a proposition Y, i.e. one is TRUE whenever the other is FALSE, create a prob:Clause node x whose prob:negationOf is a prob:Clause y.
_:x a prob:Clause;
prob:nagationOf _:y.
To Describe Unconditional Probabilities
To describe that a proposition X holds with probability P, create a prob:ProbabilisticStatement node whose prob:consequence is x and prob:hasProbability is p, where x is an instance of prob:Clause representing X and p is an instance of prob:Probability representing P.
[ a prob:ProbabilisticStatement;
prob:consequence x;
prob:hasProbability p
].To Describe Conditional Probabilities
To describe that a proposition X holds with probability P given a set of premises {Y1, ..., Yn}, create a prob:ProbabilisticStatement node that has prob:consequence x, prob:condition y_1, ..., prob:condition y_n, and prob:hasProbability is p, where x,y_1, ..., y_n are instances of prob:Clause representing X and Y1, ..., Yn respectively and p is an instance of prob:Probability representing P.
[ a prob:ProbabilisticStatement;
prob:consequence x;
prob:condition y_1;
...
prob:condition y_n;
prob:hasProbability p
].To Describe Observations
To describe that a proposition O is observed with probability P, create a prob:Observation node whose prob:proposition is o and prob:hasProbability is p, where o is an instance of prob:Clause representing O and p is an instance of prob:Probability representing P.
[ a prob:Observation;
prob:proposition o;
prob:hasProbability p
].To Describe Posteriors
To describe that a proposition X is concluded to hold with probability P,
create a prob:Belief node whose prob:consequence is x,
and prob:hasProbability is p,
accompanied by y's for each observation with label prob:observation.
Note that the observation node is of type prob:Observation, not prob:Clause.
[ a prob:Belief;
prob:consequence x;
prob:observation y;
prob:hasProbability p
].Metastatic Cancer Case (2) - Representation in RDF
Using the vocabulary above, we can represent our metastatic cancer case in RDF. For example, RDF description of the HeadAche proposition is like this:
_:HeadAche a prob:Clause;
prob:predicate ex:hasSevereHeadAche.
[ a prob:ProbabilisticStatement;
prob:consequence _:HeadAche;
prob:condition _:BrainTumor;
prob:hasProbability [a prob:Probability;
rdf:value 0.80]
].
[ a prob:ProbabilisticStatement;
prob:consequence _:HeadAche;
prob:condition _:NotBrainTumor;
prob:hasProbability [a prob:Probability;
rdf:value 0.60]
].The full description of the case is here. And this is a simplified graph for the case.
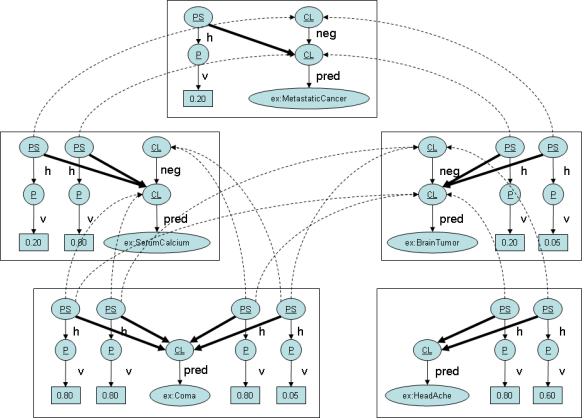
PS, CL, P, neg, pred, h, vstands forprob:ProbablisticStatement, prob:Clause, prob:Probability, prob:negationOf, prob:preditate, prob:hasProbability, rdf:valuerespectively.- a node with underlined string in it is an instance of the class whose name is equal to the underlined string. for example a node with CL is an instance of the Class prob:Clause.
- Dotted lines and bold lines represents prob:condition's and prob:consequence's, respectively.
Probability Calculations
Framework
As a use case of the vocabulary, I'd like to present a framework for probability calculations using RDF and Bayesian network, .
- Describe the problem by a RDF graph using above proposed vocabulary
- Convert the graph into a Bayesian network, and export it to a Bayesian network store.
- Describe the observation by a RDF graph
- Convert the observation graph into a query for a Bayesian reasoner on the store and hand it to the reasoner.
- Do the calculations on the reasoner and import the result back to the RDF store and merge.
Bayesian Network
A Bayesian network is a directed acyclic graph (DAG), representing probabilistic dependencies among values of the variables. The nodes and links represent the variables, and the causal relationship between them, respectively. Each node is accompanied with a conditional probability table (CPT) that represents the probabilistic relationship between the variables. The posterior probability distributions ("beliefs")for each variable could be calculated by propagating beliefs. For an example see the example below.
When exporting Bayesian networks, the XMLBIF format is used here. The XMLBIF is a XML-based format for exchanging Bayesian networks, proposed by Fabio Cozamn et al.
Metastatic Cancer Case (3) - Probability Calculation
Corresponding Bayesian Network
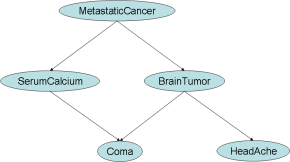
This is the Bayesian network for the metastatic cancer case. Its serialization in the XMLBIF is here. The XML fragments concerning the HeadAche node are, for example, as following.
In XMLBIF, nodes and accompanying CPTs in a Bayesian network are represented by
VARIABLE and DEFINITION elements respectively.
<VARIABLE TYPE="nature">
<NAME>ex:hasSevereHeadAche</NAME>
<OUTCOME>TRUE</OUTCOME>
<OUTCOME>FALSE</OUTCOME>
</VARIABLE>
<DEFINITION>
<FOR>ex:hasSevereHeadAche</FOR>
<GIVEN>ex:hasBrainTumor</GIVEN>
<TABLE>0.8 0.2 0.6 0.4</TABLE>
</DEFINITION>Observations
The graph representing the observation that the patient has severe headaches but is not in coma, is represented by the following graph. This should be handed to the Bayesian network reasoner in an appropriate form.
[ a prob:Observation;
prob:proposition _:HeadAche;
prob:hasProbability [a prob:Probability;
rdf:value 1.0]
].
[ a prob:Observation;
prob:proposition _:NotComa
prob:hasProbability [a prob:Probability;
rdf:value 1.0]
].Probability Calculation
The Bayesian network above is "multiply-connected", i.e. there is one or more "loop" when seeing the links undirected, so the calculation (propagation) of the probability needs some technique (Junction Tree, Cutset Conditioning, Sampling...). As the result of the calculation, we get P(MetastaticCancer | HeadAche & !Coma) = 0.097.
Importing Back the Result
The graph representing the result of the calculation is as follows. It should be merged to the graph representing the knowledge along with those for the observations.
[ a prob:Belief;
prob:consequence _:MetastaticCancer;
prob:observation _:ObsHeadAche;
prob:observation _:ObsNotComa;
prob:hasProbability [a prob:Probability;
rdf:value 0.097]
].Issues
The proposal in this paper is still in its experimental stage and needs public review and discussion. I am now writing converting rules from a RDF graph like the one above to the corresponding Bayesian network in XMLBIF format, using cwm.
Open issues include:
- Relationship with OWL, SWRL, etc.
- How to standardize Query Languages against Bayesian network store
- How to learn Bayesian networks from data or/and partial description in RDF.
- How to deal with / avoid cyclic probabilistic description in RDF
- How to deal with continuous probabilistic distributions
- Whether we need to standardize a format for literal description of Bayesian networks in RDF
Related Works and References
- [Pearl, 88]Pearl, J. , Probabilistic reasoning in intelligent systems: networks of plausible inference, Morgan Kaufmann, 1988.
is one of the most cited textbooks on Bayesian networks in general. - XMLBIF: To see the historic background and details of XMLBIF, refer to the Fabio Cozman's page. For another XML-based format for Bayesian networks, see the XBN's page by Microsoft Research.
- Bayesian network software packages: There are dozens of Bayesian network software packages. Among them are HUGIN EXPERT, Bayese Builder, Belief Network Power Constructor, BNJ. See the comparison page by K.Murphy for more comprehensive list.
- N3 and cwm: N3 is a language which is a compact and readable alternative to RDF's XML syntax, but also is extended to allow greater expressiveness. For example, one can write rules using "formulae" in N3. Cwm is a general-purpose data processor for the semantic web. It is written in Python, among whose functions are format converting, reasoning, filtering ... See W3C Tutorial page for detail.